Неорганические материалы, 2022, T. 58, № 6, стр. 651-657
Некоторые закономерности перехода натриевогерманатных стекол из жидкого в стеклообразное состояние
Д. С. Сандитов 1, 2, А. А. Машанов 1, *
1 Бурятский государственный университет им. Доржи Банзарова
670000 Улан-Удэ, ул. Смолина, 24а, Россия
2 Институт физического материаловедения СО Российской академии наук
670047 Улан-Удэ, ул. Сахьяновой, 6, Россия
* E-mail: Mashanov@bsu.ru
Поступила в редакцию 14.01.2022
После доработки 11.03.2022
Принята к публикации 15.03.2022
- EDN: UNTPQM
- DOI: 10.31857/S0002337X22060112
Аннотация
Настоящая работа посвящена исследованию температурной зависимости вязкости натриево-германатных стекол с разным содержанием оксида натрия и обсуждению на их основе некоторых аспектов перехода жидкость-стекло, в частности, кинетического критерия стеклования. По данным о параметрах уравнения Вильямса-Ландела-Ферри (ВЛФ) проведен расчет полосы температур, характеризующей область стеклования, а также время релаксации структуры при температуре стеклования исследуемых стекол. Предлагается обобщение и обоснование кинетического критерия стеклования Шмельцера.
ВВЕДЕНИЕ
У разных классов аморфных веществ в области стеклования замораживается подвижность различных кинетических единиц, связанных с различным характером взаимодействия между частицами. Однако примечательно то обстоятельство, что основные закономерности перехода жидкость–стекло в качественном отношении оказываются одинаковыми для различных стеклующихся систем независимо от их природы, что подтверждается наличием для области стеклования универсальных правил и уравнений [1, 2].
При охлаждении стеклообразующих расплавов в области стеклования резко возрастает их вязкость. В первом приближении они стеклуются при достижении одной и той же предельной вязкости ηg = η(Tg)
Это соотношение представляет собой широко распространенное приближенное правило постоянства вязкости при температуре стеклования Tg. Из обзора и детального анализа Мазурина [3] следует, что у большинства исследованных до сих пор стекол Tg соответствует температурам, при которых значения вязкости ηg находятся в пределах от 1011 до 1012 Па с, т.е. колеблются в области приближенного значения 1012 Па с (1) с заметным разбросом. Постоянство ηg лучше выполняется для стеклообразных систем одного класса.
Температурная зависимость вязкости простых маловязких жидкостей описывается известным уравнением Френкеля [1, 4]
с постоянной энергией активации U = const (η0 – высокотемпературный предел вязкости). В отличие от них у стеклообразующих расплавов энергия активации вязкого течения в области стеклования довольно сильно (практически экспоненциально) зависит от температуры: U = U(T). В связи с этим предложены эмпирические уравнения вязкости, которые учитывают эту зависимость (часто в неявном виде). Среди них широкое распространение получило соотношение Вильямса-Ландела-Ферри (уравнение ВЛФ) [5]
(3)
$\begin{gathered} \ln {\kern 1pt} {{a}_{T}} = - \,{{C}_{1}}\frac{{T - {{T}_{g}}}}{{T - {{T}_{g}} + {{C}_{2}}}}, \\ {{a}_{T}} = \frac{{\eta \left( T \right)}}{{\eta \left( {{{T}_{g}}} \right)}} \cong \frac{{\tau \left( T \right)}}{{\tau \left( {{{T}_{g}}} \right)}}, \\ \end{gathered} $Таблица 1.
Параметры уравнения ВЛФ (3) С1 и С2 для натриевосиликатных стекол Na2O–SiO2 и характеристики процесса стеклования [6, 7]
| № | Na2O, мол. % | С1 | С2, К | Tg, К | δTg, К | fg | Cg × 103 | τg, c |
|---|---|---|---|---|---|---|---|---|
| 1 | 15 | 36 | 430 | 782 | 12 | 0.028 | 7.8 | 240 |
| 2 | 20 | 36 | 390 | 759 | 11 | 0.028 | 7.8 | 220 |
| 3 | 25 | 35 | 355 | 739 | 10 | 0.028 | 7.8 | 200 |
| 4 | 30 | 35 | 322 | 721 | 9 | 0.028 | 7.8 | 180 |
| 5 | 33 | 35 | 304 | 712 | 9 | 0.028 | 7.8 | 180 |
| 6 | 35 | 35 | 291 | 705 | 8 | 0.028 | 7.8 | 160 |
Настоящая работа посвящена исследованию стеклования натриевогерманатных стекол и обсуждению на их основе некоторых аспектов перехода жидкость–стекло, в частности кинетического критерия стеклования.
ПРИМЕНИМОСТЬ УРАВНЕНИЯ ВЛФ К НАТРИЕВОГЕРМАНАТНЫМ СТЕКЛАМ
Представим соотношение ВЛФ (3) в виде уравнения прямой
и проверим линейность зависимости y = – (T – ‒ Tg)/lnaT от x = (T – Tg). Мы использовали экспериментальные данные о температурной зависимости вязкости стекол Na2O–GeO2, приведенные в электронном справочнике SciGlass [8] (табл. 2).
Таблица 2.
Температурная зависимость вязкости η(T) натриевогерманатных стекол [8]
| № | Na2O, мол. % |
lgη [Пз] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 К | 2 К | 3 К | 4 К | 5 К | 6 К | 7 К | 8 К | 9 К | 10 К | 11 К | 12 К | 13 К | ||
| 1 | 15 | 1513 | 1351 | 1235 | 1147 | 1078 | 1023 | 977 | 938 | 905 | 876 | 850 | 827 | 807 |
| 2 | 20 | 1464 | 1294 | 1178 | 1092 | 1026 | 974 | 931 | 895 | 865 | 839 | 816 | 796 | 778 |
| 3 | 25 | 1405 | 1239 | 1126 | 1044 | 982 | 933 | 893 | 860 | 832 | 808 | 788 | 769 | 753 |
| 4 | 30 | 1323 | 1175 | 1073 | 998 | 942 | 897 | 860 | 830 | 804 | 782 | 763 | 746 | 731 |
Из рис. 1 видно, что для одного из составов этих стекол указанная зависимость у(х) в области стеклования является линейной, что подтверждает применимость уравнения ВЛФ. Аналогичные прямые получены для других составов исследуемых натриевогерманатных стекол. Из прямых y–x определены значения параметров уравнения ВЛФ С1 и С2 (табл. 3).
Рис. 1.
Температурная зависимость вязкости натриевогерманатных стекол в координатах, соответствующих уравнению ВЛФ (использованы данные [8], содержание Na2O 15 мол. %).
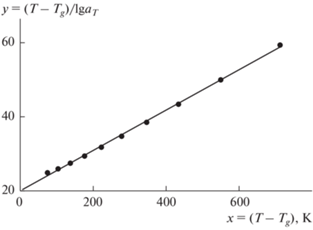
Таблица 3.
Параметры уравнения ВЛФ (3) С1 и С2 для натриевогерманатных стекол Na2O–GeO2 и рассчитанные на их основе характеристики процесса стеклования
| № | Na2O, мол. % | С1 | С2, К | Tg, К | δTg, К | fg | Cg × 103 | τg, c |
|---|---|---|---|---|---|---|---|---|
| 1 | 15 | 41 | 342 | 807 | 8.3 | 0.024 | 6.5 | 167 |
| 2 | 20 | 39 | 290 | 778 | 7.4 | 0.026 | 7.2 | 149 |
| 3 | 25 | 39 | 252 | 753 | 6.5 | 0.026 | 7.2 | 129 |
| 4 | 30 | 39 | 240 | 731 | 6.1 | 0.026 | 7.2 | 123 |
О ПРИРОДЕ ПАРАМЕТРА УРАВНЕНИЯ ВЛФ С1
При рассмотрении данных табл. 1 и 3 обращает на себя внимание слабая зависимость параметра уравнения ВЛФ С1 от природы стекол, как и у других стеклообразных систем [6, 9]. У натриевосиликатных и натриевогерманатных стекол с разным содержанием компонентов величина С1 в первом приближении оказывается практически постоянной
Хотя известно, что уравнение Френкеля (2) с постоянной энергией активации “не работает” в области стеклования, тем не менее, рассмотрим вывод соотношений (3) с его привлечением:
Равенство (6) не соответствует действительности, т.к. реальное значение С2 заметно ниже температуры стеклования: С2 < Tg (табл. 1 и 3). В отличие от равенства (6) выражение (5) для параметра С1, оказывается, имеет вполне определенный физический смысл. Убедимся в этом.
Из уравнения Френкеля (2) при Т = Tg следует соотношение
сравнение которого с выражением (5) приводит к заключению о том, что величина C1 определяется логарифмом отношения предельных вязкостей ηg и η0
Подставив в равенство (7) приближенные значения ηg ≈ 1012 Па с и η0 ≈ 10–3–10–5 Па с [1–3], получаем оценку
которая находится в удовлетворительном согласии с экспериментальными данными (4), полученными непосредственно из уравнения ВЛФ.
Таким образом, из приведенных выкладок вытекает, что слабая зависимость C1 от природы стекол объясняется приближенным постоянством вязкости при температуре стеклования ηg ≈ const и постоянством ее высокотемпературного предела η0 ≈ const.
Из интерпретации уравнения ВЛФ в рамках модели делокализованных атомов [6, 9, 10] следует, что параметр C1 является обратной величиной доли флуктуационного объема fg, замороженной при температуре стеклования,
Флуктуационный объем аморфного вещества ΔVe обусловлен тепловыми смещениями атомов (кинетических единиц) [9, 10]
где Ne – число делокализованных атомов, $\Delta {{v}_{e}}$ – элементарный флуктуационный объем, необходимый для делокализации атома – его предельного смещения из локального равновесного положения. Объемная доля флуктуационного объема fg, полученная по данным о параметре С1, естественно, слабо зависит от природы аморфных веществ [6, 9] (табл. 1, 3)РЕЛАКСАЦИОННЫЕ АСПЕКТЫ ПЕРЕХОДА ЖИДКОСТЬ–СТЕКЛО
В области стеклования молекулярные перегруппировки становятся настолько медленными, что изменения структуры расплава при охлаждении не успевают следовать за изменением температуры. При этом, как и вязкость, резко возрастает время релаксации структуры τ(Т), которое тесно связано со скоростью охлаждения жидкости q = (dT/dt). В 1951 году Бартенев [11], исходя из общих соображений, предложил следующую связь между этими величинами (кинетический критерий стеклования)
где τg – время структурной релаксации при температуре стеклования Tg, C – эмпирический параметр с размерностью температуры. Здесь и далее под q следует понимать абсолютную величину скорости изменения температуры |q| при охлаждении расплава или при нагревании стекла.Волькенштейн и Птицын [12] разработали релаксационную теорию, в соответствии с которой частицы стеклующейся системы могут находиться в двух состояниях (в основном и возбужденном), разделенных энергетическим барьером. Решение составленного кинетического уравнения приводит к заключению о том, что при некоторой температуре Тg происходит замораживание доли частиц в возбужденном состоянии, что означает стеклование системы (прекращаются переходы частиц между указанными двумя состояниями). Температура Tg отвечает условию
(10)
${{\left( {\frac{{{\text{d}}\tau }}{{{\text{d}}T}}} \right)}_{{T = {{T}_{g}}}}} = - \frac{1}{q}.$В данной теории кинетическим критерием перехода жидкость–стекло служит уравнение стеклования [10]
Обозначение правой части этого равенства через δTg предложено Немиловым [13]. Величина δTg характеризует температурный интервал перехода от жидкости к стеклу при охлаждении. Параметр уравнения Бартенева С в теории Волькенштейна-Птицына приобретает смысл полосы температур δTg.
Остановимся на оценке параметра уравнения стеклования δTg для исследуемых натриевогерманатных стекол.
Подстановка зависимости τ(T) из уравнения ВЛФ (3) в соотношение (10) приводит к равенству
сравнение которого с уравнением стеклования (11) позволяет получить формулу для расчета полосы температур δTg по данным о параметрах уравнения ВЛФ
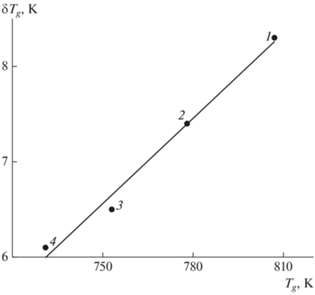
Для натриевогерманатных стекол (табл. 3) величина δTg составляет δTg = 6–8 К, что по порядку величины совпадает с данными для натриевосиликатных стекол (табл. 1).
Второй параметр уравнения ВЛФ С2 равен отношению fg к коэффициенту теплового расширения флуктуационного объема при температуре стеклования βf [9]
причем произведение βfTg является однозначной функцией fg
(15)
${{\beta }_{f}}{{T}_{g}} = {{f}_{g}}\ln \left( {{1 \mathord{\left/ {\vphantom {1 {{{f}_{g}}}}} \right. \kern-0em} {{{f}_{g}}}}} \right).$Из равенств (8), (13) и (14) с учетом (15) следует, что параметр уравнения стеклования (11) δTg определяется температурой стеклования и долей флуктуационного объема fg
(16)
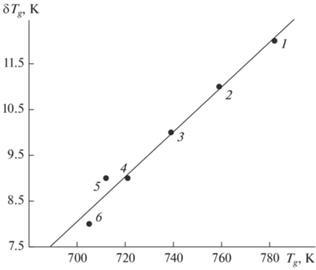
$\delta {{T}_{g}} = \frac{{{{f}_{g}}}}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 {{{f}_{g}}}}} \right. \kern-0em} {{{f}_{g}}}}} \right)}}{{T}_{g}}.$Поскольку у стекол одного класса fg ≈ const, можно ожидать линейной корреляции между величинами δTg и Tg. В самом деле, как видно из рис. 2, у натриевогерманатных стекол полоса температур δTg, в пределах которой происходит переход от жидкости к стеклу, линейно зависит от температуры стеклования Tg, как и у натриевосиликатных стекол (рис. 3).
ОБОСНОВАНИЕ И ОБОБЩЕНИЕ КРИТЕРИЯ СТЕКЛОВАНИЯ ШМЕЛЬЦЕРА
Шмельцер [14, 15] вводит характерное время изменения температуры: τT = T/q. При τ $ \ll $ τT жидкость находится в состоянии термодинамического равновесия, а при τ $ \gg $ τT – в замороженном стеклообразном состоянии. Предполагается, что переход жидкость-стекло соответствует условию τ ≈ τT. Исходя из этих соображений Шмельцер сформулировал следующий кинетический критерий стеклования [14, 15]:
(17)
${{\left[ {\frac{1}{T}\left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)\tau } \right]}_{{T = {{T}_{g}}}}} = {{C}_{3}},\,\,\,\,{{C}_{3}} \approx 1.$Уравнение стеклования (11) с учетом выражения (16) для полосы температур δTg получает следующую интерпретацию:
(18)
$q{{\tau }_{g}} = \frac{{{{f}_{g}}}}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 {{{f}_{g}}}}} \right. \kern-0em} {{{f}_{g}}}}} \right)}}{{T}_{g}}.$Разделив обе части этого равенства на температуру стеклования Тg, при усредненном значение fg ≈ 0.025 приходим к обобщенному варианту кинетического критерия стеклования
(19)
$\frac{{q{{\tau }_{g}}}}{{{{T}_{g}}}} = {{C}_{g}} = \frac{{{{f}_{g}}}}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 {{{f}_{g}}}}} \right. \kern-0em} {{{f}_{g}}}}} \right)}} \approx 7 \times {{10}^{{ - 3}}},$который с учетом q = (dT/dt) можно записать в виде выражения для определения температуры перехода Тg
(20)
${{\left[ {\frac{1}{T}\left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)\tau } \right]}_{{T = {{T}_{g}}}}} = {{C}_{g}},\,\,\,\,{{C}_{g}} \approx 7 \times {{10}^{{ - 3}}}.$Данное соотношение можно рассматривать как обоснование и обобщение критерия стеклования Шмельцера (17). При этом постоянная С3 приобретает определенный физический смысл и другое численное значение
(21)
${{С}_{3}} = {{С}_{g}} = \frac{{{{f}_{g}}}}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 {{{f}_{g}}}}} \right. \kern-0em} {{{f}_{g}}}}} \right)}} \approx {\text{const}} \approx 7 \times {{10}^{{ - 3}}}.$Этим самым устраняется недостаток критерия Шмельцера (17), сводящийся к приравниванию постоянной С3 и единице: С3 ≈ 1, причем фактически в виде постулата, без особого обоснования.
Легко видеть, что критерий Шмельцера (17) приводит к ошибочному равенству
которое противоречит уравнению стеклования (11), следующему из классической теории Волькенштейна-Птицына [12]. Например, у силикатных и германатных стекол при Tg ≈ 800 К, согласно критерию Шмельцера, произведение qτg равно ≈800 K [13], тогда как типичные значения произведения qτg у этих стекол составляют лишь около 5–10 K [6].
Обобщенный кинетический критерий стеклования (20) для qτg применительно к указанным стеклам (Tg ≈ 700–800 К) приводит к значениям
которые находятся в согласии с типичными данными для произведения qτg.
Значение Cg ≈ 7 × 10–3 в равенствах (19) и (21) получено при усредненной величине fg ≈ 0.025. Хотя величина fg меняется в небольших пределах у различных аморфных веществ, тем не менее она не является универсальной постоянной [6, 9, 10]. Это же замечание относится и к параметру Cg в обобщенном кинетическом критерии стеклования (20). Постоянство Cg наблюдается у стекла одного класса. Из соотношений (7) и (8) следует, что величина fg (как и Cg) определяется вязкостью ηg ≈ const при Tg и высокотемпературным пределом вязкости η0 ≈ const
В отличие от подходов Бартенева (1), Волькенштейна-Птицына (11) и Шмельцера (17) в обобщенном кинетическом критерии (19) появляются температура стеклования и практически универсальная безразмерная постоянная, которая определяется долей флуктуационного объема, замороженной при температуре стеклования.
Предлагаемый обобщенный критерий (19) можно сформулировать следующим образом: жидкость переходит в замороженное стеклообразное состояние, когда скорость охлаждения q достигает определенной постоянной доли Cg от характерной скорости охлаждения q = (Tg/τg), тесно связанной со временем релаксации структуры τg при температуре стеклования Tg,
(23)
$\frac{q}{{{{q}_{g}}}} = \frac{q}{{\left( {{{{{T}_{g}}} \mathord{\left/ {\vphantom {{{{T}_{g}}} {{{\tau }_{g}}}}} \right. \kern-0em} {{{\tau }_{g}}}}} \right)}} = {{C}_{g}} \approx {\text{const}} \approx 7 \times {{10}^{{ - 3}}}.$Возможна аналогичная, но несколько другая формулировка: жидкость стеклуется при достижении времени структурной релаксации τg значения, соответствующего постоянной доли Cg от характерного времени изменения температуры τT = (Tg/q), тесно связанного с температурой стеклования Tg и скоростью охлаждения расплава q,
РАСЧЕТ ВРЕМЕНИ РЕЛАКСАЦИИ СТРУКТУРЫ ПРИ ТЕМПЕРАТУРЕ СТЕКЛОВАНИЯ
Температура стеклования хотя и слабо, но зависит от скорости охлаждения расплава q. Температура, при которой достигается вязкость ηg ≈ 1012 Па с, названа стандартной температурой стеклования Tg, а соответствующая скорость охлаждения
(25)
$q = {{3}^{{}}}{{\text{К}} \mathord{\left/ {\vphantom {{\text{К}} {{\text{мин}}}}} \right. \kern-0em} {{\text{мин}}}} = {{0.05}^{{}}}{{\text{К}} \mathord{\left/ {\vphantom {{\text{К}} {\text{с}}}} \right. \kern-0em} {\text{с}}},$принимается за стандартную скорость охлаждения [1, 3, 16, 17]. В дилатометрии стекол и полимеров практически во всех странах мира используют как правило примерно такую же скорость охлаждения (25). Ввиду слабой (логарифмической) зависимости Tg от q небольшие колебания q около стандартного значения (25) не оказывают влияния на величину Tg. Поэтому обычно полагают, что подавляющее большинство имеющихся данных о Tg относится фактически к стандартной скорости охлаждения. Для других скоростей q мало данных.
По формуле (12) при стандартной скорости охлаждения q = 0.05 К/с по данным о параметрах уравнения ВЛФ С1 и С2 рассчитали время структурной релаксации τg натриевогерманатных стекол при температуре стеклования (табл. 3)
(26)
${{\tau }_{g}} = \frac{{{{C}_{2}}}}{{q{{C}_{1}}}} \approx 123{\kern 1pt} - {\kern 1pt} {{149}_{{}}}{\text{c}}{\text{.}}$По порядку величины полученные значения совпадают с данными для натриевосиликатных стекол (табл. 1).
Примерно к таким же результатам приводит известная формула Максвелла: τ = η/G, где G – модуль сдвига. У большинства оксидных неорганических стекол, в том числе силикатных и германатных, мгновенный модуль сдвига G∞ составляет около (20–25) × 109 Па и мало изменяется с температурой. При Т = Tg он всего лишь на 3–5% меньше, чем при комнатной температуре. У большой совокупности оксидных неорганических стекол при стандартной скорости охлаждения q = = 0.05 К/с логарифм вязкости lgηg [Па с] при температуре стеклования составляет 12.76 ± 0.26. По-видимому, при стандартной скорости охлаждения приблизительно постоянное значение вязкости при температуре стеклования составляет ηg ≈ 1012–1013 Па с. Из данных о величинах G∞ и ηg на уровне качественных оценок имеем [3, 13, 16, 18]
что по порядку величины совпадает с результатами расчета по формуле (26) по данным о параметрах уравнения ВЛФ С1 и С2.
ЗАКЛЮЧЕНИЕ
На примере оксидных натриевогерманатных стекол рассмотрены закономерности перехода жидкости в стеклообразное состояние. В результате модифицированы условия стеклования Шмельцера и предложен обобщенный кинетический критерий перехода жидкость–стекло, согласно которому жидкость стеклуется при достижении времени структурной релаксации τg до постоянной доли Cg от характерного времени изменения температуры τТ = Tg/q, тесно связанного с температурой стеклования и со скоростью охлаждения расплава q.
Список литературы
Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. Новосибирск: Наука, 1982. 259 с.
Ростиашвили В.Г., Иржак В.И., Розенберг Б.А. Стеклование полимеров. Л.: Химия, 1987. 192 с.
Мазурин О.В. Проблемы обеспечения совместимости значений температур стеклования, публикуемых в мировой литературе // Физика и химия стекла. 2007. Т. 33. № 1. С. 34–55.
Френкель Я.И. Введение в теорию металлов. Л.-М.: Гостехиздат, 1948. 291 с.
Ферри Дж. Вязкоупругие свойства полимеров. М.: Изд-во иностр. лит., 1963. 535 с.
Сандитов Д.С. О природе уравнения перехода жидкость-стекло // ЖЭТФ. 2016. Т. 150. Вып. 3(9). С. 501–515.
Сандитов Д.С., Бадмаев С.С. Стеклование жидкости и замороженная деформация стекол // Неорган. материалы. 2019. Т. 55. № 10. С. 1108–1115.
MDL ® SciGlass – 7.8 Institute of Theoretical Chemistry, Shrewsbury, MA, 2012.
Сандитов Д.С. Модель делокализованных атомов в физике стеклообразного состояния // ЖЭТФ. 2012. Т. 142. Вып. 1(7). С. 123–137.
Сандитов Д.С., Бадмаев С.С. Модель делокализованных атомов и свойства сульфатно-фосфатных стекол // Неорган. материалы. 2019. Т. 55. № 1. С. 99–100.
Бартенев Г.М. О зависимости между температурой стеклования силикатного стекла и скоростью охлаждения или нагревания // ДАН. 1951. Т. 76. № 2. С. 227–230.
Волькенштейн М.В., Птицын О.Б. Релаксационная теория стеклования // ЖТФ. 1956. Т. 26. № 10. С. 2204–2222.
Немилов С.В. Уравнение Максвелла и классические теории стеклования как основа прямого расчета вязкости при температуре стеклования // Физика и химия стекла. 2013. Т. 39. № 6. С. 857–878.
Schmelzer J.W.P. Kinetic Criteria of Glass Formation and the Pressure Dependence of the Glass Transition Temperature // J. Chem. Phys. 2012. V. 36. P. 074512. https://doi.org/10.1063/1.3685510
Тропин Т.В., Шмельцер Ю.В.П., Аксенов В.Л. Современные аспекты кинетической теории стеклования // Успехи физ. наук. 2016. Т. 186. № 1. С. 47–73.
Бартенев Г.М. Строение и механические свойства неорганических стекол. М.: Стройиздат, 1966. 216 с.
Бартенев Г.М., Лукьянов И.А. Зависимость температуры стеклования аморфных веществ от скорости нагревания и связь температуры стеклования с энергией активации // Журн. физ. химии. 1955. Т. 29. № 8. С. 1486–1498.
Ojovan M.I. Viscosity and Glass Transition in Amorphous Oxides // Adv. Cond. Matter. Phys. 2008. Article ID 817829. 23 p.
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы