1. На главную
  2. Электронные версии
  3. Неорганические материалы
  4. T. 58, № 8, 2022

Неорганические материалы, 2022, T. 58, № 8, стр. 891-896

Коэффициенты разделения и числа Пекле в испарительных процессах рафинирования веществ с простой основой при температурах вблизи от температур плавления

А. И. Кравченко 1, *, А. И. Жуков 1

1 Национальный научный центр “Харьковский физико-технический институт” Национальной академии наук Украины
61108 Харьков, ул. Академическая, 1, Украина

* E-mail: krwchnko@gmail.com

Поступила в редакцию 22.02.2022
После доработки 17.03.2022
Принята к публикации 22.03.2022

Полный текст (PDF)

Аннотация

С помощью уравнения Бартона-Прима-Слихтера на примерах веществ с простой основой (Sm, Yb, Mg, Eu, Te, Zn, Cd, Be, Tb) показано, что их дистилляционное или сублимационное рафинирование при T = (0.9–1.2)Tm (где Tm – температура плавления) может ухудшаться с повышением температуры вследствие роста эффективного коэффициента разделения β < 1 и/или роста диффузионного числа Пекле Pe = wX/ρD (где w – скорость испарения вещества с единицы поверхности, D – коэффициент диффузии примеси, ρ – плотность вещества, X – размерный фактор испаряемого материала) – с бóльшим или меньшим влиянием β или Pe в зависимости от природы основы и примесей. Также показано, что в кристаллизационных процессах рафинирования Pe малó и основным параметром является коэффициент разделения.

Ключевые слова: дистилляция, сублимация, кристаллизация, очистка, рафинирование, коэффициент разделения, температура плавления, уравнение Бартона-Прима-Слихтера, диффузионное число Пекле

ВВЕДЕНИЕ

Дистилляция, направленная кристаллизация и сублимация – основные методы получения высокочистых веществ [1–3]. В этих методах многокомпонентное вещество подвергается фазовому превращению при перемещении поверхности раздела фаз со скоростью $v$ с перераспределением примесей между фазами.

В испарительных методах (дистилляция и сублимация) скорость v определяется скоростью испарения w вещества с единицы поверхности. Если жидкость содержится в контейнере простой (например, цилиндрической) формы, то $v$ = w/ρ, где ρ – плотность вещества (та же зависимость имеет место при сублимации материала в виде диска, плотно вложенного в цилиндрический тигель). Разработано математическое описание процесса испарения вещества “основа–примесь” – в виде системы уравнений, связывающих чистоту продукта со степенью перегонки g (т.е. с выходом продукта). Параметрами уравнений являются эффективный коэффициент разделения β (отношение концентрации примеси в паре, покидающем поверхность испарения, к концентрации примеси в жидкости, из которой образуется пар – вблизи поверхности испарения) и число Пекле Pe = $v$X/D, где D – коэффициент диффузии примеси, а X – размерный фактор испаряемого материала (начальная толщина слоя жидкости в тигле при дистилляции; или начальная толщина испаряемой пластины, плотно вложенной в тигель; или начальный радиус шара при сублимации) [4, 5].

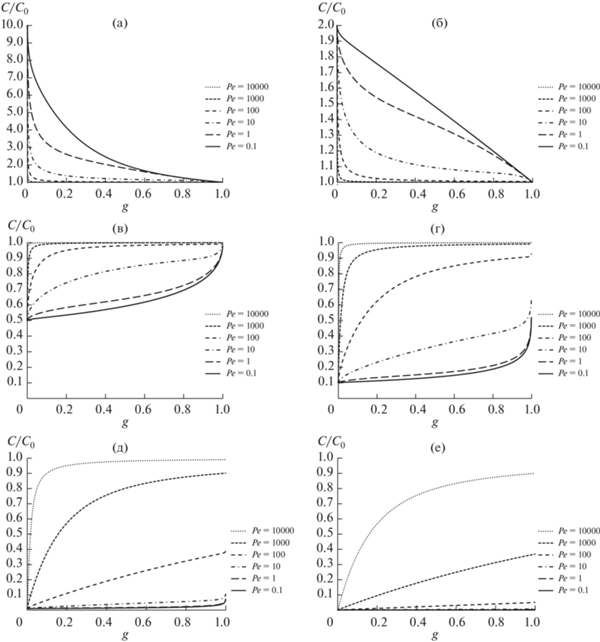
При β < 1 эффективность очистки конденсата повышается с уменьшением числа Pe (рис. 1). Если g = 1, то С/С0 = 1. При заданном β рассматриваемая зависимость при Pe = 0.1 практически совпадает с зависимостью при Pe = 0. Если Pe = 0, то (как это отмечено ранее [5–7]) зависимость С/С0 от g имеет вид известного уравнения дистилляции с идеальным перемешиванием жидкости (которое описывает и нормальную направленную кристаллизацию):

$\frac{C}{{{{C}_{0}}}} = \frac{{1 - {{{(1 - g)}}^{\beta }}}}{g}.$
Рис. 1.

Зависимости относительной усредненной концентрации С/С0 примеси в конденсате от степени перегонки g материала в виде плоского слоя при его одностороннем испарении в вакууме при различных значениях числа Пекле Ре и коэффициенте разделения β = 10 (a), 2 (б), 0.5 (в), 0.1 (г), 0.01 (д), 0.001 (е) (С0 – исходная концентрация примеси).

Важно отметить, что описание дистилляции и сублимации с помощью двух параметров (β и Ре) предполагает, что процесс определяется только диффузией примесей. Между тем, факторами реальных процессов могут быть захват примесей паром основного компонента в процессах дистилляции и сублимации, а также конвекция в процессах дистилляции (хотя отмечалось, что конвекция мала при малых X [4]).

Была рассмотрена температурная зависимость числа Пекле как следствия температурных зависимостей $v$(Т) и D(Т): зависимости D(Т) и Pe(Т) для той или иной примеси определяются энергией активации диффузии примеси в системе “основа–примесь” [6, 7].

Напротив, в процессах направленной кристаллизации скорость $v$ задается скоростью изменения тепловых условий процесса – например, скоростью перемещения нагревателя вдоль материала удлиненной формы или скоростью вытягивания кристалла из расплава. Выведены уравнения, связывающие чистоту продукта с долей закристаллизованного материала при заданном эффективном коэффициенте разделения k при кристаллизации [1–3].

Эффективный коэффициент разделения в фазовых превращениях зависит от скорости процесса. Известно уравнение Бартона-Прима-Слихтера, связывающее k с равновесным коэффициентом разделения k0 и линейной скоростью процесса $v$ [1–3, 8, 9]:

(1)
$k = \frac{{{{k}_{0}}}}{{{{k}_{0}} + (1 - {{k}_{0}})\exp \left( { - v\frac{\delta }{D}} \right)}},$
где δ – толщина диффузионного слоя в 1-й фазе перед поверхностью раздела фаз в процессе перехода 1-й фазы во 2-ю. Согласно этому уравнению, если $v$δ/D → 0, то k → k0; если же $v$δ/D растет, то k → 1, т.е. при больших значениях $v$δ/D эффективность очистки мала. (Число $v$δ/D в этом уравнении, по сути, является числом Пекле для материала в диффузионном слое.) Уравнение (1) выведено в предположении, что расхождение между k и k0 определяется только диффузией примеси в жидкости. Данные о равновесном коэффициенте k0 для ряда систем “основа–примесь” при фазовых равновесиях жидкость–кристалл и жидкость–пар содержатся в монографии Нисельсона и Ярошевского [10].

Известен порядок значений δ и D в жидкостях при температурах вблизи температуры плавления Tm: в большинстве систем “основа–примесь” δ ~ 10–3–10–2 см, D ~ 10–5 см2/с, т.е. δ/D ~ ~ 102–103 с/см [1–3, 8, 9]. Также известно, что вблизи Tm в твердом теле для большинства систем “основа–примесь” D ~ 10–6 см2/с [11, 12].

Отмечалось подобие уравнений дистилляции и направленной кристаллизации при соответствующей подстановке в них β или k ([2, гл. 15] и [4, 13]). Так, в работе [4] было отмечено, что уравнение (1), изначально выведенное для рассмотрения кристаллизационных процессов, не имеет запретов на применение также для рассмотрения процессов дистилляции или сублимации, если считать, что k – это межфазовый коэффициент разделения в рассматриваемом испарительном процессе. В то же время, применение уравнения (1) для расчета эффективного коэффициента разделения в испарительных процессах при выбранной температуре наталкивается на препятствие, связанное с отсутствием соответствующих данных о значениях δ/D. Между тем, технологические испарительные процессы рафинирования тех или иных веществ с простой основой зачастую проводятся при температурах, не слишком удаленных от Tm, и можно предполагать, что в этих процессах и при кристаллизации значения δ/D близки. Также можно ожидать, что дополнительные (помимо диффузии примесей) факторы этих процессов (конвекция и/или захват примесей паром основного компонента) несильно проявляются при данных температурах.

В то же время, можно отметить, что описание дистилляции и сублимации с помощью двух параметров (β и Ре) [4, 5] не содержит запретов рассматривать подобным образом и кристаллизационные процессы, в связи с чем возникает вопрос о вычислении в них числа Ре.

В настоящем исследовании была поставлена цель, используя уравнение Бартона-Прима-Слихтера, вычислить значения β/β0 в процессах испарения веществ “основа–примесь” (где основа – простое вещество) при температурах вблизи Tm (т.е. в предположении, что δ/D ~ 102–103 с/см, как в процессах кристаллизации), а также вычислить значения диффузионного числа Пекле при этих температурах для выяснения влияния температуры на эффективность рафинирования веществ в испарительных процессах. Также ставилась задача вычислить значения Ре в процессах кристаллизации.

ВЫПОЛНЕНИЕ РАСЧЕТОВ

Вычисление числа Pe в процессах нормальной направленной кристаллизации. В этих процессах Pe = $v$X/D, где $v$ – скорость кристаллизации, D – коэффициент диффузии примеси, X – длина горизонтального контейнера или толщина слоя расплава в тигле.

Коэффициент β и число Pe в процессах дистилляции и сублимации. Рассматривалось испарение веществ с простой основой, для которых дистилляция и сублимация как процессы рафинирования имеют практический смысл [14–16].

Для расчетов β/β0 использовалось уравнение (1) (с заменой k0 и k на β0 и β соответственно) при значениях δ/D = 100 и 1000 с/см (как для процессов кристаллизации [8, 9]). Для простоты расчетов считалось, что материал и контейнер имеют простые формы, при которых $v$ = w/ρ. Скорость w [г/(см2 с)] вычислялась по уравнению Ленгмюра с помощью известной формулы для числовых расчетов [17]

$w = {\text{0}}.058p{{\left( {\frac{M}{T}} \right)}^{{1/2}}},$
где p – давление пара [мм рт. ст.] при температуре Т [К], М – атомная (или молярная) масса пара вещества [а.е.м. или г/моль].

Справочные данные о давлении p почти всех веществ брали из монографии Несмеянова [18] (для Те учитывалась особенность испаряться в виде молекул Те4), а данные о давлении p для Tb – из [16].

Рассматривалось испарение веществ при Tm и T ≠ Tm при не слишком большом отклонении T от Tm. Поскольку повышение (понижение) температуры процесса увеличивает (уменьшает) одновременно как δ, так и D, предполагалось, что отклонение T от Tm не отражается существенно на значении δ/D. Для вычислений числа Пекле использовалась формула [6, 7]

$Pe\left( T \right) = \frac{{w\left( T \right)X}}{{\rho D\left( T \right)}} = \frac{{{\text{0}}.058p{{{\left( {\frac{M}{T}} \right)}}^{{1/2}}}X}}{{\rho {{D}_{m}}\exp \left[ {\frac{Q}{R}\left( {\frac{1}{{{{T}_{m}}}} - \frac{1}{T}} \right)} \right]}},$
где ρ – плотность вещества, г/см3; Q/R – отношение энергии активации диффузии примеси к универсальной газовой постоянной, К; Dm – коэффициент диффузии примеси в веществе при температуре вблизи Tm, см2/с. В выполняемых расчетах использовалось значение Dm = 5 × 10–5 см2/с для жидкости и Dm = 5 × 10–6 см2/с для твердого тела. Как и в работах [6, 7], расчеты выполнялись при трех значениях Q и одном (для сопоставимости результатов) значении X = 1 см.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Число Pe в процессах направленной кристаллизации. При обычных значениях $v$ < 10 см/ч = 3 × × 10–5 м/с, L ~ 0.1 м и D ~ 10–5 м2/с [3, 8, 9] вычисленное значение Pe < 0.1. При этом изменение $v$ в интервале от 0 до 10 см/ч сопровождается изменением k от k = k0 до k = 1. Таким образом, в кристаллизационных процессах рафинирования учет числа Ре не имеет смысла, при этом (как известно [3, 8, 9]) имеет смысл учет зависимости k от скорости кристаллизации.

Коэффициент β и число Pe в процессах дистилляции и сублимации. Результаты вычислений β, отношения β/β0 и числа Пекле при указанных температурах, δ/D и β0 < 1 приведены в табл. 1 и 2. Обращает на себя внимание то, что в отдельных случаях β/β0 сильно зависит от выбора значения δ/D (100 или 1000 с/см). Сопоставление табл. 1 и 2 позволяет оценить влияние температуры на β/β0 и Pe (при заданном значении X) того или иного вещества, т.е. выяснить роль температуры в процессе его очистки.

Таблица 1.  

Отношение β/β0 и число Pe = $v$X/D при X = 1 см для веществ при известных Tm и различных значениях β0 и δ/D

Вещество Tm, К рm, мм рт. ст. M, а. е. м. ρ, г/см3 w, г/(см2 с) $v$, см/с β/β0 при δ/D = 100 с/см β/β0 при δ/D = 1000 с/см $Pe$
при X = = 1 см 
β0 = = 0.1 β0 = = 0.01 β0 = = 0.001 β0 = 0.1 β0 = = 0.01 β0 = = 0.001
Sm 1350 4.4 150 7.5 0.08 0.011 3 3 3 10 100 1000 ~103
Yb 1097 3.1 173 7.0 0.07 0.010 2 3 3 10 100 1000 ~103
Mg 923 2.8 24 1.7 0.03 0.018 4 6 6 10 100 1000 ~103
Eu 1099 1.1 152 5.2 0.02 0.004 1.4 1.5 1.5 9 36 53 ~102
Te 723 0.18 128 × 4 6.2 0.006 0.0009 1.1 1.1 1.1 1.1 1.1 1.1 ~10
Zn 693 0.15 65 7.1 0.003 0.0004 1.0 1.0 1.0 1.0 1.0 1.0 ~10
Cd 594 0.12 112 8.7 0.003 0.0004 1.0 1.0 1.0 1.0 1.0 1.0 ~10
Be 1551 0.032 9 1.8 0.00014 0.00008 1.0 1.0 1.0 1.1 1.1 1.1 ~1
Tb 1629 <0.001 159 8.2 <1 × 10–5 <1 × 10–5 1.0 1.0 1.0 1.0 1.0 1.0 ≈0
Таблица 2.  

Отношение β/β0 и число Pe = $v$X/D при X = 1 см для веществ при температуре испарения T ≠ Tm и различных значениях β0 и δ/D (p – давление пара вещества при температуре Т)

Вещество Tm, К T, К T/Tm р, мм рт. ст. w, г/(см2 с) $v$, см/с β/β0
при δ/D = 100 с/см 		β/β0
при δ/D = 1000 с/см 		$Pe$ при X = 1 см
β0 = = 0.1 β0 = = 0.01 β0 = = 0.001 β0 = 0.1 β0 = = 0.01 β0 = = 0.001 Q/R = 1 × × 104 К Q/R = 2 × × 104 К Q/R = 3 × × 104 К
Sm 1350 1200 0.9 0.63 0.013 0.0017 1.2 1.2 1.2 4 5 6 1 × 103 2 × 103 5 × 103
Yb 1097 1000 0.9 0.55 0.013 0.0019 1.2 1.2 1.2 4 6 7 1 × 103 2 × 103 6 × 103
Mg 923 800 0.9 0.16 0.002 0.0009 1.1 1.1 1.1 2 2 2 1 × 103 6 × 103 5 × 105
Eu 1099 1000 0.9 0.18 0.004 0.0008 1.1 1.1 1.1 2 2 2 4 × 102 5 × 102 3 × 103
Te 723 800 1.1 0.18 0.008 0.0013 1.1 1.3 1.5 3 12 48 57 14 4
Zn 693 800 1.2 2.40 0.040 0.0056 1.6 1.7 1.8 10 73 213 17 2.5 0.36
Cd 594 700 1.2 2.42 0.056 0.0065 1.7 1.9 1.9 10 87 400 11 0.9 0.07
Be 1551 1700 1.1 0.24 0.001 0.0006 1.0 1.1 1.1 2 2 2 4.4 3.5 2.0
Mg 923 1000 1.1 10.7 0.010 0.0566 9.7 74 222 10 100 1000 510 220 100
Tb 1629 2100 1.2 0.9 0.004 0.0005 1.1 1.1 1.2 3 4 4 550 150 40

Снижение Т по отношению к Tm при сублимации Sm, Yb, Mg, Eu заметно понижает β/β0, увеличивая или уменьшая Pe (по сравнению со значениями этих величин при Т = Tm) в зависимости от Q. Повышение Т по отношению к Tm при дистилляции Te, Zn, Cd несколько повышает β/β0, увеличивая или уменьшая Pe в зависимости от Q. Такое же изменение температуры процесса при дистилляции Be и Tb почти не изменяет β/β0, но заметно увеличивает Pe. Влияние коэффициента β и числа Pe на рафинирование того или иного вещества зависит от природы вещества.

Несмотря на отсутствие в литературе надежных данных о Q и Dm для той или иной системы “основа–примесь”, выполненные расчеты дают представление о влиянии температуры на эффективность рафинирования веществ в испарительных процессах.

ЗАКЛЮЧЕНИЕ

Эффективный коэффициент разделения и число Пекле рассматриваются как два параметра процессов рафинирования веществ кристаллизацией, дистилляцией и сублимацией. Показано, что в кристаллизационных процессах рафинирования число Pe малó и основным параметром является коэффициент разделения (для которого известна зависимость от скорости кристаллизации: уравнение Бартона-Прима-Слихтера с известными значениями δ/D). Для дистилляции и сублимации рассматривались коэффициент разделения и число Pe при температурах испарения, не слишком отличающихся от температур плавления вещества (т.е. при тех же значениях δ/D, что и при кристаллизации).

С помощью названного уравнения при δ/D = 100 и 1000 с/см для ряда веществ с простой основой (Sm, Yb, Mg, Eu, Te, Zn, Cd, Be, Tb) сделано сравнение эффективного (β) и равновесного (β0) коэффициентов разделения при температурах испарения T = (0.9–1.2)Tm, а отдельно вычислены значения числа Pe = $v$X/D при X = 1 см и тех же температурах.

Показано, что повышение T может ухудшать дистилляционное и сублимационное рафинирование рассмотренных веществ как вследствие увеличения расхождения между β и β0, так и вследствие увеличения Pe (при заданном X и β < 1), при этом раздельное влияние коэффициента β и числа Pe на процессы рафинирования различных веществ различно.

Выполненные расчеты дают качественное представление о влиянии температуры на эффективность рафинирования веществ в испарительных процессах.

Список литературы

  1. Девятых Г.Г., Еллиев Ю.Е. Глубокая очистки веществ. М.: Высшая школа, 1990. 192 с.

  2. Дытнерский Ю.И. Процессы и аппараты химической технологии. Изд. 2. В 2 кн. Часть 2. Массообменные процессы и аппараты. М.: Химия, 1995. 368 с.

  3. Кристаллизация из расплавов: Справочное изд. Пер. с нем. Бартел И. и др. М.: Металлургия, 1987. 320 с.

  4. Кириллов Ю.П., Кузнецов Л.А., Шапошников В.А., Чурбанов М.Ф. Влияние диффузии на глубину очистки веществ дистилляцией // Неорган. материалы. 2015. Т. 51. № 11. С. 1177–1182. https://doi.org/10.7868/S002337X15100085

  5. Жуков А.И., Кравченко А.И. Расчет сублимации с учетом диффузии примеси // Неорган. материалы. 2017. Т. 53. № 6. С. 662–668. https://doi.org/10.1134/S0020168517060161

  6. Кравченко А.И., Жуков А.И. Температурная зависимость диффузионного числа Пекле в процессах сублимации некоторых простых веществ // Неорган. материалы. 2021. Т. 57. № 7. С. 789–795. https://doi.org/10.1134/S0020168521070101

  7. Kravchenko A.I., Zhukov A.I., Datsenko O.A. Temperature Dependences of the Peclet Number in Sublimation Processes of Simple Substances // Probl. At. Sci. Technol. 2022. № 1. P. 13–16. https://vant.kipt.kharkov.ua/

  8. Burton J.A., Prim R.C., Slichter W.P. The Distribution of Solute in Crystals Growth from the Melt. 1. Theoretical // J. Chem. Phys. 1953. V. 21. № 11. P. 1987–1991.

  9. Бартон Дж.А., Прим Р.К., Слихтер В.Р. Распределение примесей в кристаллах, выращенных из расплава. Ч. 1. Теория // Германий / Под ред. Петрова Д.А. М.: Иностранная литература, 1955. С. 74–81.

  10. Нисельсон Л.А., Ярошевский А.Г. Межфазовые коэффициенты распределения. Равновесия кристалл–жидкость и жидкость–пар. М.: Наука, 1992. 399 с.

  11. Бокштейн Б.С., Ярославцев А.Б. Диффузия атомов и ионов в твердых телах. М.: МИСиС, 2005. 362 с.

  12. Бокштейн Б.С. Атомы блуждают по кристаллу. М.: Наука, 1984. 208 с.

  13. Kravchenko A.I. Simple Substances Refining: Efficiency of Distillation Methods // Funct. Mater. 2000. V. 7. № 2. P. 315–318.

  14. Кравченко А.И. Уравнение распределение примеси в твердом дистилляте // Неорган. материалы. 2007. Т. 43. № 8. С. 1021–1022.

  15. Кравченко А.И. Соотношение между эффективным и идеальным коэффициентами разделения при дистилляции и сублимации // Неорган. материалы. 2016. Т. 52. № 4. С. 423–430. https://doi.org/10.1134/S0020168516040096

  16. Ke L., Zhang L., Zhang X., Li Z., Wang Z., Chen D., Zhou L., Chen S., Zheng L., Zhou X. Medium-Volatile Impurity Distribution in Purification of Terbium Metal by Vacuum Distillation // Sep. and Purif. Technol. 2021. V. 266. https://doi.org/10.1016/j.seppur.2021.118566

  17. Пазухин В.А., Фишер А.Я. Разделение и рафинирование металлов в вакууме. М.: Металлургия, 1969. 204 с.

  18. Несмеянов А.Н. Давление пара химических элементов. М.: Из-во АН СССР, 1961. 396 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Неорганические материалы

Архивы выпусков Информация о журнале Отправить рукопись в журнал