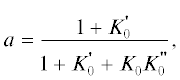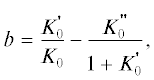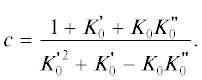Журнал неорганической химии, 2023, T. 68, № 2, стр. 191-202
Уравнение состояния периклаза на основе функций Планка–Эйнштейна
А. В. Перевощиков a, А. И. Максимов a, И. И. Бабаян a, Н. А. Коваленко a, И. А. Успенская a, *
a Московский государственный университет имени М.В. Ломоносова
119991 Москва, Ленинские горы, 1, стр. 3, Россия
* E-mail: ira@td.chem.msu.ru
Поступила в редакцию 15.08.2022
После доработки 26.09.2022
Принята к публикации 28.09.2022
- EDN: LPBWCJ
- DOI: 10.31857/S0044457X22601407
Аннотация
Представлено расширение метода Воронина–Куценка для совместного описания объемных и термохимических свойств кристаллических фаз с помощью функций Планка–Эйнштейна и модифицированного уравнения Тайта. Предложены два подхода, которые основаны на описании энергии Гиббса или Гельмгольца. В качестве тестовой системы выбран оксид магния (периклаз). Проведена оптимизация параметров уравнений состояния с использованием литературных данных в широком интервале термодинамических переменных (до 3000 K и 145 ГПа). Оценена предсказательная способность обоих подходов.
ВВЕДЕНИЕ
Развитие вычислительных методов и термодинамических баз данных является одним из важнейших современных направлений в области химической термодинамики. Моделирование фазовых и химических равновесий позволяет существенно сократить объем эксперимента за счет его грамотного планирования, но для проведения таких расчетов термодинамические функции всех фаз изучаемой системы должны быть представлены в аналитическом виде, т.е. построены соответствующие термодинамические модели или уравнения состояния.
Вывод выражений, связывающих между собой термодинамические свойства твердого вещества, является неотъемлемой частью теоретической разработки любого уравнения состояния (УС), так как оно должно удовлетворять всем термодинамическим соотношениям во всем диапазоне термодинамических переменных. Однако во многих случаях исследователи используют разные наборы функций для описания различных свойств, например, термического расширения, изотермической сжимаемости, PVT-соотношений или теплоемкости, о чем свидетельствует многообразие форм уравнений состояния, представленных в литературе. Использование различных функциональных зависимостей для описания определенных типов данных приводит к корректной аппроксимации результатов измерения именно этих свойств, но при этом не гарантирует термодинамическую согласованность рассчитанных величин с другими термодинамическими функциями.
Температурные зависимости объема при атмосферном давлении могут быть описаны через
коэффициент термического расширения 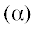 в виде полиномиальных функций [1]. Термическое расширение также может быть представлено полуэмпирическими квазигармоническими
моделями в диапазоне от 0 K до температуры плавления [2]. При параметризации УС часто используют информацию об объеме при различных температурах
и давлениях. В литературе представлены зависимости V(T) для большого количества соединений. Высокая точность определения объема и температуры
при атмосферном давлении обусловливает хорошее качество предложенных моделей и расширяет
набор веществ, для которых предложены УС. Данные по изотермической сжимаемости описаны
в литературе с помощью различных изотермических УС; одним из наиболее популярных является
уравнение Берча–Мурнагана третьего порядка, которое до сих пор используется для описания
P–V-соотношений веществ различных типов [3–6]. Наиболее востребованные изотермические УС были проанализированы в работах [7, 8]. Показано, что экспериментальные данные по изотермической сжимаемости могут быть
описаны в пределах погрешности измерения до очень высоких давлений с помощью трех
или четырех параметров, один из которых может быть зафиксирован. Для изотермических
условий в работах [7, 9] рекомендовали применять модифицированное уравнение Тайта [10], которое использовано и в настоящей работе.
в виде полиномиальных функций [1]. Термическое расширение также может быть представлено полуэмпирическими квазигармоническими
моделями в диапазоне от 0 K до температуры плавления [2]. При параметризации УС часто используют информацию об объеме при различных температурах
и давлениях. В литературе представлены зависимости V(T) для большого количества соединений. Высокая точность определения объема и температуры
при атмосферном давлении обусловливает хорошее качество предложенных моделей и расширяет
набор веществ, для которых предложены УС. Данные по изотермической сжимаемости описаны
в литературе с помощью различных изотермических УС; одним из наиболее популярных является
уравнение Берча–Мурнагана третьего порядка, которое до сих пор используется для описания
P–V-соотношений веществ различных типов [3–6]. Наиболее востребованные изотермические УС были проанализированы в работах [7, 8]. Показано, что экспериментальные данные по изотермической сжимаемости могут быть
описаны в пределах погрешности измерения до очень высоких давлений с помощью трех
или четырех параметров, один из которых может быть зафиксирован. Для изотермических
условий в работах [7, 9] рекомендовали применять модифицированное уравнение Тайта [10], которое использовано и в настоящей работе.
В то время как для описания изотермических данных предложено много различных УС, для моделирования свойств в широком интервале температур и давлений используется существенно меньшее число аналитических зависимостей [11]. Многие авторы для получения PVT-уравнений добавляют к изотермическому УС термическое давление [12–15], которое можно выразить различными способами: от простой линейной зависимости до сложного интеграла, например, как в уравнении Ми–Грюнайзена–Дебая [16].
Простейшим способом описания теплоемкости является полиномиальная зависимость от температуры. В литературе представлены различные аналитические зависимости, применяемые непосредственно (например, [17]) или в виде линейных комбинаций [18]. Помимо полиномиальных функций для описания температурной зависимости теплоемкости могут быть использованы функции Эйнштейна и Дебая [19]. Достаточно распространенным способом моделирования теплоемкости является подход CALPHAD третьего поколения, в котором теплоемкость при фиксированном давлении представляется как комбинация эйнштейновской модели с полиномиальной коррекцией на ангармоничность и наличие электронных эффектов [20]. В работе [21] предложен метод описания температурной зависимости теплоемкости с помощью комбинации функций Планка–Эйнштейна и показано, что этот подход позволяет описывать весь набор экспериментальных данных в пределах погрешности их определения, при этом количество параметров модели обычно не превышает 9–10. Такой метод был применен для аппроксимации термохимических измерений различных веществ [20, 22, 23]; при этом особо подчеркивалось, что параметры модели не имеют строгого физического смысла, однако возможность адекватного описания результатов измерений и корректное предельное поведение свойств делают его перспективным для использования в термодинамических базах данных.
Практический интерес представляет описание разнообразных наборов термодинамических данных единым УС. В литературе представлено несколько работ, в которых реализован такой подход. Авторы [13] определили параметры ранее упомянутого уравнения Ми–Грюнайзена–Дебая с помощью как PVT-данных, так и сведений по адиабатическому модулю упругости (KS). Однако другие термодинамические свойства (теплоемкость, приращения энтальпии) не были включены в оптимизацию. Даже с учетом возможности расчета этих свойств качество их описания такими уравнениями оставляет желать лучшего. Аналитические зависимости сложны и при этом не позволяют воспроизвести термохимические данные с экспериментальной точностью (доли процента).
Если при построении УС исходить из аналитических зависимостей энергии Гиббса [24, 25] или Гельмгольца [26, 27], то с помощью подобных уравнений можно описать как PVT-соотношения, так и любые термодинамические свойства веществ. Например, авторы [28] провели параметризацию предложенного ими полуэмпирического уравнения для энергии Гельмгольца и получили для ряда веществ хорошее описание значений теплоемкости, коэффициента термического расширения, адиабатического модуля упругости при атмосферном давлении, а также предсказали с приемлемой точностью имеющиеся PVT-данные при высоких давлении и температуре.
Разрабатывать УС на основе комбинации эйнштейновских функций предлагалось ранее в работах [24, 27]. Целью настоящей работы является анализ возможности расширения метода Воронина–Куценка [21] для построения УС кристаллической фазы. Помимо изобарной теплоемкости с помощью функций Планка–Эйнштейна можно описывать также и изохорную теплоемкость [21]. Поэтому в настоящей работе приведены два варианта УС на основе комбинации функций Планка–Эйнштейна, в основу которых положены зависимости энергии Гиббса или энергии Гельмгольца от естественных переменных, а также проведено сравнение интерполяционных и экстраполяционных характеристик предложенных УС.
В качестве тестовой системы был выбран оксид магния (периклаз), для которого в литературе представлено большое количество различных экспериментальных данных в широком диапазоне давлений и температур. В процессе оптимизации уравнений состояния использовали следующие термодинамические свойства: изобарную теплоемкость и приращение энтальпии, термическое расширение, PVT-соотношения и адиабатический модуль упругости при различных температурах и давлениях.
РАСЧЕТНАЯ ЧАСТЬ
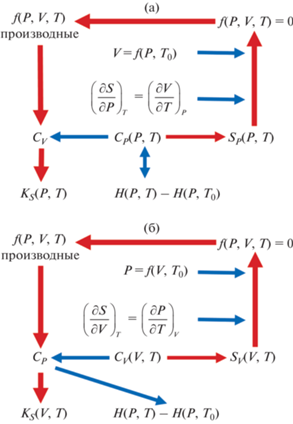
Как было показано ранее [21], применение комбинаций функций Планка–Эйнштейна демонстрирует удовлетворительные результаты в описании функций CP(T), $S_{P}^{^\circ }(T)$ и H°(T) – H°(Tref) кристаллических соединений. Расширить этот подход для описания различных свойств кристаллических веществ при изменении давления (или объема) можно с помощью основных соотношений химической термодинамики. В данной работе рассмотрены два способа: первый основан на параметризации функции CP(P, T), которую можно преобразовать в зависимость энергии Гиббса от давления и температуры; второй – на параметризации функции ${{C}_{V}}$(V,T), которую можно преобразовать в зависимость энергии Гельмгольца от объема и температуры. Далее эти модели будут обозначаться как CP-подход и ${{C}_{V}}$-подход, соответственно. Взаимосвязь между термодинамическими функциями и последовательность математических преобразований схематически представлены на рис. 1.
CP-подход. Исходное выражение для изобарной теплоемкости CP в рамках модели Воронина–Куценка [21] имеет вид:
(1)
${{C}_{P}} = 3R\sum\limits_{i = 1}^m {\alpha _{i}^{P}\frac{{{{{\left( {x_{i}^{P}} \right)}}^{2}}{{e}^{{x_{i}^{P}}}}}}{{{{{\left( {{{e}^{{x_{i}^{P}}}} - 1} \right)}}^{2}}}}} ,$(2)
$\begin{gathered} {{S}_{P}}\left( T \right) = \\ = \,\,3R\sum\limits_{i = 1}^n {\alpha _{i}^{P}} \left( {\frac{{x_{i}^{P}}}{{\left( {\exp \left( {x_{i}^{P}} \right) - 1} \right)}} - \ln \left( {1 - \exp \left( { - x_{i}^{P}} \right)} \right)} \right). \\ \end{gathered} $С помощью одного из соотношений Максвелла можно связать энтропию и объемные свойства:
(3)
${{\left( {\frac{{\partial V}}{{\partial T}}} \right)}_{P}} = - {{\left( {\frac{{\partial S}}{{\partial P}}} \right)}_{T}}.$Далее, используя выражение для S(T) в виде линейной комбинации функций Планка–Эйнштейна, можно описать термическое расширение, интегрируя соотношение Максвелла:
(4)
$V\left( {P,T} \right) - V\left( {P,0} \right) = - \int\limits_0^T {{{{\left( {\frac{{\partial S}}{{\partial P}}} \right)}}_{T}}dT} ,$(5)
$\begin{gathered} {{\Delta }}{{V}_{{PE}}}\left( {P,T} \right) = V\left( {P,T} \right) - V\left( {P,0} \right) = \\ = 3R\sum\limits_{i = 1}^n {\left( {{{{\left( {\frac{{\partial \alpha _{i}^{P}}}{{\partial P}}} \right)}}_{T}}T\ln \left( {1 - \exp \left( { - x_{i}^{P}} \right)} \right)} \right. + } \\ + \left. {\alpha _{i}^{P}{{{\left( {\frac{{\partial x_{i}^{P}}}{{\partial P}}} \right)}}_{T}}\frac{T}{{\exp \left( {x_{i}^{P}} \right) - 1}}} \right). \\ \end{gathered} $Анализ предложенного УС показал, что параметр $\alpha _{i}^{P}$ целесообразно принять независимым от давления, т.е. ${{\left( {\frac{{\partial \alpha _{i}^{P}}}{{\partial P}}} \right)}_{T}} = 0.$
Для определения других термодинамических свойств необходимо воспользоваться производными V(P, T) по давлению и температуре:
(6)
$\begin{array}{*{20}{c}} \begin{gathered} {{\left( {\frac{{\partial V}}{{\partial P}}} \right)}_{T}} = {{\left( {\frac{{\partial V\left( {P,0} \right)}}{{\partial P}}} \right)}_{T}} + 3R\sum\limits_{i = 1}^n {\alpha _{i}^{P}} T \times \\ \times \,\,\left( {{{{\left( {\frac{{{{\partial }^{2}}x_{i}^{P}}}{{\partial {{P}^{2}}}}} \right)}}_{T}}\frac{1}{{\exp \left( {x_{i}^{P}} \right) - 1}} - \left( {\frac{{\partial x_{i}^{P}}}{{\partial P}}} \right)_{T}^{2}\frac{{\exp \left( {x_{i}^{P}} \right)}}{{{{{\left( {\exp \left( {x_{i}^{P}} \right) - 1} \right)}}^{2}}}}} \right), \\ \end{gathered} \end{array}$(7)
${{\left( {\frac{{\partial V}}{{\partial T}}} \right)}_{P}} = 3R\sum\limits_{i = 1}^n {\alpha _{i}^{P}\left( {{{{\left( {\frac{{\partial x_{i}^{P}}}{{\partial P}}} \right)}}_{T}}x_{i}^{P}\frac{{\exp \left( {x_{i}^{P}} \right)}}{{{{{\left( {\exp \left( {x_{i}^{P}} \right) - 1} \right)}}^{2}}}}} \right)} .$Изохорная теплоемкость ${{C}_{V}}$, изотермический (KT) и адиабатический (KS) модули упругости могут быть рассчитаны с помощью соотношений (8)–(10):
(8)
${{C}_{V}} = {{C}_{P}} + T\frac{{\left( {\frac{{\partial V}}{{\partial T}}} \right)_{P}^{2}}}{{{{{\left( {\frac{{\partial V}}{{\partial P}}} \right)}}_{T}}}},$${{C}_{V}}$-подход. В качестве исходной для последующих преобразований может быть выбрана не только изобарная, но и изохорная теплоемкость:
(11)
${{C}_{V}} = 3R\sum\limits_{i = 1}^m {\alpha _{i}^{V}\frac{{{{{\left( {x_{i}^{V}} \right)}}^{2}}{{e}^{{x_{i}^{V}}}}}}{{{{{\left( {{{e}^{{x_{i}^{V}}}} - 1} \right)}}^{2}}}}} ,$(12)
$\begin{gathered} {{S}_{V}}\left( T \right) = ~ \\ = 3R\sum\limits_{i = 1}^n {\alpha _{i}^{V}\left( {\frac{{x_{i}^{V}}}{{\left( {\exp \left( {x_{i}^{V}} \right) - 1} \right)}} - \ln \left( {1 - \exp \left( { - x_{i}^{V}} \right)} \right)} \right)} . \\ \end{gathered} $Если воспользоваться соотношением Максвелла:
(13)
${{\left( {\frac{{\partial P}}{{\partial T}}} \right)}_{V}} = {{\left( {\frac{{\partial S}}{{\partial V}}} \right)}_{T}},$(14)
$\begin{gathered} P\left( {V,T} \right) - P\left( {V,0} \right) = \\ = - 3R\sum\limits_{i = 1}^n {\alpha _{i}^{V}\left( {{{{\left( {\frac{{\partial x_{i}^{V}}}{{\partial V}}} \right)}}_{T}}\frac{T}{{\exp \left( {x_{i}^{V}} \right) - 1}}} \right)} = {{\Delta }}{{P}_{{PE}}}\left( {V,T} \right). \\ \end{gathered} $Необходимые для последующих преобразований частные производные давления по объему и температуре записаны ниже (уравнения (15), (16)):
(15)
$\begin{gathered} {{\left( {\frac{{\partial P}}{{\partial V}}} \right)}_{T}} = {{\left( {\frac{{\partial P\left( {V,0} \right)}}{{\partial V}}} \right)}_{T}} - 3R\sum\limits_{i = 1}^n {\alpha _{i}^{V}} T \times \\ \times \,\,\left( {{{{\left( {\frac{{{{\partial }^{2}}x_{i}^{V}}}{{\partial {{V}^{2}}}}} \right)}}_{T}}\frac{1}{{\exp \left( {x_{i}^{V}} \right) - 1}} - {{{\left( {\frac{{\partial x_{i}^{V}}}{{\partial V}}} \right)}}_{T}}^{2}\frac{{\exp \left( {x_{i}^{V}} \right)}}{{{{{\left( {\exp \left( {x_{i}^{V}} \right) - 1} \right)}}^{2}}}}} \right), \\ \end{gathered} $(16)
${{\left( {\frac{{\partial P}}{{\partial T}}} \right)}_{V}} = - 3R\sum\limits_{i = 1}^n {\alpha _{i}^{V}\left( {{{{\left( {\frac{{\partial x_{i}^{V}}}{{\partial V}}} \right)}}_{T}}x_{i}^{V}\frac{{\exp \left( {x_{i}^{V}} \right)}}{{{{{\left( {\exp \left( {x_{i}^{V}} \right) - 1} \right)}}^{2}}}}} \right)} .$С помощью этих производных может быть рассчитана изобарная теплоемкость:
(17)
${{C}_{P}} = {{C}_{V}} - T\frac{{\left( {\frac{{\partial P}}{{\partial T}}} \right)_{V}^{2}}}{{{{{\left( {\frac{{\partial P}}{{\partial V}}} \right)}}_{T}}}}$и приращение энтальпии как интеграл от функции CP(Т). При расчете адиабатического модуля упругости KS использованы те же уравнения (уравнения (9), (10)), что и в CP-подходе. В настоящей работе эти расчеты осуществлялись с помощью численных методов.
Гибкость модели. В записанных выше интегральных уравнениях присутствуют функции V(P, 0) и P(V, 0), представляющие собой уровни отсчета. Поскольку большинство экспериментальных данных определено при комнатной температуре или выше, за референсную температуру удобнее выбрать 300 K; в этом случае требуется провести элементарные алгебраические преобразования:
(18)
$\begin{gathered} V\left( {P,T} \right) - V\left( {P,300} \right) = ~\,\,V\left( {P,T} \right) - V\left( {P,0} \right) - \\ - \,\,V\left( {P,300} \right) + V\left( {P,0} \right) = \\ = {{\Delta }}{{V}_{{PE}}}\left( {P,T} \right) - {{\Delta }}{{V}_{{PE}}}\left( {P,300} \right), \\ \end{gathered} $(19)
$\begin{gathered} P\left( {V,T} \right) - P\left( {V,300} \right) = P\left( {V,T} \right) - P\left( {V,0} \right) - \\ - \,\,P\left( {V,300} \right) + P\left( {V,0} \right) = \\ = {{\Delta }}{{P}_{{PE}}}\left( {V,T} \right) - {{\Delta }}{{P}_{{PE}}}\left( {V,300} \right), \\ \end{gathered} $Слагаемые V(P, 300) и P(V,300) в уравнениях (18) и (19) могут быть описаны любым изотермическим уравнением состояния. В настоящей работе для этого было использовано уравнение Тайта, модифицированное авторами [10]. Основными достоинствами этого уравнения являются аналитическая инвертируемость и хорошие аппроксимационные характеристики [7]:
(21)
$P = \frac{{{{{\left[ {1 - \frac{1}{a}\left( {1 - \frac{V}{{{{V}_{0}}}}} \right)} \right]}}^{{ - \frac{1}{c}}}} - 1}}{b},$В записанных выше уравнениях V0 – объем при давлении P = 1 бар и температуре $T = 300\,\,{\text{K;}}$ K0, $K_{0}^{'},$ 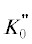 – изотермический модуль упругости и его первая и вторая производные соответственно.
При равенстве нулю параметра
– изотермический модуль упругости и его первая и вторая производные соответственно.
При равенстве нулю параметра 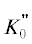 уравнение Хуан и Чоу преобразуется в хорошо известное уравнение Мурнагана [29]:
уравнение Хуан и Чоу преобразуется в хорошо известное уравнение Мурнагана [29]:
(22)
$\frac{V}{{{{V}_{0}}}} = {{\left( {1 + \frac{{K_{0}^{'}}}{{{{K}_{0}}}}P} \right)}^{{ - \frac{1}{{K_{0}^{'}}}}}}.$Варьируемым параметром предложенной нами модели является параметр θi, зависящий от давления (СP-вариант) или объема (${{C}_{V}}$-вариант). В первом случае:
(23)
$\theta _{i}^{P}\left( P \right) = \theta _{i}^{{0P}}\frac{{{{{\left( {1 + {{B}_{i}}P} \right)}}^{{{{C}_{i}}}}}}}{{{{{\left( {1 + {{B}_{i}}{{P}_{0}}} \right)}}^{{{{C}_{i}}}}}}},$Во втором случае вид зависимости $\theta _{i}^{V}(V)$ был аналогичен использованному в работе [30]:
(24)
$\theta _{i}^{V}\left( V \right) = \theta _{i}^{{0V}}\exp \left( {\frac{{\gamma _{i}^{0} - {{\gamma }_{i}}}}{{{{q}_{i}}}}} \right),\,\,\,\,{{\gamma }_{i}} = \gamma _{i}^{0}{{\left( {\frac{V}{{{{V}_{0}}}}} \right)}^{{{{q}_{i}}}}},~$Все выражения, использованные в настоящей работе для расчета свойств MgO в рамках двух подходов, приведены в табл. S1 .
Оптимизация параметров модели. Два варианта уравнения состояния, предложенные в настоящей работе, включают следующие
варьируемые параметры: V0, K0, $K_{0}^{'},$  для изотермической части, несколько пар αi, $\theta _{i}^{0},$ описывающих теплоемкость при постоянном давлении (P = 1 бар) или постоянном объеме (объем при давлении P = = 1 бар и выбранной температуре), и несколько дополнительных параметров для учета
зависимости θi от давления (Bi, Ci) или объема ($\gamma _{i}^{0},$ qi) в зависимости от использованного подхода. Для получения достоверных оценок параметров
необходимо проводить оптимизацию с использованием как можно большего числа разных
типов экспериментальных данных. В настоящей работе при оптимизации учитывали результаты
измерений теплоемкости и приращения энтальпии при P = 1 бар, объемные свойства и адиабатический модуль упругости при различных давлениях
и температурах.
для изотермической части, несколько пар αi, $\theta _{i}^{0},$ описывающих теплоемкость при постоянном давлении (P = 1 бар) или постоянном объеме (объем при давлении P = = 1 бар и выбранной температуре), и несколько дополнительных параметров для учета
зависимости θi от давления (Bi, Ci) или объема ($\gamma _{i}^{0},$ qi) в зависимости от использованного подхода. Для получения достоверных оценок параметров
необходимо проводить оптимизацию с использованием как можно большего числа разных
типов экспериментальных данных. В настоящей работе при оптимизации учитывали результаты
измерений теплоемкости и приращения энтальпии при P = 1 бар, объемные свойства и адиабатический модуль упругости при различных давлениях
и температурах.
При параметризации обоих вариантов УС использовали идентичную целевую функцию, которая
представляла собой сумму квадратов отклонений экспериментальных значений от расчетных
с учетом статистических весов для каждого типа данных. Для CP-подхода параметры оценивали следующим образом: при аппроксимации теплоемкости и приращения
энтальпии рассчитывали параметры αi и $\theta _{i}^{0},$ далее по изотермическим данным при 300 K оценивали параметры V0, K0, $K_{0}^{'},$ 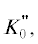 после чего находили полный набор параметров с учетом всех доступных экспериментальных
данных, используя ранее подобранные значения параметров в качестве начального приближения.
В случае ${{C}_{V}}$-варианта модели предварительно можно было оценить только значения параметров изотермического
УС, все остальные параметры рассчитывали при оптимизации всего набора экспериментальных
данных. Параметр V0 был изначально фиксирован для обоих вариантов модели и принят равным 74.71 Å3 как результат усреднения значений молярного объема из разных источников [12, 14, 31, 32].
после чего находили полный набор параметров с учетом всех доступных экспериментальных
данных, используя ранее подобранные значения параметров в качестве начального приближения.
В случае ${{C}_{V}}$-варианта модели предварительно можно было оценить только значения параметров изотермического
УС, все остальные параметры рассчитывали при оптимизации всего набора экспериментальных
данных. Параметр V0 был изначально фиксирован для обоих вариантов модели и принят равным 74.71 Å3 как результат усреднения значений молярного объема из разных источников [12, 14, 31, 32].
Рассчитанные параметры охарактеризованы 95%-ными доверительными интервалами; все рекомендованные значения являются статистически значимыми. Дополнительные параметры, не представленные в финальном наборе, принимали равными Bi = 0 или Ci = 1 (CP-вариант), $\gamma _{i}^{0}$ = 0 или qi = 1 (${{C}_{V}}$-вариант). Для адекватного описания экспериментальных данных оказалось достаточно четырех–пяти пар параметров αi и θi. Модель с тремя парами недостаточно хорошо описывала теплоемкость, а при использовании более шести пар параметров некоторые из них становились статистически незначимыми. Было также замечено, что дополнительные параметры Bi, Ci и $\gamma _{i}^{0},$ qi требуются в первую очередь в термах с наибольшими значениями $\theta _{i}^{0}.$ Введение зависимости от давления или объема в термы с наименьшими значениями $\theta _{i}^{0}$ не влияло на качество описания в целом, так как эти параметры “отвечают” за низкотемпературные вклады, а экспериментальные данные при высоком давлении и низкой температуре отсутствуют.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Численные значения параметров для CP- и ${{C}_{V}}$-вариантов УС приведены в табл. 1; в первом случае для адекватного описания различных типов данных потребовалось 19, а во втором – 13 параметров. Общая сводка информации об источниках экспериментальных значений и точности аппроксимации данных предложенными моделями представлена в табл. 2.
Таблица 1.
Параметры предложенных УС
| Параметр | Значение | Параметр | Значение |
|---|---|---|---|
| CP-подход | ${{C}_{V}}$-подход | ||
| V0, Å3 | 74.71* | V0, Å3 | 74.71* |
| K0, ГПа | 161.9 ± 0.30 | K0, ГПа | 161.7 ± 0.1 |
| $K_{0}^{'}$ | 4.662 ± 0.06 | $K_{0}^{'}$ | 4.530 ± 0.03 |
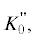 1/ГПа 1/ГПа
|
–0.06448 ± 0.008 | 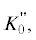 1/ГПа 1/ГПа
|
–0.048 ± 0.006 |
| $\alpha _{1}^{P}$ | 0.6571 ± 0.2 | $\alpha _{1}^{V}$ | 1.495 ± 0.06 |
| $\alpha _{2}^{P}$ | 0.2425 ± 0.05 | $\alpha _{2}^{V}$ | 0.001256 ± 0.0002 |
| $\alpha _{3}^{P}$ | 1.545 ± 0.05 | $\alpha _{3}^{V}$ | 0.4589 ± 0.05 |
| $\alpha _{4}^{P}$ | 0.307 ± 0.06 | $\alpha _{4}^{V}$ | 0.02022 ± 0.003 |
| $\alpha _{5}^{P}$ | 0.01570 ± 0.003 | $\theta _{1}^{{0\,V}},$ K | 629.4 ± 11 |
| $\alpha _{6}^{P}$ | 0.001090 ± 0.0002 | $\theta _{2}^{{0\,V}},$ K | 52.55 ± 2 |
| $\theta _{1}^{{0P}},$ K | 8065 ± 1118 | $\theta _{3}^{{0\,V}},$ K | 347.4 ± 12 |
| $\theta _{2}^{{0P}},$ K | 1432.7 ± 215 | $\theta _{4}^{{0\,V}},$ K | 143.5 ± 6 |
| $\theta _{3}^{{0P}},$ K | 583.0 ± 18 | γ1 | 1.866 ± 0.07 |
| $\theta _{4}^{{0P}},$ K | 316.3 ± 17 | q1 | 1.115 ± 0.05 |
| $\theta _{5}^{{0P}},$ K | 134.2 ± 8 | ||
| $\theta _{6}^{{0P}},$ K | 50.34 ± 3 | ||
| B1 | 0.03822 ± 0.003 | ||
| B2 | 0.03294 ± 0.006 | ||
| B3 | 0.02927 ± 0.006 | ||
| С3 | 0.2865 ± 0.04 | ||
Таблица 2.
Экспериментальные термодинамические свойства MgO и результаты их описания с помощью предложенных УС
| Источник | T, K | P, ГПа | N* | MRD** | |||||
|---|---|---|---|---|---|---|---|---|---|
| Опт-1*** | Опт-2**** | Опт-3***** | |||||||
| CP-подход | ${{C}_{V}}$-подход | CP-подход | ${{C}_{V}}$-подход | CP-подход | ${{C}_{V}}$-подход | ||||
| Теплоемкость, P = 1 бар | |||||||||
| Barron et al. [33] | 10–270 | 10–4 | 123 | 0.76 | 0.97 | 1.17 | 0.97 | 1.17 | 0.97 |
| Kruppka at al. [34] | 350–680 | 10–4 | 21 | 0.38 | 0.46 | 0.53 | 0.47 | 0.53 | 0.47 |
| Bosenick et al. [35] | 332–972 | 10–4 | 433 | 0.44 | 0.53 | 0.58 | 0.54 | 0.58 | 0.54 |
| Приращение энтальпии, P = 1 бар | |||||||||
| Victor and Douglas [36] | 273–1173 | 10–4 | 9 | 0.25 | 0.24 | 0.25 | 0.24 | 0.25 | 0.24 |
| Pankratz and Kelly [37] | 402–1799 | 10–4 | 15 | 0.28 | 0.21 | 0.23 | 0.22 | 0.23 | 0.22 |
| Richet and Fuqiet [38] | 815–1755 | 10–4 | 11 | 0.46 | 0.47 | 0.46 | 0.47 | 0.46 | 0.47 |
| Объемные свойства при различных давлениях | |||||||||
| Dubrovinsky and Saxena [1] | 298–3000 | 10–4 | 27 | 0.15 | 0.20 | 0.23 | 0.16 | 0.23 | 0.16 |
| Fiquet et al. [40] | 1474–2973 | 10–4 | 15 | 0.17 | 0.19 | 0.25 | 0.17 | 0.25 | 0.17 |
| Utsumi et al. [41] | 300 | 1–8 | 8 | 0.16 | 0.16 | 0.11 | 0.14 | 0.11 | 0.14 |
| Dewaele and Fiquet [31] | 300–2500 | 0–52 | 59 | 0.33 | 0.33 | 0.27 | 0.32 | 0.27 | 0.32 |
| Zhang [42] | 300–1073 | 0–8 | 27 | 0.14 | 0.14 | 0.11 | 0.12 | 0.11 | 0.12 |
| Speziale et al. [12] | 300 | 5–52 | 20 | 0.36 | 0.34 | 0.11 | 0.24 | 0.11 | 0.22 |
| Fei et al. [32] | 1273–2173 | 8–24 | 24 | 0.25 | 0.30 | 0.21 | 0.37 | 0.20 | 0.36 |
| Hirose et al. [43] | 300–2080 | 10–145 | 22 | 0.57 | 0.20 | 0.15 | 0.40 | 0.15 | 0.47 |
| Адиабатический модуль упругости | |||||||||
| Anderson and Andreatch [44] | 20–296 | 10–4 | 39 | 0.57 | 0.70 | 0.13 | 0.30 | 0.13 | 0.29 |
| Sumino et al. [45] | 80–1300 | 10–4 | 34 | 0.23 | 0.25 | 0.30 | 0.18 | 0.30 | 0.18 |
| Isaak et al. [46] | 300–1800 | 10–4 | 31 | 0.30 | 0.36 | 0.38 | 0.50 | 0.38 | 0.49 |
| Kono et al. [14] | 300–1650 | 2–24 | 113 | 0.89 | 0.80 | 2.17 | 0.75 | 2.29 | 0.75 |
| Li et al. [48] | 300 | 1–11 | 17 | 0.95 | 1.13 | 3.30 | 1.48 | 3.35 | 1.52 |
| Sinogeikin et al. [47] | 295–1510 | 10–4 | 15 | 0.49 | 3.84 | 0.30 | 4.92 | 0.30 | 4.94 |
* N – число экспериментальных точек. **Средние относительные отклонения $MRD\left( X \right)\% = {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}\sum {{\left| {{{X}_{{{\text{exp}}}}}~ - ~{{X}_{{{\text{calc}}}}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{X}_{{{\text{exp}}}}}~ - ~{{X}_{{{\text{calc}}}}}} \right|} {{{X}_{{{\text{calc}}}}}}}} \right. \kern-0em} {{{X}_{{{\text{calc}}}}}}} \times 100\% ,$ где ${{X}_{{{\text{exp}}}}}~$ и ${{X}_{{{\text{calc}}}}}~$ – экспериментальные и расчетные значения. *** Оптимизация с использованием всех доступных данных. **** Оптимизация данных без KS при высоком давлении. ***** Оптимизация данных без KS при высоком давлении и PVT-данных при высоких температуре и давлении.
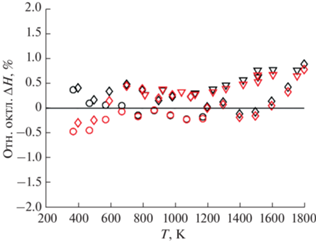
Визуально о качестве предложенных моделей можно судить по рис. 2–8. На рис. 2 представлены экспериментальные данные по теплоемкости при атмосферном давлении; символами обозначены измеренные значения, линиями – результаты расчета. Видно, что низкотемпературные данные [33], полученные методом адиабатической калориметрии, вполне согласуются с результатами ДСК-опытов [34, 35] и значениями приращения энтальпии, полученными с помощью калориметрии сброса [36–38] (рис. 2, 3). Выше 100 K предложенные УС описывают теплоемкость с точностью до 2%, а приращение энтальпии – до 1%. Если в случае энтальпии точность совпадает с погрешностью экспериментального определения, то для теплоемкости разница между экспериментальными и расчетными данными выше, чем заявлено в оригинальных работах [34, 35] (0.5% для интервала 10 < T < 20 K и 0.2% для T > > 20 K). Однако следует отметить, что разброс значений CP, полученных разными авторами, превышает указанные погрешности. Учитывая, что в качестве погрешности обычно приводят разницу между измеренными и рекомендуемыми значениями теплоемкости стандартов, полученное расхождение экспериментальных и расчетных значений можно считать удовлетворительным.
Рис. 2.
Сравнение экспериментальной теплоемкости (P = 1 бар) для MgO с расчетными значениями: абсолютные (a), относительные значения (б). Красные линии (а) и красные символы (б) соответствуют CP‑подходу, черные пунктирные линии (а) и черные символы (б) – CV-подходу. Треугольники – данные [33], квадраты – [34], круги – [35].
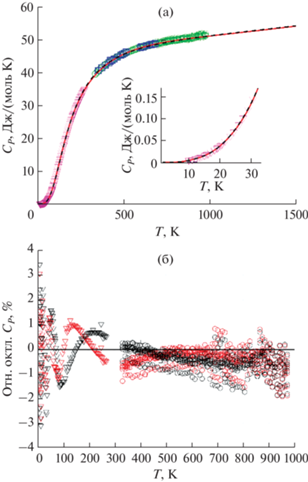
Рис. 4.
Сравнение экспериментальных объемных данных при P = 1 бар для MgO с расчетными значениями: абсолютные (a) и относительные значения (б). Красная линия (а) и красные символы (б) соответствуют CP-подходу, черная пунктирная линия (а) и черные символы (б) – CV-подходу. Круги – данные [1], квадраты – [40].

Рис. 5.
Изотермическая сжимаемость MgO при Т = 300 K, линии – расчетные значения (красная сплошная – CP-подход, черная пунктирная – CV-подход), символы – экспериментальные значения (красные квадраты – данные [41], черные пятиугольники – [42], зеленые ромбы – [43], синие круги – [31], розовые треугольники – [12]).
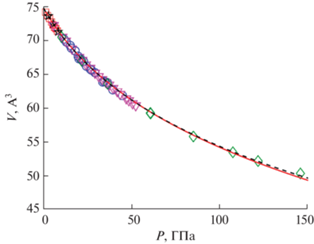
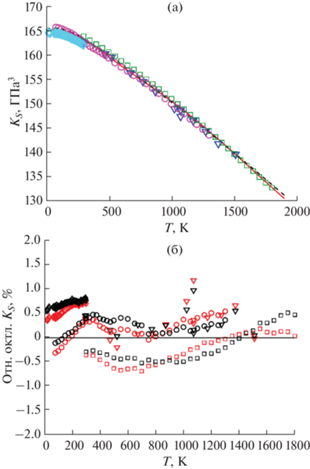
Рис. 7.
Сравнение экспериментальных данных адиабатического модуля упругости при P = 1 бар для MgO с расчетными значениями: абсолютные (a) и относительные значения (б). Красная линия (а) и красные символы (б) соответствуют CP-подходу, черная пунктирная линия (а) и черные символы (б) – CV-подходу. Ромбы – данные [46], круги – [45] квадраты – [44], треугольники – [47].
Расхождение между измеренными и сглаженными значениями CP(T) при низких температурах может быть уменьшено за счет увеличения количества параметров $\alpha _{i}^{0}$ и $\theta _{i}^{0}.$ В настоящей работе мы ограничились представленными наборами, так как ошибка 3–4% в описании теплоемкости при T < 50 K оказывает незначительное влияние на значения стандартных термодинамических функций при комнатной температуре и выше [39].
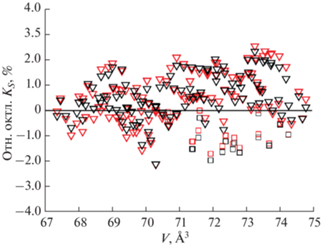
Оба варианта УС показывают близкое описание данных по термическому расширению периклаза до 3000 K; расхождение между расчетом и экспериментом не превышает ошибку эксперимента, соответствующую 0.5% [1]. На рис. 4 изображены результаты измерений объема MgO в диапазоне температур 300–3000 K при стандартном давлении P = 1 бар; видно хорошее согласие между данными разных авторов [1, 40] и модельным описанием. Результаты работ [12, 31, 32, 41–43] по изотермической сжимаемости (300 K) MgO также хорошо согласуются между собой (рис. 5) и с результатами расчетов с помощью предложенных вариантов УС. В случае изучения объемных свойств при высоких давлениях есть определенные проблемы, связанные непосредственно со способом определения значения P; его рассчитывают на основании свойств вещества сравнения (так называемого калибранта давления). В работе [43] показано, что использование разных уравнений состояния одного и того же вещества сравнения при фиксированной температуре приводит к разнице в 20 ГПа при абсолютном значении 140 ГПа. С учетом этого разница рассчитанных и измеренных PVT-данных на рис. 6 не представляется существенной, она соответствует возможной разнице в шкалах веществ сравнения [43]. Следует также подчеркнуть, что CV-вариант УС лучше описывает PVT-данные при высоких давлениях.
С высокой точностью объемные свойства можно определить через адиабатический модуль упругости, так как измеряемые значения не зависят от веществ сравнения. На рис. 7а представлена температурная зависимость адиабатического модуля упругости KS при атмосферном давлении. Оба подхода (CP и CV) хорошо описывают результаты измерений [44–47], укладываясь в погрешность эксперимента 1% согласно данным [47] (рис. 7б). Адиабатический модуль упругости при высоких давлениях можно получить комбинацией сверхзвуковой интерферометрии и рентгеновской дифракции; в работах [14, 48] такие измерения были выполнены до температуры 1650 K и давления 23 ГПа. На рис. 8 представлены относительные отклонения измеренных и рассчитанных значений KS при давлениях до 24 ГПа и температуре от 300 до 1650 K. Оба варианта УС демонстрируют близкое описание KS–V–T данных; относительные отклонения не превышают 2%, что немного превышает экспериментальную погрешность 1.2%, указанную в работе [14].
Таким образом, можно сделать вывод, что обе модели демонстрируют в целом схожее и адекватное описание эксперимента, в то время как CP-подход немного точнее описывает данные при атмосферном давлении, а CV-подход – данные при высоком давлении.
Предсказательная способность. Стандартным способом проверки предсказательной способности любой модели является воспроизведение данных, не использованных при ее параметризации. В настоящей работе для такой проверки при оптимизации были: а) исключены из общей выборки данные по адиабатическому модулю упругости при высоких давлениях, б) учтены результаты измерений коэффициентов термического расширения, адиабатического модуля упругости, теплоемкости и приращения энтальпии при стандартном давлении, а также объемные свойства при 300 K, в) учтены только изотермические PV-данные, теплоемкости, приращения энтальпии и значения коэффициента термического расширения при P = 1 бар. После получения статистически значимых параметров обеих моделей были рассчитаны средние относительные отклонения для разных типов литературных данных.
Вариант (а). В табл. 2 приведены характеристики модельного описания для полного (Опт-1) и ограниченного (Опт-2) наборов данных. Видно (столбцы Опт-1(CP) и Опт-2(CP)), что в случае CP-варианта УС, построенного по усеченному набору данных, получается менее точная оценка значений KS при высоком давлении, в то время как другие свойства воспроизводятся более точно. Частичное ухудшение описания теплоемкости и энтальпии связано с меньшим количеством использованных пар параметров αi и $\theta _{i}^{0}.$ Параметры УС, рассчитанные при оптимизации ограниченного набора данных (Опт-2), перечислены в табл. S2 . При использовании CV-варианта модели значения MRD практически одинаковы при полном и усеченном наборе данных (столбцы Опт-1(CV) и Опт-2(CV)).
Вариант (б). В этом случае (Опт-3) наблюдалось приемлемое описание PVT-свойств при высоких температурах и давлениях. Данные по изотермической сжимаемости были использованы для получения параметров изотермического УС, которые затем фиксировали при последующей оптимизации. Лучшие варианты описания (с 4 или 5-ю парами αi и $\theta _{i}^{0}$) ограниченного набора данных для CP- и CV-подходов перечислены в табл. 2 (Опт-3(CP) и Опт-3(CV) соответственно). Параметры, полученные при оптимизации Опт-3 по ограниченному набору данных, представлены в табл. S3 . Как видно из табл. 2, исключение из оптимизации определенных данных (PVT-данные при высоких температурах и давлениях) лишь незначительно ухудшает их расчет для обоих подходов с небольшим улучшением описания оставшихся данных. При этом качество оценки исключенных еще в оптимизации Опт-2 данных также меняется незначительно.
Вариант (в). При использовании CP-варианта УС не удалось получить разумную оценку адиабатического модуля упругости, в то время как CV-подход позволил рассчитать значения KS при атмосферном давлении вплоть до температур 700–800 K.
На основании изложенного сделан вывод о том, что CP-вариант обладает лучшими интерполяционными свойствами, а CV-подход – экстраполяционными свойствами.
ЗАКЛЮЧЕНИЕ
Уравнения состояния периклаза, предложенные в настоящей работе, обладают рядом достоинств, в первую очередь возможностью адекватного описания высокоточных термохимических свойств при сохранении качества аппроксимации объемных характеристик индивидуальных веществ.
Если сравнивать между собой CV- и CP-подходы, то главным преимуществом последнего является возможность независимого описания отдельных типов данных с последующей комбинацией аналитических зависимостей, что придает модели большую гибкость и приводит к лучшему описанию данных. В случае CV-подхода параметры могут быть получены только при одновременной оптимизации всех доступных типов данных, но этот вариант модели обладает лучшими прогнозирующими характеристиками.
Выявленные закономерности получены только на одном тестовом объекте – оксиде магния. О том, насколько они универсальны, можно будет судить при расширении круга изученных систем.
Список литературы
Dubrovinsky L.S., Saxena S.K. // Phys. Chem. Miner. 1997. V. 24. № 8. P. 547. https://doi.org/10.1007/s002690050070
Reeber R.R., Goessel K., Kai Wang // Eur. J. Mineral. 1995. V. 7. № 5. P. 1039. https://doi.org/10.1127/ejm/7/5/1039
Fedotenko T., Dubrovinsky L., Khandarkhaeva S. et al. // J. Alloys Compd. 2020. V. 844. P. 156179. https://doi.org/10.1016/j.jallcom.2020.156179
Wang X., Wang B., Tan D. et al. // J. Alloys Compd. 2021. V. 875. P. 159926. https://doi.org/10.1016/j.jallcom.2021.159926
Díaz-Anichtchenko D., Santamaria-Perez D., Marqueño T. et al. // J. Alloys Compd. 2020. V. 837. P. 155505. https://doi.org/10.1016/j.jallcom.2020.155505
Irshad K.A., Anees P., Rajitha R. et al. // J Alloys Compd. 2020. V. 822. P. 153657. https://doi.org/10.1016/j.jallcom.2020.153657
Freund J., Ingalls R. // J. Phys. Chem. Solids. 1989. V. 50. № 3. P. 263. https://doi.org/10.1016/0022-3697(89)90486-1
Roy P.B., Roy S.B. // J. Phys. Condens. Matter. 2005. V. 17. № 39. P. 6193. https://doi.org/10.1088/0953-8984/17/39/007
Holland T.J.B., Powell R. // J. Metamorph. Geol. 2011. V. 29. № 3. P. 333. https://doi.org/10.1111/j.1525-1314.2010.00923.x
Huang Y.K., Chow C.Y. // J. Phys. D: Appl. Phys. 1974. V. 7. № 15. P. 2021. https://doi.org/10.1088/0022-3727/7/15/305
Perevoshchikov A.V., Maksimov A.I., Kovalenko N.A. et al. // Russ. J. Phys. Chem. 2022. V. 96. № 10. P. 2059. https://doi.org/10.1134/S0036024422100259
Speziale S., Zha C.-S., Duffy T.S. et al. // J. Geophys. Res. 2001. V. 106. P. 515. https://doi.org/10.1029/2000JB900318
Tange Y., Nishihara Y., Tsuchiya T. // J. Geophys. Res. Solid Earth. 2009. V. 114. № 3. P. 1. https://doi.org/10.1029/2008jb005813
Kono Y., Irifune T., Higo Y. et al. // Phys. Earth Planet. Inter. 2010. V. 183. № 1–2. P. 196. https://doi.org/10.1016/j.pepi.2010.03.010
Huang X., Li F., Zhou Q. et al. // Sci. Rep. 2016. V. 6. P. 19923. https://doi.org/10.1038/srep19923
Anderson O.L. Equations of State of Solids for Geophysics and Ceramic Science. Oxford: Oxford University Press, 1995. 405 p.
Berman R.G., Brown T.H. // Contrib. Mineral. Petrol. 1985. V. 89. № 2–3. P. 168. https://doi.org/10.1007/BF00379451
Pechkovskaya K.I., Nikiforova G.E., Tyurin A.V. et al. // Russ. J. Inorg. Chem. 2022. V. 67. № 4. P. 476. https://doi.org/10.1134/S0036023622040155
Nikiforova G.E., Kondrat’eva O.N., Tyurin A.V. et al. // Russ. J. Inorg. Chem. 2021. V. 66. № 2. P. 242. https://doi.org/10.1134/S0036023621020145
Khvan A.V., Uspenskaya I.A., Aristova N.M. et al. // Calphad. 2020. V. 68. P. 101724. https://doi.org/10.1016/j.calphad.2019.101724
Voronin G.F., Kutsenok I.B. // J. Chem. Eng. Data. 2013. V. 58. № 7. P. 2083. https://doi.org/10.1021/je400316m
Khvan A.V., Dinsdale A.T., Uspenskaya I.A. et al. // Calphad. 2018. V. 60. P. 144. https://doi.org/10.1016/j.calphad.2017.12.008
Khvan A.V., Babkina T., Dinsdale A.T. et al. // Calphad. 2019. V. 65. P. 50. https://doi.org/10.1016/j.calphad.2019.02.003
Gerya T.V., Podlesskii K.K., Perchuk L.L. et al. // Phys. Chem. Miner. 2004. V. 31. № 7. P. 429. https://doi.org/10.1007/s00269-004-0409-8
Feistel R., Wagner W. // J. Phys. Chem. Ref. Data. 2006. V. 35. P. 1021. https://doi.org/10.1063/1.2183324
Trusler J.P.M. // J. Phys. Chem. Ref. Data. 2011. V. 40. № 4. https://doi.org/10.1063/1.3664915
Jacobs M.H.G., Schmid-Fetzer R., van den Berg A.P. // Phys. Chem. Miner. 2013. V. 40. № 3. P. 207. https://doi.org/10.1007/s00269-012-0562-4
Dorogokupets P.I., Oganov A.R. // Phys. Rev. B: Condens. Matter Mater. Phys. 2007. V. 75. № 2. P. 1. https://doi.org/10.1103/PhysRevB.75.024115
Murnaghan F.D. // Proc. Natl. Acad. Sci. USA. 1944. V. 30. P. 244. https://doi.org/10.1073/pnas.30.9.244
Jackson I., Ridgen S.M. // Phys. Earth Planet. Inter. 1996. V. 96. № 2–3. P. 85. https://doi.org/10.1016/0031-9201(96)03143-3
Dewaele A., Fiquet G., Andrault D. et al. // J. Geophys. Res. Solid Earth. 2000. V. 105. № B2. P. 2869. https://doi.org/10.1029/1999jb900364
Fei Y., Li J., Hirose K. et al. // Phys. Earth Planet. Inter. 2004. V. 143. № 1–2. P. 515. https://doi.org/10.1016/j.pepi.2003.09.018
Barron T.H.K., Berg W.T., Morrison J.A. // Proc. R. Soc. A: Math. Phys. Eng. Sci. 1959. V. 250. № 1260. P. 70. https://doi.org/10.1098/rspa.1959.0051
Krupka K.M., Robie R.A., Hemingway B.S. // Am. Mineral. 1979. V. 64. P. 86.
Bosenick A., Geiger C.A., Cemič L. // Geochim. Cosmochim. Acta. 1996. V. 60. № 17. P. 3215. https://doi.org/10.1016/0016-7037(96)00150-0
Victor A.C., Douglas T.B. // J. Res. Natl. Bur. Stand. A: Phys. Chem. 1963. V. 67A. № 4. P. 325. https://doi.org/10.6028/jres.067a.034
Pankratz L.B., Kelley K.K. // Bur. Mines Res. 1963. V. 6295.
Richet P., Fiquet G. // J. Geophys. Res. 1991. V. 96. № B1. P. 445. https://doi.org/10.1029/90JB02172
Uspenskaya I.A., Kulikov L.A. // J. Chem. Eng. Data. 2015. V. 60. № 8. P. 2320. https://doi.org/10.1021/acs.jced.5b00217
Fiquet G., Richet P., Montagnac G. // Phys. Chem. Miner. 1999. V. 27. № 2. P. 103. https://doi.org/10.1007/s002690050246
Utsumi W., Weidner D.J., Liebermann R.C. // Geophys. Monogr. Ser. 1998. V. 101. P. 327. https://doi.org/10.1029/GM101p0327
Zhang J. // Phys. Chem. Minerals. 2000. V. 27. P. 145. https://doi.org/10.1007/s002690050001
Hirose K., Sata N., Komabayashi T. et al. // Phys. Earth Planet. Inter. 2008. V. 167. № 3–4. P. 149. https://doi.org/10.1016/j.pepi.2008.03.002
Anderson O.L., Andreatch P. // J. Am. Ceram. Soc. 1966. V. 49. № 8. P. 404. https://doi.org/10.1111/j.1151-2916.1966.tb15405.x
Sumino Y., Anderson O.L., Suzuki I. // Phys. Chem. Miner. 1983. V. 9. № 1. P. 38. https://doi.org/10.1007/BF00309468
Isaak D.G., Anderson O.L., Goto T. // Phys. Chem. Miner. 1989. V. 16. № 7. P. 704. https://doi.org/10.1007/BF00223321
Sinogeikin S.V., Jackson J.M., O’Neill B. et al. // Rev. Sci. Instrum. 2000. V. 71. № 1. P. 201. https://doi.org/10.1063/1.1150183
Li B., Woody K., Kung J. // J. Geophys. Res. 2006. V. 111. № 11. P. 1. https://doi.org/10.1029/2005JB00425
Дополнительные материалы
- скачать EMS.docx
- Приложение 1.
Табл. S1. Некоторые термодинамические функции и их производные, упомянутые в основной работе.
Табл. S2. Параметры CP- и CV-подхода для оптимизации Опт-2.
Табл. S3. Параметры CP- и CV-подхода для оптимизации Опт-3.
Инструменты
Журнал неорганической химии