1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 68, № 8, 2023

Журнал неорганической химии, 2023, T. 68, № 8, стр. 1077-1082

Начальные стадии формирования надмолекулярной структуры оксидов Ca и Mg

Р. А. Сакович a, А. Ю. Шаулов a, *

a Федеральный исследовательский центр химической физики им. Н.Н. Семенова РАН
119334 Москва, ул. Косыгина, 4, Россия

* E-mail: ajushaulov@yandex.ru

Поступила в редакцию 25.03.2023
После доработки 25.04.2023
Принята к публикации 27.04.2023

Полный текст (PDF)

Аннотация

С помощью квантово-химических расчетов методом DFT найдены оптимальные геометрии в вакууме кластеров (CaO)n и (MgO)n при n = 2–30 и определены энтальпии образования 1D-, 2D- и 3D-структур. Показано, что линейные цепи оксидов Са и Mg практически не образуются, в то время как формирование двумерной (плиточной) и трехмерной (кубической) структур протекает с большим выделением энергии. Рассмотрен конкурирующий процесс образования молекулярных стержней, состоящих из плоских шестичленных циклов (МО)3, и показано, что процесс протекает не через стадию предварительного образования шестичленных циклов, а непосредственно из мономерных звеньев.

Ключевые слова: оксиды кальция и магния, квантово-химические расчеты, молекулярные структуры

ВВЕДЕНИЕ

Оксиды кальция и магния и их производные – распространенные природные соединения, нашедшие широкое применение. Оксид кальция является компонентом производства силикатных стекол, служит основой для цементов, строительных материалов и т.д., тогда как оксид магния наряду с широким применением рассматривается для решения таких важных задач, как сокращение содержания СО2 в атмосфере (геологическая секвестрация) [1], хранение водорода [2] и др. Широкое развитие получили исследования керамических композиций, содержащих СаО и MgO [3, 4].

Наряду с этим большое значение имеют наночастицы оксидов, размер и форма которых позволяют использовать их в качестве катализаторов, адсорбентов, химических агентов и т.д. [5–7].

Оксиды химических элементов в зависимости от природы связей являются соединениями с различным пространственным строением и энергией межмолекулярных взаимодействий, которые определяют их надмолекулярную структуру [8–13].

Одними из таких соединений являются оксиды магния и кальция, относящиеся к классу полиоксидов и обладающие близкой к ионной химической связью.

Существенным отличием неорганических полиоксидов от полиуглеводородов является высокая энергия химических и межмолекулярных связей, определяемая большой разницей в значениях электроотрицательности элементов. Наличие сильных полярных связей предопределяет и сильные межмолекулярные взаимодействия, оказывающие существенное влияние на свойства и надмолекулярную структуру твердого тела.

Изучению строения, стабильности и определению теплот образования катионных, анионных и нейтральных кластеров оксидов (CaO)n и (MgO)n с n ≤ 40, не определяющих еще термодинамические свойства твердого тела, посвящен ряд работ: n = 1–6 [14], 1–29 [15], 1–5 [16], 2–10 [17], 1–5 [18], 2–7 [19], 3–16 [20], 2–7 [21], 1–6 [22], 6–24 [23], 1–40 [24], 1–40 [25], 1–24 [26].

В настоящей работе рассмотрена возможность описания структуры оксидов кальция и магния на начальной стадии формирования (МО)n при n = 2–18 с использованием квантово-химических расчетов с целью определения длин связей, теплот образования линейных (1D-) и формирования 2D- и 3D-структур, а также энергии межмолекулярных взаимодействий.

Проведена оптимизация геометрии основных электронных состояний соединений, рассчитаны колебательные частоты и вычислены энтальпии реакции присоединения Са–О, Mg–O и межмолекулярных взаимодействий. При расчете использован метод теории функционала плотности DFT [27] с функционалом B3LYP [28] в базисе QZVP [29] при помощи квантово-химического пакета Turbomole [30].

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Квантово-химическое моделирование

Оксиды кальция и магния являются соединениями двухвалентных металлов и имеют кубическую решетку с химической связью, близкой к ионной, и координационным числом ионов, равным 6 [31].

Нами рассмотрены молекулярные структуры образующихся в процессе взаимодействия мономерных звеньев оксидов кальция и магния. При расчетах выполняли оптимизацию геометрии основного электронного состояния до получения на поверхности потенциальной энергии глобального минимума и проводили расчеты колебательных частот. При наличии мнимых частот весь процесс оптимизации повторялся.

С целью выбора основного метода расчета вычислены теплоты образования при 0 K гидроксидов кальция и магния в различных гибридных функционалах и тройном- (TZVP) и четверном (QZVP) ζ‑базисах (табл. 1). Наибольшую близость к экспериментальным данным показал функционал B3LYP, при этом переход к QZVP существенно улучшал результаты, поэтому в качестве основного функционала был выбран B3LYP с базисом QZVP.

Таблица 1.  

Сравнение рассчитанных и экспериментальных стандартных энтальпий образования при 0 K для гидроксидов кальция и магния, ккал/моль

Параметр Ca(OH)2 Mg(OH)2
TZVP QZVP TZVP QZVP
BHLYP –112.7 –121.8 –98.8 –105.2
PBE0 –132.0 –137.2 –113.2 –118.5
M06-2X –133.7 –138.9 –120.4 –124.2
PW6B95 –136.3 –142.1 –118.0 –122.3
B3LYP –134.8 –141.3 –121.5 –125.7
Эксперимент [30] –144.2 ± 9.0 –135.0 ± 8.0

Для оценки энергетического эффекта реакций рассчитывали энтальпию реакции как разность сумм электронной и колебательной энергий нулевых колебаний продуктов и реагентов при 0 K в вакууме, отнесенную к числу атомов металла, участвующих в реакции:

(1)
${\text{A}} + {\text{B}} \to {\text{C}} + {\text{D}},$
(2)
$\Delta {{H}_{{\text{р}}}} = \left( {E({\text{C)}} + E({\text{D}})--E({\text{A}})--E({\text{B}})} \right){\text{/}}n,$
где E = Eel + Evib0 – сумма электронной и колебательной энергий нулевых колебаний, n – число атомов металла, участвующих в реакции.

Отрицательная энтальпия реакции соответствует энергетически выгодной реакции, протекающей с выделением тепла.

1D -линейная цепь

Образование оксидов рассматривали в соответствии с уравнением:

(3)
$n{\text{M}}{{({\text{OH)}}}_{2}} \to {\text{HO(}}{\kern 1pt} --{\kern 1pt} {\text{MO}}--{{{\text{)}}}_{n}}{\text{H}} + (n--1){{{\text{Н}}}_{{\text{2}}}}{\text{O}}.$

Рассчитаны удельные энтальпии реакций образования линейных цепей ΔHр(n) для HO(–MgO–)nH и HO(–CaO–)nH при n = 2–15 (табл. 2).

Таблица 2.  

Удельные энтальпии образования линейных цепей HO(–M–O–)nH

n ΔHр(HO(–MgO–)nH), ккал/моль ΔHр(HO(–CaO–)nH), ккал/моль
2 –0.2 12.9
3 0.0 13.2
4 0.1 13.4
5 0.1 13.6
6 0.2 13.7
7 0.2 13.8
8 0.2 13.8
9 0.3 13.9
10 0.3 13.9
11 0.3 13.9
12 0.3 13.9
15 0.3 14.0

Из проведенных расчетов следует, что небольшой выигрыш в энергии получается только для линейного димера оксида магния (–0.2 ккал/моль), для всех остальных соединений магния энтальпия образования немного выше нуля, это свидетельствует о том, что формирование линейных цепей возможно, но протекает крайне медленно. Для оксида кальция энтальпии имеют большие положительные значения, следовательно, линейные цепи в вакууме образовываться не могут.

2D-структуры

Рассмотрена возможность образования двумерных структур (HO(–M–O–)nH)m с плоской ячейкой размером nm из исходных гидроксидов при n = 2–0 и m = 2–3:

(4)
$\begin{gathered} nm{\text{M(OH}}{{{\text{)}}}_{2}} \to \\ \to {{\left( {{\text{HO(}}{\kern 1pt} --{\kern 1pt} {\text{MO}}--{{{\text{)}}}_{n}}{\text{H}}} \right)}_{m}} + (n--1)m{{{\text{Н}}}_{{\text{2}}}}{\text{O}}. \\ \end{gathered} $

Рассчитанные удельные энтальпии реакций ΔHр(n, m) приведены в табл. 3 и на рис. 1.

Таблица 3.  

Энтальпии образования планарных структур (HO(–M–O–)nH)m

N m ΔHр((HO(–MgO–)nH)m), ккал/моль ΔHр((HO(–CaO–)nH)m), ккал/моль
2 2 –24.1 –19.0
3 2 –22.4 –15.8
4 2 –21.6 –14.1
5 2 –21.0 –12.9
6 2 –20.7 –12.2
7 2 –20.4 –11.6
8 2 –20.2 –11.1
9 2 –20.1 –10.9
10 2 –20.1 –10.8
2 3 –30.4 –26.5
3 3 –29.2 –24.6
4 3 –28.7 –24.0
5 3 –28.5 –23.5
6 3 –28.4 –23.0
7 3 –28.3 –22.6
8 3 –28.3 –22.2
9 3 –28.2 –22.0
10 3 –28.1 –21.9
Рис. 1.

Зависимости удельных энтальпий образования планарных структур с квадратной ячейкой размера 2n и 3n, где n = 2–10. 1 – (HO(–CaO–)nH)2, 2 – (HO(–MgO–)nH)2, 3 – (HO(–CaO–)nH)3, 4 – (HO(–MgO–)nH)3.

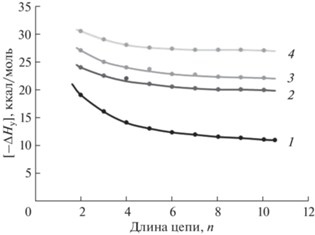
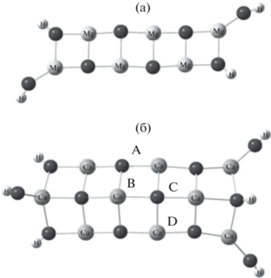
При переходе от m = 2 к m = 3 выигрыш в энергии возрастает, что объясняется образованием дополнительных поперечных связей M–O (рис. 2).

Рис. 2.

Двумерные структуры полиоксидов магния (HO(–MgO–)3H)2 (а) и кальция (HO(–CaO–)3H)3 (б).

Представленные значения энтальпии показывают, что процесс образования 2D-структур может протекать достаточно эффективно.

Полученные структуры при m = 2 лежат полностью в одной плоскости, но при m = 3 изгибаются, при этом двугранный угол ABCD составляет 130° (рис. 3б). Длины краевых связей отличаются от длин центральных на ≤0.01 нм, длины связей Mg–O лежат в диапазоне 0.195–2.02 нм, тогда как длины Ca–O равны 0.224–0.234 нм. Эти значения близки к литературным данным. Так, длина связи Са–О при n = 1 равна 0.1818 нм, при n = 6–0.224 нм [26], а длина связи Мg–O составляет 0.175 нм [32, 33].

Рис. 3.

Трехмерная структура полиоксида магния ((HO(–MgO–)2H)2)2.

3D -структуры

Аналогично рассчитаны теплоты образования трехмерных структур с объемной ячейкой размером nmk, образующихся из планарных структур в соответствии с уравнением реакции:

(5)
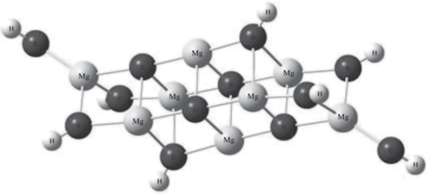
$\begin{gathered} nmk{\text{M}}{{\left( {{\text{OH}}} \right)}_{2}} \to {{\left( {{{{\left( {{\text{HO(}}{\kern 1pt} --{\kern 1pt} {\text{MO}}--{{{\text{)}}}_{n}}{\text{H}}} \right)}}_{m}}} \right)}_{k}} + \\ + \,\,(n--1)mk{{{\text{Н}}}_{{\text{2}}}}{\text{O}}. \\ \end{gathered} $

Оптимизация геометрии таких структур затруднена из-за большого числа степеней свободы, поэтому расчеты были ограничены одним соединением 2 2 2 (рис. 3).

В результате получены высокие абсолютные значения удельной энтальпии, составившие для оксида магния –38.6 ккал/моль, для оксида кальция –31.2 ккал/моль. Эти значения по модулю выше энергий образований 2D-структур, что свидетельствует о большей эффективности образования трехмерных структур.

Молекулярные шестигранные стержни

При расчете удельной энтальпии образования метаструктуры шестичленного цикла (MO)3 в соответствии с уравнением реакции

(6)
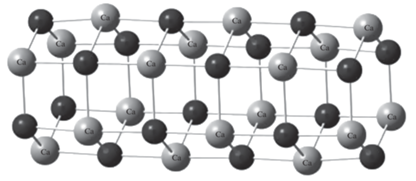
${\text{M(OH}}{{{\text{)}}}_{2}} \to {{({\text{MO}})}_{3}} + {\text{3}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}$
получены положительные значения: для оксида магния 16.9 ккал/моль, для оксида кальция 18.1 ккал/моль, что свидетельствует о маловероятном образовании одиночных циклов в вакууме.

Наряду с этим рассчитаны энтальпии образования кластеров молекулярных стержней (МС), состоящих из шестичленных циклов с n = 2–10 и образующихся непосредственно из мономерных звеньев (рис. 4) в соответствии с реакцией:

(7)
$3n{\text{M(OH}}{{{\text{)}}}_{2}} \to {{\left( {{{{({\text{MO}})}}_{3}}} \right)}_{n}} + 3n{{{\text{H}}}_{{\text{2}}}}{\text{O}}.$
Рис. 4.

Молекулярный стержень кальция ((CaO)3)6.

Полученные положительные значения энтальпии, достигающие 14.8 ккал/моль у оксида магния и 18.7 ккал/моль у оксида кальция, позволяют эффективно рассматривать образование молекулярных стержней. (табл. 4). Аналогичный вывод о высокой эффективности образования гексагональной тубулярной структуры MgO представлен в работе [22].

Таблица 4.  

Удельные энтальпии образования молекулярных стержней ((MO)3)n

n ΔHр(((MgO)3)n) ΔHр(((CaO)3)n)
ккал/моль
2 –9.3 –7.2
3 –21.1 –17.3
4 –22.2 –18.4
5 –22.9 –19.2
7 –23.3 –19.6
8 –23.6 –19.7
9 –23.8 –19.9
10 –23.9 –20.0

В данном случае, аналогично планарным структурам, наблюдается резкий скачок энергии при переходе от n = 2 к n = 3 из-за образования дополнительных связей M–O, направленных вдоль стержня.

Для сравнения эффективности протекания рассмотренных процессов на оксидах магния и кальция приведены тепловые эффекты образования различных структур на базе димеров (табл. 5).

Таблица 5.  

Удельные энтальпии образования 1D-, 2D- и 3D-структур на базе димеров, ккал/моль

Структура MgO СаО
1D –0.2 12.9
2D –24.1 –19.0
3D-кубическая ячейка –38.6 –31.2
Молекулярный стержень (n = 3) –21.1 –17.3

ЗАКЛЮЧЕНИЕ

Обобщая полученные данные и сравнивая энтальпии образования 1D-, 2D- и 3D-структур, можно определить следующие тенденции в процессе формирования базовых структур:

– образование 1D-структуры и шестичленных циклов сильно затруднено из-за отрицательного энергетического эффекта реакции,

– эффективное образование из мономерных звеньев коротких 2D-структур с большим выделением энергии,

– эффективное образование трехмерных структур за счет межмолекулярных взаимодействий мономерных звеньев и 2D-структур,

– эффективное образование молекулярных шестигранных стержней.

Из полученных данных следует, что для СаО и MgO с высокой вероятностью характерно образование плиточной 2D- и кубической 3D-структур и с меньшей вероятностью параллельное формирование молекулярных шестигранных стержней.

Список литературы

  1. Edmonds J.A., Freund P., Dooley J.J. // Greenhouse Gas Control Technologies. 2001. P. 46.

  2. Juan Pablo Mojica-Sánchez, Tania Isabel Zarate-López, José Manuel Flores-Álvarez et al. // Phys. Chem. Chem. Phys. 2019. https://doi.org/10.1039/c9cp05075b

  3. Гаркушин И.К., Лаврентьева О.В., Штеренберг А.М. // Физика и химия стекла. 2023. Т. 49. № 2. С. 148. https://doi.org/10.31857/S0132665122100109

  4. Gu Guoxuan, Li Sheng, Liu Xin et al. // Ceramics-Silikáty. 2022. V. 66. P. 480. https://doi.org/10.13168/cs.2022.0044480

  5. Utamapanya S., Klabunde K.J., Schlup J.R. // Chem. Materials. 1991. V. 3. P. 175.

  6. Сергеев Г.Б. Нанохимия. М.: Изд-во МГУ, 2003. 288 с.

  7. Суздалев И.П. Нанотехнология: физико-химия нанокластеров, наноструктур и наноматериалов М.: КомКнига, 2006. 592 с.

  8. Ray N.H. // Inorganic Polymers. London: Acad. Press, 1978. 172 p.

  9. Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. Новосибирск: Наука, 1982. 256 с.

  10. Фельц А. Аморфные и стеклообразные неорганические твeрдые тела. М.: Мир, 1986. 326 с.

  11. Ropp R.C. Inorganic Polymer Glasses. Amsterdam: Elsevier, 1992. 201 p.

  12. Сироткин О.С. Безуглеродные полимерные элементооксаны, Дис. … докт. техн. наук. Казань, 1992. 364 с.

  13. Шаулов А.Ю., Владимиров Л.В., Грачев А.В. и др. // Химическая физика. 2020. Т. 14. С. 183. https://doi.org/10.1134/S1990793120010157

  14. Malliavin M.-J., Coudray C. // J. Chem. Phys. 1997. V. 106. P. 2323.

  15. Aguado A., López-Gejo F., López J.M. // J. Chem. Phys. 1999. V. 110. P. 4788.

  16. Gutowski M., Skurski P., Li X. et al. // Phys. Rev. Lett. 2000. V. 85. P. 3145.

  17. Dong R., Chen X., Wang X. et al. // J. Chem. Phys. 2008. V. 129. P. 044705.

  18. Vasili M.L.S., Felle D. et al. // J. Phys. Chem. A. 2010. V. 114. P. 9349.

  19. Kwapien K., Sierka M., Döbler J. et al. // Angew. Chem., Int. Ed. 2011. V. 50. P. 1716.

  20. Haertelt M., Fielicke A., Meijer G. et al. // Phys. Chem. Phys. 2012. V. 14. P. 2849.

  21. Hong L., Wang H., Cheng J. et al. // Comput. Theor. Chem. 2012. V. 980. P. 62.

  22. Priynka Batra, Ritu Gaba, Upasana Issar et al. // J. Theor. Chem. 2013. P. 720794. https://doi.org/10.1155/2013/720794

  23. Zhang Y., Chen H.S., Yin Y.H. et al. // J. Phys. B: At., Mol. Opt. Phys. 2014. V. 47. P. 025102.

  24. Chen Mingyang, Felmy A.R., Dixon D.A. // J. Phys. Chem. A. 2014. V. 118. P. 3136. https://doi.org/10.1021/jp412820z

  25. Mingyang Chen, Kanchana Sahan Thanthiriwatte, David A. // J. Phys. Chem. C. 2017. V. 121. P. 23025. https://doi.org/10.1021/acs.jpcc.7b09062

  26. Motoyoshi Nakano, Daiki Hebiguchi, Shohei Azuma et al. // J. Phys. Chem. A. 2020. V. 124. P. 101.

  27. Gross E.K.U., Kohn W. // Adv. Quantum Chem. 1990. V. 21. P. 255.

  28. Becke A.D. // J. Chem. Phys. 1993. V. 98. P. 5648.

  29. Schafer A., Horn H., Ahlrichs R. // J. Chem. Phys. 1992. V. 97. P. 2571.

  30. Furche F., Ahlrichs R., Hattig C. et al. // Comput. Mol. Sci. 2014. V. 4. P. 91.

  31. Уэллс А.Ф. Строение неорганических веществ. М.: Изд-во иностр. литер., 1948. 690 с.

  32. Vasiliu M., Feller D., Gole J.L., Dixon D.A. // J. Phys. Chem. A. 2010. V. 114. P. 9349.

  33. Bawa F., Panas I. // Phys. Chem. Chem. Phys. 2002. V. 4. P. 103.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал