Проблемы машиностроения и надежности машин, 2019, № 7, стр. 80-87

Автомобильные прицепы в процессе эксплуатации подвергаются различным интенсивным нерегулярным воздействиям, которые рандомизируются и адекватное математическое описание которых возможно только методами теории вероятностей и методами теории случайных функций [1, 2].

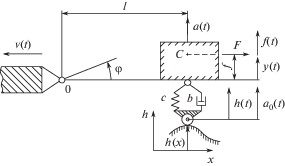
Одна из расчетных схем автомобильного прицепа представлена на рис. 1.

Здесь φ(t) – угол поворота подрессоренной массы относительно точки ее крепления к автомобилю O; $v(t)$ – скорость буксировки прицепа; h(x) – высота неровностей дороги; h(t) – кинематическое воздействие на колесо; c, b – жесткость и коэффициент демпфирования системы подрессоривания; l, r – линейные размеры; $F$– сила инерции; y(t), a(t) – вертикальное перемещение и ускорение подрессореной массы; f(t) – расчетное воздействие.

Дифференциальное уравнение для определения угла φ(t) получаем в виде [3]

а для определения перемещения $y(t) = l{\varphi }$ имеем уравнение где $2n = \frac{{{{l}^{2}}b}}{J}$; ${\omega }_{0}^{2} = \frac{{{{l}^{2}}c}}{J}$; $f(t) = \frac{{lr}}{J}F(t)$; ${\varepsilon }(t) = \frac{1}{{lc}}F(t)$.

Здесь интенсивности случайного силового воздействия f(t) и кинематических воздействий h(t) и $\dot {h}(t)$ зависят от средней скорости движения $\bar {v}(t) = const$, а интенсивность параметрического воздействия ε(t) – от ее флуктуационной составляющей $\tilde {v}(t)$, и при $\tilde {v}(t) = 0$ имеем ε(t) = 0.

Из (1) следуют уравнения для определения устойчивости движения прицепа

реакций y(t) на воздействия f(t) и h(t), для определения деформации упругого элемента $u(t) = h(t) - y(t)$и для определения ускорения подрессоренной массы $a(t) = \ddot {y}(t)$

Для анализа устойчивости движения прицепа с переменной случайной скоростью $v(t)$ уравнение (2) дополним внешним воздействием в виде белого шума q(t) с малой интенсивностью k_q, а процесс ε(t) будем считать независимым от процесса q(t) белым шумом с заданной интенсивностью k_ε. Задача состоит в определении интенсивности параметрического воздействия ε(t), при котором движение прицепа будет неустойчивым.

Для решения этой задачи имеем уравнение

Правую часть уравнения (6), обозначенную как P(t), можно считать белым шумом с интенсивностью

и спектральной плотностью где $s_{y}^{2}$ – дисперсия процесса y(t).

Квадрат модуля передаточной функции уравнения (6) будет определяться как

а для определения дисперсии $s_{y}^{2}$ получаем алгебраическое уравнение

Отсюда получаем

При ${{k}_{{\varepsilon }}} \to \frac{{4n}}{{{\omega }_{0}^{2}}}$ имеем $s_{y}^{2} \to \infty $.

Заключаем, что движение прицепа будет устойчивым при выполнении условия

Здесь величина ${{k}_{{\varepsilon }}} \equiv {{k}_{{\varepsilon }}}(\tilde {v})$ зависит от флуктуационной составляющей скорости движения $\tilde {v}$. Так что из (9) имеем возможность определить критическую скорость буксировки ${{v}_{{{\text{кр}}}}}$.

Если параметрическое воздействие ε(t) не является белым шумом и имеет некоторую спектральную плотность ${{S}_{{\varepsilon }}}({\omega }) \ne {\text{const}}$, то его (в соответствии с понятием о главном параметрическом резонансе) можно приближенно заменить на белый шум интенсивностью ${{k}_{{\varepsilon }}} = 2{\pi }{{S}_{{\varepsilon }}}(2{{{\omega }}_{0}})$. В этом случае условие устойчивости движения прицепа (9) принимает вид

Здесь также величина S_ε(2ω₀) зависит от скорости $\tilde {v}$.

Реакцию системы y(t) на воздействие в виде белого шума f(t) с интенсивностью k_f определяем из решения уравнения (3). В соответствии с (7) и (8) дисперсия процесса y(t) в этом случае будет определяться как

Если процесс f(t) не является белым шумом и имеет спектральную плотность S_f(ω) ≠ const, то, в соответствии с фильтрующими свойствами системы реагировать в основном на воздействия по частоте близкие к частоте собственных колебаний ω₀, его можно заменить на белый шум с интенсивностью ${{k}_{f}} = 2{\pi }{{S}_{f}}({{{\omega }}_{0}})$ и после этого искомую дисперсию определять по формуле (11) [4].

Реакцию системы y(t) на кинематическое воздействие h(t) определим из решения уравнения (4), квадрат модуля передаточной функции которого от h(t) к y(t) будет определяться по формуле

Полагая процесс h(t) белым шумом с интенсивностью k_h и спектральной плотностью ${{S}_{h}}({\omega }) = \frac{1}{{2{\pi }}}{{k}_{h}}$, получим для определения дисперсии процесса y(t) выражение

Из соотношений (11) и (13) следует, что требования к системе виброзащиты противоречивы: для уменьшения перемещения y(t) от воздействия f(t) требуется увеличивать ее жесткость, а для уменьшения этого перемещения от h(t) ее требуется уменьшать. Оптимальное значение квадрата частоты собственных колебаний ${\tilde {\omega }}_{0}^{2}$ определяем из условия минимума суммарного от этих воздействий перемещения. Имеем

При k_f  = 0 имеем ${\tilde {\omega }}_{0}^{2} = 0$, а при k_h = 0 ${\tilde {\omega }}_{0}^{2} \to \infty $.

Дисперсия процессов u(t) и a(t) определяется из решения уравнений (4) и (5). Получаем

где первая передаточная функция определяется по формуле (7), а вторая – по формуле (12); ${{S}_{{{{a}_{0}}}}}({\omega })$ – спектральная плотность процесса ${{a}_{0}}(t)$.

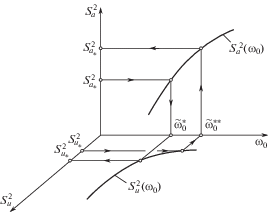
Зависимости дисперсий процессов u(t) и a(t) от частоты собственных колебаний системы ω₀ имеют вид, показанный на рис. 2.

Из рис. 2 видно, что требования к системе виброзащиты по жесткости противоречивы: при ее увеличении ускорение объекта виброзащиты возрастает, а деформация упругого элемента уменьшается; при ее уменьшении – ускорение уменьшается, а деформация возрастает.

Определение оптимальной жесткости усложняется тем, что требования к системе виброзащиты формулируются в различных единицах измерения: по перемещениям u(t) – в единицах длины, а по ускорениям a(t) – в единицах ускорения.

Определив оптимальную частоту ${\tilde {\omega }}_{0}^{*}$ из условия ограничения дисперсии ускорения $s_{a}^{2} \leqslant s_{{{{a}_{*}}}}^{2}$, получаем вполне определенную дисперсию перемещения $s_{{{{u}_{*}}}}^{2}$. Определив оптимальную частоту ${\tilde {\omega }}_{0}^{{**}}$ из условия ограничения дисперсии деформации упругого элемента $s_{u}^{2} \leqslant s_{{{{u}_{*}}}}^{2}$, получаем вполне определенное значение для дисперсии ускорения $s_{{{{a}_{*}}}}^{2}$.

За оптимальное значение частоты собственных колебаний ${\tilde {\omega }}_{0}^{{}}$ можно принять ее промежуточное значение

где α – значимость (вес) первого условия, β – значимость (вес) второго условия, а α + β =1.

Надежность функционирования рассматриваемой механической системы [5] можно оценить:

– вероятностью того, что перемещение y(t) подрессоренной массы за время t ни разу не превысит допустимого значения y_* (т.е. вероятностью непробоя за это время амортизатора)

– вероятностью того, что деформация u(t) упругого элемента за время $t$ ни разу не превысит допустимого значения ${{u}_{*}}$ (т.е. при ${{u}_{*}} = mg{\text{/}}c$ – вероятностью того, что за это время не произойдет отрыва колеса от дороги)

– вероятностью того, что дифферент φ(t) прицепа за время t ни разу не превысит допустимого значения ${{\varphi }_{*}}$

– вероятностью того, что ускорение a(t) подрессоренной массы за время t ни разу не превысит допустимого значения ${{a}_{*}}$ (т.е. вероятностью того, что сила инерции при $m\ddot {y}$, действующая на ограничитель хода, не превысит допустимого значения $m{{a}_{*}}$)

– вероятностью того, что “резкость” движения, определяемая как, $k(t) = \dddot y(t)$ за время t ни разу не превысит допустимого значения ${{k}_{*}}$

Соотношения (14)–(18) можно обобщить и записать в виде одной формулы для расчета надежности как вероятности того, что параметр качества x(t) функционирования системы за время t ни разу не превысит допустимого значения ${{x}_{*}}$, определяемого как

где $n(t) = \frac{t}{{2{\pi }}}\frac{{{{s}_{{\dot {x}}}}}}{{{{s}_{x}}}}$ – ожидаемое за время $t$ число максимумов процесса x(t); $s_{x}^{2}$ – дисперсия процесса $x(t)$; $s_{{\dot {x}}}^{2}$ – дисперсия его первой производной.

Из соотношения (19) следует, что наиболее вероятное за время t наибольшее значение x* процесса x(t) ориентировочно можно вычислить по формуле

а надежность системы оценить коэффициентом запаса надежности за время t как

Из соотношения (20) следует, что обычно принимаемое в технике правило “трех стандартов” требует уточнения. При n = 100 имеем x* ≈ 3S_x, а при n = 10 000 x* ≈ 4.29S_x.

В заключение отметим, что практическая реализация предложенной методики расчета надежности механических систем при случайных внешних воздействиях связана с определенными трудностями:

1. Определение вероятностных характеристик кинематических воздействий h(t) по вероятностным характеристикам пути h(x) и скорости движения машины v обусловлена возможностью вычисления производных от h(t), тогда как эти процессы описываются обычно формально недифференциальными случайными функциями. Это требует предварительного статистического сглаживания этих траекторий, например, так как это сделано в работе [2].

2. Определение вероятностных характеристик процесса F(t), а, следовательно, и вероятностных характеристик процесса ε(t), требует решения задачи о переезде случайных неровностей пути, приводящее к флуктуации скорости движения машины и появлению соответствующих сил инерции [6]. Эта задача может быть решена с использованием энергетического соотношения

и методов статистической линеаризации нелинейных функций.

При линеаризации соотношения (21) по методу равенства дисперсий дисперсия пульсационной составляющей скорости движения будет определяться по формуле

где g = 9.8 м с^–2; s_h – стандарт высоты неровностей.

Спектральные плотности $v(t)$ и $\dot {v}(t)$ определяются известными методами теории случайных функций [7].

3. Возможность использования в работе метода сведения случайных процессов с переменными по частоте спектрами к белым шумам с постоянными спектрами обусловлена фильтрующими свойствами динамических систем реагировать в основном на воздействия по частоте близкие к частоте собственных колебаний системы. При большом демпфировании это может приводить к определенным неточностям.

4. Возможность практического использования в расчетах устойчивости приближенного соотношения (10) требует его экспериментальной проверки. Здесь это было сделано путем вычислительного эксперимента – численного решения стохастического аналога уравнения Матье–Хилла вида

При спектральной плотности процесса ε(τ) вида

где $s_{{\varepsilon }}^{2}$ – дисперсия процесса ε(τ); τ – безразмерное время; n – безразмерный коэффициент демпфирования.

Условие устойчивости (10) получаем в виде

где число 5 соответствует некоторой скорости ${\tilde {v}}$.

Из (23) следует, что при увеличении демпфирования система становится более устойчивой. При n = 0 система всегда устойчива.

Траектория процесса ε(τ) моделируется по следующей формуле Шинозуки

где $c_{i}^{2} = {{S}_{\varepsilon }}({{{\omega }}_{i}})\Delta {\omega }_{i}^{{}}$, $\Delta {{{\omega }}_{i}}$ – шаг квантования спектральной плотности (22) , α_i – случайная величина равномерно распределенная в интервале (0; 2π).

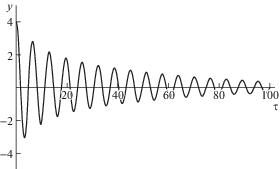
Одна из полученных траекторий процесса y(τ) для устойчивой системы при n = = 0.05, y(0) = 4, $s_{{\varepsilon }}^{2} = 0.2$ показана на рис. 3.

По результатам численных экспериментов был сделан вывод о возможности использования соотношения (10) для практических расчетов.

Заключение. В статье рассмотрен комплекс вопросов, возникающих при создании новой техники, предназначенной функционировать в условиях одновременного воздействия на нее интенсивных случайных силовых, кинематических и параметрических воздействий. Получены формулы для расчета надежности рассмотренной механической системы как вероятности непревышения параметрами качества ее функционирования (перемещениями, ускорениями и т.п.) допустимых для них значений.

Разработана методика выбора оптимальных параметров систем виброзащиты мобильных машин и методика расчета критической скорости их движения по дорогам со случайными неровностями.

Полученное приближенное условие устойчивости движения экспериментально проверено численно на моделях со случайными параметрическими воздействиями.