1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 3, 2020

Проблемы машиностроения и надежности машин, 2020, № 3, стр. 26-35

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭФФУЗИИ ГАЗА В ВАКУУМЕ

В. А. Котельников 2, *, М. В. Котельников 2, Г. С. Филиппов 1, 2, **, М. А. Платонов 2

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

2 Московский авиационный институт (национальный исследовательский университет) (МАИ)
Москва, Россия

* E-mail: mvk_home@mail.ru
** E-mail: filippov.gleb@gmail.com

Поступила в редакцию 06.09.2018
Принята к публикации 31.01.2020

Полный текст (PDF)

Аннотация

Методами математического моделирования исследована эффузия газа через небольшое отверстие прямоугольной формы в разреженное пространство. Получены функции распределения частиц газа, истекающих из отверстия и моменты этих функций: поля концентраций и скоростей частиц газа. Исследована зависимость эффузии от объема, из которого происходит истечение.

Ключевые слова: функция распределения, уравнение Власова, эффузия, разгерметизация

Истечение газа через относительно малые отверстия в результате теплового движения молекул часто встречается в природе и современной технике. Например, при движении космических аппаратов в ионосфере всегда существует опасность разгерметизации жилых отсеков в результате столкновений с метеоритами, частицами космического мусора, деградации сварных швов, различных аварий и других причин. Появлению больших течей часто предшествуют малые течи, которые трудно поддаются диагностике. Авария на орбитальной станции “Мир” в 1997 году привела к разгерметизации одного из ее модулей [1]. Тогда удалось изолировать поврежденный модуль, однако в конечном итоге это повлияло на срок ее функционирования.

Появление электроракетных двигателей (ЭРД) привело к необходимости создания вакуумных стендов больших размеров для их исследования, диагностики, совершенствования конструкции. Первые работы в области создания ЭРД начались в 60-х годах прошлого столетия по инициативе С.П. Королева и продолжаются до настоящего времени [2]. В практике использования вакуумных стендов приходится уделять много внимания исключению течей при герметизации люков, смотровых окон, в местах введения измерительных систем, в сварных швах и т.д.

Явление эффузии лежит в основе ряда технологических процессов, связанных с разделением смесей газов на отдельные компоненты путем ее пропускания через пористые вещества.

В настоящей статье методами математического моделирования исследуется эффузия газа в разреженное пространство. По этому вопросу встречается достаточно много опубликованных работ [3–18], однако строгого решения задачи на кинетическом уровне найти не удалось. Отсутствуют детальные исследования особенностей функций распределения частиц газа, истекающих в разреженное пространство.

При выборе физических, математических и численных моделей эффузии газа авторы использовали опыт, накопленный при исследовании динамики потоков разреженной плазмы в теоретических и прикладных задачах [19–22].

Физическая, математическая и численная модели задачи. Рассмотрим разреженный газ, истекающий из объема V в вакуумное пространство через отверстие, размер которого много меньше средней длины свободного пробега частиц газа. Газ в объеме V предполагается равновесным, толщиной стенок пренебрегаем, в струе газа, истекающей из отверстия, столкновениями пренебрегаем.

В общем случае такая задача оказывается шестимерной в фазовом пространстве и нестационарной [19–22]. С целью сокращения размерности задачи отверстие, через которое происходит утечка газа, берется в форме удлиненного прямоугольника. Соответствующие этой физической модели проблемы встречаются на практике в виде малых течей через трещины в обшивках летательных аппаратов и корпусах вакуумных камер.

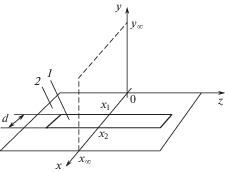
С учетом сдвиговой симметрии математическая модель задачи оказывается четырехмерной. В декартовой системе координат (рис. 1) функция распределения частиц газа зависит от четырех фазовых переменных ($x$, $y$, ${{{v}}_{x}}$, ${{{v}}_{y}}$) и времени t.

Рис. 1.

Расположение отверстия на плоскости (x, z). 1 – отверстие прямоугольной формы; 2 – элемент поверхности; ${{x}_{2}} - {{x}_{1}} = d$ – ширина отверстия.

В этом случае кинетическое уравнение (уравнение Власова) имеет вид [19–22]

(1)
$\frac{{\partial f}}{{\partial t}} + {{{v}}_{x}}\frac{{\partial f}}{{\partial x}} + {{{v}}_{y}}\frac{{\partial f}}{{\partial y}} = 0.$

Уравнение (1) решается при следующих начальных и граничных условиях: за начальный момент времени принимается момент образования щели. На срезе отверстия (граница “втекания”) функция распределения предполагается Максвелловской [24]

(2)
${{\left. f \right|}_{\begin{subarray}{l} {\text{граница}} \\ {\text{втекания}} \end{subarray} }} = \frac{{{{n}_{0}}}}{\pi }{{\left( {\frac{m}{{2kT}}} \right)}^{{3/2}}}\exp \left[ { - \frac{m}{{2kT}}({v}_{x}^{2} + {v}_{y}^{2})} \right],$
где ${{n}_{0}}$ – невозмущенная концентрация частиц газа в объеме V, m – масса молекул газа, T – температура, k – постоянная Больцмана.

Функция распределения f на срезе отверстия совпадает с (2) с учетом того, что по мере истечения газа из объема V концентрация частиц ${{n}_{0}}$ изменяется со временем.

На границе “вытекания” ставились “мягкие” граничные условия, получаемые путем экстраполяции функции распределения с прилегающих расчетных слоев.

Формулы для расчета средних скоростей частиц газа и их потоков имеют вид

(3)
$\left\langle {{{{v}}_{x}}} \right\rangle = \frac{{\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {{{{v}}_{x}}fd{{{v}}_{x}}d{{{v}}_{y}}} } }}{{\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {fd{{{v}}_{x}}d{{{v}}_{y}}} } }},\quad \left\langle {{{{v}}_{y}}} \right\rangle = \frac{{\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {{{{v}}_{y}}fd{{{v}}_{x}}d{{{v}}_{y}}} } }}{{\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {fd{{{v}}_{x}}d{{{v}}_{y}}} } }},$
(4)
${{J}_{{{\text{из}}\;{\text{отверстия}}}}} = {{\left( {\frac{{2kT}}{m}} \right)}^{{1/2}}}\int\limits_{{{x}_{1}}}^{{{x}_{2}}} {\int\limits_{ - \infty }^{ + \infty } {\int\limits_0^{ + \infty } {{{{\left. {{{{v}}_{y}}f({{{v}}_{x}},{{{v}}_{y}})} \right|}}_{\begin{subarray}{l} {\text{граница}} \\ {\text{втекания}} \end{subarray} }}} } } dxd{{{v}}_{x}}d{{{v}}_{y}},$
(5)
$\begin{gathered} {{J}_{{{\text{внешняя}}\;{\text{граница}}}}} = {{\left( {\frac{{2kT}}{m}} \right)}^{{1/2}}}\int\limits_0^{{{x}_{\infty }}} {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^0 {{{{v}}_{y}}f(t,x,{{y}_{0}},{{{v}}_{x}},{{{v}}_{y}})} } } dxd{{{v}}_{x}}d{{{v}}_{y}} + \\ + \;{{\left( {\frac{{2kT}}{m}} \right)}^{{\frac{1}{2}}}}\int\limits_0^{{{x}_{\infty }}} {\int\limits_{ - \infty }^{ + \infty } {\int\limits_0^{ + \infty } {{{{v}}_{y}}f(t,x,{{y}_{\infty }},{{{v}}_{x}},{{{v}}_{y}})} } } dxd{{{v}}_{x}}d{{{v}}_{y}} + \\ + \;{{\left( {\frac{{2kT}}{m}} \right)}^{{\frac{1}{2}}}}\int\limits_0^{{{y}_{\infty }}} {\int\limits_{ - \infty }^0 {\int\limits_{ - \infty }^{ + \infty } {{{{v}}_{y}}f(t,{{x}_{0}},y,{{{v}}_{x}},{{{v}}_{y}})} } } dyd{{{v}}_{x}}d{{{v}}_{y}} + \\ + \;{{\left( {\frac{{2kT}}{m}} \right)}^{{\frac{1}{2}}}}\int\limits_0^{{{y}_{\infty }}} {\int\limits_0^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {{{{v}}_{y}}f(t,{{x}_{\infty }},y,{{{v}}_{x}},{{{v}}_{y}})} } } dyd{{{v}}_{x}}d{{{v}}_{y}}. \\ \end{gathered} $

Математическая модель (1)–(5) приводилась к безразмерному виду с помощью системы масштабов: ${{M}_{n}} = {{n}_{\infty }}$ – масштаб концентраций; ${{M}_{L}} = d$ – масштаб длины; ${{M}_{V}} = {{\left( {2kT{\text{/}}m} \right)}^{{1/2}}}$ – масштаб скорости. Остальные масштабы выражаются через данные по формулам размерности.

Вычислительная модель задачи основана на методе последовательных итераций по времени, когда моделируется переходный процесс от начального к конечному стационарному состоянию, которое соответствует установлению параметров газа в расчетной области. При этом уравнение Власова (1) решается методом характеристик [23].

Алгоритм расчета реализован в виде компьютерной программы на языке С++ с использованием средств графической библиотеки Open GL. При этом были задействованы более миллиарда ячеек расчетной сетки (400 × 400 × 80 × 80). Область исследования струи имела размер 10 × 10 безразмерных единиц. Расчет на настольном компьютере (четырехъядерный процессор Intel Core i7-6700K, тактовая частота каждого ядра составляет 4 ГГц, оперативная память компьютера 32 Гб) продолжался 44 часа.

Контроль времени окончания счета (момента установления решения) осуществляется визуально с использованием графического окна, выводимого на экран монитора в режиме реального времени [24]. Визуально фиксировался момент, когда поток частиц, вытекающий из отверстия, становился равным потоку через внешние границы расчетной области (рис. 2).

Рис. 2.

Эволюция потока частиц газа через границы расчетной области. 1 – поток частиц газа, истекающий из отверстия в расчетную область; 2 – поток частиц газа, вытекающий из расчетной области.

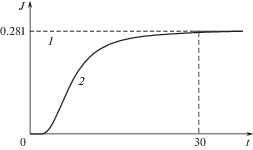
Это свидетельствовало о сохранении массы газа в расчетной области в установившемся стационарном состоянии при реализации вычислительного алгоритма.

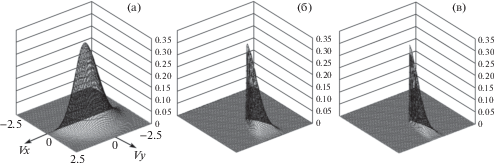
Результаты вычислительных экспериментов. На рис. 3 представлены функции распределения частиц истекающего из отверстия газа на различных расстояниях от отверстия на оси симметрии.

Рис. 3.

Зависимость функции распределения частиц газа от координаты y (x = 5; t = 30): (а) y = 0.025; (б) y = 1.5; (в) y = 3.

На рис. 4 для наглядности те же функции распределения представлены на плоскости (${{{v}}_{x}}$, ${{{v}}_{y}}$) в виде изолиний.

Рис. 4.

Изолинии функции распределения частиц газа в зависимости от координаты y (x = 5; t = 30): (а) y = 0.025; (б) y = 1.5; (в) y = 3.

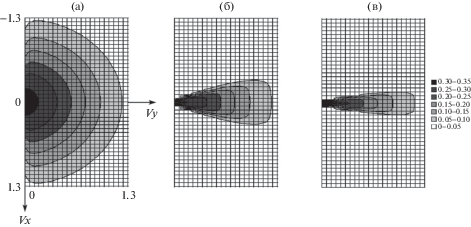
Из графиков следует, что функция распределения частиц газа деформируется с удалением от отверстия. Каждая последующая функция является частью предыдущей, что является следствием рассеяния струи. Таким образом, форма функции распределения зависит от взаимного расположения исследуемой точки и эффузионного отверстия.

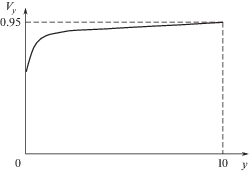
Изменение формы функции распределения при перемещении по оси y ведет к смещению ее “центра тяжести” в сторону увеличения составляющей ${{{v}}_{y}}$. В свою очередь смещение “центра тяжести” функции распределения ведет к увеличению средней скорости частиц в струе (рис. 5).

Рис. 5.

Зависимость средних скоростей частиц от координаты y вдоль оси симметрии струи (t = 30).

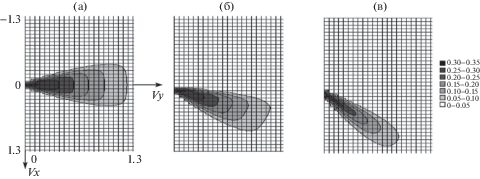
На рис. 6, 7 показана зависимость функции распределения частиц газа и ее изолиний от координаты x. Отчетливо просматривается рассеивание частиц газа с ростом координаты x. Если на оси симметрии струи (рис. 6а, 7а) средняя скорость частиц направлена по оси y, то с увеличением x угол поворота вектора средней скорости относительно оси симметрии струи увеличивается (рис. 6б, в; 7б, в).

Рис. 6.

Зависимость функции распределения частиц газа от координаты x (y = 1.5; t = 30): (а) x = 5; (б) x = 5.75; (в) x = 6.5.

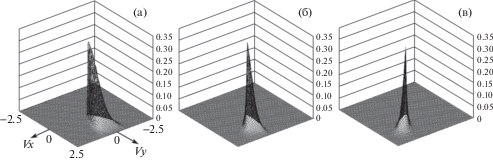
Рис. 7.

Изолинии функции распределения частиц газа в зависимости от координаты x (y = 1.5; t = 30): (а) x = 5; (б) x = 5.75; (в) x = 6.5.

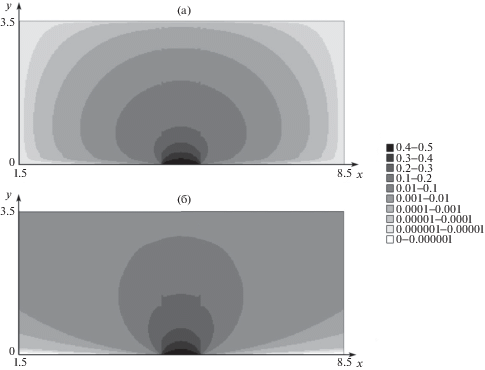
Перейдем теперь к рассмотрению моментов функции распределения. На рис. 8а, б приведено поле концентраций в расчетной области при t = 1.5 (начало эволюции) и в момент t = 30 (установившееся решение).

Рис. 8.

Изолинии концентраций частиц газа в расчетной области: (а) t = 1.5; (б) t = 30.

Распределение концентрации частиц газа вдоль оси симметрии струи приведено на рис. 9.

Рис. 9.

Эволюция распределения концентрации компонент газа по оси y (x = 5).

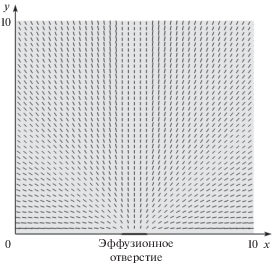
На рис. 10 дано поле скоростей частиц газа на момент установления решения. Поле скоростей имеет осевую симметрию. Из рис. 10 видно, что рассеяние струи усиливается к краям отверстия.

Рис. 10.

Поле скоростей частиц газа (t = 30).

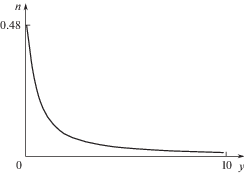
Уточнение граничного условия на срезе отверстия. Граничная функция распределения на срезе отверстия (2) содержит параметр ${{n}_{0}}$, соответствующий невозмущенной концентрации газа в объеме V. Этот параметр принят за масштаб концентрации, вследствие чего не входит в безразмерный вид уравнений. Для корректной интерпретации полученных результатов необходимо учитывать, что концентрация в объеме V вследствие эффузии уменьшается. Поэтому зависимость ${{n}_{0}}\left( t \right)$ является частью решения данной задачи.

Рассмотрим следующую модельную задачу. Имеется резервуар объемом V (например, жилой отсек космической станции), заполненный газом при нормальных условиях. На стенке резервуара образуется микротрещина площадью S, через которую начинает истекать газ. Считаем, что температура T газа в резервуаре постоянна и равновесное состояние газа со временем не нарушается вследствие малого размера микротрещины. Число частиц $\Delta N$ в объеме V, участвующих в хаотическом движении и пересекающих площадку S за интервал времени $\Delta t$ равно [25]

(6)
$\Delta N = \frac{1}{6}n\left\langle {v} \right\rangle S\Delta t.$

Если в момент времени $t = 0$ концентрация частиц ${{n}_{0}}$, то в момент времени $t = \Delta t$ концентрация равна ${{n}_{1}}$, в момент $t = 2\Delta t$ – ${{n}_{2}}$ и т.д. Элементарный расчет позволяет получить

$t = 0;\quad n = {{n}_{0}};$
$t = \Delta t;\quad n = {{n}_{1}} = {{n}_{0}}\left( {1 - \frac{{\left\langle {v} \right\rangle S}}{{6V}}\Delta t} \right);$
$t = 2\Delta t;\quad n = {{n}_{2}} = {{n}_{1}}\left( {1 - \frac{{\left\langle {v} \right\rangle S}}{{6V}}\Delta t} \right) = {{n}_{0}}{{\left( {1 - \frac{{\left\langle {v} \right\rangle S}}{{6V}}\Delta t} \right)}^{2}};$
$...$
$t = N\Delta t;\quad n = {{n}_{N}} = {{n}_{0}}{{\left( {1 - \frac{{\left\langle {v} \right\rangle S}}{{6V}}\Delta t} \right)}^{N}} = {{n}_{0}}{{\left( {1 - \frac{{\left\langle {v} \right\rangle S}}{{6V}}\Delta t} \right)}^{{\frac{t}{{\Delta t}}}}}.$

Итак,

(7)
$\frac{{n\left( t \right)}}{{{{n}_{0}}}} = {{\left( {1 - \frac{{\left\langle {v} \right\rangle S}}{{6V}}\Delta t} \right)}^{{\frac{t}{{\Delta t}}}}}.$

При этом должно выполняться неравенство $\frac{{\left\langle {v} \right\rangle S}}{{6V}}\Delta t < 1$, или $\Delta t < \frac{{6V}}{{\left\langle {v} \right\rangle S}}$.

Численные эксперименты показали, что расчет  $\frac{{n\left( t \right)}}{{{{n}_{0}}}}$ по формуле (7) практически не зависит от шага по времени $\Delta t$, если безразмерный шаг по времени

$\Delta {{t}_{{{\text{безразм}}}}} = \frac{{\Delta t}}{{{{M}_{t}}}} < {{10}^{{ - 2}}}.$

Еще один вывод зависимости ${{n}_{0}}\left( t \right)$ приведен в работе [6].

(8)
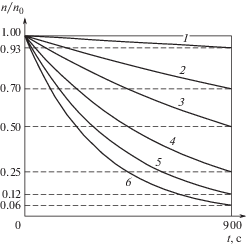
$\frac{{n\left( t \right)}}{{{{n}_{0}}}} = {{e}^{{ - \frac{1}{6}\left\langle {v} \right\rangle \frac{S}{V}t}}}.$

Расчет зависимости $\frac{{n\left( t \right)}}{{{{n}_{0}}}}$ по формулам (7) и (8) практически совпадает и приведен на рис. 11, при этом параметр S/V варьировался.

Рис. 11.

Зависимость концентрации в резервуаре от времени по формулам (7) и (8) (T  = 300 K; µ = 0.029 кг/моль; Δt = 1 с): 1 – S/V = 10–6 м–1; 2 – 5 × 10–6 м–1; 3 – 10–5 м–1; 4 – 2 × 10–5 м–1; 5 – 3 × 10–5 м–1; 6 – 4 × 10–5 м–1.

При исследовании эффузии методами математического моделирования установление решения в расчетной области наступает при времени расчета t = 30 единиц безразмерного времени. При ширине микротрещин d = 10–4 м [6]

(9)
${{t}_{{{\text{уст}}}}} = {{t}_{{{\text{безраз}}}}}{{M}_{t}} \approx 7.5 \times {{10}^{{ - 6}}}\;{\text{с}}.$

Из (7) и (9) следует, что изменение концентрации в резервуаре в результате эффузии за время установления решения незначительно и им можно пренебречь.

Заключение. Математическое моделирование эффузии разреженного газа в вакуумное пространство позволило получить функции распределения истекающих частиц. Исследована эволюция этих функций в процессе установления решения. Получена зависимость функции распределения от координат ($x$, $y$). Вычислены моменты функций распределения: поля концентраций частиц и их скоростей. Сравнение полученных данных с результатами работ [5] и [6] показало удовлетворительное согласование.

Приведенные результаты математического моделирования эффузии газа в вакуумное пространство могут быть полезны разработчикам портативных приборов диагностики малых течей, используемых в вакуумной промышленности и в космической технике. Разработанный оригинальный программный код, основанный на кинетическом подходе к решению эффузионных задач, который сопровождается компьютерной графикой, позволяющей получить наглядное представление об исследуемых физических явлениях, может быть полезен специалистам в области математического моделирования, а также в учебном процессе.

Список литературы

  1. Пономарева В.Л. Космонавтика в личном измерении. М.: Космоскоп, 2016. 386 с.

  2. Кубарев Ю.В. Полеты на Марс, электрореактивные двигатели настоящего и будущего // Наука и технологии в промышленности. 2006. № 2. С. 19.

  3. Дэшман С. Научные основы вакуумной техники. М.: Мир, 1964. 715 с.

  4. Саксаганский Г.Л. Молекулярные потоки в сложных вакуумных структурах. М.: Атомиздат, 1980. 216 с.

  5. Ананьин А.А., Занин А.Н., Семкин Н.Д. Моделирование процессов утечки газа из модуля космического аппарата // Измерительная техника. 2001. № 4. С. 29.

  6. Занин А.Н. Устройство регистрации места утечки воздуха из модуля космической станции: Дисс…. к.т.н. СГАУ, 2009. 185 с.

  7. Нестеров С.Б., Васильев Ю.И., Андросов А.В. Расчет сложных вакуумных систем. М.: МЭИ, 2001. 180 с.

  8. Нестеров С.Б., Асташина М.А., Незнамова Л.О., Васильев Ю.К. Задачи и методы исследования среды разреженного газа вблизи космического аппарата // Вакуумная техника и технология. 2007. Т. 18. № 3. С. 183.

  9. Асташина М.А. Молекулярные потоки в сложных объектах с учётом газовыделения поверхностей. Дисс…. к.т.н. М.: МЭИ, 2009. 156 с.

  10. Розанов Л.Н., Скрябнев А.Ю. Течение газа через круглый трубопровод при больших перепадах давления // Вакуумная техника и технология. 2010. Т. 20. № 1. С. 3.

  11. Скрябнев А.Ю. Вакуумметрический метод мониторинга герметичности крупных технических объектов. Дисс…. к.т.н. Санкт-Петербург. СПбГПУ, 2012. 146 с.

  12. Tang M.J., Cox R.A., Kalberer M. Compilation and evaluation of gas phase diffusion coefficients ofreactive trace gases in the atmosphere: v. 1. Inorganiccompounds // Atmos. Chem. Phys. 2014. № 14. P. 9233.

  13. Krewinkel R. A review of gas turbine effusion cooling studies // International Journal of Heat and Mass Transfer. 2013. V. 66. P. 706.

  14. Schumacher J.C., Zupanc F.J. Rodolphe Dudebout Segmented effusion cooled gas turbine engine combustor // US Patent US7546737B2, 2006.

  15. Wahlbeck P.G. Effusion. VII. The Failure of Isotropy of a Gas in an Effusion Cell and the Transition Region // J. Chem. Phys. 2003. V. 55. № 1709 (1971).

  16. Malhotra M., Kumar S. Thermal gas effusion from diamond-like carbon films // Diamond and Related Materials, 1997. V. 6. Iss. 12. P. 1830.

  17. Bronson T.J., Zupanc F.J., Yankowich P., Rudrapatna N. Effusion cooled dual wall gas turbine combustors // US Patent US9897320B2, 2010.

  18. Iczkowski R.P., Margrave J.L., Robinson S.M. Effusion of Gases through Conical Orifices // J. Phys. Chem. 1963. № 67. 2. P. 229.

  19. Котельников В.А., Ульданов С.В., Котельников М.В. Процессы переноса в пристеночных слоях плазмы. М.: Наука, 2004. 422 с.

  20. Котельников В.А., Котельников М.В., Гидаспов В.Ю. Математическое моделирование обтекания тел потоками столкновительной и бесстолкновительной плазмы. М.: Физматлит, 2010. 266 с.

  21. Котельников М.В., Котельников В.А., Морозов А.В. Математическое моделирование взаимодействия потока разреженной плазмы с поперечным магнитным полем. М.: Издательство МАИ, 2015. 170 с.

  22. Котельников В.А., Гурина Т.А., Демков В.П., Попов Г.А. Математическое моделирование электродинамики летательного аппарата в разреженной плазме. М.: Изд-во Нац. Акад. Прикл. Наук РФ, 1999. 255 с.

  23. Котельников М.В., Котельников В.А. Усовершенствованный метод характеристик // Математическое моделирование. 2017. Т. 29. № 5. С. 85.

  24. Котельников М.В., Нгуен Суан Тхау. Методика использования компьютерной графики в вычислительных экспериментах // Электронный журнал “Труды МАИ”. 2011. № 53.

  25. Савельев И.В. Курс физики. М.: Наука, главная редакция физ. мат. Литературы. 1989. Т. 1. 352 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал