Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 3, стр. 77-83
Угловое распределение пучка заряженных частиц при многократном рассеянии в веществе
Н. Н. Михеев *
Институт кристаллографии им. А.В. Шубникова
ФНИЦ “Кристаллография и фотоника” РАН
248640 Москва, Россия
* E-mail: kmikran@spark-mail.ru
Поступила в редакцию 26.06.2019
После доработки 17.07.2019
Принята к публикации 17.07.2019
Аннотация
На основе полученного ранее решения транспортного уравнения впервые проведено аналитическое описание спектральных распределений по углу для заряженных частиц моноэнергетического пучка после многократного рассеяния в веществе. Получена новая универсальная функция двумерного распределения по углу для заряженных частиц при нормальном падении пучка на поверхность образца, а также новые формулы для расчета наиболее вероятного угла отклонения для частиц, прошедших пленку вещества заданной толщины. Учтено влияние поверхности мишени на регистрируемые спектры выходящих из пленки частиц. Приведены результаты всесторонней проверки полученных соотношений на основе сопоставления модельных расчетов угловых распределений с экспериментальными спектрами электронов и протонов, взятыми из научных публикаций.
ВВЕДЕНИЕ
Для современных нано-технологий и большого числа количественных методов локальных исследований, которые используют электронные и ионные пучки, распределение заряженных частиц, прошедших пленку вещества, по углу является одной из важнейших характеристик, определяющих возможности проведения контролируемого технологического воздействия на материал и возможности изучения свойств материала с высоким пространственным разрешением. Задача по расчету таких спектральных распределений решалась и решается либо на основе выбора подходящей аппроксимирующей функции [1], либо с применением различных моделей кратного и многократного рассеяния [2–5], а также с использованием метода Монте-Карло [6]. Все эти подходы, в целом, как показано в работе [6], приводят к весьма близким друг другу результатам, рассчитываемым угловым распределениям. В тоже время истинные распределения угловых отклонений при многократном рассеянии заряженных частиц во всей области регистрации углов несколько отличаются от рассчитываемых. При угловых отклонениях, превышающих величину полной ширины углового распределения на половине максимума, истинное распределение идет выше рассчитываемых. Это отмечалось еще Р. Штернхеймером [7], и сохраняется поныне. Другой недостаток связан с отсутствием единого системного подхода при нахождении и расчете базового параметра угловых распределений – угла наиболее вероятного отклонения θp частиц, прошедших пленку: формул много, но точность их не велика, и они не обеспечивают нужного соответствия результатам, получаемым непосредственно из измерений θp по экспериментальным спектрам.
В данной работе представлены результаты использования статистической модели многократного рассеяния работ [8–12] для описания двумерного распределения заряженных частиц моноэнергетического пучка по углу их отклонения θ от начального направления после прохождения пленки вещества заданной толщины и при нормальном падении на поверхность образца. Получена новая универсальная функция F(θ, θp) для углового распределения прошедших частиц, а также новые формулы для расчета наиболее вероятного угла отклонения θp легких частиц (электронов) и тяжелых (протонов). Приводятся результаты всесторонней проверки полученных соотношений на основе сопоставления проведенных модельных расчетов угловых распределений с экспериментальными спектрами угловых отклонений электронов и протонов, взятых из научных публикаций.
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ F(θ, θp) ЗАРЯЖЕННЫХ ЧАСТИЦ
В работе [10] при решении одномерного транспортного уравнения впервые была учтена зависимость дифференциального сечения неупругого рассеяния частиц от числа испытанных ими неупругих взаимодействий. Также было получено решение транспортного уравнения F(ΔE, ΔEp), в котором более полно учтена статистика дискретного процесса многократного рассеяния для пучка частиц. Соответствующее распределение электронов пучка с начальной энергией E0 по потерянной энергии: ΔE = E0 – E и при наиболее вероятной потере энергии ΔEp = E0 – Ep имеет вид:
(1)
$\begin{gathered} F(\Delta {{E}_{p}},u) = \\ = A\exp \left\{ { - \frac{{b\Delta {{E}_{p}}}}{{0.125{{E}_{0}}}}\exp \left[ { - \int\limits_{{{u}_{{\min }}}}^u {\frac{{dk}}{{0.5\ln k + 1 - k}}} } \right]} \right\}, \\ \end{gathered} $В отличие от функции распределения потерь энергии Ландау [13] функция (1) имеет два первых приближенных решения, которые представимы через элементарные функции. После разложения ln k в ряд Грегори и последующего учета вклада только первого члена разложения мы получаем функцию первого приближения решения (1) в виде:
(2)
${{F}_{1}}\left( {\Delta {{E}_{p}},\Delta E} \right) = {{A}_{1}}\exp \left\{ { - \frac{{b{{{\left( {\Delta E - \Delta {{E}_{p}}} \right)}}^{2}}}}{{0.125{{E}_{0}}\Delta E}}} \right\}.$Если абстрагироваться от конкретной переменной ΔE и перейти к любой монотонно изменяющейся переменной, которую обозначим ε, то выражение (2) может быть записано как
(3)
$F\left( {\varepsilon ,{{\varepsilon }_{p}}} \right) = A\exp \left[ { - \frac{{{{{\left( {\varepsilon - {{\varepsilon }_{p}}} \right)}}^{2}}}}{{K\varepsilon }}} \right],$Эта функция представляет распределение частиц по переменной ε и описывает результат многократно повторяющего процесса через вероятность отклонения переменной ε от своего наиболее вероятного значения εp.
В случае многократного рассеяния заряженных частиц пучка при транспорте через пленочную мишень и при нормальном падении на поверхность образца распределение частиц F(θ, φ) в пространстве зависит только от полярного угла θ и не зависит от азимутального угла φ. Как следствие, экспериментально регистрируемое распределение частиц строго симметрично относительно первоначального направления движения частиц. Это позволяет применить функцию (3) для описания двумерного процесса многократного рассеяния. Пусть θ – угловое отклонение частицы от первоначального направления пучка после прохождения пленки известной толщины x. Тогда функция F(θ, θp) может быть получена из (3) введением новой переменной θ = (ε – εp), а также введением в знаменатель показателя экспоненты величины (θ + θp) вместо (θ + εp):
(4)
$\begin{gathered} F\left( {\theta ,{{\theta }_{p}}} \right) = \frac{{dN}}{{d\Omega }} = \frac{{dN}}{{2\pi \sin \theta d\theta }} = \\ = A\exp \left[ { - \frac{{{{\theta }^{2}}}}{{K\left( {\theta + {{\theta }_{p}}} \right)}}} \right]. \\ \end{gathered} $(5)
$\begin{gathered} F\left( {\theta ,{{\theta }_{p}}} \right) = \frac{{dN}}{{d\Omega }} = \frac{{dN}}{{2\pi \theta d\theta }} = \\ = A\exp \left[ { - \frac{{{{\theta }^{2}}}}{{0.75{{\theta }_{p}}\left( {\theta + {{\theta }_{p}}} \right)}}} \right]. \\ \end{gathered} $(6)
${\text{Г}} = {{\left( {4\ln 2 \times 1.5 \times \theta _{p}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = 2.039{{\theta }_{p}} \approx 2{{\theta }_{p}}.$Другой важный момент, который необходимо учитывать при расширении диапазона угловых отклонений заряженных частиц, это зависимость вероятности выхода частицы из пленки от величины суммарного углового отклонения θ, которое частица приобрела в процессе многократного рассеяния в мишени. Как показано в работе [8], это может быть достигнуто путем учета угловой зависимости коэффициента пропускания Ф(ξ) поверхности мишени для частиц, выходящих из пленки, и реализуется простым добавлением его сомножителем в выражение (5). Окончательно имеем:
(7)
$\begin{gathered} F\left( {\theta ,{{\theta }_{p}}} \right) = \frac{{dN}}{{d\Omega }} = \frac{{dN}}{{2\pi \sin \theta d\theta }} = \\ = {{A}_{N}}\exp \left[ { - \frac{{{{\theta }^{2}}}}{{0.75{{\theta }_{p}}\left( {\theta + {{\theta }_{p}}} \right)}}} \right]\Phi \left( \xi \right), \\ \end{gathered} $ЗАВИСИМОСТЬ θp ОТ ТОЛЩИНЫ ПЛЕНОЧНОЙ МИШЕНИ
Во многих физических приложениях теории столкновений в качестве величины, характеризующей рассеяние заряженных частиц, фигурирует интеграл:
который называется транспортным сечением. Данный интеграл представляет собой усредненное по всем возможным угловым отклонениям сечение взаимодействия первичных частиц с веществом. Для расчета транспортных сечений по упругому каналу рассеяния электронов в данной работе использовались результаты работы [15], а для протонов – результаты работы [16]. Для расчета транспортных сечений по неупругому каналу рассеяния электронов использовались результаты работы [17].В случае малоуглового рассеяния частиц в материале с числом атомов в единице объема N0 из-за независимости результата усреднения от азимута φ:
(9)
${{\theta }_{p}} = \frac{\pi }{4}\frac{x}{{{{L}_{{{\text{tr}}}}}}},\,\,{\text{при}}\,\,x < {{L}_{{{\text{tr}}}}}\,\,{\text{и}}\,\,{{\theta }_{p}} = \frac{\pi }{4}\,\,{\text{при}}\,\,x \geqslant {{L}_{{{\text{tr}}}}}.$(10)
${{R}_{p}} = \frac{{\frac{{{{m}_{e}}}}{{{{M}_{p}}}}E_{0}^{2}}}{{4\pi {{q}^{4}}{{N}_{0}}Z\frac{1}{{{{{\left( {1 - {{\beta }^{2}}} \right)}}^{{\frac{1}{2}}}}}}\ln \left\{ {\frac{{2{{m}_{e}}V_{0}^{2}}}{{J{{{\left( {1 - {{\beta }^{2}}} \right)}}^{{\frac{1}{4}}}}}}} \right\}F_{M}^{N}}},$ПРОВЕРКА СООТВЕТСТВИЯ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТАЛЬНЫМ СПЕКТРАМ
Всесторонняя проверка полученных аналитических соотношений проведена на основе сопоставления выполненных модельных расчетов угловых распределений F(θ, θp) и f(θ, θp) = 2π sin θF(θ, θp) с экспериментальными спектрами угловых отклонений протонов и электронов, взятыми из известных научных публикаций [14, 19–21]. Представлен достаточно широкий набор материалов (от алюминия до золота) и диапазон энергий E0 пучков протонов (от 30 кэВ до 10.3 МэВ). Результаты приведены на рис. 1–5. На рис. 1 представлены результаты использования полученного в данной работе распределения (7) и формулы (11) при расчете углового распределения пучка протонов с E0 = 50 кэВ, прошедших пленку никеля известной толщины. Видно, что обеспечивается адекватное соответствие расчетов и эксперимента во всем регистрируемом угловом диапазоне. Для сравнения возможностей различных подходов при описании одного и того же экспериментального спектра угловых отклонений протонов, прошедших мишень известной толщины, на рис. 2 приведены данные, полученные из работы [6], и представляющие рассчитанные угловые распределения для таких же протонов и такой же мишени, но по методикам многократного рассеяния и методу Монте-Карло. Видно, что наблюдается хорошее соответствие расчетов и моделирования друг другу, но заметное отличие их от экспериментального спектра, в том числе и по углу θp. На рис. 3, 4 для сравнения с рассчитанными функциями F(θ, θp) пунктирными линиями изображены угловые распределения, соответствующие функции Гаусса, с θp, аналогичным использованным при расчетах функции углового распределения (6). Наглядно видно, насколько хорошо используемое при выводе функции распределения (7) решение транспортного уравнения передает особенности физики дискретного процесса многократного рассеяния. А именно: с ростом числа испытанных частицами взаимодействий происходит монотонное возрастание статистической вероятности для них быть рассеянными на больший угол.
Рис. 1.
Угловое распределение пучка протонов с E0 = = 50 кэВ, прошедших пленку никеля толщиной 0.0225 мкм (Ltr = 1.334 мкм, Rp = 0.31 мкм, $\theta _{p}^{{{\text{calc}}}}$ = = 3.27°, $\theta _{p}^{{\exp }}$ = 3.33°): сплошная линия – расчет по полученным формулам, ⚪ – эксперимент работы [21].

Рис. 2.
Угловые распределения пучка протонов с E0 = = 50 кэВ, прошедших пленку никеля толщиной 0.0225 мкм. Взяты из работы [6] и представляют собой рассчитанные угловые распределения по методикам многократного рассеяния и методу Монте-Карло: сплошная линия – расчет по методике многократного рассеяния работы [5], ⚪ – расчет методом Монте-Карло работы [6], ∆ – расчет по методике многократного рассеяния работы [4], ⚫ – эксперимент работы [21].
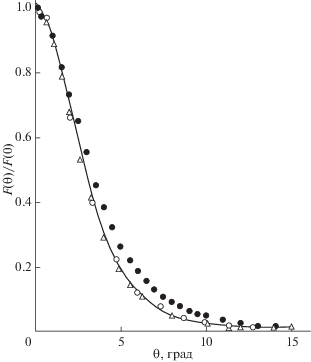
Рис. 3.
Угловое распределение пучка протонов с E0 = = 30 кэВ, прошедших пленку золота толщиной 300 Å (Rp = 0.169 мкм, θp ≈ 8°): сплошная линия – расчет по полученным формулам; пунктир – функция Гаусса; ⚪ – эксперимент работы [20].
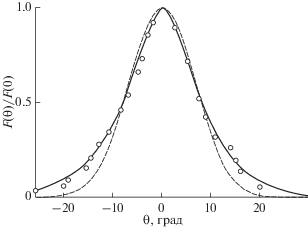
Рис. 4.
Угловое распределение пучка протонов с E0 = = 10.3 МэВ, прошедших пленку кремния толщиной 0.91 мкм в режиме “Random” (Ltr = 1.54 см; Rp = = 0.0744 cм; $\theta _{p}^{{{\text{calc}}}}$ = 0.055°; $\theta _{p}^{{\exp }}$ = 0.057°): сплошная линия – расчет по полученным формулам; пунктир – функция Гаусса; ⚪ – эксперимент работы [19].
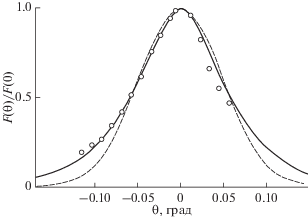
Рис. 5.
Угловое распределение пучка электронов с энергией 20 кэВ, прошедших пленку алюминия толщиной x = 1.79 мкм (Ltr = 1.69 мкм; $\theta _{p}^{{{\text{calc}}}}$ = 45°): сплошные линии, пунктир и штрих пунктир – расчеты функций F(θ, θp) и f(θ,θp) = 2π sin θF(θ,θp) по формулам данной работы; ⚪ – экспериментальные результаты из работы [14].
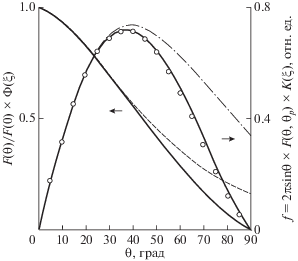
И наконец, рис. 5 приведен для того, чтобы проиллюстрировать выше сказанное о том, почему максимальное значение параметра $\theta _{p}^{{\exp }}$ угловых распределений электронов, измеренное на толстых пленочных мишенях (x > Ltr) и равное ≈38° [14], всегда меньше расчетного максимального значения θp = 45°, используемого в данной работе. На данном рисунке рассчитанные значения распределения F(θ)/F(0) в объеме пленки изображены пунктирной линией, а значения распределения F(θ)/F(0) электронов, вышедших из пленки, сплошной линией. Видно, что учет влияния угловой зависимости коэффициента пропускания Ф(ξ) на F(θ)/F(0) уменьшает θp углового распределения примерно на 1.5°. В то же время по определению и по способу измерения $\theta _{p}^{{\exp }}$ является угловым отклонением, при котором функция f = 2π sin θF(θ, θp) достигает своего максимального значения. В виду того, что в данном случае процесс многократного рассеяния не является малоугловым и sin θ < θ, то более быстрое уменьшение f с ростом угла θ приводит к смещению углового положения максимума функции в сторону меньших углов. На рис. 5 распределение f в объеме пленки изображено штрихпунктирной линией, а распределение f электронов, вышедших из пленки, сплошной линией. Итоговый результат выполненных расчетов: максимальное значение распределения f пучка электронов, вышедших из пленки, реализуется при θ = 37.5°. Открытыми кружками на рис. 5 представлены экспериментально измеренные значения функции f, взятые из работы [14]. Очевидно, что наблюдается хорошее согласие расчетов, выполненных на основе полученных распределений и формул, с экспериментальными спектрами угловых отклонений электронов.
ЗАКЛЮЧЕНИЕ
В результате использования статистической модели многократного рассеяния и решения транспортного уравнения получена новая функция, описывающая угловое распределение заряженных частиц после прохождения ими пленки вещества заданной толщины при нормальном падении моноэнергетического пучка на поверхность образца. Определены формулы для расчета базового параметра угловых распределений – наиболее вероятного угла отклонения легких (электроны) и тяжелых (протоны) частиц. Учтено влияние поверхности образца на распределение угловых отклонений, выходящих из образца заряженных частиц. Проведенная проверка полученных соотношений показала исключительно хорошее соответствие между выполненными модельными расчетами и экспериментальными результатами, полученными из научных публикаций, во всем регистрируемом диапазоне угловых отклонений.
Список литературы
Bothe W. // Hand. Phys. 1933. B. 22. S. 1.
Bethe H.A., Rose M.E., Smith L.P. // Proc. Amer. Phil. Soc. 1938. V. 78. P. 573.
Moliere G. // Z. Naturf. 1947. B. 2a. S. 133.
Gouldsmit S., Saunderson J. // Phys. Rev. 1940. V. 57. P. 24.
Meyer L. // Phys. Stat. Sol. (b). 1971. V. 44. P. 253.
Möller W., Pospiech G., Schrieder G. // Nuclear Instruments and Methods. 1975. V. 130. P. 265.
Штернхеймер Р. Принципы и методы регистрации элементарных частиц, / под ред. Арцимовича Л.А., М.: Издательство иностранной литературы, 1963. С. 9.
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 1998. № 10. С. 37.
Михеев Н.Н. // Известия РАН. Серия физическая. 2000. Т. 64. № 11. С. 2137.
Михеев Н.Н., Степович М.А., Юдина С.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2009. № 3. С. 53.
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2010. № 4. С. 25.
Михеев Н.Н., Колесник А.С. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 12. С. 88. https://doi.org/10.7868/S0207352817120083
Ландау Л.Д. Собрание трудов. М.: Наука, 1969. Т. 1. С. 482.
Cosslett V.E., Thomas R.N. // Brit. J. Appl. Phys. 1964. V. 15. P. 883.
Тилинин И.С. // ЖЭТФ. 1988. Т. 94. С. 96.
Тилинин И.С. // Поверхность. Физика, химия, механика. 1991. № 9. С. 109.
Михеев Н.Н., Степович М.А., Широкова Е.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2013. № 12. С. 84. https://doi.org/10.7868/S0207352813120123
Бедняков А.А., Жукова Ю.Н., Иферов Г.А., Чернов В.Л. // ЖЭТФ. 1976. Т. 70. С. 427.
Cano G.L. // J. Appl. Phys. 1972. V. 43. № 4. P. 1504.
Ведьманов Г.Д., Лазарев Ю.Г., Николайчук Л.И., Радченко В.И., Хижняк Н.А. // Известия РАН. Серия физическая. 1995. Т. 59. № 10. С. 141.
Schäffler H.G. // Dissertation IPP 9/14. Institute fur Plasmaphysik. Garching b. Műnchen. 1971.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


