Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 5, стр. 3-12
Применение метода фазово-амплитудных функций в рентгеновской и нейтронной рефлектометрии
Ю. А. Саламатов a, *, Е. А. Кравцов a, b, **
a Институт физики металлов им. М.Н. Михеева УрО РАН
620137 Екатеринбург, Россия
b Уральский федеральный университет им. Б.Н. Ельцина
620002 Екатеринбург, Россия
* E-mail: salamatov@imp.uran.ru
** E-mail: kravtsov@imp.uran.ru
Поступила в редакцию 22.07.2020
После доработки 18.09.2020
Принята к публикации 22.09.2020
Аннотация
Рассмотрено применение метода фазово-амплитудных функций для расчета рефлектограмм, получаемых при отражении нейтронов или рентгеновских лучей от планарных наноструктур. Описаны несколько приближений и подстановок, которые могут быть полезны для различных задач. Показано, что данным методом можно рассчитывать рефлектометрические кривые с меньшими вычислительными затратами, чем в других подходах. Приведено сравнение модельных численных результатов для различных алгоритмов. Для решения обратной задачи и восстановления потенциала рассеяния металлической пленки по экспериментальной интенсивности отражения применен алгоритм Левенберга-Марквардта. Представлены экспериментальные результаты для двух систем: пленки Al2O3//Cr(200 Å) и металлической сверхрешетки Al2O3//Cr(100 Å)/[Gd(50 Å)/Cr(11 Å)]6/ Cr(100 Å). Полученные потенциалы рассеяния позволяют сделать выводы о слоистых структурах образцов и определить их зависимость от условий роста.
ВВЕДЕНИЕ
Рентгеновская и нейтронная рефлектометрия представляет собой удобный и точный метод определения структуры тонких наноразмерных пленок и сверхрешеток. Она основана на измерении коэффициента зеркального отражения фотонов или нейтронов, падающих на образец под скользящими углами падения. Для типичных длин волн (единицы ангстрем) эти углы достаточно малы – не превышают 10° относительно поверхности. Особенно активно рефлектометрия применяется для изучения металлических многослойных наноструктур, обладающих необычными электрическими и магнитными свойствами и составляющих элементную базу квантовой наноспинтроники. Рефлектометрия позволяет определить такие характеристики, как толщины и плотности слоев отдельных элементов и сплавов, вид переходных областей между слоями, шероховатость поверхности и межслойных границ. Рефлектометрия является неразрушающим методом и никак не изменяет свойства образца. Все это обусловило довольно широкое применение данного подхода как в фундаментальных исследованиях свойств многослойных пленок, так и для текущей аттестации качества изготавливаемых образцов.
Математическая обработка рефлектометрического эксперимента заключается в анализе зависимости интенсивности зеркального отражения рентгеновских лучей от величины изменения волнового вектора. Углы падения, в отличие от углов падения при дифракции, очень малы – примерно 0°–5° относительно поверхности образца (для наиболее широко используемых длин волн 1–10 Å). Такие углы часто называют углами скольжения. Малость углов скольжения приводит к тому, что показатель преломления рентгеновских лучей, хоть он и отличается от единицы на величину порядка 10–5, начинает играть заметную роль и полностью определяет наблюдаемую картину интенсивности отражения.
Следует отметить, что показатель преломления для рентгеновских лучей и нейтронов меньше единицы, что означает, что воздух или вакуум оказываются оптически более плотными средами, чем материал образца. Это приводит к явлению полного внешнего отражения, когда ниже некоторого угла, называемого критическим, лучи почти полностью отражаются от поверхности. Коэффициент отражения в этой области примерно равен единице. Слабое проникновение первичного пучка в образец все же есть, это обусловлено ненулевой мнимой частью потенциала взаимодействия, который линейно связан с квадратом показателя преломления.
Зависимость показателя преломления от глубины проникновения в образец описывает структуру многослойной пленки. Зная эту функцию, можно определить последовательность слоев в пленке, их оптические характеристики, толщины и плотность, характер межслойного перемешивания. Для удобства чаще ищут не показатель преломления, а непосредственно численные значения указанных параметров. Эти значения позволяют при необходимости построить показатель преломления как функцию глубины. Минус данного подхода заключается в том, что особенности, не учтенные в слоистой модели пленки, не будут корректно определены. Показатель преломления позволяет описать любую структуру, не обязательно слоистую.
Существует несколько способов расчета интенсивности отражения по известному показателю преломления или набору параметров слоев. Абеле [1] связал эти величины с коэффициентами отражения и прохождения посредством оптических матриц размерности 2 × 2, которые рассчитываются для каждого слоя, затем перемножаются между собой, и из полной оптической матрицы определяются искомые коэффициенты. Если показатель преломления изменяется непрерывно, то образец разбивается на множество слоев, достаточно тонких, для того чтобы считать показатель преломления постоянным в пределах одного слоя. Соответственно, увеличивается количество оптических матриц, и существенно возрастают вычислительные затраты.
Парратт [2] предложил рекуррентные соотношения, которые позволяют последовательно рассчитать коэффициенты отражения и прохождения для всех слоев и для полной структуры. Здесь также используется разбиение образца на тонкие слои с постоянным показателем преломления. Поэтому алгоритм тоже требует много вычислительного времени в случае большого количества слоев.
Подходы Абеле и Парратта дают точное решение задачи рефлектометрии во всем диапазоне углов. Они относятся к динамической теории рассеяния и учитывают взаимодействие отраженной волны с атомами пленки, так называемое многократное рассеяние. Это явление особенно существенно вблизи области полного внешнего отражения, т.е. при углах, близких к критическому. В динамической теории рассеяния показатель преломления и интенсивность рассеяния связаны нелинейными соотношениями, поэтому алгоритмы Абеле и Парратта не допускают простого обращения. Обратная задача решается различными методами оптимизации.
Если достаточно рассмотреть отражение вдали от критического угла, можно применить кинематическую теорию, которая не учитывает многократное рассеяние [3, 4]. Его рассматривают как возмущение и считают малым по сравнению с амплитудой падающей волны. По сути кинематическая теория является первым порядком теории возмущений, поэтому ее иногда называют борновским приближением в рефлектометрии. Для кинематической теории предложено несколько корректировок и более сложных аппроксимаций, которые существенно улучшают ее точность вблизи критического угла [4]. Подробное описание этих аппроксимаций, пределов их применимости и связи с точным решением в динамической теории можно найти в [3] и более широком обзоре [5]. Там же рассматриваются причины нелинейности уравнений динамической теории и условия, когда этой нелинейностью можно пренебречь, упростив расчеты.
Кинематическое приближение сводится к линейному интегральному уравнению Фредгольма первого рода, которое может быть решено путем прямого обращения интегрального оператора, при необходимости можно использовать методы регуляризации [6]. Таким образом, в кинематической теории возможно полностью модельно-независимое решение, но, к сожалению, не все ее модификации допускают обращение интегрального оператора. Кинематическое приближение может быть использовано только вдали от области полного внешнего отражения, но там коэффициенты отражения для различных потенциалов могут быть очень близки и практически неразличимы. Из-за этого иногда невозможно однозначно интерпретировать решение, полученное в рамках кинематического подхода.
В настоящей работе рассматривается метод расчета интенсивности отражения в рефлектометрии, основанный на использовании фазово-амплитудных функций [7, 8]. Он заключается в решении нелинейного дифференциального уравнения первого порядка для коэффициента отражения. Такой подход требует меньше вычислительных ресурсов, чем матричный формализм Абеле и рекуррентные соотношения Парратта. Уравнение точное, оно соответствует динамической теории. Рассмотрены несколько приближений и подстановок, которые могут быть полезны в различных ситуациях. Показано, что метод оказывается достаточно эффективным для анализа экспериментальных данных рентгеновской рефлектометрии и позволяет получить зависимость показателя преломления от глубины как для простой, так и для более сложной многослойной системы – сверхрешетки. Уравнение для использования в нейтронной рефлектометрии аналогично и отличается только видом потенциала рассеяния.
ТЕОРИЯ МЕТОДА
В основе метода лежит представление о так называемой фазовой функции $\alpha (r),$ которая имеет простой и наглядный физический смысл [7]. При заданном центральном потенциале значение этой функции в некоторой точке r является фазой рассеяния на части потенциального барьера, заключенного в сфере радиуса r. Фаза рассеяния $\alpha $ на всем потенциальном барьере определяется как предел $\alpha = \mathop {\lim }\limits_{r \to \infty } \alpha (r).$ Фазовая функция удовлетворяет дифференциальному уравнению Риккати, которое называется фазовым уравнением. Фазовая функция характеризует эффект действия потенциала и равна нулю, если равен нулю потенциал.
Задача описания отражения рентгеновских лучей от металлических пленок представляет собой вариант одномерной задачи о взаимодействии частицы (нейтрона или рентгеновского фотона) с потенциальным барьером (ядерной или электронной структурой отражающего слоя). Волновое уравнение в этом случае имеет вид (в случае рентгеновских лучей волновая функция имеет смысл напряженности электрического поля $E(x)$):
Волновая функция представляется в виде суперпозиции падающей и отраженной волн:(2)
$\psi (x) = A(x)\left[ {{\text{exp(}}ikx{\text{)}} + B(x){\text{exp(}}{\kern 1pt} - {\kern 1pt} ikx{\text{)}}} \right].$(3)
$\begin{gathered} \frac{d}{{dx}}B(x) = \\ = - \frac{1}{{2ik}}V(x){{\left[ {{\text{exp(}}ikx{\text{)}} + B(x){\text{exp(}}{\kern 1pt} - {\kern 1pt} ikx{\text{)}}} \right]}^{2}}. \\ \end{gathered} $Описанный выше подход к решению задачи одномерного прохождения через барьер иногда называется методом амплитудных функций [9]. В указанной работе также получено уравнение, аналогичное (3), и предложено использовать метод Рунге-Кутты для его численного решения. Рассматривается применение к задачам рассеяния нуклонов на ядрах атомов, и анализируются теоретические задачи с потенциалами различных видов.
Фазовое уравнение (3) довольно широко применяют в самых разнообразных теоретических и прикладных задачах квантовой механики. В [10, 11] использован иной вид фазового уравнения, с логарифмической производной показателя преломления и эйконалом. В этом случае несколько упрощается поиск аналитических решений для ряда задач оптики, в основном с нормальным падением луча на слоистую среду. Авторы [12] в достаточно общем виде обсуждают возможность сведения уравнения Шредингера (1) к уравнению Риккати и находят собственные значения и векторы для различных потенциалов. Уравнение (3) также может быть сведено к форме уравнения Риккати. Данное уравнение может быть использовано в случае нелокальных потенциалов и потенциалов, зависящих от импульса [7]. Метод позволяет решать задачи поиска стационарных и квазистационарных состояний (мнимые значения $k$) и туннелирования (например, при проводимости квантовых нитей) [13]. Та же группа авторов [14], рассматривая нелокальные потенциалы, приводит (3) к интегро-дифференциальному уравнению Вольтерры первого рода для амплитуды рассеяния и применяет его для поиска стационарных состояний в нейтральном атоме водорода и его отрицательном ионе.
К фазовому уравнению можно также прийти, начиная не с уравнения Шредингера, а с рекуррентных соотношений для амплитуд прохождения и отражения [15]. Потенциал для этого разбивается на малые интервалы. Тогда коэффициент отражения можно представить в виде бесконечной дроби. Если уменьшить длину интервалов разбиения до нуля, то рекуррентные соотношения в пределе переходят в уравнение Риккати, аналогичное (3). Другие авторы [16] комбинируют радиальное уравнение Шредингера и выражение для логарифмической производной волновой функции, получая уравнение Риккати. Затем, используя метод вариации постоянных, выводят фазовое уравнение, аналогичное (3). В [17] эти же авторы получают фазовые уравнения уже в рамках суперсимметричной квантовой механики.
Довольно глубокой связи между уравнением Шредингера, фазовым уравнением и уравнением Риккати посвящены отдельные работы (например, [18]), в которых свойства этих уравнений рассматривают с математической точки зрения. Этой связи придают даже несколько философский смысл. Так, в [19] утверждают, что есть некоторое противоречие между описанием явлений макромира, которым соответствуют преимущественно нелинейные уравнения, и квантового микромира, основным уравнением которого является линейное уравнение Шредингера. Но последнее может быть сведено к нелинейному квадратичному уравнению Риккати, что позволяет связать две теории. У этой связи есть свои плюсы. Во-первых, уравнение Риккати допускает линеаризацию, что позволяет получить аналог принципа суперпозиции, важного для квантовой механики. Во-вторых, нелинейные уравнения часто бывают более наглядными, чем линейные, и отражают сильную зависимость решения от начальных условий. В-третьих, как уже было сказано выше, уравнения первого порядка, даже нелинейные, решаются проще, чем уравнения второго порядка. Все это свидетельствует о большой значимости нелинейных уравнений типа (3), как для теоретического анализа явлений, так и для практических расчетов. В [19] показана связь уравнения Риккати со многими физическими системами, как квантовыми, так и классическими. Автор применяет его даже к достаточно экзотическим задачам, типа поиска пифагоровых троек и космологического поведения Вселенной.
Таким образом, настоящая работа призвана дополнить этот широкий спектр исследований, посвященный фазовому уравнению и его представлению в форме уравнения Риккати, и дать последовательный вывод для применения метода фазово-амплитудных функций в прикладных экспериментальных областях – рентгеновской и нейтронной рефлектометрии.
ПРИЛОЖЕНИЕ К ЗАДАЧАМ РЕФЛЕКТОМЕТРИИ
При непосредственном рассмотрении уравнения (3) предполагают нормальное падение волны на потенциальный барьер, т.е. пучок рентгеновских лучей или нейтронов должен падать на пленку перпендикулярно ее поверхности. На самом деле рефлектометрия имеет дело со скользящими углами падения. В этом случае в отражении от барьера участвует лишь нормальная составляющая волнового вектора. Тогда в уравнении (3) $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }\sin \theta {\text{,}}$ где $\theta $ – угол падения, отсчитанный от поверхности пленки, $\lambda $ – длина волны рентгеновского либо нейтронного излучения. Вводя обозначение ${{k}_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda },$ получим $k = {{k}_{0}}\sin \theta {\text{.}}$ В рефлектометрии также часто используют величину $q = 2k,$ которая имеет смысл нормальной компоненты изменения волнового вектора при отражении. В дальнейшем будем использовать именно такую нотацию.
В случае рентгеновской рефлектометрии потенциал взаимодействия $V(x)$ связан с рентгенооптическими характеристиками вещества следующим соотношением [4]:
(4)
$V(x) = k_{0}^{2}\left( {1 - {{{\left( {1 - \delta (x) - i{\kern 1pt} \beta (x)} \right)}}^{2}}} \right),$При определении начального условия к уравнению (3) предполагали, что слева и справа от пленки находится вакуум. В случае рефлектометрии это соответствовало бы изолированной металлической пленке. К сожалению, такие пленки слишком тонки, чтобы они могли существовать сами по себе. Их всегда синтезируют на подложках, очень толстых (~10–3 м) по сравнению с характерными толщинами пленок (~10–9–10–8 м), и их можно рассматривать как полубесконечную среду с одной стороны пленки. Это приводит к тому, что за исследуемой структурой пленки тоже возникает отраженная от подложки волна, и именно ее амплитуда должна быть взята в качестве граничного условия для уравнения (3).
Амплитуда отражения от поверхности среды с показателем преломления $n$ описывается формулой Френеля [4]:
(5)
${{r}_{{\text{F}}}}(k) = \frac{{{{n}^{2}}k - {{k}_{0}}\sqrt {{{n}^{2}} - {{{\cos }}^{2}}\theta } }}{{{{n}^{2}}k + {{k}_{0}}\sqrt {{{n}^{2}} - {{{\cos }}^{2}}\theta } }}.$Для дальнейшего анализа удобно свести (3) к уравнению Риккати – простыми алгебраическими преобразованиями, после которых получаем:
(6)
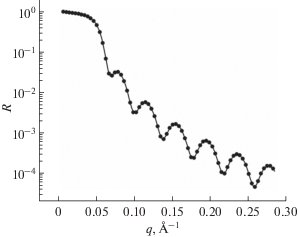
$\begin{gathered} \frac{d}{{dx}}B(x) = \left( { - \frac{{V(x){\text{exp(}}{\kern 1pt} - {\kern 1pt} 2ikx{\text{)}}}}{{2ik}}} \right){{B}^{2}}(x) + \\ + \,\,\left( { - \frac{{V(x)}}{{ik}}} \right)B(x) + \left( { - \frac{{V(x){\text{exp}}(2ikx)}}{{2ik}}} \right). \\ \end{gathered} $Для проверки численного решения уравнения (3) проведем расчет для простейшей рефлектометрической задачи: пленка хрома толщиной 200 Å на подложке из сапфира Al2O3, длина волны падающего пучка 1.79 Å, что соответствует средневзвешенной линии ${{K}_{\alpha }}$ излучения кобальта. Аналогичный расчет был осуществлен и методом Парратта. Результаты показаны на рис. 1. По оси ординат отложен коэффициент отражения $R\left( q \right)$ = = $B\left( {2k,0} \right)$ = ${{\left| {B\left( q \right)} \right|}^{2}}.$ Видно, что расчетные кривые, полученные двумя методами, хорошо совпадают. Отклонение в точке не превышает 6.6%, полное несоответствие двух кривых составляет 0.14%. Эти расхождения, по-видимому, объясняются особенностями программной реализации двух алгоритмов, поскольку уравнение (3) получено без каких-либо приближений, и неточности могут возникать только во время его численного решения.
Рис. 1.
Рефлектометрическая кривая для системы Al2O3//Cr(200 Å), рассчитанная с использованием двух алгоритмов: Парратта (кривая); метод фазово-амплитудных функций (точки).
Теперь предположим, что $\left| {B(x)} \right| \ll 1.$ Это условие выполняется вдали от области полного внешнего отражения, при больших k. Тогда можно пренебречь квадратичным и линейным членом. Уравнение (6) принимает вид:
Уравнение может быть решено путем разделения переменных. Для потенциала произвольного вида имеем: Это соответствует выражению в кинематической теории [4], здесь никак не учитывается многократное рассеяние. Потенциал взаимодействия показан на рис. 2. На рис. 3 представлен результат расчета отражения по формуле (8) в сравнении с решением точного уравнения (6). Модельная система – металлическая сверхрешетка Al2O3//Cr(100 Å)/ [Gd(50 Å)/Cr(11 Å)]6/Cr(75 Å)/Cr2O3(25 Å).Рис. 2.
Потенциал взаимодействия системы Al2O3//Cr(100 Å)/[Gd(50 Å)/Cr(11 Å)]6/Cr(75 Å)/ Cr2O3(25 Å), глубина отсчитывается от подложки.
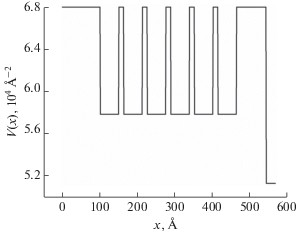
Рис. 3.
Решение точного уравнения (6) (сплошная линия) и приближение, описываемое уравнением (7) (штриховая линия).
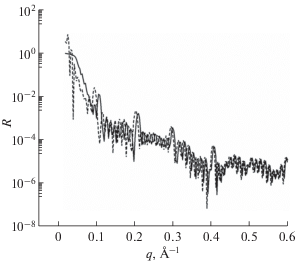
Приближенное решение удовлетворительно совпадает с точным при $q > 10{{q}_{{\text{с}}}},$ где ${{q}_{{\text{с}}}}$ соответствует критическому углу для данной системы. В этой области оправдано использование описанного приближения. При меньших $q$ наблюдается смещение пиков влево. Здесь нельзя проводить количественный анализ и определять характеристики системы, поскольку возникнет большая погрешность. Но качественно оценить поведение интенсивности вполне возможно. Приближение нельзя использовать при $q < 2{{q}_{{\text{с}}}},$ поскольку в этот участок интенсивности существенный вклад дает именно многократное отражение. Таким образом, в методе фазово-амплитудных функций легко получить кинематическое приближение для рентгеновской и нейтронной рефлектометрии.
Качество приближения можно существенно улучшить, если, по-прежнему полагая $B(x) \ll 1,$ пренебречь только квадратичным членом в уравнении (6). Тогда
(9)
$\frac{d}{{dx}}B(x) = \left( { - \frac{{V(x)}}{{ik}}} \right)B(x) + \left( { - \frac{{V(x){\text{exp(}}2ikx{\text{)}}}}{{2ik}}} \right).$(10)
$\begin{gathered} B(x) = \frac{i}{{2k}}{\text{exp}}\left( {\frac{i}{k}F(x)} \right) \times \\ \times \,\,\left[ {\int {V(x){\text{exp}}} \left( {2ik\left( {x - \frac{1}{{2{{k}^{2}}}}F(x)} \right)} \right)dx + C} \right], \\ \end{gathered} $Рис. 4.
Решение точного уравнения (6) (сплошная линия) и приближение, описываемое уравнением (9) (штриховая линия).
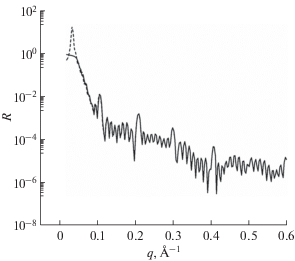
Данное приближение хорошо совпадает с решением точного уравнения практически во всем диапазоне значений q. Исключение составляет область вблизи критического угла, в которой заметно влияние отброшенного квадратичного члена. При $q = {{q}_{{\text{с}}}}$ возникает острый пик, не имеющий физического смысла. Сходные пики в этой области появляются при расчете интенсивности методом искаженных волн [3, 5]. В обзоре [5] представлено еще несколько приближенных методов, но практически все они не вполне корректно описывают область полного внешнего отражения в случае сложных систем с большим количеством переходных областей между слоями. Для некоторых потенциалов хороший результат в этой области дает приближение взвешенной суперпозиции, но его расчетная формула существенно сложнее уравнения (9). Приближение, описываемое данным уравнением, можно использовать для количественного анализа данных при $q > 1.5{{q}_{{\text{с}}}},$ что вполне достаточно для большинства рефлектометрических задач.
Рассмотрим несколько подстановок, которые позволяют получить иные формы уравнения (3). Будем искать решение в виде $B(x) = {\text{exp}}\left( {2i\theta (x)} \right),$ где $\theta (x)$ – комплексная функция. После преобразований уравнение (3) примет вид:
Эту компактную форму удобно использовать в нейтронной рефлектометрии, поскольку потенциалы там преимущественно действительные вследствие очень слабого поглощения тепловых нейтронов в веществе. Численное решение уравнения (11) при некоторых $k$ может давать большую погрешность. Это связано с особенностями косинуса комплексного аргумента – он периодичен, но может принимать сколь угодно большие значения. Погрешность можно уменьшить, если использовать методы интегрирования с переменным шагом. При малых $k$ уравнение (11) устойчиво интегрируется и с постоянным шагом. Это также упрощает его использование в нейтронной рефлектометрии, поскольку там диапазоны k, как правило, меньше, чем в случае рентгеновской рефлектометрии и обычно не превышают 0.05–0.1 Å–1.Комплексное уравнение (3) можно свести к системе двух действительных уравнений. Пусть $B(x)$ = $G(x){\text{exp}}\left( {2i\theta (x)} \right),$ где $G(x)$ и $\theta (x)$ – действительные функции. Тогда получаем систему для их определения:
(12)
$\left\{ \begin{gathered} \frac{d}{{dx}}G = \frac{1}{{2k}}\left[ {({{G}^{2}} - 1)V\sin \varphi - ({{G}^{2}} + 1)\tilde {V}\cos \varphi - 2G\tilde {V}} \right], \hfill \\ \frac{d}{{dx}}\theta = \frac{1}{{4Gk}}\left[ {({{G}^{2}} + 1)V\cos \varphi + ({{G}^{2}} - 1)\tilde {V}\sin \varphi + 2GV} \right]. \hfill \\ \end{gathered} \right.$В виде системы можно представить и уравнение (11), если заменить $\theta (x) = \rho (x) + i\gamma (x),$ где $\rho (x)$ и $\gamma (x)$ – действительные функции. Они изменяются плавно, что несколько улучшает точность численных расчетов при больших значениях k. Система в этом случае имеет вид:
(13)
$\left\{ \begin{gathered} \frac{d}{{dx}}\rho = - \frac{1}{{2k}}\left[ {V\sin \varphi {\text{sh}}y + \tilde {V}\cos \varphi {\text{ch}}y + \tilde {V}} \right], \hfill \\ \frac{d}{{dx}}\theta = \frac{1}{{2k}}\left[ {V\cos \varphi {\text{ch}}y - \tilde {V}\sin \varphi {\text{sh}}y + V} \right]. \hfill \\ \end{gathered} \right.$Итак, показано, что метод фазово-амплитудных функций позволяет рассчитывать коэффициент отражения по известному потенциалу, причем можно использовать различные приближения и формы уравнений. Но при обработке эксперимента возникает обратная задача – зная зависимость интенсивности от угла падения, нужно определить потенциал взаимодействия и характеристики слоистой структуры образца. К сожалению, представленные уравнения не допускают непосредственного обращения в силу нелинейности исходной задачи. Для поиска потенциала рассеяния можно использовать различные методы спуска, например, алгоритм Левенберга-Марквардта [23].
ЭКСПЕРИМЕНТАЛЬНАЯ АПРОБАЦИЯ
Проверим применимость метода фазово-амплитудных функций для анализа экспериментальных данных рентгеновской рефлектометрии. Для этой цели был изготовлен образец металлической пленки, аналогичный рассматриваемой выше модели, Al2O3//Cr(200 Å). Синтез образца проводили в Институте физики металлов УрО РАН (г. Екатеринбург) на установке молекулярно-лучевой эпитаксии “Катунь-С”. Подложка размером 15 × 15 мм2 вырезана в ориентации R-плоскости (кристаллографическая плоскость $(1\bar {1}02)$, совпадающая с поверхностью). Для очистки от загрязнений подложку промывали в изопропиловом спирте в ультразвуковой ванне в течение 2 мин, остатки спирта удаляли деионизированой водой. Затем подложку прокаливали в вакууме до 900°С. Хром напыляли из эффузионной ячейки при температуре подложки 350°С, чтобы увеличить коэффициент поверхностной диффузии и обеспечить бездефектный рост пленки. Давление остаточных газов в камере роста во время синтеза составляло 10–7 Па.
Рефлектометрические кривые измеряли также в Институте физики металлов УрО РАН на дифрактометре PANalytical Empyrean Series 2 в геометрии параллельного пучка с использованием излучения CoKα (длина волны $\lambda = 1.79$ Å). Параллельный пучок формировали с помощью параболического зеркала Si/W, высота пучка на образце, задаваемая системой щелей, составляла 0.05 мм. Экспериментальные данные были обработаны методом фазово-амплитудных функций с использованием алгоритма Левенберга-Марквардта, начальное приближение было выбрано с учетом номинальной толщины слоя Cr. При обработке эксперимента также применяли коррекцию при условии, что при малых углах падения засвечиваемое пучком пятно больше, чем размер образца [24]. Этот эффект снижает интенсивность полного внешнего отражения по сравнению с теоретической за счет потери части первичного пучка, попадающей мимо образца. На экспериментальных рефлектометрических кривых это проявляется как спад интенсивности в самых малых углах.
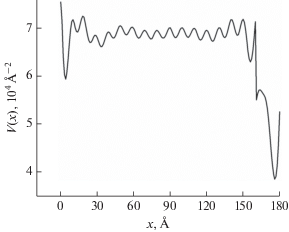
Экспериментальные данные и результат обработки для образца Al2O3//Cr(200 Å) представлены на рис. 5 и 6. Относительное отклонение расчетной рефлектометрической кривой от экспериментальной на рис. 5 составляет 1.6%. Относительная погрешность значения потенциала в каждой точке не превышает этого значения. Учитывая величину погрешности, можно сказать, что в области от 0 до 160 Å потенциал является постоянным или меняется слабо, что соответствует небольшим вариациям плотности слоя чистого хрома, возникающим в процессе синтеза. Высокочастотные осцилляции и скачок вблизи подложки являются следствием ограниченного диапазона величины $q$ и зашумления экспериментальной интенсивности. Они не несут структурной информации, их величина не превышает относительной погрешности. Спад потенциала в диапазоне от 0 до 10 Å связан с шероховатостью подложки. Спад в хвосте кривой обусловлен наличием на поверхности пленки окисленного слоя Cr2O3 толщиной примерно 16 Å. В конце диапазона (т.е. на поверхности пленки) потенциал должен обращаться в ноль. Но ввиду плохой обусловленности обратной задачи рефлектометрии, нулевые или очень малые величины определяются с очень большой погрешностью. Этим объясняется скачок потенциала вблизи поверхности пленки.
Рис. 5.
Экспериментальная рефлектометрическая кривая (точки) образца Al2O3//Cr(200 Å) и ее аппроксимация в результате решения (линия).
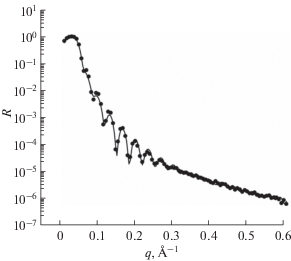
Рис. 6.
Потенциал взаимодействия для образца Al2O3//Cr(200 Å), рассчитанный методом фазово-амплитудных функций, глубина отсчитывается от подложки.
Результаты, полученные методом фазово-амплитудных функций, сравнивали с результатами, полученными методом Парратта с использованием коммерческой программы X'pert Reflectivity, поставляемой в комплекте с дифрактометром. Согласно обработке методом Парратта, толщина слоя Cr составляет 163 Å, толщина Cr2O3 13 Å. Это находится в хорошем соответствии с приведенным выше анализом потенциала рассеяния. Общая толщина пленки совпадает в пределах погрешности в обоих подходах и составляет 176 Å. Полученную толщину пленки использовали для калибровки скорости напыления хрома на установке молекулярно-лучевой эпитаксии.
Также был изготовлен образец металлической сверхрешетки Al2O3//Cr(100 Å)/[Gd(50 Å)/Cr(11 Å)]6/ Cr(100 Å). Использовали аналогичную подложку и методику подготовки. Гадолиний и хром напыляли из эффузионных ячеек. Синтез буферного слоя хрома проводили при температуре подложки 350°С, все последующие слои напыляли при комнатной температуре, чтобы подавить диффузию компонентов и перемешивание слоев. Для усложнения структуры образца и проверки возможности ее аттестации предлагаемым методом был имитирован отказ оборудования – уменьшение температуры эффузионной ячейки хрома в процессе напыления до такого значения, при котором рост слоя невозможен. Температура ячейки была восстановлена при напылении закрывающего слоя хрома, чтобы предотвратить окисление гадолиния.
Эксперимент по рентгеновской рефлектометрии проводили в тех же условиях, что и для предыдущего образца. Результаты представлены на рис. 7 и 8. Относительное отклонение расчетной кривой от экспериментальной составляет 2.5%. На рис. 8 видно, что в первых трех периодах сверхрешетки (считая от подложки) есть заметные слои хрома, а в последних трех хром практически отсутствует. Эта часть пленки представляет собой слой гадолиния с небольшими добавками хрома. Это приводит к видимому отсутствию брэгговских пиков на рефлектометрической кривой, соответствующих сверхрешетке. На самом деле брэгговские пики есть, но из-за несовершенства структуры они слабы, а начиная со второго порядка затухают совсем.
Рис. 7.
Экспериментальная рефлектометрическая кривая (точки) образца Al2O3//Cr(100 Å)/[Gd(50 Å)/ Cr(11 Å)]6/Cr(100 Å) и ее аппроксимация в результате решения (линия).
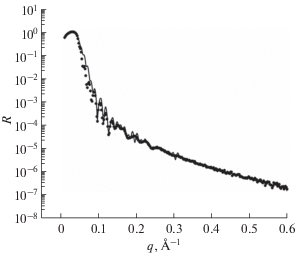
Рис. 8.
Потенциал взаимодействия для образца Al2O3//Cr(100 Å)/[Gd(50 Å)/Cr(11 Å)]6/Cr(100 Å), рассчитанный методом фазово-амплитудных функций, глубина отсчитывается от подложки.
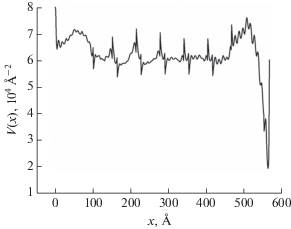
Анализ потенциала рассеяния дает возможность определить, что после падения температуры ячейки вместо роста слоев происходит лишь образование очень малых кластеров хрома в толстом слое гадолиния. При расчете только характеристик слоев это было бы сделать сложнее, поскольку необходимо моделировать кластерно-слоистую структуру. А предположить ее существование можно, только заранее зная об изменениях строения образца в результате отказа оборудования.
Скорость расчета рефлектометрической кривой методом фазово-амплитудных функций примерно в два раза выше, чем при использовании формализма оптических матриц. Это связано с тем, что нет необходимости проводить вычисление элементов и перемножение большого количества матриц.
ЗАКЛЮЧЕНИЕ
В работе было рассмотрено применение метода фазово-амплитудных функций для решения прикладных экспериментальных задач рефлектометрии. Показано, что нелинейное дифференциальное уравнение метода можно свести к линейному в рамках различных приближений и получить его аналитическое решение. Исходное уравнение не имеет аналитического решения для потенциала общего вида. Приведены несколько подстановок, позволяющих представить уравнение в более компактном виде или в форме системы действительных уравнений. Рефлектометрические кривые, рассчитанные методом фазово-амплитудных функций, хорошо совпадают с данными, полученными с использованием алгоритма Парратта и формализма оптических матриц. Программно реализован метод решения обратной задачи (определение потенциала рассеяния по известной зависимости интенсивности от угла падения) на основе алгоритма Левенберга-Марквардта. Для проверки возможности решения обратной задачи использованы экспериментальные данные для двух образцов. Для тонкой пленки хрома из анализа потенциала выведены толщины слоя хрома и окисленного слоя на поверхности. Эти величины с хорошей точностью совпали со значениями, полученными при обработке с использованием алгоритма Парратта. Потенциал для сверхрешетки Gd/Cr четко отражает изменения в структуре образце, возникшие в результате имитации отказа оборудования во время синтеза.
Таким образом, предлагаемый метод может быть достаточно эффективен как для исследования структурных свойств образцов, так и для их аттестации. Плюсом метода фазово-амплитудных функций можно также считать более высокую скорость расчетов.
Список литературы
Abeles F. // Annales de Physique. 1950. T. 12. № 5. P. 596. https://doi.org/10.1051/anphys/195012050596
Parratt L.G. // Phys. Rev. 1954. V. 95. № 2. P. 359. https://doi.org/10.1103/PhysRev.95.359
Zhou X.-L. // Phys. Rev. E. 1995. V. 52. № 2. P. 1938. https://doi.org/10.1103/PhysRevE.52.1938
Zimmerman K.M. Advanced Analysis Techniques for X‑Ray Reflectivities: Theory and Application: Дис. … д-ра наук. Карлсруэ: Университет Дортмунда, 2005. 190 с.
Zhou X.-L., Chen S.-H. // Phys. Rep. 1995. V. 257. № 4–5. P. 223. https://doi.org/10.1016/0370-1573(94)00110-O
Babanov Y., Salamatov Y., Vasin V., Ustinov V. // Superlatt. Microstr. 2015. V. 82. P. 612. https://doi.org/10.1016/j.spmi.2015.02.035
Бабиков В.В. Метод фазовых функций в квантовой механике. М: Наука, 1976. 288 с.
Calogero F. Variable Phase Approach to Potential Scattering. N-Y.: Academic Press Inc., 1967. 243 p.
Tikochinsky Y. // Ann. Phys. 1977. V. 103. № 1. P. 185. https://doi.org/10.1016/0003-4916(77)90268-8
Крайнов В.П., Пресняков Л.П. // Успехи физических наук. 1993. Т. 163. № 7. С. 85. https://doi.org/10.3367/UFNr.0163.199307f.0085
Presnyakov L.P. // Progress in Optics. 1995. V. 34. P. 159. https://doi.org/10.1016/S0079-6638(08)70325-1
Mielnik B., Reyes M.A. // J. Phys. A. 1996. V. 29. P. 6009. https://doi.org/10.1088/0305-4470/29/18/029
Kidun O., Fominykh N., Berakdar J. // Phys. Rev. A. 2005. V. 71. P. 022703. https://doi.org/10.1103/PhysRevA.71.022703
Kidun O., Fominykh N., Berakdar J. // J. Phys. A. 2002. V. 35. P. 9413. https://doi.org/10.1088/0305-4470/35/44/310
Игнатович В.К. // Теоретическая и математическая физика. 1991. Т. 88. № 3. С. 477. https://doi.org/10.1007/BF01027704
Jana A.K., Bera P.K., Das U., Talukdar B. // J Phys. A. 1990. V. 23. № 2. P. 153. https://doi.org/10.1088/0305-4470/23/2/012
Bera P.K., Nandi T.K., Talukdar B. // J. Phys. A. 1993. V. 26. № 20. P. L1073. https://doi.org/10.1088/0305-4470/26/20/003
Kryachko E.S. // Collection Czech. Chem. Commun. 2005. V. 70. № 7. P. 941. https://doi.org/10.1135/cccc20050941
Schuch D. // J. Phys.: Conf. Ser. 2014. V. 538. P. 012019. https://doi.org/10.1088/1742-6596/538/1/012019
CXRO X-Ray Interactions with Matter. http://henke.lbl.gov/optical_constants/
Costa E.D’M., Cordeiro L., Lemes N.H.T., Braga J.P. // Química Nova. 2016. V. 39. № 7. P. 882. https://doi.org/10.5935/0100-4042.20160061
Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. М: Физматлит, 2001. 576 с.
Поляк Б.Т. // Тр. Ин-та системного анализа РАН. 2006. Т. 28. С. 48.
Gibaud A., Vinaud G., Sinha S.K. // Acta Crystallogr. A. 1993. V. 49. P. 642. https://doi.org/10.1107/S0108767392013126
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


