1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 3, 2022

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 3, стр. 79-88

Расщепление уровней энергии поперечного движения позитронов при каналировании в направлении [100] кристалла кремния

В. В. Сыщенко a, *, А. И. Тарновский a, В. И. Дроник a, А. Ю. Исупов b

a Белгородский государственный национальный исследовательский университет
308015 Белгород, Россия

b Лаборатория физики высоких энергий ОИЯИ
141980 Дубна, Россия

* E-mail: syshch@yandex.ru

Поступила в редакцию 30.04.2021
После доработки 25.06.2021
Принята к публикации 30.06.2021

Полный текст (PDF)

Аннотация

Движение заряженных частиц в кристалле может быть как регулярным, так и хаотическим. На квантовом уровне хаотичность проявляется в статистических свойствах массива уровней энергии. Особый интерес представляют системы, в которых области регулярного движения разделены в фазовом пространстве областью динамического хаоса. На статистику уровней таких систем существенно влияет возможность туннелирования между динамически изолированными друг от друга областями фазового пространства. В настоящей работе выполнена оценка матричных элементов таких туннельных переходов. С этой целью численно рассчитаны все уровни энергии поперечного движения позитронов с энергией 20 ГэВ, движущихся в режиме аксиального каналирования в направлении [100] кристалла кремния, а также соответствующие этим состояниям собственные функции гамильтониана. Найдены суперпозиции этих собственных функций, соответствующие классическим орбитам, локализованным в симметричных друг другу, но динамически изолированных областях фазового пространства. Величина расщепления уровней энергии позволяет оценить матричные элементы туннельных переходов.

Ключевые слова: регулярная динамика, хаотическая динамика, квантовый хаос, каналирование, квазиклассическое приближение, статистика межуровневых расстояний, распределение Берри–Робника, динамическое туннелирование, туннелирование сопровождаемое хаосом, распределение Подольского–Нариманова.

ВВЕДЕНИЕ

Статистические свойства массива уровней энергии квантовой системы, хаотической в классическом пределе, резко отличаются от таковых для интегрируемой системы, обладающей регулярной динамикой [1–4]. Эти различия обусловлены тем обстоятельством, что уровни энергии интегрируемой системы не взаимодействуют друг с другом, в то время как между уровнями энергии неинтегрируемой (хаотической в классическом пределе) системы имеет место взаимодействие уровней, приводящее к их взаимному отталкиванию. Проявления динамического хаоса в каналировании электронов [5, 6] исследовались в работах [7–11] для случая движения вблизи направления [110] кристалла кремния. В этом случае пары соседних атомных цепочек создают двухъямный потенциал, выше седловой точки которого движение электронов оказывается почти полностью хаотическим. Было установлено, что статистические свойства уровней в этой области хорошо описываются распределением Вигнера [1–4].

Более сложным является тот случай, когда классическая динамика частицы оказывается при заданной энергии регулярной для одних начальных условий и хаотической для других, при этом области регулярного движения разделены в фазовом пространстве областью динамического хаоса. Такая ситуация реализуется, например, при движении электрона вблизи направления [100] кристалла кремния [12, 13]. В работе [14] предполагалось, что эти области порождают две независимые друг от друга последовательности уровней. Однако, туннелирование между динамически изолированными друг от друга областями фазового пространства будет приводить к взаимодействию уровней энергии, порождаемых локализованными в таких областях состояниями. Теория, учитывающая влияния туннельных переходов на статистику уровней, была предложена в [15].

В настоящей работе выполнена оценка матричных элементов таких переходов для случая каналирования позитронов высокой энергии в направлении [100] кристалла кремния. На основе установленной в работе [13] структуры фазового пространства системы дана интерпретация величины расщепления уровней энергии.

МЕТОДИКА

Движение релятивистской частицы в кристалле под малым углом $\psi $ к плотно упакованной атомами кристаллографической оси может быть описано как двумерное движение в поперечной (по отношению к оси) плоскости под воздействием непрерывных потенциалов, усредненных вдоль атомных цепочек, перпендикулярных этой плоскости, с сохранением продольной компоненты импульса частицы ${{p}_{\parallel }}.$ Непрерывный потенциал отдельной атомной цепочки может быть аппроксимирован формулой [5]:

(1)
${{U}_{1}}(x,y) = {{U}_{0}}\ln \left( {1 + \frac{{\beta {{R}^{2}}}}{{{{x}^{2}} + {{y}^{2}} + \alpha {{R}^{2}}}}} \right),$
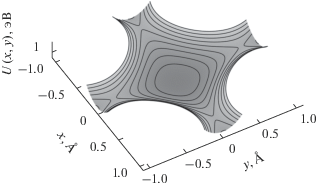
где для цепочки [100] кристалла кремния ${{U}_{{\text{0}}}} = {\text{66}}{\text{.6}}$ эВ, $\alpha = {\text{0}}{\text{.48,}}$ $\beta = {\text{1}}{\text{.5,}}$ $R = {\text{0}}{\text{.194}}~$ Å (радиус Томаса–Ферми). Такие цепочки образуют в плоскости (100) квадратную решетку с периодом $a \approx {\text{1}}{\text{.92}}$ Å. Для позитрона непрерывный потенциал цепочки является отталкивающим, и вблизи центра квадрата, в вершинах которого находятся четыре ближайшие друг к другу цепочки, возникает небольшая потенциальная ямка (рис. 1), в которой возможно финитное движение позитрона в поперечной плоскости, называемое аксиальным каналированием [5, 6]. Потенциальная энергия позитрона с учетом вкладов этих четырех цепочек будет описываться следующей суммой:
(2)
$\begin{gathered} U(x,y) = {{U}_{1}}(x - {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2},y - {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}) + \\ + \,\,{{U}_{1}}(x - {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2},y + {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}) + \\ + \,\,{{U}_{1}}(x + {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2},y - {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}) + \\ + \,\,{{U}_{1}}(x + {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2},y + {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}) - 7.96\,\,{\text{эВ,}} \\ \end{gathered} $
где константа добавлена для того, чтобы сделать потенциал равным нулю в центре ячейки.

Рис. 1.

Потенциальная энергия (2) позитрона, движущегося вблизи направления [100] кристалла кремния.

Квантовое описание аксиального каналирования дается двумерным уравнением Шредингера с гамильтонианом:

(3)
$\hat {H} = - \frac{{{{\hbar }^{2}}}}{{{{2{{E}_{\parallel }}} \mathord{\left/ {\vphantom {{2{{E}_{\parallel }}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right) + U\left( {x,y} \right),$
в котором величина ${{{{E}_{\parallel }}} \mathord{\left/ {\vphantom {{{{E}_{\parallel }}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}$ играет роль массы частицы, а ${{E}_{\parallel }} = {{({{m}^{2}}{{c}^{4}} + p_{\parallel }^{2}{{c}^{2}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – энергия продольного движения [5]. В настоящей работе рассмотрено каналирование позитронов с энергией ${{E}_{\parallel }} = 20$ ГэВ. Собственные значения (уровни энергии каналированных позитронов) и собственные функции гамильтониана (3) были найдены численно с помощью так называемого спектрального метода [16], детали которого применительно к задаче каналирования описаны в работах [7–10].

Поскольку потенциал (2) обладает симметрией квадрата, все доступные состояния поперечного движения можно классифицировать по неприводимым представлениям группы ${{D}_{{\text{4}}}}$ (или изоморфной ей ${{C}_{{{\text{4v}}}}},$ например, [17]) в зависимости от типа симметрии волновой функции. Эта группа имеет четыре одномерных неприводимых представления, обозначаемых ${{A}_{{\text{1}}}},$ ${{A}_{{\text{2}}}},$ ${{B}_{{\text{1}}}},$ ${{B}_{{\text{2}}}},$ соответствующих невырожденным уровням энергии, и одно двумерное, обозначаемое E, соответствующее двукратно вырожденным уровням. В дальнейшем мы будем исследовать только невырожденные уровни.

Механизм взаимодействия уровней энергии хорошо описан в [18] (главы 6–8) на примере двухуровневой системы. Напомним результаты этого описания, следуя использованным в [18] обозначениям. Рассмотрим пару вырожденных состояний $\left| 1 \right\rangle $ и $\left| 2 \right\rangle $ с ясным квазиклассическим смыслом. Если амплитуда перехода между этими двумя состояниями $\left\langle {2\left| {\hat {H}} \right|1} \right\rangle $ отлична от нуля, $\left\langle {2\left| {\hat {H}} \right|1} \right\rangle = {{V}_{{21}}} \equiv - A,$ это приведет к снятию вырождения, так что стационарными состояниями с определенной энергией будут линейные комбинации состояний $\left| 1 \right\rangle $ и $\left| 2 \right\rangle {\text{:}}$

(4)
$\left| {\text{I}} \right\rangle = \frac{{\left| 1 \right\rangle - \left| 2 \right\rangle }}{{\sqrt 2 }},\,\,\,\,\left| {{\text{II}}} \right\rangle = \frac{{\left| 1 \right\rangle + \left| 2 \right\rangle }}{{\sqrt 2 }}.$
Отвлекаясь от наличия всех остальных состояний, такую двухуровневую систему можно описать феноменологическим гамильтонианом
(5)
${\mathbf{H}} = \left( {\begin{array}{*{20}{c}} E&{ - A} \\ { - A}&E \end{array}} \right),$
диагональным в новом базисе $\left| I \right\rangle ,$ $\left| {II} \right\rangle {\text{:}}$
(6)
${\mathbf{H}}{\kern 1pt} ' = \left( {\begin{array}{*{20}{c}} {E + A}&0 \\ 0&{E - A} \end{array}} \right).$
В настоящей работе перед нами стоит обратная задача: исходя из найденного численно набора стационарных состояний, определить матричные элементы переходов ${{V}_{{ij}}}$ между состояниями с наглядным квазиклассическим смыслом (каковыми являются состояния, отвечающие в классическом пределе движению в динамически изолированных друг от друга областях фазового пространства). Для пар близких уровней достаточно найти матрицу преобразования от базиса стационарных состояний $\left| {\text{I}} \right\rangle ,$ $\left| {{\text{II}}} \right\rangle $ к базису состояний с простым квазиклассическим смыслом:
(7)
$\left( {\begin{array}{*{20}{c}} {\left| {\text{I}} \right\rangle } \\ {\left| {{\text{II}}} \right\rangle } \end{array}} \right) = {\mathbf{T}}\left( {\begin{array}{*{20}{c}} {\left| 1 \right\rangle } \\ {\left| 2 \right\rangle } \end{array}} \right),$
и тогда
(8)
${\mathbf{H}} = {{{\mathbf{T}}}^{{ - 1}}}{\mathbf{H}}{\kern 1pt} '{\mathbf{T}},$
откуда легко найти искомые недиагональные матричные элементы H. В рассмотренном выше простейшем случае (4) матрица преобразования имеет вид:
(9)
${\mathbf{T}} = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1&{ - 1} \\ 1&1 \end{array}} \right).$
В следующем разделе мы рассмотрим, как взаимодействия такого рода, так и более сложные случаи взаимодействия четырех уровней энергии поперечного движения каналированных позитронов.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Среди всех состояний поперечного движения позитронов с энергией ${{E}_{\parallel }} = 20$ ГэВ встречается множество пар, близких по энергии поперечного движения состояний, относящихся к разным представлениям группы симметрии нашей задачи. Например, на рис. 2 представлены графики собственных функций состояния с энергией ${{E}_{ \bot }} = 1.193{\text{0125}}$ эВ, принадлежащего представлению ${{B}_{{\text{2}}}}$ (в наших обозначениях это будет состояние $\left| {\text{I}} \right\rangle $), и состояния с энергией ${{E}_{ \bot }} = 1.1930000$ эВ, принадлежащего представлению ${{A}_{{\text{1}}}}$ (это будет состояние $\left| {{\text{II}}} \right\rangle $). Нетрудно видеть, что комбинации $\left| 1 \right\rangle $ и $\left| 2 \right\rangle {\text{:}}$

(10)
$\left| 1 \right\rangle = \frac{{\left| {\text{I}} \right\rangle + \left| {{\text{II}}} \right\rangle }}{{\sqrt 2 }},\,\,\,\,\left| 2 \right\rangle = \frac{{\left| {{\text{II}}} \right\rangle - \left| {\text{I}} \right\rangle }}{{\sqrt 2 }},$
представляют собой состояния, локализованные в двух динамически изолированных областях фазового пространства. На двух рисунках внизу (рис. 2) поверх графиков волновых функций изображены периодические орбиты, реализующиеся в классическом пределе при энергии ${{E}_{ \bot }} = {{({{E}_{{\text{I}}}} + {{E}_{{{\text{II}}}}})} \mathord{\left/ {\vphantom {{({{E}_{{\text{I}}}} + {{E}_{{{\text{II}}}}})} 2}} \right. \kern-0em} 2}.$ Амплитуда перехода между этими двумя состояниями сразу находится из величины расщепления, по абсолютной величине она составляет $A = {{({{E}_{{\text{I}}}} - {{E}_{{{\text{II}}}}})} \mathord{\left/ {\vphantom {{({{E}_{{\text{I}}}} - {{E}_{{{\text{II}}}}})} 2}} \right. \kern-0em} 2} = 6.25 \times {{10}^{{ - 6}}}$ эВ. Абсолютные значения амплитуд перехода для всех найденных пар уровней отмечены точками на рис. 3а.

Рис. 2.

Собственные функции гамильтониана (3), принадлежащие представлениям ${{B}_{{\text{2}}}}$ (собственное значение энергии поперечного движения ${{E}_{ \bot }} = 1.{\text{1930125}}$ эВ) (а) и ${{A}_{{\text{1}}}}$ (${{E}_{ \bot }} = 1.{\text{1930000}}$ эВ), белыми линиями показаны классические границы движения (а) и (б); суперпозиции (10) этих функций, черными линиями показаны соответствующие классические орбиты (в) и (г).

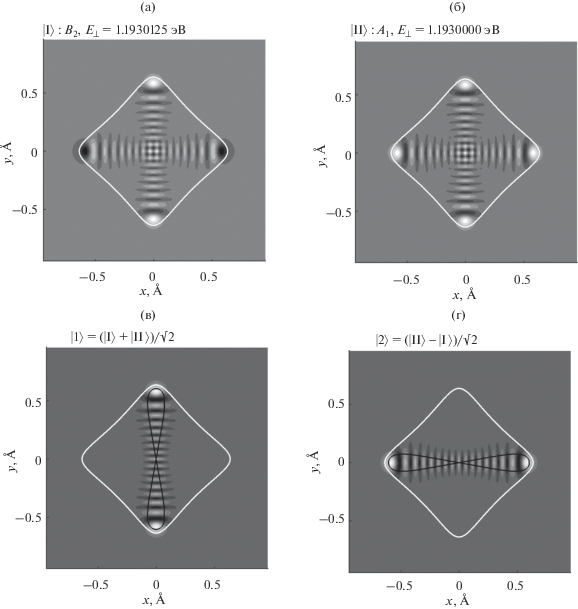
Рис. 3.

Абсолютные значения матричных элементов перехода между квазиклассическими состояниями, штриховая линия – фит (featuring) всех найденных значений полиномом четвертой степени; сплошная линия (шкала справа) – найденная в [13] доля хаотической динамики в фазовом пространстве системы (а); то же с классификацией состояний, участвующих в парных взаимодействиях (состояния, относящиеся к одному классу, соединены пунктирными линиями) (б).

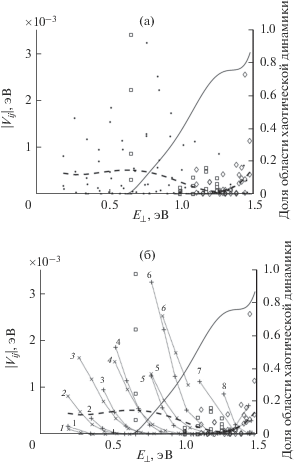
Закономерность в величине амплитуд перехода можно увидеть, если классифицировать состояния по числу полуволн, укладывающихся вдоль узкой стороны квазиклассической волновой функции, рассматривая при этом отдельно состояния, соответствующие классическим орбитам, соединяющим два противоположных угла потенциальной ямы (такие состояния отмечены на рис. 3б прямыми крестиками, +), и состояния, соответствующие орбитам, соединяющим противоположные стороны квадратной потенциальной ямы (отмечены косыми крестиками, $ \times $). Например, состояния на рис. 2 в наших обозначениях относятся к типу +1. Семейства состояний каждого типа объединены на рис. 3б пунктирными линиями.

Для каждого из таких семейств величина расщепления в зависимости от энергии состояния сначала убывает, а затем снова возрастает. Такое поведение объясняется следующим образом. В глубине потенциальной ямы (2) динамика частиц носит регулярный характер практически для всех начальных условий, так что границы различных, динамически изолированных друг от друга областей регулярного движения соприкасаются друг с другом (рис. 4а, 4б). Поэтому, если волновая функция состояния достигает краев такой области, вероятность туннельного проникновения в регулярную область, соответствующую состоянию-партнеру, будет достаточно велика, что приведет к значительной величине расщепления собственных энергий симметричной и антисимметричной комбинаций вида (4) для этих состояний. С увеличением энергии уменьшается характерное значение дебройлевской длины волны, поэтому состояние с малым числом полуволн в поперечном направлении будет локализовано в фазовом пространстве в области меньшего относительного объема, окруженной областями локализации других регулярных состояний. Поэтому вероятность туннелирования сквозь динамически недоступные области будет снижаться, что приводит к уменьшению величины расщепления соответствующих уровней энергии. Однако при дальнейшем увеличении энергии доля фазового объема, соответствующего регулярной динамике, будет сокращаться (сплошная кривая на рис. 3 показывает возрастающую долю области хаотической динамики). Так что вблизи верхнего края потенциальной ямы фазовое пространство содержит несколько динамически изолированных друг от друга областей, соответствующих разным типам регулярных орбит, разделенных областью хаотической динамики (рис. 4в, 4г). Поэтому волновые функции выбранного типа могут снова существенно отличаться от нуля вблизи границ областей регулярного движения. И хотя ширина динамически недоступной для движения частицы области будет велика, вероятность туннелирования сквозь нее начнет возрастать благодаря механизму, известному как туннелирование, сопровождаемое хаосом (chaos-assisted tunneling) [15, 19–21]. В этом случае частице достаточно лишь проникнуть наружу из своей динамически разрешенной области, и она будет подхвачена хаотическим потоком, который рано или поздно доставит ее к границе области-партнера, где частица сможет успешно завершить процесс туннелирования. Этим и обусловлено увеличение расщепления уровней вблизи верха потенциальной ямы.

Рис. 4.

Сечения Пуанкаре (а), (в) и проекции четырехмерных областей регулярной динамики в фазовом пространстве на подпространство $(x,y,{{v}_{x}})$ (б), (г) для значений энергии поперечного движения ${{E}_{ \bot }} = 0.{\text{7687125}}$ эВ (а), (б) и ${{E}_{ \bot }} = 1.{\text{386475}}$ эВ (в), (г).

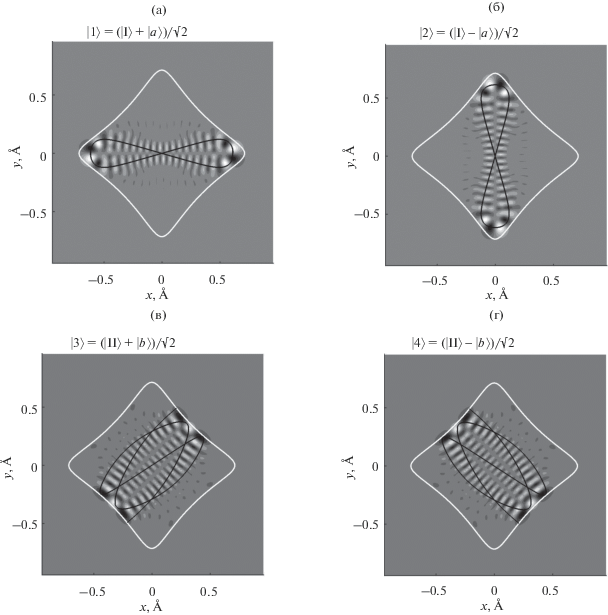
Помимо рассмотренных выше многочисленных случаев парного взаимодействия уровней, нами найдены двенадцать случаев, когда между собой взаимодействуют четыре уровня энергии, соответствующих трем типам симметрии; для одного из таких случаев волновые функции стационарных состояний представлены на рис. 5. Здесь из двух состояний, относящихся к одному типу симметрии, $\left| {{\text{III}}} \right\rangle ,$ $\left| {{\text{IV}}} \right\rangle ,$ оказывается возможным построить комбинации (рис. 6):

(11)
$\begin{gathered} \left| a \right\rangle = \cos \alpha \left| {{\text{III}}} \right\rangle - \sin \alpha \left| {{\text{IV}}} \right\rangle , \\ \left| b \right\rangle = \sin \alpha \left| {{\text{III}}} \right\rangle + \cos \alpha \left| {{\text{IV}}} \right\rangle , \\ \end{gathered} $
парные к состояниям $\left| {\text{I}} \right\rangle $ и $\left| {{\text{II}}} \right\rangle .$ С учетом этого, нетрудно обобщить (7) на случай четырех базисных состояний:
(12)
$\left( {\begin{array}{*{20}{c}} {\left| {\text{I}} \right\rangle } \\ {\left| {{\text{II}}} \right\rangle } \\ {\left| {{\text{III}}} \right\rangle } \\ {\left| {{\text{IV}}} \right\rangle } \end{array}} \right) = {\mathbf{T}}\left( {\begin{array}{*{20}{c}} {\left| 1 \right\rangle } \\ {\left| 2 \right\rangle } \\ {\left| 3 \right\rangle } \\ {\left| 4 \right\rangle } \end{array}} \right),$
где матрица преобразования будет иметь вид
(13)
${\mathbf{T}} = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1&1&0&0 \\ 0&0&1&1 \\ {\cos \alpha }&{ - {\kern 1pt} \cos \alpha }&{\sin \alpha }&{ - {\kern 1pt} \sin \alpha } \\ { - {\kern 1pt} \sin \alpha }&{\sin \alpha }&{\cos \alpha }&{ - {\kern 1pt} \cos \alpha } \end{array}} \right).$
Графики волновых функций состояний $\left| 1 \right\rangle ,$ …, $\left| 4 \right\rangle $ и соответствующие им классические периодические орбиты представлены на рис. 7. Найденные после преобразования (8) с учетом (13) величины недиагональных матричных элементов гамильтониана отмечены на рис. 3 ромбиками.

Рис. 5.

Четыре собственные функции гамильтониана (3), принадлежащие трем различным представлениям группы симметрии задачи, с близкими собственными значениями энергии поперечного движения.

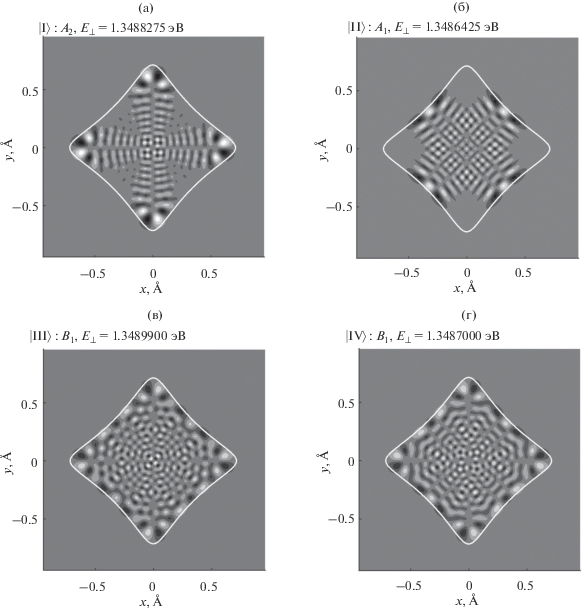
Рис. 6.

Суперпозиции вида (11) функций, представленных на рис. 5в, 5г. Угол смешивания в данном случае составляет $\alpha = {\text{45}}^\circ {\text{.}}$

Рис. 7.

Суперпозиции четырех функций, представленных на рис. 5а, 5б и на рис. 6а, 6б, определяемые соотношением (12), и соответствующие классические орбиты.

Имеются также четыре случая, когда взаимодействуют между собой две пары уровней, относящихся к двум типам симметрии. Для них матрица преобразования будет определяться двумя углами смешивания между состояниями, образующими пары одного и того же типа симметрии:

(14)
${\mathbf{T}} = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} {\cos \beta }&{ - {\kern 1pt} \sin \beta }&{\cos \alpha }&{ - {\kern 1pt} \sin \alpha } \\ {\cos \beta }&{ - {\kern 1pt} \sin \beta }&{ - {\kern 1pt} \cos \alpha }&{\sin \alpha } \\ {\sin \beta }&{\cos \beta }&{\sin \alpha }&{\cos \alpha } \\ {\sin \beta }&{\cos \beta }&{ - {\kern 1pt} \sin \alpha }&{ - {\kern 1pt} \cos \alpha } \end{array}} \right).$
Соответствующие величины недиагональных матричных элементов гамильтониана отмечены на рис. 3 (квадраты).

На рис. 8 представлено распределение найденных значений, отличных от нуля недиагональных матричных элементов гамильтониана, описывающих переходы между различными состояниями, соответствующими динамически изолированным друг от друга классическим траекториям каналированного позитрона (для массива уровней ${{E}_{ \bot }} \geqslant 1$ эВ, для которых доля области хаотической динамики в фазовом пространстве составляет значительную величину). Среднеквадратичное отклонение этих значений составляет 4.2 × 10–4 эВ. Именно эта величина фигурирует в качестве параметра в распределении Подольского–Нариманова [15], описывающем статистику межуровневых расстояний квантовой системы, классический аналог которой содержит в своем фазовом пространстве несколько регулярных областей, разделенных областью хаотической динамики.

Рис. 8.

Распределение найденных значений отличных от нуля недиагональных матричных элементов гамильтониана для массива уровней с ${{E}_{ \bot }} > 1$ эВ. Штриховыми линиями отмечено среднеквадратичное отклонение, составляющее 4.2 × 10–4 эВ.

ЗАКЛЮЧЕНИЕ

В работе рассмотрено каналирование позитронов с энергией 20 ГэВ вблизи направления [100] кристалла кремния. Численными методами найдены все уровни энергии поперечного движения позитронов и соответствующие им волновые функции. Среди этих стационарных состояний выделены группы, которые можно интерпретировать как результат взаимодействия квазиклассических состояний, соответствующих локализации частицы в динамически изолированных друг от друга областях фазового пространства. Найдены значения матричных элементов переходов между такими квазиклассическими состояниями.

Показано, что вблизи верхнего края потенциальной ямы фазовое пространство содержит несколько динамически изолированных друг от друга областей, соответствующих разным типам регулярных орбит, разделенных областью хаотической динамики. Согласно концепции туннелирования, сопровождаемого хаосом (chaos-assisted tunneling, CAT), наличие этой хаотической области способствует туннелированию частицы между динамически изолированными друг от друга областями регулярного движения, что приводит к усилению расщепления уровней энергии поперечного движения каналированных позитронов. Найденные матричные элементы переходов согласуются с этой интерпретацией.

Полученные результаты (в частности, величина среднеквадратичного отклонения для массива матричных элементов туннельных переходов) могут быть использованы для статистического анализа межуровневых расстояний рассматриваемой квантовой системы в рамках теории квантового хаоса.

Список литературы

  1. Berry M.V. // Proceedings of the Royal Society A. 1987. V. 413. P. 183. https://doi.org/10.1098/rspa.1987.0109

  2. Bohigas O., Giannoni M.-J. Chaotic Motion and Random Matrix Theories // Lecture Notes in Physics. 1984. V. 209. P. 1–99. https://doi.org/10.1007/3-540-13392-5_1

  3. Штокман Х.-Ю. Квантовый хаос. М.: ФИЗМАТЛИТ, 2004. 376 с.

  4. Райхл Л.Е. Переход к хаосу в консервативных классических и квантовых системах. М.–Ижевск: РХД, 2008. 756 с.

  5. Ахиезер А.И., Шульга Н.Ф. Электродинамика высоких энергий в веществе. М.: Наука, 1993. 344 с.

  6. Ахиезер А.И., Шульга Н.Ф., Трутень В.И., Гриненко А.А., Сыщенко В.В. // УФН. 1995. Т. 165. № 10. С. 1165.

  7. Шульга Н.Ф., Сыщенко В.В., Нерябова В.С. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2013. № 3. С. 91. https://doi.org/10.1134/S1027451013020183

  8. Шульга Н.Ф., Сыщенко В.В., Тарновский А.И., Исупов А.Ю. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2015. № 7. С. 72. https://doi.org/10.7868/S0207352815070197

  9. Shul’ga N.F., Syshchenko V.V., Tarnovsky A.I., Isupov A.Yu. // Nuclear Instrum. Methods B. 2016. V. 370. P. 1. https://doi.org/10.1016/j.nimb.2015.12.040

  10. Shul’ga N.F., Syshchenko V.V., Tarnovsky A.I., Isupov A.Yu. // J. Physics: Conference Series. 2016. V. 732. P. 012028. https://doi.org/10.1088/1742-6596/732/1/012028

  11. Сыщенко В.В., Тарновский А.И. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2021. № 7. С. 84. https://doi.org/10.31857/S1028096021070207

  12. Сыщенко В.В., Тарновский А.И., Исупов А.Ю., Соловьев И.И. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 3. С. 103. https://doi.org/10.31857/S1028096020030188

  13. Shul’ga N.F., Syshchenko V.V., Tarnovsky A.I., Dronik V.I., Isupov A.Yu. // Journal of Instrumentation. 2019. V. 14. P. C12022. https://doi.org/10.1088/1748-0221/14/12/C12022

  14. Berry M.V., Robnik M. // J. Phys. A.: Math. Gen. 1984. 17. P. 2413. https://doi.org/10.1088/0305-4470/17/12/013

  15. Podolskiy V.A., Narimanov E.E. // Phys. Lett. A. 2007. V. 362. P. 412. https://doi.org/10.1016/j.physleta.2006.10.065

  16. Feit M.D., Fleck J.A., Jr., Steiger A. // J. Computational Physics. 1982. V. 47. P. 412. https://doi.org/10.1016/0021-9991(82)90091-2

  17. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. В 10 томах. Том 3. Квантовая механика. Нерелятивистская теория. М.: ФИЗМАТЛИТ, 2016. 800 с.

  18. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 8. М.: Мир, 1966. 272 с.

  19. Bohigas O., Tomsovic S., Ullmo D. // Phys. Rep. 1993. V. 223(2). P. 43. https://doi.org/10.1016/0370-1573(93)90109-Q

  20. Podolskiy V.A., Narimanov E.E. // Phys. Rev. Lett. 2003. V. 91. P. 263601. https://doi.org/10.1103/PhysRevLett.91.263601

  21. Bolotin Y., Tur A., Yanovsky V. Chaos: Concepts, Control and Constructive Use. Springer International Publishing Switzerland, 2017. https://doi.org/10.1007/978-3-319-42496-5

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал