1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 1, 2023

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2023, № 1, стр. 86-91

Отражение легких ионов от поверхности тел: аналитическая модель и компьютерное моделирование

В. П. Афанасьев a, *, Л. Г. Лобанова a, **, В. И. Шульга b, ***

a Национальный исследовательский университет “МЭИ”
111250 Москва, Россия

b Московский государственный университет им. М.В. Ломоносова, НИИЯФ им. Д.В. Скобельцына
119991 Москва, Россия

* E-mail: v.af@mail.ru
** E-mail: lida.lobanova.2017@mail.ru
*** E-mail: vish008@yandex.ru

Поступила в редакцию 29.06.2022
После доработки 22.07.2022
Принята к публикации 22.07.2022

Полный текст (PDF)

Аннотация

Получено аналитическое решение уравнения для распределения плотности потока отраженных легких ионов по длине пробега и по потерям энергии в мишени. Оно основано на решении граничных задач для уравнения переноса методом инвариантного погружения в малоугловом приближении. В случае отражения протонов от медной и вольфрамовой мишеней проведено сравнение аналитических результатов с данными компьютерного моделирования, выполненного с использованием программы OKSANA, а также с экспериментальными данными. Отмечена возможность верификации тормозной способности материала мишени на основе созданной методики.

Ключевые слова: отражение легких ионов, аналитическая модель, метод инвариантного погружения, малоугловое приближение, компьютерное моделирование, тормозная способность.

ВВЕДЕНИЕ

Теоретическое описание процессов взаимодействия ускоренных ионов с поверхностью твердого тела необходимо для создания новых материалов методами ионной имплантации, послойного анализа материалов, совершенствования методик ионно-рассеивательной спектроскопии и других целей. Наиболее активные исследования в этой области были выполнены в 80-е годы прошлого века [1–5], что связано в основном с проблемой “первой стенки” в установках управляемого термоядерного синтеза. Однако количественной модели, точно и последовательно описывающей процессы взаимодействия легких ионов с твердым телом, не существует. Упрощенные аналитические модели, используемые для описания процесса ионного рассеяния в твердых телах [1–3], часто ориентированы на объяснение конкретных экспериментов и не позволяют в полной мере описать процессы отражения легких ионов с энергией от единиц до десятков кэВ. Поэтому основным методом теоретического анализа в этой области исследований стало компьютерное моделирование процессов взаимодействия потоков легких ионов с поверхностью твердого тела [6, 7].

Следует, однако, отметить, что последние десятилетия ознаменовались созданием эффективных методов расчета энергетических спектров электронов, отраженных от поверхности твердого тела [8–26], описания процессов неупругих потерь электронов с энергией более сотен эВ [8–11, 26]. Наличие вычислительных продуктов для решения интегро-дифференциальных уравнений типа Рикатти позволило решить граничные задачи для уравнения переноса электронов в твердых телах [19, 22] с использованием метода инвариантного погружения Амбарцумяна [27–31]. Были установлены границы применимости малоугловых приближений [17–19, 22, 23] и определена их погрешность [19, 22]. Созданные методики позволили получить ряд аналитических решений, эффективно описывающих сигналы электронной спектроскопии с необходимой точностью [9, 13, 19, 22, 23].

Возникает вопрос, можно ли применить указанные наработки теории электронного рассеяния в задачах отражения ионов от поверхности, учитывая, что малоугловые подходы, применяемые в задачах электронного рассеяния, в задачах ионного рассеяния применимы в гораздо более широком интервале энергии. В настоящей работе сделана попытка использовать для расчета энергетических и угловых спектров отраженных ионов аналитическую модель Освальда–Каспера–Гауклера (ОКГ) [12, 13, 19]. В рамках этой модели рассчитывают распределение отраженных частиц по длине пробега $s$ в мишени. Подход ОКГ основан на решении граничных задач для уравнения переноса в малоугловом приближении [19].

Проведено сравнение результатов аналитического рассмотрения с результатами компьютерного моделирования и экспериментальными данными. Численные расчеты выполнены для протонов с энергией порядка кэВ при различных углах падения на медную и вольфрамовую мишени.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

В модели ОКГ уравнение для плотности потока частиц $R\left( {s,{{\mu }_{0}},\mu } \right),$ отразившихся от мишени и прошедших в ней путь $s,$ имеет вид [19]:

(1)
$\begin{gathered} \left( {1 + {\partial \mathord{\left/ {\vphantom {\partial {\partial s}}} \right. \kern-0em} {\partial s}}} \right)R\left( {s,{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\left| \mu \right|}}{{{{\mu }_{0}} + \left| \mu \right|}}x\left( {{{\mu }_{0}},\mu } \right) + \\ + \,\,\int\limits_{ - 1}^0 {R\left( {s,{{\mu }_{0}},\mu {\kern 1pt} '} \right)x\left( {\mu {\kern 1pt} ',\mu } \right)d\mu {\kern 1pt} '} {\text{,}} \\ \end{gathered} $
где μ0, μ – косинусы углов падения и отражения. Углы отсчитываются от нормали к поверхности, а пробег s измеряется в длинах среднего пробега между упругими соударениями. Уравнение (1) получено в малоугловом приближении, подразумевающем малость параметра
(2)
$\zeta = {{{{x}_{{{\text{el}}}}}\left( \pi \right)} \mathord{\left/ {\vphantom {{{{x}_{{{\text{el}}}}}\left( \pi \right)} {{{x}_{{{\text{el}}}}}\left( 0 \right)}}} \right. \kern-0em} {{{x}_{{{\text{el}}}}}\left( 0 \right)}} \ll 1,$
где ${{x}_{{{\text{el}}}}}\left( \theta \right)$ – нормированное на единицу сечение упругого рассеяния электронов или ионов на угол $\theta $ – ионов. Следует отметить, что для ионов неравенство (2) справедливо в более широком интервале значений энергии, чем для электронов.

Для ионов и электронов уравнение (1) различается лишь видом сечения упругого рассеяния $x\left( \mu \right).$ Решение уравнения (1) строится на основе метода сферических гармоник с использованием методики аналитического продолжения интегралов по полярному углу рассеяния на интервал –1 < μ < 1. Это приводит к решению для функции отражения:

(3)
$\begin{gathered} R\left( {s,{{\mu }_{0}},\mu } \right) = \frac{{{{\mu }_{0}}\left| \mu \right|}}{{{{\mu }_{0}} + \left| \mu \right|}}{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}\sum\limits_{l{\kern 1pt} \, = \,{\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}} \times \\ \times \,\,\left( {{{\mu }_{0}}\mu + {{{(1 - \mu _{0}^{2})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{{(1 - {{\mu }^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right) \times \\ \times \,\,\left( {{\text{exp}}\left( { - \left( {1 - {{x}_{l}}} \right)s} \right) - {\text{exp}}\left( { - s} \right)} \right), \\ \end{gathered} $
где ${{P}_{l}}\left( \mu \right)$ – полиномы Лежандра, ${{x}_{l}}$ – коэффициенты разложения нормированного на единицу сечения упругого рассеяния $x\left( \mu \right)$ в ряд по полиномам Лежандра.

Проинтегрировав уравнение (3) по пробегам, приходим к формуле, описывающей угловое распределение отраженных ионов:

(4)
$\begin{gathered} R\left( {{{\mu }_{0}},\mu } \right) = - \frac{{{{\mu }_{0}}\left| \mu \right|}}{{{{\mu }_{0}} + \left| \mu \right|}}{\text{exp}}\left( {{{ - V} \mathord{\left/ {\vphantom {{ - V} {{{V}_{ \bot }}}}} \right. \kern-0em} {{{V}_{ \bot }}}}} \right)\sum\limits_{l{\kern 1pt} \, = \,{\kern 1pt} 0}^\infty {\frac{{2l + 1}}{2}} {{P}_{l}} \times \\ \times \,\,\left( {{{\mu }_{0}}\mu + {{{(1 - \mu _{0}^{2})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{{(1 - {{\mu }^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right)\ln \left( {1 - {{x}_{l}}} \right), \\ \end{gathered} $
где ${{V}_{ \bot }}$ – составляющая скорости иона, перпендикулярная поверхности образца, а множитель ${\text{exp}}\left( {{{ - V} \mathord{\left/ {\vphantom {{ - V} {{{V}_{ \bot }}}}} \right. \kern-0em} {{{V}_{ \bot }}}}} \right)$ учитывает вероятность “выживания” ионов в результате перезарядки на поверхности.

Энергетические спектры отраженных частиц будем определять формулой:

(5)
$R\left( {\Delta ,{{\mu }_{0}},\mu } \right) = \int\limits_0^\infty {R\left( {{z \mathord{\left/ {\vphantom {z {{{l}_{{{\text{el}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{el}}}}}}},{{\mu }_{0}},\mu } \right)T\left( {{z \mathord{\left/ {\vphantom {z {{{l}_{{{\text{in}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{in}}}}}}},\Delta } \right)dz} ,$
где $T\left( {{z \mathord{\left/ {\vphantom {z {{{l}_{{{\text{in}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{in}}}}}}},\Delta } \right)$ – функция, описывающая неупругие потери энергии ионов и ${{l}_{{{\text{in}}}}}$ – средняя длина свободного неупругого пробега ионов. Эта формула является следствием гипотезы Ферми о возможности представления дифференциального сечения элементарного акта рассеяния в виде суммы:
(6)
$\begin{gathered} \omega \left( {\Delta ,{{\mu }_{0}},\mu ,{{\varphi }_{0}},\varphi } \right) = {{\omega }_{{{\text{in}}}}}\left( \Delta \right)\delta \left( {\mu - {{\mu }_{0}}} \right)\delta \left( {\varphi - {{\varphi }_{0}}} \right) + \\ + \,\,{{\omega }_{{{\text{el}}}}}\left( {{{\mu }_{0}},\mu ,{{\varphi }_{0}},\varphi } \right)\delta \left( \Delta \right), \\ \end{gathered} $
где $\omega $ – дифференциальное сечение рассеяния, ${{\omega }_{{{\text{in}}}}},$ ${{\omega }_{{{\text{el}}}}}$ – дифференциальное сечение неупругого и упругого рассеяния соответственно.

Формула (6) указывает на то, что акт элементарного рассеяния можно разбить на два независимых процесса – упругое и неупругое рассеяние. В результате акта неупругого рассеяния теряется энергия, но не меняется направление движения быстрой частицы, упругое рассеяние идет без потерь энергии, однако с изменением направления движения.

Функция $T\left( {\tau ,\Delta } \right)$ – функция неупругого процесса, описывающая энергетический спектр частиц, прошедших в мишени путь $\tau {\text{.}}$ В случае электронного рассеяния функция $T\left( {\tau ,\Delta } \right)$ является функцией Ландау и представима в виде ряда:

(7)
$\begin{gathered} T\left( {\tau ,\Delta } \right) = {\text{exp}}\left( { - \tau } \right) \times \\ \times \,\,\left[ {\delta \left( \Delta \right) + \tau {{x}_{{{\text{in}}}}}\left( \Delta \right) + {{{{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{\tau }^{2}}} {2!}}} \right. \kern-0em} {2!}}\int\limits_0^\Delta {{{x}_{{{\text{in}}}}}\left( {\Delta - \varepsilon } \right){{x}_{{{\text{in}}}}}\left( \varepsilon \right)d\varepsilon } + } \right. \\ \left. { + \,\,... + {{{{\tau }^{k}}} \mathord{\left/ {\vphantom {{{{\tau }^{k}}} {k!}}} \right. \kern-0em} {k!}}\int\limits_0^\Delta {x_{{{\text{in}}}}^{{k\,{\kern 1pt} - {\kern 1pt} \,1}}\left( {\Delta - \varepsilon } \right){{x}_{{{\text{in}}}}}\left( \varepsilon \right)d\varepsilon + ...} } \right], \\ \end{gathered} $
где $\int_0^\Delta {{{x}_{{{\text{in}}}}}\left( {\Delta - \varepsilon } \right){{x}_{{{\text{in}}}}}\left( \varepsilon \right)d\varepsilon } = {{x}^{2}}\left( \Delta \right),$ $\int_0^\Delta {x_{{{\text{in}}}}^{{k{\kern 1pt} - {\kern 1pt} 1}}\left( {\Delta - \varepsilon } \right)} $ × × ${{x}_{{{\text{in}}}}}\left( \varepsilon \right)d\varepsilon = {{x}^{k}}\left( \Delta \right).$ Если ${{x}_{{{\text{in}}}}}\left( \Delta \right)$ – вероятность потери энергии $\Delta $ в результате одного акта неупругого рассеяния то, ${{x}^{k}}\left( \Delta \right)$ имеет смысл потери энергии $\Delta $ в результате k актов неупругого рассеяния.

Функция $T\left( {\tau ,\Delta } \right)$ в случае ионного рассеяния определяется в приближении Фоккера–Планка лишь двумя параметрами сечения неупругого рассеяния, а именно средними потерями энергии на единице длины $\bar {\varepsilon }$ (stopping power) и средним квадратом потерь энергии $\overline {{{\varepsilon }^{2}}} $ (straggling):

(8)
$T\left( {s,\Delta } \right) = \frac{1}{{{{{(2\pi \overline {{{\varepsilon }^{2}}s} )}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\text{exp}}\left( {{{ - {{{\left( {\Delta - \bar {\varepsilon }s} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {\Delta - \bar {\varepsilon }s} \right)}}^{2}}} {2\overline {{{\varepsilon }^{2}}s} }}} \right. \kern-0em} {2\overline {{{\varepsilon }^{2}}s} }}} \right).$
Отметим, что приближение Фоккера–Планка верно, если ${{x}_{{{\text{in}}}}}\left( \Delta \right)$ имеет резкий максимум при $\Delta \to 0$ и справедливо, например, для модели атома Томсона [32]. Но в теории Линдхарда, используемой для определения $\bar {\varepsilon }$ в случае торможения ионов с энергией несколько кэВ, сечение ${{x}_{{{\text{in}}}}}\left( \Delta \right)$ не имеет особенностей при $\Delta \to 0,$ и приближение Фоккера–Планка становится неприемлемым.

Подставив формулу (3) в формулу для расчета энергетических спектров отраженных ионов (5), получим:

(9)
$\begin{gathered} R\left( {\Delta ,{{\mu }_{0}},\mu } \right) = \\ = \frac{{{{\mu }_{0}}\left| \mu \right|}}{{{{\mu }_{0}} + \left| \mu \right|}}\frac{{\left( {1 - {{x}_{1}}} \right)\left( {1 - \Delta } \right)}}{{\Delta \bar {\varepsilon }}}{\text{exp}}\left( { - \frac{A}{{{{{\left( {1 - \Delta } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right) \times \\ \times \,\,\mathop \sum \limits_{l{\kern 1pt} \, = \,{\kern 1pt} 0}^\infty \frac{{2l + 1}}{2}{{P}_{l}}\left( {{{\mu }_{0}}\mu + {{{\left( {1 - \mu _{0}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{{\left( {1 - {{\mu }^{2}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right) \times \\ \times \,\,\left[ {{\text{exp}}\left( { - \frac{{\Delta \left( {1 - {{x}_{l}}} \right)\sigma {\kern 1pt} {\text{*}}}}{{\left( {1 - {{x}_{1}}} \right){{{\left( {1 - \Delta } \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \right)} \right. - \\ \left. { - \,\,{\text{exp}}\left( { - \frac{{\Delta \sigma {\kern 1pt} {\text{*}}}}{{\left( {1 - {{x}_{1}}} \right){{{\left( {1 - \Delta } \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \right)} \right]. \\ \end{gathered} $
Здесь множители ${{\left( {1 - \Delta } \right)}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$ и $\left( {1 - \Delta } \right){\text{\;}}$учитывают зависимость сечений упругого и неупругого рассеяния от энергии, а функция ${\text{exp}}\left( { - \frac{A}{{{{{\left( {1 - \Delta } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right)$ связана с учетом перезарядки отраженных ионов водорода [3, 4], $A$ – подгоночный параметр.

В формуле (9) присутствует также безразмерный параметр $\sigma {\text{*}},$ который является определяющим при аналитическом описании процесса формирования энергетических спектров отраженных ионов:

(10)
$\sigma {\text{*}} = {{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{l}_{{{\text{tr}}}}}\bar {\varepsilon },}}} \right. \kern-0em} {{{l}_{{{\text{tr}}}}}\bar {\varepsilon },}}$
где ${{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{l}_{{{\text{tr}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{tr}}}}}}}$ имеет смысл и порядок длины пробега иона до полной остановки (residual range) R0, ${{l}_{{{\text{tr}}}}}$ – транспортный пробег иона, или длина полной изотропизации.

Отметим, что именно процесс изотропизации нисходящего потока электронов позволил Г. Бете [33] создать простую теорию отражения электронов, удовлетворительно описывающую интегральные коэффициенты отражения электронов от мишеней с Z > 30. Теория Бете базируется на двух длинах: длине полной изотропизаци ${{l}_{{{\text{t}}{{{\text{r}}}_{{{\text{TOT}}}}}}}}$ и длине полного торможения ${{R}_{0}}.$ Из данной теории следует, что при ${{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{l}_{{{\text{t}}{{{\text{r}}}_{{{\text{TOT}}}}}}}}}}} \right. \kern-0em} {{{l}_{{{\text{t}}{{{\text{r}}}_{{{\text{TOT}}}}}}}}}} \to 0$ полный коэффициент отражения электронов стремится к 0.5, что удовлетворительно согласуется с экспериментальными данными.

СРАВНЕНИЕ С МОДЕЛИРОВАНИЕМ И ЭКСПЕРИМЕНТОМ

Моделирование выполнено с использованием компьютерной программы OKSANA в том ее варианте, который описан в [34]. Программа основана на приближении парных столкновений и моделирует взаимодействие ионов с аморфными, монокристаллическими и поликристаллическими материалами. В настоящей работе рассмотрены только аморфные мишени. Как и в программе MARLOWE [35], аморфная мишень моделируется вращением кристаллического атомного блока, процедура вращения повторяется от столкновения к столкновению. Углы рассеяния в парных столкновениях рассчитывают с использованием табулированных значений, найденных заранее путем решения уравнений движения для заданного межатомного потенциала (молекулярная динамика). В качестве межатомного потенциала использован потенциал Kr–C [6]. С целью сравнения с теорией, изложенной выше, для каждого бомбардирующего иона рассчитывали длину его траектории в мишени до момента остановки частицы или ее выхода из мишени. Поверхность мишени считали гладкой, какие-либо изменения в мишени, вызванные ионной бомбардировкой, не учитывали.

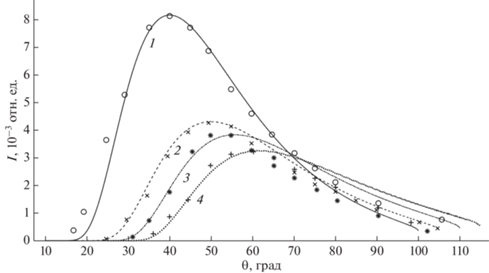
В целях апробации методики ОКГ, хорошо выверенной в задачах электронного рассеяния [13, 19], для задач рассеяния легких ионов в работе проведено сравнение расчетов на основе (3) и (4) с результатами моделирования методом Монте-Карло (рис. 1) и с экспериментальными данными (рис. 2) соответственно. Рис. 1 и 2 показывают удовлетворительные результаты сравнения расчетных данных с данными компьютерного моделирования и экспериментальными данными. Наличие хорошо выверенного решения задачи упругого рассеяния будет надежной базой для определения и верификации параметров неупругого рассеяния: средних потерь энергии на единице длины (stopping power) и параметра флуктуаций энергетических потерь (straggling).

Рис. 1.

Распределение по длине пробега протонов, отраженных от медной мишени. Угол падения 80°, угол отражения 110°, начальная энергия протонов ${{E}_{0}}{\text{:}}$ 6 (1); 20 кэВ (2). Линии – расчет на основе формулы (3), символы – компьютерное моделирование.

Рис. 2.

Угловые распределения протонов, отраженных от медной мишени. Начальная энергия протонов ${{E}_{0}}$ = 21.6 кэВ, угол падения: 80° (1); 75°(2); 70°(3); 65°(4). Линии – расчет по формуле (4), символы – эксперимент [36].

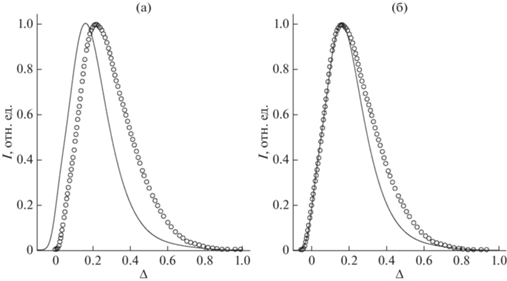
Представленные на рис. 3 графики указывают на удовлетворительное соответствие расчетов экспериментальным данным. В расчетах использовали данные базы NIST о средних потерях энергии протонов в W на единице длины, транспортное сечение протонов вычисляли по формуле Фирсова [38], параметр перезарядки $A$ = 1. Наименьшее доверие в расчетных величинах вызывают данные о средних потерях энергии на единице длины $\bar {\varepsilon }{\text{.}}$ Достаточно взглянуть на разброс данных о торможении протонов в золоте, для которого выполнено наибольшее число экспериментов [5]. Изменение средних потерь энергии от значения $\bar {\varepsilon }$ = 137.6 эВ/нм, представленного в данных NIST, до $\bar {\varepsilon }$ = 110.1 эВ/нм приводит к совпадению максимумов расчетного и экспериментального спектров (рис. 3б). По оси ординат на рис. 3 отложена безразмерная потеря энергии: ${{\left( {{{E}_{0}} - E} \right)} \mathord{\left/ {\vphantom {{\left( {{{E}_{0}} - E} \right)} {{{E}_{0}},}}} \right. \kern-0em} {{{E}_{0}},}}$ учет кинематического фактора [3] приведет в данном масштабе к сдвигу в область больших потерь энергии на величину 0.0023, которая более чем на порядок меньше погрешности эксперимента.

Рис. 3.

Энергетические спектры протонов, отраженных от вольфрамовой мишени: а – расчет на основе данных NIST; б – результат подгонки по $\bar {\varepsilon }{\text{.}}$ Начальная энергия ${{E}_{0}}$ = 25 кэВ, угол падения 71°, угол отражения 109°. Сплошные линии – расчет на основе (9), символы – эксперимент [37].

ЗАКЛЮЧЕНИЕ

В настоящей работе модель формирования энергетических спектров отраженных частиц, использованная ранее в задачах электронного рассеяния, распространена на случай ионного рассеяния. Получены аналитические формулы (3), (4), (9) для плотности потока отраженных легких ионов, справедливые в более широком диапазоне энергии по сравнению с электронным рассеянием. Основным критерием, определяющим область применимости полученных выражений, является малость отношения параметра экранирования, определяемого квадратом отношения де бройлевской длины волны частицы, к дебаевскому радиусу тормозящей среды. Параметр экранирования при фиксированном материале среды и энергии частицы на порядки меньше в случае легких ионов. Показано, что основным параметром, определяющим характеристики энергетического спектра отраженных ионов, является величина $\sigma {\text{*}},$ зависящая от величины транспортного пробега ${{l}_{{{\text{tr}}}}}$ и тормозной способности $\bar {\varepsilon }$ (формула (10)).

Численные расчеты проведены для отражения протонов с энергией 6 и 20 кэВ от медной мишени. Экспериментальные данные приведены для отражения протонов с энергией 21.6 и 25 кэВ от медной и вольфрамовой мишеней. Показано, что результаты аналитического рассмотрения находятся в хорошем согласии с данными компьютерного моделирования (программа OKSANA) и экспериментальными данными. Отмечена возможность верификации тормозной способности материала мишени на основе предложенной методики.

Список литературы

  1. Машкова Е.С., Молчанов В.А. Рассеяние ионов средних энергий поверхностями твердых тел. М.: Атомиздат, 1980. 256 с.

  2. Курнаев В.А., Машкова Е.С., Молчанов В.А. Отражение легких ионов от поверхности твердого тела. М.: Энергоатомиздат, 1985. 192 с.

  3. Mashkova E.S., Molchanov V.A. Medium Energy Ion Reflection from Solids. Amsterdam: North-Holland, 1985. 444 p.

  4. Рязанов М.И., Тилинин И.С. Исследование поверхности по обратному рассеянию частиц. М.: Энергоатомиздат, 1985. 150 с.

  5. Ziegler J.F., Biersack J.P., Littmark U. The Stopping and Range of Ions in Solids. N.Y.: Pergamon, 1985. 321 p.

  6. Экштайн В. Компьютерное моделирование взаимодействия частиц с поверхностью твердого тела. М.: Мир, 1995. 319 с.

  7. Булгадарян Д.Г. Рассеяние протонов кэвных энергий как инструмент анализа тонких слоев на поверхности материалов: Дис. … канд. физ.-мат. наук: 01.04.08. Москва: МИФИ, 2020. 116 с.

  8. Tougaard S., Kraaer J. // Phys. Rev. B. 1991. V. 43. № 2. P. 1651. https://doi.org./10.1103/PhysRevB.43.1651

  9. Afanas’ev V.P., Lubenchenko A.V., Gubkin M.K. // Eur. Phys. J. B. 2004. V. 37. № 1. P. 117. https://doi.org/10.1140/epjb/e2004-0036-x

  10. Werner W.S.M. // Surf. Sci. 2005. V. 588. № 1–3. P. 26. https://doi.org./10.1016/j.susc.2005.05.023

  11. Werner W.S.M. // Surf. Sci. 2007. V. 601. № 10. P. 2125. https://doi.org/10.1016/j.susc.2007.03.001

  12. Oswald R., Kasper E., Gaukler K.H. // J. Electron. Spectrosc. Relat. Phenom. 1993. V. 61. № 3–4. P. 251. https://doi.org/10.1016/0368-2048(93)80019-i

  13. Salvat-Pujol F., Werner W.S.M. // Phys. Rev. B. 2011. V. 83. № 19. P. 195416. https://doi.org./10.1103/PhysRevB. 83.195416

  14. Bronshtein I.M., Pronin V.P. // Sov. Phys. Solid State. 1975. V. 17. № 8. P. 2502.

  15. Pronin V.P. Elastic and Inelastic Interaction of Medium Energy Electrons with Surface of Solids. Thesis for the Degree of Doctor of Science. Saint-Petersburg: Herzen State Pedagogical University, 2014.

  16. Powell C.J., Jablonski A. // J. Electron. Spectrosc. Relat. Phenom. 2010. V. 178–179. № 3–4. P. 331. https://doi.org/10.1016/j.elspec.2009.05.004

  17. Афанасьев В.П. // Элементарные процессы и кинетика высокотемпературной неравновесной плазмы. М.: Изд-во МЭИ, 1988. С. 82.

  18. Afanas’ev V.P., Naujoks D. // Phys. Stat. Sol. 1991. V. 164. № 1. P. 133. https://doi.org/10.1002/pssb.2221640113

  19. Afanas’ev V.P., Efremenko D.S., Kaplya P.S. // J. Electron. Spectrosc. Relat. Phenom. 2016. V. 210. P. 16. https://doi.org/10.1016/j.elspec.2016.04.006

  20. Salvat-Pujol F., Jablonski A., Powell C.J. // Comput. Phys. Commun. 2005. V. 165. № 2. P. 157. https://doi.org/10.1016/j.cpc.2004.09.006

  21. Werner W.S.M. // Surf. Interface Anal. 2005. V. 37. № 11. P. 846. https://doi.org/10.1002/sia.2103

  22. Afanas’ev V.P., Kaplya P.S. // J. Surf. Invest.: X-Ray, Synchrotron Neutron Tech. 2015. V. 9. № 4. P. 715. https://doi.org/10.1134/s1027451015020238

  23. Afanas’ev V.P., Naujoks D. // Z. Phys. B. 1991. V. 84. № 3. P. 397. https://doi.org./10.1007/bf01314014

  24. Zemek J., Jiricek P., Werner W.S.M., Lesiak B., Jablonski A. // Surf. Interface Anal. 2006. V. 38. № 4. P. 615. https://doi.org./10.1002/sia.2147

  25. Jablonski A., Hansen H.S., Jansson C., Tougaard S. // Phys. Rev. B. 1992. V. 45. № 7. P. 3694.https://doi.org/10.1103/PhysRevB.45.3694

  26. Tougaard S., Chorkendorff I. // Phys. Rev. B. 1987. V. 35. № 13. P. 6570. https://doi.org/10.1103/physrevb.35.6570

  27. Dashen R.F. // Phys. Rev. B. 1964. V. 134. № 4A. P. A1025. https://doi.org/10.1103/PhysRev.134.A1025

  28. Ambartsumian V.A. // J. Phys. 1941. V. 5. № 1. P. 93.

  29. Ambartsumian V.A. // Izv. AN SSSR. 1942. V. 3. P. 97.

  30. Ambartsumian V.A. // J. Phys. 1944. V. 8. № 2. P. 65.

  31. Sobolev V.V. Light Scattering in Planetary Atmospheres. N.Y.: Pergamon Press, 1975. 256 p.

  32. Thomson J.J. // Phil. Mag. 1912. V. 23. № 136. P. 449.

  33. Bethe H. // Z. Phys. B. 1930. V. 397. № 3. P. 325. https://doi.org/10.1002/andp.19303970303

  34. Shulga V.I., Schinner A., Sigmund P. // Nucl. Instrum. Methods Phys. Res. B. 2020. V. 467. P. 91. https://doi.org/10.1016/j.nimb.2020.01.029

  35. Robinson M.T., Torrens I.M. // Phys. Rev. B. 1974. V. 9. № 12. P. 5008. https://doi.org/10.1103/PhysRevB.9.5008

  36. Morita K., Akimune H., Suita T. // Jpn. J. Appl. Phys. 1968. V. 7. № 8. P. 916. https://doi.org/10.1143/JJAP.7.916

  37. Булгадарян Д.Г., Синельников Д.Н., Ефимов Н.Е., Курнаев В.А. // Изв. РАН. Сер. Физ. 2020. Т. 84. № 6. С. 903. https://doi.org./10.31857/S036767652006006X

  38. Firsov O.B. // JETP. 1959. V. 9. № 5. P. 1076.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал