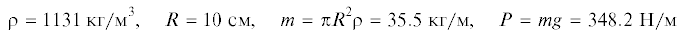Прикладная математика и механика, 2019, T. 83, № 2, стр. 215-227
ТОРМОЖЕНИЕ ЖЕСТКОГО ЦИЛИНДРА, СКОЛЬЗЯЩЕГО ПО ВЯЗКОУПРУГОМУ ОСНОВАНИЮ
И. Г. Горячева 1, *, А. А. Зобова 2, **
1 Институт проблем механики им. А.Ю. Ишлинского
Москва, Россия
2 Московский государственный университет им. М.В. Ломоносова
Москва, Россия
* E-mail: goryache@ipmnet.ru
** E-mail: azobova@mech.math.msu.su
Поступила в редакцию 07.02.2019
После доработки 14.03.2019
Принята к публикации 19.03.2019
Аннотация
Изучается торможение бесконечного жесткого цилиндра при его скольжении по поверхности вязкоупругого полупространства (ось цилиндра, движущегося плоскопараллельно, горизонтальна). Предполагается, что касательные напряжения в области контакта отсутствуют. Распределение контактных давлений, размер области контактного взаимодействия и зависимость силы сопротивления от скорости оси цилиндра определяются из решения квазистатической задачи теории вязкоупругости. На основании разработанной математической модели качественно и численно изучены особенности процесса торможения и их зависимость от вязкоупругого параметра основания.
1. Введение. При контактировании движущихся относительно друг друга тел вследствие неидеальной упругости материалов восстановление деформированной области сопровождается потерями механической энергии и возникновением сил сопротивления движению. Изучение влияния релаксационных свойств материалов на силу сопротивления движению и динамику механических систем – важная задача на стыке механики сплошной среды и теоретической механики.
В механике сплошной среды базовыми задачами являются квазистационарные задачи об относительном движении тел из деформируемых материалов. В ряде работ [1–5] рассматривалось плоско-параллельное движение бесконечного цилиндра по опорной плоскости из деформируемого материала с разными законами, связывающими напряжения и деформации в материале. При этом предполагалось, что скорость оси цилиндра, во-первых, постоянна, а во-вторых, много меньше скоростей распространения волн деформаций в материале, движение среды принимали установившимся, а инерционными членами в уравнениях механики сплошной среды пренебрегали.
Рассматривались нестационарные задачи о движении цилиндра по вязкоупругому полупространству с учетом инерционных членов в уравнениях движения среды [6, 7]. Изучалась релаксация к стационарному движению вязкоупругой среды [6], при этом скорость оси цилиндра предполагалась постоянной; найдены поправки к коэффициенту трения, вычисленному в квазистационарной постановке. Рассматривались нестационарные движения цилиндра по вязкоупругому полупространству [7]. При постановке задачи вертикальная нагрузка и скорость оси цилиндра задавались как функции времени. Построен численный алгоритм определения силы сопротивления, распределения давления и параметров области контактного взаимодействия, проведено сравнение полученного решения с квазистационарным решением. Отметим, что в этих работах динамика цилиндра под действием приложенных к нему сил не изучалась: предполагалось, что цилиндр совершает заранее предписанное движение.
Феноменологические модели вязкоупругого основания [8–11] использовались при изучении динамики цилиндра, движущегося под действием приложенных к нему сил, в том числе силы взаимодействия цилиндра с вязкоупругой средой. Аналогично подходу А.Ю. Ишлинского [12], в этих работах вязкоупругая среда описывалась моделями пружинного основания. Предполагалось [8, 9, 12], что скорость оси цилиндра и его глубина погружения в вязкоупругое полупространство постоянны. Эти параметры явно входят в выражения для распределения нормального давления и силы сопротивления. При нестационарных движениях шара [10] и цилиндра [11] параметры контактного взаимодействия зависят также от вертикальной составляющей скорости оси цилиндра или центра шара.
При условии, что касательные напряжения в контактной области описываются законом Амонтона–Кулона, поставлена и решена динамическая задача о движении диска по вязкоупругому основанию с наклонной прямолинейной границей под действием силы тяжести и силы сопротивления со стороны опоры [11]. Однако оказалось, что зависимость силы сопротивления от скорости оси цилиндра качественно отличается от полученной при решении соответствующей задачи вязкоупругости [1, 2].
Рассматривалась задача о неравномерном скольжении штампа по вязкоупругому основанию [13]. Контактные давления описывались упрощенной моделью Кельвина, сила сопротивления движению вычислялась из энергетических соотношений в предположении малой кривизны штампа, проведены расчеты торможения клиновидного штампа для модели Кельвина–Фойхта. Таким образом, одновременно решалась нестационарная задача теории вязкоупругости и динамическая задача о торможении тела.
В настоящей работе рассматривается плоскопараллельное движение жесткого кругового цилиндра, ось которого горизонтальна, по вязкоупругой горизонтальной плоскости. Предполагается, что касательные напряжения в области контактного взаимодействия равны нулю. Изучается торможение цилиндра за счет действующей на него силы сопротивления, возникающей в области контактного взаимодействия. Для расчета силы сопротивления как функции скорости скольжения цилиндра используется решение контактной задачи теории вязкоупругости в квазистатической постановке [1, 2]. Проведен качественный анализ уравнений движения. Численно найдены решения задачи Коши для некоторых реальных значений параметров вязкоупругого материала. При заданных начальных условиях найдена зависимость скорости центра цилиндра, длины участка контактного взаимодействия и его смещения от времени, распределение нормальных напряжений в области контакта, найдена зависимость времени остановки и пути торможения от вязкоупругих характеристик материала основания. Представленная работа – продолжение исследования [16, 17], в котором решение контактных задач используется для изучения динамики системы.
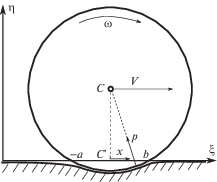
2. Постановка задачи. Рассмотрим скольжение жесткого однородного цилиндра (1) с удельной (на единицу длины) массой $m$ и радиуса $R$ по вязкоупругому основанию (2) без трения. Распределение масс в цилиндре предполагается осесимметричным, так что центр масс каждого сечения цилиндра $C$ лежит на его оси.
Введем неподвижную систему отсчета $O\xi \eta \zeta $, ось $O\xi $ которой принадлежит недеформированной опорной плоскости, ось $O\eta $ направлена вертикально вверх, ось $O\zeta $ перпендикулярна плоскости движения и сонаправлена с осью цилиндра. Горизонтальную скорость оси цилиндра обозначим ${\mathbf{V}} = V{{{\mathbf{e}}}_{\xi }}$, а угловую скорость обозначим ${\mathbf{\omega }} = - \omega {{{\mathbf{e}}}_{\zeta }}$. Положительное значение $\omega $ соответствует вращению по часовой стрелке, если смотреть с конца оси $O\zeta $ (фиг. 1). Введем также подвижную декартову систему координат $C{\kern 1pt} {\text{'}}xyz$ с осями, параллельными $O\xi \eta \zeta $ c началом в точке $C'$ – проекции центра сечения цилиндра на недеформированную плоскость. Предполагается, что скорость движения оси цилиндра мала по сравнению со скоростями распространения возмущений в вязкоупругой среде, поэтому для определения распределения давлений в области контакта цилиндра с вязкоупругим основанием будем использовать решение контактной задачи теории вязкоупругости в плоской квазистатической постановке [1, 2, 14]. Приведем далее ее постановку.
В силу предположения о малости деформаций, контур цилиндра в области контакта заменим параболой $f(x)$ = ${{x}^{2}}{\text{/}}(2R)$. Граничные условия на поверхности вязкоупругой полуплоскости отнесем к недеформированной границе ($y = 0$). Из условия контакта следует, что для всех точек площадки контакта $( - a,b)$ для перемещений ${{u}_{y}}$ по нормали к поверхности ($y = 0$) выполняется соотношение ${{u}_{y}} = f(x) + {\text{const}}$, или
Заметим, что границы $ - a$ и $b$ области контакта – функции времени. Поверхности взаимодействующих тел вне площадки контакта $( - a,b)$ не нагружены. На всей площадке контакта касательные напряжения нулевые:
Соотношения между компонентами деформации и напряжения в изотропном вязкоупругом теле примем в следующем виде (случай плоской деформации):
Величины ${{T}_{\varepsilon }}$ и ${{T}_{\sigma }}$ характеризуют вязкие свойства среды, $E$ – модуль Юнга, $\nu $ – коэффициент Пуассона соответственно. Случай плоского напряженного состояния рассматривается аналогично. Эти уравнения являются двумерным аналогом модели Максвелла–Томсона, для которой величина $H = {{T}_{\varepsilon }}E{\text{/}}{{T}_{\sigma }}$ – мгновенный модуль упругости, ${{T}_{\varepsilon }} > {{T}_{\sigma }}$.
Введем обозначение для контактного давления:
Со стороны основания на цилиндр действуют силы $P{{{\mathbf{e}}}_{y}}$ и $Q{{{\mathbf{e}}}_{x}}$, являющиеся результирующими контактного давления $p(x)$. Поскольку цилиндр жесткий, отнесем нормальные напряжения к окружности цилиндра и, пользуясь малостью контактной области, получим
Поскольку все элементарные силы, действующие на границе цилиндра, направлены к его оси, получаем, что их суммарный момент относительно оси цилиндра равен нулю: ${\mathbf{M}} = 0$.
Динамика цилиндра описывается уравнениями:
(2.1)
$m{\mathbf{a}} = m{\mathbf{g}} + P{{{\mathbf{e}}}_{y}} + Q{{{\mathbf{e}}}_{x}},\quad \frac{{d{{{\mathbf{K}}}_{C}}}}{{dt}} = 0,\quad {{{\mathbf{K}}}_{C}} = - J\omega {{{\mathbf{e}}}_{\zeta }},\quad J = \frac{1}{2}m{{R}^{2}},$В скалярном виде уравнения (2.1) имеют вид
Предполагается, что ${{a}_{\eta }} = 0$, и, следовательно, $P = mg$. Последнее уравнение показывает, что угловая скорость цилиндра остается постоянной $\omega \equiv \omega (0)$. Далее это уравнение не рассматривается. Добавим к уравнениям (2.2) кинематическое соотношение
задающее зависимость от времени абсолютной координаты оси цилиндра.Будем изучать процесс торможения, т.е., задаваясь начальной скоростью оси цилиндра $V(0)$ и начальной координатой оси цилиндра $\xi (0) = 0$, будем решать задачу Коши для уравнений (2.2) и (2.3). По полученной функции $V(t)$ будут определяться границы участка контактного взаимодействия в разные моменты времени, а также распределение давлений.
3. Безразмерные переменные, метод решения, качественные результаты. Перейдем к безрамерным переменным. Решение задачи теории вязкоупругости описывается двумя безразмерными параметрами [2]
Параметр $\alpha \geqslant 1$ задает отношение времени последействия к времени релаксации и равен единице для упругих материалов; параметр $\kappa $ представляет собой отношение радиуса цилиндра к длине участка контактного взаимодействия в покое ${{l}_{0}} = \sqrt {32RP{\text{/}}E{\text{'}}} $. Так как в постановке задачи вязкоупругости предполагается малость области контактного взаимодействия по сравнению с радиусом цилиндра [2], то $\kappa \gg 1$.
Помимо этого, для решения поставленной задачи о торможении требуется ввести третий безразмерный параметр
задающий соотношение масштаба времени, задаваемого ускорением свободного падения и радиусом цилиндра, и времени последействия ${{T}_{\varepsilon }}$.Введем безразмерные переменные
(3.1)
$\frac{{d\tilde {\xi }}}{{d\tilde {t}}} = \tilde {V},\quad \frac{{d\tilde {V}}}{{d\tilde {t}}} = \gamma \tilde {Q}$Здесь $\tilde {Q} = \tilde {Q}(\tilde {V})$ – сила сопротивления, вычисляемая по квазистатическому решению задачи теории вязкоупругости, постановка которой дана в предыдущем разделе.
Для вычисления силы в зависимости от текущего значения скорости $\tilde {V}$ требуется выполнить следующие шаги [2].
1. Вычислить безразмерную длину участка контакта
как решение уравнения(3.2)
$[1 - {{\lambda }^{2}}][{{I}_{0}}(\alpha \zeta ){{K}_{1}}(\zeta ) + {{K}_{0}}(\zeta ){{I}_{1}}(\alpha \zeta )] + \frac{2}{\zeta }\left( {\frac{1}{\alpha } - 1} \right){{\lambda }^{2}}{{I}_{1}}(\alpha \zeta ){{K}_{1}}(\zeta ) = 0$Здесь переменная
является отношением времени, за которое каждый элемент проходит расстояние, равное полуширине области контакта, ко времени последействия ${{T}_{\varepsilon }}$, ${{I}_{0}}(x)$ и ${{I}_{1}}(x)$ – бесселевы функции мнимого аргумента, ${{K}_{0}}(x)$ и ${{K}_{1}}(x)$ – цилиндрические функции мнимого аргумента.2. Вычислить относительное смещение участка контакта относительно оси $C{\kern 1pt} {\text{'}}y$
3. Вычислить силу сопротивления
(3.4)
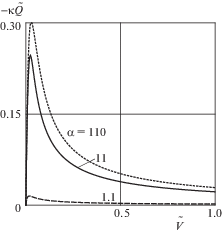
$\tilde {Q} = - {{\kappa }^{{ - 1}}}\lambda \left[ {\frac{\varepsilon }{2}(1 - {{\lambda }^{2}}) + \frac{1}{{2\zeta }}\left( {{{\lambda }^{2}} - \frac{1}{\alpha }} \right)} \right]$На фиг. 2 приведен график зависимости силы сопротивления от скорости при $\kappa = 29.1$ и α = 1.1, 11, 110.
Выражение для распределения давления $p(\tilde {x})$ по безразмерной координате $\tilde {x}$ в области контактного взаимодействия имеет вид [1, 2]
(3.5)
$\begin{gathered} \frac{{p(\tilde {x})}}{{E'}} = - \frac{\alpha }{{2\pi {{\kappa }^{2}}}}\frac{1}{{\tilde {V}}}\int\limits_{ - \tilde {a}}^{\tilde {x}} \frac{{{{\lambda }^{2}} + 4(x{\text{'}} - \kappa \tilde {V})(\lambda \varepsilon - 2x') + 1}}{{16\sqrt {(x{\text{'}} + \tilde {a})(\tilde {b} - x{\text{'}})} }}exp\left( {\frac{\alpha }{{\kappa \tilde {V}}}(\tilde {x} - x{\text{'}})} \right)dx{\text{'}} \\ \tilde {x} = \frac{x}{{{{l}_{0}}}} \in [ - \tilde {a},\tilde {b}],\quad \tilde {a} = \frac{{\lambda (1 - \varepsilon )}}{2},\quad \tilde {b} = \frac{{\lambda (1 + \varepsilon )}}{2} \\ \end{gathered} $В заключение приведем здесь важные качественные свойства силы $\tilde {Q}(\tilde {V})$ и решений уравнений (3.1). Доказательства представлены в Приложении.
1. Сила сопротивления – непрерывно дифференцируемая функция, обращающаяся в нуль при нулевой и бесконечной скорости оси цилиндра (утверждения 1, 2, 4).
2. Задание меньшего значения ${{\tilde {V}}_{0}}$ начальной скорости эквивалентно некоторому конечному сдвигу по времени исходного решения уравнения (утверждение 5).
3. Справедливо
Следствие 1. Если в начальный момент $\tilde {V}(0) \ne 0$, то функция $\tilde {V}(\tilde {t})$ строго монотонна (убывает при $\tilde {V}(0) > 0$ и возрастает при $\tilde {V}(0) < 0$) и не меняет знака, $\tilde {V}(\tilde {t}) \to 0$ при $\tilde {t} \to \infty $, $\tilde {V}(\tilde {t}) \ne 0$ $\forall \tilde {t} \in R$. Время до остановки бесконечно.
4. Путь торможения цилиндра конечен: $\tilde {\xi }(\infty ) < \infty $ (теорема 2).
Таким образом, ось цилиндра, начав движение с ненулевой скоростью, будет двигаться бесконечно долго, проходя при этом конечный путь торможения. Однако, с практической точки зрения, а также для анализа численных расчетов полезно ввести следующее определение.
Определение. Будем называть временем до остановки цилиндра время $\tilde {T}{\text{*}}$, за которое безразмерная скорость убывает от начального значения до некоторой заранее заданной малой величины $\epsilon $.
Для достаточно малых $\epsilon $ выполнено условие
Тогда справедливо
Следствие 2. Путь торможения $\tilde {\xi }(\infty )$ превышает путь $\xi {\text{*}}$, пройденный за время $\tilde {T}{\text{*}}$, не более чем на величину $\tfrac{{2\gamma \alpha }}{{\alpha - 1}}\epsilon $.
4. Пример расчета изменения контактных характеристик и скорости цилиндра при торможении. Приведем пример расчета торможения жесткого цилиндра на вязкоупругом полупространстве с параметрами материала, соответствующими некоторому образцу резины. Возьмем следующие значения размерных параметров цилиндра:
и материала вязкоупругой полуплоскости:Отметим, что при этих значениях параметров длина участка контактного взаимодействия в покое ${{l}_{0}} = 3.4$ мм. Безразмерные параметры задачи принимают значения
Пусть в начальный момент ${{\tilde {V}}_{0}} = 1$. Это значение соответствует размерному значению скорости $V = 0.54$ м/мин и выбрано так, чтобы при численном интегрировании учесть характерные участки возрастания и убывания силы сопротивления, т.е. значение ${{V}_{0}}$ больше значения скорости, при котором сила сопротивления максимальна (см. фиг. 2). Положим начальную координату оси цилиндра равной нулю: $\tilde {\xi }(0) = 0$.
При численном решении задачи использовался алгоритм Брента–Деккера решения алгебраического уравнения (3.2); алгоритм Адамса в форме Нордсика для решения задачи Коши уравнений (2.2), (2.3). Оба алгоритма реализованы в открытой библиотеке GNU Scientific Library11.
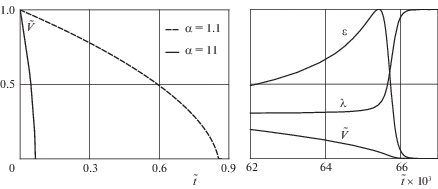
График функции $\tilde {V}(\tilde {t})$, являющейся решением уравнения (3.1), приведен в левой части фиг. 3 сплошной линией. Обратим внимание, что при малых скоростях функция $\tilde {V}(\tilde {t})$ довольно быстро убывает: этот участок соответствует максимуму функции $\tilde {Q}(\tilde {V})$. При увеличении масштаба (см. правую часть фигуры) видно, что график функции $\tilde {V}(\tilde {t})$ при $\tilde {t} \to \infty $ касается горизонтальной прямой $\tilde {V} = 0$ (решение $\tilde {V}(\tilde {t})$ не обращается в нуль, однако график практически сливается с горизонтальной осью). Там же приведены соответствующие этому решению графики зависимости смещения $\varepsilon (\tilde {t})$ и безразмерной длины $\lambda (\tilde {t})$ участка контактного взаимодействия. Отметим, что при $\tilde {t} < 0.062$ обе функции $\varepsilon (\tilde {t})$ и $\lambda (\tilde {t})$ медленно монотонно возрастают.
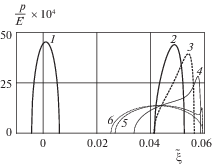
На фиг. 4 приведены графики распределения контактных давлений (3.5), ось абсцисс соответствует безразмерной абсолютной координате $\tilde {\xi }$ оси цилиндра. Распределение 1 соответствует начальному моменту времени, когда координата оси цилиндра $\tilde {\xi } = 0$; распределения (2–6) – финальному интервалу $\tilde {t}$ ∈ [0.065, 0.0672], путь торможения $\tilde {\xi }{\text{*}}$ = 0.042. Таким образом, на финальном участке движения эпюра контактного давления “расплывается” и становится симметричной.
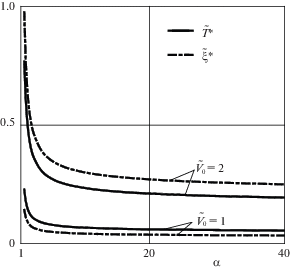
5. Анализ зависимости времени до остановки и пути торможения от параметра $\alpha $. Зафиксируем теперь безразмерные параметры $\gamma = 1.1 \times {{10}^{4}}$, $\kappa = 29.1$ и будем варьировать вязкоупругий параметр $\alpha \in (1.1,40)$. В левой части фиг. 3 представлены функции $\tilde {V}(\tilde {t})$ при $\alpha = 1.1$ (штриховая кривая) и при $\alpha = 11$ (сплошная кривая). Характер убывания скорости одинаков при разных $\alpha $, причем чем больше значение параметра $\alpha $, тем быстрее происходит остановка цилиндра. На фиг. 5 при разных начальных скоростях ${{\tilde {V}}_{0}} = 1$ и ${{\tilde {V}}_{0}} = 2$ построены графики зависимостей времени до остановки $\tilde {T}{\text{*}}$ (сплошные кривые) и пути торможения $\tilde {\xi }{\text{*}}$ (штриховые кривые) от параметра $\alpha $ (выбрано значение $\epsilon = {{10}^{{ - 7}}}$). Результаты расчетов показывают, что обе функции монотонно убывают с ростом вязкости материала основания. Заметим, что при $\alpha \to {\text{1 + }}$ (упругий материал) время до остановки и путь торможения стремятся к бесконечности: действительно, при скольжении цилиндра по упругой полуплоскости сила сопротивления равна нулю в силу симметрии распределения контактного давления по области контакта.
6. Заключение. Построено решение задачи в плоской постановке о торможении жесткого цилиндра, скользящего по вязкоупругому полупространству, проведен его качественный и численный анализ. Сила сопротивления движению цилиндра получена из решения квазистатической задачи теории вязкоупругости. Аналитически показано, что эта сила равна нулю при нулевой и бесконечной скорости оси цилиндра, а ее производная в нуле – функция отношения $\alpha $ времени последействия ко времени релаксации. Установлено, что решение задачи зависит от трех безразмерных параметров, два из которых совпадают с параметрами квазистатической задачи вязкоупругости, а третий параметр задает соотношение двух масштабов времени: динамического, задаваемого ускорением свободного падения и радиусом цилиндра, и времени последействия материала. Аналитически показано, что время до остановки цилиндра бесконечно, а путь торможения конечен. На основании численных расчетов изучены процесс торможения и характер распределения контактных давлений в разные моменты времени, а также влияние релаксационных характеристик основания на путь торможения и время до остановки. Показано, что при увеличении вязкости основания время до остановки и путь торможения монотонно убывают, при этом для упругих материалов эти величины равны бесконечности.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект 19-01-00140) и в рамках Госзадания (АААА-А17-117021310379-5).
Список литературы
Goryacheva I.G. Contact Mechanics in Tribology. Dordrecht: Kluwer, 1998. 344 p.
Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.
Carter F.W. On the action of a locomotive driving wheel // Proc. R. Soc. A. 1926. V. 112. P. 151–157.
Hunter S.C. The rolling contact of a rigid cylinder with a viscoelastic half space // J. Appl. Mech. 1961. V. 28. № 4. P. 611–617.
Golden J.M. The problem of a moving rigid punch on an unlubricated visco elastic half-plane // Quart. J. Mech. Appl. Math. 1979. V. 32. № 1. P. 25–52.
Golden J.M., Graham G.A.C. The transient quasi-static plane viscoelastic moving load problem // Intern. J. Eng. Sci. 1987. V. 25. № 1. P. 65–84.
Chertok D.L., Golden J.M., Graham G.A.C. Hysteretic friction for the transient rolling contact problem of linear viscoelasticity // J. Appl. Mech. 2001. V. 68. № 4. P. 589–595.
Pöschel T., Schwager T., Brilliantov N.V. Rolling friction of a hard cylinder on a viscous plane // Eur. Phys. J. B. 1999. V. 10. P. 169–174.
Pöchel T., Brilliantov N., Zaikin A. Bistability and noise-enhanced velocity of rolling motion // Europhys. Letters. 2005. V. 69. № 3. P. 371–377.
Вильке В.Г., Мигунова Д.С. О движении мяча по травяному газону // ПММ. 2011. Т. 75. Вып. 5. С. 801–812.
Кулешов А.С., Трещeв Д.В., Иванова Т.Б., Наймушина О.С. Твердый цилиндр на вязкоупругой плоскости // Нелин. дин. 2011. Т. 7. № 3. С. 601–625.
Ишлинский А.Ю. Трение качения // ПММ. 1938. Т. 2. Вып. 2. С. 245–260.
Солдатенков И.А. Задача о неравномерном скольжении штампа по вязкоупругому основанию с приложениями к расчету динамики подвижного контакта // ПММ. 2017. Т. 81. Вып. 3. С. 257–277.
Горячева И.Г. Об одном предельном случае качения цилиндра по вязкоупругому основанию // Научные труды аспирантов отд. мех. мех.-мат. фак. МГУ. М.: Изд-во МГУ, 1973. С. 96–105.
Abramowitz M., Stegun I.A. (Eds). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. = Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979. 832 с.
Горячева И.Г., Зобова А.А. Динамическая задача о качении с проскальзыванием упругого цилиндра по упругому основанию // ДАН. 2018. Т. 481. № 1. С. 24–26.
Горячева И.Г., Зобова А.А. Динамика движения упругого цилиндра по упругому основанию // ПММ. 2019. Т. 83. Вып. 1. С. 39–46.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика