Прикладная математика и механика, 2020, T. 84, № 2, стр. 182-195

Введение. Моделирование вязкоупругих жидких полимерных сред является популярной на сегодняшний день задачей, которую пока нельзя считать решенной. Сложная структура таких жидкостей, представляющая из себя длинные перепутанные макромолекулы, обладает бесконечным числом степеней свободы и создает значительные трудности при построении уравнений модели. Уравнения для законов сохранения в таких моделях замыкаются при помощи дополнительных уравнений – реологических определяющих соотношений. В настоящее время предложено значительное количество различных подходов к построению определяющих соотношений, но ни один из них нельзя считать основным и общепринятым. Также нужно заметить, что модели полимерных сред довольно сложны, и из-за этого их математические свойства, такие, как существование, единственность и устойчивость решений, в большинстве случаев остаются открытыми.

На сегодняшний день существует широкий круг теоретических работ, посвященных изучению течений вязкоупругих жидкостей в областях различной геометрии и с различными краевыми условиями [1–5]. Показано, что течения вязкоупругих полимерных жидкостей обладают сложными свойствами, исследование которых привело к появлению ряда реологических моделей жидких полимеров. Отличительная особенность течений вязкоупругих жидкостей – подтверждаемый экспериментально эффект памяти, т.е. зависимость характеристик потока и кривой течения от истории нагружений. Эффект памяти приводит к специфическому виду неустойчивости течений [6], расслоению потока (shear-banding) [1], возникновению тангенциальных разрывов [2]. В частности, на примере прямолинейного потока в среде Олдройда показано [7], что вопрос о неустойчивости течения связан с единственностью стационарных решений. В целом, имеющиеся на данный момент результаты оставляют актуальным исследование стационарных режимов течений и поиск точных и приближенных решений для течений различной геометрии. Понимание свойств стационарных течений необходимо как для анализа устойчивости течений, так и для исследования адекватности моделей текучих полимеров экспериментальным данным, что особенно важно при существующем разнообразии реологических уравнений состояния.

В основу данной работы положена сравнительно новая реологическая модифицированная модель Виноградова–Покровского [8], использующая мезоскопический подход для вывода определяющих соотношений. Другими словами, в данном подходе динамика несжимаемой жидкости описывается через статистическое моделирование движения одной макромолекулы в вязкоупругой анизотропной среде, свойства которой определяются несколькими феноменологическими параметрами. Таким образом, неизвестными функциями этой модели гидродинамики текучих полимеров, помимо привычных давления и трех компонент скорости, являются шесть компонент симметрического тензора анизотропии [1, 5, 8], отражающего форму макромолекул и их ориентацию в потоке. Особый интерес для этой модели, как и для других моделей жидких полимеров, представляют сдвиговые и вращающиеся течения, благодаря их применимости к вискозиметрии, позволяющей исследовать адекватность модели реальным полимерам.

Одним из типов течения, хорошо изученным в рамках теории вязкой ньютоновской жидкости, является течение над вращающимся диском. Его исследование восходит к работам Кармана [9], который предложил автомодельное представление для решения в случае слоя жидкости бесконечной высоты. В дальнейшем решение Кармана было развито и обобщено широким кругом авторов [10–12] для краевых условий разного вида. В частности изучалось движение тонкого слоя вязкой жидкости со свободной поверхностью над вращающейся горизонтальной пластиной [13, 14], в том числе и для течений неньютоновских жидкостей [3, 15]. Далее рассматривается задача, сформулированная для модифицированной модели Виноградова–Покровского. В отличие от классической “кармановской” постановки, здесь, как и в некоторых предыдущих исследованиях [13, 14], рассматривается слой вязкоупругой жидкости конечной толщины. Однако, ниже рассматриваются приближенные решения для цилиндрической зоны малого радиуса, расположенной на оси вращения диска. Высота этой зоны, предполагаемая постоянной, определяется из условия на свободной поверхности. Стационарные решения, рассматриваемые в работе, выведены по аналогии с автомодельным решением Кармана. Вид решений приведен в первом разделе статьи. Второй раздел посвящен выводу системы обыкновенных дифференциальных уравнений для стационарных решений. Наконец, третий раздел содержит описание численного метода и примеры стационарных решений для различных значений параметров задачи.

1. Предварительные сведения. Система дифференциальных уравнений, описывающих течения несжимаемой полимерной жидкости в рамках обобщенной реологической модели Виноградова–Покровского [8], в цилиндрической системе координат $r$, $\varphi $, $z$ имеет вид (см. также [4, 16]):

Здесь $t$ – время, $u$, $v$, $w$ – компоненты вектора скорости ${\mathbf{u}}$ в цилиндрической системе координат $r$, $\varphi $, $z$; $P$ – давление, ${{a}_{{rr}}}, \ldots ,{{a}_{{\varphi z}}}$ – компоненты симметричного тензора анизотропии,

где $k$, $\beta $ $(0 < \beta < 1)$ – феноменологические параметры реологической модели (см. [8, 16]), ${\text{Re}} = (\rho {{u}_{H}}l){\text{/}}{{\eta }_{0}}$ – число Рейнольдса, ${\text{W}} = ({{\tau }_{0}}{{u}_{H}}){\text{/}}l$ – число Вайсенберга, $\rho ( = \operatorname{const} )$ – плотность среды, ${{\eta }_{0}}$, ${{\tau }_{0}}$ – начальные значения сдвиговой вязкости и времени релаксации, $l$ – характерная длина, ${{u}_{H}}$ – характерная скорость,

Система (1.1)–(1.10) записана в безразмерном виде: переменные $t$, $r$, $z$, $u$, $v$, $w$, $P$, ${{a}_{{rr}}}, \ldots ,{{a}_{{\varphi z}}}$ отнесены к $l{\text{/}}{{u}_{H}}$, $l$, ${{u}_{H}}$, $\rho u_{H}^{2}$, ${\text{W/}}3$ соответственно.

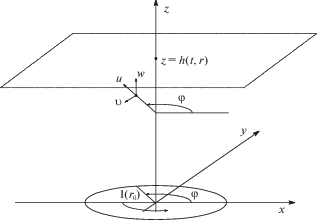
Ниже приводится алгоритм конструирования решения математической модели (1.1)–(1.10), описывающие течения вращающейся несжимаемой полимерной жидкости. Такие течения реализуются в тонком бесконечном по горизонтали слое полимерной жидкости, расположенном над вращающейся со скоростью

бесконечной пластиной с одной стороны, и имеющем свободную поверхность с другой (см. рис. 1). В формуле (1.11) угловая скорость вращения пластины – $\Omega = {\text{const}}$, ${{u}_{H}} = \Omega l$ – характерная скорость, ${{{\mathbf{e}}}_{\varphi }}$ – единичный вектор по азимутальной угловой координате $\varphi $ (см. рис. 1). Агрегат $\Lambda (t)$ – безразмерный.

В таком случае, следуя монографии [11], а также работам [10, 13, 14], будем искать эти течения несжимаемой полимерной жидкости в “кармановском” виде, т.е. будем искать у системы (1.1)–(1.10) решения вида (см. [10, 11]):

Здесь

Заметим, что у компонент ${{a}_{{rr}}}$ и ${{a}_{{\varphi \varphi }}}$ главные члены разложения одинаковы в силу системы (1.1)–(1.10).

В реальных течениях бесконечная пластина $z = 0$ заменяется конечным диском, радиус ${{r}_{0}}$ которого выбирается в качестве обезразмеривающего масштабы длины $(l = {{r}_{0}})$. Поэтому, как и для вязкой несжимаемой жидкости (см. [11] и описанную там дискуссию по этому поводу), предполагается, что разложения (1.12) справедливы при малых $r$: $0 < r < {{r}_{*}} \ll 1$. В этой связи обозначения $o(r)$, $O(r)$ и т.д. вполне приемлемы. Заметим также, что разложения (1.12) носят формальный характер до тех пор, пока не доказана сходимость соответствующих рядов.

Подставляя представление (1.12) в систему (1.1)–(1.10), собирая коэффициенты при соответствующих степенях $r$, получаем нестационарную систему для определения агрегатов $F$, $G$, $H$, ${{A}_{0}}$, $A$, $\Phi $, $C$, $\mathcal{F}$, $B$, $Q$ вида:

где $\mathcal{L} = {{{\text{W}}}^{{ - 1}}} + (k - \beta )(2{{A}_{0}} + C){\text{/}}3.$

Система уравнений (1.13)–(1.23) представляет собой замкнутую подсистему уравнений из бесконечной системы соотношений, возникающей после подстановки представлений (1.12) в систему (1.1)–(1.10).

В силу условий прилипания при $z = 0$ имеем:

Пусть свободная граница задается уравнением

Следуя [17], получим для свободной границы $z = h$ условие

Как и в [13, 14], будем полагать

(постоянная ${{h}_{*}}$ подлежит определению). Следовательно, из (1.25) получаем

2. Стационарные решения, описывающие течения “кармановского” типа вблизи оси $r = 0$. В стационарном случае математическая модель (1.13)–(1.23) примет вид (см. также (1.24)):

Здесь

При этом, $K(t) = {\text{const}} = {{K}_{0}}$, $\Lambda (t) = {\text{const}} = {{\Lambda }_{0}}$.

Рассматривая уравнения (2.6), (2.7), (2.9)–(2.11) при $z = 0$, получим

Уравнение (2.8) служит для определения $L(z)$ – давления на оси $r = 0$:

Из уравнения (2.2) следует, что $F{\kern 1pt} '(z){{{\text{|}}}_{{z = 0}}} = {{b}_{0}}$. Тогда из (2.1) $H{\kern 1pt} ''(z){{{\text{|}}}_{{z = 0}}} = - 2{{b}_{0}}$. Учитывая условия $H(0) = 0$, $H{\kern 1pt} '(z){{{\text{|}}}_{{z = 0}}} = 0$, получаем, что в окрестности нуля $H(z)$ имеет знак, обратный знаку ${{b}_{0}}$.

Можно заметить, что из (2.7) с учетом (2.1) и (2.12) следует $C(z) \equiv 0$.

Далее для простоты будем полагать, что $k = \beta $. Заметим, что численный расчет задачи (2.1)–(2.11) затруднителен из-за того, что точка $z = 0$ в силу условия $H(0) = 0$ является сингулярной для уравнений (2.6), (2.7), (2.9)–(2.11), отсутствующих в модели вихревого движения “обычной” вязкой жидкости [13]. Поэтому введем вспомогательную переменную $\xi $ по правилу

Отсюда получим

Задача (2.13) может быть решена численно конечно-разностными схемами первого порядка. Однако очевидно, что точка $z = 0$, $H = 0$ является положением равновесия в фазовой плоскости $(z,H)$. Поэтому для того, чтобы найти решение задачи (2.1)–(2.11) с независимым переменным $z$, необходимо найти фазовую траекторию, выходящую из точки $z = 0$, $H = 0$ в сторону положительных значений $z$ при условии, что все остальные начальные данные (2.13) в этой точке выполняются. Такая траектория будет бесконечно приближаться к начальной точке (2.13) в силу автономности системы. Поскольку при малых положительных $H$ производная ${\text{d}}z{\text{/d}}\xi $ отрицательна, будем считать, что начальные данные выполняются в точке $\xi {\kern 1pt} ' = + \infty $.

3. Численный поиск стационарных решений. Определим следующие значения параметров задачи, которые назовем базовыми:

Введем для системы (2.13) разностную сетку ${{\xi }_{j}} = \tau j$, $j \in \mathbb{Z}$, ${{z}_{j}} = z({{\xi }_{j}})$ и т.д. Производные неизвестных функций будем аппроксимировать по правилу

Для $\tau $ будем использовать значение ${{10}^{{ - 4}}}$. Положительные $j$ соответствуют значениям ${{z}_{j}}$, лежащим левее (ближе к нулю) некоторой начальной точки ${{z}_{0}} = z({{\xi }_{0}}) > {{z}_{j}}$, а отрицательные $j$ – значениям ${{z}_{j}} > {{z}_{0}}$, и при $\xi = - \infty $ траектория достигает свободной поверхности $z = {{h}_{*}}$, при которой $H({{h}_{*}}) = 0$.

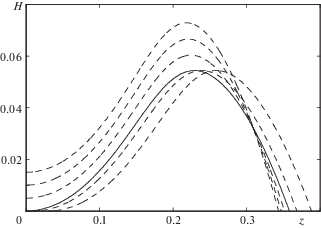
Рис. 2 показывает пример нескольких фазовых траекторий, спроектированных на плоскость $(z,H)$, проходящих рядом с началом координат этой плоскости. Из них наиболее близкой к искомому решению является траектория, обозначенная сплошной линией – она выпущена вправо по $z$ из точки ${{x}_{m}}{{ = (0,10}^{{ - 5}}},0,{{b}_{0}},{{\Lambda }_{0}},{{q}_{0}},0,{{a}_{0}},{{\phi }_{0}},{{f}_{0}})$. В силу непрерывности правых частей уравнений, можно утверждать, что среди подобных траекторий будет стремящаяся к точке, соответствующей начальным данным задачи (2.13). Для того, чтобы ее найти, из некоторой стартовой точки ${{x}^{0}}$ = (z⁰, H⁰, F⁰, B⁰, ${{G}^{0}},{{Q}^{0}},A_{0}^{0},{{A}^{0}},{{\Phi }^{0}}$, ${{\mathcal{F}}^{0}})$ выпустим численную траекторию в сторону $\xi \to + \infty $ до тех пор, пока либо $z$, либо $H$ не приблизятся к нулю. Расчет останавливается при выполнении одного из условий: $z = {{z}_{J}}{{ < 10}^{{ - 7}}}$, либо $H = {{H}_{J}}{{ < 10}^{{ - 7}}}$, соответственно, координаты точки фазового пространства обозначим индексом $J$. Введем функцию ошибки

характеризующую отклонение полученной траектории от требуемых начальных данных. Поиск искомой траектории ведется при помощи минимизации функции $T$. Правда, пока значения функции $T$ корректно определены только для таких значений аргумента ${{x}^{0}}$, у которых первые две координаты положительны $({{z}^{0}} > 0$, ${{H}^{0}} > 0)$. Для того, чтобы итерации численного метода корректно работали, необходимо доопределить функцию $T$ в областях ${{z}^{0}} < 0$ и ${{H}^{0}} < 0$ так, чтобы минимум такой функции совпадал с минимумом исходной. Для этого воспользуемся введенной ранее траекторией, выпущенной из точки ${{x}_{m}}$. Поскольку такая траектория близка к искомой, используем масштаб ее изменчивости для доопределения $T$. Обозначим за ${{z}_{m}}$ значение $z > 0$, при котором траектория, выпущенная вправо по $z$ из точки ${{x}_{m}}{{ = (0,10}^{{ - 5}}},0,{{b}_{0}},{{\Lambda }_{0}},{{q}_{0}},0,{{a}_{0}}$, ϕ₀, f₀) пересекает гиперплоскость $H = 0$. За ${{H}_{m}}$ примем максимальное значение $H$ на траектории, выходящей из ${{x}_{m}}$. Так, для траектории, обозначенной сплошной линией на рис. 2, имеем ${{z}_{m}} = 0.358$ и ${{H}_{m}} = 0.054$. Тогда доопределим

Минимум функции $T$ будем искать симплекс-методом Нелдера–Мида при помощи функции fminsearch пакета программ MATLAB. За начальную точку метода возьмем точку ${{x}_{m}}$. Точку ${{x}^{0}}$, отвечающую минимуму функции $T$, будем считать точкой, лежащей на искомой траектории – решение (2.13). Выпустим из этой точки траекторию в обе стороны $(\xi \to \pm \infty )$ до тех пор, пока с обеих сторон траектория не приблизится к значениям $H = 0$. Левая точка будет соответствовать значению $z = 0$, а правая – значению ${{h}_{*}} = z({{\xi }_{*}})$.

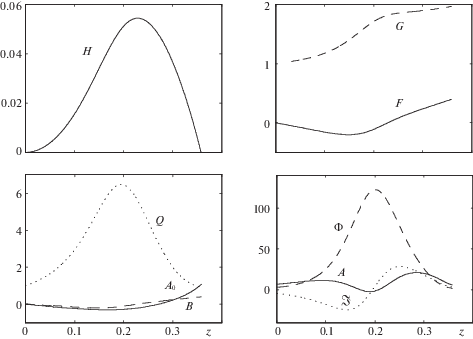
На рис. 3 приведены графики решений задачи (2.13) для базовых значений параметров, найденных описанным выше методом. Отметим, что главные коэффициенты разложения тензора анизотропии (${{A}_{0}}$, $B$, $Q$) заметно меньше побочных членов ($A$, $\Phi $, $\mathcal{F}$), что еще раз подтверждает сделанное ранее замечание о том, что такое представление решения имеет смысл только в малой окрестности оси вращения $r = 0$. Также заметим, что по высоте область течения делится на две характерные подобласти – вблизи диска жидкость течет навстречу оси вращения ($F < 0$, циклонический режим), а в верхней части, напротив, течет от центра вращения ($F > 0$, антициклонический режим).

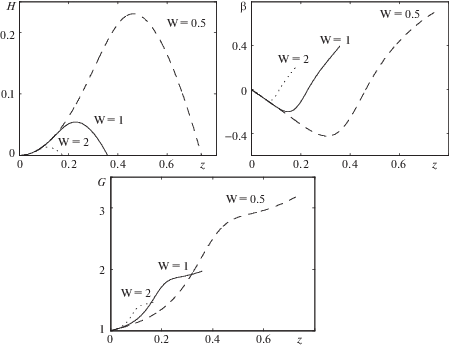
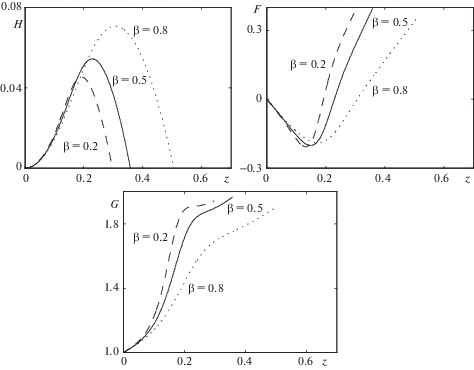
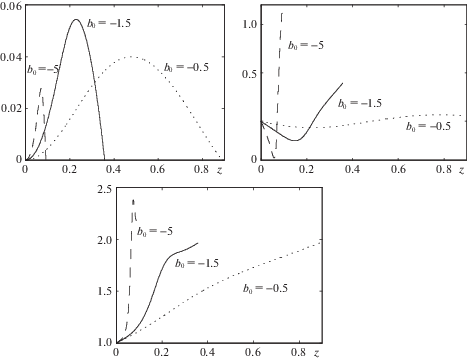
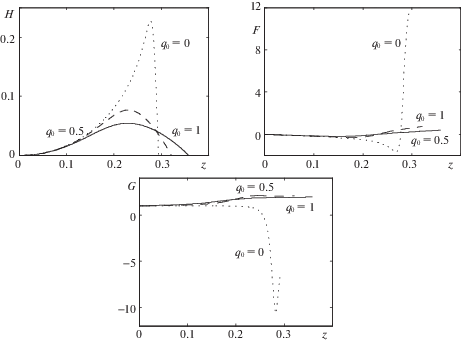
Рассмотрим влияние параметров задачи на профили скорости жидкости. Рис. 4 показывает различие в скорости при разных значениях числа Вайсенберга ${\text{W}}$. Видно, что большие значения ${\text{W}}$ соответствуют меньшим значениям скорости и меньшей высоте вихревой зоны, но в остальном характер течения существенно не меняется. Изменение феноменологического параметра $\beta $, характеризующего размер макромолекул полимера, приводит к изменению вертикальной скорости жидкости и высоты зоны течения, но практически не влияет на радиальную и угловую компоненты скорости, см. рис. 5. Более сложным представляется влияние начальных данных компонент тензора анизотропии ${{b}_{0}}$ и ${{q}_{0}}$. Так рис. 6 показывает, что ${{b}_{0}}$ оказывает немонотонный эффект на величину скорости, а также демонстрирует несколько необычный эффект: уменьшение величины ${{b}_{0}}$ в некотором диапазоне одновременно ведет к меньшим вертикальным скоростям и к более высоким вихрям. Увеличение же ${{b}_{0}}$ приводит к более сложному поведению угловой скорости, которая, в отличие от прошлых случаев, немонотонна с ростом высоты. Малые величины начального данного ${{q}_{0}}$ (рис. 7) приводят в частности к изменению знака угловой скорости с ростом $z$, то есть с ростом высоты жидкость может начать закручиваться в сторону, противоположную вращению диска. Также в этом случае наблюдается сильное увеличение амплитуды угловой скорости, а также заметная асимметрии профиля вертикальной скорости $H$. Прочие параметры оказывают сравнительно небольшое влияние на общий характер течения жидкости, и поэтому их исследование в статье не приводится.

Заключение. В работе исследовано вращательное движение слоя полимерной жидкости конечной толщины над бесконечным вращающимся диском для модифицированной реологической модели Виноградова–Покровского. Предложен вид приближенного осесимметричного решения такой задачи для малой окрестности оси вращения диска, полученного по аналогии с автомодельным решением Кармана для вязкой жидкости. Для поиска стационарных решений нами был приведен численный алгоритм, позволяющий проинтегрировать уравнения задачи в особой точке на поверхности диска. Полученные численные примеры стационарных решений для ряда значений параметров задачи показали, что различные значения параметров могут сильно влиять на характер течения, размеры вихря, направление вращения жидкости. В отличие от предыдущих исследований, например, [13, 14], были обнаружены решения только с положительным вертикальным потоком ($H > 0$), гладких решений с нисходящим потоком найдено не было. Несмотря на отсутствие общих утверждений о единственности решений решаемых задач, численными методами обнаружить множественность решений не удалось.