1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 4, 2021

Прикладная математика и механика, 2021, T. 85, № 4, стр. 469-493

Метод функционалов Ляпунова в задаче об устойчивости интегро-дифференциальных уравнений Вольтерра с бесконечным запаздыванием

А. С. Андреев 1, *, О. А. Перегудова 1, **

1 Ульяновский государственный университет
Ульяновск, Россия

* E-mail: asa5208@mail.ru
** E-mail: peregudovaoa@gmail.com

Поступила в редакцию 27.02.2021
После доработки 08.03.2021
Принята к публикации 19.03.2021

Полный текст (PDF)

Аннотация

В работе рассмотрена задача об устойчивости неавтономного нелинейного интегро-дифференциального уравнения типа Вольтерра с бесконечным запаздыванием. Проведено развитие метода функционалов Ляпунова в исследовании предельного поведения ограниченного решения, асимптотической устойчивости нулевого решения по всем и части переменных в предположении существования соответствующего функционала Ляпунова, имеющего знакопостоянную производную. Решены задачи о предельных свойствах движения механической системы с линейной эредитарностью, о стабилизации установившихся движений манипулятора с вязкоупругими цилиндрическим и сферическим шарнирами. Решена задача управления пятизвенным манипулятором с учетом вязкоупругости его шарниров.

Ключевые слова: интегро-дифференциальные уравнения Вольтерра, устойчивость, функционал Ляпунова, механическая система с вязкоупругими элементами, манипулятор, управление

1. Введение. Интенсивное развитие науки и техники стимулировало в начале 50-х годов резкое усиление интереса к теории дифференциальных уравнений с запаздыванием. Принято считать, что основу этой теории составили опубликованные ранее работы В. Вольтерра [1, 2], в которых было предложено учитывать влияние непрерывной последовательности предшествующих состояний системы или процесса на их дальнейшее изменение посредством интегральных и интегро-дифференциальных уравнений. Развитию теории в значительной степени способствовал прогресс математического и функционального анализа, других областей математики. Значимой в этом развитии явилась монография [3], в которой предложено использовать для анализа системы функциональное пространство, как более наглядное и удобное в исследовании соответствующих задач.

Вначале преимущественное развитие получила теория функционально-дифференциальных уравнений с ограниченным запаздыванием. Теория таких уравнений с неограниченным запаздыванием лишь постепенно оформилась как ветвь современного математического анализа со своими специфическими проблемами и приложениями [4, 5]. Усилия многих исследователей в этой области были направлены на разработку основ общей теории, начиная с проблемы определения фазового пространства и правой части уравнения с неограниченным запаздыванием, решением соответствующей проблемы существования, единственности, непрерывной зависимости и продолжимости решений. Из многочисленных исследований по этой проблеме можно выделить работы [6–18]. В работах [9–15, 17, 18] дано аксиоматическое построение фазовых пространств, позволяющее решать указанную проблему для любых конкретных фазовых пространств и правых частей уравнений, удовлетворяющих введенным аксиомам. Как указано в [16], некоторые из этих аксиом являются трудно проверяемыми. Предложены иные условия решения проблемы в рамках функционального пространства ограниченных непрерывных функций.

Многочисленные приложения стимулировали интенсивные исследования проблемы устойчивости как для линейных, так и для нелинейных уравнений с неограниченным запаздыванием. Выделим основные на наш взгляд известные результаты, относящиеся к изучению устойчивости прямым методом Ляпунова в направлении данной работы.

Важным элементом определения устойчивости или оценки решения является выбор между нормами исходного банахова пространства (евклидовой нормы в случае конечномерного пространства) и нормой функционального пространства. Не всегда из свойства устойчивости в евклидовом пространстве следует аналогичное свойство в функциональном пространстве [4, 5]. Указанное выше аксиоматическое описание фазовых пространств позволило определить связь между определениями устойчивости в нормах конечномерного и фазового пространства [9, 10, 12, 13].

Как и в случае функционально-дифференциальных уравнений с конечным запаздыванием [19–26], развитие прямого метода Ляпунова в исследовании устойчивости уравнений с неограниченным запаздыванием делится в основном на два направления: на основе функционалов и функций Ляпунова.

Для развития метода функционалов Ляпунова по отношению к соответствующей теории вводится знакоопределенность и свойство бесконечно малого высшего предела с использованием оценок как через норму как конечномерного пространства, так и через норму функционального пространства [4, 5].

В работах [27, 28] доказываются теоремы об асимптотической устойчивости, обобщающие теоремы типа Матросова, Руша, Красовского. В [14, 28] доказаны теоремы об экспоненциальной устойчивости и их обращении типа Красовского и Йошизавы. В [29] получены теоремы о предельном поведении и асимптотической устойчивости, развивающие предыдущие результаты автора этой работы. В [30, 31] доказаны теоремы об устойчивости на основе оценок сравнительного анализа для функционалов Ляпунова.

Динамическое свойство инвариантности положительного предельного множества ограниченного решения автономного уравнения [7, 9] позволило обобщить для такого уравнения теоремы типа Ла-Салля и Красовского о притяжении решений и асимптотической устойчивости [7].

В работе Вольтерра [1, 2] исследовались непосредственно интегро-дифференциальные уравнения. Качественные свойства этих уравнений по отношению к свойствам общих систем уравнений с запаздыванием имеют целый ряд особенностей, позволяющих построить их более глубокую качественную теорию [4, 5, 32–38], решить важные прикладные задачи [19, 39–42].

Интегро-дифференциальные уравнения типа Вольтерра разделяют на уравнения с конечным, неограниченным и бесконечным запаздыванием. Сам В. Вольтерра ограничивался, в основном, изучением уравнений первого типа. Качественные свойства решений, включая устойчивость, достаточно эффективно используются, если в качестве фазового пространства решений рассматривать исходное конечномерное пространство [34, 35, 38, 43–47]. При этом достигается решение важных прикладных задач [48–51].

Исследования уравнений третьего типа сопровождаются построением соответствующего фазового функционального пространства, как правило, с использованием методов общей теории уравнений с неограниченным запаздыванием [4, 5].

В первых двух разделах данной работы в рамках подхода [32, 33] для неавтономного нелинейного интегро-дифференциального уравнения с бесконечным запаздыванием выводятся качественные свойства решений, позволяющие решить задачи о локализации положительного предельного множества ограниченного решения, об асимптотической устойчивости нулевого решения на основе существования функционала Ляпунова, имеющего знакопостоянную производную.

Работы В.В. Румянцева [52, 53] явились основой для теории устойчивости по части переменных, имеющей многочисленные практические применения [54, 55]. Результаты исследований устойчивости относительно части переменных для функционально-дифференциальных уравнений с конечным запаздыванием с решением задач механики представлены в работах [24, 26, 55]. Проблема устойчивости по части переменных для функционально-дифференциальных уравнений с неограниченным запаздыванием является малоизученной и весьма перспективной в решении прикладных задач. Некоторые результаты в этом направлении получены в разделе 4.

Классические результаты по устойчивости и стабилизации положений равновесия и стационарных движений механических систем [56–61] получают широкое применение в управлении робототехническими системами. В разделе 5 данной работы изучается задача о влиянии наследственных свойств механической системы на устойчивость ее положений равновесия. В разделе 6 исследована задача о стабилизации установившихся движений манипуляторов с вязкоупругими цилиндрическими и сферическими шарнирами. В разделе 7 в качестве примера представлена модель управления пятизвенного манипулятора с вязкоупругими цилиндрическими и призматическим шарнирами.

2. Предварительные построения. Пусть ${{R}^{p}}$ – линейное действительное пространство $p$-векторов $x$ с некоторой нормой $\left\| x \right\|$, $R$ – действительная ось, ${{C}_{\infty }}$ – счетно-нормированное пространство всех непрерывных функций $\varphi :{{R}^{ - }} \to {{R}^{p}}$ с полунормами

${{\left| {\left| {\left| \varphi \right|} \right|} \right|}_{l}} = \max (\left\| {\varphi (s)} \right\|, - l \leqslant s \leqslant 0),\quad l = 1,2, \ldots $

Пусть $\beta = \operatorname{const} $. Для непрерывной функции $x:( - \infty ,\beta ) \to {{R}^{p}}$ и каждого $t < \beta $ функцию ${{x}_{t}} \in {{C}_{\infty }}$ определим равенством ${{x}_{t}}(s) = x(t + s)$, $s \in {{R}^{ - }}$, под $\dot {x}(t)$ будем понимать правостороннюю производную.

Рассмотрим нелинейное интегро-дифференциальное уравнение

(2.1)
$\dot {x}(t) = f(t,x(t),\quad \int\limits_{ - \infty }^t g(t,s,x(s))ds),$
где $f:R \times {{R}^{p}} \times {{R}^{p}} \to {{R}^{p}}$ и $g:S \times {{R}^{p}} \to {{R}^{p}}$, есть некоторые непрерывные функции, $S = \{ (t,s)$ : $R \in R,s \leqslant t\} $.

Решением уравнения (2.1), удовлетворяющим условию ${{x}_{\alpha }} = \varphi $, $(\alpha ,\varphi ) \in R \times {{C}_{\infty }}$, называется функция $x = x(t)$, $t \in ( - \infty ,\beta )$, ($\beta > \alpha $), такая, что ${{x}_{\alpha }}(s) = \varphi (s)$, обращающая это уравнение в тождество при всех $t \in [\alpha ,\beta )$.

Предположим, что функции $f$ и $g$ удовлетворяют условиям

$\begin{gathered} \left\| {f(t,x,g)} \right\| \leqslant {{m}_{1}}({{H}_{1}},{{H}_{2}})\quad \forall (t,x,g) \in R \times {{D}_{1}} \times {{D}_{2}} \\ {{D}_{j}} = {{D}_{j}}({{H}_{j}}) = \{ x \in {{R}^{p}}:\left\| x \right\| \leqslant {{H}_{j}}\} ,\quad j = 1,2 \\ \end{gathered} $
(2.2)
$\left\| {f({{t}_{2}},{{x}^{{(2)}}},{{g}^{{(2)}}}) - f({{t}_{1}},{{x}^{{(1)}}},{{g}^{{(1)}}})} \right\| \leqslant {{L}_{1}}\left| {{{t}_{2}} - {{t}_{1}}} \right| + {{L}_{2}}\left\| {{{x}^{{(2)}}} - {{x}^{{(1)}}}} \right\| + {{L}_{3}}\left\| {{{g}^{{(2)}}} - {{g}^{{(1)}}}} \right\|$
$\begin{gathered} {{L}_{j}} = {{L}_{j}}({{H}_{1}},{{H}_{2}}),\quad j = 1,2,3 \\ \forall ({{t}_{1}},{{x}^{{(1)}}},{{g}^{{(1)}}}),\quad ({{t}_{2}},{{x}^{{(2)}}},{{g}^{{(2)}}}) \in R \times {{D}_{1}} \times {{D}_{2}} \\ \end{gathered} $
(2.3)
$\begin{gathered} \left\| {g(t,s,x)} \right\| \leqslant {{m}_{2}}({{H}_{1}})\quad \forall (t,s,x) \in S \times {{D}_{1}} \\ \left\| {g({{t}_{2}},{{s}_{2}},{{x}^{{(2)}}}) - g({{t}_{1}},{{s}_{1}},{{x}^{{(1)}}})} \right\| \leqslant {{L}_{4}}\left| {{{t}_{2}} - {{t}_{1}}} \right| + {{L}_{5}}\left\| {{{s}_{2}} - {{s}_{1}}} \right\| + {{L}_{6}}\left\| {{{x}^{{(2)}}} - {{x}^{{(1)}}}} \right\| \\ {{L}_{j}} = {{L}_{j}}({{H}_{1}}),\quad j = 4,5,6\quad \forall ({{t}_{1}},{{s}_{1}},{{x}^{{(1)}}}),({{t}_{2}},{{s}_{2}},{{x}^{{(2)}}}) \in S \times {{D}_{1}} \\ \end{gathered} $

Кроме того, предположим, что

(2.4)
$\begin{gathered} \left\| {g(t,s,x)} \right\| \leqslant {{m}_{3}}(s - t,{{H}_{1}})\quad \forall (t,s,x) \in S \times {{D}_{1}}({{H}_{1}}) \\ \int\limits_{ - \infty }^0 {{m}_{3}}(\nu ,{{H}_{1}})d\nu \leqslant {{m}_{{30}}}({{H}_{1}}) \\ \end{gathered} $

В пространстве ${{C}_{\infty }}$ введем метрику

(2.5)
$\rho ({{\varphi }^{{(2)}}},{{\varphi }^{{(1)}}}) = \sum\limits_{l = 1}^\infty \frac{1}{{{{2}^{l}}}}\frac{{{{{\left| {\left| {\left| {{{\varphi }^{{(2)}}} - {{\varphi }^{{(1)}}}} \right|} \right|} \right|}}_{l}}}}{{1 + {{{\left| {\left| {\left| {{{\varphi }^{{(2)}}} - {{\varphi }^{{(1)}}}} \right|} \right|} \right|}}_{l}}}}$

Согласно [20, 32, 33] имеет место следующая теорема.

Теорема 2.1. Пусть функции $f$ и $g$ удовлетворяют условиям (2.2)–(2.4) (в том числе, при ${{L}_{1}} = {{L}_{4}} = {{L}_{5}} = 0$). Тогда для каждой точки $(\alpha ,\varphi ) \in R$ × $\{ \varphi \in {{C}_{\infty }}:\left\| {\varphi (s)} \right\| \leqslant H\} $ существует единственное решение $x = x(t,\alpha ,\varphi )$, ${{x}_{\alpha }} = \varphi $, определенное при $t \in ( - \infty ,\beta )$, $\beta > \alpha $, непрерывно зависящее от $(\alpha ,\varphi ) \in R \times {{C}_{\infty }}$.

Введем пространства ${{B}_{f}}$ и ${{B}_{g}}$ непрерывных функций $f:R \times {{R}^{p}} \times {{R}^{p}} \to {{R}^{p}}$ и $g:S \times {{R}^{p}} \to {{R}^{p}}$ соответственно, удовлетворяющих условиям (2.2)–(2.4). Определим сходимость в ${{B}_{f}}$ и ${{B}_{g}}$ согласно открыто-компактной топологии [62].

Аналогично построениям из [44, 45] уравнению (2.1) можно сопоставить семейство предельных уравнений вида

(2.6)
$\dot {x}(t) = f{\kern 1pt} *{\kern 1pt} (t,x(t),\quad \int\limits_{ - \infty }^t {g{\kern 1pt} *{\kern 1pt} (t,s,x(s))ds)} ,\quad (f*,g*) \in {{B}_{f}} \times {{B}_{g}}$

Определение 2.1. Пусть $x = x(t,\alpha ,\varphi )$ есть решение уравнения (2.1), ограниченное при всех $t \in R$, $\left\| {x(t,\alpha ,\varphi )} \right\| \leqslant H$ $\forall t \in R$. Функция $\varphi {\kern 1pt} * \in {{C}_{\infty }}$ называется предельной для этого решения, если $\exists {{t}_{n}} \to \infty $, такая, что соответствующая последовательность

$x_{t}^{{(n)}}(\alpha ,\varphi ) = x({{t}_{n}} + s,\alpha ,\varphi )$
сходится к $\varphi {\kern 1pt} *$ в ${{C}_{\infty }}$ при $n \to \infty $, или $\rho (x_{t}^{{(n)}}(\alpha ,\varphi ),\varphi {\kern 1pt} *) \to 0$ при $n \to \infty $.

Множество ${{\Omega }^{ + }}(\alpha ,\varphi )$ всех таких функций образует в ${{C}_{\infty }}$ положительное предельное множество данного решения $x = x(t,\alpha ,\varphi )$. Покажем, что это множество имеет следующее свойство квазиинвариантности.

Теорема 2.2. Пусть $x = x(t,\alpha ,\varphi )$ есть решение уравнения (2.1), ограниченное при всех $t \in R$, $\left\| {x(t,\alpha ,\varphi )} \right\| \leqslant {{H}_{1}}$ $\forall t \in R$. Тогда множество ${{\Omega }^{ + }}(\alpha ,\varphi )$ непусто, компактно, связно и квазиинвариантно.

Доказательство. Как и в [44], из условий (2.2) и (2.4) можно найти, что каждое ограниченное решение $x = x(t,\alpha ,\varphi )$ равномерно непрерывно по $t \geqslant \alpha $

(2.7)
$\left| {x({{t}_{2}},\alpha ,\varphi ) - x({{t}_{1}},\alpha ,\varphi )} \right| \leqslant {{m}_{1}}({{H}_{1}},{{m}_{{30}}}({{H}_{1}}))\quad \forall {{t}_{1}},{{t}_{2}} \geqslant \alpha $

Покажем, что множество ${{\Omega }^{ + }}(\alpha ,\varphi )$ решения $x = x(t,\alpha ,\varphi )$ является непустым.

Пусть ${{t}_{n}} \to \infty $ – произвольная последовательность. Для последовательности функций ${{x}^{{(n)}}}(t) = x({{t}_{n}} + t,\alpha ,\varphi )$ при всех ${{t}_{1}},{{t}_{2}} \in [\alpha - {{t}_{n}},0]$ имеет место оценка (2.7). Отсюда выводим существование подпоследовательности $\{ t_{n}^{{(k)}}\} \subset \{ {{t}_{n}}\} $ и функции $\varphi {\kern 1pt} * \in {{C}_{\infty }}$, таких, что $\{ {{x}^{{(k)}}}(t)\} $ сходится к $x = \varphi {\kern 1pt} *{\kern 1pt} (t)$ равномерно по $t \in [ - T,0]$ при каждом $T > 0$. И, значит, $\rho (x_{t}^{{(k)}},\varphi {\kern 1pt} *) \to 0$ при $k \to \infty $. Таким образом, ${{\Omega }^{ + }}(\alpha ,\varphi )$ непусто.

Стандартным подходом, как и для функционально-дифференциальных уравнений с конечным запаздыванием [24, 26], можно показать, что ${{\Omega }^{ + }}(\alpha ,\varphi )$ связно, а именно, это множество нельзя представить в виде объединения двух непересекающихся непустых замкнутых множеств, и оно компактно. Очевидно, что оно является компактным.

Покажем, что множество ${{\Omega }^{ + }}(\alpha ,\varphi )$ является квазиинвариантным, а именно, для любой функции $\varphi {\kern 1pt} * \in {{\Omega }^{ + }}(\alpha ,\varphi )$ существуют предельное уравнение (2.6) и его решение $x = x(t,0,\varphi {\kern 1pt} *)$ такие, что ${{x}_{t}}(\alpha ,\varphi {\kern 1pt} *) \in {{\Omega }^{ + }}(\alpha ,\varphi )$ для всех $t \in R$.

Без ограничения общности, можем принять, что для последовательности ${{t}_{n}} \to \infty $ имеем

$\begin{gathered} {{f}^{{(n)}}}(t,x) = f({{t}_{n}} + t,x) \to f{\kern 1pt} *{\kern 1pt} (t,x),\quad f* \in {{B}_{f}} \\ {{g}^{{(n)}}}(t,x) = g({{t}_{n}} + t,x) \to g{\kern 1pt} *{\kern 1pt} (t,x),\quad g* \in {{B}_{g}} \\ \end{gathered} $

Из того, что $x = x(t) = x(t,\alpha ,\varphi )$ есть решение уравнения (2.1), последовательно имеем

$x(t) = x(\alpha ) + \int\limits_\alpha ^t {f(\tau ,x(\tau )} ,\int\limits_{ - \infty }^\alpha {g(\tau ,s,x(s))ds} + \int\limits_\alpha ^\tau {g(\tau ,s,x(s))ds)d\tau } $
для всех $t \geqslant \alpha $,
(2.8)
$\begin{gathered} x({{t}_{n}} + t) = x({{t}_{n}}) + \int\limits_{{{t}_{n}}}^{{{t}_{n}} + t} {f(\tau ,x(\tau )} , + \int\limits_{ - \infty }^0 {g(\tau ,\alpha + s,x(\alpha + s))ds} + \int\limits_\alpha ^\tau {g(\tau ,s,x(s))ds)d\tau } \\ {{x}^{{(n)}}}(t) = {{x}^{{(n)}}}(0) + \int\limits_0^t {{{f}^{{(n)}}}(\tau ,{{x}^{{(n)}}}(\tau )} ,\int\limits_{ - \infty }^0 {g({{t}_{n}} + \tau ,\alpha + s,\varphi (s))ds} + \int\limits_{\alpha - {{t}_{n}}}^\tau {{{g}^{{(n)}}}(\tau ,s,{{x}^{{(n)}}}(s))ds)d\tau } \\ \end{gathered} $
для всех $t \in [\alpha - {{t}_{n}}, + \infty )$.

Согласно условию (2.4) имеем следующие оценки

(2.9)
$\left\| {\int\limits_{ - \infty }^0 {g({{t}_{n}} + \tau ,\alpha + s,\varphi (s))ds} } \right\| \leqslant \int\limits_{ - \infty }^0 {{{m}_{3}}(s + \alpha - {{t}_{n}} - \tau ,{{H}_{1}})ds} = \int\limits_{ - \infty }^{ - {{t}_{n}} + \alpha - \tau } {{{m}_{3}}(\nu ,{{H}_{1}})d\nu } \to 0$
при $n \to \infty $.

(2.10)
$\left\| {\int\limits_{{{t}_{0}} - {{t}_{n}}}^\tau {{{g}^{{(n)}}}(\tau ,s,{{x}^{{(n)}}}(s))ds} } \right\| \leqslant \int\limits_{ - \infty }^0 {{{m}_{3}}(\nu ,{{H}_{1}})d\nu } \leqslant {{m}_{{30}}}({{H}_{1}})$

Отсюда, переходя в равенстве (2.8) к пределу при $n \to \infty $, получаем

(2.11)
$x{\kern 1pt} *{\kern 1pt} (t) = x{\kern 1pt} *{\kern 1pt} (0) + \int\limits_0^t {f{\kern 1pt} *{\kern 1pt} (\tau ,x{\kern 1pt} *{\kern 1pt} (\tau )} ,\quad \int\limits_{ - \infty }^\tau {g{\kern 1pt} *{\kern 1pt} (\tau ,s,x{\kern 1pt} *{\kern 1pt} (s))ds)d\tau } $
при всех $t \in R$, при этом по построению $x_{0}^{*}(s) = \varphi {\kern 1pt} *{\kern 1pt} (s)$, $s \in {{R}^{ - }}$.

Дифференцируя равенство (2.11) по $t \in R$, имеем требуемое доказательство.

3. Принцип квазиинвариантности. Введем следующие пространства скалярных функций:

1) пространство $B_{V}^{1}$ функций ${{V}_{1}} \in {{C}^{1}}(R \times {{R}^{p}} \times R \to R)$;

2) $B_{V}^{{11}}$ – подпространство $B_{V}^{1}$ функций ${{V}_{1}}(t,x,{v})$, удовлетворяющих условиям вида (2.2);

3) пространство $B_{{v}}^{2}$ функций ${{V}_{2}} \in {{C}^{1}}(S \times {{R}^{p}} \to R)$, удовлетворяющих условиям вида (2.3), имеющих производную $\partial {{V}_{2}}(t,s,x){\text{/}}\partial t$ ∈ $C(S \times {{R}^{p}} \to R)$, при этом

(3.1)
$\begin{gathered} \left| {{{V}_{2}}(t,s,x)} \right| \leqslant {v}(s - t,{{H}_{1}}),\quad \left| {\frac{{\partial {{V}_{2}}}}{{\partial t}}(t,s,x)} \right| \leqslant {v}(s - t,{{H}_{1}}) \\ \forall (t,s,x) \in S \times \{ x \in {{R}^{p}}:\left\| x \right\| \leqslant {{H}_{1}}\} \\ \int\limits_{ - \infty }^0 {v}(\nu ,{{H}_{1}})d\nu \leqslant {{{v}}_{0}}({{H}_{1}}) < \infty \\ \end{gathered} $

4) пространство $B_{W}^{1}$ функций ${{W}_{1}} \in C(R \times {{R}^{p}} \times R \to {{R}^{ + }})$, удовлетворяющих условиям вида (2.2);

5) пространство $B_{w}^{2}$ функций ${{W}_{2}} \in C(S \times {{R}^{p}} \to R)$, удовлетворяющих условиям вида (2.4) и (2.6).

Для функционала $V = V(t,\varphi )$, определяемого равенством

(3.2)
$V(t,\varphi ) = {{V}_{1}}(t,\varphi (0),{{{v}}_{2}}(t,\varphi )),\quad {{{v}}_{2}}(t,\varphi ) = \int\limits_{ - \infty }^0 {{V}_{2}}(t,t + s,\varphi (s))ds,\quad \varphi \in {{C}_{\infty }}$
вдоль заданного решения $x = x(t) = x(t,\alpha ,\varphi )$, $(\alpha ,\varphi ) \in {{R}^{ + }} \times {{C}_{\infty }}$ при $t \in [\alpha ,\beta )$, ($\beta > \alpha $) можно определить функцию
(3.3)
$V(t) = V(t,{{x}_{t}}) = {{V}_{1}}(t,x(t,\alpha ,\varphi ),{{{v}}_{2}}(t,{{x}_{t}}(\alpha ,\varphi )));\quad {{{v}}_{2}}(t,{{x}_{t}}) = \int\limits_{ - \infty }^t {{V}_{2}}(t,s,x(s,\alpha ,\varphi ))ds$
и ее производную
(3.4)
$\begin{gathered} \dot {V}(t) = \dot {V}(t,{{x}_{t}}(\alpha ,\varphi )) = \\ = \;\left( {{{{\left. {\frac{{\partial V_{1}^{{^{{}}}}(t,x(t),{{{v}}_{2}})}}{{\partial t}} + \left( {\frac{{\partial {{V}_{1}}(t,x(t),{{{v}}_{2}})}}{{\partial x}}} \right)f(t,x(t),y)} \right|}}_{y}} = \int\limits_{ - \infty }^t {g(t,\tau ,x(\tau ))d\tau } + } \right. \\ {{\left. {\left. {^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}} + \;\left( {\frac{{\partial {{V}_{1}}(t,x(t),{{v}_{2}})}}{{\partial v}}} \right)\left( {{{V}_{2}}(t,t,x(t)) + \int\limits_{ - \infty }^t \frac{{\partial {{V}_{2}}(t,\tau ,x(t))}}{{\partial t}}d\tau } \right)} \right)} \right|}_{{{{{v}}_{2}}}}} = \int\limits_{ - \infty }^t {{{V}_{2}}(t,\tau ,x(\tau ))d\tau } , \\ \end{gathered} $
где $( \cdot ){\kern 1pt} '$ – операция транспонирования.

Введем соответствующий функционал $\dot {V}(t,\varphi )$, называемый в дальнейшем производной от $V$, и предположим, что производная $\dot {V}(t,\varphi )$ для некоторых ${{W}_{1}} \in B_{W}^{1}$ и ${{W}_{2}} \in B_{W}^{2}$ удовлетворяет следующему неравенству

(3.5)
$\dot {V}(t,\varphi ) \leqslant - {{W}_{1}}\left( {t,\varphi (0),\int\limits_{ - \infty }^t {{W}_{2}}(t,t + s,\varphi (s))ds} \right) \leqslant 0$

Пусть ${{V}_{1}} \in B_{V}^{{11}}$, ${{V}_{2}} \in B_{{v}}^{2}$, ${{W}_{1}} \in B_{W}^{1}$, ${{W}_{2}} \in B_{W}^{2}$. Аналогично определению $(f*,g*)$ могут быть определены семейства соответствующих предельных функций $\{ V_{1}^{*}\} $, $\{ V_{2}^{*}\} $, $\{ W_{1}^{*}\} $, $\{ W_{2}^{*}\} $. Может быть введена предельная совокупность $(f*,g*,V_{1}^{*},V_{2}^{*},W_{1}^{*},W_{2}^{*})$, задаваемая единой для предельных функций последовательностью ${{t}_{n}} \to \infty $.

Имеет место следующая теорема типа принципа квазиинвариантности.

Теорема 3.1. Предположим, что:

1) может быть найден функционал $V = V(t,\varphi )$, производная которого $\dot {V}(t,\varphi )$ удовлетворяет неравенству (3.5);

2) решение $x = x(t,\alpha ,\varphi )$ уравнения (2.1) ограничено при всех $t \in R$, $\left\| {x(t,\alpha ,\varphi )} \right\| \leqslant {{H}_{1}}$ $\forall t \in R$.

Тогда при некотором $c = {{c}_{0}} \geqslant m({{H}_{1}})$ для каждой точки $\varphi * \in {{\Omega }^{ + }}(\alpha ,\varphi )$ найдется предельная совокупность $(f*,g*,V_{1}^{*},V_{2}^{*},W_{1}^{*},W_{2}^{*})$ такая, что для соответствующего решения $x = x(t,0,\varphi *)$ предельного уравнения (2.6) имеют место включения

$\{ {{x}_{t}}(0,\varphi {\kern 1pt} *),t \in R\} \subset {{\Omega }^{ + }}(\alpha ,\varphi )$
${{x}_{t}}(0,\varphi {\kern 1pt} *) \in \{ V{\kern 1pt} *{\kern 1pt} (t,\varphi ) = {{c}_{0}}\} \cap \{ W{\kern 1pt} *{\kern 1pt} (t,\varphi ) = 0\} \quad \forall t \in R$

Доказательство.

Из условий 1 и 2 теоремы следует существование постоянной ${{c}_{0}} = \operatorname{const} \geqslant m({{H}_{1}})$ такой, что функция $V(t) = V(t,{{x}_{t}}(\alpha ,\varphi )) \searrow {{c}_{0}}$ при $t \to \infty $.

Пусть $\varphi {\kern 1pt} * \in {{\Omega }^{ + }}(\alpha ,\varphi )$ есть предельная функция, задаваемая последовательностью ${{t}_{n}} \to \infty $. Будем считать, что $(f*,g*,V_{1}^{*},V_{2}^{*},W_{1}^{*},W_{2}^{*})$ есть предельная совокупность, определяемая этой же последовательностью. Аналогично представлению (2.8) согласно (3.3) и (3.4) имеем

$V({{t}_{n}} + t,{{x}^{{(n)}}}(t)) = V_{1}^{{(n)}}(t,{{x}^{{(n)}}}(t)$
(3.6)
$\begin{gathered} \int\limits_{ - \infty }^0 {{{V}_{2}}({{t}_{n}} + t,{{t}_{0}} + s,\varphi (s))ds} + \int\limits_{{{t}_{0}} - {{t}_{n}}}^t {V_{2}^{{(n)}}(t,s,{{x}^{{(n)}}}(s))ds)} \\ V({{t}_{n}} + t) - V({{t}_{n}}) \leqslant - \int\limits_0^t {W_{1}^{{(n)}}(\tau ,{{x}^{{(n)}}}(\tau ),} \;\int\limits_{ - \infty }^0 {{{W}_{2}}({{t}_{n}} + t,{{t}_{0}} + s,\varphi (s))ds} + \\ \end{gathered} $
$ + \;\int\limits_{{{t}_{0}} - {{t}_{n}}}^t {{{W}^{{(n)}}}(\tau ,s,{{x}^{{(n)}}}(s))ds)d\tau \leqslant 0} $

В силу условия (3.1) для этих соотношений имеют место оценки вида (2.9). Соответственно из (3.6), переходя к пределу при ${{t}_{n}} \to \infty $, получаем искомые соотношения

$\begin{gathered} V_{1}^{*}(t,x{\kern 1pt} *{\kern 1pt} (t,0,\varphi {\kern 1pt} *),\int\limits_{ - \infty }^t {V_{2}^{*}(t,s,x{\kern 1pt} *{\kern 1pt} (s,0,\varphi {\kern 1pt} *))ds)} = {{c}_{0}} \\ W_{1}^{*}(t,x{\kern 1pt} *{\kern 1pt} (t,0,\varphi {\kern 1pt} *),\int\limits_{ - \infty }^t {W_{2}^{*}(t,s,x{\kern 1pt} *{\kern 1pt} (s,0,\varphi {\kern 1pt} *)ds)} = {{c}_{0}} \\ \end{gathered} $

Теорема доказана.

4. Устойчивость нулевого решения. Предположим, что $f(t,0,0) = g(t,0,0) \equiv 0$, так что уравнение (2.1) имеет нулевое решение $x(t,\alpha ,0) \equiv 0$, непрерывно зависящее от $(\alpha ,\varphi ) \in R \times {{C}_{\infty }}$.

Введем класс ${{\mathcal{K}}_{1}}$ функций ${{a}_{1}}:{{R}^{ + }} \to {{R}^{ + }}$ типа Хана [63] и класс ${{\mathcal{K}}_{2}}$ функций ${{a}_{2}}:{{R}^{ + }} \times {{R}^{ + }} \to {{R}^{ + }}$, таких, что ${{a}_{2}}(\alpha ,\nu ) \in {{\mathcal{K}}_{1}}$ при фиксированном $\alpha \in {{R}^{ + }}$. Будем полагать, что для оценки (3.1) ${{\nu }_{0}} \in {{\mathcal{K}}_{1}}$.

Примем следующее определение устойчивости в ${{R}^{n}}$ [4, 27, 28], обозначив через $\left| {\left| {\left| \varphi \right|} \right|} \right| = \sup ({{\left| {\left| {\left| \varphi \right|} \right|} \right|}_{l}},l \in N) = \sup (\left\| {\varphi (s)} \right\|,s \in {{R}^{ - }})$.

Определение 4.1. Решение $x = 0$ уравнения (2.1) является устойчивым, если $(\forall \varepsilon > 0)$ $(\forall \alpha \in {{R}^{ + }})$ $(\exists \delta = \delta (\varepsilon ,\alpha ) > 0)$ $(\forall \varphi \in {{C}_{\infty }}:\left| {\left| {\left| \varphi \right|} \right|} \right| < \delta )$ $(\forall t \geqslant \alpha )$ $\left\| {x(t,\alpha ,\varphi )} \right\| < \varepsilon $. Равномерная устойчивость означает, что $\delta = \delta (\varepsilon ) > 0$.

Определение 4.2. Решение $x = 0$ уравнения (2.1) является слабо асимптотически устойчивым, если оно равномерно устойчиво и $(\forall \alpha \in {{R}^{ + }})$ $(\exists {{\delta }_{0}} = {{\delta }_{0}}(\alpha ) > 0)$ $(\forall \varphi \in {{C}_{\infty }}:\left| {\left| {\left| \varphi \right|} \right|} \right| < {{\delta }_{0}})$ $\mathop {\lim }\limits_{t \to \infty } {\text{ }}x(t,\alpha ,\varphi ) = 0$.

Определение 4.3. Решение $x = 0$ уравнения (2.1) является равномерно асимптотически устойчивым относительно компакта $K \subset {{C}_{\infty }}$, если оно равномерно устойчиво и $(\exists {{\delta }_{0}} > 0)$ $(\forall \varepsilon > 0)$ $(\exists T = T(\varepsilon ) > 0)$ $(\forall \alpha > 0)$ $(\forall \varphi \in \in \{ \left| {\left| {\left| \varphi \right|} \right|} \right| < {{\delta }_{0}}\} \cap K)$ $(\forall t \geqslant \alpha + T)$ $\left\| {x(t,\alpha ,\varphi )} \right\| < \varepsilon $.

Теорема 4.1. Предположим, что:

1) можно найти функционал $V = V(t,\varphi )$ вида (3.3) такой, что

${{a}_{1}}(\left\| x \right\|) \leqslant {{V}_{1}}(t,x,{v}) \leqslant {{a}_{2}}(t,\left\| x \right\| + \left| {v} \right|),\quad {{a}_{1}} \in {{\mathcal{K}}_{1}},\quad {\kern 1pt} {{a}_{2}} \in {{\mathcal{K}}_{2}}$,
производная которого удовлетворяет неравенству (3.5);

2) для каждой предельной совокупности $(f{\kern 1pt} *,g{\kern 1pt} *,W_{1}^{*},W_{2}^{*})$ множество $\{ W{\kern 1pt} *{\kern 1pt} (t,\varphi ) = 0\} $ не содержит решений соответствующего предельного уравнения (2.6), кроме $x{\kern 1pt} *{\kern 1pt} (t,0,0) \equiv 0$.

Тогда решение $x = 0$ уравнения (2.1) асимптотически устойчиво.

Доказательство.

Для решения $x = x(t,\alpha ,\varphi )$ уравнения (2.1) из условия 1 теоремы при $t \in [\alpha ,\beta )$, ($\beta > \alpha $) имеем цепочку неравенств

(4.1)
$\begin{gathered} {{a}_{1}}(\left\| {x(t,\alpha ,\varphi )} \right\|) \leqslant {{V}_{1}}(t,x(t,\alpha ,\varphi ),{{V}_{2}}(t,{{x}_{t}}(\alpha ,\varphi ))) \leqslant V(\alpha ,x(\alpha ,\alpha ,\varphi ),{{V}_{2}}(\alpha ,{{x}_{\alpha }}(\alpha ,\varphi ))) = \\ = V(\alpha ,\varphi (0),{{V}_{2}}(\alpha ,\varphi )) \leqslant {{a}_{2}}(\alpha ,\left\| {\varphi (0)} \right\| + {{\nu }_{0}}(\left| {\left| {\left| \varphi \right|} \right|} \right|)) < {{a}_{1}}(\varepsilon ), \\ \end{gathered} $
если $\left| {\left| {\left| \varphi \right|} \right|} \right| + {{\nu }_{0}}(\left| {\left| {\left| \varphi \right|} \right|} \right|) < a_{2}^{{ - 1}}(\alpha ,{{a}_{1}}(\varepsilon )) = \delta (\alpha ,\varepsilon )$.

И, значит, $\left\| {x(t,\alpha ,\varphi )} \right\| < \varepsilon $ $\forall t \geqslant \alpha $.

Условие 2 теоремы означает, что для каждого решения $x = x{\kern 1pt} *{\kern 1pt} (t,0,\varphi {\kern 1pt} *)$, $\varphi {\kern 1pt} * \ne 0$, предельного уравнения (2.6) найдется $\beta \geqslant 0$, такое, что

$W{\kern 1pt} *{\kern 1pt} (\beta ,x_{\beta }^{*}(0,\varphi {\kern 1pt} *)) \ne 0$

В силу теоремы 2.1 и условия 2 данной теоремы для каждой предельной точки $\varphi {\kern 1pt} * \in {{\Omega }^{ + }}(\alpha ,\varphi )$ ограниченного решения $x = x(t,\alpha ,\varphi )$ имеем $W{\kern 1pt} *{\kern 1pt} (\beta ,x_{\beta }^{*}(0,\varphi {\kern 1pt} *)) \equiv 0$. Таким образом, находим, что $\varphi {\kern 1pt} * = 0$ $\forall \varphi {\kern 1pt} * \in {{\Omega }^{ + }}(\alpha ,\varphi )$ и, значит, $x(t,\alpha ,\varphi ) \to 0$ при $t \to \infty $. Теорема доказана.

Теорема 4.2. Предположим, что:

1) условие 1 теоремы 3.1 выполнено для функционала $V = V(t,\varphi )$ вида (3.3) и функции ${{a}_{2}} \in {{\mathcal{K}}_{1}}$;

2) для каждой предельной совокупности $(f*,g*,V_{1}^{*},V_{2}^{*},W_{1}^{*},W_{2}^{*})$ множество $\{ V{\kern 1pt} *{\kern 1pt} (t,\varphi ) = {{c}_{0}} = \operatorname{const} > 0\} $ ∩ $\{ W{\kern 1pt} *{\kern 1pt} (t,\varphi ) = 0\} $ не содержит решений соответствующего предельного уравнения (2.6).

Тогда решение $x = 0$ уравнения (2.1) равномерно асимптотически устойчиво относительно компакта $K \subset {{C}_{\infty }}$.

Доказательство.

Равномерная устойчивость $x = 0$ следует из условия 1 и (4.1) с учетом того, что ${{a}_{2}} = {{a}_{2}}(\nu )$. При этом находим, что для каждого ограниченного при всех $t \geqslant \alpha $ решения $x(t,\alpha ,\varphi )$ уравнения (2.1) функция $V(t,{{x}_{t}}(\alpha ,\varphi )) \searrow 0$ при $t \to \infty $. Далее, аналогично [24, 26], доказывается, что это свойство имеет место равномерно по $(\alpha ,\varphi ) \in {{R}^{ + }} \times K$.

5. Устойчивость по части переменных для случая конечного запаздывания. Рассмотрим задачу об устойчивости нулевого решения $x = 0$ по части переменных ${{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{l}}$ ($0 < l < p$). Для удобства переобозначим эти переменные через ${{y}_{i}} = {{x}_{i}}$ ($i = 1,2, \ldots ,l$), а остальные – через ${{z}_{j}} = {{x}_{{m + j}}}$ ($j = 1,2, \ldots $, $r = p - l$). Соответственно, $x{\kern 1pt} ' = ({{x}_{1}},{{x}_{2}}$, ... ..., ${{x}_{l}},{{x}_{{l + 1}}}, \ldots ,{{x}_{p}})$ = $(y{\kern 1pt} ',z{\kern 1pt} ')$, $y \in {{R}^{l}}$ есть вектор $l$-мерного действительного пространства с некоторой нормой $\left\| y \right\|$, $z \in {{R}^{{p - l}}}$ есть вектор $(p - l)$-мерного действительного пространства с некоторой нормой $\left\| z \right\|$, $\left\| x \right\| = \left\| x \right\| + \left\| z \right\|$.

Функцию $x = \varphi (s)$, $s \in {{R}^{ - }}$, будем представлять через соответствующие составляющие $\psi (s)$ и $\theta (s)$

$x{\kern 1pt} ' = \varphi {\kern 1pt} '(s) = (\psi {\kern 1pt} '(s),\theta {\kern 1pt} '(s)) = (y{\kern 1pt} ',z{\kern 1pt} ')$

В дополнение к условиям (2.2)–(2.4) будем полагать также z – продолжимость решений уравнения (2.1) [24, 26, 54]. Это означает, что если какое-либо решение $x = x(t,\alpha ,\varphi )$ определено лишь при $t \in ( - \infty ,\beta )$, $\alpha < \beta < + \infty $, то $\left\| {y(t,\alpha ,\varphi )} \right\| \to \infty $ при $t \to \infty $.

Будем использовать соответствующие определения устойчивости по части переменных $y$ с введенной нормой $\left\| \varphi \right\|$.

Теорема 5.1. Предположим, что:

1) каждое решение $x = x(t,\alpha ,\varphi )$, $(\alpha ,\varphi ) \in {{R}^{ + }} \times \{ \varphi \in {{C}_{\infty }}:\left\| \varphi \right\| \leqslant {{H}_{0}}\} $ уравнения (2.1) ограничено по $z$, $\left\| {z(t,\alpha ,\varphi )} \right\| \leqslant {{H}_{1}}(\alpha ,\varphi )$ $\forall t \geqslant \alpha $;

2) можно найти функционал $V = V(t,\varphi )$ вида (3.3), удовлетворяющий условиям

${{a}_{1}}(\left\| y \right\|) \leqslant {{V}_{2}}(t,x,{v}) \leqslant {{a}_{2}}(t,\left\| x \right\| + \left| {v} \right|),\quad {{a}_{1}} \in {{K}_{1}},\quad {{a}_{2}} \in {{K}_{2}}$
производная которого удовлетворяет неравенству (3.5);

3) для каждой предельной совокупности $(f{\kern 1pt} *,g{\kern 1pt} *,W_{1}^{*},W_{2}^{*})$ максимальное квазиинвариантное подмножество $M$ множества $\{ W{\kern 1pt} *{\kern 1pt} (t,\varphi ) = 0\} $ содержится в множестве $\{ \varphi \in {{C}_{\infty }}:\psi (s) \equiv 0\;\forall s \in {{R}^{ - }}\} $.

Тогда решение $x = 0$ уравнения (2.1) асимптотически устойчиво по $y$.

Доказательство.

Из условия 2 теоремы аналогично выводу соотношений (4.1) имеем оценки

${{a}_{1}}(\left\| {y(t,\alpha ,\varphi )} \right\|) \leqslant {{a}_{2}}(\alpha ,\left\| {\varphi (0)} \right\| + {{\nu }_{0}}({\text{|||}}\varphi {\text{|||}}))$
$\left\| {y(t,\alpha ,\varphi )} \right\| < \varepsilon \quad \forall t \geqslant \alpha ,\quad {\text{если}}$
$\left| {\left| {\left| \varphi \right|} \right|} \right| + {{\nu }_{0}}(\left| {\left| {\left| \varphi \right|} \right|} \right|) \leqslant a_{2}^{{ - 1}}(\alpha ,{{a}_{1}}(\varepsilon )) = \delta (\alpha ,\varepsilon )$

Учитывая условие 1 теоремы, находим, что каждое решение $x = x(t,\alpha ,\varphi )$, $(\alpha ,\varphi ) \in {{R}^{ + }}$ × $\{ \varphi \in {{C}_{\infty }}:\left| {\left| {\left| \varphi \right|} \right|} \right| < \inf ({{H}_{0}},\delta )\} $ определено и ограничено при всех $t \in {{R}^{ - }}$.

Согласно теореме 2.1 для каждого такого решения функция $\varphi {\kern 1pt} * = ((\psi {\kern 1pt} *){\kern 1pt} ',(\theta {\kern 1pt} *){\kern 1pt} ')$ ∈ ∈ ${{\Omega }^{ + }}(\alpha ,\varphi )$, если только $\psi {\kern 1pt} * = 0$. Отсюда следует, что

$\mathop {\lim }\limits_{t \to \infty } {\text{ }}y(t,\alpha ,\varphi ) = 0$

Теорема доказана.

Можно вывести также следующую теорему.

Теорема 5.2. Предположим, что:

1) существует некоторое ${{H}_{0}} > 0$ такое, что решения $x = x(t,\alpha ,\varphi )$, $(\alpha ,\varphi ) \in {{R}^{ + }}$ × × $\{ \varphi \in {{C}_{\infty }}:{\text{|||}}\varphi {\text{|||}} \leqslant {{H}_{0}}\} $ уравнения (2.1) равномерно ограничены по $z$, $\left\| {z(t,\alpha ,\varphi )} \right\| \leqslant {{H}_{1}}$ = = const $\forall t \geqslant \alpha $;

2) можно найти функционал $V = V(t,\varphi )$ вида (3.3), удовлетворяющий условию 2 теоремы 4.1 при ${{a}_{2}} \in {{K}_{1}}$;

3) для каждой предельной совокупности $(f{\kern 1pt} *,g{\kern 1pt} *,V_{1}^{*},V_{2}^{*},W_{1}^{*},W_{2}^{*})$ множество

$\{ V(t,\varphi ) = {{c}_{0}} = \operatorname{const} > 0\} \cap \{ W{\kern 1pt} *{\kern 1pt} (t,\varphi ) = 0\} $
не содержит решений $x = x{\kern 1pt} *{\kern 1pt} (t,0,\varphi {\kern 1pt} *)$ любого предельного уравнения (2.6).

Тогда решение $x = 0$ уравнения (2.1) равномерно по $(\alpha ,\varphi ) \in {{R}^{ + }} \times K$ асимптотически устойчиво относительно $y$.

6. Устойчивость положений равновесия и стационарных движений механической системы с линейной эредитарностью. Рассмотрим механическую систему с $N$ материальными точками, положения которых определяются радиус-векторами ${{\bar {r}}_{1}} = ({{x}_{1}},{{y}_{1}},{{z}_{1}})$, … …, ${{\bar {r}}_{N}} = ({{x}_{N}},{{y}_{N}},{{z}_{N}})$.

Допустим, что имеются вязкоупругие элементы с реакциями ${{\bar {F}}_{{jk}}}$ ($j = 1, \ldots ,N$; $k = 1,2, \ldots ,{{\mu }_{N}}$), приложенными к $j$-й точки.

(6.1)
$\begin{array}{*{20}{l}} {{{{\bar {F}}}_{{jk}}} = {{F}_{{jk}}}\bar {e}_{{jk}}^{0} = - ({{\rho }_{{jk}}}(t){{l}_{{jk}}}({{{\bar {r}}}_{j}}(t)) + \int\limits_{ - \infty }^t {{{g}_{{jk}}}(t,s){{l}_{{jk}}}({{{\bar {r}}}_{j}}(s))ds)\bar {e}_{{jk}}^{0}} } \end{array},$
где ${{l}_{{jk}}}$ – удлинение $k$-го элемента с учетом остаточной деформации при перемещении ${{\bar {r}}_{j}}(t)$, ${{\rho }_{{jk}}}$ и ${{g}_{{jk}}}$ – соответствующие коэффициенты жесткости и релаксации, $\bar {e}_{{jk}}^{0}$ – единичный вектор соответствующего направления.

Виртуальная работа этих реакций на элементарных перемещениях $\delta {{\bar {e}}_{{jk}}} = \delta {{e}_{{jk}}}{{\bar {e}}_{{jk}}}$ определяется равенствами

$\delta {\kern 1pt} '{\kern 1pt} A = \sum\limits_{j = 1}^N \,\sum\limits_{k = 1}^{{{\mu }_{j}}} \,{{\bar {F}}_{{jk}}}\delta {{\bar {e}}_{{jk}}} = F{\kern 1pt} '{\kern 1pt} \delta L$
(6.2)
$\begin{gathered} F{\kern 1pt} ' = ({{F}_{1}},{{F}_{2}}, \ldots ,{{F}_{p}}) = ({{F}_{{11}}}, \ldots ,{{F}_{{1{{\mu }_{1}}}}}, \ldots {{F}_{{N{{\mu }_{N}}}}}) \\ L{\kern 1pt} ' = ({{l}_{1}}, \ldots ,{{l}_{p}}) = ({{l}_{{11}}}, \ldots ,{{l}_{{1{{\mu }_{1}}}}}, \ldots {{l}_{{N{{\mu }_{N}}}}}) \\ \end{gathered} $
$p = \sum\limits_{j = 1}^N \,{{\mu }_{j}}$

Пусть на систему наложены идеальные стационарные связи, так что ее положение определяется $n$ обобщенными координатами ${{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{n}}$. Из (6.1) и (6.2) находим обобщенные силы, определяющие действие вязкоупругих элементов

$\begin{gathered} {{Q}_{1}} = \left( {\frac{{\partial L}}{{\partial q}}} \right)F;\quad L = L(q),\quad \frac{{\partial L}}{{\partial q}} = \frac{{\partial ({{L}_{1}},{{L}_{2}}, \ldots ,{{L}_{p}})}}{{\partial ({{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{n}})}} \\ F = - P(t)L(q(t)) - \int\limits_{ - \infty }^t {G(t,s)L(q(s))ds} \\ P = \operatorname{diag} ({{\rho }_{{11}}},{{\rho }_{{12}}}, \ldots ,{{\rho }_{p}}),\quad G = \operatorname{diag} ({{g}_{{11}}},{{g}_{{12}}}, \ldots ,{{g}_{p}}) \\ \end{gathered} $

Допустим, что на систему действуют также потенциальные и диссипативные силы

${{Q}_{2}} = {{Q}_{2}}(t,q,\dot {q}),\quad {{Q}_{2}}(t,q,0) \equiv 0;\quad \dot {q}{\kern 1pt} '{\kern 1pt} {{Q}_{2}} \leqslant 0,\quad {{Q}_{3}} = - \frac{{\partial \Pi (t,q)}}{{\partial q}},$
где $\Pi (t,q)$ – потенциальная энергия.

Движение системы может быть описано уравнениями Лагранжа

(6.3)
$\frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial{ \dot {q}}}}} \right) - \frac{{\partial T}}{{\partial q}} = - \frac{{\partial \Pi }}{{\partial q}} + {{Q}_{1}} + {{Q}_{2}},$
где $T = (\dot {q}{\kern 1pt} '{\kern 1pt} A(q)\dot {q}){\text{/}}2$ – кинетическая энергия, $A \in {{R}^{{n \times n}}}$ – положительно определенная при всех $q \in {{R}^{n}}$ матрица.

Будем полагать, что функции, входящие в (6.3), удовлетворяют условиям (2.2)–(2.4), равенству $L(q) = {{L}_{0}}$ при $\left\| q \right\| \leqslant {{H}_{0}}$ удовлетворяет конечное число значений.

Введем функционал, определяемый вдоль движения $(q(t),\dot {q}(t))$ системы (6.3) следующим равенством

$V(t,{{q}_{t}},\dot {q}(t)) = \tfrac{1}{2}\dot {q}{\kern 1pt} '{\kern 1pt} A(q)\dot {q} + {{\Pi }_{1}}(t,q) - \tfrac{1}{2}\int\limits_{ - \infty }^t {(L(q(t)) - L(q(s))){\kern 1pt} '{\kern 1pt} G(t,s)(L(q(t)) - L(q(s)))ds} ,$
где ${{\Pi }_{1}}(t,q)$ имеет вид

${{\Pi }_{1}}(t,q) = \Pi (t,q) + \frac{1}{2}L{\kern 1pt} '(q)P(t)L(q) + \frac{1}{2}L{\kern 1pt} '(q)\left( {\int\limits_{ - \infty }^t {G(t,s)ds} } \right)L(q)$

Для производной функционала $V$ согласно (3.4) в силу уравнений движения (6.3) находим оценку

$\begin{gathered} \dot {V}(t,{{q}_{t}},\dot {q}(t)) = \frac{{\partial {{\Pi }_{1}}(t,q)}}{{\partial t}} + {{Q}_{{2'}}}(t,q,\dot {q})\dot {q} - W(t,{{q}_{t}}) \leqslant - W(t,{{q}_{t}}) \leqslant 0 \\ W(t,{{q}_{t}}) = \frac{1}{2}\int\limits_{ - \infty }^t {(L(q(t)) - L(q(s))){\kern 1pt} '\frac{{\partial G(t,s)}}{{\partial t}}(L(q(t)) - L(q(s)))ds} , \\ \end{gathered} $
если

$\frac{{\partial {{\Pi }_{1}}(t,q)}}{{\partial t}} \leqslant 0,{\kern 1pt} \quad \forall (t,q) \in {{R}^{ + }} \times {{R}^{n}},\quad a{\kern 1pt} '\frac{{\partial G(t,s)}}{{\partial t}}a \geqslant 0\quad \forall (t,s) \in S,\quad \forall a \in {{R}^{n}}$

Определим семейство функций $\{ \Pi _{1}^{*}(t,q)\} $, предельных к функции ${{\Pi }_{1}}(t,q)$, и матриц $\{ G_{t}^{*}(t,s)\} $, предельных к $\partial G(t,s){\text{/}}\partial t$.

На основании теоремы 2.1 имеем следующее утверждение.

Утверждение 6.1. Пусть:

1) равенства $\partial \Pi {\kern 1pt} *{\kern 1pt} (t,q){\text{/}}\partial q = 0$ для всех предельных $\Pi _{1}^{*}(t,q)$ определяют одно и то же множество изолированных положений $M = \{ q = q_{0}^{{(k)}}$, $k = 1,2, \ldots ,l\} $;

2) для каждой матрицы $G_{t}^{*}(t,s)$ найдется пара значений $({{t}_{0}},{{s}_{0}}) \in S$, такая, что

$\det {{G}_{t}}({{t}_{0}},{{s}_{0}}) = \prod\limits_{j = 1}^p \,g_{j}^{*}({{t}_{0}},{{s}_{0}}) \ne 0$

Тогда каждое ограниченное движение системы (6.3) неограниченно приближается к одному из предельных положений равновесия $(\dot {q},q) = (0,q_{0}^{{(k)}})$ при $t \to + \infty $.

Без ограничения общности, допустим, что при $q = 0$ имеют место равенства

$\Pi (t,0) = 0,\quad \frac{{\partial \Pi }}{{\partial q}}(t,0) = 0,{\kern 1pt} \quad L(0) = 0$

Тогда система (6.3) имеет положение равновесия $\dot {q} = q = 0$.

Согласно теореме 3.2 имеем следующее утверждение.

Утверждение 6.2. Допустим, что:

1) функция ${{\Pi }_{1}}(t,q)$ удовлетворяет условиям

${{a}_{1}}(\left\| q \right\|) \leqslant {{\Pi }_{1}}(t,q) \leqslant {{a}_{2}}(\left\| q \right\|),\quad {{a}_{1}},{{a}_{2}} \in {{K}_{1}}$
$\left\| {\frac{{\partial {{\Pi }_{1}}(t,q)}}{{\partial q}}} \right\| \geqslant {{a}_{3}}(\left\| q \right\|),\quad {{a}_{3}} \in {{K}_{1}};$

2) выполнено условие 2 утверждения 6.1.

Тогда положение равновесия $\dot {q} = q = 0$ системы (6.3) асимптотически устойчиво равномерно по $K \subset {{C}_{\infty }}$.

Рассмотрим частный случай, когда

$\Pi = \Pi (q),\quad {{\rho }_{\rho }} = \rho _{\rho }^{0} = \operatorname{const} ,\quad {{g}_{j}}(t,s) = {{g}_{j}}(s - t)$

В этом случае находим, что $g_{j}^{*}(t,s) = {{g}_{j}}(s - t)$

${{\Pi }_{1}} = {{\Pi }_{1}}(q) = \Pi (q) + \frac{1}{2}L{\kern 1pt} '(q)PL(q) + \frac{1}{2}L{\kern 1pt} '(q)\left( {\int\limits_{ - \infty }^0 {G(\nu )d\nu } } \right)L(q)$

Условия утверждения 5.2 будут выполнены, если

${{\Pi }_{1}}(q) \geqslant {{a}_{1}}(\left\| q \right\|),\quad \left\| {\frac{{\partial {{\Pi }_{1}}(q)}}{{\partial q}}} \right\| \ne 0;\quad {{g}_{j}}(\nu ) \leqslant 0\quad (j = 1,2, \ldots ,p),\quad \prod\limits_{j = 1}^p \,{{g}_{j}}(\nu {\kern 1pt} *) \ne 0$
при $q \ne 0$ и некотором $\nu {\kern 1pt} * \in {{R}^{ - }}$.

По теореме 4.2 имеет место также следующее утверждение.

Утверждение 6.3. Допустим, что:

1) движения системы (6.3) из некоторой окрестности $\dot {q} = q = 0$ ограничены по ${{q}_{{m + 1}}}, \ldots ,{{q}_{n}}$, например, эти переменные определяются по $\bmod (2\pi )$;

2) функция ${{\Pi }_{1}}(q) \geqslant {{a}_{1}}({{\left\| q \right\|}_{m}})$

$\left\| {\frac{{\partial {{\Pi }_{1}}(q)}}{{\partial q}}} \right\| \ne 0\quad \forall q \in \{ {{\Pi }_{1}}(q) > 0\} $

Тогда положение равновесия $\dot {q} = q = 0$ равномерно асимптотически устойчиво по $\dot {q},{{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{m}}$.

7. О стабилизации установившихся движений манипуляторов с цилиндрическими и сферическими вязкоупругими шарнирами. Рассмотрим манипулятор, функционирующий в однородном поле тяжести, с указанными выше шарнирами, положение которого определяется $n$ обобщенными координатами ${{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{n}}$.

Уравнения движения системы возьмем в форме (6.3) с тем изменением, что потенциальная энергия сил тяжести $\Pi = \Pi (q)$, вязкоупругое действие в шарнирах является линейным по координатам ${{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{n}}$ таким образом, что

(7.1)
$\begin{gathered} L = (q - {{q}_{0}}),\quad P = {{P}_{0}} = \operatorname{diag} (\rho _{1}^{0},\rho _{2}^{0}, \ldots ,\rho _{n}^{0}),\quad \rho _{k}^{0} \geqslant 0 \\ G(t,s) = G(s - t) = \operatorname{diag} ({{g}_{1}}(s - t),{{g}_{2}}(s - t), \ldots ,{{g}_{n}}(s - t)) \\ {{g}_{k}}(\nu ) \leqslant 0,\quad {{g}_{{k'}}}(\nu ) \geqslant 0, \\ \end{gathered} $
обобщенная сила ${{Q}_{2}}$ есть управление, ${{Q}_{2}} = U$, подлежащее определению.

Пусть $\dot {q} = 0$, $q = {{q}^{{(0)}}}$ есть заданное положение манипулятора, создаваемое управлением

(7.2)
${{U}^{{(0)}}} = \frac{{\partial \Pi }}{{\partial q}}({{q}^{{(0)}}}) + \left( {{{P}_{0}} + \int\limits_{ - \infty }^0 G(\nu )d\nu } \right)({{q}^{{(0)}}} - {{q}_{0}})$

Введем возмущения $x = q - {{q}^{{(0)}}}$ и рассмотрим задачу нахождения управляющих воздействий ${{U}^{{(1)}}} = U - {{U}^{{(0)}}}$ без измерения скоростей, обеспечивающих стабилизацию положения $\dot {x} = 0$, $x = 0$.

Уравнения возмущенного движения могут быть представлены в виде

(7.3)
$\frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial{ \dot {x}}}}} \right) - \frac{{\partial T}}{{\partial x}} = - \frac{{\partial \Pi }}{{\partial q}}({{q}^{{(0)}}} + x) + \frac{{\partial \Pi }}{{\partial q}}({{q}^{{(0)}}}) - {{P}_{0}}x - \int\limits_{ - \infty }^r {G(s - t)x(s)ds + {{U}^{{(1)}}}} $

Выберем управляющее воздействие в виде

(7.4)
${{U}^{{(1)}}} = - \left( {\frac{{\partial f}}{{\partial x}}} \right){{U}^{{(11)}}}f + \left( {\frac{{\partial f}}{{\partial x}}} \right)\int\limits_0^t {{{U}^{{(12)}}}(s - t)(f(x(t)) - f(x(s)))ds} ,$
где ${{U}^{{(11)}}}$, ${{U}^{{(12)}}} \in {{R}^{{n \times n}}}$, ${{U}^{{(11)}}} = \operatorname{const} $, ${{U}^{{(12)}}}(\nu ) \geqslant 0$, $(U_{\nu }^{{(12)}}){\kern 1pt} '(\nu ) \leqslant 0$, $f:{{R}^{n}} \to {{R}^{n}}$ ($f(0) = 0$) есть обратимая функция, выбираемая из условия эффективности управления.

Введем функционал

(7.5)
$\begin{gathered} V = T({{q}_{0}} + x,\dot {x}) + {{\Pi }_{1}}(x) - \frac{1}{2}\int\limits_{ - \infty }^t (x(t) - x(s)){\kern 1pt} '{\kern 1pt} G(s - t)(x(t) - x(s))ds + \\ + \;\frac{1}{2}\int\limits_0^t (f(x(t)) - f(x(s))){\kern 1pt} '{{U}^{{(12)}}}(s - t)(f(x(t)) - f(x(s)))ds \\ \end{gathered} $
(7.6)
${{\Pi }_{1}}(x) = \Pi ({{q}_{0}} + x) - x{\kern 1pt} '\frac{{\partial \Pi }}{{\partial q}}({{q}_{0}}) - \Pi ({{q}_{0}}) + \frac{1}{2}x{\kern 1pt} '\left( {{{P}_{0}} + \int\limits_{ - \infty }^0 G(\nu )d\nu } \right)x + \frac{1}{2}f{\kern 1pt} '(x){{U}^{{(11)}}}f(x)$

Для производной функционала (7.5) в силу уравнений движения (7.3) имеем

(7.7)
$\begin{gathered} \dot {V} \leqslant \;\,\frac{1}{2}\int\limits_0^t (x(t) - x(s)){\kern 1pt} '{{G}_{\nu }}(s - t)(x(t) - x(s))ds - \\ - \;\frac{1}{2}\int\limits_0^t (f(x(t)) - f(x(s))){\kern 1pt} 'U_{\nu }^{{(12)}}(s - t)(f(x(t)) - f(x(s)))ds \leqslant 0 \\ \end{gathered} $

В соответствии с теоремой имеем следующий результат.

Утверждение 7.1. Пусть управление (7.4) таково, что:

1) $y{\kern 1pt} '{{G}_{\nu }}(\nu )y - z{\kern 1pt} 'U_{\nu }^{{(12)}}(\nu )z \leqslant 0{\kern 1pt} $ $( \ne 0{\text{ при }}{{y}^{2}} + {{z}^{2}} \ne 0)$;

2) функция ${{\Pi }_{1}}(x)$ является определенно-положительной, при этом

$\left\| {\frac{{\partial {{\Pi }_{1}}}}{{\partial x}}} \right\| \geqslant {{a}_{1}}(\left\| x \right\|)$

Тогда управление (7.4) решает задачу о стабилизации заданного положения $\dot {q} = 0$, $q = {{q}^{{(0)}}}$ манипулятора.

Заметим, что потенциальная энергия $\Pi = \Pi (q)$ системы представляет собой функцию периодическую по ${{q}_{1}}$, ${{q}_{2}}$, …, ${{q}_{n}}$. Поэтому значения $\rho _{1}^{0}$, $\rho _{2}^{0}$, …, $\rho _{n}^{0}$ и функция $f = f(x)$ могут быть выбраны так, что ${{\Pi }_{1}}(x) \to \infty $ при $\left\| x \right\| \to \infty $. Соответственно, имеет место утверждение о глобальной равномерной стабилизации.

Пусть координаты ${{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{m}}$ манипулятора являются позиционными, а ${{q}_{{m + 1}}},{{q}_{{m + 2}}}, \ldots ,{{q}_{n}}$ – циклическими, так что кинетическая энергия $T$ и потенциальная энергия не зависят явно от ${{q}_{{m + 1}}},{{q}_{{m + 2}}}, \ldots ,{{q}_{n}}$, соответствующие обобщенные силы равны нулю.

Следуя [59], переобозначим координаты и введем импульсы, соответствующие циклическим координатам

$\begin{gathered} r{\kern 1pt} ' = ({{r}_{1}},{{r}_{2}}, \ldots ,{{r}_{m}}) = ({{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{m}}) \\ s{\kern 1pt} ' = ({{s}_{1}},{{s}_{2}}, \ldots ,{{s}_{{n - m}}}) = ({{q}_{{m + 1}}},{{q}_{{m + 2}}}, \ldots ,{{q}_{n}}) \\ p = \frac{{\partial T}}{{\partial{ \dot {s}}}} \\ \end{gathered} $

В обозначениях из [59] имеем следующие уравнения движения

(7.8)
$\frac{d}{{dt}}\left( {\frac{{\partial R}}{{\partial{ \dot {r}}}}} \right) - \frac{{\partial R}}{{\partial r}} = - \frac{{\partial \Pi }}{{\partial r}} + {{Q}_{1}} + {{U}_{r}},{\kern 1pt} \quad \frac{{dp}}{{dt}} = {{U}_{s}},\quad \dot {s} = - \frac{{\partial R}}{{\partial p}},$
где

$\begin{gathered} 2{{R}_{2}} = \dot {r}{\kern 1pt} '({{A}_{{rr}}}(r) - {{A}_{{rs}}}(r)A_{{ss}}^{{ - 1}}(r){{A}_{{sr}}}(r))\dot {r},\quad {{R}_{1}} = p{\kern 1pt} 'A_{{ss}}^{{ - 1}}(r){{A}_{{sr}}}(r)\dot {r} \\ 2{{R}_{0}} = - p{\kern 1pt} 'A_{{ss}}^{{ - 1}}(r)p,\quad U{\kern 1pt} ' = ({{U}_{{r{\kern 1pt} '}}},{{U}_{{s{\kern 1pt} '}}}) \\ \end{gathered} $

Из уравнений (7.8) находим, что при управлении

(7.9)
${{U}_{r}} = U_{r}^{0} - \frac{{\partial {{R}_{0}}}}{{\partial r}}({{p}_{0}},{{r}_{0}}) + \frac{{\partial \Pi }}{{\partial r}}({{r}_{0}}) + \left( {{{P}_{0}} + \int\limits_{ - \infty }^0 G(\nu )d\nu )} \right)({{r}^{{(0)}}} - {{r}_{0}});\quad {{U}_{s}} = U_{s}^{0} = 0$
система имеет стационарное движение

(7.10)
$\dot {r} = 0,\quad r = {{r}^{{(0)}}},\quad p = {{p}^{{(0)}}},\quad \dot {s} = \dot {s}_{0}^{{(0)}} - {{\left. {\frac{{\partial {{R}_{0}}}}{{\partial p}}} \right|}_{{r = {{r}^{{(0)}}},p = {{p}^{{(0)}}}}}}$

Введем возмущения $y = r - {{r}_{0}}$, $z = p - {{p}^{{(0)}}}$. Выберем управляющие воздействия в виде

(7.11)
$\begin{gathered} U_{r}^{{(1)}} = {{U}_{r}} - U_{r}^{0} = - \left( {\frac{{\partial f}}{{\partial r}}} \right){{U}^{{(11)}}}f + \left( {\frac{{\partial f}}{{\partial x}}} \right)\int\limits_0^t {{{U}^{{(12)}}}(s - t)(f(x(t)) - f(x(s)))ds} \\ U_{s}^{{(1)}} = {{U}_{s}} = - K(p - {{p}^{{(0)}}}), \\ \end{gathered} $
где ${{U}^{{(11)}}},{{U}^{{(12)}}} \in {{R}^{{m \times m}}}$, ${{U}^{{(11)}}} = \operatorname{const} $, ${{U}^{{(12)}}}(\nu ) \geqslant 0$, ${{U}_{\nu }}(\nu ) > 0$; $f:{{R}^{m}} \to {{R}^{m}}$ ($f(0) = 0$) есть обратимая функция, $K \in {{R}^{{(n - m) \times (n - m)}}}$ – положительно определенная матрица.

Введем функционал

$V = {{R}_{2}}(y,y) + {{W}_{1}}({{p}_{0}},y) - \frac{1}{2}\int\limits_{ - \infty }^t {(y(t) - y(s)){\kern 1pt} 'G(s - t)(y(t) - y(s))ds} + $
(7.12)
$\begin{gathered} + \;\frac{1}{2}\int\limits_0^t {(f(y(t)) - f(y(s))){\kern 1pt} '{{U}^{{(12)}}}(s - t)(f(y(t)) - f(y(s)))ds} + \frac{1}{2}z{\kern 1pt} 'Kz \\ {{W}_{1}}({{p}_{0}},y) = \Pi ({{r}_{0}} + y) - {{R}_{0}}({{p}_{0}},{{r}_{0}} + y) - y{\kern 1pt} '\frac{{\partial \Pi ({{r}_{0}})}}{{\partial r}} + \\ \end{gathered} $
$ + \;y{\kern 1pt} '\frac{{\partial {{R}_{0}}({{p}_{0}},{{r}_{0}})}}{{\partial r}} - \Pi ({{r}_{0}}) + {{R}_{0}}({{p}_{0}},{{r}_{0}}) + \frac{1}{2}y{\kern 1pt} '\left( {{{P}_{0}} + \int\limits_{ - \infty }^0 {G(\nu )d\nu } } \right)y + \frac{1}{2}f{\kern 1pt} '(y){{U}^{{(11)}}}f(y)$

Для производной функционала (7.12) в силу уравнений движения (7.8) находим

$\begin{gathered} \dot {V} \leqslant \frac{1}{2}\int\limits_0^t {(y(t) - y(s)){\kern 1pt} '{{G}_{\nu }}(s - t)(y(t) - y(s))ds} - \\ - \;\frac{1}{2}\int\limits_0^t {(f(y(t)) - f(y(s))){\kern 1pt} 'U(s - t)(f(y(t)) - f(y(s)))ds} - \frac{1}{2}z{\kern 1pt} 'Kz \leqslant 0 \\ \end{gathered} $

В соответствии с теоремой 4.2 имеем следующий результат.

Утверждение 7.2. Пусть управляющее и вязкоупругое воздействия (7.9) и (7.11) таковы, что:

1) $f{\kern 1pt} '(y)U_{\nu }^{{(12)}}f(y) - y{\kern 1pt} '{{G}_{\nu }}y > 0$ при $y \ne 0$;

2) функция ${{W}_{1}}({{p}_{0}},y)$ является определенно положительной по $y$, при этом

$\left\| {\frac{{\partial {{W}_{1}}({{p}_{0}},y)}}{{\partial y}}} \right\| \geqslant {{a}_{1}}(\left\| y \right\|)$

Тогда имеет место стабилизация заданного стационарного движения $\dot {r} = 0$, $r = {{r}^{{(0)}}}$, $p = {{p}^{{(0)}}}$ манипулятора. Подбором $\rho _{1}^{0}$, $\rho _{2}^{0}$, $\rho _{m}^{0}$ и функции $f = f(y)$ может быть достигнута глобальная равномерная стабилизация.

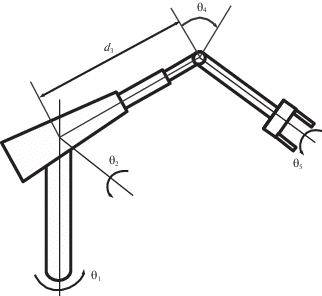
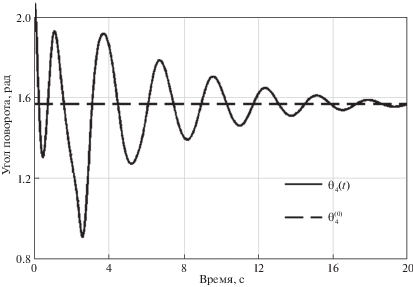
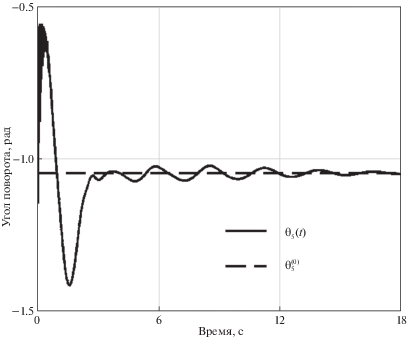
8. Стабилизация программного положения пятизвенного робота-манипулятора. В этом разделе представлено численное моделирование управляемого движения многозвенного робота-манипулятора с пятью степенями свободы (см. рис. 1). Робот имеет один призматический и четыре вращательных шарнира.

Рис. 1.

Каждое звено манипулятора представлено в виде твердого тела. Кинематические пары манипулятора считаются однозвенными, их геометрические центры обозначены символом ${{O}_{k}}$ ($k = 1,2, \ldots ,5$). Центры масс ${{C}_{k}}$ ($k = 1,2, \ldots ,5$) звеньев лежат на осях ${{O}_{k}}{{O}_{{k + 1}}}$, оси ${{O}_{k}}{{O}_{{k + 1}}}$ ($k = 1,2, \ldots ,5$) – оси симметрии звеньев. Первое базовое звено вертикальное, оно вращается вокруг ${{O}_{1}}{{O}_{2}}$, угол поворота равен ${{\theta }_{1}}$. Вторая кинематическая пара позволяет вращать второе звено вокруг горизонтальной оси, проходящей через ${{O}_{2}}$. Третья кинематическая пара допускает прямолинейное движение третьего звена по линии ${{O}_{2}}{{O}_{4}}$ (${{O}_{3}} \in {{O}_{1}}{{O}_{4}}$). Введем обозначение смещения третьего звена $x = {{d}_{3}} = {{O}_{1}}{{O}_{4}}$. Четвертое звено может вращаться вокруг горизонтальной оси, проходящей через ${{O}_{4}}$, с углом поворота ${{\theta }_{4}}$. Пятое звено, моделирующее захват, может вращаться вокруг ${{O}_{4}}{{O}_{5}}$, его угол поворота обозначается ${{\theta }_{5}}$. Будем считать, что центры масс ${{C}_{k}}$ звеньев лежат на осях ${{O}_{k}}{{O}_{{k + 1}}}$ и эти оси являются осями симметрии соответствующих звеньев ($k = 1,2, \ldots ,5$). Введем главные центральные оси ${{C}_{k}}{{x}_{k}},{{C}_{k}}{{y}_{k}},{{C}_{k}}{{z}_{k}}$ звеньев. Будем считать, что для звеньев 1 и 5 оси ${{C}_{1}}{{z}_{1}}$ и ${{C}_{5}}{{z}_{5}}$ являются осями симметрии. Для звеньев 2, 3 и 4 такими осями являются ${{C}_{2}}{{x}_{2}}$, ${{C}_{3}}{{x}_{3}}$ и ${{C}_{4}}{{x}_{4}}$ соответственно. Предположим, что оси ${{C}_{2}}{{z}_{2}}$, ${{C}_{3}}{{z}_{3}}$ и ${{C}_{4}}{{z}_{4}}$ горизонтальны. Массы звеньев обозначим через ${{m}_{k}}$ ($k = 1,2, \ldots ,5$), а их основные центральные моменты инерции обозначим через $I_{x}^{{(k)}}$, $I_{y}^{{(k)}}$ и $I_{z}^{{(k)}}$. Соответственно, имеем $I_{x}^{{(1)}} = I_{y}^{{(1)}}$, $I_{x}^{{(5)}} = I_{y}^{{(5)}}$, $I_{y}^{{(2)}} = I_{z}^{{(2)}}$, $I_{y}^{{(3)}} = I_{z}^{{(3)}}$, $I_{y}^{{(4)}} = I_{z}^{{(4)}}$. Введем длины ${{O}_{2}}{{C}_{2}} = {{l}_{2}}$, ${{C}_{3}}{{O}_{4}} = {{l}_{3}}$, ${{O}_{4}}{{O}_{5}} = 2{{O}_{4}}{{C}_{4}} = 2{{l}_{4}}$ и ${{O}_{5}}{{C}_{5}} = {{l}_{5}}$.

Используя теорему Кенига, можно найти кинетическую энергию ${{T}_{i}}$ каждого звена $i = 1,2, \ldots ,5$ как кинетическую энергию абсолютно твердого тела.

${{T}_{1}} = \frac{1}{2}I_{z}^{{(1)}}\dot {\theta }_{1}^{2},\quad {{T}_{2}} = \frac{1}{2}{{m}_{2}}l_{2}^{2}({{\sin }^{2}}{{\theta }_{2}}\dot {\theta }_{1}^{2} + \dot {\theta }_{2}^{2}) + \frac{1}{2}(I_{x}^{{(2)}}\dot {\theta }_{1}^{2}{{\cos }^{2}}{{\theta }_{2}} + I_{z}^{{(2)}}(\dot {\theta }_{1}^{2}{{\sin }^{2}}{{\theta }_{2}} + \dot {\theta }_{2}^{2}))$
${{T}_{3}} = \frac{1}{2}{{m}_{3}}({{\dot {x}}^{2}} + {{(x - {{l}_{3}})}^{2}}\dot {\theta }_{z}^{2} + (x - {{l}_{3}}){{\sin }^{2}}{{\theta }_{2}}\dot {\theta }_{1}^{2}) + \frac{1}{2}(I_{x}^{{(3)}}\dot {\theta }_{1}^{2}{{\cos }^{2}}{{\theta }_{2}} + I_{z}^{{(3)}}(\dot {\theta }_{1}^{2}{{\sin }^{2}}{{\theta }_{2}} + \dot {\theta }_{2}^{2}))$
${{T}_{4}} = \frac{1}{2}{{m}_{4}}((\dot {x} + {{l}_{4}}{{\dot {\theta }}_{4}}\sin {{\theta }_{4}}{{)}^{2}} + {{(x{{\dot {\theta }}_{2}} - {{l}_{4}}{{\dot {\theta }}_{4}}\cos {{\theta }_{4}})}^{2}} + {{(x\cos {{\theta }_{4}} - {{l}_{4}}\sin ({{\theta }_{2}} + {{\theta }_{4}}))}^{2}}\dot {\theta }_{1}^{2} + $
$ + \;\frac{1}{2}(I_{x}^{{(4)}}\dot {\theta }_{1}^{2}{{\cos }^{2}}({{\theta }_{2}} + {{\theta }_{4}}) + I_{z}^{{(4)}}(\dot {\theta }_{1}^{2}{{\sin }^{2}}({{\theta }_{2}} + {{\theta }_{4}}) + {{({{\dot {\theta }}_{2}} + {{\dot {\theta }}_{4}})}^{2}}))$
${{T}_{5}} = \frac{1}{2}{{m}_{5}}((\dot {x} + (2{{l}_{4}} + {{l}_{5}}){{\dot {\theta }}_{4}}\sin {{\theta }_{4}}{{)}^{2}} + {{(x{{\dot {\theta }}_{2}} - (2{{l}_{4}} + {{l}_{5}}){{\dot {\theta }}_{4}}\cos {{\theta }_{4}})}^{2}} + $
$ + \;{{(x\cos \theta - (2{{l}_{4}} + {{l}_{5}})\sin ({{\theta }_{2}} + {{\theta }_{4}}))}^{2}}\dot {\theta }_{1}^{2} + $
$ + \;\frac{1}{2}I_{x}^{{(5)}}{{({{\dot {\theta }}_{1}}\cos ({{\theta }_{2}} + {{\theta }_{4}}) + {{\dot {\theta }}_{5}})}^{2}} + \frac{1}{2}I_{z}^{{(5)}}(\dot {\theta }_{1}^{2}{{\cos }^{2}}({{\theta }_{2}} + {{\theta }_{4}}) + {{({{\dot {\theta }}_{2}} + {{\dot {\theta }}_{4}})}^{2}})$

Кинетическая энергия манипулятора имеет вид

$T = {{T}_{1}} + {{T}_{2}} + {{T}_{3}} + {{T}_{4}} + {{T}_{5}}$

Потенциальная энергия манипулятора выражается в виде

$\begin{gathered} \Pi = - {{m}_{2}}g{{l}_{2}}\cos {{\theta }_{2}} - {{m}_{3}}g(x - {{l}_{3}})\cos {{\theta }_{2}} - {{m}_{4}}g(x\cos {{\theta }_{2}} + {{l}_{4}}\cos ({{\theta }_{2}} + {{\theta }_{4}})) - \\ - \;{{m}_{5}}g(x\cos {{\theta }_{2}} + (2{{l}_{4}} + {{l}_{5}})\cos ({{\theta }_{2}} + {{\theta }_{4}})) \\ \end{gathered} $

Массоинерционные параметры робота выбраны следующими

${{m}_{2}} = 5{\text{ }}кг,\quad {{m}_{3}} = {{m}_{4}} = 3кг,\quad {{m}_{5}} = 4кг$
${{l}_{2}} = 0.8м,\quad {{l}_{3}} = {{l}_{4}} = 0.4м,\quad {{l}_{5}} = 0.5м$
$I_{x}^{{(2)}} = I_{y}^{{(2)}} = 0.25{\text{ }}кг{{м}^{2}},\quad I_{z}^{{(2)}} = 0.2{\text{ }}кг{{м}^{2}}$
$I_{x}^{{(3)}} = I_{y}^{{(3)}} = I_{z}^{{(3)}} = I_{x}^{{(4)}} = I_{y}^{{(4)}} = I_{z}^{{(4)}} = 0.1{\text{ }}кг{{м}^{2}}$
$I_{x}^{{(5)}} = I_{y}^{{(5)}} = 0.05{\text{ }}кг{{м}^{2}},\quad I_{z}^{{(5)}} = 0.2{\text{ }}кг{{м}^{2}}$

Программное положение робота выбрано следующим

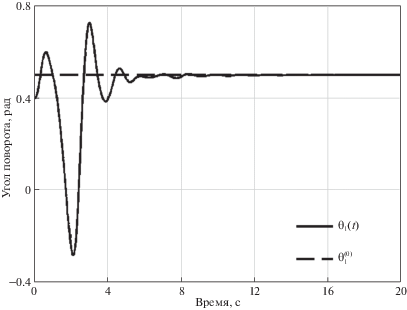
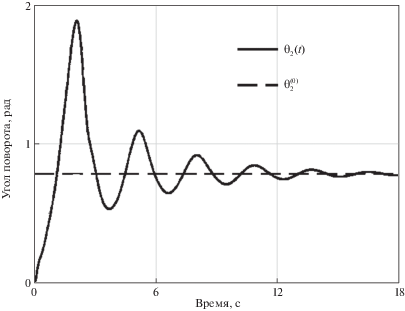
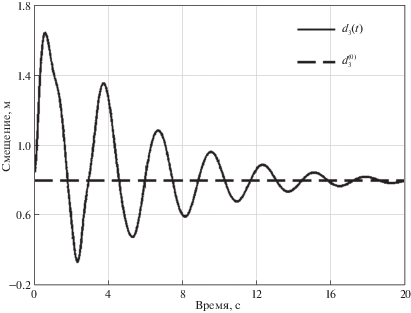
(8.1)
$\begin{gathered} \theta _{1}^{{(0)}} = 0.5\;рад,\quad \theta _{2}^{{(0)}} = \pi {\text{/}}4\;рад,\quad d_{3}^{{(0)}} = 0.8\;м \\ \theta _{4}^{{(0)}} = - \pi {\text{/}}3\;рад,\quad \theta _{5}^{{(0)}} = \pi {\text{/}}2\;рад \\ \end{gathered} $

Расчеты проведены при следующих начальных отклонениях от программного положения

(8.2)
$\begin{gathered} {{x}_{1}}(0) = {{x}_{5}}(0) = - 0.1\;рад,\quad {{x}_{2}}(0) = - 0.8\;рад,\quad {{x}_{3}}(0) = 0.05\;м,\quad {{x}_{4}}(0) = 0.5\;рад \\ {{{\dot {x}}}_{1}}(0) = {{{\dot {x}}}_{5}}(0) = - 0.01\;{\text{рад/с}},\quad {{{\dot {x}}}_{2}}(0) = {{{\dot {x}}}_{4}}(0) = - 0.02\;{\text{рад/с}},\quad {{{\dot {x}}}_{3}}(0) = 0.01\;{\text{м/с}} \\ \end{gathered} $

На рис. 2–6 представлены результаты численного моделирования процесса управления манипулятором, показывающие зависимости от времени углов поворота и линейного смещения его звеньев.

Рис. 2.
Рис. 3.
Рис. 4.
Рис. 5.
Рис. 6.

Заключение. В работе проведено развитие метода функционалов Ляпунова в исследовании устойчивости неавтономного нелинейного интегро-дифференциального уравнения с бесконечным запаздыванием. Выводятся качественные свойства решения такого уравнения типа свойства инвариантности положительного предельного множества решения динамической системы. Доказана теорема о локализации положительного предельного множества ограниченного решения в предположении существования функционала Ляпунова, имеющего знакопостоянную производную. Этот результат можно определить как принцип квазиинвариантности для исследуемого уравнения. Доказаны теоремы об асимптотической устойчивости нулевого решения по всем и части переменных при указанном выше предположении. Доказанные теоремы позволили определить достаточные условия предельных свойств движений голономной механической системы с линейной эредитарностью. Решена задача о стабилизации положений равновесия и стационарных движений манипулятора с цилиндрическим и сферическим шарнирами. Периодичность уравнений движения по обобщенным координатам позволяет вывести условия глобальной стабилизации.

Решена задача о стабилизации заданного положения пятизвенного манипулятора с цилиндрическими и призматическим шарнирами. Представлены результаты численного моделирования процесса стабилизации.

Работа выполнена при финансовой поддержке РФФИ (проект № 19-01-00791).

Список литературы

  1. Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976. 286 с.

  2. Вольтерра В. Теория функционалов, интегральных и интегро-дифференциальных уравнений. М.: Наука, 1980. 304 с.

  3. Красовский Н.Н. Некоторые задачи теории устойчивости движения. М.: Физматгиз, 1959. 211 с.

  4. Corduneanu C., Lakshmikantham V. Equations with unbounded delay: a survey // Nonlin. Anal., Theory, Meth.&Appl. 1980. V. 4. P. 831–877.

  5. Кордуняну К., Лакшмикантам В. Уравнения с неограниченным запаздыванием // Автом. и телемех. 1985. Вып. 7. С. 5–44.

  6. Colleman B.D., Dill H. On the stability of certain motions of incompressible materials with memory // Arch. Rat. Mech. Anal. 1968. V. 30. P. 197–224.

  7. Coleman B., Mizel V. On the stability of solutions of functional differential equations // Arch. Rat. Mech. Anal. 1968. V. 30. P. 173–196.

  8. Colleman B.D., Owen D.R. On the initial-value problem for a class of functional differential equations // Arch. Rat. Mech. Anal. 1974. V. 55. P. 275–299.

  9. Hale J., Kato J. Phase space for retarded equations with infinite delay // Fukcialaj Ekvacioj. 1978. V. 21. P. 11–41.

  10. Hino Y. Stability properties for functional differential equations with infinite delay // Tohoku Math. J. 1983. V. 35. P. 597–605.

  11. Hino Y., Murakami S., Naito T. Functional Differential Equations with Infinite Delay // Lect. Notes in Math. 1991. V. 1473.

  12. Murakami S. Perturbation theorems for functional differential equations with infinite delay via limiting equations // J. Differ. Eqns. 1985. V. 59. P. 314–335.

  13. Murakami S., Naito T. Fading memory spaces and stability properties for functional differential equations with infinite delay // Fukcialaj Ekvacioj. 1989. V. 32. P. 91–105.

  14. Sawano K. Exponential asymptotic stability for functional differential equations with infinite retardations // Tohoku Math. J. 1979. V. 31. P. 363–382.

  15. Sawano K. Positively invariant sets for functional differential equations with infinite delay // Tohoku Math. J. 1980. V. 32. P. 557–566.

  16. Sawano K. Some considerations on the fundamental theorems for functional differential equations with infinite retardations // Fukcialaj Ekvacioj. 1982. V. 25. P. 97–104.

  17. Schumacher K. Existence and continuous dependence for functional-differential equations with unbounded delay // Arch. Rat. Mech. Anal. 1978. V. 67. P. 315.

  18. Atkinson F.V., Haddock J.R. On determining phase spaces for functional differential equations // Funkcialaj Ekvacioj. 1988. V. 31. P. 331–347.

  19. Горяченко В.Д. Методы исследования устойчивости ядерных реакторов. М.: Атомиздат, 1977. 286 с.

  20. Колмановский В.Б., Носов В.Р. Устойчивость и периодические режимы регулирования систем с последействием. М.: Наука, 1981. 448 с.

  21. Хейл Д.К. Теория функционально-дифференциальных уравнений. М.: Мир, 1984. 421 с.

  22. Haddock J., Krisztin T., Terjeki J. Invariance principles for autonomous functional differential equations // J. Integral Eqns. 1985. V. 10. P. 123–136.

  23. Разумихин Б.С. Устойчивость эредитарных систем. М.: Наука, 1988. 108 с.

  24. Андреев А.С. Устойчивость неавтономных функционально-дифференциальных уравнений. Ульяновск: УлГУ, 2005. 328 с.

  25. Перегудова О.А. Развитие метода функций Ляпунова в задаче устойчивости функционально-дифференциальных уравнений // Диффер. уравн. 2008. Т. 44. 12. С. 1638–1647.

  26. Андреев А.С. Метод функционалов Ляпунова в задаче об устойчивости функционально-дифференциальных уравнений // Автом. и телемех. 2009. 9. С. 4–55.

  27. Hino Y. On stability of the solution of some functional differential equations // Fukcialaj Ekvacioj. 1971. V. 14. P. 47–60.

  28. Kato J. Stability problems in functional differential equations with infinite delay // Fukcialaj Ekvacioj. 1978. V. 21. P. 63–80.

  29. Burton T.A. Stability theory for delay equations // Funkcialaj Ekvacioj. 1979. V. 22. P. 67–76.

  30. Kato J. Liapunov’s second method in functional differential equations // Tohoku Math. J. 1980. V. 32. P. 487–497.

  31. Kato J. Asymptotic behavior in functional differential equations with infinite delay // Lect. Notes in Math., 1983. V. 1017. P. 300–312

  32. Тихонов А.Н. О функциональных уравнениях и их применению к некоторым задачам математической физики // Бюлл. Моск. ун-та. Сек. А, 1938. Т. 1. № 8. С. 1–25.

  33. Мышкис А.Д. Линейные дифференциальные уравнения с запаздывающим аргументом. М.: Наука, 1972. 352 с.

  34. Быков Я.В. О некоторых задачах теории интегро-дифференциальных уравнений. Фрунзе: Изд-во Киргиз. ун-та, 1957. 327 с.

  35. Филатов А.Н. Методы усреднения в дифференциальных и интегро-дифференциальных уравнениях. Ташкент: ФАН, 1971. 180 с.

  36. Керимов М.К. Библиография некоторых новых работ по интегральным и интегро-дифференциальным уравнениям // В доп. к кн.: Вольтерра В. Теория функционалов, интегральных и интегро-дифференциальных уравнений. М.: Наука, 1980. 304 с.

  37. Burton T.A. Stability and Periodic Solutions of Ordinary and Functional Differential Equations. Orlando: Acad. Press. 1985. 337 p.

  38. Сергеев В.С. Первый метод Ляпунова в исследовании систем, описываемых интегродифференциальными уравнениями типа Вольтерра. М.: ВЦ РАН, 2011. 193 с.

  39. Colleman B.D., Gurtin M.E., Ismael Herrera R., Truesdell C. Wave Propagation in Dissipative Materials. Berlin: Springer, 1965.

  40. Резван В. Абсолютная устойчивость автоматических систем с запаздыванием. М.: Наука, 1980. 360 с.

  41. Белоцерковский С.М., Скрипач Б.К., Табачников В.Г. Крыло в нестационарном потоке газа. М.: Наука, 1971. 767 с.

  42. Белоцерковский С.М., Кочетков Ю.А., Красовский А.А., Новицкий В.В. Введение в аэроавтоупругость. М.: Наука, 1980. 384 с.

  43. Sergeev V.S. Stability of solutions of Volterra integrodifferential equations // Math.&Comput. Model., 2007. V. 45. P. 1376–1394.

  44. Andreev A.S., Peregudova O.A. On the Stability and stabilization problems of Volterra integral-differential equations // Russ. J. Nonlin. Dyn. 2018. V. 14. № 3. P. 387–407.

  45. Андреев А.С., Перегудова О.А. Нелинейные регуляторы в задаче о стабилизации положения голономной механической системы // ПММ. 2018. Т. 82. № 2. С. 156–176.

  46. Андреев А.С., Перегудова О.А. О методе функционалов Ляпунова в задаче об устойчивости интегро-дифференциальных уравнений типа Вольтерра // Ж. Средневолжск. матем. об-ва. 2018. Т. 20. № 3. С. 260–272.

  47. Andreev A., Peregudova O. Volterra equations in the control problem of mechanical systems // 2019. 23rd International Conference on System Theory, Control and Computing (ICSTCC). P. 298–303.

  48. Сергеев В.С. Об устойчивости равновесия крыла в нестационарном потоке // ПММ. 2000. Т. 64. Вып. 2. С. 219–228.

  49. Сергеев В.С. Об устойчивости равновесия вязкоупругой пластины // Автомат. и телемех. 2007. Вып. 9. С. 79–86.

  50. Сергеев В.С. Устойчивость движения железнодорожной колесной пары в одном случае // Автомат. и телемех. 2009. Вып. 9. С. 157–161.

  51. Andreev A., Peregudova O. Non-linear PI regulators in control problems for holonomic mechanical systems // Syst. Sci.&Control Engng. 2018. V. 6. № 1. P. 12–19.

  52. Румянцев В.В. Об устойчивости движения по отношению к части переменных // Вестн. МГУ. Сер. Мат., Механ., Физ., Астрон., Хим. 1957. № 4. С. 9–16.

  53. Румянцев В.В. Об асимптотической устойчивости и неустойчивости по отношению к части перемменных // ПММ. 1971. Т. 35. Вып. 1. С. 147–152.

  54. Румянцев В.В., Озиранер А.С. Устойчивость и стабилизация по отношению к части переменных. М.: Наука, 1987. 253 с.

  55. Воротников В.И., Румянцев В.В. Устойчивость и управление по части координат фазового вектора динамических систем: теория, методы и приложения. М.: Научный мир, 2001. 320 с.

  56. Румянцев В.В. Об устойчивости стационарных движений // ПММ. 1966. Т. 30. Вып. 8. С. 922–933.

  57. Румянцев В.В. Об устойчивости стационарных движений спутников. М.; Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2010. 156 с.

  58. Карапетян А.В., Румянцев В.В. Устойчивость консервативных и диссипативных систем. Итоги науки и техники. Сер. Общая механика. Т. 6. М.: ВИНИТИ, 1983.

  59. Карапетян А.В. Устойчивость стационарных движений. М.: УРСС, 1998. 168 с.

  60. Каленова В.И., Карапетян А.В., Морозов В.М., Салмина М.А. Неголономные механические системы и стабилизация движения // Фундам. и прикл. матем. 2005. Т. 11. 7. С. 117–158.

  61. Карапетян А.В., Кулешов А.С. Об устойчивости стационарных движений механических систем с неизвестными первыми интегралами // Динамич. системы. 2017. Т. 7 (35). № 1. С. 3–16.

  62. Sell G. Topological Dynamics and Ordinary Differential Equations. New York: Van Nostrand Reinhold, 1971.

  63. Руш Н., Абетс П., Лалуа М. Прямой метод в теории устойчивости: учебник. М.: Мир, 1980. 300 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал