Прикладная математика и механика, 2021, T. 85, № 4, стр. 494-502
Осциллятор с сухим трением и упругим ограничителем
1 Университет Эври
Эври, Франция
* E-mail: stepsj@ya.ru
Поступила в редакцию 31.01.2021
После доработки 02.03.2021
Принята к публикации 15.03.2021
Аннотация
Рассматривается осциллятор с двумя степенями свободы, возбуждаемый сухим трением. Система состоит из двух масс, соединенных линейными пружинами. Вторая масса контактирует с приводным ремнем, движущимся с постоянной скоростью, и может сталкиваться с упругим упором. Между этой массой и ремнем действуют силы трения с кулоновскими характеристиками. Обнаружено несколько периодических движений, включающих фазы прилипания, фазы скольжения и контакта с упором.
1. Введение. В технических приложениях часто встречаются негладкие динамические системы, примерами которых являются осцилляторы с сухим трением или вибрационные системы с зазором между движущимися частями. Негладкие системы сложны, и их обычно моделируют как системы материальных точек, соединенных пружинами. Такие системы были предметом многих исследований, в основном, в случае систем с одной степенью свободы [1–4]. Для систем с несколькими степенями свободы, в основном, используются численные методы [5–7]. В [8] периодические движения для систем с двумя степенями свободы с упругим ограничителем, получены в аналитическом виде. В [9] приведено аналитическое исследование поведения двойного осциллятора с сухим трением. Данная работа является продолжением работы [10], в которой исследовался двойной осциллятор с сухим трением при наличии жесткого ограничителя. В этой статье предполагается мягкое столкновение с ограничителем. Найдено несколько периодических движений, в том числе с ударами об упругий ограничитель.
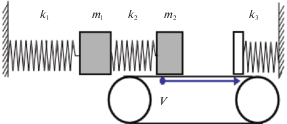
2. Постановка задачи. Система (рис. 1) состоит из двух масс (${{m}_{1}},{{m}_{2}}$), соединенных линейными пружинами (${{k}_{1}},{{k}_{2}}$). Вторая масса находится в контакте с приводным ремнем, движущимся с постоянной скоростью ${{\nu }_{0}}$. Между массой ${{m}_{2}}$ и ремнем действует сила трения $\Psi $.
Перемещение ${{x}_{2}}$ второй массы ограничивается наличием упругого упора. Когда ${{x}_{2}}$ превышает зазор, происходит контакт массы с ограничителем и возникает восстанавливающая сила, пропорциональная жесткости пружины ${{k}_{3}}$. Движение осциллятора с двумя степенями свободы описывается системой уравнений
(2.1)
$\begin{gathered} x_{1}^{{''}} + {{x}_{1}} - \chi {{x}_{2}} = 0\quad x_{2}^{{''}} + \chi \eta ({{x}_{2}} - {{x}_{1}}) = \eta u + F \\ \chi = \frac{{{{k}_{2}}}}{{{{k}_{1}} + {{k}_{2}}}},\quad \eta = \frac{{{{m}_{1}}}}{{{{m}_{2}}}},\quad t = \omega \tilde {t},\quad \omega = \sqrt {\frac{{{{k}_{1}} + {{k}_{2}}}}{{{{m}_{1}}}}} \\ (o){\kern 1pt} ' = \frac{{d(o)}}{{dt}},\quad u = \frac{\Psi }{{{{k}_{1}} + {{k}_{2}}}} \\ \end{gathered} $Здесь ${{x}_{1}},{{x}_{2}}$ обозначают перемещения масс.
Восстанавливающая сила $F$ определяется соотношениями
(2.2)
$\begin{gathered} F = 0\quad {\text{при}}\quad {{x}_{2}} \leqslant b \\ F = - \eta k({{x}_{2}} - b)\quad {\text{при}}\quad {{x}_{2}} \geqslant b;\quad k = \frac{{{{k}_{3}}}}{{{{k}_{1}} + {{k}_{2}}}}, \\ \end{gathered} $Сила трения $u$ определяется из законов Кулона
(2.3)
$x_{2}^{'} \ne V\quad u = {{u}_{s}}\operatorname{sign} (V - x_{2}^{'}),\quad V = \frac{{{{{v}}_{0}}}}{\omega }\quad (скольжение)$(2.4)
$\begin{gathered} x_{2}^{'} = V \\ u = \left\{ {\begin{array}{*{20}{l}} {\varepsilon {{u}_{s}}\quad {\text{при}}\quad \varepsilon (\chi ({{x}_{2}} - {{x}_{1}}) - F{\text{/}}\eta ) > {{u}_{r}},\quad \varepsilon = \pm 1\quad (фаза\;покоя)} \\ {\chi ({{x}_{2}} - {{x}_{1}}) - F{\text{/}}\eta \quad {\text{при}}\quad \left| {\chi ({{x}_{2}} - {{x}_{1}}) - F{\text{/}}\eta } \right| < {{u}_{r}}\quad (фаза\;скольжения)} \end{array}} \right., \\ \end{gathered} $Динамика такого осциллятора разнообразна и может включать фазы покоя и скольжения (stick–slip) без контакта с ограничителем (свободное движение) и с контактом с ограничителем (ограниченное движение). Для каждого вида движений можно получить решение в замкнутой форме.
3. Движения без контакта с ограничителем (${{x}_{2}} < b$). Движение с трением скольжения второй массы при $x_{2}^{'} < V$. Решение получается из модального анализа уравнения (2.1), где $u = {{u}_{s}}$, $F = 0$:
(3.1)
$\begin{gathered} Z(t) = H(t){{Z}_{0}}\quad Z = \left( {\begin{array}{*{20}{l}} z \\ {z{\kern 1pt} '} \end{array}} \right),\quad {{Z}_{0}} = Z(0),\quad z = X - {{d}_{0}} \\ X = ({{x}_{1}},{{x}_{2}}{{)}^{t}}\quad H(t) = \left( {\begin{array}{*{20}{c}} {{{H}_{1}}(t)}&{{{H}_{2}}(t)} \\ {{{H}_{3}}(t)}&{{{H}_{1}}(t)} \end{array}} \right), \\ \end{gathered} $(2 × 2)-матрицы ${{H}_{i}}(t)$ $(i = 1,2,3)$ получаются в аналитическом виде [9]
(3.2)
$\begin{gathered} {{d}_{0}} = ({{d}_{{01}}},{{d}_{{02}}}{{)}^{t}} \\ {{d}_{{01}}} = \frac{{{{u}_{s}}}}{{1 - \chi }},\quad {{d}_{{02}}} = \frac{{{{d}_{{02}}}}}{\chi } \\ \end{gathered} $Движение с трением скольжения второй массы при $x_{2}^{'} > V$ (с превышением скорости ремня). Решение выводится из модального анализа уравнений (2.1), где $u = - {{u}_{s}}$:
(3.3)
$\bar {Z}(t) = H(t){{\bar {Z}}_{0}}\quad \bar {Z} = \left( {\begin{array}{*{20}{c}} {X + {{d}_{0}}} \\ {X{\kern 1pt} '} \end{array}} \right)\quad {{\bar {Z}}_{0}} = \bar {Z}(0)$Движение с трением покоя второй массы, $x_{2}^{'} = V$. Это движение определяется уравнениями
(3.4)
$\begin{gathered} x_{1}^{{''}} + {{x}_{1}} - \chi {{x}_{2}} = 0 \\ x_{2}^{{''}} = 0 \\ \end{gathered} $Решение получено в аналитическом виде [9]:
(3.5)
$Z(t) = \Gamma (t){{Z}_{0}}\quad {{Z}_{0}} = Z(0),\quad \Gamma (t) = \left( {\begin{array}{*{20}{c}} {{{\Gamma }_{1}}(t)}&{{{\Gamma }_{2}}(t)} \\ {{{\Gamma }_{2}}(t)}&{{{\Gamma }_{1}}(t)} \end{array}} \right),$(2 × 2)-матрицы ${{\Gamma }_{i}}(t)$ $(i = 1,2,3)$ получены из модального анализа (2.4). Более того, при всех такого рода колебаниях выполняется неравенство
4. Движения с контактом с ограничителем (${{x}_{2}} > b$). Движение с трением скольжения второй массы при $x_{2}^{'} < V$. Решение выводится из модального анализа (2.1), где $u = {{u}_{s}}$, $F = - \eta k({{x}_{2}} - b)$:
(4.1)
$\begin{gathered} {{\delta }_{0}} = ({{\delta }_{{01}}},{{\delta }_{{02}}}{{)}^{t}} \\ {{\delta }_{{01}}} = \frac{{({{u}_{s}} + kb)\chi }}{{(k + \chi - {{\chi }^{2}})}},\quad {{\delta }_{{02}}} = {{\delta }_{{01}}}{\text{/}}\chi \\ \end{gathered} $(2 × 2)-матрицы ${{L}_{i}}(t)$ $(i = 1,2,3)$ приведены в Приложении.
Движение с трением скольжения второй массы при $x_{2}^{'} > V$ (с превышением скорости ремня). Решение выводится из модального анализа уравнений (2.1), где $u = - {{u}_{s}}$, $F = - \eta k({{x}_{2}} - b)$:
(4.2)
$\begin{gathered} \bar {Y}(t) = L(t){{{\bar {Y}}}_{0}}\quad \bar {Y} = \left( {\begin{array}{*{20}{c}} {X - {{{\bar {\delta }}}_{0}}} \\ {X{\kern 1pt} '} \end{array}} \right) \\ {{{\bar {Y}}}_{0}} = \bar {Y}(0),\quad {{{\bar {\delta }}}_{0}} = ({{{\bar {\delta }}}_{{01}}},{{{\bar {\delta }}}_{{02}}}{{)}^{t}} \\ {{{\bar {\delta }}}_{{01}}} = \frac{{(kb - {{u}_{s}})\chi }}{{(k + \chi - {{\chi }^{2}})}},\quad {{{\bar {\delta }}}_{{02}}} = {{{\bar {\delta }}}_{{01}}}{\text{/}}\chi \\ \end{gathered} $Движение с трением покоя второй массы, $x_{2}^{'} = V$. Движение определяется уравнениями (3.4). Решение получается из (3.5). Во время покоя выполняется неравенство
Далее будет получено в аналитической форме несколько видов периодических движений с выходом на контакт с ограничителем и с фазами скольжения и покоя.
5. Движения первого вида с контактом с ограничителем. Предположим, что при $t = 0$
При $t = 0$ происходит удар, при $t > 0$ система совершает движение в силу уравнений (4.1), при $t = \tau $, ${{x}_{2}}(\tau ) = b$, $x_{2}^{'}(\tau ) < 0$ и при $t > 0$, происходит движение без контакта с ограничителем, определяемое уравнением
Периодическое движение с периодом $T = \tau + {{\tau }_{1}}$ получается, если
Из (4.1) получим
(5.4)
$\begin{gathered} {{Y}_{B}} = Y(\tau ) = L(\tau ){{Y}_{0}} \\ {{Y}_{0}} = {{Z}_{0}} + {{F}_{0}},\quad {{Y}_{B}} = {{Z}_{B}} + {{F}_{0}} \\ {{F}_{0}} = \left( {\begin{array}{*{20}{c}} {{{f}_{0}}} \\ 0 \end{array}} \right),\quad {{f}_{0}} = {{d}_{0}} - {{\delta }_{0}} \\ \end{gathered} $Из (5.3) следует
(5.5)
$\begin{gathered} {{Z}_{B}} = H( - {{\tau }_{1}}){{Z}_{0}},\quad H( - {{\tau }_{1}}) = \left( {\begin{array}{*{20}{c}} {{{H}_{1}}}&{ - {{H}_{2}}} \\ { - {{H}_{3}}}&{{{H}_{1}}} \end{array}} \right) \\ {{H}_{i}} = {{H}_{i}}({{\tau }_{1}}),\quad (i = 1,2,3) \\ \end{gathered} $Из (5.4) выводим
(5.6)
$\begin{gathered} {{Z}_{B}} = L(\tau )({{Z}_{0}} + {{F}_{0}}) - {{F}_{0}} \\ L(\tau ) = \left( {\begin{array}{*{20}{c}} {{{L}_{1}}}&{{{L}_{2}}} \\ {{{L}_{3}}}&{{{L}_{1}}} \end{array}} \right),\quad {{L}_{i}} = {{L}_{i}}(\tau ),\quad (i = 1,2,3) \\ \end{gathered} $Из (5.5) следует
(5.7)
$\begin{array}{*{20}{l}} {{{z}_{B}} - {{z}_{0}} = ({{H}_{1}} - I){{z}_{0}} - {{H}_{2}}z_{0}^{'}} \\ {z_{B}^{'} + z_{0}^{'} = - {{H}_{3}}{{z}_{0}} + ({{H}_{1}} + I)z_{0}^{'}} \end{array}\quad I = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)$Принимая во внимание следующее свойство матриц ${{H}_{i}}$, $(i = 1,2,3)$
(5.8)
$H_{1}^{2} - I - {{H}_{2}}{{H}_{3}} = 0,\quad {{H}_{i}}{{H}_{j}} = {{H}_{j}}{{H}_{i}}\quad (i,j = 1,2,3)$Из (5.7) получим
Из (5.6) следует
(5.10)
$\begin{gathered} {{z}_{B}} - {{z}_{0}} = ({{L}_{1}} - I)({{z}_{0}} + {{f}_{0}}) + {{L}_{2}}z_{0}^{'} \\ z_{B}^{'} + z_{0}^{'} = {{L}_{3}}({{z}_{0}} + {{f}_{0}}) + ({{L}_{1}} + I)z_{0}^{'} \\ \end{gathered} $Из того же свойства матриц ${{L}_{i}}$, $(i = 1,2,3)$ (см. Приложение)
(5.11)
$L_{1}^{2} - I - {{L}_{2}}{{L}_{3}} = 0,\quad {{L}_{i}}{{L}_{j}} = {{L}_{j}}{{L}_{i}},\quad (i,j = 1,2,3)$Из (5.9), (5.12) следует
(5.13)
$if\;\;det\left| {\begin{array}{*{20}{c}} {{{H}_{1}} + I}&{{{H}_{2}}} \\ {{{L}_{1}} + I}&{ - {{L}_{2}}} \end{array}} \right| \ne 0,\quad {{z}_{B}} - {{z}_{0}} = 0,\quad z_{B}^{'} + z_{0}^{'} = 0$Периодическое движение зависит от пяти параметров (${{x}_{{01}}},x_{{01}}^{'},x_{{02}}^{'},\tau ,{{\tau }_{1}}$), определяемых четырьмя скалярными уравнениями, которые выводятся из уравнений (5.7), (5.10), (5.13):
(5.14)
$\begin{gathered} ({{H}_{1}} - I){{z}_{0}} - {{H}_{2}}z_{0}^{'} = 0 \\ ({{L}_{1}} - I)({{z}_{0}} + {{f}_{0}}) + {{L}_{2}}z_{0}^{'} = 0 \\ \end{gathered} $Отсюда следует, что, как и в [10], три параметра (${{x}_{{01}}},x_{{01}}^{'},x_{{02}}^{'}$) могут быть определены из (5.14) в зависимости от периода $T = \tau + {{\tau }_{1}}$.
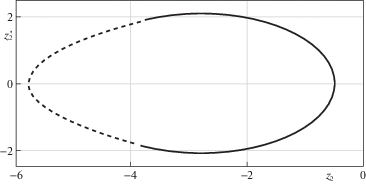
Пример
Для $\eta = 1$, $k = 0.7$, $\chi = 0.3$, ${{u}_{s}} = 1$, $V = 4$, $b = 1$, получаем:
Фазовые портреты движения масс ${{m}_{1}},{{m}_{2}}$ представлены на рис. 2, 3. Сплошнная линия соответствует движению в контакте с ограничителем, точечная линия соответствует свободному движению без контакта с ограничителем.
6. Движения второго вида с контактом с ограничителем. Предположим, что при $t = 0$:
При $0 < t < \tau $, система совершает движение в силу уравнений (3.5) в фазе покоя второй массы без контакта с ограничителем ($x_{2}^{'} = V$, ${{x}_{2}} < b$). Предположим, что
(6.2)
${{x}_{{2B}}} \equiv {{x}_{2}}(\tau ) = b,\quad \chi \left| {{{x}_{{2B}}} - {{x}_{{1B}}}} \right| < {{u}_{r}},\quad {{x}_{{1B}}} \equiv {{x}_{1}}(\tau )$При $0 < t - \tau < {{\tau }_{1}}$, вторая масса покоится на ленте и находится в контакте с ограничителем. Движение определяется уравнением
Во время этого движения выполняется неравенство
Фаза покоя прекращается, когда $t = \tau + {{\tau }_{1}}$, $\chi \left( {{{x}_{2}} - {{x}_{1}}} \right) + k\left( {{{x}_{2}} - b} \right) = {{u}_{r}}$ (4.5).
При $0 < t - T < {{\tau }_{2}}$ ($T = \tau + {{\tau }_{1}}$) имеем фазу скольжения с контактом второй массы с ограничителем (${{x}_{2}} > b$)
Это движение заканчивается в момент $t = T + {{\tau }_{2}}$, при выполнении условий
При $0 < t - T - {{\tau }_{2}} < {{\tau }_{3}}$, система находится в фазе скольжения без контакта с ограничителем (${{x}_{2}} < b$)
Периодическое движение с периодом $\Theta = \tau + {{\tau }_{1}} + {{\tau }_{2}} + {{\tau }_{3}}$ получается, если
Это движение зависит от 7 параметров (${{x}_{{10}}},x_{{10}}^{'},{{x}_{{20}}},\tau ,{{\tau }_{1}},{{\tau }_{2}},{{\tau }_{3}}$), определяемых 7 скалярными уравнениями, выводимыми из (6.1), (6.6), (4.8).
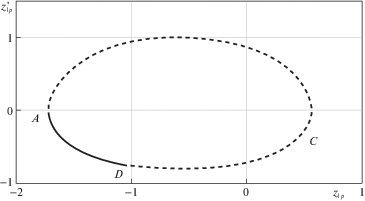
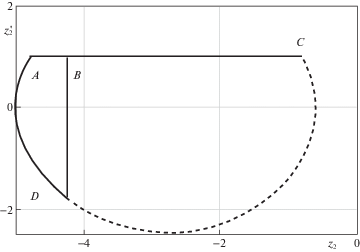
Пример
Для $\eta = 3$, $k = 0.3$, $\chi = 0.2$, ${{u}_{s}} = 1$, $V = 1$, $b = 2$, ${{u}_{r}} = 1.7695$, получим
Из фазовых портретов движения масс ${{m}_{1}},{{m}_{2}}$, показанных на рис. 4, 5, видно, что ограничения (3.6) и (6.4) выполняются в процессе движения в фазе покоя.
Заключительные замечания. В данной работе найдено несколько периодических движений двойного осциллятора с сухим трением и упругим ограничителем. Эти движения включают несколько фаз трения скольжения и трения покоя. Другие движения с фазами превышения второй массой скорости приводного ремня с последующими фазами скольжения, покоя и контакта с ограничителем предполагается исследовать в следующих работах.
Список литературы
Shaw S.W., Holmes P.J. A periodically forced piecewise linear oscillator // J. Sound&Vibr. 1983. V. 90. № 1. P. 129–155.
Hindmarsh M.B, Jeffries D.J. On the motions of the impact oscillator // J. Physics A. 1984. V. 17. P. 1791–1803.
Hong H.K., Liu C.S. Non-sticking formulae for Coulomb friction under harmonic loading // J. Sound&Vibr. 2001. V. 244. № 5. P. 883–898.
Csernak G., Stepan G. On the periodic response of a harmonically excited dry friction oscillator // J. Sound&Vibr. 2006. V. 295. № 4. P. 649–658.
Valente A.X., McClamroch N.H., Mezie I. Hybrid impact of two coupled oscillators that can impact a fixed stop // Int. J. Non-Lin. Mech. 2003. V. 38. P. 677–689.
Galvanetto U., Bishop S.R. Stick-slip vibrations of a 2-degree-of-freedom geophysical fault model // Int. J. Mech. Sci. 1994. V. 36. № 8. P. 683–698.
Khizgiyayev S.V. Self-excited oscillations of a two-mass oscillator with dry “stick-slip” friction // JAMM. 2007. V. 71. P. 905–913.
Pascal M. Dynamics and stability of a two degree of freedom oscillator with an elastic stop // J. Comput.&Nonlin. Dyn. 2006. V. 1. № 1. P. 94–102.
Pascal M. Dynamics of coupled oscillators excited by dry friction // ASME J. Comput. Nonlin. Dyn. 2008. V. 3. № 3. P. 20–26.
Pascal M. A new model of dry friction oscillator colliding with a rigid obstacle // Nonlin. Dyn. 2018. V. 91. P. 2541–2550.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика