Прикладная математика и механика, 2021, T. 85, № 4, стр. 461-468

Классические диаграммы Смейла [1] для консервативных механических систем с симметрией представляет собой в пространстве постоянных интеграла энергии $H = h$ и интегралов Нётер ${\mathbf{K}} = {\mathbf{k}}$ множество $S$ поверхностей $h = h({\mathbf{k}})$, на котором эти интегралы зависимы. Множество $S$ называется бифуркационным по Смейлу: на нем происходят перестройки топологического типа областей возможности движения системы в конфигурационном пространстве. Каждой точке множества $S$ соответствует инвариантное в фазовом пространстве множество системы (в частности, стационарное движение).

Методика Смейла с небольшими изменениями и дополнениями распространяется [2–4] на случай диссипативных механических систем с симметрией при условии, что диссипативные силы обладают частичной диссипацией и не разрушают интегралы Нётер. При этом полная механическая энергия $H$ не возрастает вдоль движений системы, сохраняет свое начальное значение $h$ на инвариантных множествах, а обобщенные диаграммы Смейла по-прежнему представляет собой множество $S$, на котором невозрастающая функция $H$ и интегралы Нётер ${\mathbf{K}} = {\mathbf{k}}$ зависимы.

Существенное отличие обобщенных диаграмм от классических состоит в следующем: в консервативном случае все точки пространства $({\mathbf{k}};h)$ инвариантны относительного фазового потока системы, а в диссипативном случае инвариантны только точки, лежащих на множестве $S$, а остальные точки этого пространства эволюционируют вдоль прямых ${\mathbf{k}} = \operatorname{const} $ в сторону уменьшения $h$ и стремятся к одной из точек множества $S$, соответствующей значению функции $H$, которое меньше начального. Таким образом, обобщенные диаграммы Смейла позволяют находить предельные движения системы только по начальному значению полной энергии и значениям постоянных интегралов Нётер.

1. Обобщенные диаграммы Смейла. Рассмотрим механическую систему с $n$ степенями свободы, находящуюся под действием потенциальных и диссипативных сил с частичной диссипацией и допускающую m-параметрическую $(m < n)$ группу симметрий. Пусть полная механическая энергия $H$ и интегралы Нётер ${\mathbf{K}}$ имеют вид

Здесь ${\mathbf{v}} \in {{\mathbb{R}}^{n}}$ – квазискорости системы, ${\mathbf{r}} \in \Sigma $ – переменные (в общем случае – зависимые), от которых зависят положительно-определенная $n \times n$ матрица ${\mathbf{A}}$ кинетической энергии, $m \times n$ – матрица ${\mathbf{B}}$ интегралов Нётер и потенциальная энергия $V$ системы, $h$ – начальное значение полной энергии, ${\mathbf{k}}$ – постоянные интегралов Нётер. Эти интегралы предполагаются независимыми, т.е. $\operatorname{rank} {\mathbf{B}} = m$ при ${\mathbf{r}} \in \Sigma $.

Согласно модифицированной теории Рауса [2–4] критические уровни полной энергии на фиксированных уровнях интегралов Нётер соответствуют инвариантным множествам системы. Учитывая структуру функций $H$ и ${\mathbf{K}}$, задачу поиска инвариантных множеств можно решать в два этапа. На первом этапе находится единственная критическая точка (точка минимума) функции $H$ по переменным ${\mathbf{v}}$ на линейном многообразии ${\mathbf{K}} = {\mathbf{k}}$ (при этом переменные ${\mathbf{r}}$ рассматриваются как параметры). Нетрудно показать, что

Функция ${{V}_{{\mathbf{k}}}}({\mathbf{r}})$ называется приведенным или эффективным потенциалом.

На втором этапе находятся критические множества (в частности, точки) эффективного потенциала, удовлетворяющие уравнению

Пусть ${{{{\gamma }}}_{1}}({\mathbf{k}})$, ${{{{\gamma }}}_{2}}({\mathbf{k}})$, … – все решения уравнения (1.5). Критические множества ${{{{\gamma }}}_{j}}({\mathbf{k}})$ $(j = 1;2;...)$ могут иметь различную размерность (в том числе, нулевую) и пересекаться при некоторых значениях ${{{\mathbf{k}}}_{0}}$:

Значения ${{{\mathbf{k}}}_{0}}$ и соответствующие множества ${{{{\gamma }}}_{0}}$ называются бифуркационными по Пуанкаре–Четаеву.

Критическим множествам ${{{{\gamma }}}_{j}}({\mathbf{k}}) \in \Sigma $ соответствуют инвариантные в фазовом пространстве ${{\mathbb{R}}^{n}} \times \Sigma $ множества

Полная механическая энергия $H$ сохраняет свое начальное значение на всех множествах (1.6). Будем называть объединение инвариантных множеств (1.6) полным, если функция $H$ убывает на всех других движениях системы.

Зафиксируем постоянные интегралов Нётер ${\mathbf{k}} = {\mathbf{c}}$. Справедливы следующие утверждения [2–4].

Теорема 1. Если множество ${{{{\gamma }}}_{j}}({\mathbf{c}})$ компактно и доставляет эффективному потенциалу строго минимальное значение, то инвариантное множество ${{\Gamma }_{j}}({\mathbf{c}})$ устойчиво, если, кроме того, объединение инвариантных множеств (1.6) является полным, а значения ${\mathbf{c}}$ постоянных интегралов Нётер не являются бифуркационными, то любое возмущенное движение системы, близкое к движениям на множестве ${{\Gamma }_{j}}({\mathbf{c}})$, стремится при $t \to \infty $ к инвариантному множеству ${{\Gamma }_{j}}({\mathbf{k}})$, соответствующему возмущенным значениям ${\mathbf{k}} = {\mathbf{c}} + {{\delta }}{\mathbf{c}}$ постоянных интегралов Нётер.

Теорема 2. Если критическое множество ${{{{\gamma }}}_{j}}({\mathbf{c}})$ компактно, не доставляет эффективному потенциалу даже нестрого минимальное значение, объединение инвариантных множеств (1.6) является полным, а значения ${\mathbf{c}}$ постоянных интегралов Нётер не являются бифуркационными, то инвариантное множество ${{\Gamma }_{j}}({\mathbf{c}})$ неустойчиво.

Обобщенные диаграммы Смейла представляют собой в пространстве $({\mathbf{k}};h)$ множество $S$ поверхностей

Все точки, лежащие на множестве $S$ инвариантны относительно фазового потока системы. Если объединение инвариантных множеств (1.6) является полным, то все точки $({\mathbf{k}};h)$, не лежащие на множестве $S$, эволюционируют вдоль прямых ${\mathbf{k}} = \operatorname{const} $ в сторону уменьшения $h$ и стремятся к одной из точек $\left( {{\mathbf{k}},{{h}_{i}}({\mathbf{k}})} \right)$, удовлетворяющей условию ${{h}_{i}}({\mathbf{k}}) < h$. При этом, если есть только одна точка ${{h}_{s}}({\mathbf{k}}) < h$, соответствующая минимуму эффективного потенциала на множестве ${{{{\gamma }}}_{s}}({\mathbf{k}})$ (в данном случае – глобальному на уровне ${\mathbf{K}} = {\mathbf{k}}$), то $h \to {{h}_{s}}({\mathbf{k}})$ либо всегда (при условии, что на уровне ${\mathbf{K}} = {\mathbf{k}}$ нет никаких других точек $({\mathbf{k}},\,\,{{h}_{i}}({\mathbf{k}}))$, удовлетворяющих неравенству ${{h}_{i}}({\mathbf{k}}) < h$, $i \ne s$), либо с вероятностью 1 (если иные точки есть, но они соответствуют не минимальным значениям эффективного потенциала на множествах ${{{{\gamma }}}_{i}}({\mathbf{k}})$). Если же при значениях функции $H$, меньших начального, есть несколько точек, $({\mathbf{k}},{{h}_{{{{s}_{1}}}}}({\mathbf{k}}))$, $({\mathbf{k}},{{h}_{{{{s}_{2}}}}}({\mathbf{k}}))$, …, которые соответствуют минимальным значениям эффективного потенциала на множествах ${{{{\gamma }}}_{{{{s}_{1}}}}}({\mathbf{k}}),{{{{\gamma }}}_{{{{s}_{2}}}}}({\mathbf{k}}),...$ (одна глобальному, а остальные – локальным), то $h$ может стремиться к ${{h}_{{{{s}_{1}}}}}({\mathbf{k}})$, ${{h}_{{{{s}_{2}}}}}({\mathbf{k}})$, с ненулевой вероятностью, причем сумма этих вероятностей равна 1. Здесь вероятность понимается как отношение меры множества начальных значений фазовых переменныx задачи, для которых имеет место соответствующий предел $h$, к полной мере всех начальных значений.

Таким образом, обобщенные диаграммы Смейла позволяют определять предельные движения системы только по значениям постоянных интегралов Нётер и начальному значению полной механической энергии, причем в ряде случаев однозначно или с вероятностью 1.

2. Волчок с вязким наполнителем. Рассмотрим задачу о движении тяжелого твердого тела с полостью, целиком заполненной однородной жидкостью. Предположим, что тело динамически симметрично, а полость представляет собой эллипсоид вращения, ось симметрии которого совпадает с осью симметрии тела, на которой расположен центр масс тела. Кроме того, предположим, что жидкость совершает простое [5] движение, причем взаимодействие жидкости со стенками полости описывается вязким трением, линейным по разности угловых скорости тела и половины вектора вихря жидкости.

Уравнения движения системы имеют вид [6]

Здесь

${\mathbf{\omega }}$ – угловая скорость тела, ${\mathbf{\Omega }}$ – половина вектора вихря жидкости, ${\mathbf{\gamma }}$ – единичный вектор восходящей вертикали, $V = mgs{{{{\gamma }}}_{3}}$ – потенциальная энергия ($m$ – масса всей системы, $g$ – ускорение свободного падения, $s$ – расстояние от неподвижной точки до центра масс системы), ${\mathbf{J}}$ – тензор инерции тела для неподвижной точки, ${{{\mathbf{J}}}_{*}}$ – тензор инерции эквивалентного [5] тела, ${\mathbf{I}}$ – центральный тензор инерции жидкости, тензор ${\mathbf{D}}$ характеризует интенсивность внутреннего трения (${{D}_{1}} > 0$, ${{D}_{3}} > 0$), ${{a}_{1}},{{a}_{2}} = {{a}_{1}}$ и ${{a}_{3}}$ – полуоси полости; все тензоры и векторы задаются в главных осях инерции тела для неподвижной точки.

Уравнения движения системы (2.1)–(2.3) допускают невозрастающую вдоль решений этой системы функцию

интеграл и геометрический интеграл

Последний определяет пространство положений вектора ${\mathbf{\gamma }}$. Минимум функции (2.4) по ${{\omega }}$ и $\Omega $ на линейном многообразии (2.5) достигается при

и определяет эффективный потенциал

Здесь $C({\mathbf{\gamma }}) = {{C}_{1}}\left( {{{\gamma }}_{1}^{2} + {{\gamma }}_{2}^{2}} \right) + {{C}_{3}}{{\gamma }}_{3}^{2}$, ${{C}_{1}} = {{A}_{1}} + {{B}_{1}} = {{J}_{1}} + {{I}_{1}}$, ${{C}_{3}} = {{A}_{3}} + {{B}_{3}} = {{J}_{3}} + {{I}_{3}}$.

Критическим точкам эффективного потенциала (2.8) на сфере (2.6) соответствуют равномерные вращения системы как твердого тела вокруг вертикали (см. (2.7)) при вертикальном (если ${{\gamma }}_{3}^{2} = 1$) или наклонном (если ${{\gamma }}_{3}^{2} < 1$) положении оси симметрии тела, причем при ${{{{\gamma }}}_{3}} = - 1$ центр масс системы занимает наинизшее, а при ${{{{\gamma }}}_{3}} = + 1$ – наивысшее положение.

Сужение эффективного потенциала (2.8) на сферу (2.6) задается соотношением ${{V}_{k}} = mgsf(x)$, где

Функция $f(x)$ при любых значениях параметров $c$ и $p$ имеет критические точки $x = \pm 1$, которым соответствуют равномерные вращения системы вокруг вертикально расположенной оси симметрии. Внутренние критические точки функции $f(x)$ определяются из уравнения $f{\kern 1pt} '(x) = df{\text{/}}dx = 0$, где

Таким образом, внутренние критические точки удовлетворяют уравнению ${{\varphi }}(x) = p > 0$ и существует либо при $c > 1$ (при этом $x \in ( - 1,0)$), либо при $c \in \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},1} \right)$ (при этом $x \in (0,1)$).

Точки $x = \pm 1$ доставляют функции $f(x)$ минимальное (максимальное) значение, если $f{\kern 1pt} '(1) < 0$ (>0), $f{\kern 1pt} '( - 1) > 0$ (<0), а внутренние критические точки – если ${{\left. {f{\kern 1pt} ''(x)} \right|}_{{p = {{\varphi }}(x)}}} > 0$ (<0), т.е. если ${{\left. {{{\varphi }}{\kern 1pt} '(x)} \right|}_{{p = {{\varphi }}(x)}}} > 0$ (<0)

Нетрудно показать, что функция ${{\varphi }}(x)$

a) при $c > 1$ монотонно возрастает от ${{p}_{0}}$ до $ + \infty $ при $x \in ( - 1,0)$;

б) при $c \in \left[ {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4},1} \right)$ монотонно убывает от $ + \infty $ до ${{p}_{0}}$ при $x \in ( + 0,1)$;

в) при $c \in \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}} \right)$ монотонно убывает от $ + \infty $ до ${{p}_{*}}$ при $x \in ( + 0,{{x}_{*}})$ и монотонно возрастает от ${{p}_{*}}$ до ${{p}_{0}}$при $x \in ({{x}_{*}},1)$.

Здесь

Следовательно, точка $x = - 1$ доставляет функции $f(x)$ минимальное значение при любых $p$, если $c < 1$, и только при $p \leqslant {{p}_{0}}$, если $c > 1$, а точка $x = + 1$ доставляет функции $f(x)$ минимальное значение только при $c < 1$ и $p > {{p}_{0}}$ (а также при $p = {{p}_{0}}$, если $c < 3{\text{/}}4$). Внутренние критические точки доставляют функции $f(x)$ минимальное значение при $c > 1$, если $p > {{p}_{0}}$, и при $c \in \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}} \right)$, если $p \in ({{p}_{*}},{{p}_{0}})$.

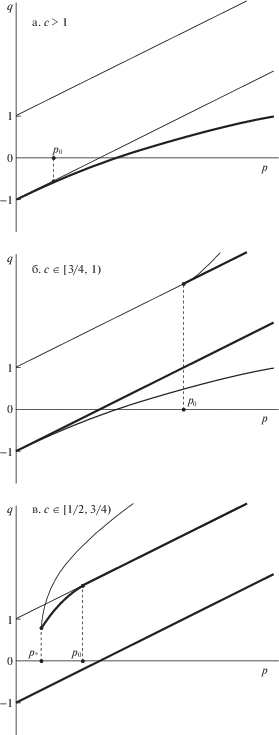
Таким образом, атлас обобщенных диаграмм Смейла состоит из трех карт (см. рис. 1). На этом рисунке $q = {h \mathord{\left/ {\vphantom {h {mgs}}} \right. \kern-0em} {mgs}}$ – безразмерное начальное значение полной энергии, прямые $q = \pm 1 + {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}$ соответствуют критическим точкам $x = \pm 1$, а кривые $q = q(p)$ задаются параметрически соотношениями

– внутренним критическим точкам функции $f(x)$, полужирные линии соответствуют устойчивым движениям системы. Бифуркационное по Смейлу множество $S$ представляет собой совокупность всех этих кривых и прямых.

Нетрудно показать, (см. уравнения (2.1)–(2.3)), что функция $H$ сохраняет свое начальное значение только на равномерных вращениях системы как твердого тела вокруг вертикали. Следовательно, любая точка плоскости $(p,q)$, удовлетворяющая условию $q > {{q}_{{\min }}}$, где ${{q}_{{\min }}} = \min f(x)$ (при $q < {{q}_{{\min }}}$ движение невозможно) и не лежащая на множестве $S$, движется под действием фазового потока системы (2.1)–(2.3) вдоль прямой $p = \operatorname{const} $ сверху вниз, асимптотически приближаясь к точке $(p;{{q}_{\infty }})$, принадлежащей множеству $S$.

Пусть, например, $c \in \left[ {{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4},1} \right)$ (см. рисунок (б)). Если $p < {{p}_{0}}$ и q < 1 + + ${p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}\left( {q > 1 + {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}} \right)$, то однозначно (с вероятностью 1) предельным движением системы будет вращение вокруг вертикально расположенной оси симметрии при наинизшем расположении центра масс. Если $q < 1 + {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}$, то аналогичное утверждение справедливо при $p \geqslant {{p}_{0}}$. Если же $p > {{p}_{0}}$ и $q > 1 + {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}$, то предельными движениями системы с ненулевой вероятностью могут быть равномерные вращения вокруг вертикально расположенной оси симметрии как при наинизшем, так и при наивысшем положении центра масс. В случае $c > 1$ и $c \in \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}} \right)$ предельными движениями могут быть равномерные вращения системы и при наклонном положении оси симметрии. В первом случае (см. рисунок (а)) при $p > {{p}_{0}}$ либо однозначно (если $q < - 1 + {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}$), либо с вероятностью 1 (если $q > - 1 + {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}$), а во втором случае (см. рисунок (в)) при $p \in ({{p}_{*}},{{p}_{0}})$ только с ненулевой вероятностью и только при $q > q(p)$, где $q(p)$ определяется соотношением (2.9) для $x \in ({{x}_{*}},1)$.

Заключительные замечания. Приведенные в разд. 1 результаты очевидным образом распространяются на случай, когда функции $H$ и ${\mathbf{K}}$ (см. (1.1) и (1.2)) содержат дополнительные слагаемые $({\mathbf{a}}({\mathbf{r}}),{\mathbf{v}})$ и ${\mathbf{b}}({\mathbf{r}})$ соответственно $\left( {{\mathbf{a}} \in {{\mathbb{R}}^{n}},{\mathbf{b}} \in {{\mathbb{R}}^{m}}} \right)$. При этом усложняются формулы (1.3) и (1.4), а все утверждения разд. 1 сохраняют справедливость.

Кроме того, приведенные в разд. 1 результаты могут быть использованы для качественного анализа диаграмм систем с полной диссипацией, если диссипативные силы зависят от малого параметра и при нулевом его значении обладают только частичной диссипацией и допускают линейные по квазискоростям интегралы. Следовательно, при нулевом значении малого параметра можно построить обобщенные диаграммы Смейла. При ненулевом значении малого параметра разрушаются как первые интегралы, так и все инвариантные множества, кроме тривиальных, соответствующих состояниям равновесия системы. Первые интегралы переходят в медленно меняющиеся (по сравнению с полной механической энергией) функции, а нетривиальные инвариантные множества – в квазиинвариантные множества. Пусть $({\mathbf{k}},\,h)$ – произвольная точка начальных значений функций (1.1) и (1.2). Под действием фазового потока системы эта точка начинает “быстро” двигаться в сторону уменьшения $h$ в окрестности прямой ${\mathbf{k}} = \operatorname{const} $ и за конечное время оказывается в окрестности бифуркационного (для нулевого значения малого параметра) множества $S$. Затем эта точка “медленно” движется в сторону уменьшения $h$ в окрестности множества $S$ и в пределе стремится к одному из состояний равновесия системы (с нулевой вероятностью – к неустойчивому и с ненулевой – к устойчивому).

Этот метод качественного анализа диссипативных систем неоднократно применялся в задаче о движении волчка тип-топ для различных видов трения в точке контакта волчка с опорной плоскостью (см. [7–12]).

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований № 19-01-00140.