Прикладная математика и механика, 2021, T. 85, № 5, стр. 587-600

1. Введение. Магнитная гидродинамика (МГД) начала интенсивно развиваться с середины прошлого века в связи с бурным развитием исследований в астрофизике, термоядерной энергетике, а также созданием новых приборов и устройств для энергетических и двигательных систем.

Большой цикл работ был связан с исследованием магнитогидродинамических пограничных слоев. Интерес к подобной проблематике связан с возможностью использования электромагнитного поля как управляющего фактора, приводящего к перестройке всего течения, что особенно актуально в связи с развитием гиперзвуковой аэродинамики и ракетной техники. Была найдена глубокая аналогия между обтеканием тел и обтеканием локальных сопротивлений.

Данное исследование обобщает предыдущие результаты [1–5]. Изучалось [1] нестационарное движение вязкой жидкости, ограниченной перемещающейся плоской стенкой. Рассматривались [2] неустановившиеся пограничные слои вязкой несжимаемой жидкости (слои Рэлея–Стокса) на вращающейся пластине в отсутствие магнитного поля. Эволюция вязкого потока на вращающейся пластине, индуцированная продольными колебаниями стенки и вдувом (отсосом) среды в отсутствие магнитного поля, изучалась в [3]. Установившееся течение идеальной электропроводной жидкости вращающейся между параллельными стенками в постоянном магнитном поле исследовалось в [4]. Неустановившееся движение вязкой электропроводной жидкости между вращающимися параллельными стенками при наличии магнитного поля представлено в [5]. В настоящей работе изучается нестационарный поток несжимаемой вязкой электропроводной жидкости на вращающейся пластине при наличии магнитного поля. Жидкость занимает полупространство, ограниченное плоской стенкой и вращается вместе со стенкой с постоянной угловой скоростью вокруг некоторой оси. В момент времени $t > 0$ стенка начинает совершать продольные колебания и в тот же момент времени по нормали к стенке включается однородное магнитное поле, индукция которого постоянна. Далее исследуется распространение возмущений в однородной проводящей среде под действием однородного магнитного поля и продольных колебаний стенки. Побудительными мотивами написания данной работы явились как фундаментальный, так и сугубо прикладной аспекты в современных геофизических исследованиях. В частности, весьма насущна проблема определения параметров искусственного источника волн, по электромагнитному эффекту вызванного им волнения. Актуальность темы обусловлена необходимостью изучения Мирового океана, играющего все большую роль в жизни человечества. Это способствовало началу исследований макроскопических движений морской воды (проводящая жидкость), находящейся в магнитном поле Земли, которые сопровождаются появлением электрических токов и, как следствие, индуцированного магнитного поля. Тем самым задача определения индуцированного электромагнитного поля распадается на две части: определение поля скоростей волнения и нахождение по заданному полю скоростей электромагнитного возмущения. При этом скорость движения среды находят или из результатов натурных наблюдений, или из решения гидродинамической задачи. Представленная работа может служить математической моделью течений морской воды, находящейся в магнитном поле Земли, а также других процессов в астрофизических задачах (магнитосферах планет, джетах и аккреционных дисках и т.п.). В работе обсуждается случай резонанса (частота продольных колебаний стенки совпадает с удвоенной частотой проекции угловой скорости вращения системы тело–жидкость). Резонанс приводит к нетривиальному физическому эффекту: амплитуда колеблющегося поля скоростей не стремится к нулю на бесконечности, а остается ограниченной.

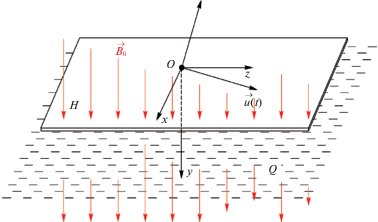
2. Аналитическое решение уравнений магнитной гидродинамики. Рассмотрим движение вязкой электропроводной несжимаемой жидкости в полупространстве, ограниченном плоской стенкой, которая вращается вместе со стенкой как одно целое с угловой скоростью ${{\omega }_{0}} = {\text{const}}$, причем вектор ${{\omega }_{0}}$ образует с этой плоскостью угол $\beta \left( {0 < \beta \leqslant \frac{\pi }{2}} \right)$. Бесконечная пластина $H$ ограничивает полупространство $Q$, заполненное несжимаемой жидкостью плотности $\rho $, кинематической вязкости $\nu $ и магнитной проницаемости $\mu $. Жидкость находится в поле массовых сил с потенциалом $U$. Схематично геометрия представлена на рис. 1.

Свяжем с пластиной декартову систему координат ${{Q}_{{xyz}}}$ с ортами ${{\vec {e}}_{x}}$, ${{\vec {e}}_{y}}$, ${{\vec {e}}_{z}}$ так, что плоскость ${{O}_{{xz}}}$ совпадает с пластиной, а ось ${{Q}_{y}}$ направлена перпендикулярно пластине внутрь жидкости.

В момент времени $t > 0$ пластина начинает двигаться в продольном направлении со скоростью $\vec {u}(t)$ и в этот момент включается однородное магнитное поле с индукцией ${{\vec {B}}_{0}}$, которое направлено перпендикулярно пластине, т.е. ${{\vec {B}}_{0}}$ = ${{B}_{0}}{{\vec {e}}_{y}}$.

Перед тем как написать уравнения движения вязкой электропроводной жидкости скажем несколько слов об уравнении индукции $\frac{{\partial{ \vec {B}}}}{{\partial t}}$ = ${\text{rot}}\left( {{\vec {v}} \times \vec {B}} \right)$ + $\frac{1}{{\mu \sigma }}\Delta \vec {B}$. Важным свойством этого уравнения является его инвариантность по отношению к переходу к вращающейся системе координат. Это объясняется тем, что в магнито-гидродинамическом приближении поле $\vec {B}$ обладает указанной инвариантностью. Другое важное свойство этого уравнения заключается в том, что в случае бесконечно проводящей жидкости сохраняется поток поля $\vec {B}$ через любую материальную поверхность в жидкости (силовые линии вморожены в движущееся вещество). Магнитное число Рейнольдса ${{\operatorname{Re} }_{m}}$ = $\frac{{VL}}{{{{\nu }_{m}}}}$, выражающее отношение по порядку величины второго члена в правой стороне этого уравнения к первому, будем считать большим. Здесь $V$ – характерная скорость задачи, $L$ – характерный размер, ${{\nu }_{m}}$ – магнитная вязкость. Случай ${{\operatorname{Re} }_{m}} \ll 1$ реализуется не только при очень высокой проводимости, но и в случае больших размеров и скоростей системы, что характерно для астрофизических задач. Поскольку представленная задача может служить математической моделью течения морской воды (проводящая жидкость) в магнитном поле вращающейся Земли, то имеет место случай ${{\operatorname{Re} }_{m}} \gg 1$. В этом случае в уравнении индукции нужно оставить только первый член.

Уравнение движения жидкости в системе координат ${{Q}_{{xyz}}}$, вращающейся с угловой скоростью ${{\vec {\omega }}_{0}}$, а также граничные и начальные условия имеет вид:

граничные и начальные условия:

Здесь t – время, $\vec {r}$ – радиус-вектор относительно полюса O, ${\vec {v}}$ – скорость жидкости, P – давление.

Решение системы уравнений (2.1), удовлетворяющее начальным и граничным условиям ищем в виде:

Тогда система (2.1) распадается на подсистемы:

Обозначим ${{\omega }_{y}} = {{\vec {\omega }}_{0}}{{\vec {e}}_{y}} = \Omega $ и введем комплексную структуру

Тогда система уравнений примет вид

граничные и начальные условия запишутся в виде

Исключая магнитную индукцию из уравнений (2.6), получаем

Решение уравнения (2.7) ищем с помощью синус-преобразования Фурье, которое введем формулой [8]

Дифференциальное уравнение (2.7) принимает вид

здесь $\begin{array}{*{20}{l}} {\mu (\lambda ,t) = \lambda \sqrt {\frac{2}{\pi }} \left( {\nu \hat {u}_{t}^{'} + \frac{{B_{0}^{2}}}{{\mu \rho }}\hat {u}} \right)} \end{array}$.

Характеристическое уравнение (2.8) и его корни

где

Решение неоднородного уравнения (2.8) имеет вид

где ${{c}_{1}},{{c}_{2}}$ находятся по методу Лагранжа вариации произвольных постоянных

Откуда

Наконец

Удовлетворяя начальным условиям, получаем

Для нахождения $\hat {V}(y,t)$ применим обратное синус-преобразование Фурье

имеем или

Вектор касательных напряжений, действующий со стороны жидкости на стенку, определяется выражением [1]

Подставляя скорость $\begin{array}{*{20}{l}} {\hat {V}(y,t)} \end{array}$ из (2.11), получаем

Найденные соотношения полностью решают задачу.

3. Продольные квазигармонические колебания пластины. Рассмотрим квазигармонический режим, т.е. будем считать, что все временные факторы задачи зависят от времени посредством множителя ${{e}^{{\lambda t}}}$: $\lambda = - \alpha + i\omega $.

Система уравнений (2.6), (2.8) имеет вид:

Исключим из уравнений (3.1) магнитную индукцию. Тогда система уравнений запишется в виде

умножим второе уравнение на $i$ и сложим с первым уравнением

Обозначим $\begin{array}{*{20}{l}} {{{{v}}_{x}} + i{{{v}}_{z}} = {{W}_{2}}} \end{array}$, ${{\left. {{{W}_{2}}} \right|}_{{y = 0}}} = {{u}_{x}}(0) + i{{u}_{z}}(0)$, тогда

Далее, умножая второе уравнение на i и вычитая из первого, получаем

при этом

Решение уравнений (3.2)–(3.4) существует при $\lambda \ne \pm i2\Omega $.

Наконец,

Или в векторной форме:

где $\begin{array}{*{20}{l}} {{{E}_{j}} = {{e}^{{{{\mu }_{j}}y}}}} \end{array}$; $j = 1,2$, $\begin{array}{*{20}{l}} {{{\mu }_{j}} = \sqrt {\frac{{\lambda \pm i2\Omega }}{{{v} + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}} } \end{array}$.

Рассмотрим резонансный случай: $\begin{array}{*{20}{l}} {\lambda = \pm i2\Omega } \end{array}$. Тогда:

В обоих случаях при $\begin{array}{*{20}{l}} {y \to \infty } \end{array}$ поле скоростей жидкости

носит колебательный характер и, оставаясь ограниченным, не стремится к нулю. В этом резонансном случае $\begin{array}{*{20}{l}} {\lambda = \pm i2\Omega } \end{array}$ решение удовлетворяет условиям на пластинке H, но не удовлетворяет условиям на бесконечности. Это так называемый “гидродинамический парадокс”.

Из соотношений (3.7) находим поле $\vec {B} = ({{B}_{x}},{{B}_{z}})$

и поле давлений

4. Структура пограничных слоев. Пусть пластина движется со скоростью $\vec {u}\left( t \right)$ = $\vec {u}\left( 0 \right){{e}^{{\lambda t}}}$, $\lambda = - \alpha + i\omega $. Поле скоростей вязкой электропроводной жидкости имеет вид

где $\begin{array}{*{20}{l}} {{{E}_{1}} = {{e}^{{{{\mu }_{1}}y}}}} \end{array}$, ${{E}_{2}} = {{e}^{{{{\mu }_{2}}y}}}$, ${{\mu }_{{1,2}}} = \sqrt {\frac{{\lambda \pm i2\Omega }}{{\nu + {{B_{0}^{2}} \mathord{\left/ {\vphantom {{B_{0}^{2}} {\mu \rho \lambda }}} \right. \kern-0em} {\mu \rho \lambda }}}}} $, $\operatorname{Re} {{\mu }_{{1,2}}} < 0$.

Рассмотрим

где $\begin{array}{*{20}{l}} {A = \nu - \frac{{\alpha B_{0}^{2}}}{{\mu \rho \left( {{{\alpha }^{2}} + {{\omega }^{2}}} \right)}}} \end{array}$, $B = - \frac{{\omega B_{0}^{2}}}{{\mu \rho \left( {{{\alpha }^{2}} + {{\omega }^{2}}} \right)}}$.

Тогда $\begin{array}{*{20}{l}} {{{A}^{2}} + {{B}^{2}} = {{\nu }^{2}} + \frac{{B_{0}^{4} - 2\nu \alpha \mu \rho B_{0}^{2}}}{{{{\mu }^{2}}{{\rho }^{2}}\left( {{{\alpha }^{2}} + {{\omega }^{2}}} \right)}}} \end{array}$.

Обозначим

Рассмотрим $\begin{array}{*{20}{l}} {{{\mu }_{{1,2}}} = \sqrt {C + iD} } \end{array}$.

Введем обозначения $\sqrt {C + iD} = {{\mu }_{{1,2}}} = \frac{1}{{{{\delta }_{{1,2}}}}} + i{{k}_{{1,2}}}$, где индекс 1 соответствует знаку +, индекс 2 – знаку –.

При этом

С учетом введенных обозначений поле скоростей принимает вид:

где ${{\hat {A}}_{1}} = \frac{1}{2}\left[ {\vec {u}\left( 0 \right) + i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}} \right]{{e}^{{ - \alpha t}}}{{e}^{{ - {y \mathord{\left/ {\vphantom {y {{{\delta }_{1}}}}} \right. \kern-0em} {{{\delta }_{1}}}}}}}$, ${{\hat {A}}_{2}} = \frac{1}{2}\left[ {\vec {u}\left( 0 \right) - i\vec {u}\left( 0 \right) \times {{{\vec {e}}}_{y}}} \right]{{e}^{{ - \alpha t}}}{{e}^{{ - {y \mathord{\left/ {\vphantom {y {{{\delta }_{2}}}}} \right. \kern-0em} {{{\delta }_{2}}}}}}}$.

Полученное решение представляет суперпозицию двух волн с волновыми числами ${{k}_{{1,2}}}$ и частотой $\omega $, распространяющихся вдоль оси $Oy$ навстречу друг другу и экспоненциально затухающих на расстояниях порядка ${{\delta }_{{1,2}}}$ соответственно. Величина пограничного слоя определяется расстоянием, на котором амплитуда волны уменьшается в “e” раз, т.е. ${{\delta }_{{1,2}}}$ это толщины пограничных слоев, примыкающих к стенке.

Плоские волны индуцированы затухающими гармоническими колебаниями пластины. Фазовые скорости этих волн различны, т.к. волновые числа ${{k}_{1}}$, ${{k}_{2}}$ различны. Кроме того, скорости зависят от частоты. Это означает, что поток вязкой электропроводной жидкости представляет собой дисперсионную среду.

Групповые скорости этих волн ${{{v}}_{{\operatorname{gr} }}} = \frac{{d\omega }}{{dk}}$ также различны. Они зависят от коэффициентов затухания и вращения системы, магнитной индукции и параметров жидкости. Амплитуды этих волн зависят от величины проекции угловой скорости на ось $y$, параметров движения стенки, магнитной индукции и параметров жидкости. Отметим, что волна, излучаемая стенкой, затухает на глубине ${{\delta }_{1}}$, а другая волна, набегающая из бесконечности на стенку, затухает на глубине ${{\delta }_{2}}$.

Выберем индукцию поля $B_{0}^{2} = 2\nu \alpha \mu \rho $. Тогда ${{A}^{2}} + {{B}^{2}} = {{\nu }^{2}}$, где $A$ = $\nu \frac{{{{\omega }^{2}} - {{\alpha }^{2}}}}{{{{\alpha }^{2}} + {{\omega }^{2}}}}$, $B$ = = $ - \nu \frac{{2\alpha \omega }}{{{{\alpha }^{2}} + {{\omega }^{2}}}}$.

В этом случае волновые числа имеют вид

Волновые числа ${{k}_{1}}$ и ${{k}_{2}}$, а также величины пограничных слоев ${{\delta }_{1}}$ и ${{\delta }_{2}}$ не зависят от магнитной проницаемости и электропроводности жидкости и определяются лишь коэффициентом затухания $\alpha $ и вязкостью жидкости $\nu $.

Кроме того, на характер распространения волн существенное влияние оказывает вращение жидкости (проекция угловой скорости вращения системы на ось $Oy$).

Введем безразмерную переменную $Y = \omega {\text{/}}\alpha $ и безразмерный параметр $S = 2\Omega {\text{/}}\alpha $. Тогда выражения для волновых чисел примут вид

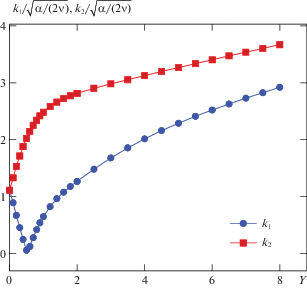
На рис. 2 представлены графики зависимости волновых чисел ${{k}_{1}}$, ${{k}_{2}}$ от $Y$ (частота $\omega $ при фиксированном $s = 2$).

В рассматриваемом случае $k(\omega )$ – волновое число, вообще говоря, комплексное. Его действительная часть характеризует зависимость фазовой скорости волны от частоты, а мнимая часть – зависимость коэффициента затухания амплитуды волны от частоты. Дисперсия, как правило, связана с внутренними свойствами материальной среды. При этом выделяются частотная (временная) дисперсия, когда поляризация в диспергирующей среде зависит от значений поля в предшествующие моменты времени (память), и пространственная дисперсия, когда поляризация в данной точке зависит от значений поля в некоторой области пространства (нелокальность). Из графиков видно, что волновое число ${{k}_{2}}$ монотонно возрастает с увеличением частоты колебаний стенки, в то время как волновое число ${{k}_{1}}$ имеет сложный характер и угловую точку.

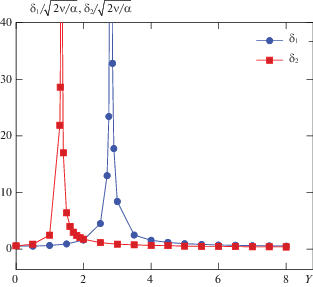
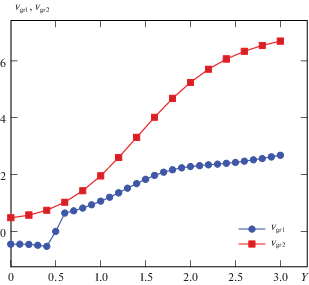
Анализ зависимостей волновых чисел ${{\delta }_{1}}$ и ${{\delta }_{2}}$ от $Y$ (частоты $\omega $) при фиксированном $s$ $(s = 2)$, представленных на рис. 3, показывает, что существуют особые точки нестационарной задачи, в окрестности которых волновые числа обращаются в бесконечность. При этом производные ${{\partial {{\delta }_{1}}} \mathord{\left/ {\vphantom {{\partial {{\delta }_{1}}} {\partial Y}}} \right. \kern-0em} {\partial Y}}$ и ${{\partial {{\delta }_{2}}} \mathord{\left/ {\vphantom {{\partial {{\delta }_{2}}} {\partial Y}}} \right. \kern-0em} {\partial Y}}$ терпят разрыв первого рода, поэтому вопрос распространения волновых пакетов в данной среде необходимо дополнительно исследовать. Для волны, излучаемой колеблющейся стенкой, особой точкой является $Y = 2.81$, в окрестности которой волновое число ${{\delta }_{1}}$ терпит разрыв и с ростом частоты стремится к нулю. При этом скорость волнового пакета ${{v}_{{{\text{gr}}1}}}$, представленная на рис. 4 терпит разрыв также в этой точке $(Y = 2.81)$. Волна, набегающая на стенку, имеет особую точку $Y = 1.31$, в которой волновое число ${{\delta }_{2}}$ имеет бесконечный разрыв и при дальнейшем росте частоты стремится к нулю.

Рассмотрим случай резонанса $\omega = 2\Omega $ (в безразмерных переменных $Y = S$). Волновое число и толщина пограничного слоя для волны, излучаемой стенкой, имеют вид

При этом набегающая волна имеет волновое число ${{k}_{2}}$ = $\sqrt {\frac{\alpha }{\nu }} \frac{S}{{\sqrt {1 + {{S}^{2}}} }}$ и толщину пограничного слоя ${{\delta }_{2}}$ = $\sqrt {\frac{\nu }{\alpha }} \sqrt {1 + {{S}^{2}}} $.

Представляет интерес сравнить полученное решение с решением задачи о колебаниях плоской стенки в вязкой несжимаемой жидкости, вращающейся в полупространстве ограниченном стенкой, рассмотренной в работе [6].

Структура решения имеет вид

где но амплитуды волн и волновые числа волн разные, т.к. корни характеристического уравнения совершенно другие, а именно ${{\mu }_{j}} = \hat {\delta }_{{1,2}}^{{ - 1}}$ + $i{{\hat {k}}_{{1,2}}}$, причем выбраны такие ветви корня, для которых $\operatorname{Re} {{\mu }_{j}} \leqslant 0$; $j = 1,2$. Полученное решение представляет суперпозицию двух волн с волновыми числами ${{k}_{j}}$ $(j = 1,2)$ и частотой $\omega $, распространяющихся вдоль оси $Oy$ навстречу друг другу и экспоненциально затухающих на расстояниях порядка ${{\delta }_{j}}$ соответственно. Решение (4.2) равномерно пригодно для всей области, как в нерезонансном, так и в резонансном случае $(2\Omega = \omega )$. Действительно, при $\Omega = \omega $т.е. в резонансном случае волна, набегающая на пластину, отсутствует, однако решение продолжает затухать вглубь жидкости. При $\alpha = 0$ однако, ${{\delta }_{2}} \to \infty $, и решение становится непригодным при $y \to \infty $, т.к. толщина одного из пограничных слоев неограниченно возрастает. Этот эффект отсутствия колебательного решения при $\omega = 2\Omega $ обсуждается в работе [2]. Важным заключением из приведенного анализа является тот факт, что затухание снимает трудности, отмеченные в [2]. В этом смысле оно играет аналогичную роль, что и отсос жидкости с поверхности пористой пластины, рассмотренный в [3]. Найдем связь между волновыми числами нашей задачи и волновыми числами задачи о колебаниях стенки в вязкой несжимаемой жидкости. Обозначим волновые числа этой задачи ${{\tilde {k}}_{{1,2}}}$, ${{\tilde {\delta }}_{{1,2}}}$. Выполняя простые, но громоздкие вычисления, получаем

Сравним волновые числа для случая резонанса $\omega = 2\Omega $ $(Y = S)$ ${{\tilde {k}}_{{1,2}}} = 0$, ${{\tilde {\delta }}_{{1,2}}} = \sqrt {\nu {\text{/}}\alpha } $. Получаем ${{k}_{2}}$ = $\frac{\alpha }{{{{{\tilde {\delta }}}_{{1,2}}}}}\frac{1}{{\sqrt {{{\omega }^{2}} + \alpha } }}$ = $\sqrt {\frac{\alpha }{\nu }} \frac{S}{{\sqrt {1 + {{S}^{2}}} }}$, ${{\delta }_{2}}$ = $\sqrt {\frac{\nu }{\alpha }} \sqrt {1 + {{S}^{2}}} $, т.е. в электропроводной жидкости в магнитном поле существует набегающая на стенку волна. Толщина пограничного слоя увеличилась в $\sqrt {1 + {{S}^{2}}} $ раз. Также различны волновые числа ${{k}_{1}}$ и ${{\hat {k}}_{1}}$. Сопоставляя результаты, видим, как магнитное поле меняет профиль скорости, толщину пограничного слоя и касательные напряжения на стенке. Интересно сопоставить результаты, полученные в [5] с результатами данной статьи. Различные краевые условия в задачах обеих работ приводят к различным решениям для поля скоростей. В [5] решение представлено в виде суперпозиции двух волн, одна из которых является отраженной от неподвижной стенки. Эти волны имеют равные волновые числа и толщины пограничных слоев, причем они отличаются от соответствующих величин в данной задаче. Скорости волновых пакетов [5] совпадают в отличие от представленной работы, где скорости волновых пакетов различны и отличны от [5]. И только в резонансном случае $\omega = 2\Omega $ волновые числа [5], которые имеют вид k = $\frac{{\sqrt {\alpha {\text{/}}\nu } }}{{\sqrt {1 + {{{{\alpha }^{2}}} \mathord{\left/ {\vphantom {{{{\alpha }^{2}}} {\left( {4{{\Omega }^{2}}} \right)}}} \right. \kern-0em} {\left( {4{{\Omega }^{2}}} \right)}}} }}$, $\delta $ = = $\sqrt {\frac{\nu }{\alpha }} \sqrt {1 + \frac{{4{{\Omega }^{2}}}}{{{{\alpha }^{2}}}}} $ совпадают с результатами для набегающей волны ${{k}_{2}}$ и ${{\delta }_{2}}$, полученными в представленной статье.

Заключение. Проведен анализ задачи неустановившегося течения вязкой электропроводной несжимаемой жидкости в плоско-параллельной конфигурации. Найдены точные решения трехмерных нестационарных уравнений магнитной гидродинамики. При этом никаких ограничений на характер движения пластины не накладывается. Определены поле скоростей в потоке и векторы касательных напряжений, действующие из жидкости на стенку. Для случая “нормальных” колебаний пластины рассмотрен случай резонанса и исследована структура пограничных слоев, примыкающих к стенке. Показано, как магнитное поле меняет характер течения электропроводной жидкости, изменяя поле скоростей жидкости, величины волновых чисел и пограничных слоев. Кроме того, меняются и касательные напряжения, действующие из жидкости на стенку.

Математическая процедура интегрирования системы дифференциальных уравнений рассматриваемой задачи может быть использована при исследовании более сложных задач. Кроме того, полученные результаты могут быть использованы для учёта силовых воздействий при движении жидкости в полостях различной формы, а также в задачах фильтрации и при моделировании различных физических явлений в движущейся жидкости.