Прикладная математика и механика, 2022, T. 86, № 2, стр. 169-185

1. Введение. Маятниковые движения тяжелого твердого тела с неподвижной точкой впервые описаны Б.К. Млодзеевским в 1894 г. [1], где было показано, что такие движения может совершать тело с центром масс в главной плоскости инерции; осью вращения является главная ось инерции, перпендикулярная этой плоскости. Позднее рассматривались вопросы об устойчивости малых маятниковых колебаний [2], а также плоских и близких к ним вращений тела с центром масс на главной оси инерции [3]. Маятниковые движения изучены для тел с геометрией масс, отвечающей случаю Ковалевской [4, 5], Горячева–Чаплыгина [6], Бобылева–Стеклова [7], а также динамически симметричного тела [8].

Теоретический и прикладной интерес представляет изучение влияния высокочастотных вибраций на движение твердого тела или системы твердых тел. Первые работы в данной области опубликованы А. Стефенсоном [9], показавшим возможность стабилизации верхнего положения математического маятника за счет вертикальных вибраций точки подвеса. Подробная библиография по динамике маятниковых систем при наличии вибраций содержится в монографиях [10, 11].

В работе А.П. Маркеева [12] были получены приближенные автономные уравнения движения тела с произвольной геометрией масс в случае произвольных высокочастотных периодических или условно-периодических вибраций точки подвеса в трехмерном пространстве. В этих уравнениях влияние вибраций точки подвеса эквивалентно наложению дополнительного (стационарного) вибрационного потенциального поля. В рамках указанной системы уравнений проведен ряд исследований частных случаев движений твердого тела с вибрирующей точкой подвеса для различных случаев геометрии масс тела и различных случаев вибраций [12–18].

Были описаны [16] (в рамках приближенной автономной системы) маятниковые движения волчка Лагранжа с вибрирующей точкой подвеса для широкого спектра вибраций, включающего и вибрации вдоль горизонтальной прямой. Была исследована орбитальная устойчивость этих движений. В этой статье угол собственного вращения волчка относительно оси симметрии являлся циклической координатой, и потому исследование устойчивости проведено по отношению к отклонению плоскости маятниковых движений волчка.

Другим классическим случаем динамики твердого тела с неподвижной точкой является случай С.В. Ковалевской [19]. В частности, было проведено [4, 5] исследование устойчивости маятниковых движений волчка Ковалевской с неподвижной точкой подвеса по отношению к возмущениям угла собственного вращения вокруг главной оси, содержащей центр масс тела.

Представляет интерес (в рамках приближенной автономной системы) изучить влияние вибраций точки подвеса волчка Ковалевской на устойчивость его маятниковых движений. В случае вибраций точки подвеса вдоль горизонтальной прямой система допускает как маятниковые движения, аналогичные таким движениям тела с неподвижной точкой, так и маятниковые движения других типов. Изучение этих движений начато [18] с линейного анализа их орбитальной устойчивости (по отношению к пространственным возмущениям).

Отметим, что первый интеграл, имеющий место в задаче о движении волчка Ковалевской вокруг неподвижной точки, исчезает при наличии вибраций точки подвеса. В такой постановке задачи отсутствует и циклическая координата (угол прецессии). При этом из-за появления выделенного направления в пространстве, определяемого направлением оси вибраций, возникает возможность стабилизации маятниковых движений, неустойчивых в случае неподвижной точки подвеса.

Целью данной работы является завершение линейного анализа орбитальной устойчивости маятниковых движений волчка Ковалевской с вибрирующим подвесом, а также проведение подробного нелинейного анализа их орбитальной устойчивости.

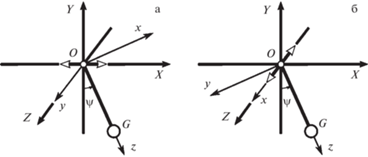
2. Постановка задачи. Рассмотрим движение тяжелого твердого тела, точка $O$ которого (называемая далее точкой подвеса) совершает периодическое движение вдоль фиксированной горизонтальной прямой с частотой $\Omega $ по закону $O{\text{'}}O = \xi (t)$ относительно фиксированной точки $O{\text{'}}$. Среднее значение $\left\langle {\xi (t)} \right\rangle $ за период считаем равным нулю.

Введем поступательно движущуюся систему координат $OXYZ$, ось $OY$ которой направлена вертикально вверх, а вибрации происходят вдоль оси $OX$ (или в отдельно оговоренном случае – вдоль оси $OZ$). Введем связанную с телом систему координат $Oxyz$ с осями, направленными вдоль главных осей инерции тела для точки $O$. Главные моменты инерции тела для точки $O$ обозначим через $A$, $B$ и $C$ и свяжем соотношениями, отвечающими волчку Ковалевской

Пусть центр масс $G$ волчка лежит на оси $Oz$, и $OG = {{z}_{G}}$, а масса тела – $m$. Ориентацию системы $Oxyz$ относительно $OXYZ$ зададим углами Эйлера $\psi $, $\theta $ и $\varphi $.

Будем считать, что наибольшее отклонение ${{h}_{*}}$ точки подвеса от точки $O{\text{'}}$ мало по сравнению с приведенной длиной тела $l = B{\text{/}}(m{{z}_{G}})$, а частота вибраций точки подвеса $\Omega $ велика по отношению к характерной частоте ${{\omega }_{*}} = \sqrt {g{\text{/}}l} $. Введем малый параметр ${{\varepsilon }^{2}} = {{h}_{*}}{\text{/}}l$ и будем считать, что ${{\omega }_{*}}\sim {{\varepsilon }^{2}}\Omega $ (т. е. ${{h}_{*}}\Omega \sim l{{\omega }_{*}}$).

Движение тела опишем с помощью канонических уравнений Гамильтона. Методами теории возмущений можно привести функцию Гамильтона к виду, главная часть которой автономна. Впервые такое преобразование проведено для уравнений Эйлера–Пуассона [12], а приведение гамильтониана к автономному виду описано в монографии [10]. Оставляя за переменными прежние обозначения, запишем приближенный автономный гамильтониан в виде

где $\alpha = {{\langle {{{\dot {\xi }}}^{2}}\rangle {{m}^{2}}z_{G}^{2}} \mathord{\left/ {\vphantom {{\langle {{{\dot {\xi }}}^{2}}\rangle {{m}^{2}}z_{G}^{2}} {({{B}^{2}}\omega _{*}^{2})}}} \right. \kern-0em} {({{B}^{2}}\omega _{*}^{2})}}$ – безразмерный параметр, характеризующий интенсивность вибраций, ${{P}_{1}}$, ${{P}_{2}}$, ${{P}_{3}}$ – безразмерные импульсы, отвечающие углам $\psi $, $\theta $ и $\varphi $ соответственно. Слагаемое ${{\hat {\Pi }}_{\nu }}$ представляет собой вибрационный потенциал.

Система с гамильтонианом (2.1), (2.2) имеет частные решения, при которых главная ось $Oz$ (или, что то же, радиус-вектор ${\mathbf{OG}}$) совершает маятниковые движения в фиксированной вертикальной плоскости вокруг одной из двух других главных осей инерции, занимающей фиксированное горизонтальное положение. При этом ось вибрации либо лежит в плоскости этих движений, либо перпендикулярна ей. В первом случае маятниковые движения будем называть продольными, во втором – поперечными.

Данная работа посвящена исследованию двух типов движения: продольных движений, при которых осью вращения является ось $Oy$ из экваториальной плоскости инерции (рис. 1а), и поперечных движений, при которых осью вращения является ось динамической симметрии $Ox$. Другие два типа движения в данной работе не рассматриваются.

Указанным продольным движениям отвечает частное решение системы (2.1), (2.2), задаваемое соотношениями

а изменение величин $\psi $ и ${{P}_{1}}$ описывается каноническими уравнениями с функцией Гамильтона

Для поперечных маятниковых движений ось $Oz$ может совпасть с осью $OZ$. Чтобы избежать вырождения, при исследовании таких движений перенаправим оси системы координат $OXYZ$ таким образом, чтобы вибрации точки подвеса происходили вдоль оси $OZ$. Гамильтониан приближенной системы запишется в виде (2.1), в котором вибрационный потенциал примет вид

Поперечным движениям отвечает частное решение системы (2.1), (2.5)

при этом величины $\psi $ и ${{P}_{1}}$  удовлетворяют каноническим уравнениям математического маятника с гамильтонианом

Ранее [18] было проведено исследование движений систем с гамильтонианами (2.4) и (2.7), а также линейный анализ орбитальной устойчивости описанных маятниковых движений по отношению к пространственным возмущениям.

Целью данной работы является завершение линейного анализа орбитальной устойчивости маятниковых движений системы с функцией Гамильтона (2.1), (2.2) и (2.1), (2.5), по отношению к пространственным возмущениям, а также выполнение подробного нелинейного исследования орбитальной устойчивости.

Отметим, что при отсутствии вибраций точки подвеса маятниковые движения тела могут совершаться в любой фиксированной вертикальной плоскости. В этом случае, вследствие имеющейся относительно вертикали симметрии силового поля (поля тяжести), в системе имеется циклическая координата, и по отношению к пространственным возмущениям маятниковые движения неустойчивы. При наличии горизонтальных вибраций точки подвеса указанная симметрия нарушается, и циклическая координата исчезает. Далее будет показано, что маятниковые движения могут быть устойчивыми и при наличии пространственных возмущений.

3. Маятниковые движения. Гамильтонианы (2.4) и (2.7) и соответствующие им системы уравнений, описывающие маятниковые движения, далее будем называть модельными.

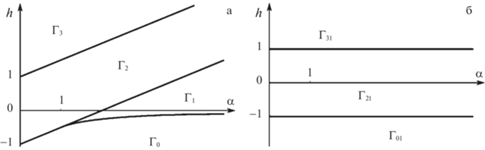
Модельные системы имеют первые интегралы (интегралы энергии) вида ${{H}_{0}} = h = \operatorname{const} $, ${{H}_{{01}}} = h = \operatorname{const} $. На рис. 2а,б построены бифуркационные диаграммы в плоскости параметров $\alpha $, $h$ для модельных систем (2.4) и (2.7), соответственно, где отображены области, отвечающие разным типам маятниковых движений.

На рис. 2а области ${{\Gamma }_{0}}$, ${{\Gamma }_{1}}$, ${{\Gamma }_{2}}$ и ${{\Gamma }_{3}}$ с различным характером движения разделены прямыми $h = \pm 1 + {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}$ и участком гиперболы $2\alpha h = - 1$ при $\alpha > 1$. Точкам гиперболы $2\alpha h = - 1$ отвечает устойчивое боковое положение равновесия ${{\psi }_{*}} = \pm \arccos ({{\alpha }^{{ - 1}}})$. Точкам прямой $h = - 1 + {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}$ при $\alpha < 1$ отвечает устойчивое нижнее положение равновесия $\psi = 0$, а при $\alpha > 1$ – неустойчивое нижнее положение и асимптотическое движение. Прямая $h = 1 + {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}$ соответствует неустойчивому верхнему положению равновесия $\psi = \pi $ и асимптотическому движению. На рис. 2б прямой $h = - 1$ при всех $\alpha $ отвечает устойчивое нижнее положение равновесия, а прямой $h = 1$ отвечают неустойчивое верхнее равновесие и асимптотическое движение.

В областях ${{\Gamma }_{0}}$ и ${{\Gamma }_{{01}}}$ на рис. 2а и 2б движение невозможно. В области ${{\Gamma }_{1}}$ центр масс тела совершает колебания около бокового равновесия $\psi = {{\psi }_{*}}$. Областям ${{\Gamma }_{2}}$ и ${{\Gamma }_{{21}}}$ отвечают колебания центра масс около нижнего положения. В областях ${{\Gamma }_{3}}$ и ${{\Gamma }_{{31}}}$ происходят вращения волчка.

Для проведения интегрирования модельных систем разрешим интегралы энергии ${{H}_{0}} = h$ и ${{H}_{{01}}} = h$ относительно импульса ${{P}_{1}}$ и, используя уравнения Гамильтона, получим дифференциальные уравнения продольных и поперечных маятниковых движений, соответственно $\dot {\psi } = {{P}_{1}}(\psi ,h)$ = $ \pm \sqrt {2h + 2\cos \psi - \alpha {{{\cos }}^{2}}\psi } $ и $\dot {\psi } = 2{{P}_{1}}(\psi ,h)$ = $ \pm 2\sqrt {(h + \cos \psi )} $.

Полагая, что $u = \cos \psi $ ($\left| u \right| \leqslant 1$), перепишем эти уравнения в виде

Здесь введены обозначения ${{u}_{{1,2}}} = {{\left( {1 \pm \sqrt {1 + 2\alpha h} } \right)} \mathord{\left/ {\vphantom {{\left( {1 \pm \sqrt {1 + 2\alpha h} } \right)} \alpha }} \right. \kern-0em} \alpha }$, (${{u}_{1}} < {{u}_{2}}$).

Интегрирование уравнений продольных и поперечных маятниковых движений (3.1) проведено в работе [18]. Для дальнейшего исследования введем обозначения

и выпишем частоты маятниковых движений ${{\omega }_{j}}$ ($j$ – индекс области)

Здесь $\operatorname{K} \left( k \right)$ – полный эллиптический интеграл первого рода, $k$ – модуль эллиптического интеграла.

В областях колебаний и вращений модельных систем введем переменные действие-угол $I$, $w$.

Переменную действие введем по формуле

где интеграл берется по полному изменению угла $\psi $ за период колебания или вращения.

Обращая соотношение (3.2), получим гамильтониан ${{H}_{0}} = h(I)$, записанный через переменную действие.

4. Гамильтониан возмущенного движения. Маятниковые движения (колебания и вращения) полных систем с тремя степенями свободы, для которых “маятниковая часть” записана через переменную действие, а остальные переменные принимают значения (2.3) или (2.6), примем за невозмущенное движение. Рассмотрим вопрос об орбитальной устойчивости этих движений.

В системе с гамильтонианом (2.1) введем возмущения по формулам $r = I - {{I}_{0}}$, ${{p}_{2}} = {{P}_{2}}$, ${{p}_{3}} = {{P}_{3}}$, ${{q}_{2}} = \theta - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, ${{q}_{3}} = \varphi - {{\varphi }_{0}}$, где ${{I}_{0}}$ и ${{\varphi }_{0}}$ – значение переменной действие и угла $\varphi $ на невозмущенном движении. Выделим слагаемые возмущенного гамильтониана до четвертого порядка включительно по переменным ${{r}^{{1/2}}}$, ${{p}_{2}}$, ${{q}_{2}}$, ${{p}_{3}}$, ${{q}_{3}}$ и представим его в виде

Здесь ${{\omega }_{0}}$ – частота невозмущенного движения, а ${{O}_{6}}$ – $2\pi $-периодические слагаемые шестого и более высоких порядков по ${{r}^{{1/2}}}$, ${{p}_{2}}$, ${{q}_{2}}$, ${{p}_{3}}$, ${{q}_{3}}$. Указанные частные производные в выражении для ${{H}_{4}}$ вычисляются следующим образом

Для продольных маятниковых движений, описываемых гамильтонианом (2.4), функции ${{\tilde {H}}_{2}}$ и ${{\tilde {H}}_{4}}$ имеют вид

В случае, когда невозмущенное движение – поперечное маятниковое движение, описываемое системой с гамильтонианом (2.7), имеем

В выражениях (4.2)–(4.5) функции $\psi \left( w \right)$ и ${{P}_{1}}\left( w \right)$ отвечают невозмущенному движению.

На уровне энергии невозмущенного движения $\hat {H} = 0$ осуществим изоэнергетическую редукцию и, принимая в качестве новой независимой переменной величину $w$, рассмотрим неавтономную редуцированную систему с двумя степенями свободы с гамильтонианом

Критерии орбитальной устойчивости тривиального положения равновесия системы с гамильтонианом (4.1) и описанной редуцированной системы с гамильтонианом (4.6) совпадают [20].

Замечание. Положения равновесия модельных систем (2.4) и (2.7) в рамках редуцированной неавтономной системы с двумя степенями свободы сохраняются. Для рассматриваемых движений устойчивость положений равновесия сохраняется и при пространственных возмущениях. В этом случае корни характеристических уравнений линеаризованных систем $ \pm i{{\Omega }_{{k,j}}}$ ($k$ – индекс области, $j = 1,2$) имеют вид

5. Критерии устойчивости маятниковых движений. В областях колебаний и вращений модельных систем рассмотрим сначала линеаризованную систему, описываемую гамильтонианом ${{K}_{2}}$. Пусть ${\mathbf{X}}(w)$ – матрица фундаментальных решений этой системы, удовлетворяющих начальным условиям ${\mathbf{X}}(0) = {{{\mathbf{E}}}_{4}}$, где ${{{\mathbf{E}}}_{4}}$ – единичная матрица четвертого порядка. Характеристическое уравнение линейной системы имеет вид

Здесь ${{a}_{1}}$ – след матрицы ${\mathbf{X}}(2\pi )$, ${{a}_{2}}$ – сумма ее главных миноров второго порядка.

Условия устойчивости в линейном приближении задаются неравенствами [21]

В областях устойчивости в линейном приближении гамильтониан ${{K}_{2}}$ при помощи $2\pi $-периодической по $w$ линейной замены переменных ${{p}_{2}},{{q}_{2}},{{p}_{3}},{{q}_{3}}$ → $p_{2}^{'},q_{2}^{'},p_{3}^{'},q_{3}^{'}$ может быть приведен к нормальной форме

где $ \pm i{{\lambda }_{{1,2}}}$ – характеристические показатели системы.

Границами областей устойчивости в линейном приближении внутри областей ${{\Gamma }_{1}}$, ${{\Gamma }_{2}}$, ${{\Gamma }_{{21}}}$, ${{\Gamma }_{3}}$ и ${{\Gamma }_{{31}}}$ являются кривые резонансов первого и второго порядков, задаваемых соотношениями

где ${{k}_{1}}$ и ${{k}_{2}}$ – целые числа.

Согласно теореме Крейна–Гельфанда–Лидского [23], эти кривые в областях ${{\Gamma }_{1}}$, ${{\Gamma }_{2}}$ и ${{\Gamma }_{{21}}}$ рождаются из точек нижних границ этих областей, где величины ${{\Omega }_{{i,j}}}$, вычисляемые по формулам (4.7) и (4.8), связаны соответствующими резонансными соотношениями. Из некоторых таких точек рождаются пары кривых резонансов, заключающие между собой области неустойчивости (области параметрического резонанса), а из других рождается по одной резонансной кривой (и области неустойчивости нет).

В областях, где выполняются условия (5.2) устойчивости в линейном приближении, проводится нелинейный анализ устойчивости тривиального положения равновесия рассматриваемой неавтономной системы с двумя степенями свободы. Для этого при помощи близкой к тождественной замены переменных $p_{2}^{'},q_{2}^{'},p_{3}^{'},q_{3}^{'}$ → ${{\hat {p}}_{2}},{{\hat {q}}_{2}},{{\hat {p}}_{3}},{{\hat {q}}_{3}}$ требуется провести нормализацию преобразованного гамильтониана возмущенного движения в слагаемых четвертой степени относительно возмущений.

Если в системе отсутствуют резонансы четвертого порядка, то есть величины ${{\lambda }_{{1,2}}}$ не связаны соотношениями вида

то имеет место нерезонансный случай, и нормальная форма гамильтониана в симплектических полярных координатах ${{\varphi }_{i}}$, ${{r}_{i}}$ (${{\hat {q}}_{i}} = \sqrt {2{{r}_{i}}} \sin {{\varphi }_{i}}$, ${{\hat {p}}_{i}} = \sqrt {2{{r}_{i}}} \cos {{\varphi }_{i}}$, $i = 2,3$) приводится к виду где ${{c}_{{20}}}$, ${{c}_{{11}}}$ и ${{c}_{{02}}}$ – постоянные коэффициенты, а $\tilde {K}({{r}_{2}},{{r}_{3}},{{\varphi }_{2}},{{\varphi }_{3}},w)$ – $2\pi $-периодическая по $w$ функция, порядок которой по ${{r}_{2}}$ и ${{r}_{3}}$ не ниже третьего.

При отсутствии вырождения в членах четвертой степени нормализованного гамильтониана (5.4), то есть при выполнении условия

положение равновесия ${{r}_{2}} = {{r}_{3}} = 0$ неавтономной редуцированной системы с двумя степенями свободы устойчиво для большинства (в смысле меры Лебега) начальных условий [22]. Если при ${{r}_{2}} \geqslant 0$, ${{r}_{3}} \geqslant 0$ квадратичная форма является знакоопределенной, то положение равновесия формально устойчиво [22].

Пусть в системе выполняется резонансное соотношение вида (5.3). В случае ${{k}_{1}}{{k}_{2}} < 0$ в системе имеется положительно определенный первый интеграл, и рассматриваемое положение равновесия формально устойчиво [22]. Если же ${{k}_{1}}{{k}_{2}} \geqslant 0$, то гамильтониан системы приводится к нормальной форме

где коэффициенты ${{a}_{{{{k}_{1}}{{k}_{2}}}}}$, ${{b}_{{{{k}_{1}}{{k}_{2}}}}}$ постоянны. При выполнении условия положение равновесия ${{r}_{2}} = 0$, ${{r}_{3}} = 0$ устойчиво с учетом в функции Гамильтона членов не выше второго порядка по ${{r}_{j}}$ ($j = 2,3$) [22]. Если условие (5.6) выполняется с обратным знаком, то имеет место неустойчивость.

Случаи вырождения $D = 0$, а также случаи кратного резонанса, требуют дополнительного исследования и в данной работе не рассматриваются.

Нормальную форму гамильтониана вида (5.4) или (5.5) можно получить, построив нормализованное отображение, порождаемое системой канонических уравнений движения системы с функцией Гамильтона $K$ за период $2\pi $ [20]. Построение отображения выполнено с использованием программного пакета MAPLE.

6. О результатах исследования устойчивости в линейном приближении. Для проверки условий (5.2) устойчивости в линейном приближении внутри областей ${{\Gamma }_{1}}$, ${{\Gamma }_{2}}$, ${{\Gamma }_{{21}}}$, ${{\Gamma }_{3}}$, и ${{\Gamma }_{{31}}}$ следует проинтегрировать уравнения движения неавтономной системы с гамильтонианом ${{K}_{2}}$ и определить коэффициенты характеристического уравнения (5.1). Интегрирование уравнений движения и вычисление необходимых коэффициентов проведено численно.

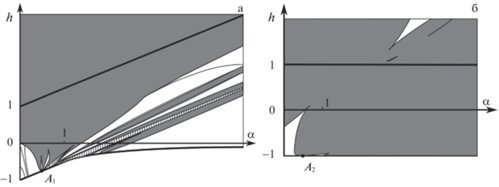
Исследование линейной орбитальной устойчивости рассматриваемых продольных и поперечных маятниковых движений волчка подробно проведено в работе [18], где в соответствующих областях в плоскости параметров $\alpha $ и $h$ построены диаграммы устойчивости. Полученные результаты показаны на рис. 3. На этих рисунках полужирными линиями отмечены границы областей, соответствующие рис. 2, тонкими линиями обозначены кривые резонансов первого и второго порядков. Серым цветом показаны области неустойчивости, области устойчивости в линейном приближении не закрашены. В областях с вертикальной штриховкой содержится счетное множество резонансных кривых первого и второго порядков.

Картина устойчивости для продольных маятниковых движений показана на рис. 3а. В области ${{\Gamma }_{2}}$ колебаний около нижнего положения кривые резонансов первого и второго порядков берут начало в точках нижней границы области с абсциссами

В области ${{\Gamma }_{2}}$ имеются шесть существенных областей устойчивости. Четыре из них примыкают к точке ${{A}_{1}}$ ($\alpha = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, $h = - {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}$), где имеет место кратный резонанс ${{\Omega }_{{2,1}}} = 2$, ${{\Omega }_{{2,2}}} = 1$. Первая из этих областей примыкает к границе $\alpha = 0$ и нижней границе области ${{\Gamma }_{2}}$ и имеет угловую точку (0; 0). Вторая и третья области устойчивости расположены между точкой кратного резонанса ${{A}_{1}}$ и угловыми точками (0.49252; –0.34305) и (0.64130; –0.17655), соответственно. Четвертая область устойчивости занимает участок нижней границы области ${{\Gamma }_{2}}$ при $\alpha \in (1{\text{/}}2;\;7{\text{/}}9)$ и заканчивается в угловой точке (1.22538; –0.05679). При $\alpha > 1$ имеются две обширные области устойчивости в линейном приближении, расширяющиеся с увеличением значения $\alpha $. На верхней границе большей из этих областей находится угловая точка (2.77955; 1.25049). Вблизи точки с абсциссой $\alpha = 1$ на нижней границе области ${{\Gamma }_{2}}$ находится счетное множество точек, порождающих резонансные кривые. Эти кривые ограничены заштрихованной областью около нижней границы ${{\Gamma }_{2}}$.

В области ${{\Gamma }_{1}}$ колебаний в окрестности бокового положения равновесия кривые резонансов первого и второго порядков выходят из точек нижней границы области, абсциссы которых

Бóльшую часть области ${{\Gamma }_{1}}$ занимает примыкающая к ее нижней границе область устойчивости в линейном приближении. Эта область ограничена сверху областью неустойчивости, выходящей из точки нижней границы области ${{\Gamma }_{1}}$ с абсциссой α = = ${{\sqrt {375 + 30\sqrt {145} } } \mathord{\left/ {\vphantom {{\sqrt {375 + 30\sqrt {145} } } {15}}} \right. \kern-0em} {15}}$ ≈ 1.80892. Над этой областью неустойчивости в окрестности верхней границы области ${{\Gamma }_{1}}$ располагается заштрихованная область, где, как и в области ${{\Gamma }_{2}}$, располагается счетное множество резонансных кривых.

В области вращений ${{\Gamma }_{3}}$ не обнаружено областей орбитальной устойчивости.

Диаграмма устойчивости поперечных маятниковых движений представлена на рис. 3б. В области ${{\Gamma }_{{21}}}$ колебаний около нижнего положения равновесия кривые резонансов первого и второго порядков выходят из точек нижней границы области с абсциссами

В этой области находятся две области устойчивости (рис. 3б), примыкающие к нижней границе ${{\Gamma }_{{21}}}$ левее и правее точки кратного резонанса ${{A}_{2}}$ ($\alpha = 1{\text{/}}2$, $h = - 1$; ${{\Omega }_{{21,1}}} = {{\Omega }_{{21,2}}} = 1{\text{/}}2$). Верхняя граница левой из этих областей заключена между точками (0; –0.37233) и (0.66882; 0.43844). Область устойчивости правее точки ${{A}_{2}}$ имеет угловую точку (1.15900; –0.37413).

В области вращений ${{\Gamma }_{{31}}}$ в рассматриваемом диапазоне параметров обнаружены три области устойчивости в линейном приближении. Наибольшая из них берет начало в точке (2.72745; 2.68839) и расширяется с ростом $h$. Две малые области устойчивости представляют собой криволинейный треугольник с угловыми точками (2.83023; 2.53740), (2.67780; 2.40480) и (2.70412; 2.41939), и тонкую полосу с угловой точкой (3.78114; 3.53085) (заключенную при $h = 4$ между точками с абсциссами α = 4.22712 и α = 4.22736).

Таким образом, для описанных маятниковых движений существуют области линейной орбитальной устойчивости по отношению к рассматриваемым в работе пространственным возмущениям. Этот результат отличает данную задачу от аналогичной задачи в случае неподвижной точки подвеса тела, когда устойчивость при наличии пространственных возмущений невозможна.

Результаты данного исследования в предельном случае отсутствия вибраций соответствуют выводам [4, 5]. В этих работах было получено, что маятниковые колебания волчка Ковалевской как вокруг оси динамической симметрии, так и вокруг оси из экваториальной плоскости орбитально устойчивы по отношению к возмущению угла собственного вращения, если амплитуда этих колебаний меньше значения ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Этим колебаниям на диаграммах рис. 1а и б отвечают отрезки $\alpha = 0$, $ - 1 < h < 1$. На рис. 1а область устойчивости колебаний при стремлении интенсивности вибраций к нулю сходится к отрезку $h \in \left[ { - 1;\;0} \right]$, что отвечает колебаниям с амплитудой до ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. На рис. 1б область устойчивости колебаний сходится к отрезку $h \in \left[ { - 1;\; - {\kern 1pt} 0.37233} \right]$, но при численном исследовании самой границы $\alpha = 0$ получаем, что условия (5.2) выполняются со знаком равенства при $h \in \left[ { - 1;\;0} \right]$, а при $h > 0$ одно их этих условий выполняется с обратным знаком, что также отвечает результатам [4, 5].

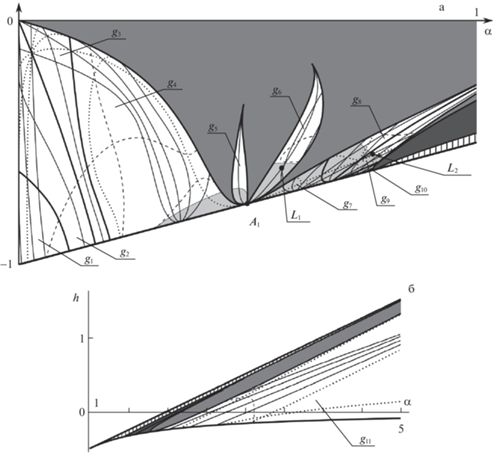
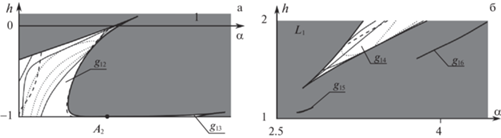
7. Нелинейный анализ устойчивости маятниковых движений. Результаты нелинейного анализа устойчивости маятниковых движений, основанные на критериях из параграфа 4, представим на рис. 4–6. На этих диаграммах полужирными линиями показаны кривые резонансов первого и второго порядков, часть которых является границами областей устойчивости в линейном приближении, а остальные кривые разделяют эти области на подобласти ${{g}_{i}}$ ($i = 1\; \ldots \;16$). Кривые резонансов четвертого порядка, соответствующие условию ${{k}_{1}}{{k}_{2}} < 0$, отображены точечными линиями, резонансные кривые с ${{k}_{1}}{{k}_{2}} \geqslant 0$ показаны сплошными тонкими линиями. Пунктирные линии – кривые вырождения, на которых имеем $D = 0$.

В незакрашенных областях для маятниковых движений выполняются условия формальной устойчивости, а в областях, закрашенных светло-серым цветом, эти условия нарушаются. В заштрихованной области содержится счетное множество кривых резонансов четвертого порядка; на них исследование не проводилось. В темно-серых областях содержится конечное число резонансных кривых четвертого порядка, однако картина устойчивости здесь весьма сложна и в данной работе не описывается. Остановимся подробнее на результатах исследования.

7.1. Области продольных колебаний волчка около нижнего положения равновесия (рис. 4а). В области ${{\Gamma }_{2}}$ продольных колебаний около нижнего положения равновесия нелинейный анализ устойчивости проведен в областях линейной устойчивости, примыкающих к точке кратного резонанса ${{A}_{1}}$ и разделенных на подобласти ${{g}_{i}}$ ($i = 1 \ldots 10$).

Часть кривых резонансов четвертого порядка берут начало в точках нижней границы области ${{\Gamma }_{2}}$ (в силу громоздкости выражения для абсцисс точек и соответствующие резонансные соотношения не приводятся).

Кроме того, в исследуемых областях обнаружены четыре резонансные кривые, граничные точки которых лежат на других границах областей устойчивости: две кривые $2{{\lambda }_{1}} - 2{{\lambda }_{2}} = 3$ (области ${{g}_{2}}$, ${{g}_{3}}$ и ${{g}_{8}}$, ${{g}_{9}}$) и кривые $4{{\lambda }_{1}} = 9$ и $3{{\lambda }_{1}} + {{\lambda }_{2}} = 8$ (область ${{g}_{6}}$).

На кривых резонансов четвертого порядка ${{\lambda }_{1}} + 3{{\lambda }_{2}} = 5$ (область ${{g}_{6}}$) и $3{{\lambda }_{1}} + {{\lambda }_{2}} = 9$ (области ${{g}_{9}}$) обнаружены два малых участка неустойчивости, местоположение которых отмечено на рис. 4а точками ${{L}_{1}}$ и ${{L}_{2}}$. Участок ${{L}_{1}}$ заключен между точками (0.57520, –0.60225) и (0.57386, –0.60567), а участок ${{L}_{2}}$ – между (0.77345, –0.54603) и (0.77360, –0.54590). Вне этих участков на данных кривых, а также на остальных резонансных кривых выполняется условие устойчивости (5.6).

В рассматриваемой части плоскости параметров обнаружены пять кривых вырождения: три из них лежат в левой области устойчивости в линейном приближении (подобласти ${{g}_{1}}$, ${{g}_{2}}$, ${{g}_{3}}$ и ${{g}_{4}}$), и по одной лежит в правых областях (подобласти ${{g}_{6}}$ и ${{g}_{8}}$, ${{g}_{9}}$).

В большей части четырех исследуемых областей устойчивости в линейном приближении имеет место формальная устойчивость. Исключение составляют части этих областей, примыкающие к точке ${{A}_{1}}$ кратного резонанса, где условие формальной устойчивости нарушается. При этом граница этой части области в подобласти ${{g}_{9}}$ пересекает участок неустойчивости ${{L}_{2}}$ на резонансной кривой.

7.2. Область продольных колебаний волчка около бокового положения равновесия (рис. 4б). Для колебаний волчка в окрестности бокового положения равновесия нелинейный анализ устойчивости проведен для области ${{g}_{{11}}}$ устойчивости в линейном приближении при $\alpha < 5$. В этой части области обнаружено семь кривых резонансов четвертого порядка, выходящих из точек нижней границы области ${{\Gamma }_{1}}$ с абсциссами

На всех рассмотренных кривых резонансов четвертого порядка условия устойчивости (5.6) выполняются. Обнаружена одна кривая вырождения, лежащая между точками (3.11532, –0.15951) и (2.71379, 0.11436) на границах области. Условия формальной устойчивости выполняются во всей области ${{g}_{{11}}}$.

7.3. Области поперечных колебаний волчка около нижнего положения равновесия (рис. 5а). В области ${{\Gamma }_{{21}}}$ поперечных колебаний десять резонансных кривых берут начало на нижней границе области, абсциссы которых

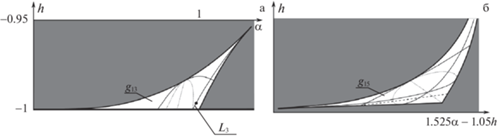
Дополнительно в области устойчивости в линейном приближении ${{g}_{{12}}}$ найдены две резонансные кривые $4{{\lambda }_{1}} = 3$, граничные точки которых лежат на боковых и верхней границах области. На всех кривых резонансов четвертого порядка в этой области условия устойчивости (5.6) выполняются. Также в области ${{g}_{{12}}}$ обнаружены две кривые вырождения и область, в которой нарушаются условия формальной устойчивости. Эта область примыкает к верхней границе области ${{g}_{{12}}}$ вблизи верхней угловой точки. Ее граница заключена между точками (0.51562, –0.01612) и (0.60296, 0.05082), и вытягивается внутрь области устойчивости до точки (0.43111, –0.19137).

Область устойчивости ${{g}_{{13}}}$ в другом масштабе изображена на рис. 6а. В этой области найдена дополнительная резонансная кривая $4{{\lambda }_{2}} = 3$. На кривой резонанса $3{{\lambda }_{1}} + {{\lambda }_{2}}$ = 1 в области ${{g}_{{13}}}$ обнаружен участок неустойчивости, заключенный между точкой (49/50, –1) нижней границы области ${{\Gamma }_{{21}}}$ и точкой (0.99119, –0.99625), отмеченной жирной точкой ${{L}_{3}}$ на рис. 6а. Условия формальной устойчивости выполняются во всей области ${{g}_{{13}}}$, и кривые вырождения отсутствуют.

7.4. Области поперечных вращений волчка (рис. 5б). Картина устойчивости поперечных вращений в области ${{g}_{{14}}}$ показана на рис. 5б. Подробная картина для области ${{g}_{{15}}}$ представлена в другом масштабе и в осях $1.525\alpha - 1.05h$ и $h$ на рис. 6б, а узкая область ${{g}_{{16}}}$ отдельно не изображена.

На всех кривых резонансов четвертого порядка (по семь кривых в областях ${{g}_{{14}}}$ и ${{g}_{{15}}}$ и одна кривая в области ${{g}_{{16}}}$) критерии устойчивости (5.6) выполнены; условия формальной устойчивости выполняются во всех точках областей ${{g}_{{14}}}$, ${{g}_{{15}}}$ и ${{g}_{{16}}}$. В областях ${{g}_{{14}}}$ и ${{g}_{{15}}}$ обнаружены по одной кривой вырождения.

Заключение. В работе исследовано влияние вибраций точки подвеса вдоль горизонтальной прямой на вид и орбитальную устойчивость маятниковых движений волчка Ковалевской. Показано, что под действием вибраций точки подвеса тела, его маятниковые движения могут оставаться такими же, как и у тела с неподвижной точкой (поперечные движения), однако, с помощью вибраций можно получить и другие маятниковые движения тела (продольные движения).

При отсутствии вибраций точки подвеса маятниковые движения тела орбитально неустойчивы по отношению к пространственным возмущениям, но с помощью вибраций вдоль горизонтали можно добиться стабилизации некоторых маятниковых движений. В таких областях орбитальной устойчивости в линейном приближении проведен строгий нелинейный анализ устойчивости. Построены области выполнения условий формальной устойчивости и устойчивости для большинства (в смысле меры Лебега) начальных условий, а также проверены критерии устойчивости на кривых резонансов четвертого порядка.

Исследование выполнено в Московском авиационном институте (национальном исследовательском университете) за счет гранта Российского научного фонда (проект № 19-11-00116).