Прикладная математика и механика, 2022, T. 86, № 2, стр. 223-234

1. Введение. Расчеты конструкций из слоистых композитов обычно проводятся по критериям прочности их одномерно армированных волокнистых монослоев. К настоящему времени предложено довольно много таких критериев. Однако задача построения новых и совершенствования существующих критериев остается по-прежнему актуальной. Коэффициент запаса прочности, учитывающий неточность применяемых критериев, для многих несущих конструкций все еще назначается очень большим. Поэтому могут продолжаться попытки построения новых, а также модификации и специализации существующих критериев. Настоящая работа также посвящена исследованию и построению вариантов одного критерия прочности монослоя по условию разрушения связующего при наличии сжатия нормально волокнам [1]. Нагружения с таким сжатием, например, могут испытывать в полете монослои композитных панелей обшивки планера самолета [2]. Компонентами этого вида нагружения наряду с поперечным сжатием могут являться сдвиг в плоскости волокон и растяжение или сжатие вдоль волокон. Соотношения данных компонент в различных участках панели различно. Однородное напряженное состояние с фиксированным соотношением компонент с высокой точностью реализуется, например, в экспериментах по осевому сжатию с кручением и внутренним или внешним давлением композитных трубчатых образцов, намотанными послойно по окружности [3, 4]. В принципе такие состояния можно получать и в плоских крестообразных образцах, вырезанных из однонаправленного листа.

Обзор работ по теориям прочности композитов приведены, например, в [5, 6]. Здесь кратко отметим только два подхода к построению наиболее известных критериев. Их общий вид таков:

Функция $f$ определяет некоторое соотношение между компонентами ${{\sigma }_{{ij}}}$ тензора напряжений, ${{k}_{l}}$ – постоянные композита.

Первый подход основывается на общих тензорных и инвариантно-полиномиальных формулировках функции $f$. Они широко используются при образовании критериев прочности анизотропных материалов (композитов), например, в [7–11]. Предполагается, что искомый критерий является инвариантным относительно группы ортогональных преобразований, соответствующих классу симметрии структуры материала. Достоинства и недостатки этого подхода отмечались в [12–14]. Нарушение таких условий прочности означает либо разрушение (обрыв, локальное выпучивание) в основном волокон, либо разрушение (скол, расщепление) в основном матрицы, однако без явного указания какой именно из этих видов (мод, механизмов) разрушения в основном произошел [7, 8, 10]. При расчетах конструкций из слоистых композитов идентификация механизма разрушения монослоя необходима. Считается, что первый механизм приводит к полной потери несущей способности слоя, а второй – только лишь к изменению некоторых его характеристик упругости. Хотя эти механизмы и можно условно отделить по доминирующим слагаемым в выражениях данных критериев [15], тем не менее, начиная с работы [9] критерии прочности по механизмам разрушения волокон и связующего, как правило, формулируются отдельно [11]. Разложение критерия по этим механизмам основывалось на рассмотрении проекций напряжений на плоскости перпендикулярные и параллельные волокнам [9]. Кроме того, каждый из полученных таким образом критериев еще подразделялся на два случая наличия растягивающих или сжимающих нормальных напряжений на данных плоскостях [9].

Если не связывать построение критерия с симметрийно-инвариантными ограничениями, то эти два вида критериев можно сразу отдельно формулировать на соответствующих площадках. В этом состоит второй подход, которого мы здесь придерживаемся. Тогда в соотношении (1.1) функция $f \equiv f\left( {{{\tau }_{n}},{{\sigma }_{n}},{{k}_{l}}} \right)$, где соответственно ${{\tau }_{n}}$ и ${{\sigma }_{n}}$ касательное и нормальное напряжения на площадке с нормалью $n$. При плоском напряженном состоянии композита критериальная функция $f$ по механизму разрушения связующего применялась в форме квадратичной зависимости между ${{\tau }_{n}}$ и ${{\sigma }_{n}}$ [16, 17]. Ориентация этой площадки полагалась одной и той же для всех напряженных состояний. Ее положение было зафиксировано перпендикулярно плоскости волокон в их направлении, так что ${{\tau }_{n}} \equiv {{\tau }_{{nl}}}$ – касательное напряжение вдоль волокон. В некоторых случаях вполне удовлетворительные результаты получались при линейной функции $f$ на той же площадке [18]. Однако, с изменением напряжений ориентация данной площадки $n$ может изменяться. Для каждого напряженного состояния ее положение соответствует максимуму функции $f\left( {{{\tau }_{{nl}}},{{\tau }_{{nt}}},{{\sigma }_{n}},{{k}_{l}}} \right)$, где ${{\tau }_{{nt}}}$ – касательное напряжение поперек волокон [9]. Эта площадка составляет с плоскостью волокон некоторый двугранный угол ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - \alpha $, ребро которого параллельно направлению волокон [1, 9, 19]. На данной площадке критерии прочности по механизму разрушения связующего при наличии сжатия перпендикулярно направлению волокон предлагались в виде [1]:

а также в форме [19]

Очевидно, что (1.3) следует из (1.2), если допустить, что $\eta _{t}^{2}\sigma _{n}^{2} = 0$ и $\eta _{l}^{2}\sigma _{n}^{2} = 0$ [1]. В (1.2)–(1.4) приняты следующие обозначения: ${{S}_{t}}$ и ${{S}_{l}}$ – сопротивление сдвигу матрицы при действии соответственно напряжения ${{\tau }_{{nt}}}$ или ${{\tau }_{{nl}}}$, ${{\eta }_{t}}$ и ${{\eta }_{l}}$ – угловые коэффициенты касательных к предельным кривым ${{\sigma }_{n}} - {{\tau }_{{nt}}}$ и ${{\sigma }_{n}} - {{\tau }_{{nl}}}$ в точке ${{\sigma }_{n}} = 0$, соответственно; угловая скобка в (1.4) означает, что для любого $x$, $\left\langle x \right\rangle = {{\left( {x + \left| x \right|} \right)} \mathord{\left/ {\vphantom {{\left( {x + \left| x \right|} \right)} 2}} \right. \kern-0em} 2}$.

Согласно аналогии, между сопротивлением сдвигу и предельной силой трения (покоя) выражения (1.2)–(1.4) учитывают на площадке $n$ влияние нормального напряжения сжатия на сопротивление сдвигу, соответствующее ортотропному закону трения [20, 21]. Критические замечания по критериям (1.2), (1.3) приводились в [11].

Ключевым элементом в применении (1.2)–(1.4) для данного напряженного состояния ${{\tau }_{{nt}}}$, ${{\tau }_{{nl}}}$, ${{\sigma }_{n}}$ на площадке $n$ является решение задачи об определении угла $\alpha = {{\alpha }_{*}}$, доставляющего максимум функции $f \equiv f\left( {{{\tau }_{{nl}}},{{\tau }_{{nt}}},{{\sigma }_{n}},{{k}_{l}}} \right)$ [9]. К настоящему времени точное решение найдено только для (1.3) [1]. Для исходного общего критерия (1.2) точное решение еще не получено. Это сдерживает возможно более широкое его приложение.

В природных волокнистых композитах наблюдаются асимметричные законы внутреннего трения, при котором сопротивление сдвигу зависит от сочетания знаков касательных напряжений вдоль и поперек волокон [21]. Применительно к таким материалам необходимо иметь, например, обобщение (1.2) на случай влияния нормального напряжения сжатия на сопротивление сдвигу, соответствующее асимметричному закону трения. Такое обобщение также еще не построено.

Квадратичные условия прочности композитов наиболее широко употребительные. Тем не менее их линейная аппроксимация в некоторых случаях может давать вполне удовлетворительные результаты [18]. Кроме того, линейное условие может быть использовано при кусочно-линейном приближении нелинейных критериев и эффективно при решении обратных задач по определению характеристик монослоев из свойств пакета [22]. Линейный аналог данных условий прочности к настоящему времени также не сформулирован.

В качестве параметров в критерии (1.2)–(1.4) входят угловые коэффициенты ${{\eta }_{t}}$ и ${{\eta }_{l}}$ касательных к соответствующим предельным кривым. Эти кривые вообще являются искомыми и для новых композитов или технологий заранее неизвестны. Для их определения нужен некоторый массив опытных данных в окрестности чистого продольного сдвига. Поэтому также актуальным является вопрос определения параметров данных критериев по результатам стандартных испытаний.

Целью настоящей работы является, применительно к случаю наличия поперечного сжатия:

• формулировка линейного и квадратичного вариантов общего условия прочности (1.2), учитывающих влияние нормального напряжения на сопротивление сдвигу на площадке $n$, соответствующее ортотропному асимметричному закону трения;

• вывод уравнения для определения ориентации площадки $n$, на которой реализуется максимум линейного критерия;

• вывод формулы для определения угла наклона площадки $n$, соответствующего максимуму квадратичного критерия;

• определение видов установочных испытаний для нахождения параметров данных критериев прочности;

• экспериментальная проверка предложенных критериев при двухкомпонентном нагружении комбинациями поперечного сжатия и продольного сдвига.

2. Линейное и квадратичное условия прочности. Линейный ${{F}_{1}}$ и квадратичный ${{F}_{2}}$ критерии прочности по условию разрушения связующего, которые учитывают влияние нормального напряжения сжатия на предельное сопротивление сдвигу, соответствующее ортотропному асимметричному закону трения на площадке $n$, записываются соответственно в виде:

где величина постоянных ${{m}_{t}}$, ${{m}_{l}}$ в зависимости от знаков касательных напряжений вдоль ${{\tau }_{{nl}}}$ и поперек ${{\tau }_{{nt}}}$ волокон может быть различной [21]:

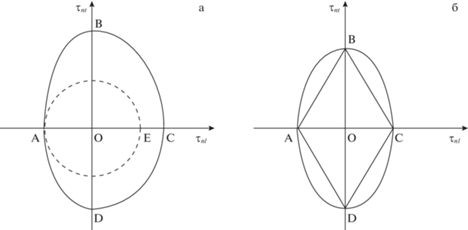
На плоскости (${{\tau }_{{nl}}},{{\tau }_{{nt}}}$) критерий (2.2) является выпуклой замкнутой гладкой кривой, составленной из дуг четырех эллипсов с общим центром и различными полуосями, как показано на схеме рис. 1а (сплошная линия). Полуоси четвертей соответствующих эллипсов в вершинах смежных дуг одинаковы,

Симметричный изотропный случай $m_{t}^{ + } = m_{t}^{ - } = m_{l}^{ + } = m_{l}^{ - } = {{m}_{l}}$, ${{Y}_{l}} = {{Y}_{t}}$ критерия (2.2) на рис. 1а представляется окружностью (пунктирная линия). Симметричные ортотропные случаи $m_{t}^{ + } = m_{t}^{ - }$, $m_{l}^{ + } = m_{l}^{ - }$ критериев (2.2) и (2.1) являются соответственно эллипсом и вписанным в этот эллипс ромбом (рис. 1б). В последнем случае (2.2) совпадает с критерием (1.2) после переопределения констант ${{m}_{t}} = {1 \mathord{\left/ {\vphantom {1 {{{\eta }_{t}}}}} \right. \kern-0em} {{{\eta }_{t}}}}$, ${{m}_{l}} = {1 \mathord{\left/ {\vphantom {1 {{{\eta }_{l}}}}} \right. \kern-0em} {{{\eta }_{l}}}}$, ${{Y}_{t}} = {{{{S}_{t}}} \mathord{\left/ {\vphantom {{{{S}_{t}}} {{{\eta }_{t}}}}} \right. \kern-0em} {{{\eta }_{t}}}}$, ${{Y}_{t}} = {{{{S}_{t}}} \mathord{\left/ {\vphantom {{{{S}_{t}}} {{{\eta }_{t}}}}} \right. \kern-0em} {{{\eta }_{t}}}}$.

При плоском напряженном состоянии в системе координат ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ напряжения на площадке $n$, наклоненной к оси ${{x}_{3}}$ под углом $\alpha $, (оси ${{x}_{1}}$, ${{x}_{2}}$ лежат в плоскости волокон в направлении армирования и перпендикулярно ему, соответственно; ось ${{x}_{3}}$ – перпендикулярна плоскости волокон) записываются в виде

В данной системе координат единичная нормаль к площадке $n = \left( {0,\cos \alpha ,\sin \alpha } \right)$. Относительно плоскости ${{x}_{1}},{{x}_{2}}$ площадка $n$ повернута вокруг оси параллельной ${{x}_{1}}$, поэтому в средней формуле (2.3) содержится только косинус в первой степени.

Согласно (2.3) напряжение ${{\sigma }_{{11}}}$ в направлении волокон не фигурирует в условиях (2.1), (2.2) и напрямую не взаимодействует с напряжениями ${{\tau }_{{nt}}}$, ${{\tau }_{{nl}}}$ и ${{\sigma }_{n}}$ на площадке $n$. Это известный недостаток всех критериев сформулированных на площадках параллельных направлению волокон [1, 16–19]. Заметим, что и в тензорно-инвариантных теориях критерии прочности по механизму разрушения матрицы также не содержат ${{\sigma }_{{11}}}$ [9, 11]. Ошибка, связанная с пренебрежением вклада ${{\sigma }_{{11}}}$ в напряжения в матрице обычно не слишком велика. Это обусловлено главным образом обычно очень большим превышением модуля упругости волокна над модулем упругости связующего. Кроме того, при наличии ${{\sigma }_{{11}}}$ прежде данных критериев возможно нарушение условия прочности по механизму разрушения волокон. Это условие здесь не рассматривается.

Однако, по причине указанного превышения модуля упругости волокна и статистической природы его прочности в связующем происходит накопление микротрещин с ростом продольного напряжения. Такое увеличение трещиноватости связующего обусловлено концентрацией и сингулярностью для напряжений у рассеянных локальных разрушений волокон. Это растрескивание уменьшает эффективную площадь связующего, воспринимающую напряжения. Достаточно высокий уровень трещиноватости оказывает существенный разупрочняющий эффект. Его можно учитывать с помощью введения в критерий параметра разупрочнения ${{q}_{w}}$. За меру такой разупрочненности может быть принята просто относительная величина продольного напряжения ${{q}_{w}} = {{{{\sigma }_{{11}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{11}}}} {{{S}_{{11}}}}}} \right. \kern-0em} {{{S}_{{11}}}}}$ [1], где ${{S}_{{11}}}$ – прочность композита при одноосном нагружении в направлении волокон. Согласно опытным данным существенное влияние этого разупрочнения наблюдается только при высоких продольных напряжениях $\left| {{{\sigma }_{{11}}}} \right| \geqslant 0.7\left| {{{S}_{{11}}}} \right|$ [1]. Далее здесь это разупрочнение не рассматривается.

Что касается определения угла $\alpha {\kern 1pt} *$ наклона площадки возможного разрушения, или кратко – угла разрушения, примем, что при $\alpha {\kern 1pt} *$ реализуется максимум функции ${{F}_{2}}({{\tau }_{{nt}}},{{\tau }_{{nl}}},{{\sigma }_{n}})$ или ${{F}_{1}}({{\tau }_{{nt}}},{{\tau }_{{nl}}},{{\sigma }_{n}})$ для данных ${{\sigma }_{{22}}}$, ${{\sigma }_{{12}}}$. Согласно этому предположению и (2.3) угол $\alpha {\kern 1pt} *$ является решением системы

Система (2.4) определяет также искомую поверхность прочности ${{f}_{i}}({{\sigma }_{{22}}},{{\sigma }_{{12}}}) = 0$, которая является огибающей для $\alpha $-семейства условий ${{F}_{i}}\left( {{{\sigma }_{{22}}},{{\sigma }_{{12}}},\alpha } \right) = 0$.

Известно множество волокнистых растительных материалов с асимметричным внутренним трением [21]. Для конструкционных композитов влияние асимметрии трения в сравнении с их анизотропией незначительно. Далее ограничимся рассмотрением симметричного анизотропного случая, когда ${{m}_{t}}$ и ${{m}_{l}}$ не изменяются при перемене знаков касательного напряжения,

При выполнении равенств (2.5) критерии (2.2) и (2.1) на плоскости (${{\tau }_{{nl}}}$, ${{\tau }_{{nt}}}$) представляют собой соответственно эллипс и вписанный в этот эллипс ромб (рис. 1б).

3. Линейный критерий. Обозначим выражения под знаком модуля в (2.1) через $T\left( {{{\tau }_{{nt}}},{{\sigma }_{n}}} \right)$ и $L\left( {{{\tau }_{{nl}}},{{\sigma }_{n}}} \right)$. При плоском напряженном состоянии

и (2.1) записывается в виде

Используя (3.1) из (3.2) получаем, согласно (2.4), уравнение для определения $\alpha {\text{*}}$:

При ${{\sigma }_{{12}}} = 0$ из (3.2) и (3.3) следует, что

где $\alpha _{ \bot }^{*}$, ${{S}_{{22}}}$ – соответственно угол разрушения и прочность композита при одноосном сжатии перпендикулярно направлению волокон.

Также из (3.2), (3.3) при ${{\sigma }_{{22}}} = 0$ получаем, что

где $\alpha _{0}^{*}$, ${{S}_{{12}}}$ – соответственно угол разрушения и сопротивление сдвигу композита при продольном сдвиге.

Согласно [1], также здесь и везде далее принимаем, что

С учетом (3.6) выражение (3.2) для ${{F}_{1}}$ и уравнение (3.3) для определения угла ${{\alpha }_{*}}$ приобретают простой вид

где

Критерий (3.7) в общем случае является физически нелинейным из-за зависимости от угла $\alpha $. Линейный случай [18] следует из (3.7), (3.8) при $\alpha = 0$ и ${{m}_{t}} = 0$. Согласно (3.7)–(3.9) в число характеристических констант композита, кроме ${{S}_{{22}}}$ и ${{S}_{{12}}}$, в общем случае входит также угол $\alpha _{ \bot }^{*}$.

В случае одинакового сопротивления сдвигу поперек и вдоль волокон ${{m}_{t}} = {{m}_{l}}$ из (3.9) следует, что угол $\alpha _{ \bot }^{*}$ не является независимой характеристической константой материала. Он определяется отношением прочностей ${{S}_{{22}}}$ и ${{S}_{{12}}}$,

Например, для углепластика при ${{S}_{{22}}} = - 200$ МПа и ${{S}_{{12}}} = 83.1$ МПа получаем $\alpha _{ \bot }^{*} \cong 50.3^\circ $.

4. Квадратичный критерий. При плоском напряженном состоянии с учетом (2.5) и (3.6) критерий (2.2) принимает вид

где параметры ${{m}_{t}}$, ${{m}_{l}}$ и $Y$ точно также как и в линейном случае определяются по формулам (3.9).

Используя (4.1) из (2.4) получаем уравнение относительно искомого угла $\alpha {\text{*}}$,

Это уравнение имеет два решения:

С учетом выражения для $Y$и ${{m}_{t}}$ в (3.9) и согласно (4.2) получаем простую формулу для нахождения угла $\alpha {\kern 1pt} *$ наклона площадки возможного разрушения,

При ${{\sigma }_{{22}}} = {{S}_{{22}}}$ формула (4.3) тождественно дает $\alpha {\kern 1pt} *{\kern 1pt} \left( {{{S}_{{22}}}} \right) = \alpha _{ \bot }^{*}$, что и следовало ожидать.

В случае ${{m}_{t}} = {{m}_{l}}$ угол $\alpha _{ \bot }^{*}$ также как и для критерия (2.1) не является независимой характеристической постоянной материала. Он определяется квадратом отношения прочностей ${{S}_{{22}}}$ и ${{S}_{{12}}}$:

При ${{S}_{{22}}} = - 200$ МПа и ${{S}_{{12}}} = 83.1$ МПа согласно (4.4) также получаем $\alpha _{ \bot }^{*} \cong 50.3^\circ $.

5. Установочные испытания. Приведем возможные виды экспериментов, определяющие все материальные параметры данных критериев.

Вначале рассмотрим более простой случай, когда в (2.1) и (2.2) коэффициенты перед касательными напряжениями вдоль и поперек волокон равны, ${{m}_{t}} = {{m}_{l}}$. При таком равенстве на плоскости (${{\tau }_{{nl}}},{{\tau }_{{nt}}}$) условие (2.1) является квадратом вписанным в окружность условия (2.2) (рис. 1).

Из соотношений (3.6), (3.9), (3.10) и (4.4) следует, что в этом случае все параметры предложенных критериев ${{m}_{t}}$, ${{m}_{l}}$, ${{Y}_{t}}$, ${{Y}_{l}}$, $\alpha _{ \bot }^{*}$ могут быть определены по результатам всего двух стандартизованных испытаний образцов на разрушение. А именно, по прочности ${{S}_{{22}}}$ при одноосном сжатии перпендикулярно направлению волокон и прочности ${{S}_{{12}}}$ при продольном сдвиге в плоскости волокон. После определения прочностей ${{S}_{{22}}}$ и ${{S}_{{12}}}$ все параметры данных критериев вычисляются по формулам (3.9), а также (3.10) или (4.4).

В общем случае, когда ${{m}_{t}} \ne {{m}_{l}}$, кроме прочностей ${{S}_{{22}}}$ и ${{S}_{{12}}}$ надо еще определить угол $\alpha _{ \bot }^{*}$ скалывания композита по матрице при одноосном сжатии перпендикулярно направлению волокон. Судя по литературе к настоящему времени отсутствует общепринятый стандарт на испытания по определению этого угла. По результатам экспериментов на разрушение призматических и трубчатых образцов стекло- и углепластиков получали узкий диапазон изменения значений этого угла, $\alpha _{ \bot }^{*} = 53^\circ \pm 3^\circ $ [23–25]. К настоящему времени в расчетах общепринято использование значения $\alpha _{ \bot }^{*}$ из данного диапазона [26]. Тогда по приведенным формулам (3.9) определяются все параметры данных критериев.

6. Экспериментальная проверка предложенных критериев. Пример расчета кривых прочности при поперечном сжатии в комбинации со сдвигом. Обычно в качестве экспериментальной проверки критериев прочности приводятся примеры их применения при одноосном нагружении под различными углами к волокнам. Такая проверка условий (1.3) и [18] для стеклопластика, углепластика и боропластика приведена в [15]. При этом расчетные кривые прочности для данных критериев и критериев, [8, 9, 16–18], различаются несущественно [15].

Для критериев (2.1), (2.2) показательным является двухкомпонентное нагружение комбинациями сжатия перпендикулярно направлению волокон и продольного сдвига в плоскости волокон.

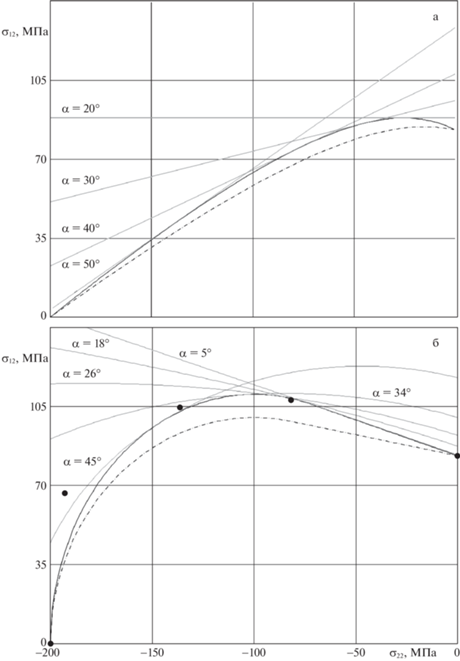
В качестве примера приложения критериев (2.1) и (2.2) на рис. 2 приведены кривые прочности (более толстые линии) углепластика при нагружении его нормальными и сдвиговыми напряжениями рассчитанные согласно (3.7)–(3.9), (рис. 2а) и (4.1), (4.3) (рис. 2б) при ${{S}_{{22}}} = - 200$ МПа, ${{S}_{{12}}} = 83.1$ МПа, $\alpha _{ \bot }^{*} = 55^\circ $, соответствующих испытаниям на поперечное сжатие в комбинации со сдвигом [24].

Для $\alpha $-семейств (более тонкие сплошные линии) прямых ${{F}_{1}}\left( {{{\sigma }_{{22}}},{{\sigma }_{{12}}},\alpha } \right) = 0$, $\alpha = {\text{const}}$ (рис. 2а) и $\alpha $-семейств эллипсов ${{F}_{2}}\left( {{{\sigma }_{{22}}},{{\sigma }_{{12}}},\alpha } \right) = 0$, $\alpha = {\text{const}}$ (рис. 2б), соответствующие этим критериям кривые прочности являются внутренними огибающими. На этих рисунках видно, что кривая прочности соответствует критическим напряжениям имеющих радиус-вектор наименьшей длины. Штрихпунктирными линиями изображены кривые прочности для случая ${{m}_{t}} = {{m}_{l}}$ когда угол $\alpha _{ \bot }^{*} \cong 50.3^\circ $ для линейного критерия по формуле (3.10) и для квадратичного критерия согласно формуле (4.4).

Влияние нелинейности обусловленной зависимостью от угла $\alpha $ критерия (2.1) видно на рис. 2а. Характерным является образование максимума сопротивления разрушению при переходе от случая нагружения чисто сдвиговыми напряжениями к случаям нагружения комбинацией сдвиговых и нормальных напряжений. На этом максимуме площадка разрушения составляет с нормалью к плоскости волокон угол равный 20°, локальный максимум ${{\sigma }_{{12}}}$ реализуется при отношении ${{\sigma }_{{22}}}$ к ${{\sigma }_{{12}}}$ равному (–3.3) и превышает ${{S}_{{12}}}$ на 6%. В случае ${{m}_{t}} = {{m}_{l}}$ такой максимум отсутствует.

Квадратичный критерий (2.2) при ${{m}_{t}} \ne {{m}_{l}}$ (рис. 2б, сплошная линия) дает максимум ${{\sigma }_{{12}}}$ превышающий ${{S}_{{12}}}$ на 33% при $\alpha * \cong 31.7^\circ $ с отношением ${{{{\sigma }_{{22}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{22}}}} {{{\sigma }_{{12}}}}}} \right. \kern-0em} {{{\sigma }_{{12}}}}} \cong - 0.9$. При ${{m}_{t}} = {{m}_{l}}$ (рис. 2б, штрихпунктирная линия) также имеет место аналогичный максимум ${{\sigma }_{{12}}}$ при $\alpha * \cong 25.3^\circ $, ${{{{\sigma }_{{22}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{22}}}} {{{\sigma }_{{12}}}}}} \right. \kern-0em} {{{\sigma }_{{12}}}}} \cong - 1$, который больше ${{S}_{{12}}}$ на 20%.

Круглые темные точки на рис. 2б соответствуют данным испытаний [24].

На рис. 2б видно, что квадратичный критерий прочности (4.1) при ${{m}_{t}} \ne {{m}_{l}}$ вполне удовлетворительно согласуется с данными эксперимента.

Заключение. Сформулированы линейный и квадратичный варианты условия прочности, учитывающие влияние нормального напряжения на сопротивление сдвигу на площадке $n$, соответствующее ортотропному асимметричному закону трения. Приведены уравнения для определения ориентации площадки $n$, на которой реализуется максимум линейного критерия. Получено точное решение в виде конечной формулы для расчета угла наклона площадки возможного разрушения по квадратичному критерию. Показано, что кривые прочности являются огибающей для семейства линий уровня данных критериев. Определены виды установочных испытаний для нахождения параметров предложенных критериев прочности. Приведены результаты экспериментальной проверки критериев на данных испытаний на разрушение углепластика при двухкомпонентном нагружении комбинациями поперечного сжатия и продольного сдвига. Установлено хорошее соответствие опыту варианта квадратичного критерия прочности, учитывающего влияние нормального напряжения на сопротивление сдвигу, соответствующее ортотропному закону трения.