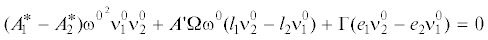Прикладная математика и механика, 2022, T. 86, № 6, стр. 814-838

1. Введение. Гиростатом называют механическую систему, состоящую из твердого тела, которое содержит массы, циклически движущиеся таким образом, что не изменяется распределение масс во всей системе [1]. Часто под гиростатом понимают систему твердых тел, состоящую из тела-носителя, в котором вокруг фиксированных в нем осей вращаются роторы, являющиеся динамически и статически уравновешенными относительно этих осей [2, 3]. История формирования понятия “гиростат” отражена в [4].

Задача о движении в поле силы тяжести гиростата с постоянным гиростатическим моментом, имеющего неподвижную точку, является непосредственным обобщением классической задачи о движении твердого тела с неподвижной точкой. В книге [4] для гиростата приведены аналоги общих случаев интегрируемости этой классической задачи и ее точных частных решений. Здесь также представлены неклассические постановки задачи о движении гиростата с неподвижной точкой, в которых рассматривается его движение не только в поле силы тяжести, но и в поле потенциальных и гироскопических сил, в ньютоновском, кулоновском и магнитном полях.

Еще одна неклассическая постановка задачи о гиростате относится к случаю переменного гиростатического момента, явно зависящего от времени [3]. Расширение постановки задачи о гиростате позволяет получить для этой задачи большое число точных частных решений [4–8]. Такие решения находят путем задания класса инвариантных соотношений для системы уравнений движения или заданием структуры решения этих уравнений. При этом в случае гиростатического момента, явно зависящего от времени, эта зависимость определяется аналитической структурой получаемых решений, а не физическими свойствами момента сил, действующего со стороны статора на ротор относительно его оси.

Для получения точных частных решений используются различные редуцированные формы уравнений движения гиростата. В [9] отмечены случаи, когда редукция с использованием первых интегралов некорректна вследствие функциональной зависимости этих интегралов.

Кроме движений, определяемых формальным заданием класса решений уравнений движения, для гиростата с постоянным или явно зависящим от времени гиростатическим моментом выделяются и анализируются движения, обладающие определенными свойствами – это стационарные движения [2, 10–13], прецессионные, маятниковые, прецессионно-изоконические, асимптотические [14–18], а также хаотические движения [19–22]. Большое развитие получили топологические методы исследования движения гиростата [23–26].

В [27] получены условия устойчивости равномерных вращений тяжелого гиростата с неподвижной точкой. Для симметричного гиростата, закрепленного на оси симметрии, в [28] найдены условия устойчивости его регулярной прецессии в центральном ньютоновском поле. В [29] рассмотрена устойчивость стационарных движений гиростата в идеальной жидкости, а в [30] изучен вопрос о стабилизации программных движений гиростата с полостью, заполненной вязкой жидкостью.

Современные исследования динамики гиростата, не имеющего неподвижной точки, посвящены, в основном, изучению вращательного движения спутника-гиростата, движущегося по орбите. В [31–34] проведен анализ достаточных и необходимых условий устойчивости относительных равновесий орбитального гиростата. Для спутника-гиростата, движущегося в центральном ньютоновском силовом поле по круговой орбите, в [35] предложен метод определения всех его равновесных ориентаций и проведен анализ достаточных условий их устойчивости. Периодические движения такого гиростата рассмотрены в [36–38]. В [39–41] изучаются динамика и устойчивость стационарных движений космических систем, в том числе и гиростатов, с тросовыми и шарнирными соединениями. Для однороторного спутника-гиростата, содержащего сферическую полость с жидкостью большой вязкости, в [42] получено приближенное решение уравнений его движения относительно центра масс. В [43, 44] рассмотрены вопросы устойчивости и стабилизации относительных равновесий спутника-гиростата с упругим стержнем. В [45] предложен алгоритм структурно-параметрической идентификации модели демпфированных колебаний упругого элемента спутника-гиростата.

При изучении большинства как прикладных, так и теоретических задач, гиростатический момент, часто даже не оговаривая это, предполагают постоянным, то есть полагают, что роторы либо вращаются по инерции без трения, либо они вращаются с постоянными относительными угловыми скоростями. Случай переменного гиростатического момента, не являющегося явно заданной функцией времени, имеет место при исследовании задач ориентации гиростата с помощью управляющих моментов, приложенных к роторам со стороны тела-носителя и зависящих от компонент вектора угловой скорости [46–48].

На практике быстро вращающийся ротор испытывает значительное тормозящее воздействие сил трения, и поэтому предположение о вращении роторов по инерции без трения нереализуемо для длительно работающих аппаратов с быстро вращающимися роторами, выполненных по схеме гиростата. Что касается предположения о вращении роторов с постоянными относительными угловыми скоростями, то устройством, которое с той или иной точностью обеспечивает реализацию этого предположения, является электромотор. Поэтому для обоснования правомерности применения модели гиростата с равномерно вращающимися роторами следует изучить модель гиростата, в которой роторы гиростата являются роторами электромоторов, а статоры электромоторов являются частью тела-носителя гиростата. Два основных типа электромоторов – асинхронный и синхронный.

После выхода статьи [49] явные модели электромоторов используются при изучении динамики гироскопа в кардановом подвесе. До недавнего времени в публикациях на эту тему рассматривались упрощенные модели электромоторов, которые явно не содержат электрических токов [49–56]. Поэтому их уместно назвать бестоковыми. В таких моделях суммарный момент M, создаваемый электромотором и силами трения относительно оси ротора (гироскопа), зависит от угловой скорости вращения ротора относительно статора в случае асинхронного электромотора, а в случае синхронного электромотора он зависит также от угла поворота ротора относительно вращающегося магнитного поля статора. В простейшем случае $M = - {{k}_{1}}\gamma - {{k}_{2}}\dot {\gamma }$ $\left( {{{k}_{1}},{{k}_{2}} > 0} \right)$, где $\gamma = \varphi {\kern 1pt} '\; - \Omega ~t$, $\varphi {\kern 1pt} '$ – угол поворота ротора электромотора $S'$ относительно его статора, ${{\Omega }} > 0$ – постоянная угловая скорость вращения магнитного поля в статоре. Для асинхронного электромотора в простейшем случае применяется линейная формула $M = - {{k}_{0}}\dot {\gamma }$ $\left( {{{k}_{0}} > 0} \right)$, где $\dot {\gamma } = \dot {\varphi }{\kern 1pt} '\; - \Omega {\kern 1pt} '$, $\Omega {\kern 1pt} '$ – угловая скорость вращения ротора, при которой вращающий момент электромотора уравновешивает момент трения ($0 < \Omega {\kern 1pt} ' < \Omega $). В [49–56] для гироскопа в кардановом подвесе используются бестоковые модели электромоторов, основанные на нелинейных аналогах этих формул.

В [57] рассмотрена двухтоковая модель синхронного электромотора, частным случаем которой является двухтоковая модель асинхронного электромотора. В [58] предложена достаточно общая многотоковая модель синхронного электромотора в виде системы обыкновенных дифференциальных уравнений, включающей уравнения для электрических токов. На основе этой модели в [59] получено условие глобальной устойчивости такого электромотора, а в [60, 61] установлен необходимый и достаточный критерий устойчивости стационарных движений гироскопа в кардановом подвесе, снабженного синхронным электромотором. Этот результат обобщает на случай многотоковой модели синхронного электромотора результат работ [54, 55].

Представляет интерес явно учесть наличие электромотора и при изучении динамики гиростата. Этому посвящена данная работа. В ней рассматривается тяжелый однороторный гиростат с неподвижной точкой, снабженный электромотором. Ротор электромотора является ротором гиростата, а статор электромотора является частью тела-носителя. Трение в сферическом шарнире, реализующем неподвижную точку, предполагается отсутствующим, а относительно оси ротора на него со стороны тела-носителя действуют момент сил трения и момент, создаваемый электромотором. Рассматриваются три модели электромотора: бестоковые модели асинхронного и синхронного электромотора и многотоковая модель синхронного электромотора.

Получены две формы дифференциальных уравнений движения гиростата, соответствующие двум определениям его тензора инерции для неподвижной точки. Дано сравнение условий существования стационарных вращений гиростата с электромотором с такими условиями для двух известных моделей гиростата без электромотора – с равномерно вращающимся ротором и с ротором, вращающимся по инерции без трения [2, 10].

2. Основные соотношения для механической части гиростата. При выводе уравнений движения гиростата с электромотором за основу взят подход, принятый в [2, 3].

2.1. Механическая часть гиростата. Рассматривается система двух твердых тел ${{S}^{0}}$ и $S{\kern 1pt} '$. Тело ${{S}^{0}}$ с произвольным распределением масс имеет неподвижную точку $O$. Предполагается, что связь, реализующая неподвижную точку, является идеальной. В теле ${{S}^{0}}$ вокруг фиксированной в нем оси $l$ вращается твердое тело $S{\kern 1pt} '$ (ротор), которое является статически и динамически уравновешенным относительно этой оси.

Система тел ${{S}^{0}}$ и $S{\kern 1pt} '$ находится в поле силы тяжести. Со стороны тела-носителя ${{S}^{0}}$ к ротору $S{\kern 1pt} '$ приложены равнодействующие сил реакции в подшипниках, на которых установлена ось $l$. Кроме того, относительно оси $l$ действует момент сил трения ${{M}_{2}}$, зависящий от угловой скорости $\dot {\varphi }{\kern 1pt} '$ вращения ротора $S{\text{'}}$ относительно тела-носителя ${{S}^{0}}$. Для поддержания вращения ротора при наличии трения используется электромотор, так что тело $S{\kern 1pt} '$ является ротором электромотора, а статор электромотора составляет часть тела-носителя ${{S}^{0}}$. Момент, создаваемый электромотором относительно оси $l$, обозначается через ${{M}_{1}}$. Далее, через ${{m}^{0}}$ и $m{\kern 1pt} '$ обозначаются массы тел ${{S}^{0}}$ и $S{\kern 1pt} '$, а через ${{C}^{0}}$ и $C{\kern 1pt} '$ – их центры масс. Точка $C{\kern 1pt} '$ лежит на оси $l$.

С телом ${{S}^{0}}$ неизменно связана правая декартова система координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$ с началом в неподвижной точке, а с ротором $S{\kern 1pt} '$ неизменно связана система координат $C{\kern 1pt} '{\kern 1pt} \xi _{1}^{'}\xi _{2}^{'}\xi _{3}^{'}$ с началом в его центре масс и осью $C{\kern 1pt} '{\kern 1pt} \xi _{1}^{'}$, направленной вдоль оси $l$ вращения ротора. Единичные векторы осей координат $O{{\xi }_{1}}$, $C{\kern 1pt} '{\kern 1pt} \xi _{1}^{'}$ и т. д. обозначаются через ${{{\mathbf{\xi }}}_{1}}$, ${\mathbf{\xi }}_{1}^{'}$ и т.д. Вектор ${\mathbf{h}} = {\mathbf{OC}}{\kern 1pt} '$ проведен из неподвижной точки $O$ в центр масс $C{\kern 1pt} '$ ротора $S{\kern 1pt} '$, а вектор ${{{\mathbf{c}}}^{0}} = {\mathbf{O}}{{{\mathbf{C}}}^{0}}$ указывает положение центра масс ${{C}^{0}}$ тела-носителя ${{S}^{0}}$.

Пусть ${\mathbf{\omega }}$ – абсолютная угловая скорость тела ${{S}^{0}}$, v – единичный вектор направления силы тяжести, $\varphi {\kern 1pt} '$ – угол поворота ротора $S{\kern 1pt} '$ вокруг оси $l$ относительно тела ${{S}^{0}}$. Единичный вектор оси $l$ обозначается через ${\mathbf{l}}$, так что ${\mathbf{l}} = {\mathbf{\xi }}_{1}^{'}$. Векторы ω, v, ${\mathbf{l}}$, ${\mathbf{h}}$, ${{{\mathbf{c}}}^{0}}$ задаются своими компонентами в системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$:

Величины ${{\omega }_{i}}$, ${{\nu }_{i}}$ $\left( {i = 1,2,3} \right)$, $\varphi {\kern 1pt} '$ являются функциями времени $t$ и входят в число фазовых переменных системы дифференциальных уравнений движения рассматриваемой электромеханической системы, а величины ${{l}_{i}}$, ${{h}_{i}}$, $c_{i}^{0}$ $\left( {i = 1,2,3} \right)$ являются постоянными параметрами этой системы.

2.2. Момент количества движения и тензор инерции гиростата в неподвижной точке. Следуя [2, 3], получаем для вектора ${\mathbf{x}}$ момента количества движения гиростата относительно неподвижной точки выражение

Здесь ${{{\mathbf{A}}}^{0}}$ – тензор инерции тела ${{S}^{0}}$ в точке O, A′ – момент инерции ротора S ′ относительно оси $l$, B′ – момент инерции ротора относительно любой оси, проведенной из его центра масс C ′ ортогонально $l$.

Выражение (2.2) записывают в виде

где A* – тензор инерции гиростата, определенный формулой

Выражение (2.2) записывают также в виде

Здесь тензор ${\mathbf{A}}$ определен формулой

а величина p′ является проекцией вектора ${\mathbf{\omega }}{\kern 1pt} ' = {\mathbf{\omega }} + \dot {\varphi }{\kern 1pt} '{\kern 1pt} {\mathbf{l}}$ абсолютной угловой скорости ротора S ′ на направление оси $l$:

Согласно (2.4), компоненты тензора ${\mathbf{A}}{\kern 1pt} *$ в системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$ выражаются по формулам

Здесь символ $\left( {1\;2\;3} \right)$ означает, что формулы для $A_{{22}}^{{\text{*}}}$, $A_{{33}}^{{\text{*}}}$, $A_{{23}}^{{\text{*}}}$, $A_{{31}}^{{\text{*}}}$ получаются из формул (2.8) путем круговой перестановки индексов 1, 2, 3. Остальные три компоненты $A_{{21}}^{{\text{*}}}$, $A_{{32}}^{{\text{*}}}$, $A_{{13}}^{{\text{*}}}$ тензора ${\mathbf{A}}{\kern 1pt} *$ равны его соответствующим компонентам с переставленными индексами.

Формула (2.6), определяющая тензор ${\mathbf{A}}$, отличается от формулы (2.4), определяющей тензор ${\mathbf{A}}{\kern 1pt} *$, отсутствием члена с $A{\kern 1pt} '$. Поэтому компоненты ${{A}_{{ij}}}$ $\left( {i,j = 1,2,3} \right)$ тензора ${\mathbf{A}}$ в системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$ выражаются по формулам, которые получаются из формул (2.8) путем отбрасывания членов, содержащих A′.

2.3. Уравнение вращения ротора. Для вывода дифференциального уравнения, описывающего вращение ротора S ′ вокруг оси $l$, воспользуемся векторным уравнением $d\left( {{\mathbf{A}}{\kern 1pt} '\; \cdot {\mathbf{\omega }}{\kern 1pt} '} \right){\text{/}}dt$ = M, которое выражает теорему об изменении момента количества движения ротора относительно его центра масс C ′. Здесь A′ – тензор инерции ротора в точке C ′, ${\mathbf{M}}$ – момент, создаваемый относительно точки C ′ силами, действующими на ротор со стороны тела-носителя ${{S}^{0}}$.

Момент ${\mathbf{M}}$ равен сумме момента ${{{\mathbf{M}}}_{1}} = {{M}_{1}}{\mathbf{l}}$, создаваемого электромотором относительно оси ротора $l$, момента ${{{\mathbf{M}}}_{2}} = {{M}_{2}}{\mathbf{l}}$, создаваемого относительно этой оси силами трения, а также момента ${{{\mathbf{M}}}_{3}}$, создаваемого относительно точки C ′ равнодействующими сил реакций в цилиндрических шарнирах, с помощью которых ось $l$ закреплена в теле ${{S}^{0}}$. В проекции на направление единичного вектора ${\mathbf{l}}$ получаем уравнение вращения ротора

где $M = {{M}_{1}} + {{M}_{2}}$. С учетом (2.7) оно записывается следующим образом

3. Модели электромотора. Дадим краткие описания используемых в данной работе бестоковых моделей асинхронного и синхронного электромоторов [52, 62], а также многотоковой модели синхронного электромотора [58], и приведем соответствующие им выражения для момента $M$ на оси ротора гиростата.

Для всех этих моделей электромотора момент, создаваемый силами трения вокруг оси ротора, предполагается монотонно убывающей и непрерывно дифференцируемой нечетной функцией ${{M}_{2}}\left( {\dot {\varphi }{\kern 1pt} '} \right)$ относительной угловой скорости ротора $\dot {\varphi }{\kern 1pt} '$. Предполагается также, что в статоре электромотора имеются обмотки провода, на которые подается переменный электрический ток. В результате этого создается магнитное поле, результирующий вектор напряженности которого B постоянен по модулю, ортогонален оси ротора и вращается вокруг нее с постоянной угловой скоростью ${{\Omega }} > 0$.

3.1. Бестоковая модель асинхронного электромотора. В случае асинхронного электромотора вращающееся магнитное поле статора индуцирует магнитное поле в роторе, и в результате взаимодействия этих двух полей возникает момент ${{M}_{1}}\left( {\dot {\varphi }{\kern 1pt} '} \right)$, увлекающий ротор во вращение. Знак этого момента противоположен знаку разности $\dot {\varphi }{\kern 1pt} '\; - {{\Omega }}$.

При ${{M}_{1}}\left( 0 \right) > - {{M}_{2}}\left( 0 \right)$ существует значение $\Omega {\kern 1pt} ' \in \left( {0,\Omega } \right)$ угловой скорости ротора $\dot {\varphi }{\kern 1pt} '$, при котором момент трения уравновешивает вращающий момент асинхронного электромотора, то есть суммарный момент $M\left( {\dot {\varphi }{\kern 1pt} '} \right)$ = ${{M}_{1}}\left( {\dot {\varphi }{\kern 1pt} '} \right)$ + ${{M}_{2}}\left( {\dot {\varphi }{\kern 1pt} '} \right)$ для такого электромотора равен нулю при $\dot {\varphi }{\kern 1pt} ' = {{\Omega }}{\kern 1pt} '{\kern 1pt} < \Omega $. Вместо угловой скорости $\dot {\varphi }{\kern 1pt} '$ удобно ввести переменную $\dot {\gamma } = \dot {\varphi }{\kern 1pt} '\; - \Omega {\kern 1pt} '$. Тогда суммарный момент $M$ для бестоковой модели асинхронного электромотора становится функцией $M\left( {\dot {\gamma }} \right)$ такой, что $\dot {\gamma }M\left( {\dot {\gamma }} \right) < 0$ $\left( {\dot {\gamma } \ne 0} \right)$, $M\left( 0 \right) = 0$.

3.2. Бестоковая модель синхронного электромотора. В рамках упрощенного подхода предполагается, что ротор S′ синхронного электромотора имеет неизменно связанное с ним магнитное поле, вектор напряженности которого B′ постоянен по модулю и ортогонален оси ротора. В результате взаимодействия магнитных полей статора и ротора возникает сила, которая стремится совместить концы векторов ${\mathbf{B}}$ и $ - {\mathbf{B}}{\kern 1pt} '$. Момент ${{M}_{1}}$, создаваемый этой силой относительно оси ротора, является синусоидальной функцией ${{M}_{1}}\left( \gamma \right) = - {{b}_{0}}\sin \gamma $ $\left( {{{b}_{0}} > 0} \right)$ угла $\gamma = \varphi {\kern 1pt} '\; - \Omega t$ между векторами ${\mathbf{B}}$ и $ - {\mathbf{B}}{\kern 1pt} '$. В результате для суммарного момента $M = {{M}_{1}} + {{M}_{2}}$ получаем формулу $M = {{M}_{2}}\left( {\dot {\varphi }{\kern 1pt} '} \right) - {{b}_{0}}{\text{\;sin\;}}\gamma $.

Поскольку функция ${{M}_{2}}\left( {\dot {\varphi }{\kern 1pt} '} \right)$ – нечетная и монотонно убывающая, при $\dot {\varphi }{\kern 1pt} ' = {{\Omega }} > 0$ она отрицательна, и поэтому, вводя обозначение ${{c}_{0}} = - {{M}_{2}}\left( {{\Omega }} \right)$, имеем ${{c}_{0}} > 0$. Пользуясь этим обозначением, запишем полученную формулу в виде

где $\Delta {{M}_{2}}\left( {\dot {\gamma }} \right) = {{M}_{2}}\left( {\dot {\gamma } + \Omega } \right) + {{с}_{0}}$. Момент ${{\Delta }}{{M}_{2}}\left( {\dot {\gamma }} \right)$ – диссипативный, так как

3.3. Многотоковая модель синхронного электромотора. Рассмотрим многотоковую модель синхронного электромотора, предложенную в [58] и откорректированную в [59]. Так же, как и в п. 3.2, предполагаем, что в статоре электромотора создано магнитное поле, результирующий вектор напряженности которого постоянен по модулю, ортогонален оси ротора и вращается вокруг этой оси с постоянной угловой скоростью ${{\Omega }} > 0$.

В роторе синхронного электромотора имеются две обмотки – демпферная обмотка и обмотка возбуждения. Демпферная обмотка обычно выполнена в виде “беличьего колеса”, то есть в виде двух металлических колец, соединенных металлическими стержнями, ортогональными плоскости каждого из этих колец. Обмотка возбуждения содержит большое число витков электрического провода, и на ее концы через угольные щетки подается постоянное напряжение.

Многотоковая модель синхронного электромотора [58] определяется системой дифференциальных уравнений [59]

с фазовым вектором $\left( {\gamma ,\dot {\gamma },x,{{i}_{1}}, \ldots ,{{i}_{{{{n}_{2}}}}}} \right)$, где $x,{{i}_{1}}, \ldots ,{{i}_{{{{n}_{2}}}}}$ – электрические токи, ${{n}_{2}}$ – число стержней в демпферной обмотке. Здесь A′ – осевой момент инерции ротора, ${{R}_{1}}$ и ${{L}_{1}}$ – активное и индуктивное сопротивления обмотки возбуждения, а ${{R}_{2}}$ и ${{L}_{2}}$ – активное и индуктивное сопротивления стержней демпферной обмотки. В уравнения (3.3) также входят диссипативный момент ${{\Delta }}{{M}_{2}}\left( {\dot {\gamma }} \right),$ постоянная ${{c}_{0}} > 0$ и постоянные параметры $\mu ,{{a}_{1}},{{a}_{2}}$, ${{b}_{0}} > 0$.

Для многотоковой модели синхронного электромотора правая часть первого из уравнений (3.3) представляет собой суммарный момент $M$, создаваемый относительно оси ротора силами, действующими на ротор со стороны статора:

4. Первая форма уравнений движения гиростата с электромотором. В этом разделе получена система дифференциальных уравнений движения гиростата с электромотором. Она включает динамические и кинематические уравнения движения системы тел ${{S}^{0}}$ и S′, в которых в качестве переменных взяты проекции ${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$ и ${{\nu }_{1}}$, ${{\nu }_{2}}$, ${{\nu }_{3}}$ векторов ω и v на главные оси тензора инерции ${\mathbf{A}}$, определенного формулой (2.6). Кроме того, эта система включает уравнение вращения ротора, а в случае многотоковой модели электромотора – и уравнения для электрических токов.

4.1. Уравнения движения тела-носителя с ротором. Чтобы вывести уравнения движения системы тел ${{S}^{0}}$, S ′, воспользуемся теоремой об изменении момента количества движения этой системы относительно неподвижной точки: $d{\mathbf{x}}{\text{/}}dt = {{{\mathbf{M}}}_{O}}$. Здесь ${\mathbf{x}}$ – суммарный момент количества движения тел ${{S}^{0}}$, $S{\text{'}}$ относительно неподвижной точки $O$, ${{{\mathbf{M}}}_{O}}$ – момент относительно точки $O$ внешних сил, действующих на систему тел ${{S}^{0}}$ и S ′. Момент ${{{\mathbf{M}}}_{O}}$ равен моменту, создаваемому относительно точки $O$ силой $({{m}^{0}} + m{\kern 1pt} ')g{\mathbf{\nu }}$ веса обоих тел, приложенной в их общем центре масс $C$. Этот центр масс определяется вектором ${\mathbf{c}} = {\mathbf{OC}}$ = ${\text{(}}m{{~}^{0}}{{{\mathbf{c}}}^{0}} + m{\kern 1pt} '{\kern 1pt} {\mathbf{h}}{\text{)/}}m$, где $m = {{m}^{0}} + m{\kern 1pt} '$ – масса всей системы, ${{{\mathbf{c}}}^{0}} = {\mathbf{O}}{{{\mathbf{C}}}^{0}}$, ${\mathbf{h}} = {\mathbf{OC}}{\kern 1pt} '$. Следовательно, ${{{\mathbf{M}}}_{O}} = mg{\mathbf{c}} \times {\mathbf{\nu }}$, и теорема об изменении момента количества движения выражается векторным уравнением

где $d{\kern 1pt} '{\kern 1pt} {\text{/}}dt$ – относительная производная по времени в системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$, ${\mathbf{e}} = {\mathbf{c}}{\text{/}}\left| {\mathbf{c}} \right|$, ${{\Gamma }} = mg\left| {\mathbf{c}} \right|$. Компоненты единичного вектора ${\mathbf{e}}$ в системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$ обозначаются через ${{e}_{1}}$, ${{e}_{2}}$, ${{e}_{3}}$:

Запишем векторное уравнение (4.1) в проекциях на оси системы координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$, связанной с телом-носителем ${{S}^{0}}$. В качестве этой системы координат выберем главные оси тензора инерции ${\mathbf{A}}$, определенного формулой (2.6). В таких осях для внедиагональных компонент этого тензора имеем ${{A}_{{ij}}} = 0$ $(i,j = 1,2,3$; $i \ne j)$, а для его диагональных компонент примем обозначения ${{A}_{1}} = {{A}_{{11}}}$, ${{A}_{2}} = {{A}_{{22}}}$, ${{A}_{3}} = {{A}_{{33}}}$. С помощью этих обозначений формула (2.5) записывается в виде

Тогда, принимая во внимание, что $A{\kern 1pt} '{\kern 1pt} \dot {p}{\kern 1pt} ' = M$ согласно (2.9), и пользуясь разложениями (2.1), (4.2), получаем из (4.1) три дифференциальных уравнения

4.2. Вывод первой формы уравнений движения гиростата с электромотором. Величина p′ в уравнениях (4.3) выражается через переменные ${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$, $\dot {\varphi }{\kern 1pt} '$ по формуле (2.7). В случае бестоковой модели асинхронного электромотора вместо $\dot {\varphi }{\kern 1pt} '$ в п. 2.1 введена переменная $\dot {\gamma }$ = $\dot {\varphi }{\kern 1pt} '\; - \Omega {\kern 1pt} '$, и тогда $p{\kern 1pt} ' = {{\omega }_{1}}{{l}_{1}} + {{\omega }_{2}}{{l}_{2}}$ + ${{\omega }_{3}}{{l}_{3}} + \dot {\gamma } + \Omega {\kern 1pt} '$. Для бестоковой и многотоковой моделей синхронного электромотора в п. 2.2, 2.3 введена переменная $\gamma = \varphi {\kern 1pt} '\; - \Omega t$, пользуясь которой имеем для величины p′ выражение $p{\kern 1pt} ' = {{\omega }_{1}}{{l}_{1}} + {{\omega }_{2}}{{l}_{2}}$ + + ${{\omega }_{3}}{{l}_{3}} + \dot {\gamma } + \Omega $.

Рассматривая случай синхронного электромотора как основной, подставляем это выражение в уравнения (4.3) и получаем следующие динамические уравнения для системы тел ${{S}^{0}}$, S ′

Они определяют изменение фазовых переменных ${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$.

Изменение фазовых переменных $\gamma $, $\dot {\gamma }$ определяет уравнение вращения ротора (2.10). Поскольку $\ddot {\varphi }{\kern 1pt} ' = \ddot {\gamma }$, это уравнение записывается в виде

Чтобы получить уравнения движения гиростата в нормальном виде, следует подставить в правую часть уравнения (4.5) выражения производных ${{\dot {\omega }}_{1}}$, ${{\dot {\omega }}_{2}}$, ${{\dot {\omega }}_{3}}$ через фазовые переменные, определяемые формулами (4.4).

Изменение компонент единичного вектора v в системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}~$определяют известные кинематические уравнения

В случае бестоковой модели синхронного электромотора момент $M$ является функцией $M = M\left( {\gamma ,\dot {\gamma }} \right)$ переменных $\gamma $, $\dot {\gamma }$ и представляется по формуле (3.1). В этом случае уравнения (4.4), (4.5), (4.6) эквивалентны замкнутой системе обыкновенных дифференциальных уравнений с фазовым вектором $y = ({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}},{{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}},\gamma $, $\dot {\gamma })$, которая описывает движение тяжелого однороторного гиростата с синхронным электроприводом ротора.

При использовании многотоковой модели синхронного электромотора момент $M$ в (4.5) является функцией (3.4): $M\left( {\gamma ,\dot {\gamma },x,{{i}_{1}}, \ldots ,{{i}_{{{{n}_{2}}}}}} \right)$ не только переменных $\gamma $, $\dot {\gamma }$, но и электрических токов $x,{{i}_{1}}, \ldots ,{{i}_{{{{n}_{2}}}}}$. Поэтому в случае многотоковой модели синхронного электромотора первая форма уравнений движения гиростата определяется уравнениями (4.4), (4.5), (4.6), к которым добавляются уравнения системы (3.3), описывающие изменение электрических токов $x,{{i}_{1}}, \ldots ,{{i}_{{{{n}_{2}}}}}$:

Она имеет фазовый вектор $\begin{array}{*{20}{l}} {y = \left( {{{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}},{{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}},\gamma ,\dot {\gamma },x,{{i}_{1}}, \ldots ,{{i}_{{{{n}_{2}}}}}} \right).} \end{array}$

5. Вторая форма уравнений движения гиростата с электромотором. Выведем уравнения движения тяжелого гиростата с электромотором, в которых динамические и кинематические уравнения движения системы тел ${{S}^{0}}$ и S ′ записаны в проекциях на главные оси тензора инерции A*, определенного формулой (2.4).

5.1. Вывод второй формы уравнений движения гиростата с электромотором. С помощью тензора A* момент количества движения гиростата выражается по формуле (2.3). В качестве осей системы координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$, связанной с телом ${{S}^{0}}$, выберем главные оси тензора A*. Тогда для внедиагональных компонент этого тензора имеем $A_{{ij}}^{{\text{*}}} = 0$ $(i,j = 1,2,3;$ $i \ne j)$, а для его диагональных компонент принимаем обозначения $A_{1}^{{\text{*}}} = A_{{11}}^{{\text{*}}}$, $A_{2}^{{\text{*}}} = A_{{22}}^{{\text{*}}}$, $A_{3}^{{\text{*}}} = A_{{33}}^{{\text{*}}}$. Проекции векторов ω, v на главные оси тензора A* обозначим через ${{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}}$ и ${{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}$. Формула (2.3) в этом случае записывается следующим образом

Подставив выражение (5.1) в векторное уравнение (4.1) и воспользовавшись разложениями (2.1), (4.2), получаем вторую форму динамических уравнений

Вращение ротора описывается дифференциальным уравнением (4.5). После подстановки в него выражений производных ${{\dot {\omega }}_{1}}$, ${{\dot {\omega }}_{2}}$, ${{\dot {\omega }}_{3}}$, определяемых уравнениями (5.2), приходим к следующему уравнению вращения ротора

Ниже доказана нереализуемость сингулярного случая, когда коэффициент при $\ddot {\gamma }$ в уравнении (5.3) равен нулю. Подставив определяемое этим уравнением выражение $\ddot {\gamma }$ в уравнения (5.2), получим уравнения нормального вида, определяющие изменение переменных ${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$, которые не приводим из-за их громоздкости.

Изменение переменных ${{\nu }_{1}}$, ${{\nu }_{2}}$, ${{\nu }_{3}}$ описывается уравнениями (4.6).

Итак, вторая форма уравнений движения гиростата с электромотором определяется системой уравнений (5.2), (5.3), (4.6) с добавлением уравнений (4.7) в случае многотоковой модели электромотора.

5.2. Доказательство нереализуемости условия сингулярности. Коэффициент при $\ddot {\gamma }$ в уравнении (5.3) запишем в виде A′D, где

Равенство $D = 0$ является условием сингулярности второй формы уравнений движения гиростата с электромотором.

В качестве системы координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$, связанной с телом-носителем ${{S}^{0}}$, пользуемся системой координат, оси которой являются главными осями тензора A*. Диагональные компоненты $A_{{ii}}^{*}$ $\left( {i = 1,2,3} \right)$ тензора A* в этой системе координат обозначены через $A_{i}^{*}$, а его внедиагональные компоненты равны нулю. Компоненты тензора ${\mathbf{A}}$ в неглавной для него системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$ обозначим через ${{\tilde {A}}_{{ij}}}$ $\left( {i,j = 1,2,3} \right)$.

Согласно определениям (2.4), (2.6) тензоров A*, ${\mathbf{A}}$, величины ${{\tilde {A}}_{{ij}}}$ $\left( {i,j = 1,2,3} \right)$ выражаются по формулам, которые получаются из формул (2.8) для компонент $A_{{ij}}^{*}$ $\left( {i,j = 1,2,3} \right)$ тензора A* путем отбрасывания членов, содержащих $A{\kern 1pt} '{\kern 1pt} {{l}_{i}}{{l}_{j}}$. Следовательно, ${{\tilde {A}}_{{ii}}}$ = $A_{i}^{*} - A{\kern 1pt} '{\kern 1pt} l_{i}^{2}$ $\left( {i = 1,2,3} \right)$, ${{\tilde {A}}_{{ij}}} = {{\tilde {A}}_{{ji}}}$ = $ - A{\kern 1pt} '{\kern 1pt} {{l}_{i}}{{l}_{j}}$ $(i,j = 1,2,3$; $i \ne j)$. Поэтому определитель матрицы $\tilde {A}$ с элементами ${{\tilde {A}}_{{ij}}}$ $\left( {i,j = 1,2,3} \right)$ представляется в виде

где ${{\varepsilon }_{i}} = {{l}_{i}}\sqrt {A{\kern 1pt} '} $ $\left( {i = 1,2,3} \right)$. Вычислив здесь определитель, с учетом формулы (5.4) для $D$ получаем

Таким образом, равенство $D = 0$, являющееся условием сингулярности второй формы уравнений движения гиростата с электромотором, означает вырожденность матрицы $\tilde {A}$, элементами которой служат компоненты тензора инерции ${\mathbf{A}}$ в системе координат $O{{\xi }_{1}}{{\xi }_{2}}{{\xi }_{3}}$, главной для тензора A*. Свойство вырожденности матрицы, составленной из компонент тензора ${\mathbf{A}}$, сохраняется при ортогональных преобразованиях координат. Поэтому при $D = 0$ после перехода к главным осям тензора ${\mathbf{A}}$ должно равняться нулю произведение его главных диагональных компонент, которые положительны согласно их определению. Следовательно, условие $D = 0$ нереализуемо.

6. Условия существования стационарных движений гиростата с электромотором. В этом разделе найдены условия, при которых система дифференциальных уравнений движения тяжелого однороторного гиростата с электромотором имеет стационарные решения. Они описывают стационарные движения гиростата – состояния покоя и равномерные вращения тела-носителя ${{S}^{0}}~$ вокруг вертикали. Если для вывода таких условий воспользоваться первой формой уравнений движения гиростата (п. 4.2), то это приведет к труднообозримым соотношениям из-за наличия большого числа членов с $A{\kern 1pt} '{\kern 1pt} {{\omega }_{i}}{{\omega }_{j}}$ в правых частях динамических уравнений (4.4). Поэтому удобнее вывести такие условия на основе второй формы уравнений движения гиростата.

В качестве основной будем рассматривать модель гиростата, включающую многотоковую модель синхронного электромотора. Она описывается системой дифференциальных уравнений (4.5), (4.6), (4.7), (5.2). Стационарные решения этой системы определяются набором постоянных значений фазовых переменных

Поскольку ${{\dot {\gamma }}^{0}} = d{{\gamma }^{0}}{\text{/}}dt = 0$, из уравнений (4.7) для электрических токов следует, что

Поэтому в случае многотоковой модели синхронного электромотора стационарные решения уравнений движения гиростата определяются фазовым вектором

компоненты которого – постоянные величины.

При таких значениях фазовых переменных уравнение вращения ротора (4.5) удовлетворяется при условии $M = 0$, которое с учетом определения (3.4) момента $M$ и отмеченного в (3.2) равенства ${{\Delta }}{{M}_{2}}\left( 0 \right) = 0$ эквивалентно тригонометрическому уравнению

Далее предполагается, что ${{c}_{0}}{\text{/}}{{b}_{0}} < 1$. Тогда уравнение (6.3) определяет два счетных набора стационарных значений ${{\gamma }^{0}}$ угла $\gamma $ для многотоковой модели синхронного электромотора:

Здесь

Рассмотрим теперь кинематические уравнения (4.6). При постоянных значениях фазовых переменных они принимают вид соотношений

которые означают равенство нулю векторного произведения ${\mathbf{\omega }} \times {\mathbf{\nu }}$, то есть выполнение условий

Отсюда следует

Утверждение 1. Стационарное решение (6.2) дифференциальных уравнений движения тяжелого однороторного гиростата с синхронным электромотором либо соответствует состоянию покоя тела-носителя ${{S}^{0}}$ (при ${{\omega }^{0}} = 0$), либо оно описывает равномерное вращение тела ${{S}^{0}}$ в неподвижном пространстве с некоторой угловой скоростью ${{\omega }^{0}} \ne 0$ вокруг неизменно связанной с этим телом и установленной по вертикали вниз полуоси, направление которой в теле ${{S}^{0}}$ определяет единичный вектор с компонентами $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$.

Обратившись, наконец, к динамическим уравнениям (5.2), потребуем, чтобы они выполнялись при постоянном значении ${{\gamma }^{0}}$ угла $\gamma $, постоянных значениях $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$ компонент единичного вектора вертикали и постоянных значениях (6.4) компонент вектора угловой скорости. В результате получаем три соотношения

Таким образом, приходим к следующему выводу.

Утверждение 2. Пусть $y = {{y}^{0}}$ – стационарное решение второй формы уравнений движения однороторного тяжелого гиростата в случае многотоковой модели синхронного электромотора, определенное формулой (6.2). Условиями существования такого решения являются соотношения (6.1), (6.3), (6.4), (6.5).

Замечание 1. При использовании бестоковой модели синхронного электромотора уравнения движения гиростата получаются из уравнений его многотоковой модели, если отбросить уравнения для электрических токов, а в формуле (3.4) для момента $M$ положить $\mu ,{{a}_{1}},{{a}_{2}} = 0$. Условиями существования стационарных решений таких уравнений являются соотношения (6.3), (6.4), (6.5).

Замечание 2. Уравнения движения гиростата при использовании бестоковой модели асинхронного электромотора формально следуют из уравнений для многотоковой модели синхронного электромотора, если отбросить уравнения для электрических токов, в выражении (3.4) для момента $M$ положить $\mu ,{{a}_{1}},{{a}_{2}},{{b}_{0}},{{c}_{0}} = 0$ и заменить в формулах величину ${{\Omega }}$ на Ω′. Стационарные решения в этом случае существуют при условии (6.4) и условии (6.5), где вместо ${{\Omega }}$ используется Ω′.

Соотношения (6.4), (6.5) совпадают с условиями существования стационарных решений уравнений движения тяжелого гиростата с неподвижной точкой, у которого ротор вращается с постоянной относительной угловой скоростью ${{\Omega }}$, но здесь они получены для модели гиростата с электромотором, включающей дифференциальные уравнения для электрических токов.

Основными условиями существования стационарных решений являются соотношения (6.5).

Замечание 3. Легко проверить, что скалярное произведение вектора, компонентами которого служат правые части соотношений (6.5), на вектор с компонентами $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$ тождественно равно нулю. Поэтому одно из соотношений (6.5) выполняется при выполнении двух других.

Отсюда следует, что для описания структуры множества стационарных движений гиростата достаточно получить из трех соотношений (6.5) два независимых соотношения, одно из которых определяет направления полуосей равномерного вращения в теле ${{S}^{0}}$, то есть величины $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$, а другое определяет соответствующие этим направлениям угловые скорости ${{\omega }^{0}}$ равномерных вращений.

7. Анализ основных условий существования стационарных движений гиростата с электромотором. Анализ соотношений (6.5) проводится известными методами, и его результаты сформулированы ниже в виде утверждений 3–7. Сначала рассмотрен случай, когда ${{\Gamma }} = 0$, то есть центр масс гиростата совпадает с неподвижной точкой, а затем рассмотрен случай, когда ${{\Gamma }} \ne 0$.

7.1. Случай, когда $\Gamma = 0$. Пусть функции $V{\kern 1pt} *$, $\Delta {\kern 1pt} *{\kern 1pt} (\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0})$ определены формулами

При ${{\Gamma }} = 0$ соотношения (6.5) переходят в условия равенства нулю трех выражений, которые содержат ${{\omega }^{0}}$ в качестве множителя. Поэтому при ${{\Gamma }} = 0$ соотношения (6.5) выполняются в случае, когда ${{\omega }^{0}} = 0$, а величины $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$ – любые, а также в случае, когда величины $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$, ${{\omega }^{0}}$ удовлетворяют трем равенствам $(A_{2}^{*} - A_{3}^{*}){{\omega }^{0}}\nu _{2}^{0}\nu _{3}^{0}$ + + $A{\kern 1pt} '{\kern 1pt} \Omega ({{l}_{2}}\nu _{3}^{0} - {{l}_{3}}\nu _{2}^{0})$ = 0 $\left( {1\;2\;3} \right)$. Умножив эти равенства на ${{l}_{1}},{{l}_{2}},{{l}_{3}}$ и сложив, получаем ${{\omega }^{0}}V{\kern 1pt} *{\kern 1pt} (\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0})$ = 0, здесь функция V* определена в (7.1). Таким образом, при ${{\Gamma }} = 0$ существуют два варианта выполнения соотношений (6.5): вариант 1, когда ${{\omega }^{0}} = 0$, и вариант 2, когда, вообще говоря, ${{\omega }^{0}} \ne 0$, а величины ${{\nu }}_{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$ удовлетворяют условию $V{\kern 1pt} *{\kern 1pt} (\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0})$ = 0. Дальнейший анализ приводит к следующим выводам.

Утверждение 3. Пусть ${{\Gamma }} = 0$. Тогда

A) Имеются два варианта выполнения условий (6.5) существования стационарных движений гиростата с электромотором. Вариант 1, когда ${{\omega }^{0}} = 0$, соответствует состояниям покоя тела ${{S}^{0}}$ при любых значениях величин $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$, определяющих ориентацию этого тела в неподвижном пространстве. Вариант 2 соответствует равномерному вращению тела ${{S}^{0}}$ с ненулевой, вообще говоря, угловой скоростью ${{\omega }^{0}}$ вокруг установленной по вертикали вниз полуоси, направление которой в теле ${{S}^{0}}$ определяют направляющие косинусы $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$, удовлетворяющие условию

B) Если для варианта 2 выполнены равенства

то $V{\kern 1pt} *{\kern 1pt} (\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}) \equiv 0$ согласно (7.1), и тогда направление полуоси равномерного вращения в теле ${{S}^{0}}$ может быть любым.

C) Если для варианта 2 не выполнено хотя бы одно из равенств (7.3), то условие (7.2) определяет в теле ${{S}^{0}}$ конус второго порядка – конус осей (пар противоположно направленных полуосей), вокруг которых может происходить вертикальное равномерное вращение этого тела с угловой скоростью ${{\omega }^{0}}$, вообще говоря, отличной от нуля.

D) Для каждого набора значений $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$, удовлетворяющих условию (7.2), угловая скорость ${{\omega }^{0}}$ равномерного вращения при $\Delta {\kern 1pt} *{\kern 1pt} (\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}) \ne 0$ определена однозначно и выражается по формуле

при этом для соответствующего набора значений $ - \nu _{1}^{0}$, $ - \nu _{2}^{0}$, $ - \nu _{3}^{0}$, согласно этой формуле, угловая скорость равномерного вращения имеет противоположный знак.

E) В случае, когда для набора значений $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$, удовлетворяющего соотношению (7.2), выполнено равенство $\Delta {\kern 1pt} *{\kern 1pt} (\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}) = 0$, равномерное вращение существует при ${{l}_{2}}\nu _{3}^{0} - {{l}_{3}}\nu _{2}^{0} = 0$, ${{l}_{3}}\nu _{1}^{0} - {{l}_{1}}\nu _{3}^{0} = 0$, ${{l}_{1}}\nu _{2}^{0} - {{l}_{2}}\nu _{1}^{0} = 0$, то есть при ${\mathbf{l}} \times {{{\mathbf{\nu }}}^{0}} = 0$, и его угловая скорость ${{\omega }^{0}}$ может быть любой.

Кроме условия (7.2), величины $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$, должны удовлетворять условию $\nu {{_{1}^{0}}^{{^{2}}}} + \nu {{_{2}^{0}}^{{^{2}}}} + \nu {{_{3}^{0}}^{{^{2}}}}$ = 1.

Определение (7.2) направлений осей равномерных вращений гиростата при ${{\Gamma }} = 0$ по форме аналогично определению [27, 28] конуса Штауде, то есть конуса осей равномерных вращений тяжелого твердого тела с неподвижной точкой, но отличается от него тем, что в определение конуса Штауде вместо параметров $A_{1}^{{\text{*}}}$, $A_{2}^{{\text{*}}}$, $A_{3}^{{\text{*}}}$, ${{l}_{1}}$, ${{l}_{2}}$, ${{l}_{3}}$ входят параметры $A_{1}^{0}$, $A_{2}^{0}$, $A_{3}^{0}$, ${{e}_{1}}$, ${{e}_{2}}$, ${{e}_{3}}$.

7.2. Случай, когда ${{\Gamma }} \ne 0$. При ${{\Gamma }} \ne 0$ сразу выделим вариант, когда ${{\omega }^{0}} = 0$. Непосредственно из условий (6.5) получаем такой результат.

Утверждение 4. При ${{\Gamma }} \ne 0$ вариант ${{\omega }^{0}} = 0$, соответствующий состоянию покоя гиростата, имеет место, когда

то есть ${\mathbf{e}} \times {{{\mathbf{\nu }}}^{0}} = 0$. Это означает, что центр масс гиростата находится на вертикали над неподвижной точкой $O$ или под этой точкой.

Рассмотрим теперь вариант, когда ${{\omega }^{0}} \ne 0$ в случае ${{\Gamma }} \ne 0$. Чтобы вывести соотношение, связывающее $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$, сначала умножим равенства (6.5) на ${{e}_{1}},{{e}_{2}},{{e}_{3}}$ и сложим. Приходим к соотношению,

содержащему ${{\omega }^{0}}$ в первой степени. Здесь приняты обозначения

Получим теперь из равенств (6.5) соотношение, содержащее ${{\omega }^{0}}$ только во второй степени. Для этого умножим равенства (6.5) на ${{l}_{1}},{{l}_{2}},{{l}_{3}}$ и сложим. Приходим к соотношению

где функция $V{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right)$ определена в (7.1).

Проанализируем соотношения (7.4), (7.7) и получим из них условия, определяющие значения $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$ и соответствующие им значения ${{\omega }^{0}}$.

Утверждение 5. Пусть ${{\Gamma }} \ne 0$ и ${{\omega }^{0}} \ne 0$. Вырожденный случай, когда выполняется тождественное равенство $S{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right) \equiv 0$, имеет место при условиях

которые следуют из (7.5). Если условия (7.8) выполнены, то соотношение (7.4) имеет место только при дополнительном условии $\Pi {\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right) \equiv 0$, то есть, согласно (7.6), при

Тогда, согласно (7.1), (7.5), (7.6), в этом случае имеем $S*,\Pi {\kern 1pt} *$, $V{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right) \equiv 0$, и поэтому оба соотношения (7.4), (7.7) выполняются при любых значениях $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$ и ${{\omega }^{0}}$.

Для варианта, когда ${{\Gamma }} \ne 0$ и ${{\omega }^{0}} \ne 0$, рассмотрим теперь общий невырожденный случай, когда 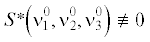, то есть не выполнено хотя бы одно из условий (7.8). В этом случае функция $S{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right)$ обращается в нуль лишь при некоторых значениях своих аргументов, но не исключено, что $\Pi {\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right)$ ≡ 0.

Сначала рассмотрим особый подслучай общего невырожденного случая.

Утверждение 6. Пусть ${{\Gamma }} \ne 0$ и ${{\omega }^{0}} \ne 0$. Особый подслучай общего невырожденного характеризуется тем, что 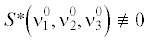, но $S{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right) = 0$ при некоторых особых значениях $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$. Для этих значений соотношения (7.4), (7.7), определяющие направления полуосей и угловые скорости равномерных вращений, выполнены лишь при $\Pi {\kern 1pt} *$, $V{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right)$ = 0, и тогда соотношениям (7.4), (7.7) удовлетворяет любое значение ${{\omega }^{0}}$.

Рассмотрим, наконец, общий неособый подслучай невырожденного случая, когда при данных значениях $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$ выполнено неравенство $S{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right) \ne 0$. Так как, по предположению, ${{\omega }^{0}} \ne 0$, то из (7.4) следует, что в этом подслучае выполняется также неравенство

а угловая скорость ${{\omega }^{0}}$ однозначно определяется по формуле

Подставив это выражение в (7.7), приходим к соотношению, которое с учетом неравенства (7.9) записывается в виде

Запишем соотношение (7.11) в виде

С учетом (7.10) следует, что угловая скорость равномерного вращения выражается также по формуле

Утверждение 7. Пусть ${{\Gamma }} \ne 0$ и ${{\omega }^{0}} \ne 0$. Пусть компоненты $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$ единичного вектора вертикали ${{{\mathbf{\nu }}}^{0}}$ в главных осях тензора инерции A* удовлетворяют неравенству $S{\kern 1pt} *{\kern 1pt} \left( {\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}} \right) \ne 0$ и условию (7.11). Тогда полуось, определяемая в теле ${{S}^{0}}$ вектором ${{{\mathbf{\nu }}}^{0}}$ с такими компонентами, является полуосью равномерного вращения тела ${{S}^{0}}$, если оно установлено так, что эта полуось направлена по вертикали вниз. Угловая скорость этого равномерного вращения выражается по любой из формул (7.10) или (7.12).

Левая часть соотношения (7.11) является суммой однородных полиномов четвертой и третьей степени по отношению к $\nu _{1}^{0},\nu _{2}^{0},\nu _{3}^{0}$. Это соотношение определяет в теле-носителе ${{S}^{0}}$ неизменно связанную с ним поверхность четвертого порядка. Пересечение поверхности (7.11) с единичной сферой $\nu {{_{1}^{0}}^{{^{2}}}} + \nu {{_{2}^{0}}^{{^{2}}}} + \nu {{_{3}^{0}}^{{^{2}}}}$ = 1 определяет неизменно связанную с телом-носителем ${{S}^{0}}$ кривую, называемую сферической линией. Конус с вершиной в точке $O$, направляющей линией которого служит сферическая линия, является конусом полуосей равномерных вращений гиростата. Геометрическое место концов векторов угловой скорости равномерного вращения в теле ${{S}^{0}}$ называется направляющей линией.

8. Сравнение условий существования стационарных движений гиростата с электромотором и без электромотора. В большинстве работ, посвященных динамике тяжелого гиростата без электромотора, имеющего неподвижную точку, рассматриваются две модели гиростата. Первая из этих моделей основана на предположении, что динамически и статически уравновешенный ротор вращается с постоянной относительной угловой скоростью вокруг своей оси симметрии, фиксированной в теле-носителе. Другая модель гиростата основана на предположении, что ротор вращается по инерции без трения. Обе эти модели описываются одинаковыми по форме уравнениями движения, отличающимися определением тензора инерции, и поэтому обычно подразумевается, что результаты, полученные с помощью таких уравнений, справедливы для обеих моделей. Это относится и к уравнению, определяющему направления полуосей равномерных вращений гиростата, полученному в [2, 10] и, позже, в [13]. Однако между этими двумя известными моделями гиростата имеется различие, которое необходимо учитывать при определении полуосей равномерных вращений.

На примере однороторного тяжелого гиростата с неподвижной точкой рассмотрим подробнее вопрос об условиях существования стационарных движений для двух указанных моделей гиростата, основываясь на полученных выше уравнениях его движения.

8.1. Условия существования стационарных движений гиростата с ротором, вращающимся с фиксированной угловой скоростью. Уравнения движения тяжелого гиростата с ротором, вращающимся с фиксированной относительной угловой скоростью ${{\Omega }}$, получаются из второй формы уравнений движения гиростата с синхронным электромотором, то есть из уравнений (5.2), (5.3), (4.6), (4.7), если отбросить уравнение вращения ротора (5.3) и уравнения для электрических токов (4.7) и положить $\ddot {\gamma } = 0$ в динамических уравнениях (5.2). Получившаяся из (5.2), (4.6) система дифференциальных уравнений является результатом проектирования на главные оси тензора A* известных векторных уравнений

Здесь A* – тензор, определенный формулой (2.4), ${\mathbf{\lambda }}* = A{\kern 1pt} '{\kern 1pt} \Omega ~l$ – гиростатический момент.

Cтационарные решения этой системы соответствуют значениям $\omega _{1}^{0}$, $\omega _{2}^{0}$, $\omega _{3}^{0}$, $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$ фазовых переменных, при которых ее правые части обращаются в нуль.

Из условий обращения в нуль правых частей скалярных уравнений, соответствующих векторному кинематическому уравнению ${\mathbf{\dot {\nu }}} = {\mathbf{\nu }} \times {\mathbf{\omega }}$, следуют уже полученные выше выражения (6.4) для $\omega _{1}^{0},\omega _{2}^{0},\omega _{3}^{0}$. В результате их подстановки в скалярные уравнения (5.2), соответствующие входящему в (8.1) векторному динамическому уравнению, условия обращения в нуль правых частей динамических уравнений принимают тот же вид (6.5), что и для гиростата с синхронным электромотором.

Поэтому для тяжелого гиростата с ротором, вращающимся с постоянной относительной угловой скоростью ${{\Omega }}$, направляющие косинусы $\nu _{1}^{0}$, $\nu _{2}^{0}$, $\nu _{3}^{0}$ полуосей равномерного вращения и угловые скорости ${{\omega }^{0}}$ равномерного вращения определены теми же формулами (7.11), (7.10), что и для гиростата с синхронным электромотором, в котором угловая скорость вращения магнитного поля в статоре равна ${{\Omega }}$.

Сферическая и направляющая линии для этого случая изучены в [11, 12].

8.2. Условия существования стационарных движений гиростата с ротором, вращающимся по инерции без трения. Уравнение вращения ротора S ′ получено выше в форме (2.9): $A{\kern 1pt} '{\kern 1pt} \dot {p}{\kern 1pt} ' = M$. Здесь $M$ – момент, создаваемый относительно оси ротора силами, действующими на ротор со стороны тела-носителя ${{S}^{0}}$, а величина p′ определяется формулой (2.7). Для модели гиростата с ротором, вращающимся по инерции без трения, имеем $M = 0$. Тогда $p{\kern 1pt} '{\kern 1pt} \left( t \right) = p{\kern 1pt} '{\kern 1pt} \left( {{{t}_{0}}} \right)$ при $t \geqslant {{t}_{0}}$, то есть величина p′ является интегралом движения.

Поэтому уравнения движения гиростата с ротором, вращающимся по инерции без трения, следуют из первой формы уравнений движения гиростата с электромотором, а именно, из уравнений (4.3), (4.6), если положить в них $M = 0$. Они получаются также путем проектирования на главные оси тензора ${\mathbf{A}}$ векторных уравнений

которые имеют тот же вид, что и уравнения (8.1). Их отличие от уравнений (8.1) состоит в том, что вместо тензора A* и вектора ${\mathbf{\lambda }}* = A{\kern 1pt} '\;{{\Omega }}\;{\mathbf{l}}$ здесь используются тензор ${\mathbf{A}}$, определенный формулой (2.6), и вектор ${\mathbf{\lambda }} = A{\kern 1pt} '{\kern 1pt} p{\kern 1pt} '{\kern 1pt} {\mathbf{l}}$.

Отсюда следует, что для гиростата с вращающимся по инерции ротором конус полуосей равномерных вращений и угловые скорости равномерных вращений определяются формулами такого же вида, как формулы (7.11), (7.10) для гиростата с ротором, вращающимся с постоянной относительной угловой скоростью. Но вместо моментов инерции $A_{1}^{{\text{*}}}$, $A_{2}^{{\text{*}}}$, $A_{3}^{{\text{*}}}$ в эти формулы входят моменты инерции ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$, а вместо фиксированной угловой скорости ${{\Omega }}$ в них входит угловая скорость p′, определяемая начальными условиями. Таким образом, при использовании первой формы уравнений движения, с тензором ${\mathbf{A}}$, для гиростата с вращающимся по инерции ротором вместо фиксированного в теле-носителе конуса полуосей равномерных вращений в общем случае существует семейство таких конусов, зависящих как от параметра от величины p′.

Условия существования стационарных движений гиростата с вращающимся по инерции ротором и уравнение конуса полуосей его равномерных вращений можно также получить, воспользовавшись второй формой уравнений движения гиростата, а именно уравнениями (5.2), (4.5), (4.6), взятыми при $M = 0$. В этом случае, в отличие от гиростата с электромотором, нет выделенной угловой скорости вращения ротора, и поэтому в уравнениях (5.2), (4.5) следует заменить $\dot {\gamma } + {{\Omega }}$, $\ddot {\gamma }$ на $\dot {\varphi }{\kern 1pt} '$, $\ddot {\varphi }{\kern 1pt} '$.

Пусть в некоторый момент времени ${{t}_{0}}$ для полученной таким образом системы уравнений движения гиростата заданы начальные значения ее фазовых переменных: ${{\omega }_{i}}\left( {{{t}_{0}}} \right) = \omega _{i}^{0}$, ${{\nu }_{i}}\left( {{{t}_{0}}} \right) = \nu _{i}^{0}$ $\left( {i = 1,2,3} \right)$, $\dot {\varphi }{\kern 1pt} '{\kern 1pt} \left( {{{t}_{0}}} \right) = {{\Omega }^{0}}$.

Они определяют стационарное движение гиростата, если такие постоянные значения фазовых переменных удовлетворяют всем уравнениям движения (5.2), (4.5), (4.6), в которых $M = 0$, а $\dot {\gamma } + {{\Omega }}$, $\ddot {\gamma }$ заменены на $\dot {\varphi }{\kern 1pt} '$, $\ddot {\varphi }{\kern 1pt} '$. Для уравнений (5.2) это означает выполнение условий

а для уравнений (4.6) – выполнение условий

Уравнение вращения ротора (4.5) в случае $M = 0$ удовлетворяется при любых постоянных значениях фазовых переменных.

Из соотношений (8.3) следуют выражения (6.4). Подставив их в соотношения (8.2), получаем условия существования стационарных движений гиростата с ротором, вращающимся по инерции без трения. По форме они совпадают с полученными выше условиями (6.5) существования стационарных движений гиростата с синхронным электромотором, которые, в свою очередь, совпадают с условиями существования стационарных движений для гиростата с ротором, вращающимся с постоянной относительной угловой скоростью. Существенное отличие этих условий от условий (6.5) состоит в том, что вместо фиксированной относительной угловой скорости ${{\Omega }}$ вращения ротора в них входит произвольное начальное значение ${{{{\Omega }}}^{0}}$ этой угловой скорости.

Таким образом, при использовании второй формы уравнений движения, с тензором A*, для гиростата с вращающимся по инерции ротором вместо фиксированного в теле-носителе конуса полуосей равномерных вращений в общем случае существует семейство таких конусов, зависящих от величины ${{\Omega }^{0}} = \dot {\varphi }{\kern 1pt} '\left( {{{t}_{0}}} \right)$ как от параметра.

Заключение. В статье дана математическая постановка задачи о движении однороторного гиростата с неподвижной точкой, помещенного в поле силы тяжести и снабженного электромотором, который поддерживает вращение ротора при наличии момента сил трения относительно его оси. Связь, реализующая неподвижную точку, предполагается идеальной. Рассмотрены три модели электромотора: бестоковые модели асинхронного и синхронного электромотора и многотоковая модель синхронного электромотора. Дифференциальные уравнения движения гиростата с электромотором получены в двух формах, соответствующих двум определениям тензора инерции в неподвижной точке. В случае многотоковой модели синхронного электромотора эти уравнения включают уравнения для электрических токов.

Проанализированы условия, при которых существуют стационарные решения таких дифференциальных уравнений. Эти решения описывают стационарные движения гиростата – состояния покоя и равномерные вращения тела-носителя вокруг вертикали. Установлено, что в общем случае направления полуосей равномерных вращений гиростата с электромотором образуют в теле-носителе конус, совпадающий с конусом полуосей равномерных вращений для известной модели гиростата с ротором, вращающимся с постоянной относительной угловой скоростью.