Радиотехника и электроника, 2020, T. 65, № 3, стр. 240-244

ВВЕДЕНИЕ

Рассматривается двумерная задача дифракции плоской поляризованной ТМ-волны на структуре, состоящей из двух идентичных сплошных серебряных наноцилиндров в световом диапазоне длин волн $300\,\,{\text{нм}} < \lambda < 900\,\,{\text{нм}}{\text{.}}$ Как известно, в этом диапазоне длин волн относительная диэлектрическая проницаемость ${{\varepsilon }_{с}}$ серебра отрицательна. Это приводит не только к существованию поверхностных волн (плазмонов), но и к их резонансам [1]. Такое свойство структур из благородных металлов было использовано в спектроскопии для создания сенсоров [1]. Отметим, что случаи одиночных структур из серебра (золота) исследовались в [2–6]. Двухэлементные (трехэлементные) структуры из серебряных цилиндров прямоугольного сечения рассмотрены в [3, 4], а для случая двух эллиптических цилиндров – в [7]. Случай двух сплошных или полых цилиндров из метаматериала рассматривался в [8].

Цель данной работы состоит в строгом электродинамическом исследовании особенностей резонансного рассеяния плоской волны светового диапазона длин волн в структуре, образованной двумя одинаковыми серебряными наноцилиндрами одинакового радиуса.

1. ФОРМУЛИРОВКА ЗАДАЧИ. МЕТОД РЕШЕНИЯ

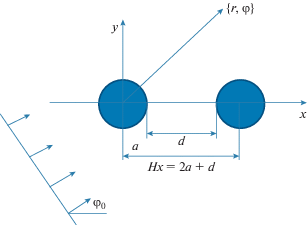
Рассмотрим двумерную задачу дифракции плоской поляризованной электромагнитной ТМ-волны на структуре, состоящей из двух одинаковых диэлектрических (серебряных) цилиндров одинакового радиуса $a$, расположенных на расстоянии $d$ между собой. Предполагается, что длина электромагнитной волны $\lambda $ принадлежит световому диапазону λ ≈ 300…900 нм. Геометрия исследуемой задачи представлена на рис. 1. Диэлектрическую проницаемость серебра 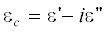≡ $\operatorname{Re} ({{\varepsilon }_{c}}) - i\operatorname{Im} ({{\varepsilon }_{c}})$ определяли путем аппроксимации кубичными сплайнами экспериментальных данных работы [10]. Зависимость действительной и мнимой частей относительной диэлектрической проницаемости серебра от длины волны $\lambda $ представлена на рис. 2. Отметим, что использование результатов работы [10], так же как и аналитического представления диэлектрической проницаемость серебра ${{\varepsilon }_{c}}$ в теории Друде-Зоммерфельда [1], накладывает ограничение на минимальный диаметр ($2a$) серебряных цилиндров $\min (2a) \geqslant 10\,\,{\text{нм,}}$ поскольку при $2a < 10\,\,{\text{нм}}$ необходимо учитывать явление пространственной дисперсии [1].

Рис. 1.

Геометрия задачи.

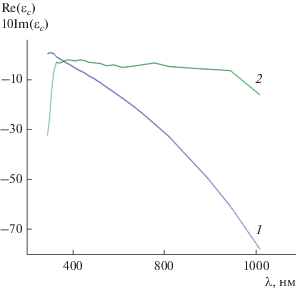
Рис. 2.

Частотные зависимости действительной (1) и мнимой (2) частей относительной диэлектрической проницаемости серебра.

Очевидно, что с точки зрения классической электродинамики речь идет о решении задачи дифракции плоской электромагнитной волны на двух цилиндрах из диэлектрика с потерями. Исследуем случай ТМ-поляризации, когда в электромагнитном поле присутствуют компоненты ${{H}_{z}}(x,y),$ ${{E}_{x}}(x,y),$ ${{E}_{y}}(x,y)$. Задача дифракции в этом случае сводится к нахождению скалярной функции $U(x,y) = {{H}_{z}}(x,y),$ а волновое поле падающей плоской волны задается выражением

где угол ${{\varphi }_{0}}$ определяет направление распространения волны. Используем гауссовскую систему физических единиц, зависимость от времени выбрана в виде $\exp (i\omega t).$

Полное поле $U(x,y)$ в кусочно-однородной среде удовлетворяет уравнению Гельмгольца

где диэлектрическая проницаемость $\varepsilon (x,y)$ среды определяется выражением

для задачи, геометрия которой представлена на рис. 1.

Уравнение (1) необходимо дополнить условием непрерывности величин

на границах цилиндров. В формуле (3) через $N$ обозначена нормаль к границам цилиндров.

Полное поле вне цилиндров состоит из падающего ${{U}^{0}}$ и рассеянного ${{U}^{S}}$ полей

Рассеянное поле ${{U}^{S}}$ в цилиндрической системе координат ($x = r\cos \varphi ,$ $y = r\sin \varphi $) должно удовлетворять в дальней зоне условию излучения

где $\Phi (\varphi )$ – диаграмма рассеяния структуры. Полное сечение рассеяния ${{\sigma }_{s}}$ и сечение поглощения ${{\sigma }_{a}}$ выражаются через решение краевой задачи (1)–(4) по формулам

Интегрирование в (7) проводится по внешним контурам цилиндров.

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численное решение краевой задачи проводилось модифицированным методом дискретных источников [11–13]. Точность численного решения оценивалась невязкой граничных условий $\Delta $ в линейной норме на цилиндрах и во всех расчетах была не хуже, чем $\Delta = {{10}^{{ - 3}}}.$

На рис. 3 изображены зависимости полных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для структуры с фиксированным значением радиуса цилиндров $a = 25\,\,нм,$ угле падения плоской волны ${{\varphi }_{0}} = 0$ и расстояниях между цилиндрами 1, 2.5, 5, 10 и 25 нм. Из рисунка видно, что число максимумов спектра сечения рассеяния $k{{\sigma }_{s}}$, их взаимное расположение, а также величина и расположение максимума зависят от расстояния между цилиндрами. Так, наибольший максимум спектра сечения рассеяния $k{{\sigma }_{s}}$ у кривой 1 (что соответствует расстоянию между цилиндрами $d = 1\,\,{\text{нм}}$) расположен при меньших значениях $\lambda $, чем два других побочных максимума. Такое же явление наблюдается и у кривых 2, 3. Однако для кривых 4 и 5 (что соответствует расстояниям между цилиндрами 10 и 25 нм) имеет место обратный эффект – главный максимум находится при бóльших значениях $\lambda $ (правее), чем другой побочный максимум. Также наблюдается и уменьшение числа максимумов, что свидетельствует о их вырождении.

Рис. 3.

Влияние расстояния между цилиндрами на частотную зависимость нормированного поперечника рассеяния при радиусе цилиндров $a = 25\,\,нм$ и угле падения плоской волны ${{\varphi }_{0}} = 0$: d = 1 (1), 2.5 (2), 5 (3), 10 (4) и 25 нм (5).

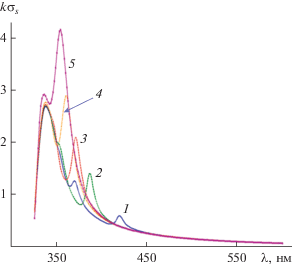
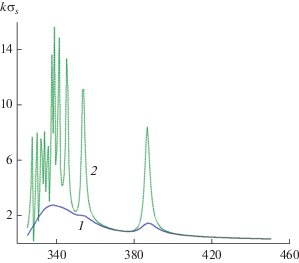
Рисунок 4 иллюстрирует влияние потерь серебра на зависимость полных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для структуры с фиксированным значением радиуса цилиндров $a = 25\,нм$, угле падения плоской волны ${{\varphi }_{0}} = 0$ и расстоянием между цилиндрами $d = 2.5\,\,{\text{нм}}{\text{.}}$ На рисунке представлен случай реальных потерь серебра, которые определяются значениями мнимой части относительной диэлектрической проницаемости серебра $\operatorname{Im} ({{\varepsilon }_{c}})$ (см. рис. 2), и случай, когда мнимая часть относительной диэлектрической проницаемости серебра равна $0.001\operatorname{Im} ({{\varepsilon }_{c}}).$ Из этого рисунка следует, что при малых потерях серебра наблюдаются как дипольный резонанс $k{{\sigma }_{s}}$ (в окрестности $\lambda \approx 384\,\,{\text{нм}}$), так и мультипольные резонансы. Однако реальные потери серебра приводят не только к уменьшению амплитуд максимумов резонансов $k{{\sigma }_{s}},$ но к фактическому исчезновению мультипольных резонансов, так как они сливаются в один общий максимум.

Рис. 4.

Влияние потерь серебра на частотную зависимость сечения рассеяния $k{{\sigma }_{s}}$ для структуры при фиксированном значении радиуса цилиндров $a = 25\,\,нм,$ угле падения плоской волны ${{\varphi }_{0}} = 0,$ расстоянии между цилиндрами d = 2.5, в случае $\operatorname{Im} ({{\varepsilon }_{c}})$ (кривая 1) и $0.001\operatorname{Im} ({{\varepsilon }_{c}})$(кривая 2).

На рис. 5а изображены зависимости полных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для структуры с фиксированным значением радиуса цилиндров $a = 25\,\,нм,$ угле падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0em} 4}$ и расстояниях между цилиндрами 1, 2.5, 5, 10 и 25 нм. Из рисунка видно, что здесь, как и в случае угла падения ${{\varphi }_{0}} = 0,$ число максимумов спектра сечения рассеяния $k{{\sigma }_{s}},$ их взаимное расположение, а также величина и расположение максимума зависят от расстояния между цилиндрами. Отметим, что при расстоянии между цилиндрами $d = 1\,\,{\text{нм}}$ (кривая 1) наблюдаются хорошо выделенные три максимума $k{{\sigma }_{s}}$, при этом наибольший максимум спектра сечения рассеяния $k{{\sigma }_{s}}$ расположен при меньших значениях λ, чем другие два максимума. Такое же явление отмечаем и при $d$ = 2.5 нм (кривая 2). Однако при расстояниях между цилиндрами 5, 10 и 25 нм (кривые 3–5) наблюдается эффект уменьшения числа максимумов и их вырождения (фактическое исчезновение второго максимума у кривой 5).

Рис. 5.

Влияние расстояния между цилиндрами на частотную зависимость нормированного поперечника рассеяния при радиусе цилиндров $a = 25\,\,нм,$ углах падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0em} 4}$ (а) и –π/2 (б) и различном расстоянии между цилиндрами: d = 1 (1), 2.5 (2), 5 (3), 10 (4) и 25 нм (5).

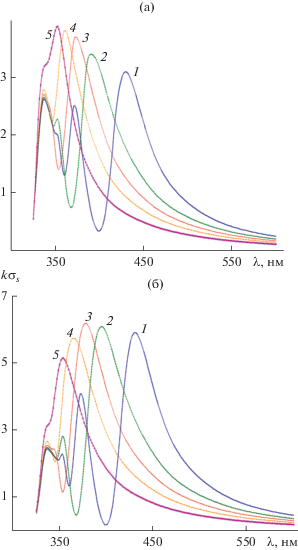
Аналогичные тенденции видны и на рис. 5б, который отличается от рис. 5а только величиной угла падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}.$

Таким образом, из результатов, представленных на рис. 3–5, следует, что у поперечника рассеяния $k{{\sigma }_{s}}$ наблюдается эффект вырождения резонансов.

Рассмотрим теперь ситуацию, когда радикс цилиндров равен $a = 75\,\,нм,$ т.е. увеличен в три раза по отношению к рассмотренному выше случаю. Так, на рис. 6а изображены зависимости полных сечений рассеяния $k{{\sigma }_{s}}$ от длины волны $\lambda $ для структуры с фиксированным значением радиуса цилиндров $a = 75\,\,нм,$ угле падения плоской волны ${{\varphi }_{0}} = 0$ и расстояниях между цилиндрами 2, 7.5, 15, 30 и 75 нм. Видно, что на кривой 1, соответствующей расстоянию между цилиндрами $d$= 2 нм, имеется три четко выраженных и два слабо выраженных максимума $k{{\sigma }_{s}}$. При этом слабо выраженные максимумы $k{{\sigma }_{s}}$ расположены по обе стороны главного максимума $k{{\sigma }_{s}}$. Увеличение расстояния $d$ между цилиндрами приводит к тому, что побочные максимумы $k{{\sigma }_{s}}$ сначала перемещаются на левую сторону главного максимума $k{{\sigma }_{s}}$ (см. кривую 2), а затем поодиночке исчезают (см. кривые 3–5).

Рис. 6.

Зависимость нормированного поперечника рассеяния от частоты при радиусе цилиндров $a = 75\,\,нм,$ углах падения плоской волны ${{\varphi }_{0}} = 0$ (а), ‒π/4 (б), ‒π/2 (в) и различных расстояниях между цилиндрами: d = 2 (1), 7.5 (2), 15 (3), 30 (4) и 75 нм (5).

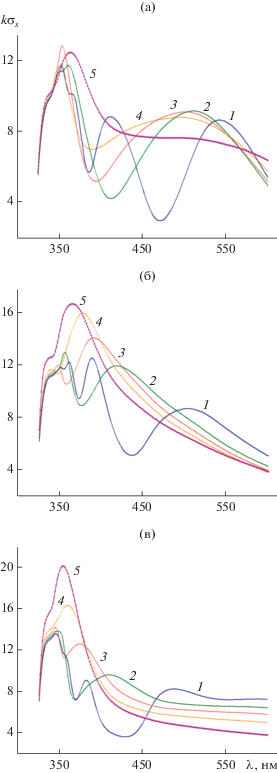
На рис. 6б представлены результаты расчетов той же зависимости при тех параметрах, но при угле падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 4}} \right. \kern-0em} 4}.$ Из рис. 6б видно, что кривая 1 содержит два четко выделенных максимума $k{{\sigma }_{s}}$ и три слабо выраженных (побочных) максимума $k{{\sigma }_{s}}$, расположенных при $\lambda < 352\,\,{\text{нм}}{\text{.}}$ Увеличение расстояния между цилиндрами $d$ приводит к тому, что при $d \geqslant 7.5\,\,{\text{нм}}$ сначала исчезают два побочных (кривые 2, 3), а затем и третий побочный максимум стремится к исчезновению (кривая 5).

Такие же тенденции можно наблюдать и на рис. 6в, где представлены рассчитанные графики рассматриваемой зависимости $k{{\sigma }_{s}}$ при угле падения плоской волны ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}.$

Таким образом, из результатов, изображенных на рис. 6а–6в, следует, что увеличение радиуса цилиндров вызывает увеличение числа побочных максимумов сечений рассеяния $k{{\sigma }_{s}}$, а увеличение расстояния между цилиндрами – их постепенное исчезновение.

ЗАКЛЮЧЕНИЕ

Исследованы связанные колебания плазмонов, возбуждаемых при падении плоской поляризованной ТМ-волны светового диапазона длин волн, на структуру, состоящую из двух одинаковых сплошных серебряных нано цилиндров. Результаты исследования позволили сделать следующие выводы. Поперечник рассеяния для рассмотренных структур характеризуется резонансными свойствами в области длин волн $330\,{\text{нм}} < \lambda < 550\,\,{\text{нм}}{\text{.}}$ Реальные потери серебра приводят к существенному уменьшению амплитуд мультипольных резонансов и к эффекту их слияния в один общий максимум. Положение максимумов поперечника рассеяния, их взаимное расположение и вырождение зависит как от расстояния между цилиндрами, так и величины их радиусов.