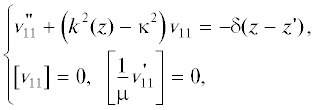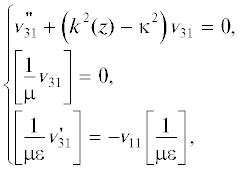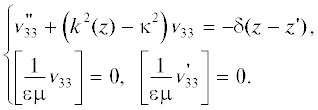Радиотехника и электроника, 2020, T. 65, № 7, стр. 644-652
Решение задачи дифракции на плоском экране, расположенном в плоскослоистой среде, с помощью метода продолженных граничных условий
А. Г. Кюркчан a, b, c, С. А. Маненков a, *
a Московский технический университет связи и информатики
111024 Москва, ул. Авиамоторная, 8а, Российская Федерация
b Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация
c ФГУП Центральный научно-исследовательский институт связи
111141 Москва, 1-й проезд Перова поля, 8, Российская Федерация
* E-mail: mail44471@mail.ru
Поступила в редакцию 12.12.2019
После доработки 12.12.2019
Принята к публикации 14.01.2020
Аннотация
На основе метода продолженных граничных условий разработан алгоритм численного решения трехмерной задачи дифракции поля точечного источника на плоском экране, расположенном на границе раздела плоскослоистой среды. В частности, рассмотрен случай, когда экран находится на границе раздела двух сред и на верхней границе диэлектрического слоя, окруженного одинаковыми диэлектрическими полупространствами. Для контроля правильности получаемых результатов проведена проверка точности выполнения оптической теоремы. Построены угловые зависимости диаграммы рассеяния для экрана круговой, прямоугольной и эллиптической формы.
ВВЕДЕНИЕ
Задача дифракции на тонких экранах представляет большой практический интерес, например, при анализе полосковых антенн. Существует много работ, посвященных как двумерным, так и трехмерным вариантам задачи дифракции на тонких экранах расположенных в однородной и плоскослоистой средах [1–6]. Однако трехмерные задачи исследованы достаточно слабо. В литературе рассматриваются различные методы решения задачи дифракции на тонких экранах, например, такие, как метод интегральных уравнений [1], метод полуобращения [2, 3], метод задачи Римана–Гильберта [5] и ряд других.
В данной работе рассмотрена трехмерная задача дифракции поля вертикального электрического диполя, который расположен либо над плоским экраном, лежащим на границе раздела двух однородных диэлектрических полупространств, либо на верхней границе однородного диэлектрического слоя, окруженного одинаковыми полупространствами. Для решения рассматриваемой задачи дифракции был использован метод продолженных граничных условий (МПГУ) [7, 8], который ранее применялся к решению двумерных и трехмерных задач дифракции [9–11]. Основная идея метода состоит в переносе граничных условий с поверхности экрана на некоторое небольшое расстояние $\delta $ в область над экраном. Такой подход позволяет свести задачу дифракции к интегральному уравнению первого рода относительно неизвестного тока на поверхности тонкого экрана. При этом ядро интегрального уравнения не имеет особенности при совпадении аргументов, что очень удобно при численном решении задачи. В то же время в силу малости расстояния $\delta $ ядро имеет максимум при совпадении аргументов, что делает соответствующий численный алгоритм устойчивым. Отметим, что настоящая работа является обобщением работы [11] на векторный случай дифракции на плоском экране, расположенном в плоскослоистой среде.
При решении задачи дифракции на экране, расположенном на границе раздела плоскослоистой среды, использовалась функция Грина (ФГ) данной среды, которая аналитически учитывает граничные условия сопряжения на всех границах раздела. В результате задача сводится к нахождению тока только на поверхности экрана, т.е. отпадает необходимость искать токи на границах раздела сред. Однако при этом возникает проблема, связанная со сходимостью интегралов Зоммерфельда, через которые выражается ФГ. Для ее преодоления мы выделяли асимптотики подынтегральных выражений в соответствующих интегралах, с последующим интегрированием в явном виде этих асимптотик. Для решения интегрального уравнения в работе использован метод Крылова–Боголюбова. При этом ядра системы скалярных интегральных уравнений, к которым сводится задача дифракции, разбивали на две части: сингулярную, обусловленную описанными выше асимптотиками, и оставшуюся регулярную часть. Сингулярная часть является быстроменяющейся функцией координат, в то время как регулярная меняется медленно. Поэтому можно использовать более “грубую” аппроксимацию подынтегральной функции при численной оценке интегралов от регулярной части ФГ [12]. Этот факт позволяет существенно ускорить вычисления.
1. ПОСТАНОВКА ЗАДАЧИ
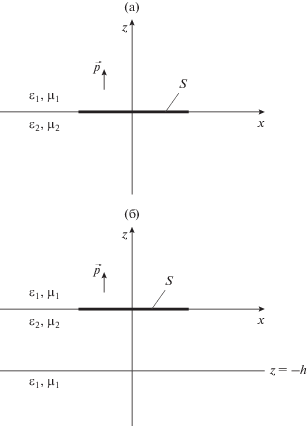
Рассмотрим математическую постановку задачи. Пусть плоский бесконечно тонкий экран $S$ расположен на границе раздела $z = 0$ плоскослоистой среды, а именно пусть он находится либо на границе однородного диэлектрического полупространства с характеристиками ${{\mu }_{2}}$ и ${{\varepsilon }_{2}}$, либо на верхней границе диэлектрического слоя с проницаемостями ${{\mu }_{2}}$ и ${{\varepsilon }_{2}}$, окруженного двумя одинаковыми полупространствами (рис. 1). Характеристики верхнего полупространства (при $z > 0$) или полупространств, окружающих слой, обозначим через ${{\mu }_{1}},\;{{\varepsilon }_{1}}$. На поверхности экрана выполняется условие
где ${{\vec {i}}_{z}}$ – единичный орт по оси z, $\vec {E}$ – полное электрическое поле. На границах раздела сред, т.е. либо при $z = 0$, в случае когда экран расположен на границе однородного полупространства, либо при $z = 0$ и $z = - h$, при решении задачи дифракции на экране, находящемся на границе диэлектрического слоя, выполнены условия сопряжения следующего вида:(2)
$\left[ {{{{\vec {i}}}_{z}} \times \vec {E}} \right] = 0,\,\,\,\,\left[ {{{{\vec {i}}}_{z}} \times \vec {H}} \right] = 0,$(3)
${{\vec {E}}_{i}} = - \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\nabla \left( {\nabla {{{\vec {A}}}_{i}}} \right) + k_{1}^{2}{{{\vec {A}}}_{i}}} \right),$(5)
${{\vec {A}}_{i}} = \vec {p}\frac{{\exp ( - i{{k}_{1}}{{R}_{0}})}}{{4\pi {{R}_{0}}}},\,\,\,\,{{R}_{0}} = \left| {\vec {r} - {{{\vec {r}}}_{0}}} \right|.$Рис. 1.
Геометрия задачи: рассеяние на экране, лежащем на границе полупространства (а), и на верхней границе диэлектрического слоя (б).
В формулах (3)–(5) ${{k}_{1}} = \omega \sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}} $ – волновое число среды вне слоя ($\omega $ – круговая частота), ${{\zeta }_{1}} = \sqrt {{{{{\mu }_{1}}} \mathord{\left/ {\vphantom {{{{\mu }_{1}}} {{{\varepsilon }_{1}}}}} \right. \kern-0em} {{{\varepsilon }_{1}}}}} $ – волновой импеданс среды верхнего полупространства, $\vec {p}$ – момент диполя, причем $\vec {p} = {{\vec {i}}_{z}}$. В результате полное поле представляется в виде суммы первичного и вторичного (рассеянного) полей. А именно
(6)
$\vec {E} = \vec {E}_{{}}^{0} + \vec {E}_{{}}^{1},\,\,\,\,\vec {H} = \vec {H}_{{}}^{0} + \vec {H}_{{}}^{1},$где первичные поля $\vec {E}_{{}}^{0},\;\vec {H}_{{}}^{0}$ определяются из задачи дифракции поля диполя в отсутствие экрана. Решение данной задачи общеизвестно и здесь не приводится. Будем также считать, что на бесконечности выполнены условия излучения для рассеянного поля:
(7)
$\begin{gathered} \mathop {\lim }\limits_{r \to \infty } \vec {E}_{{}}^{1} = 0,\,\,\,\,\mathop {\lim }\limits_{r \to \infty } \vec {H}_{{}}^{1} = 0, \\ \operatorname{Im} {{\varepsilon }_{p}},{{\mu }_{p}} < 0,\,\,\,\,p = 1,2, \\ \end{gathered} $2. ВЫВОД ОСНОВНЫХ СООТНОШЕНИЙ
Будем решать поставленную задачу при помощи МПГУ. С этой целью “перенесем” граничное условие с поверхности экрана на некоторое расстояние $\delta > 0$ [7–11]. Тогда граничное условие (при $z = \delta $) примет вид
(8)
${{\vec {i}}_{z}} \times \vec {E}_{{}}^{1} = - {{\vec {i}}_{z}} \times \vec {E}_{{}}^{0},\,\,\,\,\vec {r} \in {{S}_{\delta }},$(9)
$\vec {E}_{{}}^{1} = - \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\nabla (\nabla \vec {A}) + k_{1}^{2}\vec {A}} \right).$В формуле (9) потенциал $\vec {A}$ определяется из соотношения (в декартовых координатах) [1]:
(10)
$\vec {A} = \int\limits_S {\hat {G}(\vec {r},\vec {r}{\kern 1pt} ')\vec {j}(\vec {r}{\kern 1pt} ')ds{\kern 1pt} '} ,$(11)
$\hat {G}\vec {j} = \left( {\begin{array}{*{20}{c}} {{{g}_{{11}}}}&0&0 \\ 0&{{{g}_{{11}}}}&0 \\ {\frac{{\partial {{g}_{{31}}}}}{{\partial x}}}&{\frac{{\partial {{g}_{{31}}}}}{{\partial y}}}&{{{g}_{{33}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{j}_{{x{\kern 1pt} '}}}} \\ {{{j}_{{y\,'}}}} \\ 0 \end{array}} \right).$Функции ${{g}_{{11}}},\;{{g}_{{31}}},\;{{g}_{{33}}}$ в формуле (11) представляются в виде:
(12)
${{g}_{{11}}} = \frac{1}{{2\pi }}\int\limits_0^\infty {{{v}_{{11}}}(\kappa ,z,z{\kern 1pt} '){{J}_{0}}(\kappa {{R}_{ \bot }})\kappa d\kappa } ,$(13)
${{g}_{{31}}} = \frac{1}{{2\pi }}\int\limits_0^\infty {{{v}_{{31}}}(\kappa ,z,z{\kern 1pt} '){{J}_{0}}(\kappa {{R}_{ \bot }})\kappa d\kappa } ,$(14)
${{g}_{{33}}} = \frac{1}{{2\pi }}\int\limits_0^\infty {{{v}_{{33}}}(\kappa ,z,z{\kern 1pt} '){{J}_{0}}(\kappa {{R}_{ \bot }})\kappa d\kappa } ,$причем спектральные функции ${{v}_{{11}}},{{v}_{{31}}},{{v}_{{33}}}$ являются решениями одномерных краевых задач:
В формулах (15)–(17) квадратные скобки вновь означают скачки соответствующих величин либо при $z = 0$, либо при $z = 0$ и $z = - h$ соответственно для задач дифракции на экране, лежащем или на границе диэлектрического полупространства, или на верхней границе диэлектрического слоя. Функция $k(z)$ в указанных двух случаях слоистой среды имеет вид
(18)
$k(z) = \left\{ \begin{gathered} {{k}_{1}},\,\,\,\,z > 0, \hfill \\ {{k}_{2}},\,\,\,\,z < 0, \hfill \\ \end{gathered} \right.$либо
(19)
$k(z) = \left\{ \begin{gathered} {{k}_{1}},\,\,\,\,z > 0,\,\,\,\,z < - h, \hfill \\ {{k}_{2}},\,\,\,\, - h < z < 0. \hfill \\ \end{gathered} \right.$Решения задач (15)–(17) получаются аналогично тому, как это рассмотрено в работе [1] (см. также ниже).
Подставим формулу (9) в граничное условие (8). В результате с учетом (10) и (11) получим следующее интегральное уравнение первого рода относительно неизвестного тока $\vec {j}$:
(20)
${{\vec {i}}_{z}} \times \left[ {\frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\int\limits_S {\left( {{{\nabla }_{ \bot }}\left( {\left( {\nabla _{ \bot }^{'}\tilde {g}} \right)\vec {j}} \right) - k_{1}^{2}{{g}_{{11}}}\vec {j}} \right)ds{\kern 1pt} '} } \right] = - {{\vec {i}}_{z}} \times {{\vec {E}}^{0}},$(21)
${{g}_{{11}}} = - \frac{i}{{4\pi }}\int\limits_0^\infty {(1 + {{R}_{{11}}}} )\exp ( - i{{\gamma }_{1}}\delta ){{J}_{0}}(\kappa {{R}_{ \bot }})\frac{{\kappa d\kappa }}{{{{\gamma }_{1}}}},$(22)
$\begin{gathered} \tilde {g} = - \frac{i}{{4\pi }}\int\limits_0^\infty {({{\kappa }^{2}} + k_{1}^{2}{{R}_{{11}}}} + \gamma _{1}^{2}{{R}_{{33}}}) \times \\ \times \,\,\exp ( - i{{\gamma }_{1}}\delta ){{J}_{0}}(\kappa {{R}_{ \bot }})\frac{{d\kappa }}{{{{\gamma }_{1}}\kappa }}, \\ \end{gathered} $(23)
${{R}_{{11}}} = \frac{{{{\gamma }_{1}} - {{\mu }_{{12}}}{{\gamma }_{2}}}}{{{{\gamma }_{1}} + {{\mu }_{{12}}}{{\gamma }_{2}}}},\,\,\,\,{{R}_{{33}}} = \frac{{{{\gamma }_{1}} - {{\varepsilon }_{{12}}}{{\gamma }_{2}}}}{{{{\gamma }_{1}} + {{\varepsilon }_{{12}}}{{\gamma }_{2}}}},$(24)
$\begin{gathered} {{R}_{{11}}} = \frac{{\left( {\gamma _{2}^{2}{{\mu }_{{12}}} - \gamma _{1}^{2}{{\mu }_{{21}}}} \right)\operatorname{tg} \left( {{{\gamma }_{2}}h} \right)}}{{2i{{\gamma }_{1}}{{\gamma }_{2}} - \left( {\gamma _{2}^{2}{{\mu }_{{12}}} + \gamma _{1}^{2}{{\mu }_{{21}}}} \right)\operatorname{tg} \left( {{{\gamma }_{2}}h} \right)}}, \\ {{R}_{{33}}} = \frac{{\left( {\gamma _{2}^{2}{{\varepsilon }_{{12}}} - \gamma _{1}^{2}{{\varepsilon }_{{21}}}} \right)\operatorname{tg} \left( {{{\gamma }_{2}}h} \right)}}{{2i{{\gamma }_{1}}{{\gamma }_{2}} - \left( {\gamma _{2}^{2}{{\varepsilon }_{{12}}} + \gamma _{1}^{2}{{\varepsilon }_{{21}}}} \right)\operatorname{tg} \left( {{{\gamma }_{2}}h} \right)}}. \\ \end{gathered} $Для дальнейшего удобно считать, что граница поверхности экрана совпадает с координатной линией в некоторой ортогональной системе координат $(\xi ,\eta )$. Пусть в этой системе координат
(25)
$\begin{gathered} x = x(\xi ,\eta ),\,\,\,\,y = y(\xi ,\eta ), \\ \xi \in [{{\xi }_{1}},{{\xi }_{2}}],\,\,\,\,\eta \in [{{\eta }_{1}},{{\eta }_{2}}]. \\ \end{gathered} $Нетрудно показать, что в этом случае уравнение (20) сводится к следующей системе двумерных интегральных уравнений (СИУ) относительно неизвестных компонент тока ${{j}_{{\xi '}}},\;{{j}_{{\eta '}}}$:
(26)
$\begin{gathered} \int\limits_{{{\eta }_{1}}}^{{{\eta }_{2}}} {\int\limits_{{{\xi }_{1}}}^{{{\xi }_{2}}} {{{K}_{{11}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} '){{{\tilde {j}}}_{{\xi {\kern 1pt} '}}}(\xi {\kern 1pt} ',\eta {\kern 1pt} ')d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } + \\ + \,\,\int\limits_{{{\eta }_{1}}}^{{{\eta }_{2}}} {\int\limits_{{{\xi }_{1}}}^{{{\xi }_{2}}} {{{K}_{{12}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} '){{{\tilde {j}}}_{{\eta {\kern 1pt} '}}}(\xi {\kern 1pt} ',\eta {\kern 1pt} ')d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } = - E_{\xi }^{0}(\xi ,\eta ), \\ \int\limits_{{{\eta }_{1}}}^{{{\eta }_{2}}} {\int\limits_{{{\xi }_{1}}}^{{{\xi }_{2}}} {{{K}_{{21}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} '){{{\tilde {j}}}_{{\xi {\kern 1pt} '}}}(\xi {\kern 1pt} ',\eta {\kern 1pt} ')d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } + \\ + \,\,\int\limits_{{{\eta }_{1}}}^{{{\eta }_{2}}} {\int\limits_{{{\xi }_{1}}}^{{{\xi }_{2}}} {{{K}_{{22}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} '){{{\tilde {j}}}_{{\eta {\kern 1pt} '}}}(\xi {\kern 1pt} ',\eta {\kern 1pt} ')d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } = - E_{\eta }^{0}(\xi ,\eta ), \\ \end{gathered} $(27)
$\begin{gathered} {{K}_{{11}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} ') = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\xi }}}}\frac{{{{\partial }^{2}}\tilde {g}}}{{\partial \xi \partial \xi {\kern 1pt} '}} - k_{1}^{2}{{g}_{{11}}}{{t}_{{11}}}{{h}_{{\xi {\kern 1pt} '}}}} \right), \\ {{K}_{{12}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} ') = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\xi }}}}\frac{{{{\partial }^{2}}\tilde {g}}}{{\partial \xi \partial \eta {\kern 1pt} '}} - k_{1}^{2}{{g}_{{11}}}{{t}_{{12}}}{{h}_{{\eta {\kern 1pt} {\kern 1pt} '}}}} \right), \\ {{K}_{{21}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} ') = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\eta }}}}\frac{{{{\partial }^{2}}\tilde {g}}}{{\partial \eta \partial \xi {\kern 1pt} '}} + k_{1}^{2}{{g}_{{11}}}{{t}_{{12}}}{{h}_{{\xi \,'}}}} \right), \\ {{K}_{{22}}}(\xi ,\eta ,\xi {\kern 1pt} ',\eta {\kern 1pt} ') = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\eta }}}}\frac{{{{\partial }^{2}}\tilde {g}}}{{\partial \eta \partial \eta {\kern 1pt} '}} - k_{1}^{2}{{g}_{{11}}}{{t}_{{11}}}{{h}_{{\eta {\kern 1pt} '{\kern 1pt} }}}} \right). \\ \end{gathered} $В формуле (26) обозначено ${{\tilde {j}}_{{\xi \,'}}} = {{h}_{{\eta {\kern 1pt} '}}}{{j}_{{\xi {\kern 1pt} '}}},$ ${{\tilde {j}}_{{\eta {\kern 1pt} '}}} = {{h}_{{\xi {\kern 1pt} '}}}{{j}_{{\eta \,'}}}$ (${{h}_{{\xi {\kern 1pt} '}}},{{h}_{{\eta {\kern 1pt} '}}}$ – коэффициенты Ламе соответствующей системы координат). Величины ${{t}_{{11}}}$ и ${{t}_{{12}}}$ представляют собой элементы матрицы перехода, определяемой из соотношения
(28)
$\left( {\begin{array}{*{20}{c}} {{{j}_{\xi }}} \\ {{{j}_{\eta }}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{t}_{{11}}}}&{{{t}_{{12}}}} \\ { - {{t}_{{12}}}}&{{{t}_{{11}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{j}_{{\xi {\kern 1pt} '}}}} \\ {{{j}_{{\eta {\kern 1pt} '}}}} \end{array}} \right).$СИУ (26) решали с использованием метода Крылова–Боголюбова, для чего была введена сетка
где ${{\Delta }_{1}} = \frac{{{{\xi }_{2}} - {{\xi }_{1}}}}{{2{{N}_{1}}}},$ ${{\Delta }_{2}} = \frac{{{{\eta }_{2}} - {{\eta }_{1}}}}{{2{{N}_{2}}}}$. Далее заменяли неизвестные компоненты токов (точнее функции ${{\tilde {j}}_{{\xi \,'}}},{{\tilde {j}}_{{\eta {\kern 1pt} '}}}$) линейной комбинацией кусочно-постоянных функций(31)
$\begin{gathered} {{{\tilde {j}}}_{{\xi {\kern 1pt} '}}}(\xi ,\eta ) = \sum\limits_{j = 1}^{{{N}_{1}}} {\sum\limits_{l = 1}^{{{N}_{2}}} {{{c}_{{jl}}}{{f}_{j}}(\xi ){{q}_{l}}(\eta )} } , \\ {{{\tilde {j}}}_{{\eta {\kern 1pt} '}}}(\xi ,\eta ) = \sum\limits_{j = 1}^{{{N}_{1}}} {\sum\limits_{l = 1}^{{{N}_{2}}} {{{d}_{{jl}}}{{f}_{j}}(\xi ){{q}_{l}}(\eta )} ,} \\ \end{gathered} $(32)
${{f}_{j}}(\xi ) = \left\{ \begin{gathered} 1,\,\,\,\,\xi \in [{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}},{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}], \hfill \\ 0,\,\,\,\,\xi \notin [{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}},{{{\bar {\xi }}}_{j}} + \Delta _{1}^{{}}], \hfill \\ \end{gathered} \right.$(33)
${{q}_{l}}(\eta ) = \left\{ \begin{gathered} 1,\,\,\,\,\eta \in [{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}},{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}], \hfill \\ 0,\,\,\,\,\eta \notin [{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}},{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}]. \hfill \\ \end{gathered} \right.$После подстановки формул (31) в СИУ (26) и приравнивания левых и правых частей полученных равенств в точках коллокации, получим следующую систему линейных алгебраических уравнений (СЛАУ):
(34)
$\begin{gathered} \sum\limits_{j = 1}^{{{N}_{1}}} {\sum\limits_{l = 1}^{{{N}_{2}}} {\left( {A_{{11}}^{{st,jl}}{{c}_{{jl}}} + A_{{12}}^{{st,jl}}d_{{jl}}^{{}}} \right)} } = u_{1}^{{st}}, \\ \sum\limits_{j = 1}^{{{N}_{1}}} {\sum\limits_{l = 1}^{{{N}_{2}}} {\left( {A_{{21}}^{{st,jl}}c_{{jl}}^{{}} + A_{{22}}^{{st,jl}}d_{{jl}}^{{}}} \right)} } = u_{2}^{{st}}, \\ \end{gathered} $(35)
$A_{{pq}}^{{st,jl}} = \int\limits_{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}^{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}} {\int\limits_{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}^{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}} {{{K}_{{pq}}}({{{\bar {\xi }}}_{s}},{{{\bar {\eta }}}_{t}},\xi {\kern 1pt} ',\eta {\kern 1pt} ')d\xi {\kern 1pt} 'd\eta {\kern 1pt} ',} } $(36)
$\begin{gathered} u_{1}^{{st}} = - E_{\xi }^{0}({{{\bar {\xi }}}_{s}},{{{\bar {\eta }}}_{t}}),\,\,\,u_{2}^{{st}} = - E_{\eta }^{0}({{{\bar {\xi }}}_{s}},{{{\bar {\eta }}}_{t}}),\,\,\,p,q = 1,2, \\ s = 1,2,...,{{N}_{1}},\,\,\,t = 1,2,...,{{N}_{2}}. \\ \end{gathered} $Рассмотрим вопрос о вычислении матричных элементов СЛАУ (34). Повторные интегралы в формуле (35) сводятся к следующим:
(37)
$\begin{gathered} A_{{11}}^{{st,jl}} = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\xi }}}}\int\limits_{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}^{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}} {\left. {\frac{{\partial{ \tilde {g}}}}{{\partial \xi }}} \right|_{{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}}^{{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}}}d\eta '{\kern 1pt} } - k_{1}^{2}\int\limits_{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}^{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}} {\int\limits_{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}^{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}} {{{g}_{{11}}}{{t}_{{11}}}{{h}_{{\xi {\kern 1pt} '}}}d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } } \right), \hfill \\ A_{{12}}^{{st,jl}} = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\xi }}}}\int\limits_{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}^{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}} {\left. {\frac{{\partial{ \tilde {g}}}}{{\partial \xi }}} \right|_{{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}}^{{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}}}d\xi {\kern 1pt} '} + k_{1}^{2}\int\limits_{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}^{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}} {\int\limits_{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}^{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}} {{{g}_{{11}}}{{t}_{{12}}}{{h}_{{\eta {\kern 1pt} '}}}d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } } \right), \hfill \\ A_{{21}}^{{st,jl}} = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\eta }}}}\int\limits_{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}^{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}} {\left. {\frac{{\partial{ \tilde {g}}}}{{\partial \eta }}} \right|_{{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}}^{{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}}}d\eta {\kern 1pt} '} - k_{1}^{2}\int\limits_{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}^{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}} {\int\limits_{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}^{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}} {{{g}_{{11}}}{{t}_{{12}}}{{h}_{{\xi {\kern 1pt} '}}}d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } } \right), \hfill \\ A_{{22}}^{{st,jl}} = \frac{{i{{\zeta }_{1}}}}{{{{k}_{1}}}}\left( {\frac{1}{{{{h}_{\eta }}}}\int\limits_{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}^{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}} {\left. {\frac{{\partial{ \tilde {g}}}}{{\partial \eta }}} \right|_{{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}}^{{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}}}d\xi {\kern 1pt} '} + k_{1}^{2}\int\limits_{{{{\bar {\eta }}}_{l}} - {{\Delta }_{2}}}^{{{{\bar {\eta }}}_{l}} + {{\Delta }_{2}}} {\int\limits_{{{{\bar {\xi }}}_{j}} - {{\Delta }_{1}}}^{{{{\bar {\xi }}}_{j}} + {{\Delta }_{1}}} {{{g}_{{11}}}{{t}_{{11}}}{{h}_{{\eta {\kern 1pt} '}}}d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } } \right). \hfill \\ \end{gathered} $Нетрудно видеть, что подынтегральные функции в формулах (37) выражаются через величины ${{g}_{{11}}}$ и ${{\partial{ \tilde {g}}} \mathord{\left/ {\vphantom {{\partial{ \tilde {g}}} {\partial {{R}_{ \bot }}}}} \right. \kern-0em} {\partial {{R}_{ \bot }}}}$. Как следует из асимптотик подынтегральных функций, в интегралах (21) и (22) данные интегралы сходятся очень медленно (при малых $\delta $). Для ускорения сходимости мы выделили асимптотики соответствующих функций при $\kappa \to \infty $. В результате будем иметь
(38)
$\begin{gathered} {{g}_{{11}}} = g_{{11}}^{s} + g_{{11}}^{r} \equiv (1 + R_{{11}}^{\infty })\frac{{\exp ( - i{{k}_{1}}R)}}{{4\pi R}} - \\ - \,\,\frac{i}{{4\pi }}\int\limits_0^\infty {({{R}_{{11}}} - R_{{11}}^{\infty }} )\exp ( - i{{\gamma }_{1}}\delta ){{J}_{0}}(\kappa {{R}_{ \bot }})\frac{{\kappa d\kappa }}{{{{\gamma }_{1}}}}, \\ \end{gathered} $(39)
$\begin{gathered} \frac{{\partial{ \tilde {g}}}}{{\partial {{R}_{ \bot }}}} = \frac{{\partial {{{\tilde {g}}}^{s}}}}{{\partial {{R}_{ \bot }}}} + \frac{{\partial {{{\tilde {g}}}^{r}}}}{{\partial {{R}_{ \bot }}}} \equiv \\ \equiv \left[ {(1 - R_{{33}}^{\infty })\frac{d}{{d{{R}_{ \bot }}}}\left( {\frac{{\exp ( - i{{k}_{1}}R)}}{{4\pi R}}} \right) + \frac{i}{{4\pi }}{{F}_{\infty }}\frac{{R - \delta }}{{{{R}_{ \bot }}}}} \right] + \\ + \,\,\frac{i}{{4\pi }}\int\limits_0^\infty {\left[ {\left( {{{\kappa }^{2}}(R_{{33}}^{\infty } - {{R}_{{33}}}) + k_{1}^{2}({{R}_{{11}}} + {{R}_{{33}}})} \right)_{{}}^{{}}} \right.} \times \\ \times \,\,\left. {\exp ( - i{{\gamma }_{1}}\delta ) - \frac{{{{F}_{\infty }}{{\gamma }_{1}}}}{\kappa }\exp ( - \kappa \delta )} \right]{{J}_{1}}(\kappa {{R}_{ \bot }})\frac{{d\kappa }}{{{{\gamma }_{1}}}}, \\ \end{gathered} $где в случае задачи дифракции на экране, расположенном на границе полупространства, получаем
(40)
$\begin{gathered} R_{{11}}^{\infty } = \frac{{{{\mu }_{{21}}} - 1}}{{{{\mu }_{{21}}} + 1}},\,\,\,R_{{33}}^{\infty } = \frac{{{{\varepsilon }_{{21}}} - 1}}{{{{\varepsilon }_{{21}}} + 1}}, \\ {{F}_{\infty }} = i\left( {k_{1}^{2}(R_{{11}}^{\infty } + R_{{33}}^{\infty }) + \frac{{\left( {k_{1}^{2} - k_{2}^{2}} \right){{\varepsilon }_{{21}}}}}{{{{{({{\varepsilon }_{{21}}} + 1)}}^{2}}}}} \right), \\ \end{gathered} $а в случае рассеяния на экране, лежащем на верхней границе диэлектрического слоя, –
(41)
$\begin{gathered} R_{{11}}^{\infty } = \frac{{{{\mu }_{{21}}} - {{\mu }_{{12}}}}}{{2 + {{\mu }_{{21}}} + {{\mu }_{{12}}}}},\,\,\,\,R_{{33}}^{\infty } = \frac{{{{\varepsilon }_{{21}}} - {{\varepsilon }_{{12}}}}}{{2 + {{\varepsilon }_{{21}}} + {{\varepsilon }_{{12}}}}}, \\ {{F}_{\infty }} = i\left( {k_{1}^{2}(R_{{11}}^{\infty } + R_{{33}}^{\infty }) + \frac{{k_{1}^{2} - k_{2}^{2}}}{{2 + {{\varepsilon }_{{21}}} + {{\varepsilon }_{{12}}}}}} \right). \\ \end{gathered} $В формулах (38) и (39) $R = \sqrt {R_{ \bot }^{2} + {{\delta }^{2}}} $. Заметим, что при выводе формулы (39) использовано тождество [13]
(42)
$\int\limits_0^\infty {{{J}_{1}}(\kappa {{R}_{ \bot }})\exp ( - \kappa \delta )\frac{{d\kappa }}{\kappa }} = \frac{{R - \delta }}{{{{R}_{ \bot }}}}.$Как нетрудно показать, подынтегральные выражения в интегралах в формулах (38) и (39) убывают как ${1 \mathord{\left/ {\vphantom {1 {{{\kappa }^{{5/2}}}}}} \right. \kern-0em} {{{\kappa }^{{5/2}}}}}$ (для малых $\delta $) при $\kappa \to \infty $, т.е. легко могут быть найдены численно.
Отметим, что в случае дифракции на экране, расположенном на верхней границе диэлектрического слоя, подынтегральные выражения в формулах (38) и (39) содержат особенности на комплексной плоскости $\kappa $. А именно имеются полюсы, которые расположены на действительной оси (в случае отсутствия поглощения в среде слоя) или вблизи нее. Для преодоления трудностей, связанных с интегрированием в окрестности полюсов при условии, что поглощение в среде мало (считаем, что имеются малые потери в среде слоя), используем методику, аналогичную той, которая предложена работе [14]. Будем предполагать, что ${{k}_{2}} > {{k}_{1}}$. Сделаем замену $\kappa = {{k}_{1}}\sin \psi $ в интегралах в формулах (38) и (39) и запишем их в виде
(43)
$\begin{gathered} \int\limits_0^\infty {\frac{{F(\kappa )}}{{\chi (\kappa )}}d\kappa } = \int\limits_0^{\pi /2 + i\infty } {\frac{{{{F}_{1}}(\psi )}}{{\chi (\psi )}}} d\psi = \int\limits_0^{\pi /2} {\frac{{{{F}_{1}}(\psi )}}{{\chi (\psi )}}} d\psi + \\ + \,\,\int\limits_{\pi /2}^{\pi /2 + i{{\beta }_{{12}}}} {\frac{{{{F}_{1}}(\psi )}}{{\chi (\psi )}}} d\psi + \int\limits_{\pi /2 + i{{\beta }_{{12}}}}^{\pi /2 + i\infty } {\frac{{{{F}_{1}}(\psi )}}{{\chi (\psi )}}} d\psi , \\ \end{gathered} $В формуле (43) для упрощения записи мы не стали вводить новых обозначений для функции $\chi (\psi )$, которая получается после замены переменной. Первый и третий интегралы в (43) берем от гладких функций и вычисляем стандартными методами. Второй интеграл в (43) находим при помощи замены $\psi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + i\beta $ с последующим применением равенства [14]
(44)
$\begin{gathered} i\int\limits_0^{{{\beta }_{{12}}}} {\frac{{{{F}_{1}}(\beta )}}{{\chi (\beta )}}} d\beta = i\int\limits_0^{{{\beta }_{{12}}}} {\left( {\frac{{{{F}_{1}}(\beta )}}{{\chi (\beta )}} - \sum\limits_l {\frac{{{{\omega }_{l}}}}{{\beta - {{\beta }_{l}}}}} } \right)} d\beta + \\ + \,\,i\sum\limits_l {{{\omega }_{l}}\left[ {\ln \left( {{{\beta }_{{12}}} - {{\beta }_{l}}} \right) - \ln \left( { - {{\beta }_{l}}} \right)} \right]} , \\ \end{gathered} $Сделаем также замечание относительно вычисления интегралов в формуле (37). Для их оценки мы использовали тот факт, что в формулах (38) и (39) функции $g_{{11}}^{s}$ и ${{\partial {{{\tilde {g}}}^{s}}} \mathord{\left/ {\vphantom {{\partial {{{\tilde {g}}}^{s}}} {\partial {{R}_{ \bot }}}}} \right. \kern-0em} {\partial {{R}_{ \bot }}}}$ (которые мы назовем сингулярными частями величин $g_{{11}}^{{}}$ и ${{\partial{ \tilde {g}}} \mathord{\left/ {\vphantom {{\partial{ \tilde {g}}} {\partial {{R}_{ \bot }}}}} \right. \kern-0em} {\partial {{R}_{ \bot }}}}$, т.е. внеинтегральные слагаемые в (38) и (39)) являются быстро меняющимися функциями координат (при приближении точек наблюдения и источника), а оставшиеся интегралы по переменной $\kappa $ меняются медленно в зависимости от координат. Таким образом, интегралы от сингулярных частей следует вычислять, используя, например, адаптивные программы численного интегрирования, а к оставшимся интегралам от регулярных частей можно применить формулу интегрирования, являющуюся двумерным аналогом формулы прямоугольников [12]. Данный факт позволяет существенно сократить время счета матричных элементов на ЭВМ.
В качестве выходной характеристики задачи рассмотрим диаграмму рассеяния $\vec {F}(\theta ,\varphi )$ волнового поля. Диаграмма получается при помощи перехода к асимптотике рассеянного поля при $r \to \infty $. Эта величина определяется по формуле
где в случае полупространства $p = 1,2$, а в случае диэлектрического слоя $p = 1$. Предполагая отсутствие поглощения в средах, можно получить следующее представление для диаграммы рассеяния:
(46)
$\begin{gathered} \vec {F}(\theta ,\varphi ) = {{F}_{\theta }}(\theta ,\varphi ){{{\vec {i}}}_{\theta }} + {{F}_{\varphi }}(\theta ,\varphi ){{{\vec {i}}}_{\varphi }} = \\ = \int\limits_S {{{{\hat {G}}}_{\infty }}(\vec {r},\vec {r}{\kern 1pt} ')\vec {j}(\vec {r}{\kern 1pt} ')ds{\kern 1pt} '} , \\ \end{gathered} $где
(47)
${{\hat {G}}_{\infty }}\vec {j} = \left( {\begin{array}{*{20}{c}} {f_{{11}}^{\infty }}&{f_{{12}}^{\infty }} \\ {f_{{21}}^{\infty }}&{f_{{22}}^{\infty }} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{{\tilde {j}}}_{{\xi {\kern 1pt} '}}}} \\ {{{{\tilde {j}}}_{{\eta {\kern 1pt} '}}}} \end{array}} \right),$(48)
$f_{{11}}^{\infty } = - i{{\zeta }_{1}}{{k}_{1}}{{h}_{{\xi {\kern 1pt} '}}}\left( {\cos \theta ({{\tau }_{{11}}}\cos \varphi - {{\tau }_{{12}}}\sin \varphi )g_{{11}}^{\infty } + \frac{1}{{{{h}_{{\xi '}}}}}\frac{{\partial g_{{31}}^{\infty }}}{{\partial {{R}_{ \bot }}}}\frac{{\partial {{R}_{ \bot }}}}{{\partial \xi {\kern 1pt} '}}\sin \theta } \right),$(49)
$\begin{gathered} f_{{12}}^{\infty } = - i{{\zeta }_{1}}{{k}_{1}}{{h}_{{\eta {\kern 1pt} '}}}\left( {\cos \theta ({{\tau }_{{12}}}\cos \varphi + {{\tau }_{{11}}}\sin \varphi )g_{{11}}^{\infty } + \frac{{^{{}}}}{{}}} \right. \\ \left. { + \,\,\frac{1}{{{{h}_{{\eta {\kern 1pt} '}}}}}\frac{{\partial g_{{31}}^{\infty }}}{{\partial {{R}_{ \bot }}}}\frac{{\partial {{R}_{ \bot }}}}{{\partial \eta {\kern 1pt} '}}\sin \theta } \right), \\ \end{gathered} $(50)
$f_{{21}}^{\infty } = i{{\zeta }_{1}}{{k}_{1}}{{h}_{{\xi {\kern 1pt} '}}}\left( {{{\tau }_{{11}}}\sin \varphi + {{\tau }_{{12}}}\cos \varphi } \right)g_{{11}}^{\infty },$(51)
$f_{{22}}^{\infty } = i{{\zeta }_{1}}{{k}_{1}}{{h}_{{\eta {\kern 1pt} '}}}\left( {{{\tau }_{{12}}}\sin \varphi - {{\tau }_{{11}}}\cos \varphi } \right)g_{{11}}^{\infty },$(52)
$\begin{gathered} g_{{11}}^{\infty } = \frac{1}{{4\pi }}{{F}_{{11}}}(\theta )\exp ( - i{{k}_{p}}(x{\kern 1pt} '\sin \theta \cos \varphi + \\ + \,\,y{\kern 1pt} '\sin \theta \sin \varphi )), \\ \end{gathered} $(53)
$\begin{gathered} \frac{{\partial g_{{31}}^{\infty }}}{{\partial {{R}_{ \bot }}}} = \pm \frac{1}{{4\pi }}{{F}_{{31}}}(\theta ) \times \\ \times \,\,\operatorname{ctg} \theta \exp ( - i{{k}_{p}}(x{\kern 1pt} '\sin \theta \cos \varphi + y{\kern 1pt} '\sin \theta \sin \varphi )), \\ \end{gathered} $верхний знак относится к верхнему полупространству $z > 0$, $p = 1$ или $p = 2$ в случае дифракции на экране, лежащем на границе полупространства, и $p = 1$ в случае диэлектрического слоя. Величины ${{\tau }_{{11}}}$ и ${{\tau }_{{12}}}$ представляют собой элементы матрицы перехода, определяемой из соотношения
(54)
$\left( {\begin{array}{*{20}{c}} {{{j}_{{x{\kern 1pt} '}}}} \\ {{{j}_{{y{\kern 1pt} '}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\tau }_{{11}}}}&{{{\tau }_{{12}}}} \\ { - {{\tau }_{{12}}}}&{{{\tau }_{{11}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{j}_{{\xi {\kern 1pt} '}}}} \\ {{{j}_{{\eta {\kern 1pt} '}}}} \end{array}} \right).$При этом в случае, когда экран расположен на границе диэлектрического полупространства, получаем
(55)
${{F}_{{11}}}(\theta ) = \left[ \begin{gathered} 1 + {{R}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z > 0, \hfill \\ {{T}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z < 0, \hfill \\ \end{gathered} \right.$(56)
${{F}_{{31}}}(\theta ) = \left[ \begin{gathered} {{R}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}) + {{R}_{{33}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z > 0, \hfill \\ {{T}_{{33}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}) - \frac{{{{\gamma }_{2}}}}{{{{\gamma }_{1}}}}{{T}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z < 0, \hfill \\ \end{gathered} \right.$где в верхних формулах в (55) и (56) $\kappa = {{k}_{1}}\sin \theta ,$ ${{\gamma }_{1}} = {{k}_{1}}\cos \theta ,$ ${{\gamma }_{2}} = \sqrt {k_{2}^{2} - k_{1}^{2}{{{\sin }}^{2}}\theta } $, а в нижних $\kappa = {{k}_{2}}\sin \theta ,$ ${{\gamma }_{1}} = \sqrt {k_{1}^{2} - k_{2}^{2}{{{\sin }}^{2}}\theta } ,$ ${{\gamma }_{2}} = - {{k}_{2}}\cos \theta .$
В случае наличия диэлектрического слоя имеем
(57)
${{F}_{{11}}}(\theta ) = \left[ \begin{gathered} 1 + {{R}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z > 0, \hfill \\ {{T}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z < - h, \hfill \\ \end{gathered} \right.$(58)
${{F}_{{31}}}(\theta ) = \left[ \begin{gathered} {{R}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}) + {{R}_{{33}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z > 0, \hfill \\ {{T}_{{33}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}) - {{T}_{{11}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}}),\,\,\,\,z < - h, \hfill \\ \end{gathered} \right.$где $\kappa = {{k}_{1}}\sin \theta ,$ ${{\gamma }_{1}} = \pm {{k}_{1}}\cos \theta ,$ ${{\gamma }_{2}} = \sqrt {k_{2}^{2} - k_{1}^{2}{{{\sin }}^{2}}\theta } $ (верхний знак относится к верхнему полупространству $z > 0$). В формулах (55)–(58) ${{T}_{{11}}},\;\;{{T}_{{33}}}$ – коэффициенты прохождения плоской волны для диэлектрического полупространства и слоя. В этих формулах мы выделили в явном виде зависимость коэффициентов отражения и прохождения плоской волны от величин ${{\gamma }_{{1,2}}}$.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ
В качестве критерия правильности получаемых результатов мы проверили точность выполнения оптической теоремы [15]. Был рассмотрен случай дифракции поля вертикального диполя на экране, лежащем на границе раздела двух сред (см. рис. 1а). По аналогии с работой [15] можно показать, что оптическая теорема для данной геометрии имеет вид
(59)
$\begin{gathered} \frac{1}{{{{\zeta }_{1}}}}\int\limits_0^{2\pi } {\int\limits_0^{\pi /2} {{{{\left| {{{{\vec {F}}}_{\Sigma }}(\theta ,\varphi )} \right|}}^{2}}} } \sin \theta d\theta + \\ + \,\,\frac{1}{{{{\zeta }_{2}}}}\int\limits_0^{2\pi } {\int\limits_{\pi /2}^\pi {{{{\left| {{{{\vec {F}}}_{\Sigma }}(\theta ,\varphi )} \right|}}^{2}}} } \sin \theta d\theta = - \mathop {\lim }\limits_{\vec {r} \to {{{\vec {r}}}_{0}}} \left( {\operatorname{Re} {{E}_{z}}(\vec {r})} \right). \\ \end{gathered} $Здесь ${{\vec {F}}_{\Sigma }}(\theta ,\varphi )$ – диаграмма рассеяния полного поля в верхнем и нижнем полупространствах. Эта величина имеет вид
(60)
${{\vec {F}}_{\Sigma }}(\theta ,\varphi ) = \left( {F_{\theta }^{0}(\theta ,\varphi ) + {{F}_{\theta }}(\theta ,\varphi )} \right){{\vec {i}}_{\theta }} + {{F}_{\varphi }}(\theta ,\varphi ){{\vec {i}}_{\varphi }},$(61)
$\begin{gathered} {{F}^{0}}(\theta ,\varphi ) = \frac{{i{{k}_{p}}{{\zeta }_{p}}}}{{4\pi }}{{F}_{{33}}}(\theta ) \times \\ \times \,\,\exp ( - i{{k}_{p}}({{x}_{0}}\sin \theta \cos \varphi + {{y}_{0}}\sin \theta \sin \varphi )), \\ \end{gathered} $(62)
${{F}_{{33}}}(\theta ) = \left[ \begin{gathered} \exp (i{{\gamma }_{1}}{{z}_{0}}) + {{R}_{{33}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}})\exp ( - i{{\gamma }_{1}}{{z}_{0}}), \hfill \\ \theta \in (0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}), \hfill \\ {{T}_{{33}}}(\kappa ,{{\gamma }_{1}},{{\gamma }_{2}})\exp ( - i{{\gamma }_{1}}{{z}_{0}}),\,\,\,\,\theta \in ({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},\pi ), \hfill \\ \end{gathered} \right.$$p = 1,2$. Причем в верхней строке в формуле (62) $\kappa = {{k}_{1}}\sin \theta ,$ ${{\gamma }_{1}} = {{k}_{1}}\cos \theta ,$ ${{\gamma }_{2}} = \sqrt {k_{2}^{2} - k_{1}^{2}{{{\sin }}^{2}}\theta } $, а в нижней $\kappa = {{k}_{2}}\sin \theta ,$ ${{\gamma }_{1}} = \sqrt {k_{1}^{2} - k_{2}^{2}{{{\sin }}^{2}}\theta } ,$ γ2 = $ = - {{k}_{2}}\cos \theta .$
В правой части формулы (59) стоит значение вертикальной компоненты полного поля в точке источника. Эта величина представляется в виде
(63)
$ - \mathop {\lim }\limits_{\vec {r} \to {{{\vec {r}}}_{0}}} \left( {\operatorname{Re} {{E}_{z}}(\vec {r})} \right) = - \mathop {\lim }\limits_{\vec {r} \to {{{\vec {r}}}_{0}}} \left( {\operatorname{Re} E_{z}^{0}(\vec {r}) + \operatorname{Re} E_{z}^{1}(\vec {r})} \right),$где
(64)
$\begin{gathered} - \mathop {\lim }\limits_{\vec {r} \to {{{\vec {r}}}_{0}}} \left( {\operatorname{Re} E_{z}^{0}(\vec {r})} \right) = \frac{{{{\zeta }_{1}}k_{1}^{2}}}{{6\pi }} + \\ + \,\,\frac{{{{\zeta }_{1}}}}{{4\pi {{k}_{1}}}}\operatorname{Re} \left( {\int\limits_0^\infty {{{R}_{{33}}}} (\kappa )\exp ( - 2i{{\gamma }_{1}}{{z}_{0}})\frac{{{{\kappa }^{3}}d\kappa }}{{{{\gamma }_{1}}}}} \right), \\ \end{gathered} $(65)
$\begin{gathered} - \mathop {\lim }\limits_{\vec {r} \to {{{\vec {r}}}_{0}}} \left( {\operatorname{Re} E_{z}^{1}(\vec {r})} \right) = \\ = \operatorname{Re} \left( {\int\limits_{{{\eta }_{1}}}^{{{\eta }_{2}}} {\int\limits_{{{\xi }_{1}}}^{{{\xi }_{2}}} {\left( {\frac{{\partial {{{\tilde {g}}}_{1}}}}{{\partial \xi {\kern 1pt} '}}{{{\tilde {j}}}_{{\xi {\kern 1pt} '}}} + \frac{{\partial {{{\tilde {g}}}_{1}}}}{{\partial \eta {\kern 1pt} '}}{{{\tilde {j}}}_{{\eta {\kern 1pt} '}}}} \right)d\xi {\kern 1pt} 'd\eta {\kern 1pt} '} } } \right), \\ \end{gathered} $(66)
${{\tilde {g}}_{1}} = - \frac{1}{{4\pi }}\int\limits_0^\infty {\left( {1 - {{R}_{{33}}}} \right)\exp ( - i{{\gamma }_{1}}{{z}_{0}}){{J}_{0}}(\kappa {{R}_{ \bot }})\kappa d\kappa } .$В формуле (66) обозначено ${{R}_{ \bot }} = $ $ = \sqrt {{{{({{x}_{0}} - x{\kern 1pt} ')}}^{2}} + {{{({{y}_{0}} - y{\kern 1pt} ')}}^{2}}} .$ При численной оценке интегралов в формулах (46) и (65) мы использовали кусочно-постоянную аппроксимацию неизвестных функций ${{\tilde {j}}_{{\xi {\kern 1pt} '}}},{{\tilde {j}}_{{\eta {\kern 1pt} '}}}$ с последующим вычислением двойных интегралов по формуле, являющейся двумерным аналогом формулы прямоугольников.
Был рассмотрен экран круговой, эллиптической и прямоугольной формы, лежащий на границе раздела сред. Параметры сред имели значения ${{\varepsilon }_{1}} = 1,{{\varepsilon }_{2}} = 10$ (магнитная проницаемость всюду равна единице). Размеры экранов были следующие: радиус круглого экрана $ka = 3.1416$, полуоси эллиптического $ka = 3.1416,$ $kb = 1.5708$, половины сторон прямоугольного экрана $ka = 3.1416,$ $kb = 1.5708$, где $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$, $\lambda $ – длина волны. Источник располагался в точках с координатами $(0,0,{{z}_{0}})$, $({a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2},0,{{z}_{0}})$ и $(a,0,{{z}_{0}})$, где $k{{z}_{0}} = 1$. При численном решении задачи дифракции на круговом экране использовались полярные координаты
а на прямоугольном – декартовы $x = \xi ,$ $y = \eta $. При анализе задачи дифракции на эллиптическом экране в качестве подходящих координат применялись следующие:
(68)
$\begin{gathered} x = \frac{d}{2}\left( {\xi + \frac{1}{\xi }} \right)\cos \eta ,\,\,\,\,y = \frac{d}{2}\left( {\xi - \frac{1}{\xi }} \right)\sin \eta , \\ \xi \in [1,{{\xi }_{{\max }}}],\,\,\,\,\eta \in [0,2\pi ]. \\ \end{gathered} $Здесь $d$ – межфокусное расстояние, ${{\xi }_{{\max }}} = \sqrt {\frac{{a + b}}{{a - b}}} $. Число точек коллокации для круглого экрана было выбрано равным ${{N}_{1}} = 7,$ ${{N}_{2}} = 43$, для эллиптического ${{N}_{1}} = 6,$ ${{N}_{2}} = 32$, а для прямоугольного ${{N}_{1}} = 18,$ ${{N}_{2}} = 8$. В табл. 1 представлены значения модуля относительной разности правой и левой части в формуле (59) для рассматриваемых форм экрана. Как видно из таблицы, относительная разность правой и левой части равенства (59) не превосходит $3 \times {{10}^{{ - 3}}}$, т.е. достаточно мала.
Таблица 1.
Проверка точности выполнения оптической теоремы для разных форм экрана
| Форма экрана | Точность выполнения оптической теоремы | ||
|---|---|---|---|
| ${{x}_{0}} = 0$ | ${{x}_{0}} = {a \mathord{\left/ {\vphantom {a 2}} \right. \kern-0em} 2}$ | ${{x}_{0}} = a$ | |
| Круглый | $7.27 \times {{10}^{{ - 4}}}$ | $1.82 \times {{10}^{{ - 3}}}$ | $2.18 \times {{10}^{{ - 3}}}$ |
| Эллиптический | $4.3 \times {{10}^{{ - 4}}}$ | $3.24 \times {{10}^{{ - 4}}}$ | $9.43 \times {{10}^{{ - 4}}}$ |
| Прямоугольный | $5.81 \times {{10}^{{ - 4}}}$ | $1.5 \times {{10}^{{ - 4}}}$ | $1.21 \times {{10}^{{ - 3}}}$ |
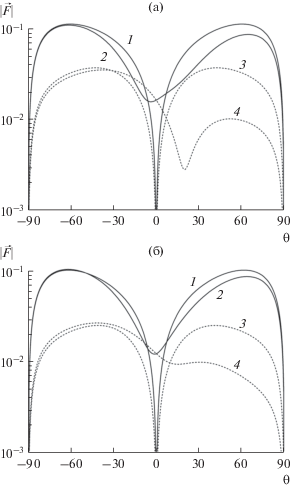
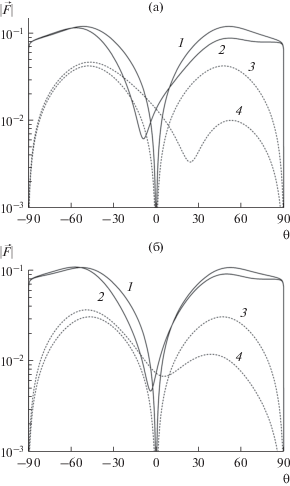
На рис. 2, 3 представлены угловые зависимости модуля диаграммы рассеяния для кругового и прямоугольного экранов, расположенных на границе полупространства и диэлектрического слоя. Размеры экранов были выбраны такими же, что и выше. Параметры сред имели значения ${{\varepsilon }_{1}} = 1,$ ${{\varepsilon }_{2}} = 10 - i{{10}^{{ - 3}}}$. Толщина диэлектрического слоя $kh = 6.2832$. Величина $k{{z}_{0}} = 1$. На рисунках сплошные кривые иллюстрируют угловые зависимости модуля диаграммы полного поля, а штриховыми кривыми показаны зависимости для диаграммы рассеянного поля. Зависимости диаграммы построены для двух углов $\varphi = 0^\circ $ и $\varphi = 180^\circ $ (рассматривалось верхнее полупространство). Как показывают расчеты, угловые зависимости диаграммы рассеяния эллиптического экрана (для выбранных размеров экрана) мало отличаются от соответствующих зависимостей прямоугольного, поэтому мы их не приводим. Как следует из рисунков, в том случае, когда диполь находится на оси z, диаграмма как полного, так и рассеянного поля обращается в нуль при $\theta = 0$. Видно также, что при дифракции на экране круговой формы диаграмма рассеянного поля имеет “провал” примерно при θ = 20°…25° в отличие от случая дифракции на прямоугольном экране, при условии, что источник расположен в точке $(a,0,{{z}_{0}})$. Отметим, что при дифракции на экране, расположенном на верхней границе диэлектрического слоя, зависимости диаграммы рассеяния полного поля имеют достаточно резкие изломы при $\theta = \pm 90^\circ $.
ЗАКЛЮЧЕНИЕ
На основе МПГУ разработан численный алгоритм решения трехмерной задачи дифракции поля электрического диполя на планарном экране, расположенном в плоскослоистой среде. Получены формулы, позволяющие находить диаграмму рассеяния для задачи дифракции на экране, расположенном на границе раздела двух сред или на верхней границе диэлектрического слоя, окруженного одинаковыми однородными полупространствами. В последнем случае предложен эффективный алгоритм нахождения функции Грина слоя. Для тестирования метода проведена проверка точности выполнения оптической теоремы для случая дифракции на экранах круговой, эллиптической и прямоугольной формы, лежащих на границе полупространства. Показано, что точность выполнения оптической теоремы составляет примерно $2 \times {{10}^{{ - 3}}}$ для выбранных параметров задачи. Построены угловые зависимости модуля диаграммы рассеяния для экранов круговой и прямоугольной формы, расположенных на границе полупространства и верхней границе диэлектрического слоя.
Список литературы
Захаров Е.В., Пименов Ю.В. Численный анализ дифракции радиоволн. М.: Радио и связь, 1982.
Литвиненко Л.Н., Просвирнин С.Л. Спектральные операторы рассеяния в задачах дифракции волн на плоских экранах. Киев: Наукова думка, 1984.
Воробьев С.Н., Литвиненко Л.Н., Просвирин С.Л. // Журн. вычисл. математики и мат. физики. 1986. Т. 26. № 6. С. 894.
Nosich A.I., Andrienko A.S. // IEEE Trans. 1994. V. MTT-42. № 2. P. 298.
Панин С.Б., Поединчук А.Е. // Изв. вузов. Радиофизика. 2002. Т. 45. № 8. С. 690.
Schuchinsky A.G., Zelenchuk D.E., Lerer A.M., Dickie R. // IEEE Trans. 2006. V. AP-54. № 2. P. 490.
Кюркчан А.Г., Анютин А.П. // Докл. АН. 2002. Т. 385. № 3. С. 309.
Кюркчан А.Г., Смирнова Н.И. Математическое моделирование в теории дифракции с использованием априорной информации об аналитических свойствах решения. М.: Медиа Паблишер, 2014.
Maнeнкoв C.A. // PЭ. 2007. T. 52. № 12. C. 1413.
Maнeнкoв C.A. // PЭ. 2009. T. 54. № 10. C. 1196.
Кюркчан А.Г., Маненков С.А. // Акуст. журн. 2015. Т. 61. № 3. С. 302.
Маненков С.А. // Радиотехника и электроника. 2019. Т. 64. № 10. С. 943.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971.
Кюpкчан А.Г., Маненков С.А. // Изв. вузов. Радиофизика. 1998. Т. 41. № 7. С. 874.
Еремин Ю.А., Свешников А.Г. // Вестник Моск. ун‑та. Физика. 2015. Т. 70. № 4. С. 43.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника