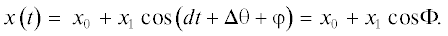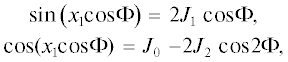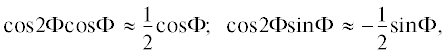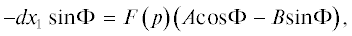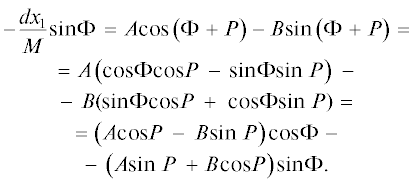Радиотехника и электроника, 2021, T. 66, № 8, стр. 782-790
Анализ фазовой автоподстройки при воздействии гармонической помехи и шума
Б. И. Шахтарин *
Московский государственный технический университет им. Н.Э. Баумана
105005 Москва, 2-я Бауманская ул., Российская Федерация
* E-mail: shakhtarin@mail.ru
Поступила в редакцию 27.10.2020
После доработки 27.10.2020
Принята к публикации 24.03.2021
Аннотация
Рассмотрены приоритетные работы В.И. Тихонова в изучении статистических характеристик фазовой автоподстройки (ФАП), когда на ее вход воздействует помеха в форме шума. В продолжение работ В.И. Тихонова получены основные соотношения метода гармонического баланса, и в процессе их вывода отмечены стадии упрощения, по которым можно судить о степени точности полученных соотношений. В частном случае уравнения совпадают с соотношениями, полученными автором ранее. Найдены значения выходных параметров предполагаемого решения ДУ ФАП.
ВВЕДЕНИЕ
Воздействие помех на системы синхронизации в устройствах радионавигации (ГЛОНАСС, GPS и др.), радиосвязи и радиолокации рассматривалось в ряде работ [1–16]. Среди помех особое внимание уделяется шумовым и активным помехам, к которым, в частности, относятся гармонические прицельные и перестраиваемые помехи. Особое внимание в последние годы уделяется воздействию гармонических помех на системы фазовой автоподстройки.
Определяющая роль в исследовании воздействия помех на систему фазовой автоподстройки (ФАП) принадлежит В.И. Тихонову. Основные статистические характеристики ФАП при воздействии шумовых и гармонических помех получены В.И. Тихоновым и его ближайшими учениками.
К статистическим характеристикам ФАП относятся плотность распределения вероятности (ПРВ) сигнала ошибки, его числовые характеристики в стационарном и переходящих режимах, частота вращательных движений, время достижения указанным сигналом соответствующих порогов и, в частности, среднее время до срыва слежения.
Первые исследования приведенных характеристик были начаты В.И. Тихоновым. К этим работам он активно привлекал своих учеников. В результате комплекса работ была создана теория ФАП, функционирующая под воздействием помех, что имело большое практическое значение и породило массу работ его последователей.
При содействии В.И. Тихонова начато исследование ФАП и при воздействии на нее гармонических помех [11], которое продолжилось в работах [12, 13] на основе применения метода гармонического баланса [17].
В [17, 18] методом гармонического баланса найден ряд динамических характеристик ФАП при условии, что частота гармонической помехи лежит за пределами полосы синхронизации ФАП, причем в [17] это сделано при условии малой амплитуды биений.
1. РАБОТЫ В.И. ТИХОНОВА И ЕГО БЛИЖАЙШИХ УЧЕНИКОВ ПО ИССЛЕДОВАНИЮ ВОЗДЕЙСТВИЯ ШУМОВ И ГАРМОНИЧЕСКИХ ПОМЕХ НА СИСТЕМУ ФАП
Рассмотрим подробно вывод основного соотношения метода гармонического баланса, из которого видна степень приближения полученного результата и, следовательно, возможность оценки его точности. В работе [1, с. 1192] была получена ставшая общеизвестной формула Тихонова
(1)
$W\left( x \right) = \frac{1}{{2\pi {{I}_{0}}\left( r \right)}}\exp \left( {r\cos x} \right),\,\,\,\,~~\left| x \right| \leqslant \pi ~,~$Формула Тихонова (1) соответствует нулевой начальной расстройке ${{{\text{Д}}}_{0}}$ по частоте сигналов, подаваемых на фазовый дискриминатор (рис. 1).
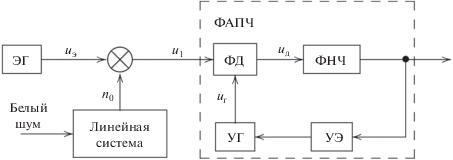
Рис. 1.
Структурная схема ФАП (по В.И. Тихонову): ЭГ – эталонный генератор, ФД – фазовый детектор (дискриминатор), ФНЧ – фильтр низкой частоты, УЭ – управляющий элемент, УГ – управляемый генератор, сигналы uэ – эталонный, uг – от генератора, uд – от дискиминатора, u1 – на входе ФАП.
Там же [1] представлена ПРВ $W\left( x \right)$ в интегральной форме для случая ${{{\text{Д}}}_{0}} \ne 0$ [1, ф-ла (21)] с нормирующим множителем N, в который входит квадрат модуля модифицированной функции Бесселя с мнимым индексом ${{\left| {{{I}_{{iv}}}\left( r \right)} \right|}^{2}},~\left( {v = {{{\text{Д}}}_{0}}} \right)$. В этом случае при вычислениях ПРВ $W\left( x \right)$ требовалось использовать известные таблицы Моргана.
В работе [3, ф-ла (9)] интегральная формула Тихонова была преобразована в быстросходящийся ряд по модифицированным функциям Бесселя с целочисленным индексом и исследована сходимость полученного ряда. Величина ${{\left| {{{I}_{{iv}}}\left( r \right)} \right|}^{2}}$ была представлена (рис. 2) [1, рис. 2.2 ; 4, ф-ла (XIX)] в форме ряда
(2)
${{\left| {{{I}_{{iv}}}\left( r \right)} \right|}^{2}} = \frac{{{\text{sh}}\left( {\pi v} \right)}}{{\pi v}}\left[ {I_{0}^{2}\left( r \right) + 2{{v}^{2}}\mathop \sum \limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{n}}{{I}_{n}}\left( r \right)}}{{{{n}^{2}} + {{v}^{2}}}}} \right],$Рис. 2.
Зависимость квадрата модуля модифицированной функции Бесселя от аргумента и чисто мнимого порядка iv.

Впервые результаты расчета ПРВ $W\left( x \right)$ (при ${{{\text{Д}}}_{0}} \ne 0$) опубликованы в работе [5].
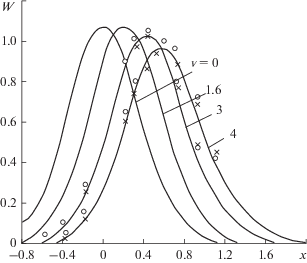
С учетом оценки сходимости ряда для ПРВ $W\left( x \right)$ [3] при точности $\varepsilon = {{10}^{{ - 4}}}$ получено, что число слагаемых отрезка ряда равно $N = 4,~7,~10,~15,~22,~26$ при ОСШ $r = 1,~2.7,~4.5,~7.4,~12.2,~17.$ На рис. 3 приведены ПРВ $W\left( x \right)$ при $r = 7.4$ и различных значениях $v = {{{\text{Д}}}_{0}}$ [3].
Рис. 3.
Плотность распределения вероятностей фазовой ошибки при отношении сигнал/шум r = 7.4 и разных значениях частотной расстройки, приближенные значения ПРВ отмечены крестиками и кружками.
На основе ПРВ $W\left( x \right)$ в форме рядов получены формулы для начальных моментов ${{m}_{{1x}}}$ и ${{m}_{{2x}}}$ сигнала рассогласования ФАП [4], а также формула дисперсии (при $v = 0$) [7]:
(3)
$\sigma _{x}^{2} = \frac{{{{\pi }^{2}}}}{3} + 4\mathop \sum \limits_{n = 1}^\infty \frac{{{{{\left( { - 1} \right)}}^{n}}{{I}_{n}}\left( r \right)}}{{{{n}^{2}}{{I}_{0}}\left( r \right)}}.$Была разработана разностная схема для уравнения [1, ф-ла (13)] и найдена ПРВ $W\left( {x,t} \right)$ в переходном режиме (рис. 4) при $r = 2.5;~\,\,v = 0$ и ${{x}_{0}} = 1;$ $~{{W}_{0}}\left( x \right) = \delta \left( {x - {{x}_{0}}} \right).$
Рис. 4.
Плотность распределения вероятностей фазовой ошибки W(x, t) в переходном режиме при r = 2.5 и нулевой расстройке по частоте.

Следует отметить, что в первой работе [1] В.И. Тихоновым решена и другая (в отличие от ПРВ $W\left( x \right)$) проблема статистической динамики ФАП, а именно получена характеристика вращательных движений ${{\beta }_{c}}$ в системе ФАП, которая после преобразований может быть представлена в виде [4]
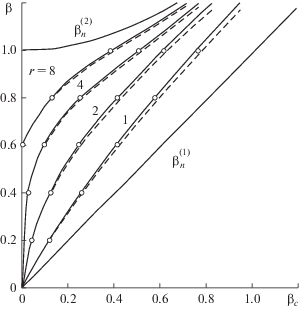
где $c\left( {v,r} \right) = {{{\text{sh}}(\pi v)} \mathord{\left/ {\vphantom {{{\text{sh}}(\pi v)} {2{{\pi }^{2}}}}} \right. \kern-0em} {2{{\pi }^{2}}}}{{\left| {{{I}_{{iv}}}\left( r \right)} \right|}^{2}}~.~$ Эта зависимость представлена на рис. 5, где $\beta = {v \mathord{\left/ {\vphantom {v r}} \right. \kern-0em} r}$.Рис. 5.
Характеристика вращательных движений ФАП (сплошные кривые), где β = v/r, βc – нормированная частота вращательных движений; асимптотика βc для систем ФАП второго порядка (штриховые).
В работе [10], а также [5, 8] аналитически, экспериментально и посредством моделирования была детально исследована проблема срыва слежения в системе ФАП. В частности, рассмотрена задача достижения границ марковским процессом [10], найдены формулы для начальных моментов времени ${{T}_{1}}$ до срыва слежения. Показано, что нормированное среднее время ${{\gamma }_{c}} = {{\Omega }}{{T}_{c}}$ (${{\Omega }}$ – полоса синхронизации ФАП, ${{T}_{c}} = {{T}_{1}}$) может быть представлено в виде (рис. 6, $\beta = {v \mathord{\left/ {\vphantom {v r}} \right. \kern-0em} r}$)
Рис. 6.
Зависимости нормированного среднего значения времени до срыва слежения от параметров ФАП (сплошные кривые), расчет по асимптотическим формулам (штриховые) и нормированное среднеквадратическое значение времени до срыва слежения (крестики).

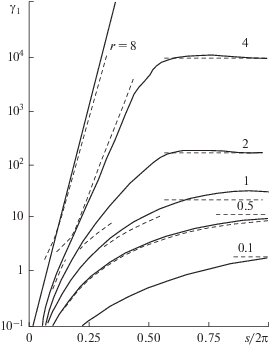
Получены также зависимости ${{\gamma }_{1}}\left( s \right) = \Omega {{T}_{1}}\left( s \right)$ от порога s (рис. 7). Найдена вероятность срыва слежения (рис. 8) на основе разностной схемы уравнения Понтрягина.
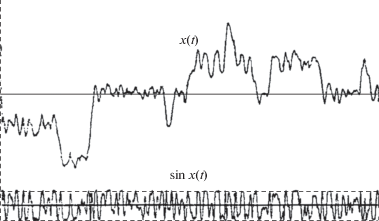
Экспериментально показано, что срыв слежения в системе ФАП определяется не только простым пересечением сигналом рассогласования фазовых уровней ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и π, а также циклом вращения вокруг фазового цилиндра с последующим переходом от от состояния равновесия к соседнему (рис. 9). Данные явления срыва подтверждены результатами моделирования ФАП (рис. 10).
Исследования В.И. Тихонова шумовых воздействий на ФАП продолжены его учениками. В результате наряду с шумовыми помехами рассмотрены и воздействия на ФАП и гармонических помех [11–13].
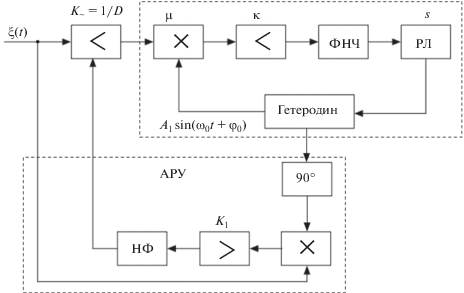
Следует отметить, что наряду с анализом ФАП под воздействием помех В.И. Тихонов получил ряд результатов в области синтеза оптимальных систем ФАП [7, 14] (рис. 11).
2. ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ПОМЕХИ НА СИСТЕМУ ФАП
2.1. Основные соотношения метода гармонического баланса
Можно показать, что при воздействии на ФАП наряду с сигналом и гармонической помехи дифференциальное уравнение ФАП имеет вид [17]
(6)
$px~ = {\text{\;}}\beta - F\left( p \right)\left[ {{\text{sin\;}}x + \varepsilon ~{\text{sin}}\left( {x + dt + {{\Delta }}\theta } \right)} \right],$Предполагаемое решение дифференциального уравнения (6) в методе гармонического баланса при учете лишь одной гармоники принимается в виде [17]
Параметры предполагаемого решения (7) – постоянная составляющая ${{x}_{0}}$, амплитуда первой гармоники ${{x}_{1}}$ и фазовый угол ${{\Phi }}$ – найдены в процессе гармонического баланса подстановкой (7) в левую и правую части дифференциального уравнения (6).
В работе [17] эти параметры были нами найдены при условии малого значения амплитуды ${{x}_{1}}$ и при условии $d > 1$, что обусловило использование приближенных соотношений [17] (нулевое приближение):
Затем нами были получены уточняющие соотношения на основе первого приближения.
В данной статье при использовании дифференциального уравнения (6) и предполагаемого решения в форме (7) используем более строгий подход (второе приближение), когда вместо (8) используются приближения более высокого порядка, в связи с чем повышается точность полученных результатов: динамических характеристик и критических значений параметров ФАП и помехи.
В данном случае используются отрезки рядов
где ${{J}_{0}} = {{J}_{0}}({{x}_{1}})$, ${{J}_{1}} = {{J}_{1}}({{x}_{1}})$, ${{J}_{2}} = {\text{\;}}{{J}_{2}}({{x}_{1}})$ – функции Бесселя соответствующих порядков, причем здесь добавляется в разложении (9) вторая гармоника ${\text{cos\;}}2{{\Phi }}$.В результате вместо (8) используются соотношения
Подставляя предполагаемое решение (2) в исходное дифференциальное уравнение (6), получим
Воспользуемся соотношением (9). В результате получим (первая стадия упрощения)
На второй стадии упрощения пренебрегаем второй гармоникой во втором слагаемом в фигурных скобках, при перемножении воспользуемся приближенными равенствами (отбросим третьи гармоники):
а также отбросим вторые гармоники, возникающие в произведениях,
В результате в правой части приведенного соотношения останутся лишь первые гармоники
вида 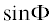 и
и  :
:
Выделим в правой части данного соотношения постоянную составляющую
(11)
$\beta ~\,\, - {{M}_{0}}\left[ {{{J}_{{\text{o}}}}{\text{\;sin}}{{x}_{0}}{\text{\;}} + \varepsilon {{J}_{1}}{\text{\;cos}}\left( {{{x}_{0}}{\text{\;}} - \,\,~\psi } \right)} \right] = {\text{\;}}0,$В результате оставшиеся переменные характеризуются соотношениями
гдеЗапишем передаточную функцию фильтра в комплексной форме
где $M = \left| {F~\left( p \right)} \right|~$, $P = {\text{arg}}F\left( p \right).~$В результате из (12) с учетом (13) находим
После гармонического баланса по 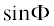 и
и 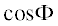 получим два уравнения относительно величин ${\text{cos}}P$ и ${\text{sin\;}}P$:
получим два уравнения относительно величин ${\text{cos}}P$ и ${\text{sin\;}}P$:
(18)
$\begin{gathered} A{\text{cos}}P - B~{\text{sin}}P = {\text{\;}}0, \\ B{\kern 1pt} {\text{cos}}P + A{\text{sin}}P = \frac{{d{{x}_{1}}}}{M}. \\ \end{gathered} $Определитель ${{\Delta }}$ системы уравнений (14) имеет вид
В результате решения системы уравнений (14) находим искомые величины ${\text{cos}}{\kern 1pt} P$ и ${\text{sin}}P$ в виде
(15)
${\text{cos}}P~\, = {{{{{{\Delta }}}_{1}}} \mathord{\left/ {\vphantom {{{{{{\Delta }}}_{1}}} {{\Delta }}}} \right. \kern-0em} {{\Delta }}};\,\,\,{\text{sin}}P\,\,~ = {{{{{{\Delta }}}_{2}}} \mathord{\left/ {\vphantom {{{{{{\Delta }}}_{2}}} {{\Delta }}}} \right. \kern-0em} {{\Delta }}}.$Очевидно, что
Отсюда имеем
Таким образом, эквивалентная запись определителя имеет вид
Поэтому окончательно получим
(16)
$d{{x}_{1}}~{\text{cos}}P~ = {\text{\;}}\varepsilon M\left( {{{J}_{0}}{\text{\;}} + {\text{\;}}{{J}_{2}}{\text{\;}}} \right){\text{cos}}\left( {\psi ~ - ~{{x}_{0}}} \right),$(17)
$\begin{gathered} d{{x}_{1}}~{\text{sin\;}}P = \\ = M\left[ {\varepsilon \left( {{{J}_{0}} - ~{{J}_{2}}{\text{\;}}} \right){\text{sin}}\left( {\psi ~ - ~{{x}_{0}}} \right) - \,~2{{J}_{1}}{\text{\;cos\;}}{{x}_{0}}} \right], \\ \end{gathered} $Полученные соотношения (11), (16), (17) совпадают с соответствующими уравнениями (7)–(9), приведенными в [18] без вывода, теперь по приведенному процессу их вывода можно судить о степени приближенности найденных соотношений.
При ${{J}_{2}} = {{J}_{2}}\left( {{{x}_{1}}} \right) = 0~$ по (16), (17) следует частный случай, полученный ранее.
2.2. Соотношения для параметров${{x}_{0}}$, ${{x}_{1}}$, $\psi $ предполагаемого решения дифференциального уравнения
По (16) и (17) может быть найдена система уравнений относительно величин ${\text{cos}}\psi $ и ${\text{sin}}\psi $, имеющая вид
(18)
$\begin{array}{*{20}{c}} {\cos ~{{x}_{0}}~\cos \psi + \sin {{x}_{0}}\sin ~\psi = {{c}_{1}},} \\ { - ~{\kern 1pt} \sin ~{{x}_{0}}\cos \psi + \cos ~{{x}_{0}}\sin ~\psi = {{c}_{2}},} \end{array}$Определитель системы (18) равен единице, поэтому
гдеПри малых значениях амплитуды ${{x}_{1}}$ функция ${{J}_{2}}\left( {{{x}_{1}}} \right) \approx 0$, поэтому в этом случае из (19) находим
(20)
$\begin{gathered} {{{{\Delta }}}_{1}} = \frac{{{{x}_{1}}}}{{\varepsilon M{{J}_{0}}}} \times \\ \times \,\,\left[ {d{\text{\;cos}}\left( {P~ + {\text{\;}}{{x}_{0}}} \right) - \,\,~\frac{1}{2}\frac{2}{{{{x}_{1}}}}{{J}_{1}}M{\text{sin}}2{{x}_{0}}} \right] = {{\gamma }_{{10}}}{{F}_{{10}}}, \\ \end{gathered} $(21)
$\begin{gathered} {{{{\Delta }}}_{1}} = \frac{{{{x}_{1}}}}{{\varepsilon M{{J}_{0}}}} \times \\ \times \,\,\left[ {d{\text{\;cos}}\left( {P~ + {\text{\;}}{{x}_{0}}} \right) - ~\,\,\frac{2}{{{{x}_{1}}}}{{J}_{1}}M{\text{co}}{{{\text{s}}}^{2}}{{x}_{0}}} \right] = {{\gamma }_{{20}}}{{F}_{{20}}}. \\ \end{gathered} $Далее из (17) находим
Тогда
(22)
$\psi = \left\{ \begin{gathered} ~{{x}_{0}}{\text{\;}} + \varphi {\kern 1pt} ,\,\,\,\,~{\text{при}}\,\,\,\,d > ~~0,{\text{\;}}\beta ~\,\, > \,\,~0, \hfill \\ {{x}_{0}} - \varphi + \pi ,\,\,\,\,\,{\text{при}}\,\,\,\,\,d~~ < 0,\,\,\beta \,\,~ > \,\,~0; \hfill \\ \end{gathered} \right.$Графики зависимости $\psi \,\,~ = f\left( d \right)$ представлены на рис. 12 при $\varepsilon $ = 0.5, $a$ = 0.8; $~\alpha _{0}^{{ - 2}}$ = 6.25, при невырожденном и вырожденном фильтре для $\beta $ = 0.9, 0.7 и 0.5.
Рис. 12.
Зависимость фазового угла ψ от относительной разности частот d помехи и сигнала при ε = 0.5; a = 0.8; Ωτ = 6.25 (τ – постоянная времени фильтра) и различных β = 0.9 (1, 2); 0.7 (3, 4); 0.5 (5, 6) в случае невырожденного (1, 3, 5) и вырожденного фильтров (2, 4, 6).

Соотношение для постоянной составляющей $~{{x}_{0}}$ находится по (11) с учетом (16) и имеет вид
(23)
${\text{sin\;}}{{x}_{0}} = \frac{1}{{{{J}_{0}}}}\left[ {\frac{\beta }{{{{M}_{0}}}} - {{J}_{1}}\frac{{d{{x}_{1}}{\text{cos}}P}}{{M\left( {{{J}_{0}} + {{J}_{2}}} \right)}}} \right].$Графики зависимости ${{x}_{0}} = f\left( d \right)$ изображены на рис. 13а при $\varepsilon $ = 0.5; $a$ = 0.8; $\alpha _{0}^{{ - 2}}$ = 6.25 при невырожденном и вырожденном фильтре для $\beta $ = 0.9, 0.7 и 0.5.
Рис. 13.
Зависимость постоянной составляющей x0 (а) и амплитуды первой гармоники x1 (б) от относительной разности частот d помехи и сигнала при ε = 0.5; a = 0.8; Ωτ = 6.25 и различных β = 0.9 (1, 2); 0.7 (3, 4); 0.5 (5, 6) в случае невырожденного (1, 3, 5) и вырожденного фильтров (2, 4, 6).
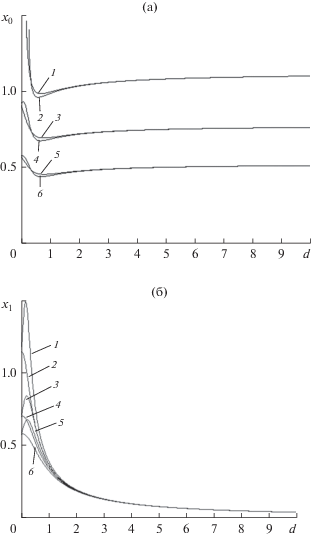
Остается найти зависимость амплитуды$~{{x}_{1}}$ первой гармоники предполагаемого решения от параметров ФАП и отстройки $d$. По (19) находим неявную зависимость
(24)
$x_{1}^{2} = \frac{{{{{\left( {\varepsilon M} \right)}}^{2}}{{{\left( {J_{0}^{2} - J_{2}^{2}} \right)}}^{2}}}}{{{{d}^{2}}{{{\left( {F_{1}^{2} + F_{2}^{2}} \right)}}^{2}}}}.$При больших отстройках $d$ находим
(25)
$x_{1}^{2} = \frac{{\varepsilon J_{0}^{2}}}{{{{d}^{2}} + {{{[{{2{{J}_{1}}} \mathord{\left/ {\vphantom {{2{{J}_{1}}} {{{x}_{1}}}}} \right. \kern-0em} {{{x}_{1}}}}]}}^{2}}{\text{cos}}{{x}_{0}}}} \approx \frac{{{{\varepsilon }^{2}}}}{{{{d}^{2}} + 1 - {{\beta }^{2}}}}.$Графики зависимости ${{x}_{1}} = f\left( d \right)$ представлены на рис. 13б при тех же параметрах, что и на рис. 13а.
ЗАКЛЮЧЕНИЕ
Таким образом, определяющая роль в создании теории ФАП под воздействием помех принадлежит В.И. Тихонову и его ближайшим ученикам. Были создали не только методы анализа стохастической ФАП, но и ее синтеза на основе нелинейной теории оптимальной фильтрации Р.Л. Стратоновича [19] (научным руководителем Р.Л. Стратоновича на раннем этапе его творчества был B.И. Тихонов).
Следует также отметить заметный вклад В.И. Тихонова в исследование теории выбросов случайных процессов [20] и теории передачи сообщений [21].
Список литературы
Тихонов В.И. // Автоматика и телемеханика. 1959. Т. 20. № 9. С. 1188.
Тихонов В.И. // Автоматика и телемеханика. 1960. Т. 21. № 3. С. 301.
Тихонов В.И., Шахтарин Б.И. // Автоматика и телемеханика 1965. Т. 26. № 9. С. 1563.
Шaxтapин Б.И. // PЭ. 1968. T. 13. № 2. C. 247.
Челышев К.Б. // Автоматика и телемеханика. 1963. Т. 24. № 7. С. 942.
Тихонов В.И., Челышев К.Б. // РЭ. 1963. Т. 8. № 2. С. 331.
Тихонов В.И. Статистическая радиотехника. М.: Сов. радио, 1966.
Шахтарин Б.И., Щепкин Ю.Н. Электросвязь. 1966. № 9. С. 18.
Тихонов В.И., Журавлев А.Г. Радиотехника. 1962. Т. 17. № 9. С. 40.
Тихонов В.И. // Изв. вузов СССР. Радиоэлектроника. 1972. Т. 15. № 4. С. 413.
Журавлев А.Г. // Радиотехника. 1963. Т. 18. № 9. С. 38.
Шaxтapин Б.И. // PЭ. 2012. T. 57. № 6. C. 649.
Шaxтapин Б.И. // PЭ. 2012. T. 57. № 8. C. 858.
Ярлыков М.С. Применение марковской теории нелинейной фильтрации в радиотехнике. М.: Сов. радио, 1980.
Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Горячая линия – Телеком, 2015.
Тихонов В.И., Миронов М.А. Марковские процессы. М.: Сов. радио, 1977.
Шахтарин Б.И. Статистическая динамика систем синхронизации. М.: Радио и связь, 1998.
Karsi M.F., Lindsey W.C. // IEEE Trans. 2000. V. 48. № 5. P. 886.
Шaxтapин Б.И. // PЭ. 2006. T. 51. № 11. C. 1324.
Тихонов В.И. Выбросы случайных процессов. М.: Наука, 1970.
Тихонов В.И., Кульман Н.К. Нелинейная фильтрация и квазикогерентный прием сигналов. М.: Сов. радио, 1975.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника