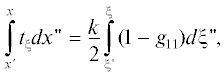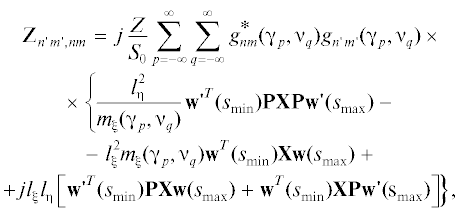Радиотехника и электроника, 2022, T. 67, № 6, стр. 546-556

ВВЕДЕНИЕ

Выпуклые фазированные антенные решетки (ФАР) могут применяться для широкоугольного (полусферического и более) электрического сканирования или совмещения поверхности ФАР с выпуклой поверхностью летательного аппарата (конформные ФАР) [1–3].

Для корректной оценки характеристик выпуклых ФАР необходимо учитывать взаимное влияние ее излучающих элементов. При больших по сравнению с длиной волны размерах поверхности ФАР для расчета взаимного влияния элементов используются асимптотические (коротковолновые) методы. Один из них основан на так называемом поэлементном подходе [4], при котором на основе геометрической теории дифракции (ГТД) вычисляется матрица взаимных проводимостей (в случае вибраторов − матрица импедансов) элементов, являющаяся матрицей коэффициентов системы линейных уравнений, решение которой позволяет найти амплитуды напряжений (токов) в излучателях при заданном распределении падающих волн в питающих фидерах излучателей [5, 6]. Недостатком поэлементного подхода при большом числе излучающих элементов ФАР является необходимость вычисления и обращения матрицы взаимных проводимостей (импедансов) большого размера, что представляет определенные вычислительные трудности.

Альтернативный асимптотический метод первоначально развит для периодических цилиндрических ФАР с произвольной выпуклой направляющей [1, 5, 7] и в дальнейшем распространен на квазипериодические выпуклые антенные решетки, характеризующиеся плавно меняющимися размерами единичной ячейки антенной решетки, для случая апертурных излучателей [8, 9]. Для представления электромагнитного ФАР в данном методе используются периодические граничные условия на боковой поверхности единичной ячейки решетки. Аналогично методу разложения Флоке для бесконечной плоской ФАР, разложение электромагнитного поля вблизи выпуклой поверхности антенны представляется в виде ряда пространственных гармоник, выражающихся, в отличие от случая плоской ФАР, через функции Эйри.

Для периодических выпуклых цилиндрических ФАР, как и для плоской ФАР, определение амплитуд напряжений или токов в излучателях сводится к решению системы линейных алгебраических уравнений, получающихся в результате применения численного метода для определения электромагнитного поля в одной ячейке решетки [1, 7, 8]. Порядок этой системы уравнений не зависит от числа элементов ФАР, а только от сложности описания поля одного элемента. Первоначально для квазипериодических ФАР система линейных уравнений заменялась системой интегральных уравнений той же размерности вдоль некоторой кривой на поверхности антенны [8, 9]. В дальнейшем для сферической решетки щелевых излучателей было показано, что решение на основе системы интегральных уравнений может быть с хорошей точностью заменено решением на основе системы линейных алгебраических уравнений [10]. Это позволяет существенно упростить решение задачи и применить данный метод для других типов излучающих элементов.

Цель данной работы – представить общие асимптотические выражения электромагнитного поля в приповерхностном слое выпуклой квазипериодической ФАР с учетом выявленной возможности упрощений и применить их для анализа взаимного влияния многовибраторных излучателей в составе осесимметричной выпуклой ФАР.

1. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ФАР

1.2. Электромагнитное поле вблизи поверхности ФАР

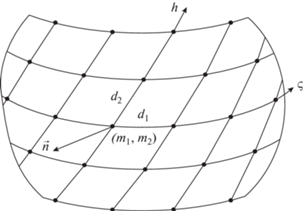
Введем на гладкой выпуклой поверхности антенны систему поверхностных координат ς, h, в которых излучатели расположены с постоянными шагами d_ς и d_h соответственно (рис. 1). При этом расстояния между элементами

${{d}_{1}} = \int\limits_{{\varsigma }}^{{{\varsigma }} + {{d}_{{{\varsigma }}}}} {\sqrt {{{g}_{{{{\varsigma \varsigma }}}}}} } d\varsigma ,\,\,\,\,{{d}_{2}} = \int\limits_h^{h + {{d}_{h}}} {\sqrt {{{g}_{{hh}}}} } dh$

в общем случае зависят от координат точки на поверхности ς, h. Условием применимости предлагаемого метода является квазипериодичность выпуклой ФАР, означающая, что изменение размеров ее единичной ячейки должно быть не более среднего размера ячейки на размере поверхности порядка характерного радиуса кривизны ρ. Это можно выразить в виде условий медленности изменения компонент метрического тензора (коэффициентов первой квадратичной формы) поверхности ${{g}_{{{{\varsigma \varsigma }}}}}$, ${{g}_{{hh}}}$, ${{g}_{{{{\varsigma }}h}}}$

(5)

$\frac{1}{{\sqrt[4]{g}}}\left| {grad\sqrt[4]{g}} \right| = O\left( {\frac{1}{\rho }} \right),$

где grad – функция градиента на поверхности, g – определитель метрического тензора. Излучатели ФАР должны быть идентичны и расположены одинаковым образом в единичной ячейке.

Рис. 1.

Система координат на поверхности выпуклой ФАР, точки обозначают положение центров нормальных проекций элементов на проводящую поверхность ФАР.

Электрическое и магнитное поля в свободном пространстве вблизи проводящей поверхности при парциальном возбуждении (3) в этом случае могут быть представлены в виде двойного ряда пространственных гармоник [8, 9]

(6а)

$\vec {E}({{\varsigma }},h,n) = \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {\vec {\hat {E}}\left( {{{\varsigma }},h,n;{{{{\gamma }}}_{p}},{{{{\nu }}}_{q}}} \right)} } \exp \left( { - j({{{{\gamma }}}_{p}}{{\varsigma }} + {{{{\nu }}}_{q}}h)} \right),$

(6б)

$\vec {H}({{\varsigma }},h,n) = \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {\vec {\hat {H}}\left( {{{\varsigma }},h,n;{{{{\gamma }}}_{p}},{{{{\nu }}}_{q}}} \right)} } \exp \left( { - j({{{{\gamma }}}_{p}}{{\varsigma }} + {{{{\nu }}}_{q}}h)} \right),$

где $n$ – длина отрезка нормали от поверхности до точки наблюдения вблизи поверхности,

(7)

${{{{\gamma }}}_{p}} = {{\gamma }} + \frac{{2{{\pi }}p}}{{{{d}_{{{\varsigma }}}}}},\,\,\,\,{{{{\nu }}}_{q}} = {{\nu }} + \frac{{2{{\pi }}q}}{{{{d}_{h}}}};$

(8)

${{\gamma }} = \frac{{{{u}_{1}}}}{{{{d}_{{{\varsigma }}}}}},\,\,\,\,{{\nu }} = \frac{{{{u}_{2}}}}{{{{d}_{h}}}}.$

Амплитуды пространственных гармоник для квазипериодической антенной решетки представляются интегралами по бесконечному спектру

(9а)

$\vec {\hat {E}}\left( {{{\varsigma }},h,n;{{\gamma ,\nu }}} \right) = \sum\limits_{i = 1}^2 {\sum\limits_{l = 1}^2 {\int\limits_{ - \infty }^\infty {{{C}_{{il}}}(n;{{\gamma ,\nu }};t)} {\kern 1pt} {{{\vec {e}}}^{{(il)}}}} } \left( {t;{{\varsigma }},h,n;{{\gamma ,\nu }}} \right)\exp \left( {j\int\limits_0^x {({{t}_{{{\xi }}}} - t)dx{\kern 1pt} '} } \right)dt,$

(9б)

$\vec {\hat {H}}\left( {{{\varsigma }},h,n;{{\gamma ,\nu }}} \right) = \sum\limits_{i = 1}^2 {\sum\limits_{l = 1}^2 {\int\limits_{ - \infty }^\infty {{{C}_{{il}}}(n;{{\gamma ,\nu }};t)} {\kern 1pt} {{{\vec {h}}}^{{(il)}}}} } \left( {t;{{\varsigma }},h,n;{{\gamma ,\nu }}} \right)\exp \left( {j\int\limits_0^x {({{t}_{{{\xi }}}} - t)dx{\kern 1pt} '} } \right)dt,$

где векторные функции ${{\vec {e}}^{{(il)}}}$, ${{\vec {h}}^{{(il)}}}$, характеризующие пространственные гармоники поля вблизи поверхности, имеют индексы i = 1 для стоячих у поверхности волн и i = 2 для уходящих от поверхности волн. Индекс l = 1, 2 разделяет волны двух поляризаций (квази-LSE-волны). Компоненты векторных пространственных гармоник имеют вид

(10а)

$\begin{gathered} e_{{{\xi }}}^{{(il)}} \cong \frac{1}{{j{{m}_{{{\xi }}}}}}\frac{{\partial {{\psi }}_{1}^{{(il)}}}}{{\partial s}}, \\ e_{\eta }^{{(il)}} \cong {{\psi }}_{2}^{{(il)}},\,\,\,\,e_{n}^{{(il)}} \cong \frac{1}{{\sqrt {{{g}_{{11}}}} }}{{\psi }}_{1}^{{(il)}}, \\ \end{gathered} $

(10б)

$\begin{gathered} h_{\xi }^{{(il)}} \cong \frac{1}{{jZ{{m}_{{{\xi }}}}}}\frac{{\partial {{\psi }}_{2}^{{(il)}}}}{{\partial s}},\,\,\,\,h_{\eta }^{{(il)}} \cong - \frac{1}{Z}{{\psi }}_{1}^{{(il)}}, \\ h_{n}^{{(il)}} \cong \frac{1}{{Z\sqrt {{{g}_{{11}}}} }}{{\psi }}_{2}^{{(il)}}, \\ \end{gathered} $

где Z = 120π; i, l = 1, 2; функции ${{\psi }}_{{1,2}}^{{(il)}}$ в наиболее компактном виде можно записать как

(11)

${{\psi }}_{1}^{{(il)}} = {\mathbf{P}}{{{\mathbf{x}}}^{{(il)}}}{\mathbf{w}}(s),\,\,\,\,{{\psi }}_{2}^{{(il)}} = {{{\mathbf{x}}}^{{(il)}}}{\mathbf{w}}(s).$

Здесь вектор-столбец w(s) составлен из первой и второй функций Эйри

(12)

${\mathbf{w}}(s) = \left( {\begin{array}{*{20}{c}} {{{w}_{1}}(t - s + {{x}_{{{\xi }}}})} \\ {{{w}_{2}}(t - s + {{x}_{{{\xi }}}})} \\ {{{w}_{1}}(t - s - {{x}_{{{\xi }}}})} \\ {{{w}_{2}}(t - s - {{x}_{{{\xi }}}})} \end{array}} \right),$

(13)

$s = \frac{{kn}}{{{{m}_{{{\xi }}}}}},$

− приведенная координата вдоль нормали,

(14)

${{m}_{{{\xi }}}} = {{\left( {\frac{{k{{{{\rho }}}_{{{\xi }}}}}}{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}$

– большой параметр, по степеням которого разлагается асимптотическое решение; ρ_ξ – радиус кривизны нормального сечения поверхности вдоль направления движения фронта пространственной гармоники, k = 2π/λ;

(15)

${{t}_{{{\xi }}}} = m_{{{\xi }}}^{2}\left( {g_{{11}}^{{ - 1}} - 1} \right),$

(16)

${{x}_{{{\xi }}}} = \frac{1}{{{{m}_{{{\xi }}}}}}\sqrt[{}]{{\frac{{{{g}_{{11}}}}}{{{{g}_{{22}}}}}}}\frac{{{{b}_{{12}}}}}{{{{b}_{{11}}}}},$

где g₁₁, g₂₂ – компоненты метрического тензора, а b₁₁, b₁₂ – компоненты тензора кривизны поверхности в координатах ξ, η, первая из которых направлена вдоль направления движения фронта пространственной гармоники

(17)

${{\xi }} = \frac{{{\gamma }}}{k}{{\varsigma }} + \frac{{{\nu }}}{k}h,$

а вторая ей ортогональна;

(18а)

$\begin{gathered} {{{\mathbf{x}}}^{{(11)}}} = \frac{1}{4}\left( {\begin{array}{*{20}{c}} { - w_{2}^{'}(t + {{x}_{{{\xi }}}})} \\ {w_{1}^{'}(t + {{x}_{{{\xi }}}})} \\ {w_{2}^{'}(t - {{x}_{{{\xi }}}})} \\ { - w_{1}^{'}(t - {{x}_{{{\xi }}}})} \end{array}} \right), \\ {{{\mathbf{x}}}^{{(12)}}} = \frac{{{{m}_{{{\xi }}}}}}{4}\left( {\begin{array}{*{20}{c}} { - {{w}_{2}}(t + {{x}_{{{\xi }}}})} \\ {{{w}_{1}}(t + {{x}_{{{\xi }}}})} \\ { - {{w}_{2}}(t - {{x}_{{{\xi }}}})} \\ {{{w}_{1}}(t - {{x}_{{{\xi }}}})} \end{array}} \right), \\ \end{gathered} $

(18б)

$\begin{gathered} {{{\mathbf{x}}}^{{(21)}}} = \frac{{{{m}_{{{\xi }}}}}}{{{\omega }}}\left( {\begin{array}{*{20}{c}} 0 \\ {{{w}_{2}}(t - {{x}_{{{\xi }}}})} \\ 0 \\ { - {{w}_{2}}(t + {{x}_{{{\xi }}}})} \end{array}} \right), \\ {{{\mathbf{x}}}^{{(22)}}} = \frac{1}{{{\omega }}}\left( {\begin{array}{*{20}{c}} 0 \\ {w_{2}^{'}(t - {{x}_{{{\xi }}}})} \\ 0 \\ {w_{2}^{'}(t + {{x}_{{{\xi }}}})} \end{array}} \right), \\ \end{gathered} $

(19)

${{\omega }} = w_{2}^{'}(t + {{x}_{{{\xi }}}}){{w}_{2}}(t - {{x}_{{{\xi }}}}) + {{w}_{2}}(t + {{x}_{{{\xi }}}})w_{2}^{'}(t - {{x}_{{{\xi }}}});$

(20)

${\mathbf{P}} = j\left( {\begin{array}{*{20}{c}} { - 1}&0&0&0 \\ 0&{ - 1}&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right).$

Верхний предел интегрирования по dx' в (9) связан с координатой ξ соотношением

(21)

$x = \int\limits_0^{{\xi }} {\frac{{{{g}_{{11}}}m_{{{\xi }}}^{{}}}}{{{{\rho }_{{{\xi }}}}}}} d{{\xi }}{\text{.}}$

Спектральные амплитуды пространственных гармоник ${{\vec {e}}^{{(il)}}}$, ${{\vec {h}}^{{(il)}}}$ являются медленно меняющимися функциями точки на поверхности. Касательные составляющие электрического вектора стоячих пространственных гармоник равны нулю при n = 0.

Приведенные выражения поля справедливы в поверхностном слое n ~ λ при больших размерах поверхности (m_ξ$ \gg $ 1), медленности изменения радиусов кривизны поверхности gradρ ~ 1 и условии квазипериодичности ФАР (5). Численные расчеты показывают, что метод дает хорошее приближение к результатам строгого решения уже при m_ξ > 2 [10]. Условия применимости асимптотических выражений нарушаются на скачках кривизны поверхности, разрывах непрерывности поверхностных координат ς, h и в точках их сгущения g = 0. При наличии таких неоднородностей выражения поля справедливы на достаточном удалении от них, чтобы полем дифракции на неоднородностях можно было пренебречь.

Интегральное представление (9) является преобразованием Фурье, что позволяет связать коэффициенты разложения с токами излучателей с помощью леммы Лоренца, примененной к единичной ячейке антенной решетки так же, как в случае периодической антенной решетки [8]. Вспомогательное поле в лемме Лоренца выберем в виде

$\begin{gathered} {{{\vec {E}}}_{{i{\kern 1pt} 'j{\kern 1pt} '}}}( - {{\gamma }}, - {{\nu }}) = {{{\vec {e}}}^{{(i{\kern 1pt} 'j{\kern 1pt} ')}}}({{\gamma ,\nu }}) \times \\ \times \,\,\exp \left( {j({{\gamma \varsigma }} + {{\nu }}h) - j\int\limits_0^x {({{t}_{{{\xi }}}} - t{\kern 1pt} ')dx{\kern 1pt} '} } \right), \\ \end{gathered} $

$\begin{gathered} {{{\vec {H}}}_{{i{\kern 1pt} '{\kern 1pt} j{\kern 1pt} '}}}( - {{\gamma ,}} - {{\nu }}) = {{{\vec {h}}}^{{(i{\kern 1pt} '{\kern 1pt} j{\kern 1pt} ')}}}({{\gamma ,\nu }}) \times \\ \times \,\,\exp \left( {j({{\gamma \varsigma }} + {{\nu }}h) - j\int\limits_0^x {({{t}_{{{\xi }}}} - t{\kern 1pt} ')dx{\kern 1pt} '} } \right). \\ \end{gathered} $

При интегрировании по поперечному сечению ячейки используем ортогональность пространственных гармоник, считая, что изменением амплитуд пространственных гармоник в пределах единичной ячейки можно пренебречь. Затем выполним интегрирование по dx с применением известного соотношения

$\int\limits_{ - \infty }^\infty {\exp \left( { - j(t - t{\kern 1pt} ')x} \right)\,} dx = 2{{\pi \delta }}(t - t{\kern 1pt} ').$

В результате получаем коэффициенты разложения

(22)

$\begin{gathered} {{C}_{{il}}}(n;{{\gamma ,\nu }};t) = \frac{Z}{{2\pi {{S}_{0}}}}\int\limits_{ - \infty }^\infty {\int\limits_{{{V}_{{(3 - i)}}}(n)} {\left( {{{{\vec {j}}}^{e}}{{{\vec {e}}}^{{(3 - i)l}}} - {{{\vec {j}}}^{m}}{{{\vec {h}}}^{{(3 - i)l}}}} \right)} } \times \hfill \\ \times \,\,\exp \left( {j\left( {{{\gamma \varsigma }}{\kern 1pt} {\text{'}} + {{\nu }}h{\kern 1pt} '} \right)} \right)dV{\kern 1pt} '\exp \left( { - j\int\limits_0^x {({{t}_{{{\xi }}}} - t)dx{\kern 1pt} '} } \right)dx, \hfill \\ \end{gathered} $

где ${{\vec {j}}^{e}}$ – электрический ток, ${{\vec {j}}^{m}}$ – магнитный ток излучателя; V₁(n) ‒ часть объема единичной ячейки, расположенная между сечениями 0 ≤ n' ≤ n, V₂(n) ‒ часть объема единичной ячейки, расположенная между сечениями n ≤ n' ≤ n₀, где n₀ – толщина поверхностного слоя, содержащего излучатели; S₀ ‒ площадь единичной ячейки. В области протекания токов излучателей коэффициенты возбуждения пространственных гармоник C_il зависят от координаты n; при n ≥ n₀, C_1l = 0, а C_2l не зависят от n.

В области протекания токов, при наличии продольных компонент электрических и магнитных токов относительно нормали к поверхности, к нормальным компонентам выражений для электрического (9а) и магнитного (9б) полей необходимо прибавить дополнительные слагаемые [8, 13]:

(23а)

$\Delta {{E}_{n}}({{\varsigma }},h,n) = \frac{j}{{\omega \varepsilon }}j_{n}^{e} = \frac{j}{{\omega \varepsilon }}\sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{B}^{{(e)}}}(n;\gamma ,\nu ;t)\exp \left( { - j({{{{\gamma }}}_{p}}{{\varsigma }} + {{{{\nu }}}_{q}}h) + j\int\limits_0^x {({{t}_{{{\xi }}}} - t)dx{\kern 1pt} '} } \right),} } } $

(23б)

$\Delta {{H}_{n}}({{\varsigma }},h,n) = \frac{j}{{\omega \mu }}j_{n}^{m} = \frac{j}{{\omega \mu }}\sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{B}^{{(m)}}}(n;\gamma ,\nu ;t)\exp \left( { - j({{{{\gamma }}}_{p}}{{\varsigma }} + {{{{\nu }}}_{q}}h) + j\int\limits_0^x {({{t}_{{{\xi }}}} - t)dx{\kern 1pt} '} } \right),} } } $

также представленные здесь в виде разложений, коэффициенты которых имеют вид

(24)

$\begin{gathered} {{B}^{{(e,m)}}}(n;\gamma ,\nu ;t) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{1}{{{{S}_{0}}(n)}}} \times \\ \times \,\,\int\limits_{{{S}_{0}}(n)} {j_{n}^{{(e,m)}}\exp \left( {j\left( {\gamma \varsigma {\kern 1pt} '\,\, + \nu h{\kern 1pt} '} \right)} \right)dS} \times \\ \times \,\,\exp \left( { - j\int\limits_0^x {({{t}_{\xi }} - t)dx{\kern 1pt} '} } \right)dx. \\ \end{gathered} $

Выражения (6), (9), (22)−(24) обобщают и развивают аналогичные выражения для апертурных излучателей [9] на общий случай произвольных излучателей, представимых системой электрических и магнитных токов в приповерхностном слое выпуклой квазипериодической ФАР.

Подставим (22), (24) в (9), (23) и выполним интегрирование по dtdx' методом стационарной фазы. Точка стационарной фазы x' = x, t = t_ξ(x); определитель, составленный из вторых частных производных фазовой функции, (гессиан) равен −1, и в результате применения метода стационарной фазы [15] получаем

(25а)

$\begin{gathered} \vec {\hat {E}}({{\varsigma }},h,n;{{\gamma ,\nu }}) = \\ = \sum\limits_{i = 1}^2 {\sum\limits_{l = 1}^2 {\left[ {{{{\overline C }}_{{il}}}(n;{{\gamma ,\nu }};{{t}_{{{\xi }}}}){{{\vec {e}}}^{{(il)}}}\left( {{{t}_{{{\xi }}}};{{\varsigma }},h,n;{{\gamma ,\nu }}} \right)\frac{{^{{}}}}{{}}} \right.} } + \\ \left. { + \,\,\frac{j}{{\omega \varepsilon }}{{{\bar {B}}}^{{(e)}}}(\varsigma ,n;{{\gamma ,\nu }})\vec {n}} \right], \\ \end{gathered} $

(25б)

$\begin{gathered} \vec {\hat {H}}({{\varsigma }},h,n;{{\gamma ,\nu }}) = \\ = \sum\limits_{i = 1}^2 {\sum\limits_{l = 1}^2 {\left[ {{{{\bar {C}}}_{{il}}}(n;{{\gamma ,\nu }};{{t}_{{{\xi }}}}){{{\vec {h}}}^{{(il)}}}\left( {{{t}_{{{\xi }}}};{{\varsigma }},h,n;{{\gamma ,\nu }}} \right) + \frac{{^{{}}}}{{}}} \right.} } \\ \left. { + \,\,\frac{j}{{\omega \mu }}{{{\bar {B}}}^{{(m)}}}(\varsigma ,n;{{\gamma ,\nu }})\vec {n}} \right], \\ \end{gathered} $

(26)

$\begin{gathered} {{{\bar {C}}}_{{il}}}(n;{{\gamma ,\nu }};t) = \frac{Z}{{{{S}_{0}}}} \times \\ \times \,\,\int\limits_{{{V}_{{(3 - i)}}}(n)} {\left( {{{{\vec {j}}}^{e}}{{{\vec {e}}}^{{(3 - i)l}}} - {{{\vec {j}}}^{m}}{{{\vec {h}}}^{{(3 - i)l}}}} \right)\exp \left( {j\left( {{{\gamma \varsigma }}{\kern 1pt} {\text{'}} + {{\nu }}h{\kern 1pt} '} \right)} \right)} dV{\kern 1pt} ', \\ \end{gathered} $

(27)

$\begin{gathered} {{{\bar {B}}}^{{(e,m)}}}(\varsigma ,n;\gamma ,\nu ) = \\ = \frac{1}{{{{S}_{0}}(n)}}\int\limits_{{{S}_{0}}(n)} {j_{n}^{{(e,m)}}\exp \left( {j\left( {{{\gamma \varsigma }}{\kern 1pt} {\text{'}} + {{\nu }}h{\kern 1pt} '} \right)} \right)} dS{\kern 1pt} '. \\ \end{gathered} $

Так как

то формально большим параметром для метода стационарной фазы является волновое число k, а фактически kρ_ξ$ \gg $ 1. Применение метода стационарной фазы математически не вполне обосновано в переходной области (области “полутени”) t_ξ(x) ~ 1, так как в этой области изменение амплитудного множителя не может считаться достаточно медленным. Несмотря на эту слабость математического обоснования, результаты численного исследования осесимметричной сферической ФАР щелевых излучателей в данном приближении, названном автором асимптотическим приближением первого порядка, показали их хорошее совпадение с результатами строгого решения [10].

Выражения для амплитуд пространственных гармоник (9), (22) дают в переходной области t_ξ ~ 1 порядок отброшенных асимптотических членов разложения (6), (23) $O\left( {m_{{{\xi }}}^{{ - 2}}} \right)$. Для приближения первого порядка (25)–(27) порядок первой производной амплитуд пространственных гармоник в этой области равен

$\frac{{\partial {{e}^{{(il)}}}}}{{\partial {{\xi }}}} = O\left( {\frac{{{{e}^{{(il)}}}}}{{{{m}_{{{\xi }}}}}}} \right).$

Отсюда следует, что порядок отброшенных членов асимптотического приближения первого порядка (25) в переходной области увеличился и равен $O\left( {m_{{{\xi }}}^{{ - 1}}} \right)$. Вне переходной области |t_ξ| $ \gg $ 1 действует приближение геометрической оптики, порядок отброшенных членов $O\left( {m_{{{\xi }}}^{{ - 3}}} \right)$ в обоих случаях и выражения (6), (23) и (25) асимптотически эквивалентны. Для ФАР с периодической сеткой расположения элементов разложения (6), (25) переходят в ранее полученные для этого частного случая в [8], а порядок отброшенных членов становится $O\left( {m_{{{\xi }}}^{{ - 4}}} \right)$.

Выражения (25)−(27) носят локальный характер: с их помощью амплитуды токов и напряжений в излучающих элементах ФАР могут быть найдены из рассмотрения только текущей ячейки антенной решетки без решения интегрального уравнения (или системы таких уравнений), связывающего амплитуды токов в соседних ячейках, к которой приводит преставление (6), (22).

1.3. Поле в дальней зоне

Учтем, что электромагнитное поле ФАР при парциальном возбуждении не изменяется при изменении фазовых сдвигов между излучателями u₁, u₂ на 2πm, где m – любое целое число. Тогда диаграмма направленности элемента в составе антенной решетки (парциальная диаграмма элемента) с использованием (4) и спектра падающих волн при возбуждении одного элемента $F({\mathbf{u}}) = \exp \left( {j({{m}_{1}}{{u}_{1}} + {{m}_{2}}{{u}_{2}})} \right)$ может быть записана в виде

(28)

$\begin{gathered} {{{\vec {f}}}_{{{{m}_{1}}{{m}_{2}}}}}({{\theta ,}}\varphi ) = \frac{{k{{d}_{{{\varsigma }}}}{{d}_{h}}}}{{4\pi \sqrt {2\pi Z} }} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{{\vec {F}}}_{0}}({{\theta }},\varphi ;{{\gamma ,\nu ;\varsigma }},h)\exp \left( {j\left( {{{\gamma }}{{{{\varsigma }}}_{{{{m}_{1}}}}} + {{\nu }}{{h}_{{{{m}_{2}}}}}} \right)} \right)} } d{{\gamma }}d{{\nu ,}} \\ \end{gathered} $

где ${{\vec {F}}_{0}}$ – диаграмма направленности одной пространственной гармоники, которая определяется по электромагнитному полю на поверхности S ': n = n₀, охватывающей излучатели ФАР, формулой типа Гюйгенса–Кирхгофа [8, 14]:

(29)

$\begin{gathered} {{{\vec {F}}}_{0}}({{\theta }},\varphi ;{{\gamma }},{{\nu }}) = \frac{1}{{2{{\pi }}}} \times \\ \times \,\,\iint\limits_{S'} {\vec {M}({{\gamma ,\nu ;\varsigma }},h)\exp \left[ {jk\left( {{{{\vec {i}}}_{R}}\vec {r} - {{\xi }}} \right)} \right]dS}, \\ \end{gathered} $

где ${{\vec {i}}_{R}} = {{\vec {k}} \mathord{\left/ {\vphantom {{\vec {k}} k}} \right. \kern-0em} k}$ – единичный вектор в направлении наблюдения, $\vec {r}$ – радиус-вектор точки на поверхности S ', а величину

(30)

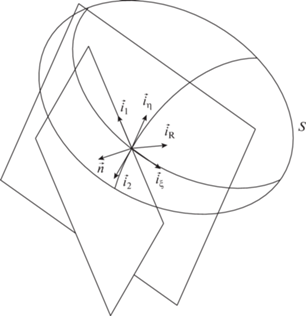
$\vec {M} = \left[ {\left[ {\vec {n},\vec {\hat {E}}} \right],{{{\vec {i}}}_{R}}} \right] + \left[ {{{{\vec {i}}}_{R}},\left[ {{{{\vec {i}}}_{R}},\left[ {\vec {n},Z\vec {\hat {H}}} \right]} \right]} \right]$

назовем для удобства изложения “вектором излучения”, $\vec {\hat {E}}$, $\vec {\hat {H}}$ – амплитуды векторов поля пространственной гармоники. Поверхность интегрирования в (29) можно перенести на проводящую поверхность S (n = 0), так как в вектор излучения входит поле только уходящей пространственной гармоники (С_1l(n₀) = 0), источники которого находятся на поверхности S, а результат интегрирования по формуле типа Гюйгенса–Кирхгофа не зависит от того, по какой охватывающей источники поверхности производится интегрирование. При этом коэффициенты возбуждения гармоники С_2l(n₀), конечно, должны быть вычислены при n = n₀.

Поскольку вектор излучения ортогонален единичному вектору ${{\vec {i}}_{R}}$, направленному в точку наблюдения, введем для его представления ортонормированный поляризационный базис (рис. 2):

(31)

${{\vec {i}}_{1}} = \frac{1}{{\sqrt {1 - {{{\left( {\vec {n}{{{\vec {i}}}_{R}}} \right)}}^{2}}} }}\left[ {{{{\vec {i}}}_{R}}{\text{,}}\vec {n}} \right],\,\,\,\,{{\vec {i}}_{2}} = \left[ {{{{\vec {i}}}_{R}}{\text{,}}{{{\vec {i}}}_{1}}} \right].$

Рис. 2.

Базисы на поверхности антенной решетки.

Проекции вектора излучения в этом базисе

(32)

$\begin{gathered} {{M}_{{\text{1}}}} = \frac{1}{{\sqrt {1 - {{{\left( {\vec {n}{{{\vec {i}}}_{R}}} \right)}}^{2}}} }}\left\{ { - \left[ {{{{\hat {E}}}_{{{\xi }}}}\left( {\vec {n}{{{\vec {i}}}_{R}}} \right) + Z{{{\hat {H}}}_{{{\eta }}}}} \right]\left( {{{{\vec {i}}}_{R}}{{{\vec {i}}}_{{{\eta }}}}} \right)} \right. + \\ \left. { + \,\,\left[ {{{{\hat {E}}}_{{{\eta }}}}\left( {\vec {n}{{{\vec {i}}}_{R}}} \right) - Z{{{\hat {H}}}_{{{\xi }}}}} \right]\left( {{{{\vec {i}}}_{R}}{{{\vec {i}}}_{\xi }}} \right)} \right\}, \\ {{M}_{{\text{2}}}} = - \frac{1}{{\sqrt {1 - {{{\left( {\vec {n}{{{\vec {i}}}_{R}}} \right)}}^{2}}} }}\left\{ {\left[ {{{{\hat {E}}}_{{{\eta }}}} - \left( {\vec {n}{{{\vec {i}}}_{R}}} \right)Z{{{\hat {H}}}_{{{\xi }}}}} \right]\left( {{{{\vec {i}}}_{R}}{{{\vec {i}}}_{{{\eta }}}}} \right)} \right. + \\ \left. { + \,\,\left[ {{{{\hat {E}}}_{\xi }} + \left( {\vec {n}{{{\vec {i}}}_{R}}} \right)Z{{{\hat {H}}}_{\eta }}} \right]\left( {{{{\vec {i}}}_{R}}{{{\vec {i}}}_{\xi }}} \right)} \right\}, \\ \end{gathered} $

где ${{\vec {i}}_{{{\xi }}}} = {{{{{\vec {r}}}_{{{\xi }}}}} \mathord{\left/ {\vphantom {{{{{\vec {r}}}_{{{\xi }}}}} {\sqrt {{{g}_{{11}}}} }}} \right. \kern-0em} {\sqrt {{{g}_{{11}}}} }}$, ${{\vec {i}}_{{{\eta }}}} = {{{{{\vec {r}}}_{{{\eta }}}}} \mathord{\left/ {\vphantom {{{{{\vec {r}}}_{{{\eta }}}}} {\sqrt {{{g}_{{22}}}} }}} \right. \kern-0em} {\sqrt {{{g}_{{22}}}} }}$ ‒ единичные векторы вдоль координатных линий ξ и η.

Вычисление интегралов (28), (29) в общем случае даже асимптотическими методами затруднительно. Однако в случае отсутствия условий возникновения дифракционных лепестков (шаги антенной решетки меньше λ/2 для прямоугольной ячейки и меньше ${{{\lambda }} \mathord{\left/ {\vphantom {{{\lambda }} {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }}$ для гексагональной ячейки) диаграмма элемента приближенно может быть вычислена методом стационарной фазы, примененным к четырехкратному интегралу, получающемуся после подстановки (29) в (28).

Стационарная точка единственная и определяется соотношениями

(33)

$\begin{gathered} {{{{\gamma }}}_{s}} = k{{{\vec {i}}}_{R}}{{{\vec {r}}}_{{{\varsigma }}}}({{{{\varsigma }}}_{{{{m}_{1}}}}},{{h}_{{{{m}_{2}}}}}),\;\;\,\,{{{{\nu }}}_{s}} = k{{{\vec {i}}}_{R}}{{{\vec {r}}}_{h}}({{{{\varsigma }}}_{{{{m}_{1}}}}},{{h}_{{{{m}_{2}}}}}), \\ {{{{\varsigma }}}_{s}} = {{{{\varsigma }}}_{{{{m}_{1}}}}},\,\,\,\,{{h}_{s}} = {{h}_{{{{m}_{2}}}}}. \\ \end{gathered} $

В результате применения общей формулы метода стационарной фазы [15] получим простое выражение для парциальной диаграммы элемента

(34)

$\begin{gathered} {{{\vec {f}}}_{{{{m}_{1}}{{m}_{2}}}}}({{\theta }},\varphi ) \cong \frac{{k{{S}_{0}}}}{{2\sqrt {2\pi Z} }} \times \\ \times \,\,\vec {M}({{{{\gamma }}}_{s}},{{{{\nu }}}_{s}};{{{{\varsigma }}}_{{{{m}_{1}}}}},{{h}_{{{{m}_{2}}}}},{{n}_{0}})\exp \left( {jk{{{\vec {i}}}_{R}}{{{\vec {r}}}_{{{{m}_{1}}{{m}_{2}}}}}} \right), \\ \end{gathered} $

где ${{S}_{0}} = {{d}_{{{\varsigma }}}}{{d}_{h}}\sqrt g $ – площадь единичной ячейки. Это выражение остается равномерно непрерывным для всех углов наблюдения, как при ${{\vec {i}}_{R}}\vec {n}({{{{\varsigma }}}_{{{{n}_{1}}}}},{{h}_{{{{n}_{2}}}}}) > 0$ (освещенная элементом область), так и при ${{\vec {i}}_{R}}\vec {n}({{{{\varsigma }}}_{{{{n}_{1}}}}},{{h}_{{{{n}_{2}}}}}) < 0$ (теневая область). Выражения для вектора излучения (32) в стационарной точке упрощаются:

(35)

${{M}_{{\text{1}}}} = {{\hat {E}}_{{{\eta }}}}\left( {\vec {n}{{{\vec {i}}}_{R}}} \right) - Z{{\hat {H}}_{{{\xi }}}},\,\,\,\,{{M}_{{\text{2}}}} = - {{\hat {E}}_{{{\xi }}}} - \left( {\vec {n}{{{\vec {i}}}_{R}}} \right)Z{{\hat {H}}_{{{\eta }}}}.$

Переход к проекциям на орты сферической системы координат ${{{{\vec {\theta }}}}^{0}}$, ${{\vec {\varphi }}^{{\text{0}}}}$ осуществляется преобразованием вращения поляризационного базиса

(36)

$\left( {\begin{array}{*{20}{c}} {{{M}_{{{\theta }}}}} \\ {{{M}_{\varphi }}} \end{array}} \right) = {\mathbf{T}}\left( {\begin{array}{*{20}{c}} {{{M}_{1}}} \\ {{{M}_{2}}} \end{array}} \right),$

(37)

${\mathbf{T}} = \frac{1}{{\sqrt {1 - {{{(\vec {n}{{{\vec {i}}}_{R}})}}^{2}}} }}\left( {\begin{array}{*{20}{c}} {\vec {n}{{{\vec {\varphi }}}^{{\text{0}}}}}&{\vec {n}{{{{{\vec {\theta }}}}}^{{\text{0}}}}} \\ {\vec {n}{{{{{\vec {\theta }}}}}^{{\text{0}}}}}&{\vec {n}{{{\vec {\varphi }}}^{{\text{0}}}}} \end{array}} \right),$

где $\vec {n} = \vec {n}({{{{\varsigma }}}_{{{{m}_{1}}}}},{{h}_{{{{m}_{2}}}}})$.

Диаграмма направленности ФАР в целом с учетом взаимной связи элементов может быть получена суммированием парциальных диаграмм элементов ФАР с весовыми коэффициентами, равными амплитудам падающих волн на их входах.

2. АНТЕННАЯ РЕШЕТКА ВИБРАТОРНЫХ ИЗЛУЧАТЕЛЕЙ

Применим асимптотическое приближение первого порядка для анализа антенной решетки вибраторных (в общем случае многовибраторных, директорных) излучателей ленточного типа, плоскость ленты которых параллельна проводящей поверхности антенной решетки (рис. 3). Ширину лент примем достаточно узкой для того, чтобы токи вибраторов можно было считать параллельными их продольной оси. На входе излучателей предполагается наличие включенной в узком зазоре активного вибратора согласующей цепочки, эквивалентная схема которой приведена на рис. 4.

Рис. 3.

Излучатель с тремя вибраторами в единичной ячейке ФАР: n₁, n₂, n₃ – высота вибраторов над экраном; b – ширина вибратора; χ – угол между осями вибраторов и координатной линией.

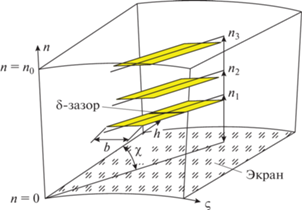
Рис. 4.

Эквивалентная схема входной цепи излучателя: Z – входное сопротивление излучателя; W ‒ волновое сопротивление подводящего фидера; X – согласующая реактивность; n – коэффициент трансформации входной цепи; U, I – напряжение и ток в зазоре вибратора.

Для определения токов в вибраторах одного элемента при парциальном возбуждении (3) воспользуемся методом моментов. Взаимные сопротивления базисных функций тока имеют вид [11]

Использовав разложение электрического поля по пространственным гармоникам (25), (26), запишем (38) в виде

Использовав выражения (10), (11), преобразуем (39) к виду

(41)

Вектор коэффициентов разложения плотности тока по базисным функциям x находится из решения системы линейных уравнений

где W ‒ волновое сопротивление подводящего фидера, n – коэффициент трансформации входной цепи (рис. 4). Коэффициенты матрицы ${\mathbf{\bar {Z}}}$ определяются по формуле

Выражения для парциальной диаграммы элемента, пригодные при произвольном расстоянии между элементами по направляющей, получены в виде ряда по азимутальным гармоникам для случая осесимметричной выпуклой антенной решетки щелевых излучателей [12]. Они применимы и для осесимметричной вибраторной ФАР при использовании в них вектора излучения (55), где величины M_il в этом случае выражаются через функции $e_{{{{\xi }},{{\eta }}}}^{{2l}}$, $h_{{{{\xi }},{{\eta }}}}^{{2l}}$ по формуле (32). Там же приведены выражения для проекций единичного вектора ${{\vec {i}}_{R}}$ на орты системы координат поверхности ${{\vec {i}}_{{{\kern 1pt} \xi }}},{{\vec {i}}_{{{\kern 1pt} {{\eta }}}}},\vec {n}$, а также для других параметров дифференциальной геометрии поверхности осесимметричной ФАР.

3. ИССЛЕДОВАНИЕ СФЕРИЧЕСКОЙ ВИБРАТОРНОЙ ФАР

Результаты расчета парциальной диаграммы элемента вибраторной осесимметричной сферической ФАР приведены на рис. 5. Вибраторы длиной l₁ = 0.5λ расположены на высоте n₁ = 0.243λ над проводящей поверхностью сферы радиусом a = 4.016λ в узлах прямоугольной сетки параллелей и меридианов и ориентированы вдоль меридианов. Число элементов вдоль параллелей N_φ = 46, вдоль меридианов N_θ = 23; расстояние между элементами вдоль меридианов d_θ = 0.56λ, вдоль экватора d_φmax = 0.56λ. Входная цепь настроена на согласование элементов, расположенных на экваторе, в синфазном режиме.

Рис. 5.

Парциальная диаграмма аксиального вибратора в сферической антенной решетке в сечении θ = 90° (а) и θ = = 30° (б); ϑ_n = 90°: 1, 2 − θ-поляризация; 3, 4 – φ-поляризация; 1, 3 − ряд Фурье; 2, 4 – метод стационарной фазы.

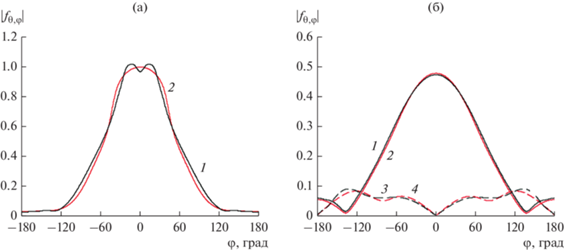
Диаграммы рассчитаны в зависимости от азимутального угла φ для двух значений угла θ с помощью ряда азимутальных гармоник [12] и по методу стационарной фазы (34) и нормированы на корень квадратный из коэффициента направленного действия (КНД) единичной ячейки. Активный излучающий элемент расположен при ϑ_n = 90°.

Поскольку вклад быстрых ползущих волн [1] в случае шагов решетки, близких к половине длины волны, достаточно мал, метод стационарной фазы достаточно близко описывает парциальную диаграмму вибраторного элемента, причем интересно отметить, что не только в освещенной, но и в теневой области излучателя.

Парциальные диаграммы элементов позволяют определить зависимость максимального коэффициента усиления (КУ) ФАР от углов сканирования, иначе, диаграмму сканирования [8]:

Диаграммы сканирования осесимметричных сферических ФАР аксиальных и азимутальных вибраторов с прямоугольной сеткой размещения при радиусе поверхности сферы a = 13.5λ, размерах вибраторов n₁ = 0.243λ, l₁ = 0.5λ и расстоянии между ними по меридианам d_θ = 0.5λ приведены на рис. 6. Активные элементы располагаются в поясе сферы 30° ≤ ϑ ≤ 120°. Для сравнения также приведена зависимость максимального КНД в приближении физической оптики, равного КНД равномерного эквивалентного плоского раскрыва [1, 10]. Угол сканирования отсчитывается от экваториальной плоскости ε₀ = π/2 – θ₀ (угол места). Значения КУ и КНД нормированы на КНД D₀ при ε₀ = 0.

Рис. 6.

Диаграммы сканирования сферических ФАР аксиальных (а) и азимутальных (б) вибраторов: d_φmax = 0.5λ (1), 0.6λ (2); КНД (3).

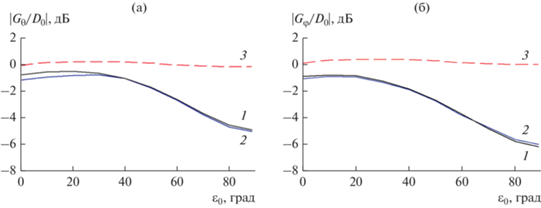
Уменьшение КУ ФАР при сканировании связано с отражением части падающей мощности от входов элементов (уменьшение КПД), неоптимальной поляризацией части излучающих элементов, приводящей к кроссполяризационным потерям, и в случае d_φmax = 0.6λ – с наличием дифракционных лепестков. Как следует из расчета, меньшие потери КУ имеет ФАР аксиальных вибраторов.

Учет эффектов взаимного влияния излучателей позволяет также определить амплитуды отраженных волн на входах излучателей и рассчитать КПД ФАР [10]. На рис. 7 приведены зависимости КПД η рассматриваемых вибраторных сферических ФАР при возбуждении, соответствующем максимальному КУ ФАР [8], от угла сканирования.

Рис. 7.

КПД сферической ФАР аксиальных (а) и азимутальных (б) вибраторов для d_φmax = 0.5λ (1) и 0.6λ (2).

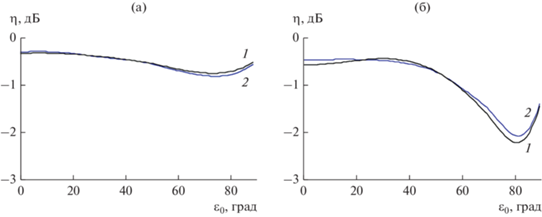
Потери из-за рассогласования входов и поляризационные потери меньше для ФАР аксиальных вибраторов. Для уменьшения потерь из-за рассогласования входов могут быть использованы более сложные излучающие элементы, например, такие как охватываемые соотношениями работы директорные излучатели. Поляризационные потери можно устранить только за счет использования в каждом элементе ФАР вибраторов двух ортогональных поляризаций с независимым управлением их возбуждением при сканировании.

ЗАКЛЮЧЕНИЕ

Электромагнитное поле выпуклой ФАР представлено в виде линейной суперпозиции полей при парциальных возбуждениях, при которых амплитуды падающих волн в фидерах излучателей ФАР имеют одинаковую амплитуду и постоянный сдвиг фазы между соседними излучателями. Для электромагнитного поля в приповерхностном слое квазипериодической выпуклой ФАР при парциальном возбуждении получено приближенное асимптотическое представление в виде ряда пространственных гармоник, обобщающее разложение Флоке для плоских ФАР. Пространственные гармоники имеют вид уходящих и стоячих волн двух поляризаций у выпуклой поверхности, зависимость которых от продольной координаты, направленной по нормали к поверхности, описывается функциями Эйри. Коэффициенты разложения связаны интегральным преобразованием с электрическими и магнитными токами излучателей. В приближении первого порядка связь локальна, так что поле в данной ячейке ФАР определяется токами излучателя, расположенного в этой же ячейке. Выражения поля в приближении первого порядка использованы для анализа выпуклой квазипериодической вибраторной или директорной ФАР методом моментов. Для парциальной диаграммы направленности излучающего элемента в составе ФАР получено равномерное приближенное асимптотическое выражение, справедливое при расстоянии между элементами ФАР не более порядка половины длины волны.

Метод позволяет рассчитать характеристики ФАР большого электрического размера с большим числом элементов при учете их взаимного влияния. Так, для вибраторных осесимметричных сферических ФАР с числом элементов N = 6106…7310 рассчитаны зависимости от угла сканирования коэффициента усиления и коэффициента полезного действия, определяемого рассогласованием на входах элементов. Все численные расчеты выполнены в математической среде Mathcad 15.