Радиотехника и электроника, 2022, T. 67, № 6, стр. 557-561
Применение метода конформного отображения для расчета характеристического сопротивления канала Флоке сверхширокополосной синфазной антенной решетки ТЕМ-рупоров
С. Е. Банков a, М. Д. Дупленкова a, *
a Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация
* E-mail: duplenkova@yandex.ru
Поступила в редакцию 22.10.2021
После доработки 02.12.2021
Принята к публикации 25.12.2021
- EDN: CRMVSM
- DOI: 10.31857/S0033849422060043
Аннотация
Развит метод анализа бесконечной синфазной сверхширокополосной решетки ТЕМ-рупоров, основанный на теории длинных линий. Для определения характеристического сопротивления в каждом сечении бесконечной синфазной решетки использованы методы матриц рассеяния и конформного отображения. Изложен алгоритм, реализующий метод конформного отображения. Проведено сравнение результатов расчета с использованием предлагаемой методики и электродинамического моделирования в программной среде ANSYS HFSS.
ВВЕДЕНИЕ
Сверхширокополосные (СШП) антенные решетки ТЕМ-рупоров интенсивно исследуются в настоящее время. Интерес к ним связан с требованием расширения полосы рабочих частот радиотехнических систем. При этом большинство известных работ (см., например, [1–5]) посвящено численному и экспериментальному исследованию конструкций таких решеток. В отличие от линейных и кольцевых решеток при использовании ТЕМ-рупора в качестве элемента двумерной решетки возникает эффект аномально высокого заднего излучения [6, 7], а использование металлического экрана приводит к значительному сужению полосы согласования. Для частичного преодоления указанной проблемы были предложены [8, 9] двумерные решетки ТЕМ-рупоров с металлизацией межрупорного пространства. В указанных работах моделирование проводилось численно-аналитическим методом Бубнова–Галеркина для решения интегрального уравнения, а также при помощи электродинамического моделирования.
Для моделирования больших антенных решеток было использовано приближение бесконечной решетки [7, 8, 10]. Анализ такой структуры сводится к анализу одного ее периода, получившего название канала Флоке, т.е. фактически исследовали собственные волны канала Флоке. Аналогичный подход использован для решеток антенн Вивальди без диэлектрического заполнения [11, 12].
В рамках указанного метода канал Флоке рассматривается как ступенчатый волноводный трансформатор, преобразующий волны, возбужденные источником, в волны пустого канала Флоке (т.е. свободного пространства). Анализ неоднородного канала Флоке проводится в два этапа. На первом решается задача о собственных волнах однородного канала. Иными словами, строится математическая модель, связывающая параметры собственных волн с геометрическими параметрами структуры. На втором этапе строится математическая модель неоднородной структуры: исследуемый ТЕМ-рупор разбиваем на парциальные ступеньки и для каждой определяем волновую матрицу передачи, а затем находим результирующую матрицу путем их перемножения.
В работе [10] для нахождения импеданса в сечении канала Флоке использовали метод Бубнова–Галеркина [7]. Цель данной работы – развитие альтернативного способа анализа СШП-решеток ТЕМ-рупоров с металлизацией межрупорного пространства с помощью метода конформного отображения.
2. МЕТОД КОНФОРМНОГО ОТОБРАЖЕНИЯ
Метод конформного отображения является строгим методом решения электростатических задач. Определение характеристического сопротивления (импеданса) одиночного ТЕМ-рупора методом конформного отображения проводилось в [13], причем было показано, что импеданс регулярного бесконечного ТЕМ-рупора в квазистатическом приближении зависит только от двух угловых параметров и не меняется вдоль его длины. В данной работе аналогичный метод был применен для определения импеданса в сечении бесконечной решетки ТЕМ-рупоров.
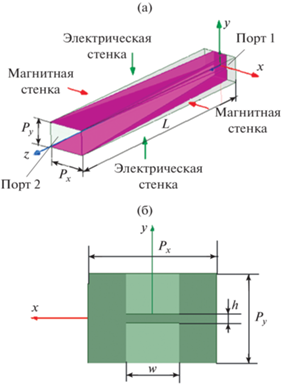
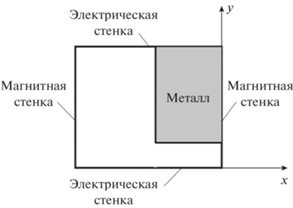
На рис. 1а и 1б показаны соответственно канал Флоке и его поперечное сечение. В синфазной решетке на боковых поверхностях канала Флоке могут быть установлены идеальные электрические и идеальные магнитные стенки. В результате задача сводится к четверти поперечного сечения канала Флоке (рис. 2).
Чтобы определить импеданс, отобразим этот элемент на прямоугольник, причем на его горизонтальных ребрах выполняются граничные условия идеальной электрической проводимости, а на вертикальных ребрах – идеальной магнитной проводимости. Такую структуру принято называть ТЕМ-волноводом. Его импеданс определяется как отношение его сторон [14]. В связи с тем, что не существует прямого решения для конформного отображения многоугольника на прямоугольник, отображение будем осуществлять в два этапа, используя известные отображения многоугольника на полуплоскость интеграла Шварца–Кристоффеля и полуплоскости на прямоугольник. Конформное отображение многоугольника на полуплоскость [15] осуществляют с использованием выражения (1), которое устанавливает соответствие между вершинами многоугольника на плоскости z1 и точками ${{a}_{n}}$ на нижней границе верхней полуплоскости Im(ω) > 0. Для произвольного многоугольника преобразование Шварца–Кристоффеля имеет следующий вид:
(1)
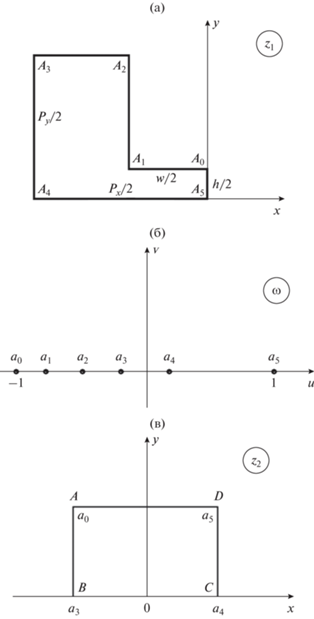
$\begin{gathered} {{z}_{1}} = {{C}_{1}}\int\limits_{{{\omega }_{0}}}^\omega ( \omega - {{a}_{0}}{{)}^{{{{\alpha }_{0}} - 1}}}{{(\omega - {{a}_{1}})}^{{{{\alpha }_{1}} - 1}}}...{{(\omega - {{a}_{{n - 1}}})}^{{{{\alpha }_{{n - 1}}} - 1}}}d\omega + \\ + \,\,{{C}_{2}},\,\,\,\sum\limits_{j = 0}^{n - 1} {{{\alpha }_{j}}} = n - 1, \\ \end{gathered} $Первый этап преобразования отображает плоскость z1 (рис. 3а) на комплексную плоскость ω (рис. 3б). Тогда общее выражение (1) принимает вид
(2)
$\begin{gathered} {{z}_{1}} = {{C}_{1}}\int\limits_{\omega 0}^\omega {f(\omega )} d\omega + {{C}_{2}}, \\ f(\omega ) = {{(\omega - {{a}_{0}})}^{{{{\alpha }_{0}} - 1}}}{{(\omega - {{a}_{1}})}^{{{{\alpha }_{1}} - 1}}}...{{(\omega - {{a}_{5}})}^{{{{\alpha }_{5}} - 1}}}, \\ \end{gathered} $Введем длины сторон многоугольника ${{I}_{j}}$:
(3)
${{I}_{j}} = {{A}_{n}}{{A}_{{n + 1}}} = \int\limits_{{{a}_{n}}}^{{{a}_{{n + 1}}}} {f(\omega )d\omega \,} ,\,\,\,\,j = 0,...,5.$(4)
$\frac{{\left| {{{I}_{0}}} \right|}}{{\left| {{{I}_{4}}} \right|}} = \frac{w}{{{{P}_{x}}}},\,\,\,\,\frac{{\left| {{{I}_{1}}} \right|}}{{\left| {{{I}_{3}}} \right|}} = 1 - \frac{h}{{{{P}_{y}}}},\,\,\,\,\frac{{\left| {{{I}_{3}}} \right|}}{{\left| {{{I}_{4}}} \right|}} = \frac{{{{P}_{x}}}}{{{{P}_{y}}}}.$Постоянную С1, задающую масштаб фигуры, находят из следующего равенства:
Постоянная C2 определяет положение многоугольника на плоскости z1 относительно начала координат. Примем ее равной $i\left| {{{I}_{5}}} \right|{{C}_{1}}$. Тогда вершина А5 окажется в точке z = 0.
Соотношения (4) используем для определения параметров а0, …, а5. Видно, что число неизвестных превышает число уравнений, что дает нам возможность сформулировать для параметров а0, …, а5 дополнительные условия. Потребуем выполнения следующих соотношений:
С учетом равенств (6) находим три неизвестные постоянные а1, …, а3 и три уравнения (4) для их определения.
Зададим положение точек а1, …, а3 с помощью коэффициентов k1, …, k3:
(7)
${{a}_{1}} = - {{k}_{1}},\,\,\,\,{{a}_{2}} = - {{k}_{1}}{{k}_{2}},\,\,\,\,{{a}_{3}} = - {{k}_{1}}{{k}_{2}}{{k}_{3}},$Введем следующие функции:
(8)
$\begin{gathered} {{A}_{1}}({{k}_{1}},{{k}_{2}},{{k}_{3}}) = \frac{{\left| {{{I}_{0}}} \right|}}{{\left| {{{I}_{4}}} \right|}},\,\,\,\,{{A}_{2}}({{k}_{1}},{{k}_{2}},{{k}_{3}}) = \frac{{\left| {{{I}_{1}}} \right|}}{{\left| {{{I}_{3}}} \right|}}, \\ {{A}_{3}}({{k}_{1}},{{k}_{2}},{{k}_{3}}) = \frac{{\left| {{{I}_{3}}} \right|}}{{\left| {{{I}_{4}}} \right|}}. \\ \end{gathered} $Подстановка (8) приводит нас к системе трех уравнений относительно коэффициентов k1, …, k3. Непосредственное ее решение представляет собой достаточно трудоемкий процесс, связанный с численным определением интегралов (3). Чтобы избежать больших затрат компьютерного времени, мы использовали процедуру многомерной аппроксимации. Для этого функции А1, …, А3 были рассчитаны для дискретных значений аргументов:
(9)
$\begin{gathered} {{k}_{{1r}}} = {r \mathord{\left/ {\vphantom {r N}} \right. \kern-0em} N},\,\,\,\,r = 0,\,\,1,\,\,...,N, \\ {{k}_{{2s}}} = {s \mathord{\left/ {\vphantom {s N}} \right. \kern-0em} N},\,\,\,\,s = 0,\,\,1,\,\,...,N, \\ {{k}_{{3t}}} = {t \mathord{\left/ {\vphantom {t N}} \right. \kern-0em} N},\,\,\,\,r = 0,\,\,1,\,\,...,N. \\ \end{gathered} $По полученным массивам данных строится сплайн-аппроксимация. Для контроля точности получаемого решения введем параметр Δ:
(10)
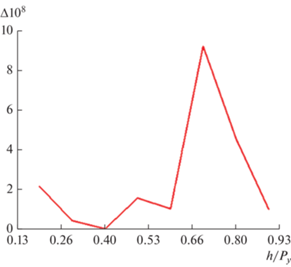
$\Delta = \left| {{{A}_{1}} - {w \mathord{\left/ {\vphantom {w {{{P}_{x}}}}} \right. \kern-0em} {{{P}_{x}}}}} \right| + \left| {{{A}_{2}} - 1 + {h \mathord{\left/ {\vphantom {h {{{P}_{y}}}}} \right. \kern-0em} {{{P}_{y}}}}} \right| + \left| {{{A}_{3}} - {{{{P}_{x}}} \mathord{\left/ {\vphantom {{{{P}_{x}}} {{{P}_{y}}}}} \right. \kern-0em} {{{P}_{y}}}}} \right|.$Он позволяет оценить отличие между фигурой на плоскости ${{z}_{1}}$ и истинным сечением канала Флоке. На рис. 4 показана зависимость параметра Δ от расстояния h (см. рис. 1). Кривая получена для ${w \mathord{\left/ {\vphantom {w {{{P}_{x}}}}} \right. \kern-0em} {{{P}_{x}}}}$ = 0.4. Видно, что конформное отображение в описываемом примере осуществляется с относительной погрешностью, не превышающей 10–7.
На втором этапе с помощью эллиптического интеграла первого рода (11) конформно отобразим верхнюю полуплоскость Im(ω) > 0 на прямоугольник АВСD в плоскости z2 (см. рис. 3в).
(11)
${{z}_{2}} = I(\omega ) = {{С}_{3}}\int\limits_0^\omega {\frac{{du}}{{\sqrt {(1 - {{u}^{2}})(1 - {{k}^{2}}{{u}^{2}})} }}} ,\,\,\,\,k < 1.$При этом потребуем, чтобы вершины А0–А3 на плоскости z1 перешли на левую вертикальную границу прямоугольника на плоскости z2, а вершины А4, А5 на его правую границу. В этом случае получаем искомое расположение электрических и магнитных стенок, позволяющее записать для импеданса Zc простое соотношение
(12)
${{Z}_{c}} = {{{{W}_{0}}\left| {AD} \right|} \mathord{\left/ {\vphantom {{{{W}_{0}}\left| {AD} \right|} {\left| {CD} \right|}}} \right. \kern-0em} {\left| {CD} \right|}},$Отображение в форме (11) переводит точку ω = 0 на плоскости ω в нулевую точку на плоскости z2. Точкам а0, а3, а4, а5 на плоскости ω будут соответствовать точки АBCD на плоскости z2. Параметр k, задающий положение точки перехода с горизонтальной стороны прямоугольника на вертикальную, выбирается из условия k = 1/a4. При 0 < u < 1/k, u = Re(ω) подынтегральное выражение в формуле (11) будет чисто действительным, т.е. движению точки в этом интервале в плоскости ω соответствует движение точки вдоль стороны ВС (от 0 до С) в плоскости z2, а при 1/k < u < 1 выражение становится чисто мнимым и движению точки в этом интервале на плоскости ω будет соответствовать вертикальный отрезок СD. Вычисляя соответствующие интегралы, определяем длины отрезков ВС и СD. Отметим, что величина постоянной С3, входящей в отображение (11), не влияет на характеристическое сопротивление, так как в него входит отношение длин отрезков и данная константа сокращается.
Отметим, что в результате отображений исходной фигуры на прямоугольник ее две электрические стенки перешли в вертикальные отрезки АВ и CD, а магнитные соответственно в горизонтальные AD и BC, т.е. мы пришли к так называемому ТЕМ-волноводу, для которого известно соотношение (12). Физически это отношение разности потенциалов между двумя металлическими пластинами к полному току на одной из них.
Таким образом, осуществив преобразования (1) и (11) и определив необходимые константы, мы получили решение задачи о характеристическом сопротивлении (импедансе) в сечении канала Флоке.
5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
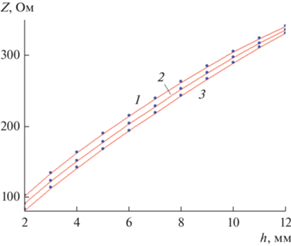
Результаты расчетов импеданса, полученных при использовании конформного отображения и расчетов с помощью системы электродинамического моделирования HFSS приведены на рис. 5. Расчет был проведен для ячеек Флоке, имеющих вдоль оси 0z постоянное сечение при w = 3, 4, 5 мм и изменении параметра h от 2 до 12 мм. Как видно на рисунке, результаты совпадают с графической точностью.
Рис. 5.
Зависимость характеристического сопротивления от геометрических параметров структуры: w = = 4 (1), 5 (2) и 6 мм (3).
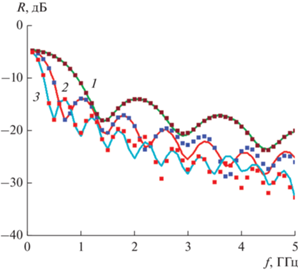
На рис. 6 представлены зависимости коэффициента отражения от частоты для решетки регулярных ТЕМ-рупоров, расчитанные методом матрицы рассеяния и конформного отображения (точки) и при помощи НFSS (сплошные линии). Результаты совпадают с графической точностью до уровня ‒20 дБ.
ЗАКЛЮЧЕНИЕ
Представленные результаты показали, что метод конформного отображения может быть применен для расчета характеристического сопротивления (импеданса) в сечениях канала Флоке сверхширокополосной синфазной антенной решетки ТЕМ-рупоров с металлизацией межрупорного пространства. Этот вывод подтверждается результатами сравнения с расчетами регулярных ячеек Флоке с использованием HFSS, а также сопоставлением расчетов частотной зависимости коэффициента отражения бесконечной двумерно-периодической решетки регулярных ТЕМ-рупоров.
Список литературы
McGrath D.T., Baum C.E. // IEEE Trans. 1999. V-AP. 47. № 3. P. 469.
Elmansouri M.A., Ha J., Filipovic D.S. // IEEE Trans. 2017. V-AP. 65. № 3. P. 1374.
Elmansouri M.A., Filipovic D.S. // IET Microwaves, Antennas and Propagation. 2017. V. 11 № 15. P. 2134.
Калошин В.А., Ле Н.Т., Фролова Е.В. // Журн. радиоэлектроники. 2020. № 4. http://jre.cplire.ru/jre/apr20/2/text.pdf.
Fedorov V.M., Efanov M.V., Ostashev V.Y. et al. // Electronics. 2021. V. 10. № 9. https://doi.org/10.3390/electronics10091011
Калошин В.А., Нгуен К.З. // Журн. радиоэлектроники. 2017. № 5. http://jre.cplire.ru/jre/may17/ 14/text.pdf.
Банков С.Е., Калошин В.А., Нгуен К.З. // РЭ. 2018. Т. 63. № 7. С. 702.
Банков С.Е, Калошин В.А, Ле Н.Т. // РЭ. 2018. Т. 63. № 12. С. 1263.
Калошин В.А., Ле Н.Т. // Журн. радиоэлектроники. 2020. № 3. http://jre.cplire.ru/jre/mar20/8/text.pdf.
Дупленкова М.Д., Калошин В.А. // РЭ. 2022. Т. 68. № 5. С. 419.
Банков С.Е., Скородумова Е.А. // РЭ. 2015. Т. 60. № 5. С. 470.
Банков С.Е., Дупленкова М.Д. // РЭ. 2018. Т. 63. № 1. С. 25.
Yang F.C., Lee K.S.H. // Sensor and Simulation Note. 1976. № 221. P. 1.
Справочник по расчету и конструированию СВЧ полосковых устройств / Под ред. В.И. Вольмана. М.: Радио и связь, 1982.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1977.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника