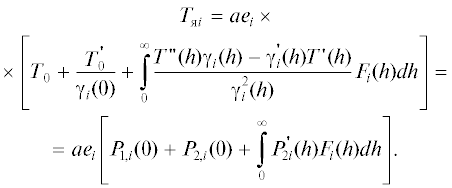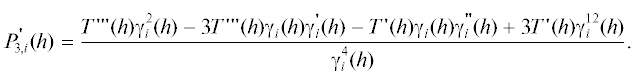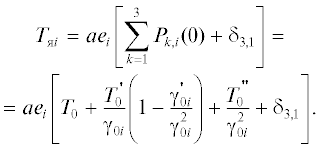Радиотехника и электроника, 2022, T. 67, № 6, стр. 541-545

О некоторых канонических представлениях радиометрических задач

В. В. Климов^*

Фрязинский филиал Института радиотехники и электроники им. В.А. Котельникова РАН
141190 Фрязино, Московской обл., пл. Введенского, 1, Российская Федерация

^* E-mail: klimov47@list.ru

Поступила в редакцию 28.05.2019
После доработки 15.10.2021
Принята к публикации 25.12.2021

EDN: USKPFY
DOI: 10.31857/S0033849422060110

Полный текст (PDF)

Аннотация

Рассмотрен и обоснован новый подход к построению комплекса математических и программных средств для экологического мониторинга окружающей среды на основе многоканальной регистрации радиометрической информации и ее анализа и качественной интерпретации. Для решения прямой и обратной задачи получены простые аналитические соотношения, связывающие основные радиофизические параметры с параметрами среды. Подробно рассмотрен случай однородной среды с оценкой диапазона рабочих частот, а также случаи среды с экспоненциальным и полиномиальным поглощением.

В исследовании природных ресурсов Земли важную роль играют дистанционные методы измерения физических характеристик, основное преимущество которых по сравнению с контактными измерениями заключается в высокой скорости регистрации данных. Наряду с оптическими в последнее время все более широкое применение находят радиометрические методы исследования, которые позволяют получать не только поверхностные характеристики Земного покрова, но также и глубинные характеристики покрова [1, 2]. Такие характеристики позволяют, например, следить за влажностью почвы сельскохозяйственных полей, обнаруживать очаги пожаров, возникающие в торфяных образованиях, и решить ряд других народно-хозяйственных задач.

В измерениях, производимых с помощью радиометров различных диапазонов, устанавливаемых на борту самолета или искусственного спутника Земли, широко используется соотношение, связывающее радиояркостную температуру T_яi на рабочей частоте ν_i с термодинамическими и электрофизическими характеристиками среды [3, 6]:

(1)

$\begin{gathered} {{T}_{{{\text{я}}i}}} = ae\int\limits_0^\infty {T(h){{\gamma }_{i}}(h)\exp \left[ { - \int\limits_0^h {{{\gamma }_{i}}(h{\kern 1pt} ')dh{\kern 1pt} '} } \right]} dh = \\ = - a{{e}_{i}}\int\limits_0^\infty {T(h)d{{F}_{i}}(h)} \kappa , \\ \end{gathered} $

где h – глубина проникновения электромагнитной волны в поглощающую среду; γ_i(h) – коэффициент поглощения энергии радиосигнала (γ_i(h) > 0); ae_i – излучательная способность среды; T(h) – термодинамическая температура среды.

Соотношение (1) позволяет по T(h) и γ_i(h) находить значение T_яi (прямая задача) и по T_яi находить T(h) и γ_i(h) (обратная задача). Поиск аналитических соотношений, связывающих радиояркостную температуру среды с ее термодинамическими и электрофизическими характеристиками, является актуальным как для решения прямой, так и обратной радиометрических задач.

Приводимые ниже соотношения являются относительно простыми формулами, включающими в себя значения T(h) и γ_i(h) и их производных в точке h = 0. Опыт работы, проведенной автором по вычислению радиояркостных температур чистой атмосферы и паров воды в диапазоне волн 0.7…2.0 мм, показал эффективность вычислений на основе таких соотношений. Так, применение этих соотношений позволило сократить объем вычислений по сравнению с прямым просчетом в среднем в пять раз. Приведем фрагмент алгоритма, соответствующий вычислению радиояркостной температуры по предлагаемому методу:

for i: =1 step 1 until BB do begin x:=0;

for i1:=j step 1 until HH do begin

h:=(W[i1+1,1] – W[i1,1])/5; dT:=(W[i1+1,4] – W[i1,4]/5;

d3:=(i,i1+1) – G(I, i1))/5; GH:=G(i, i1) – d3/2; TH:=W[i1, 4] – dT/2;

for j1:=1 step 1 until 5 do begin

GH:=GH+d3; TH:=TH+dT;

x:=x+TH·(1 – exp(-GH·H))·exp(–x1);

x1:=x1+GH·H end end; G3[i]:=x end; вывод (G3).

Здесь i – номер частоты, i1 – номер высоты, j – текущая высота наблюдения, G3 – значение радиояркостной температуры, W[i1, 1] – заданная моделью атмосферы высота, W[i1, 4] – заданная моделью атмосферы температура.

Перейдем к обобщению этого алгоритма. Отметим, что

(2)

${{F}_{i}}(h) = \exp \left[ {\int\limits_0^h {{{\gamma }_{i}}(x)dx} } \right],$

(3)

${{F}_{i}}\left( 0 \right) = 1,\,\,\,\,{{F}_{i}}\left( \infty \right) = 0.$

Для удобства дальнейшего рассмотрения введем следующие обозначения:

(4)

$\begin{gathered} {{P}_{{{\text{1,}}i}}}(h) = T(h);\,\,\,\,{{P}_{{2,i}}} = \frac{{T'(h)}}{{{{\gamma }_{i}}(h)}}; \ldots ; \\ {{P}_{{k,i}}}(h) = \frac{{P_{{k - 1,i}}^{'}(h)}}{{{{\gamma }_{i}}(h)}}. \\ \end{gathered} $

Представление яркостной температуры дает следующая лемма.

Лемма 1. Пусть функции T(h) и γ_i(h) таковы, что

(5)

$\int\limits_0^\infty {P_{{N,i}}^{'}(h)} {{F}_{i}}(h)dh = {{\delta }_{{Ni}}},$

тогда

(6)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\sum\limits_{k = 1}^N {{{P}_{{k,i}}}(0) + a{{e}_{i}}{{\delta }_{{Ni}}}} ,$

где P_k,i(0) – значение P_k,i(h) при h = 0.

Доказательство. Интегрируя (1) по частям и учитывая (3) получим

(7)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}{{T}_{0}} + \left[ {\int\limits_0^\infty {T{\kern 1pt} '(h){{F}_{i}}(h)dh} } \right],$

где T₀= T(0) – температура поверхности.

Таким образом, имеем

${{T}_{{{\text{я}}i}}} = ae({{T}_{0}} + {{\delta }_{{1i}}}) = a{{e}_{i}}({{P}_{{1,i}}}(0) + {{\delta }_{{1i}}}).$

Разделив и умножив подынтегральное выражение (7) на γ_i(h) и интегрируя полученное выражение, получим

(8)

Таким образом, имеем

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\left[ {{{P}_{{1,i}}}(0) + {{P}_{{2,i}}}(0) + {{\delta }_{{2,i}}}} \right].$

Разделив и умножив подынтегральное выражение (8) на γ_i(h) и интегрируя полученное выражение, получим

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\left[ {{{P}_{{1,i}}}(0) + {{P}_{{2,i}}}(0) + {{P}_{{3,i}}}(0) + \int\limits_0^\infty {P_{{3,i}}^{'}(h){{F}_{i}}(h)dh} } \right],$

где

Покажем, что при любом N справедливо

(9)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\left[ {\sum\limits_{k = {\text{1}}}^N {{{P}_{{k,i}}}(0) + \int\limits_0^\infty {P_{{N,i}}^{'}(h){{F}_{i}}(h)dh} } } \right].$

Для N = 1, 2, 3 справедливость (9) доказана. Пусть утверждение справедливо для N = l, докажем его для N = l + 1. Имеем

(10)

${{T}_{{{\text{я}}i}}} = \left[ {\sum\limits_{k = {\text{1}}}^l {{{P}_{{k,i}}}(0) + \int\limits_0^\infty {P_{{l,i}}^{'}(h){{F}_{i}}(h)dh} } } \right].$

Учитывая, что ${{P}_{{l + 1,i}}}(h) = {{P_{{l,i}}^{'}(h)} \mathord{\left/ {\vphantom {{P_{{l,i}}^{'}(h)} {{{\gamma }_{i}}(h)}}} \right. \kern-0em} {{{\gamma }_{i}}(h)}}$, получим

(11)

$\begin{gathered} \int\limits_0^\infty {P_{{l,i}}^{'}(h){{F}_{i}}(h)dh} = \int\limits_0^\infty {\frac{{{{P}_{{e,i}}}(h)}}{{\gamma _{i}^{{}}(h)}}{{F}_{i}}(h){{\gamma }_{i}}(h)dh} = \\ = - \int\limits_0^\infty {{{P}_{{l + 1,i}}}(h)d{{F}_{i}}(h)} \\ \end{gathered} $

и, интегрируя (11) по частям, получим

(12)

$\int\limits_0^\infty {P_{{l,i}}^{'}(h){{F}_{i}}(h)dh} = {{P}_{{l + 1,i}}}(0) + \int\limits_0^\infty {P_{{l,i}}^{'}(h){{F}_{i}}(h)dh} .$

Подставляя (12) в разложение (10), получим требуемый результат.

Лемма 2. Пусть ${{P}_{{N + 1,i}}}(h) = {{\delta }_{{N,i}}}{{\varphi }_{{N,i}}}(h),$ тогда соотношение (5) выполняется по крайней мере для следующих функций:

(13)

${{\varphi }_{{N,i}}}(h) \equiv 1,$

(14)

${{\varphi }_{{N,i}}}(h) = \frac{{\gamma _{i}^{2}(h) - \gamma _{i}^{'}(h)}}{{{{\gamma }_{i}}(h){{\gamma }_{i}}(0)}},$

(15)

${{\varphi }_{{N,i}}}(h) = - \,(k + 1)F_{i}^{k}(h).$

Доказательство. Пусть справедливо (13), тогда, используя (4), получим

$\begin{gathered} \int\limits_0^\infty {P_{{l,i}}^{'}(h){{F}_{i}}(h)dh} = \int\limits_0^\infty {{{P}_{{N + 1,i}}}(h){{\gamma }_{i}}(h){{F}_{i}}(h)dh = } \\ = \int\limits_0^\infty {{{\delta }_{{N,i}}}{{\varphi }_{{N,i}}}(h){{\gamma }_{i}}(h){{F}_{i}}(h)dh = } \\ = {{\delta }_{{N,i}}}\int\limits_0^\infty {{{\gamma }_{i}}(h){{F}_{i}}(h)dh = } - {\kern 1pt} \,{{\delta }_{{N,i}}}\int\limits_0^\infty {d{{F}_{i}}(h)} = {{\delta }_{{N,i}}}. \\ \end{gathered} $

Пусть справедливо (14). Поскольку

$F_{i}^{{''}}(h) = \left[ {\gamma _{i}^{2}(h) - \gamma _{i}^{'}(h)} \right]{{F}_{i}}(h),$

то

В предпоследнем равенстве использовалось F_i(h) = = γ_i(h)F_i(h). Пусть выполняется (15), тогда

$\begin{gathered} \int\limits_0^\infty {{{P}_{{N + 1,i}}}(h){{\gamma }_{i}}(h){{F}_{i}}(h)dh} = \\ = - \,{{\delta }_{{N,i}}}(k + 1)\int\limits_0^\infty {F_{i}^{k}} (h)d{{F}_{i}}(h) = {{\delta }_{{N,i}}}. \\ \end{gathered} $

Рассмотрим теперь несколько примеров вычисления радиояркостной температуры для различных видов γ_i(h). В случае однородной среды, т.е. когда γ_i(h) ≡ γ_i(0) = γ_i> 0, используя соотношение (4) и лемму 1, получим

(16)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\sum\limits_{k = {\text{1}}}^N {{{T}^{{(k - 1)}}}{{(0)} \mathord{\left/ {\vphantom {{(0)} {\gamma _{i}^{{k - 1}}}}} \right. \kern-0em} {\gamma _{i}^{{k - 1}}}}} + a{{e}_{i}}{{\delta }_{{N,i}}}.$

Лемма 3. Пусть φ_N,i(h) ≡ $1$, тогда

(17)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\sum\limits_{k = {\text{1}}}^N {\sum\limits_{t = k - {\text{1}}}^N {\frac{{t!}}{{(t - k + 1)!}}{{B}_{{ti}}}\Lambda _{i}^{{t - k + 1}}(0)} } + {{\delta }_{{N,i}}}a{{e}_{i}},$

где Λ_i(h) – первообразная функция для γ_i(h), B_N,i = = δ_N,i /N!, B_ti – некоторые константы при t = 0, 1,…, N – 1.

Пусть

${{\gamma }_{i}}(h) = \sum\limits_{l = 0}^n {{{C}_{{il}}}{{h}^{l}}} ,$

тогда

${{\Lambda }_{i}}(h) = \sum\limits_{l = 0}^n {{{C}_{{il}}} + \frac{{{{h}^{{l + 1}}}}}{{l + 1}} + {{C}_{i}}} ,$

где C_i – некоторая константа, и по лемме 3 получим

(18)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\sum\limits_{k = {\text{1}}}^N {\sum\limits_{t = k - {\text{1}}}^N {\frac{{{{B}_{{ti}}}t!}}{{(t - k + 1)!}}C_{i}^{{t - k + 1}}} } + {{\delta }_{{N,i}}}a{{e}_{i}}.$

Рассмотрим случай, когда ${{\gamma }_{i}}(h) = {\text{exp(}}{{a}_{i}}h)$, при этом

${{\Lambda }_{i}}(h) = \frac{{\exp ({{a}_{i}}h)}}{{{{a}_{i}}}} + {{C}_{i}},$

где C_i – некоторая константа. Находясь в условии леммы 3, получим

(19)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\sum\limits_{k = {\text{1}}}^N {\sum\limits_{t = k - {\text{1}}}^N {\frac{{{{B}_{{ti}}}t!}}{{(t - k + 1)!}}\left( {\frac{1}{{{{a}_{i}}}} + {{C}_{i}}} \right)_{{}}^{{t - k + 1}}} } + {{\delta }_{{N,i}}}a{{e}_{i}}.$

И, наконец, если

${{\gamma }_{i}}(h) = \exp ({{a}_{i}}h)\sum\limits_{k = 0}^n {{{C}_{{ik}}}{{h}^{k}}} ,$

то

(20)

$\begin{gathered} {{\Lambda }_{i}}(h) = \exp ({{a}_{i}}h) \times \\ \times \,\,\sum\limits_{k = 0}^n {\left[ {\frac{{{{h}^{k}}}}{{{{a}_{i}}}} + \sum\limits_{p = 1}^k {\frac{{{{{( - 1)}}^{p}}k!}}{{(k - p)!a_{i}^{{p + 1}}}}{{h}^{{k - p}}}} } \right]} {{C}_{{ik}}} + {{C}_{i}}. \\ \end{gathered} $

Находясь в условии леммы 3, получим

(21)

${{T}_{{{\text{я}}i}}} = ae\sum\limits_{k = {\text{1}}}^N {\sum\limits_{t = k - {\text{1}}}^N {\frac{{{{B}_{{ti}}}t!}}{{(t - k + 1)!}}\left[ {\sum\limits_{l = 0}^n {\frac{{{{{( - 1)}}^{l}}}}{{a_{i}^{{l + 1}}}}l!{{C}_{{il}}} + {{C}_{i}}} } \right]{\kern 1pt} } } ,$

где C_i – некоторая константа.

Представление термодинамической температуры дает следующая лемма.

Лемма 4. Пусть ${{P}_{{N + 1,l}}}(h) = {{\delta }_{{N,i}}}(h)$, тогда

(22)

$T(h) = \sum\limits_{k = 0}^{N - 1} {{{B}_{{ki}}}\Lambda _{i}^{k}(h)} + {{\delta }_{{N,i}}}{{\Phi }_{{N + 1,i}}}(h),$

где Λ_i(h) – первообразная функция для γ_i(h), Φ_N + _1,i(h) – первообразная функция для [γ_i(h)Φ_N,i(h)], …., Φ_0,i(h) = φ_N,i(h), B_k,i – некоторая константа.

Доказательство. Из соотношений (4) следует, что

(23)

$P_{{N,i}}^{'}(h) = {{\delta }_{{N,i}}}{{\varphi }_{{N,i}}}(h){{\varphi }_{i}}(h).$

Интегрируя (23), находим

(24)

${{P}_{{N,i}}}(h) = \int {{{\delta }_{{N,i}}}(h){{\varphi }_{{N,i}}}(h)dh = {{\delta }_{{N,i}}}(h){{\varphi }_{{1,i}}}(h) + {{B}_{{1i}}}.} $

Подставляя (24) в (4), получим дифференциальное уравнение

$P_{{N - {\text{1,}}i}}^{'}(h) = {{\gamma }_{i}}(h)({{\delta }_{{N,i}}}{{\Phi }_{{1,i}}}(h) + {{B}_{{1i}}}),$

решение которого имеет вид

${{P}_{{N - {\text{1,}}i}}}(h) = {{\delta }_{{N,i}}}{{\Phi }_{{2,i}}}(h) + {{B}_{{1i}}}{{\Lambda }_{i}}(h) + {{B}_{{0i}}}.$

Повторяя эту процедуру (N – 1) раз, получим разложение (22).

Лемма 5. Если φ_N,i(h) ≡ 1, то

(25)

${{P}_{{k,i}}}(h) = \sum\limits_{t = k - 1}^N {\frac{{t!}}{{(t - k + 1)!}}{{B}_{{ti}}}\Lambda _{i}^{{t - k + 1}}} (h),$

где Λ_i(h) – первообразная функция для γ_i(h), B_Ni = = δ_N,i/N!, B_ti – некоторые константы при t = 0, 1,…, N – 1.

Доказательство. В силу сделанных предположений

$\Phi _{{N + {\text{1,}}i}}^{{}}(h) = \frac{{\Lambda _{i}^{N}}}{{N{\text{!}}}}$

и значит, по лемме 4 имеем

(26)

$T(h) = \sum\limits_{k = 0}^{N - 1} {{{B}_{{ki}}}\Lambda _{i}^{k}} (h) + {{\delta }_{{Ni}}}\frac{{\Lambda _{i}^{N}(h)}}{{N!}}.$

При k =1 разложение (25) очевидно, при k = 2 имеем

$\begin{gathered} {{P}_{{2,i}}} = \frac{{T{\kern 1pt} '(h)}}{{{{\gamma }_{i}}(h)}} = \frac{1}{{{{\gamma }_{i}}(h)}}\sum\limits_{t = 1}^N {t{{B}_{{ti}}}\Lambda _{i}^{{t - 1}}} (h)\Lambda _{i}^{'}(h) = \\ = \sum\limits_{t = 1}^N {t{{B}_{{ti}}}\Lambda _{i}^{{t - 1}}} (h). \\ \end{gathered} $

Предполагая, что (25) справедливо для k = l, докажем его для k = l + 1. Имеем

$\begin{gathered} {{P}_{{l + 1,i}}}(h) = \frac{{P_{{li}}^{'}(h)}}{{{{\gamma }_{i}}(h)}} = \\ = \frac{1}{{{{\gamma }_{i}}(h)}}\sum\limits_{t = 1}^N {\frac{{{{B}_{{ti}}}t!(t - l + 1)}}{{(t - l + 1)!}}\Lambda _{i}^{{t - l}}} (h)\Lambda _{i}^{'}(h) = \\ = \sum\limits_{t = l}^N {\frac{{t!}}{{(t = l)!}}{{B}_{{ti}}}\Lambda _{i}^{{t - l}}} (h). \\ \end{gathered} $

Таким образом, справедливость (25) доказана.

Теперь справедливость леммы 3 не вызывает сомнений. Действительно, если в выражение (6) подставить P_k,i(h), вычисленное по формуле (25) при h = 0, то полученное выражение даст нам формулу (17).

Рассмотрим более подробно случай, когда φ_N,i(h) ≡ 1. В этом случае термодинамическая температура запишется в виде (26). Пусть ${{\gamma }_{i}}(h) = {{\gamma }_{{1i}}}h + {{\gamma }_{{0i}}}$, тогда

${{\Lambda }_{i}}(h) = \frac{{{{\gamma }_{{1i}}}{{h}^{2}}}}{2} + {{\gamma }_{{0i}}}h + {{C}_{i}}.$

Будем искать T(h) в виде $T(h) = \sum\nolimits_{i = 0}^\infty {{{T}_{i}}{{h}^{i}}} $. Приравнивая коэффициенты при одинаковых степенях, получим при N = 1:

(27)

$\begin{gathered} {{T}_{0}} = {{B}_{{0i}}} + {{\delta }_{{1i}}}С_{i}^{{}},\,\,\,\,{{T}_{1}} = {{\delta }_{{1i}}}\gamma _{{0i}}^{{}}, \\ {{T}_{2}} = \frac{{{{\delta }_{{1i}}}}}{2}\gamma _{{1i}}^{{}},\,\,\,\,{{T}_{3}} = {{T}_{{\text{4}}}} = ... = 0. \\ \end{gathered} $

Как следует из (27), произвольным образом можно задавать только T₀. Приравнивая коэффициенты при одинаковых степенях при N = 2, получим

(28)

$\begin{gathered} {{T}_{0}} = {{B}_{{0i}}} + {{B}_{{1i}}}{{C}_{i}} + \frac{{{{\delta }_{{2,i}}}}}{2}C_{i}^{2},\,\,\,\,{{T}_{1}} = {{B}_{{1i}}}{{\gamma }_{{0i}}} + \frac{{{{\delta }_{{2,i}}}}}{2}C_{i}^{{}}{{\gamma }_{{0i}}}, \\ {{T}_{2}} = {{B}_{{1i}}}{{\gamma }_{{1i}}} + \frac{{{{\delta }_{{2,i}}}}}{2}\gamma _{{0i}}^{2} + \frac{{{{\delta }_{{2,i}}}}}{4}{{C}_{i}}{{\gamma }_{{1i}}}, \\ {{T}_{3}} = \frac{{{{\delta }_{{2,i}}}{{\gamma }_{{0i}}}{{\gamma }_{{1i}}}}}{4},\,\,\,\,{{T}_{4}} = \frac{{{{\delta }_{{2,i}}}\gamma _{{1i}}^{2}}}{8},\,\,\,\,{{T}_{5}} = {{T}_{6}} = ... = 0. \\ \end{gathered} $

Как это следует из формул (28), коэффициенты T₀ и T₁ можно задавать произвольно. Таким образом, увеличивая N, мы можем варьировать коэффициенты T_i при больших значениях индекса i.

Если

${{\delta }_{i}}(h) = \sum\limits_{l = 0}^n {{{C}_{{il}}}{{h}^{l}},} $

то по лемме 4 имеем

$T(h) = {{\sum\limits_{k = 0}^N {{{B}_{{ki}}}\left[ {\sum\limits_{l = 0}^n {{{C}_{{il}}}\frac{{{{h}^{{l + 1}}}}}{{(l + 1)}} + {{C}_{i}}} } \right]} }^{k}},$

где ${{B}_{{ki}}} = {{{{\delta }_{{N,i}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{N,i}}}} {N!}}} \right. \kern-0em} {N!}},{{C}_{{i,}}}{{B}_{{ki}}}$ – некоторые константы при k = 0, 1, …, N – 1.

В случае ${{\gamma }_{i}}(h) = \exp ({{a}_{i}}h)$ термодинамическая температура будет равна

$T(h) = {{\sum\limits_{k = 0}^N {{{B}_{{ki}}}\left[ {\frac{{\exp ({{a}_{i}}h)}}{{{{a}_{i}}}} + {{C}_{i}}} \right]} }^{k}}.$

Если

${{\gamma }_{i}}(h) = \exp ({{a}_{i}}h)\sum\limits_{k = 0}^n {{{C}_{{ik}}}{{h}^{k}},} $

то

$T(h) = \sum\limits_{k = 0}^{N - 1} {{{B}_{{ki}}}\exp (k{{a}_{i}}h){{Q}_{{nk}}}(h)} ,$

где Q_nk(h) – многочлен степени (n × k).

Для многих практических ситуаций достаточная степень точности расчета обеспечивается при N = 3 или когда

(29)

Из этого соотношения, в частности, следует, что в коротковолновой части спектра коэффициент поглощения реальных сред достаточно большой и значение радиояркостной температуры определяется в основном температурой на поверхности. С увеличением длины волны уменьшается поглощение среды и становится существенным вклад второго и третьего члена в разложении (29). При этом для частоты ν₁, для которой $\gamma _{j}^{'} = \gamma _{j}^{2}(0)$, происходит смена знака второго члена. Это обстоятельство свидетельствует о взаимности появления локального экстремума в спектре радиояркостной температуры, что, в частности, подтверждается рядом натурных экспериментов, выполненных с торфяными образованиями с борта самолета [4, 5].

Для иллюстрации возможности использования полученных выше соотношений при решении обратных задач будем считать, что функции γ_i(h) заданы и требуется определить термодинамический профиль по известным значениям ${{T}_{{{\text{я}}i}}}(i = 1,...,\overline k )$.

При сделанных предположениях в соответствии с (6) образуется система линейных уравнений вида

(30)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\sum\limits_{k = 1}^N {{{A}_{{ik}}}{{T}^{{(k - 1)}}}(0) + a{{e}_{i}}{{\delta }_{{N,i}}}} ,$

где A_ik определяется соотношениями (4) через значения ${{\gamma }_{i}}(0),\gamma _{i}^{'}(0),...,\gamma _{i}^{{(N - 1)}}(0)$. Если при каждом i можно пренебречь членом ae_iδ_N,i, то указанная система решается относительно T(0), T'(0),…, T^(N ^– 1)(0) обычными методами. Если при некоторых i членом ae_iδ_N,i пренебречь нельзя, то система решается относительно $T{\text{(0),}}T{\kern 1pt} {\kern 1pt} '{\text{(0),}}...{\text{,}}{{T}^{{{\text{(}}N - {\text{1)}}}}}(0),$ ${{\delta }_{{N,1}}},{{\delta }_{{N,2}}},...,{{\delta }_{{N,{{i}_{m}}}}}$ после присоединения к системе (30) необходимого числа уравнений с пренебрежимым членом ae_iδ_N,i.

Рассмотрим случай однородной среды $({{\gamma }_{i}}(h) \equiv {{\gamma }_{i}}(0) = {{\gamma }_{i}})$. В этом случае система (30) запишется в виде

(31)

${{T}_{{{\text{я}}i}}} = a{{e}_{i}}\sum\limits_{k = 1}^N {\frac{{{{T}^{{(k - 1)}}}(0)}}{{\gamma _{i}^{{k - 1}}}}} + a{{e}_{i}}{{\delta }_{{N,i}}}.$

Предположим, что членами ae_iδ_N,i можно пренебречь. Пусть i = 1, 2, …, N и W_N – определитель системы (31) относительно T(0), T'(0),…, T^(N^{– 1)}(0), тогда

${{W}_{N}} = \left\| {\begin{array}{*{20}{c}} {a{{e}_{i}}}&{\frac{{a{{e}_{1}}}}{{{{\gamma }_{1}}}}}&{\frac{{a{{e}_{1}}}}{{\gamma _{1}^{2}}}}&{\frac{{a{{e}_{1}}}}{{\gamma _{1}^{{N - 1}}}}} \\ {::::}&{::::}&{::::}&{::::} \\ {a{{e}_{N}}}&{\frac{{a{{e}_{N}}}}{{{{\gamma }_{N}}}}}&{...}&{\frac{{a{{e}_{N}}}}{{\gamma _{N}^{{N - 1}}}}} \end{array}} \right\|.$

Нетрудно заметить, что

${{W}_{N}} = {{D}_{N}}\prod\limits_{i = 1}^N {a{{e}_{i}}} ,$

где D_N – определитель Вандермонда, и, значит,

${{W}_{N}} = \prod\limits_{i = 1}^N {a{{e}_{i}}\prod\limits_{p > k}^N {\frac{{{{\gamma }_{p}} - {{\gamma }_{k}}}}{{{{\gamma }_{p}}{{\gamma }_{k}}}}.} } $

Таким образом, если γ_p ≠ γ_k ни при каких p > k, то W_N ≠ 0 и система уравнений (31) имеет единственное решение при любой левой части. Значит, частоты следует выбирать из диапазона, на котором функция γ₁ = γ(ν₁) монотонна.

Список литературы

Арманд Н.А., Башаринов А.Е., Шутко А.И. // Изв. вузов СССР. Радиофизика. 1977. Т. 20. № 6. С. 809.
Арманд Н.А., Крапивин В.Ф., Мкртчян Ф.А. Методы обработки данных радиофизического исследования окружающей среды. М: Наука, 1987.
Башаринов А.Е., Тучков Л.Т., Поляков В.М., Ананов Н.И. Измерение радиотепловых и плазменных излучений в СВЧ-диапазоне. М.: Сов. радио, 1968.
Бородин Л.Ф., Миронов А.С. // Экологические системы и приборы. 2009. № 11. С. 15.
Крапивин В.Ф., Бородин Л.Ф., Миронов А.С. и др. // Экологические системы и приборы. 2009. № 11. С. 28.
Тучков Л.Т. Естественные шумовые излучения в радиоканалах. М.: Сов. радио, 1968.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал