Радиотехника и электроника, 2022, T. 67, № 6, стр. 533-540

ВВЕДЕНИЕ

Как известно, в нанопроводах (цилиндрах) из благородных металлов (например, из серебра или золота) в оптическом диапазоне волн существуют резонансы поверхностных волн (плазмон-поляритонов) [1–3]. Поэтому такие нанопровода находят применение в спектроскопии, а также используются в качестве сенсоров. Спектры рассеяния и поглощения на одиночных цилиндрах с прямоугольной формой поперечного сечения рассчитаны в [4–6]. В работах [5–11] исследовано рассеяние на цилиндрах прямоугольного, круглого или эллиптического сечения из золота, серебра и метаматериала. Случаи линейных кластеров из двух или трех цилиндров из серебра рассматривался в [4–6, 12–14].

Цель данной работы состоит в строгом электродинамическом исследовании особенностей резонансного рассеяния плоской волны светового диапазона длин волн линейным кластером, образованным шестью одинаковыми серебряными цилиндрами.

1. ФОРМУЛИРОВКА ЗАДАЧИ. МЕТОД РЕШЕНИЯ

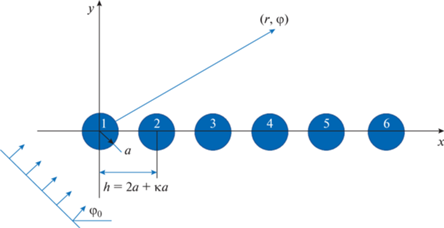
Рассмотрим двумерную задачу дифракции плоской электромагнитной волны на линейном кластере (структуре), состоящем из шести одинаковых серебряных наноцилиндров. Считается, что цилиндры расположены вдоль оси $x$ декартовой системы координат ($x,y$) на одинаковом расстоянии $h = 2a + d$ и имеют одинаковые радиусы ${{a}_{l}} = a$ ($l = 1,2$, …, 6) (рис. 1). Предполагается, что длина электромагнитной волны $\lambda $ принадлежит световому диапазону длин волн ($\lambda \approx 300...900нм$).

Геометрия исследуемой задачи представлена на рис. 1. Относительную диэлектрическую проницаемость серебра 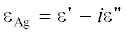$ \equiv \operatorname{Re} ({{\varepsilon }_{{{\text{Ag}}}}}) - i\operatorname{Im} ({{\varepsilon }_{{{\text{Ag}}}}})$ в световом диапазоне длин волн определяли путем аппроксимации кубическими сплайнами экспериментальных данных работы [15]. Отметим, что использование результатов работы [15], так же как и теории Друде [1], накладывает ограничение на минимальный диаметр $2a$ серебряных цилиндров $2a > 10$ нм, так как при $2a < 10$ нм необходимо учитывать явления пространственной дисперсии [1].

Таким образом, с точки зрения классической электродинамики речь идет о решении задачи дифракции плоской электромагнитной волны на шести диэлектрических цилиндрах.

Исследуем случай ТМ-поляризации, когда в электромагнитном поле присутствуют компоненты ${{H}_{z}}(x,y),$ ${{E}_{x}}(x,y),$ ${{E}_{y}}(x,y)$. При этом задача дифракции сводится к нахождению скалярной функции $U(x,y) = {{H}_{z}}(x,y)$, а волновое поле падающей плоской волны задается выражением

где угол ${{\varphi }_{0}}$ определяет направление распространения волны. В работе используется гауссовская система физических единиц, зависимость от времени выбрана в виде $\exp (i\omega t)$, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda } = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}$ – волновое число вакуума, $\omega $ – круговая частота, $с$ – скорость света в вакууме.

Полное поле $U(x,y)$ в кусочно-однородной среде удовлетворяет уравнению Гельмгольца

где диэлектрическая проницаемость $\varepsilon (x,y)$ среды определяется выражением Уравнение (2) необходимо дополнить условием непрерывности величин на границах цилиндров, где $N$ – нормаль к границам цилиндров.

Полное поле вне цилиндров состоит из падающего ${{U}^{0}}$ и рассеянного ${{U}^{s}}$ полей

где рассеянное поле ${{U}^{s}}$ представляет собой сумму полей $U_{l}^{s}$, рассеянных каждым цилиндром

Отметим, что в цилиндрической системе координат ($x = r\cos \varphi ,\;y = r\sin \varphi $) рассеянное ${{U}^{s}}$ поле должно удовлетворять в дальней зоне условию излучения

где $\Phi (\varphi )$ – диаграмма рассеяния кластера. Полное сечение рассеяния ${{\sigma }_{s}}$ выражается через решение краевой задачи (1)–(5) по формуле

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Численное решение краевой задачи проводили модифицированным методом дискретных источников [16–18]. Точность численного решения оценивали невязкой граничных условий $\Delta $ в линейной норме на цилиндрах, и во всех расчетах она была не хуже чем $\Delta = {{10}^{{ - 3}}}$.

Рассмотрим сначала случай кластера, когда радиусы цилиндров из реального серебра полагались равными a = 25 нм. На рис. 2а–2в представлены результаты расчетов спектра нормированного поперечника рассеяния $k{{\sigma }_{S}}$ для трех углов падения плоской волны φ = 0, π/4 и π/2. Расстояния между цилиндрами на всех рисунках κа = = 0.05а, 0.1а, 0.2а, 0.5а, 1а и 2а.

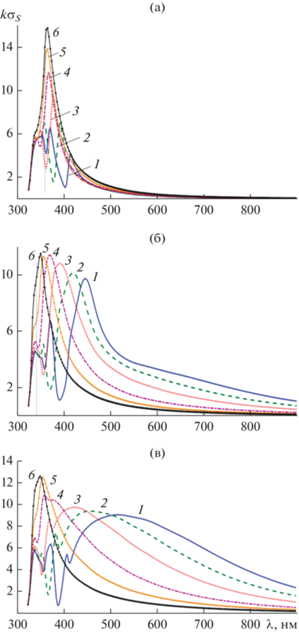
Из рис. 2 видно, что кривые спектра нормированного поперечника рассеяния $k{{\sigma }_{S}}$ содержат максимумы (резонансы), число и положение которых зависят от угла падения плоской волны и расстояния между цилиндрами. Так, при угле падения плоской волны ${{\varphi }_{0}} = 0$ и κа = 0.05а первый максимум поперечника рассеяния $k{{\sigma }_{S}}$ располагается при $\lambda \approx 410\,\,{\text{нм}}$ (см. рис. 2а), при ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ – $\lambda \approx 450\,\,{\text{нм}}$ (см. рис. 2б), а при ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ – $\lambda \approx 500\,\,{\text{нм}}$ (см. рис. 2в). Увеличение κa приводит к смешению резонансных максимумов в сторону меньших длин волн и уменьшению их числа (при κа = 2а остается только один максимум $k{{\sigma }_{S}}$). Отметим, что характер поведения процесса уменьшения числа максимумов свидетельствует о наличии процесса вырождения резонансов плазмонов.

На рис. 3 приведены результаты расчетов спектра нормированного поперечника рассеяния $k{{\sigma }_{S}}$ для кластера с параметрами κa = 0.2a при угле падения плоской волны ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ и четырех значениях радиуса цилиндров:

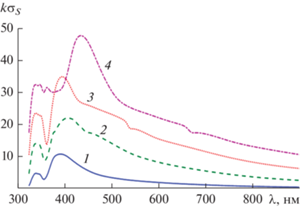
a = 25, 50, 75 и 100 нм. Из представленных результатов следует, что каждая кривая имеет “главный” максимум, значения которого увеличиваются и смещаются в сторону больших длин волн при увеличении радиуса цилиндров.

Выше была рассмотрена интегральная характеристика рассеянного поля, теперь обсудим структуру ближнего поля кластера при его различных параметрах.

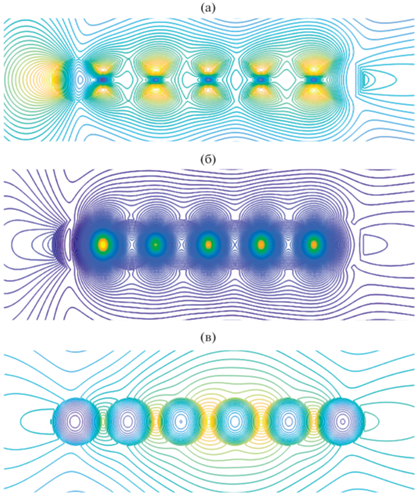
На рис. 4а–4в изображены пространственные распределения линий равных амплитуд компоненты магнитного поля ${{H}_{z}}$ в линейном кластере из шести одинаковых серебряных наноцилиндров при радиусе цилиндра а = 25 нм, угле падения плоской волны φ₀ = 0, расстоянии между цилиндрами κа = 0.1а и трех разных длинах волн: двух резонансных λ = 390.2 и 356.64 нм и одной нерезонансной λ = 600.2 нм. Отметим, что при таком угле падения падающая волна “освещает” первый цилиндр и “бежит” вдоль линейного кластера, взаимодействуя поочередно с каждым цилиндром. Из представленных результатов следует, что структуры ближнего поля кластера в резонансном и нерезонансном случаях существенно различаются друг от друга. Так, в резонансных случаях (см. рис. 4а, 4б) наблюдаются связанные резонансы, возникающие только между частями двух соседних цилиндров, лежащих друг против друга. В нерезонансном случае (см. рис. 4в) наблюдаем взаимодействие плазмонов как между соседними цилиндрами, так и цилиндрами 1–6, 2–6, 2–5, 3–5.

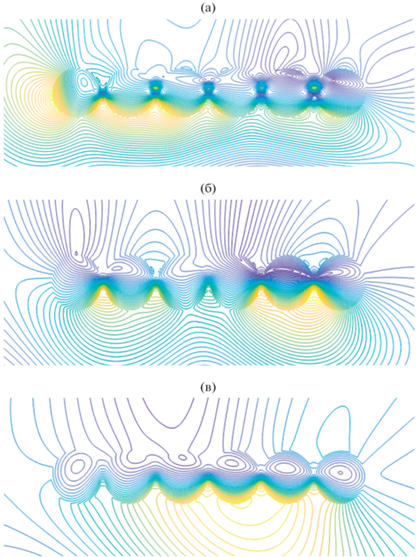
На рис. 5а–5в изображены пространственное распределение линий равных амплитуд компоненты магнитного поля ${{H}_{z}}$ в том же самом линейном кластере но при угле падения плоской волны φ₀ = π/4 и двух резонансных длинах волн λ = 354.9 и 418.4 нм и нерезонансной λ = 600 нм. При таком падении плоской волны “освещается” вся нижняя часть всех цилиндров кластера. Из рис. 5 видно, что в этом случае изолированные связанные резонансы между двумя соседними цилиндрами уже не имеют место и заменяются на связанные резонансы, объединяющие несколько цилиндров. В нерезонансном случае (см. рис. 5в) структура ближнего поля напоминает рассмотренный выше нерезонансный случай падения плоской волны φ₀ = 0.

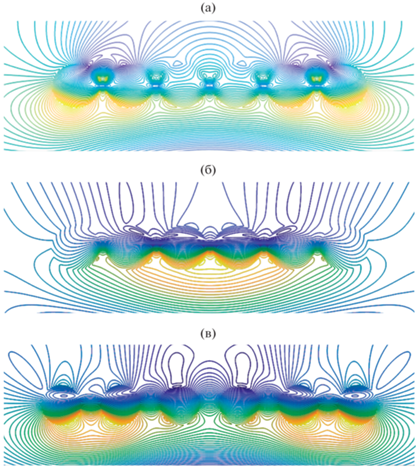
Пространственное распределение линий равных амплитуд компоненты магнитного поля ${{H}_{z}}$ в том же самом линейном кластере, но при нормальном угле падения плоской волны φ₀ = π/2 и длинах волн λ = 350 и 410 нм представлены соответственно на рис. 5а, 5б, а для кластера с расстоянием между цилиндрами κа = 1а на резонансной длине волны λ = 360 нм – на рис. 5в. Отметим, что при длине волны λ = 350 нм наблюдается минимум нормированного поперечника рассеяния $k{{\sigma }_{S}}$, а при длине волны λ = 410 нм – его максимум (см. рис. 2в, кривая 3). Как видно из рис. 5а, при таком падении плоской волны наиболее сильно связанные резонансы проявляются в первых двух и последних двух (крайних) цилиндрах. Структура ближнего поля в резонансном случае для расстояний между цилиндрами κа = 0.2а и 1.0а существенно различается. Так, при κа = 0.2а связанные резонансы возбуждаются только в средней части кластера (цилиндры 2–5, см. рис. 1) и не возбуждаются в крайних цилиндрах (1 и 6). В случае κа = 1а связанные резонансы возбуждаются во всех цилиндрах, но наиболее сильно – в первых двух и последних двух цилиндрах.

Наконец обсудим результаты расчетов диаграмм рассеяния. На рис. 7а представлены диаграммы рассеяния для случая кластера с параметрами а = 25 нм, угле падения плоской волны φ₀ = 0, κа = 0.1а и двух резонансных длинах волн λ = 390.2 и 356.64 нм и нерезонансной длине волны λ = 600.2 нм.

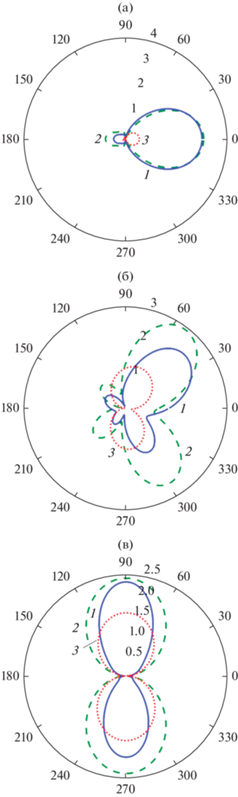
Из представленных результатов видно, что диаграмма рассеяния имеет только два лепестка как в резонансных, так и в нерезонансном случае. При этом направления максимумов диаграммы рассеяния соответствуют углам φ = 0, π. Отсутствие большего числа лепестков связано с отмеченным выше эффектом вырождения ближнего поля кластера. На рис.7б представлены расчеты диаграмм рассеяния для случая такого же кластера, но при угле падения плоской волны φ₀ = π/4, двух резонансных длинах волн λ = 354.9, 418.4 нм и одной нерезонансной длине волны λ = 600 нм. Здесь диаграммы рассеяния для резонансных и нерезонансного случаев отличаются числом лепестков. Следует отметить, что направления максимумов диаграмм рассеяния в резонансных случаях отличаются друг от друга. Расчеты диаграммы рассеяния при нормальном угле падения плоской волны φ₀ = π/2 и длинах волн λ = 350, 410 и 700 нм представлены на рис. 7в. В этом случае диаграммы рассеяния имеют только два лепестка и максимумы излучения в направлениях углов φ = ±π/2.

ЗАКЛЮЧЕНИЕ

Из представленных выше результатов следует, что в световом диапазоне длин волн дифракция ТМ-поляризованной плоской волны на линейном кластере, состоящем из шести серебряных круговых наноцилиндров одинакового диаметра, сопровождается образованием плазмонов, их вырождением и наличием связанных резонансов. Показано, что на эти процессы, а также на спектры поперечника рассеяния и диаграммы рассеяния оказывают существенное влияние угол падения плоской волны, величина радиуса цилиндров и расстояния между цилиндрами.