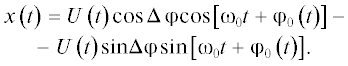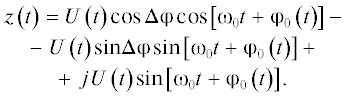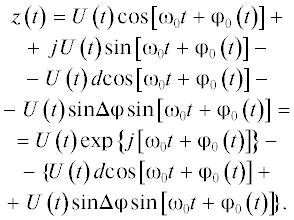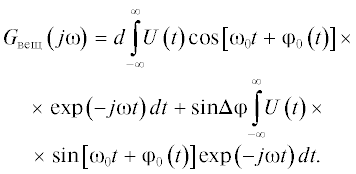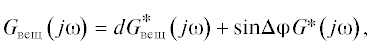Радиотехника и электроника, 2022, T. 67, № 6, стр. 562-566

Спектр комплексного сигнала при рассогласовании квадратурных составляющих

С. И. Зиатдинов^*

Санкт-Петербургский государственный университет аэрокосмического приборостроения
190000 Санкт-Петербург, ул. Большая Морская, 67, Российская Федерация

^* E-mail: ziat.53@mail.ru

Поступила в редакцию 12.03.2021
После доработки 24.10.2021
Принята к публикации 30.10.2021

EDN: MFHGXT
DOI: 10.31857/S0033849422060213

Полный текст (PDF)

Аннотация

Рассмотрен вопрос формирования квадратурных составляющих когерентной системы обработки сигналов, представленной двумя каналами со сдвинутыми на 90° опорными напряжениями. Исследовано влияния практически неизбежных амплитудных и фазовых рассогласований параметров квадратурных каналов на частотные свойства комплексного сигнала. Получены выражения для спектральной плотности комплексного сигнала в случае неравенства коэффициентов передачи каналов и отличия от 90° фазового сдвига опорных напряжений при преобразовании на видеочастоту высокочастотных входных радиосигналов. Показано, что отклонение коэффициентов передачи и фазовое рассогласование квадратурных каналов когерентной системы приводит к появлению в выходном сигнале дополнительной вещественной составляющей, уровень которой определяется величиной отклонения коэффициентов передачи квадратурных каналов и значением фазового рассогласования опорных напряжений.

ВВЕДЕНИЕ

В импульсных радиосистемах реализация когерентной обработки на радиочастоте при длительностях радиоимпульсов от десятых долей микросекунд до наносекунд с частотами заполнения от сотен до тысяч мегагерц является сложной технической задачей. Поэтому в ряде практических случаев при построении когерентных систем, таких как обнаружители и измерители параметров сигналов, систем селекции движущихся целей (СДЦ), систем автоматического сопровождения по дальности и угловым координатам используют преобразование принимаемых высокочастотных радиосигналов на видеочастоту, что позволяет существенно упростить реализацию устройств обработки [1]. Данное преобразование осуществляется с помощью пары преобразователей (квадратурных каналов) со сдвинутыми на 90° опорными напряжениями. В результате формируется на видеочастоте комплексный сигнал в виде двух квадратурных составляющих, используя которые решаются все задачи обработки сигналов [2].

Рассмотренные в литературе вопросы обработки комплексных сигналов на основе их квадратурных составляющих базируются на безошибочном преобразовании высокочастотных сигналов на видео-частоту [3]. На практике реализовать квадратурные каналы с абсолютно одинаковыми характеристиками не представляется возможным. Каналы могут иметь различные коэффициенты передачи, а используемые опорные напряжения могут иметь фазовый сдвиг, отличный от 90°. Данные погрешности приводят к ошибкам оценки параметров комплексного сигнала [4], снижению качества работы системы СДЦ [5], систем автоматического сопровождения. Так, в работе [4] показано, что наличие амплитудных и фазовых рассогласований квадратурных каналов приводит к ошибкам оценки таких важнейших параметров комплексного сигнала, как его амплитуда и частота. При незначительных отклонениях коэффициентов передачи квадратурных каналов возникающие ошибки измерения амплитуды и частоты пропорциональны величине отклонения коэффициентов передачи. При этом ошибка измерения амплитуды комплексного сигнала, вызванная фазовым рассогласованием квадратурных каналов, пропорциональна отклонению коэффициентов передачи каналов. В то же время ошибка измерения частоты комплексного сигнала пропорциональна квадрату фазового рассогласования.

В работе [5] дана оценка влияния рассогласований параметров квадратурных каналов на работу адаптивной системы селекции движущихся целей. В результате показано, что наличие амплитудных и фазовых рассогласований квадратурных каналов приводит к существенному уменьшению коэффициента подавления пассивных помех.

В связи с этим представляет интерес установление на уровне параметров обрабатываемых сигналов причины ухудшения характеристик систем обработки при наличии погрешностей в настройке квадратурных каналов.

Цель данной работы – исследовать влияние погрешностей реализации квадратурных каналов когерентной системы на частотные свойства комплексного сигнала.

1. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ КОМПЛЕКСНОГО СИГНАЛА

Рассмотрим случай, когда для формирования квадратурных сигналов в когерентных системах обработки используются два фазовых детектора со сдвинутыми по фазе на 90° опорными напряжениями. При подаче на входы фазовых детекторов принимаемого высокочастотного сигнала на выходах фазовых детекторов появляются на видео-частоте два квадратурных сигнала, образующие комплексный сигнал, который запишем в виде

$z\left( t \right) = x\left( t \right) + jy\left( t \right),$

где x(t) и y(t) – квадратурные составляющие комплексного выходного сигнала квадратурных каналов. В случае отсутствия ошибок преобразования данные сигналы можно представить следующим образом [6]:

(1)

$\begin{gathered} x\left( t \right) = U\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right], \\ y\left( t \right) = U\left( t \right)\sin \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right], \\ \end{gathered} $

где U(t) и φ₀(t) – флуктуирующие амплитуда и начальная фаза квадратурных сигналов; ω₀ – средняя частота.

Выражения (1) позволяют записать комплексный сигнал z(t) в виде

(2)

$z\left( t \right) = U\left( t \right){\text{exp}}\left\{ {j\left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]} \right\}.$

Применим к (2) прямое преобразование Фурье. Тогда спектральная плотность комплексного сигнала z(t) будет определяться выражением

(3)

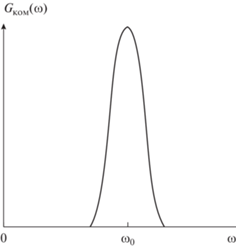
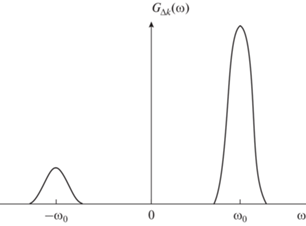
$\begin{gathered} {{G}_{{{\text{ком}}}}}\left( {j{{\omega }}} \right) = \\ = \int\limits_{ - \infty }^\infty {U\left( t \right)} \exp \left\{ {j\left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]} \right\}\exp \left( { - j{{\omega t}}} \right)dt = \\ = \int\limits_{ - \infty }^\infty {U\left( t \right)} {\kern 1pt} {\text{exp}}\{ - j\left[ {({{\omega }} - {{{{\omega }}}_{0}}} \right)t + {{{{\varphi }}}_{0}}\left( t \right)]\} dt. \\ \end{gathered} $

Вид модуля спектральной плотности (3) показан на рис. 1. Спектральная плотность комплексного сигнала является односторонней относительно нуля частот и может располагаться как в области положительных частот, так и в области отрицательных частот.

Рис. 1.

Модуль спектральной плотности комплексного сигнала.

В дальнейшем будем считать, что квадратурные каналы имеют различные коэффициенты передачи, а фазовые сдвиги опорных напряжений имеют отличный от 90° фазовый сдвиг. В этом случае выходные сигналы квадратурных каналов можно представить следующим образом:

(4)

$\begin{gathered} x\left( t \right) = kU\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right) + {{\Delta \varphi }}} \right]; \\ y\left( t \right) = U\left( t \right)\sin \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right], \\ \end{gathered} $

где k = 1 + Δk; Δk – отклонение коэффициентов передачи квадратурных каналов; Δφ – отклонение от 90° фазового сдвига опорных напряжений.

2. ВЛИЯНИЕ ОТКЛОНЕНИЯ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ КВАДРАТУРНЫХ КАНАЛОВ НА СПЕКТРАЛЬНУЮ ПЛОТНОСТЬ КОМПЛЕКСНОГО СИГНАЛА

Рассмотрим отдельно влияние параметров Δk и Δφ на частотные свойства комплексного сигнала (4). Для этого положим в (4) Δk ≠ 0 и Δφ = 0. Тогда выражения (4) примут вид

(5)

$\begin{gathered} x\left( t \right) = kU\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right], \\ y\left( t \right) = U\left( t \right)\sin \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]. \\ \end{gathered} $

Используя соотношения (5), найдем спектральную плотность комплексного сигнала:

(6)

$\begin{gathered} {{G}_{{{{\Delta }}k}}}\left( {j{{\omega }}} \right) = \mathop \smallint \limits_{ - \infty }^\infty \left[ {x\left( t \right) + jy\left( t \right)} \right]{\text{exp}}\left( { - j{{\omega }}t} \right)dt = \\ = \mathop \smallint \limits_{ - \infty }^\infty \{ kU\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right] + \\ + \,\,jU\left( t \right)\sin \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]\} {\text{exp}}\left( { - j{{\omega }}t} \right)dt. \\ \end{gathered} $

Подставим в (6) k = 1 + Δk. В результате получим

(7)

$\begin{gathered} {{G}_{{{{\Delta }}k}}}\left( {j{{\omega }}} \right) = \mathop \smallint \limits_{ - \infty }^\infty \{ U\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right] + \hfill \\ + \,\,jU\left( t \right)\sin \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]\} {\text{exp}}\left( { - j{{\omega }}t} \right)dt + \hfill \\ + \,\,{{\Delta }}k\mathop \smallint \limits_{ - \infty }^\infty U\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]{\text{exp}}\left( { - j{{\omega }}t} \right)dt. \hfill \\ \end{gathered} $

Перепишем (7) в виде

(8)

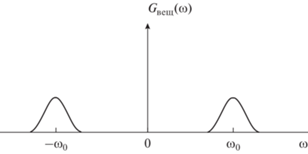
$\begin{gathered} {{G}_{{{{\Delta }}k}}}\left( {j{{\omega }}} \right) = \mathop \smallint \limits_{ - \infty }^\infty U\left( t \right)\exp \left\{ {j\left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]} \right\} \times \\ \times \,\,{\text{exp}}\left( { - j{{\omega }}t} \right)dt + \\ + \,\,{{\Delta }}k\mathop \smallint \limits_{ - \infty }^\infty U\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]{\text{exp}}\left( { - j{{\omega }}t} \right)dt. \\ \end{gathered} $

В выражении (8) первый интеграл представляет спектральную плотность комплексного сигнала G_ком(jω), соответствующую спектральной плотности (3), модуль которой показан на рис. 1. Второй интеграл в (8) представляет спектральную плотность G_вещ(jω) вещественного сигнала ΔkU(t)cos[(ω₀t + φ₀(t)], которая является двухсторонней относительно нуля частот [7]. Модуль данной спектральной плотности показан на рис. 2.

Рис. 2.

Модуль спектральной плотности вещественного сигнала.

Таким образом, можно записать, что

(9)

${{G}_{{{{\Delta }}k}}}\left( {j{{\omega }}} \right) = {{G}_{{{\text{ком}}}}}\left( {j{{\omega }}} \right) + {{G}_{{{\text{вещ}}}}}\left( {j{{\omega }}} \right),$

где

$\begin{gathered} {{G}_{{{\text{ком}}}}}\left( {j{{\omega }}} \right) = \\ = \mathop \smallint \limits_{ - \infty }^\infty U\left( t \right){\text{exp}}\left\{ {j\left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]} \right\}{\text{exp}}\left( { - j{{\omega }}t} \right)dt; \\ \end{gathered} $

$\begin{gathered} {{G}_{{{\text{вещ}}}}}\left( {j{{\omega }}} \right) = \\ = {{\Delta }}k\mathop \smallint \limits_{ - \infty }^\infty U\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]{\text{exp}}\left( { - j{{\omega }}t} \right)dt. \\ \end{gathered} $

Графически модуль спектральной плотности (9) показан на рис. 3.

Рис. 3.

Модуль спектральной плотности сигнала при амплитудном (фазовом) рассогласовании квадратурных составляющих.

Из полученных результатов следует, что при отклонении коэффициентов передачи квадратурных каналов в спектре выходного сигнала кроме спектральной плотности комплексного сигнала появляется спектральная плотность вещественного сигнала, величина которой определяется разностью коэффициентов передачи квадратурных каналов.

3. ВЛИЯНИЕ ФАЗОВОГО РАССОГЛАСОВАНИЯ КВАДРАТУРНЫХ КАНАЛОВ НА СПЕКТРАЛЬНУЮ ПЛОТНОСТЬ КОМПЛЕКСНОГО СИГНАЛА

Примем в (4) Δk = 0 и Δφ ≠ 0. Для этих условий квадратурные составляющие (4) записываются в виде

(10)

$\begin{gathered} x\left( t \right) = U\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right) + {{\Delta \varphi }}} \right], \\ y\left( t \right) = U\left( t \right)\sin \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]. \\ \end{gathered} $

Первое выражение в (10) можно представить следующим образом:

Тогда комплексный сигнал записывается в виде

(11)

В выражении (11) сделаем следующую подстановку cos ∆φ = 1 – d. В результате (11) можно представить как

(12)

В полученном соотношении (12) первое слагаемое является комплексным сигналом и определяет спектральную плотность G_ком(jω) комплексной составляющей выходного сигнал квадратурных каналов, второе слагаемое является вещественным сигналом и определяет спектральную плотность G_вещ(jω) вещественной составляющей выходного сигнала квадратурных каналов.

Найдем составляющую G_вещ(jω) выходного сигнала квадратурных каналов. Для этого ко второму слагаемому выражения (12) применим прямое преобразование Фурье

(13)

Соотношение (13) перепишем в виде

(14)

где

$G_{{{\text{вещ}}}}^{*}\left( {j{{\omega }}} \right) = \mathop \smallint \limits_{ - \infty }^\infty U\left( t \right)\cos \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]{\text{exp}}\left( { - j{{\omega }}t} \right)dt,$

$G{\text{*}}\left( {j{{\omega }}} \right) = \mathop \smallint \limits_{ - \infty }^\infty U\left( t \right)\sin \left[ {{{{{\omega }}}_{0}}t + {{{{\varphi }}}_{0}}\left( t \right)} \right]{\text{exp}}\left( { - j{{\omega }}t} \right)dt$

– спектральные плотности вещественных сигналов U(t)cos[ω₀t + φ₀(t)] и U(t)sin[ω₀t + φ₀(t)] соответственно.

При малых углах фазового рассогласования квадратурных каналов ∆φ, не превышающих единиц градусов, с учетом того, что d ≈ Δφ²/2 $ \ll $ Δφ выражение (14) можно представить следующим образом:

${{G}_{{{\text{вещ}}}}}\left( {j{{\omega }}} \right) \approx {{\Delta \varphi }}G{\text{*}}\left( {j{{\omega }}} \right).$

В результате спектральная плотность выходного сигнала квадратурных каналов принимает вид

(15)

${{G}_{{{{\Delta \varphi }}}}}\left( {j{{\omega }}} \right) = {{G}_{{{\text{ком}}}}}\left( {j{{\omega }}} \right) + {{G}_{{{\text{вещ}}}}}\left( {j{{\omega }}} \right).$

Графически модуль спектральной плотности (15) имеет такой же вид, как и спектральная плотность (9), представленная на рис. 3.

Полученные результаты позволяют сделать вывод о том, что при фазовом рассогласовании квадратурных каналов в спектре выходного сигнала присутствует спектральная плотность как комплексного, так и вещественного сигнала, величина которой определяется уровнем фазового рассогласования каналов. Возможные по разным причинам изменения параметров настройки квадратурных каналов могут быть скомпенсированы путем использования устройства автоматического регулирования усиления и схемы фазовой автоподстройки.

ЗАКЛЮЧЕНИЕ

К качеству настройки квадратурных каналов когерентной системы обработки сигналов должны предъявляться весьма жесткие требования. Наличие амплитудных и фазовых рассогласований квадратурных каналов обусловливает искажение спектральной плотности выходного комплексного сигнала. Ошибки настройки квадратурных каналов когерентной системы приводят к появлению в выходном сигнале каналов вещественной составляющей, уровень которой пропорционален разности коэффициентов передачи и величине фазового отклонения опорных напряжений от 90°. Наличие в выходном сигнале квадратурных каналов когерентной системы вещественной составляющей приводит к ошибкам оценки параметров комплексного сигнала, к ошибкам при решении задач обнаружения сигналов, снижению качества работы систем селекции движущихся целей.

Список литературы

Бакулев П.А., Стенин В.М. Методы и устройства селекции движущихся целей. М.: Радио и связь, 1986.
Бакулев П.А. Радиолокационные системы. М.: Радиотехника, 2004.
Попов В.И. // Радиопромышленность. 2017. Т. 27. № 1. С. 57.
Мичурин С.В. // Изв. вузов. Приборостроение. 2020. Т. 63. № 6. С. 495.
Зиатдинов С.И. // Изв. вузов. Радиоэлектроника. 2020. Т. 23. № 3. С. 25.
Попов Д.И. // Цифровая обработка сигналов. 2014. № 4. С. 32.
Тихонов В.И. Статистическая радиотехника. М.: Радио и связь, 1982.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал