Радиотехника и электроника, 2022, T. 67, № 6, стр. 576-583
Дисперсионные свойства гиромагнитной волны в диссипативной среде
П. А. Макаров a, b, *, В. Г. Шавров c, В. И. Щеглов c, **
a Сыктывкарский государственный университет им. П. Сорокина
167001 Сыктывкар, Октябрьский просп., 55, Российская Федерация
b Физико-математический институт ФИЦ Коми НЦ УрО РАН
127982 Сыктывкар, ул. Оплеснина, 4, Российская Федерация
c Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация
* E-mail: makarovpa@syktsu.ru
** E-mail: vshcheg@cplire.ru
Поступила в редакцию 09.03.2021
После доработки 09.03.2021
Принята к публикации 30.03.2021
- EDN: FJBILY
- DOI: 10.31857/S003384942206016X
Аннотация
Рассмотрены дисперсионные свойства электромагнитных волн, распространяющихся в касательно намагниченной ферритовой пластине, обладающей бигиротропными свойствами в сочетании с магнитной диссипацией. Получено дисперсионное соотношение, имеющее комплексный характер благодаря диссипации. Обнаружены ветви дисперсионных кривых, свойственные только диссипативной среде. Установлено критическое значение параметра затухания, разделяющее две области дисперсии, различающиеся по характеру существенным образом. Показано, что критическое значение параметра затухания соответствует переходу магнитных колебаний из периодического режима в апериодический.
ВВЕДЕНИЕ
Электромагнитные и магнитостатические волны (ЭМВ, МСВ) являются основой для устройств обработки аналоговой информации в диапазоне СВЧ. Малые габариты, широкий частотный диапазон и легкость управления путем перестройки магнитного поля обеспечили создание широкого класса таких устройств начиная еще с 60-х годов ХХ в. [1–3]. В последние годы важное значение приобретают работы, направленные на обработку информации в цифровой форме, для чего используется воздействие на магнитную среду мощными импульсами света от фемтосекундного лазера [4–6].
Предметом внимания большинства перечисленных работ являются короткие МСВ, длина которых на несколько порядков меньше длины электромагнитных волн той же частоты. Рассмотрение базируется на приближении магнитостатики без учета диэлектрических свойств среды [7–9]. Однако в работах [10, 11] показана важность рассмотрения волн в магнитных средах на основе полных уравнений электродинамики с учетом диэлектрической проницаемости среды. Исследуются в первую очередь гиромагнитные волны, распространяющиеся в касательно намагниченной ферритовой пластине перпендикулярно приложенному постоянному полю [9]. В работе [12] рассмотрены свойства гиромагнитных волн в широком диапазоне частот, от нуля и до частот, превышающих частоты традиционных МСВ в несколько раз. Выявлено существование ряда новых ветвей и диапазонов волн, в которых электрическое поле участвует наравне с магнитным.
Распространение и дисперсия волн рассматривались в среде, полностью бездиссипативной, однако в работах [13, 14] было показано, что учет магнитной диссипации уже в магнитостатическом приближении приводит к ограничению допустимого диапазона волновых чисел и появлению новых диссипативных ветвей, в среде без потерь отсутствующих. В работах [15, 16] отмечено ограничение сектора допустимых направлений распространения магнитостатических волн, а также получены изочастотные зависимости. В работах [17–24] в том же магнитостатическом приближении были получены дисперсионные соотношения для действительной и мнимой частей волнового числа, определены диапазоны существования диссипативных волн по частоте и по волновому числу.
В работе [25] рассмотрение проведено уже в рамках полной электродинамики, то есть с учетом диэлектрических свойств среды, что позволило выявить сложный характер дисперсии и предсказать существование ряда новых ветвей, в том числе имеющих обратный характер. Настоящая работа является продолжением исследований, выполненных в работе [25], причем основное внимание уделяется вариации параметра затухания.
1. ОБЩАЯ ГЕОМЕТРИЯ ЗАДАЧИ
Общая геометрия задачи совпадает с принятой в [25]. Ее схема показана на рис. 1. Основу геометрии составляет пластина толщины $d$, намагниченная в плоскости полем $\vec {H}$. Декартова система координат $Oxyz$ ориентирована так, что плоскость $Oxy$ совпадает с плоскостью пластины, а ось $Ox$ ей перпендикулярна. Поле направлено вдоль оси $Oz$, волна, имеющая волновой вектор $\vec {k}$, распространяется вдоль оси $Oy$. Такая геометрия подобна геометрии классической задачи Дэймона–Эшбаха [7–9]. Главное отличие состоит в том, что здесь задача рассматривается не в магнитостатическом приближении, а в рамках полной электродинамики, т.е. с учетом как магнитного, так и электрического поля.
2. ДИСПЕРСИОННОЕ СООТНОШЕНИЕ
Материал пластины будем считать бигиротропной средой, электродинамические свойства которой описываются двумя тензорами – диэлектрической и магнитной проницаемости [26, 9 ]:
(1)
$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\varepsilon } = \left( {\begin{array}{*{20}{c}} \varepsilon &{i{{\varepsilon }_{a}}}&0 \\ { - i{{\varepsilon }_{a}}}&\varepsilon &0 \\ 0&0&{{{\varepsilon }_{\parallel }}} \end{array}} \right),\,\,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } = \left( {\begin{array}{*{20}{c}} \mu &{i{{\mu }_{a}}}&0 \\ { - i{{\mu }_{a}}}&\mu &0 \\ 0&0&{{{\mu }_{\parallel }}} \end{array}} \right).$В работе [9] показано, что в этом случае в пластине может распространяться гиромагнитная волна, в отсутствие зависимости от координаты $z$ определяемая уравнениями
(2)
$\frac{{\partial {{E}_{z}}}}{{\partial y}} = - i{{k}_{0}}\left( {\mu {{H}_{x}} + i{{\mu }_{a}}{{H}_{y}}} \right),$(3)
$\frac{{\partial {{E}_{z}}}}{{\partial x}} = - i{{k}_{0}}\left( {i{{\mu }_{a}}{{H}_{x}} - \mu {{H}_{y}}} \right),$Разрешение этой системы относительно ${{H}_{x}}$ и ${{H}_{y}}$ дает поля гиромагнитной волны в виде [12]
(4)
${{H}_{x}} = - \frac{{{{\mu }_{a}}}}{{{{k}_{0}}\left( {{{\mu }^{2}} - {{\mu }_{a}}} \right)}}\frac{{\partial {{E}_{z}}}}{{\partial x}} + \frac{{i\mu }}{{{{k}_{0}}\left( {{{\mu }^{2}} - {{\mu }_{a}}} \right)}}\frac{{\partial {{E}_{z}}}}{{\partial y}},$(5)
${{H}_{y}} = - \frac{{i\mu }}{{{{k}_{0}}\left( {{{\mu }^{2}} - {{\mu }_{a}}} \right)}}\frac{{\partial {{E}_{z}}}}{{\partial x}} - \frac{{{{\mu }_{a}}}}{{{{k}_{0}}\left( {{{\mu }^{2}} - {{\mu }_{a}}} \right)}}\frac{{\partial {{E}_{z}}}}{{\partial y}}.$При координатной зависимости волны вида ${\text{exp}}\left( { - i{{k}_{x}}x - i{{k}_{y}}y} \right)$ эти формулы переходят в приведенные в [9].
В рамках полной электродинамики условие равенства нулю ротора от магнитного поля не выполняется, так что введение магнитостатического потенциала исключено, поэтому следует воспользоваться решением задачи Дэймона–Эшбаха через поля [27]. Следуя такому способу решения и полагая координатно-временную зависимость полей волны в виде
(6)
${\text{exp}}i\left( {\omega t - \vec {k}\vec {r}} \right) = {\text{exp}}\left( {i\omega t} \right){\text{exp}}\left( { - i{{k}_{x}}x} \right){\text{exp}}\left( { - i{{k}_{y}}y} \right)$(7)
$\frac{{{\text{exp}}\left( {kd{{\alpha }_{0}}} \right) - {\text{exp}}\left( { - kd{{\alpha }_{0}}} \right)}}{{\exp \left( {kd{{\alpha }_{0}}} \right) + {\text{exp}}\left( { - kd{{\alpha }_{0}}} \right)}} - \frac{{2\mu {{\alpha }_{0}}}}{{{{\beta }_{0}}}} = 0,$(8)
${{\alpha }_{0}} = \sqrt {1 - \frac{{k_{0}^{2}}}{{{{k}^{2}}}}\frac{{\varepsilon \left( {{{\mu }^{2}} - \mu _{a}^{2}} \right)}}{\mu }} ,$(9)
${{\beta }_{0}} = \frac{{\sqrt {{{k}^{2}} - k_{0}^{2}\varepsilon } }}{k}\left\{ {\mu _{a}^{2} - {{\mu }^{2}} - \frac{{{{k}^{2}}}}{{{{k}^{2}} - k_{0}^{2}\varepsilon }}\frac{{\alpha _{0}^{2}{{\mu }^{2}} - \mu _{a}^{2}}}{{{{\mu }^{2}} - \mu _{a}^{2}}}} \right\},$3. ДИСПЕРСИОННОЕ СООТНОШЕНИЕ В СРЕДЕ С ДИССИПАЦИЕЙ
В среде с диссипацией соотношение (7)–(9) содержит три комплексные величины: волновое число $k$ и компоненты магнитной проницаемости $\mu $ и ${{\mu }_{a}}$. В результате и само дисперсионное соотношение приобретает комплексный характер. Дальнейшая задача состоит в том, чтобы выделить действительную и мнимую части этого соотношения, чтобы каждая из частей была бы действительной. Тогда, поскольку дисперсионное соотношение в целом (7)–(9) равно нулю, то можно считать и действительную и мнимую его части также равными нулю. При этом равенство нулю действительной части даст закон дисперсии волны как соотношение между частотой и действительной частью волнового числа. Реализация такой задачи в аналитическом виде [25] является довольно громоздкой. Вместе с тем при численном решении нет необходимости аналитическим путем выделять действительную и мнимую части соотношения (7)–(9), а достаточно поручить такое выделение машинной программе. То есть, задавая действительное значение частоты, можно так подобрать действительную часть волнового числа, чтобы действительная часть соотношения (7)–(9) равнялась нулю. Такой подбор можно осуществить с помощью процедуры поиска нуля. Таким образом, следует вычислить параметры ${{\alpha }_{0}}$ и ${{\beta }_{0}}$, подставить их в (7) и осуществить поиск нуля действительной части полученного соотношения, что и даст искомый закон дисперсии.
4. ТЕНЗОР МАГНИТНОЙ ПРОНИЦАЕМОСТИ И ХАРАКТЕРНЫЕ ЧАСТОТЫ
Из выражений (7)–(9) можно видеть, что параметрами, определяющими закон дисперсии, являются компоненты тензора магнитной проницаемости $\mu $ и ${{\mu }_{a}}$. В среде с диссипацией эти компоненты включают в себя параметр затухания Гильберта $\alpha $ [26]. С точностью до первой степени этого параметра компоненты тензора проницаемости принимают вид [25]
(10)
$\mu = \frac{{\Omega _{H}^{2} - {{\Omega }^{2}} + {{\Omega }_{H}}}}{{\Omega _{H}^{2} - {{\Omega }^{2}}}} - i\alpha \frac{{\Omega \left( {\Omega _{H}^{2} + {{\Omega }^{2}}} \right)}}{{{{{\left( {\Omega _{H}^{2} - {{\Omega }^{2}}} \right)}}^{2}}}},$(11)
${{\mu }_{a}} = \frac{\Omega }{{\Omega _{H}^{2} - {{\Omega }^{2}}}} - i\alpha \frac{{2{{\Omega }^{2}}{{\Omega }_{H}}}}{{{{{\left( {\Omega _{H}^{2} - {{\Omega }^{2}}} \right)}}^{2}}}},$(12)
$\Omega = \frac{\omega }{{4\pi \gamma {{M}_{0}}}},\,\,\,\,{{\Omega }_{H}} = \frac{{{{H}_{0}}}}{{4\pi {{M}_{0}}}}.$(14)
${{f}_{2}} = \gamma \sqrt {{{H}_{0}}\left( {{{H}_{0}} + 4\pi {{M}_{0}}} \right)} = 2739{\text{ Э}},~$(16)
${{f}_{4}} = \gamma \sqrt {{{{\left( {{{H}_{0}} + 2\pi {{M}_{0}}} \right)}}^{2}} + {{{\left( {2\pi {{M}_{0}}} \right)}}^{2}}} = \,\,4417{\text{ Э,}}$Процедура поиска нуля состоит в определении изменения знака дисперсионного соотношения при изменении варьируемого параметра с последующим уточнением полученного значения путем уменьшения шага варьирования до величины, требуемой желаемой точностью.
5. ДИСПЕРСИЯ В ОТСУТСТВИЕ ДИССИПАЦИИ
В качестве отправной точки для дальнейшего исследования, рассмотрим сначала дисперсию волны в геометрии рис. 1 в случае отсутствия диссипации. На рис. 2 показаны соответствующие дисперсионные кривые, полученные в рамках полной электродинамики с помощью соотношений (7)–(9). Видно, что спектр имеет несколько ветвей, подобных наблюдавшимся ранее [12]. Рассмотрим эти ветви по отдельности.
Рис. 2.
Дисперсионные кривые в отсутствие диссипации ($\alpha $ = 0): кривая 1 соответствует дисперсии волны в свободном пространстве, кривая 2 – классической поверхностной волне Дэймона–Эшбаха, кривая 3 – дополнительной ветви прямых волн, кривые 4 и 5 – ветвям аномальной дисперсии; параметры: ${{H}_{0}}$= 437.5 Э, $4\pi {{M}_{0}}$ = 1750 Гс, $d$ = 15 мкм, $\varepsilon $ = 1.

Кривая 1 соответствует дисперсии электромагнитной волны в свободном пространстве, т.е. представляет собой прямую, описываемую формулой
Все остальные кривые являются решениями дисперсионного соотношения (7)–(9), т.е. соответствуют волнам, распространяющимся в пластине с магнитными свойствами.
Кривая 2 при достаточной величине волнового числа (более 10 см–1) отражает закон дисперсии для классической поверхностной волны Дэймона–Эшбаха, полученной в магнитостатическом приближении. Здесь показан только начальный участок кривой, где частота из-за крайней малости волнового числа еще не смогла удалиться на заметное расстояние от величины ${{f}_{2}}$, так что кривая смотрится как горизонтальная линия. Однако проверка показывает, что при дальнейшем увеличении волнового числа эта кривая практически точно следует дисперсионной кривой Дэймона–Эшбаха, асимптотически приближаясь к горизонтальной прямой на частоте ${{f}_{3}}$.
Кривая 3 соответствует ветви прямых волн, имеющей место только в рамках полной электродинамики. При достаточных волновых числах она превращается в горизонтальную прямую на частоте ${{f}_{4}}$.
Кривые 4 и 5 представляют собой дополнительные ветви, подобные ветвям аномальной дисперсии в оптике. Эти ветви располагаются левее прямой 1, так что их фазовая скорость превышает скорость света, т.е. они не являются физически реализуемыми. Однако такое положение имеет место только при небольших значениях диэлектрической проницаемости. В работе [25] показано, что при $\varepsilon $ = 10 эти кривые смещаются в сторону больших значений волнового числа и трансформируются в две ветви, расположенные намного правее кривой 1 (см. [25, рис. 5, кривые 4, 5]), т.е. их физическая реализация становится возможной.
Замечание. В рамках данной работы авторы ограничиваются рассмотрением случая $\varepsilon $ = 1 и исследуют далее кривые 4 и 5 с формальной стороны, отвлекаясь от вопроса об их физической реализации, более подробное решение которого оставляют для дальнейших исследований.
6. ДИСПЕРСИЯ ВОЛНЫ ПРИ РАЗЛИЧНЫХ УРОВНЯХ ЗАТУХАНИЯ
Предварительное исследование дисперсионных кривых при наличии диссипации выявило существенное различие их характера в случае малого и большого затухания. При этом имеется критическое значение параметра затухания ${{\alpha }_{c}}$, при переходе через которое характер кривых коренным образом меняется. Величина критического значения параметра затухания при принятых в разд. 5 параметрах составляет около 0.75. Рассмотрим случаи большого и малого затухания по отдельности.
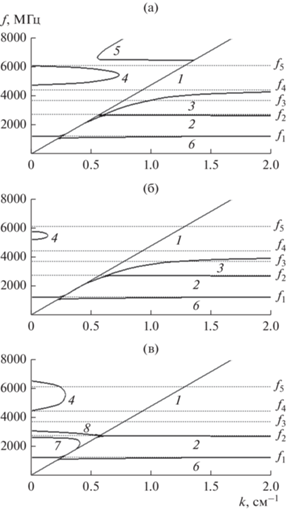
Затухание малое. На рис. 3 представлены дисперсионные кривые при различных значениях параметра затухания $\alpha $, номера кривых 1…5 сохранены теми же, что на рис. 2. Как и ранее кривая 1 соответствует дисперсии волны в свободном пространстве, кривая 2 – классической поверхностной волне Дэймона–Эшбаха, кривая 3 – дополнительной ветви прямых волн, кривые 4 и 5 – ветвям аномальной дисперсии. Видно, что характер кривых 1 и 2 при всех значениях параметра затухания не меняется, т.е. от диссипации не зависит. Кривая 3 имеет место только при значениях $\alpha $ = = 0.1 (а) и 0.4 (б), а при $\alpha $ = 0.7 (в) отсутствует, т.е. условием существования этой ветви является сравнительно небольшое затухание. Кривые 4 и 5 уже при малом затухании, $\alpha $ = 0.1 (а), претерпевают значительное изменение. Так, на кривой 4 появляется загиб в сторону меньших значений волнового числа, а на кривой 5 – загиб в сторону больших, причем оба загиба наблюдаются в окрестности частоты ${{f}_{5}}$, равной 6125 МГц при принятых параметрах. Картина соответствует как бы расщеплению первоначально цельных ветвей 4 и 5 на две части, которые “расталкиваются” в окрестности этой частоты.
При увеличении затухания до $\alpha $ = 0.4 (б) кривая 5 вообще исчезает, а кривая 4 смещается в сторону меньших значений волнового числа. Однако при дальнейшем увеличении затухания до $\alpha $ = 0.7 (в) кривая 4 как бы слегка возвращается в сторону больших значений волнового числа, однако не достигая кривой 1. Кроме перечисленных кривых при наличии затухания в спектре волн появляются новые ветви. Так, на частоте ${{f}_{1}}$ = 1225 МГц появляется ветвь 6, которая далее сохраняется при всех значениях параметра затухания.
При достаточно большом уровне затухания $\alpha $ = 0.7 (в) кривая 2 в области, левее кривой 1, расщепляется на две ветви 7 и 8, из которых 7, как бы отщепляясь от кривой 1 при повышении частоты вблизи ${{f}_{2}}$, поворачивает в сторону уменьшения волнового числа, создавая иллюзию расталкивания ветвей, подобную расталкиванию кривых 4 и 5 при $\alpha $ = 0.1 (а).
Затухание большое. Рассмотрим теперь дисперсию волны при большом затухании, для чего обратимся к рис. 4, где показаны дисперсионные кривые в случае большой диссипации ($\alpha $ > 0.75) при различных значениях параметра затухания $\alpha $. Видно, что в этом случае кривые 1, 2, 6 и 7 сохраняются теми же, что и при малом затухании, однако кривая 7 исчезает. Главным отличием от случая малого затухания является полное исчезновение кривых 4 и 5 и появление на их месте кривой 9, являющейся как бы продолжением кривой 2 левее кривой 1. В процессе увеличения затухания кривая 9 является как бы разрастанием кривой 4 на рис. 3в в сторону меньшей частоты, где она претерпевает изгиб в сторону больших значений волнового числа и сливается левым концом c кривой 2. По мере увеличения затухания верхняя часть кривой 9 наклоняется в сторону больших значений волнового числа, приближаясь к кривой 1.
Рис. 4.
Дисперсионные кривые в случае большой диссипации ($\alpha $ > 0.75) при $\alpha $ = 0.8 (а), 1.0 (б), 1.5 (в); обозначения кривых 1…8 см. на рис. 2 и 3, кривая 9 – новая диссипативная ветвь, являющаяся продолжением кривой 2 в области малых волновых чисел; параметры те же, что на рис. 2.
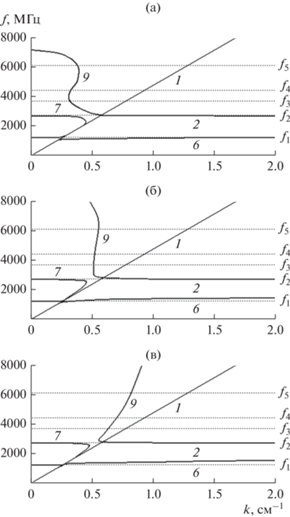
Рис. 5.
Зависимость времени релаксации от параметра затухания, точки – результаты машинного эксперимента, сплошная линия построена по формуле (19); на вставке – зависимость амплитуды колебаний намагниченности от параметра затухания; параметры те же, что на рис. 2.

7. ЗАВИСИМОСТЬ КРИТИЧЕСКОГО ЗНАЧЕНИЯ ПАРАМЕТРА ЗАТУХАНИЯ ОТ ВРЕМЕНИ РЕЛАКСАЦИИ
Главным результатом разд. 6 является резкое изменение характера дисперсионных кривых при переходе через критическое значение параметра затухания. Для выяснения причины такого изменения было выполнено исследование развития колебаний во времени после включения возбуждающего воздействия. Возбуждение осуществлялось на частоте 2800 МГц, постоянное поле составляло 2750 Э, амплитуда возбуждающего поля равнялась 0.01 Э. Остальные параметры задачи совпадали с введенными ранее. Наблюдение развития колебаний во времени позволило определить две величины – время релаксации колебаний магнитной системы и амплитуду колебаний намагниченности, установившуюся после окончания релаксации.
Полученные результаты представлены на рис. 5. Основную часть рисунка составляет зависимость времени релаксации от параметра затухания. Приведены результаты машинного эксперимента (точки) и аппроксимирующая их плавная кривая в виде полинома четвертого порядка:
(19)
$\begin{gathered} {{\tau }_{c}} = (4.12{{\alpha }^{4}} - 15.32{{\alpha }^{3}} + 20.53{{\alpha }^{2}} - \\ - \,\,12.06\alpha + 2.89) \times {{10}^{{ - 8}}}, \\ \end{gathered} $Из рис. 5 видно, что с увеличением параметра затухания время релаксации сначала падает довольно быстро, однако далее его падение замедляется, при достаточно больших значениях параметра затухания стремясь к нулю. Наиболее сильно выраженное изменение характера спада времени релаксации происходит при значении параметра затухания ${{\alpha }_{c}}$ = 0.75, которое как раз и является критическим для резкого изменения характера дисперсии, представленного на рис. 3 и 4.
По вертикальной оси сплошными горизонтальными линиями дополнительно отложено время периода возбуждаемых колебаний ${{T}_{0}}$ = $3.57 \times {{10}^{{ - 10}}}$ с, а также его половина ${{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} 2}} \right. \kern-0em} 2}$ = $1.78 \times {{10}^{{ - 10}}}$ с. Видно, что замедление падения времени релаксации происходит как раз при значениях параметра затухания, соответствующих близости между временем релаксации и периодом или полупериодом возбуждаемых колебаний. Затухание колебаний за время собственного периода означает, что они становятся апериодическими. Это происходит как раз при значении параметра затухания, равном критическому по изменению характера дисперсии. То есть можно считать, что изменение характера дисперсии обусловлено именно установлением апериодического характера магнитных колебаний. Из вставки на рисунке можно видеть, что падение амплитуды колебаний при этом замедляется и стремится к постоянному значению около 0.05 отн. ед., с резонансом никак не связанному.
ЗАКЛЮЧЕНИЕ
Рассмотрены дисперсионные свойства электромагнитных волн, распространяющихся в касательно намагниченной ферритовой пластине, обладающей бигиротропными свойствами в сочетании с магнитной диссипацией. В геометрии задачи Дэймона–Эшбаха рассмотрено общее волновое уравнение для гиромагнитной волны. Получено дисперсионное соотношение, по структуре совпадающее с классическим соотношением Дэймона–Эшбаха. Показано, что благодаря диссипации составляющие дисперсионного соотношения и само соотношение в целом имеют комплексный характер, происходящий из-за комплексного характера тензора магнитной проницаемости среды. Установлено, что закон дисперсии гиромагнитной волны в среде с диссипацией определяется равенством нулю действительной части комплексного дисперсионного соотношения. Решение полученного уравнения методом поиска нуля позволило получить закон дисперсии гиромагнитной волны в широком диапазоне значений параметра затухания. Рассмотрены дисперсионные кривые в случаях отсутствия и наличия диссипации. Отмечено, что в отсутствие диссипации дисперсионные кривые, кроме обычной ветви поверхностной волны типа Дэймона–Эшбаха, имеют еще одну ветвь, лежащую выше по частоте. При наличии диссипации характер дисперсионных кривых усложняется, появляются ветви, свойственные только диссипативной среде. Установлено критическое значение параметра затухания, разделяющее две области, различающиеся по характеру дисперсии существенным образом. Показано, что при величине параметра затухания меньшей критического значения в области частот выше волны Дэймона–Эшбаха имеют место разделенные промежутком две диссипативные ветви, характер которых подобен аномальной дисперсии в оптике. При величине параметра затухания, большей критической, две диссипативные ветви сливаются в одну, начинающуюся с частоты волны Дэймона–Эшбаха и уходящую по частоте в бесконечность, стремясь к дисперсионной ветви волны в свободном пространстве. Показано, что критическое значение параметра затухания соответствует переходу магнитных колебаний из периодического режима в апериодический.
Список литературы
Адам Дж.Д. // ТИИЭР. 1988. Т. 76. № 2. С. 73.
Исхак В.С. // ТИИЭР. 1988. Т. 76. № 2. С. 86.
Adam J.D., Davis L.E., Dionne G.F. et al. // IEEE Trans. 2002. V. MTT-50. № 3. P. 721.
Kirilyuk A., Kimel A.V., Rasing T. // Rev. Mod. Phys. 2010. V. 82. № 3. P. 2731.
Janusonis J., Chang C.L., Jansma T. et al. // Phys. Rev. B. 2016. V. 94. № 2. P. 024415(7).
Власов В.С., Макаров П.А., Шавров В.Г., Щеглов В.И. // Журн. радиоэлектроники. 2017. № 6. http://jre.cplire.ru/jre/jun17/5/text.pdf.
Damon R.W., Eshbach J.R. // J. Phys. Chem. Solids. 1961. V. 19. № 3/4. P. 308.
Шавров В.Г., Щеглов В.И. Магнитостатические волны в неоднородных полях. М.: Физматлит, 2016.
Шавров В.Г., Щеглов В.И. Магнитостатические и электромагнитные волны в сложных структурах. М.: Физматлит, 2017.
Вашковский А.В., Локк Э.Г. // РЭ. 2001. Т. 46. № 10. С. 1257.
Вашковский А.В., Локк Э.Г. // Успехи физ. наук. 2011. Т. 181. № 3. С. 293.
Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // Журн. радиоэлектроники. 2018. № 4. http://jre.cplire.ru/jre/apr18/7/text.pdf.
Вызулин С.А., Розенсон А.Э., Шех С.А. // РЭ. 1991. Т. 36. № 1. С. 164.
Ползикова Н.И., Раевский А.О. // ФТТ. 1996. Т. 38. № 10. С. 2937.
Annenkov A.Yu., Gerus S.V. // Book of Abstracts of Moscow Intern. Symp. on Magnetism (MISM). Moscow: Publ. “Изд-во Физ.фак. МГУ”, 2014. P. 863.
Анненков А.Ю., Герус С.В. // Сб. трудов XXII Междунар. конф. “Электромагнитное поле и материалы”. М.: НИУ МЭИ, 2014. С. 99.
Макаров П.А., Шавров В.Г., Щеглов В.И. // Журн. радиоэлектроники. 2014. № 7. http://jre.cplire.ru/ jre/jul14/8/text.pdf.
Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // Журн. радиоэлектроники. 2016. № 2. http://jre.cplire.ru/jre/feb16/2/text.pdf.
Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // Журн. радиоэлектроники. 2016. № 3. http://jre.cplire.ru/jre/mar16/1/text.pdf.
Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // Журн. радиоэлектроники. 2016. № 3. http:// jre.cplire.ru/jre/mar16/2/text.pdf
Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // РЭ. 2018. Т. 63. № 6. С. 577.
Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // РЭ. 2018. Т. 63. № 9. С. 974.
Makarov P., Maltceva L., Kotov L., Shcheglov V. // Eur. Phys. J. Web of Conf. 2018. V. 185. № 2. P. 02012.
Makarov P., Maltceva L., Kotov L., Shcheglov V. // Eur. Phys. J. Web of Conf. 2018. V. 185. № 2. P. 02015.
Макаров П.А., Шавров В.Г., Щеглов В.И. // Журн. радиоэлектроники. 2018. № 9. http://jre.cplire.ru/jre/sep18/10/text.pdf.
Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит, 1994.
Шавров В.Г., Щеглов В.И. Динамика намагниченности в условиях изменения ее ориентации. М.: Физматлит, 2019.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника