1. На главную
  2. Электронные версии
  3. Сенсорные системы
  4. T. 33, № 1, 2019

Сенсорные системы, 2019, T. 33, № 1, стр. 7-14

Оптимальная аффинная аппроксимация проективного преобразования изображений

И. А. Коноваленко 1, 2, *, В. В. Кохан 1, Д. П. Николаев 1, 2

1 Институт проблем передачи информации им. А.А. Харкевича РАН
127051 Москва, Большой Каретный пер., 19, Россия

2 Smart Engines Ltd.
117312 Москва, проспект 60-летия Октября, д. 9, Россия

* E-mail: konovalenko@iitp.ru

Поступила в редакцию 06.09.2018

Полный текст (PDF)

Аннотация

Замена проективного преобразования существенно более простым аффинным преобразованием встречается во многих областях технического зрения. В то же время понятие точности аффинной аппроксимации проективного преобразования в литературе не формализуется. Это в свою очередь приводит к отсутствию постановок задач и теоретически обоснованных методов аффинной аппроксимации проективного преобразования. Настоящая работа направлена на заполнение этого пробела. Авторами предложено в качестве критериев точности аффинной аппроксимации проективного преобразования изображения использовать среднеквадратичную и максимальную поточечную невязку в координатах преобразованного изображения. На основе этих критериев сформулированы задачи поиска оптимальных аффинных аппроксимаций. Доказана выпуклость полученных задач оптимизации. Предложен метод использования оптимальных аффинных аппроксимаций для экономии вычислительных ресурсов при преобразовании изображений.

Ключевые слова: проективное преобразование, точность проективного преобразования, аффинная аппроксимация преобразований, линеаризация, выпуклый анализ

ВВЕДЕНИЕ

Проективное исправление

Рассмотрим произвольную оптическую систему. Оптическая система обладает дисторсией, если коэффициент линейного увеличения изменяется по полю зрения ее объектива. Оптическая система, свободная от дисторсии, называется ортоскопической оптической системой (ООС). Любую оптическую систему можно с произвольной точностью свести к ООС посредством процедуры калибровки, поэтому далее будем рассматривать только ООС. Они обладают тем важнейшим свойством, что образы прямых линий сцены, которые они порождают, тоже являются прямыми линиями или точками.

Под коррекцией перспективы порожденного ООС изображения будем понимать такое геометрическое преобразование этого изображения, которое устраняет на нем перспективное схождение прямых линий, параллельных в сцене. Будем рассматривать частный случай, когда сцену можно считать плоской. Тогда коррекция перспективы существует и является проективным преобразованием. Поэтому коррекцию перспективы для случая плоской сцены будем называть проективным исправлением.

Большое количество прикладных и теоретических исследований на тему проективного исправления подтверждает ее актуальность. Например, в работах (Orrite, Herrero, 2004; Zhukovsky et al., 2015) предлагаются алгоритмы для проективного сопоставления контуров и отрезков соответственно. В работе (Povoltskiy et al., 2017) описывается сегментация проективно исправленных номерных знаков автомобилей, а в (Чернов и др., 2016) – паспортов. В статьях (Шемякина и др., 2017; Шемякина, 2017) анализируются подходы к решению задачи проективного наведения на примере страховых свидетельств. В работах (Болотова и др., 2017; Skoryukina et al., 2018) рассматриваются алгоритмы проективного наведения на документы. В статье (Skoryukina et al., 2017) описывается система “Snapscreen”, которая детектирует и проективно исправляет фотографию экрана телевизора с дальнейшим распознаванием телевизионной передачи. В статьях (Karpenko et al., 2015; Холопов, 2017) задача проективного исправления возникает при картировании местности по снимкам с бортовой камеры БПЛА. Теоретические исследования проективных инвариантов представлены, например, в работах (Николаев, 2016; Савчик, Николаев, 2016; Балицкий и др., 2017).

Аффинная аппроксимация проективного преобразования

Мы будем исследовать замену проективного преобразования существенно более простым аффинным преобразованием. Соображение, что на практике аффинное преобразование с хорошей точностью локально приближает проективное преобразование, было высказано в статье (Gruen, 1985). Это свойство было использовано в работе (Tu-ichi et al., 1981) для упрощения дальнейших математических построений. Аффинное приближение повсеместно используется в рендеринге изображений (Heckbert, 1989; Lorenz, Dollner, 2009) и в завершении изображений (Darko, 2006). В работе (Huang et al., 2015) проективное преобразование заменяется на более простое аффинное с целью борьбы с переобучением. Близкая идея используется в “слабой перспективной модели” (Alter, 1992, Kutulakos,Vallino, 1996; Aradhye, Myers, 2010), где аппроксимация носит частичный характер. Строить аффинно инвариантные методы (вместо существенно более сложных проективно инвариантных) принято в популярной технологии особых точек (Mikolajczyk, Schmid, 2002; Mikolajczyk, Schmid, 2004; Morel, Yu, 2009), как и в родственной задаче поиска значимых регионов (Kadir et al., 2004), хотя оба подхода практически обеспечивают инвариантность к ракурсу съемки. Деление на аффинные и проективные методы имеется и в области стереореконструкции (Faugeras, 1992).

Существует критика аффинной аппроксимации, как ведущей к практической потере точности (Zwicker, 2004). Однако само понятие точности аффинной аппроксимации проективного преобразования в литературе не формализуется. Это в свою очередь делает невозможным поиск оптимальной аффинной аппроксимации проективного преобразования. Основное содержание данной работы состоит в введении понятия точности аффинной аппроксимации проективного преобразования и обоснования вычислительной возможности нахождения оптимальной по точности аффинной аппроксимации.

Критерии точности проективного исправления

Пусть дано два проективных преобразования H и ${\hat {H}}$. Первое – имеет смысл идеального исправления входного изображения, которым обычно является фотография. На практике H неизвестно, но при тестировании может задаваться экспертно. Второе – некоторое практическое приближение или оценка первого, как правило, получаемое автоматически. В результате применения H к входному изображению получается некоторое изображение, называемое идеально исправленным, а в результате применения ${\hat {H}}$ – практически исправленным.

Кроме того, пусть дана область интереса R – множество тех и только тех точек идеально исправленного изображения, в которых нам важно, чтобы ${\hat {H}}$ хорошо приближало H. Обычно R соответствует документу, автомобильному номеру, зданию и прочим интересующим нас объектам сцены, либо же задает идеально исправленное изображение целиком. Множество R известно, постоянно для конкретной задачи и не зависит от H и ${\hat {H}}$. Например, при проективном исправлении фотографии водительских прав мы заранее задаем, какая область изображения при идеальном его исправлении должна оказаться занятой образом прав.

Также введем зависимое множество $Q\;\mathop = \limits^{{\text{def}}} \;{\hat {H}}{{{\text{H}}}^{{ - 1}}}(R)$, содержащее образы тех же точек сцены, что и R, но на практически исправленном изображении. Тогда встает задача формализации точности приближения преобразованием $\hat {H}$ преобразования H. Наиболее часто в литературе встречаются следующие способы такой формализации:

• Коэффициент Жаккара (Jaccard, 1901), равняющийся площади пересечения множеств Q и R, отнесенной к площади их объединения:

(1)
${{K}_{{{\text{Jaccard}}}}}(Q,R)\;\mathop = \limits^{{\text{def}}} \;\frac{{S(Q \cap R)}}{{S(Q \cup R)}}.$

Этот коэффициент является целевым, например, на конкурсе по анализу и распознаванию документов “ICDAR” (Zhukovsky et al., 2015).

• Метрика Хаусдорфа (Huttenlocher, 1993) и ее многочисленные модификации (Ефимов, Новиков, 2016; Dubuisson, Jain, 1994; Коноваленко, Шемякина, 2018; Fresche, 1906). Она равняется наибольшему расстоянию от точек одного множества до соответствующих им ближайших точек второго множества:

(2)
$\begin{gathered} {{d}_{{{\text{Hausdorff}}}}}(Q,R)\;\mathop = \limits^{{\text{def}}} \\ = \;\max \left\{ {\mathop {\max }\limits_{q \in Q} \mathop {\min }\limits_{r \in R} {{{\left\| {q - r} \right\|}}_{2}},\;\mathop {\max }\limits_{r \in R} \mathop {\min }\limits_{q \in Q} {{{\left\| {r - q} \right\|}}_{2}}} \right\}. \\ \end{gathered} $

Например, в работе (Dong-Gyu, 1999) метрика Хаусдорфа используется для проективного сопоставления объектов, в (Orrite, Herrero, 2004) – для проективного выравнивания частично заслоненных контуров, а в статье (Jesorsky, Kirchberg, 2001) – для робастной детекции лиц.

Рассмотрим две важные модификации метрики Хаусдорфа:

– Критерий максимальной невязки (Коноваленко, Шемякина, 2018), который отличается от метрики Хаусдорфа тем, что в нем вместо ближайшей точки для данной точки выбирается фактически соответствующая ей точка:

$\begin{gathered} {{L}_{\infty }}({\hat {H}},{\text{H}};R)\;\mathop = \limits^{{\text{def}}} \\ = \;\max \left\{ {\mathop {\max }\limits_{q \in Q} {{{\left\| {q - {\text{H}}{{{{\hat {H}}}}^{{ - 1}}}(q)} \right\|}}_{2}},\;\mathop {\max }\limits_{r \in R} {{{\left\| {r - {\hat {H}}{{{\text{H}}}^{{ - 1}}}(r)} \right\|}}_{2}}} \right\}. \\ \end{gathered} $

Заметим, что аргументы под первым максимумом равны, поэтому

(3)
${{L}_{\infty }}({\hat {H}},{\text{H}};R) = \mathop {\max }\limits_{r \in R} {{\left\| {r - {\hat {H}}{{{\text{H}}}^{{ - 1}}}(r)} \right\|}_{2}}.$

Этот критерий использовался в качестве точности нормализации фотографии документа перед распознаванием его текстового содержания (Коноваленко, Шемякина, 2018).

– Расстояние Фреше (Frechet, 1906) и его разновидности. Оно определяется следующим образом:

(4)
$F(Q,R) = \mathop {\inf }\limits_{\alpha ,\beta } \;\mathop {\max }\limits_{t \in [0,1)} {{\left\| {\delta Q(\alpha (t)),\delta R(\beta (t))} \right\|}_{2}},$
где $\delta Q$ и $\delta R$ – непрерывные биекции множества $[0,1)$ в границы множеств Q и R соответственно, а $\alpha ,\beta $ – непрерывные монотонные сюръекции множества [0, 1) в себя (репараметризация). Расстояние Фреше применялось, например, для измерения степени близости двух контуров после проективного выравнивания в задаче проективно-инвариантного распознавания плоских замкнутых контуров (Притула и др., 2014), для оценки качества сегментации изображений (Березский, Березская, 2015), для оценки качества сопоставления карт (Wei et al., 2013).

• Наиболее часто точность проективной нормализации рассчитывается как среднеквадратичная невязка координат:

(5)
${{L}_{2}}({\hat {H}},{\text{H}};R)\;\mathop = \limits^{{\text{def}}} \;\sqrt {\frac{1}{{S(R)}}\int\limits_R \left\| {r - {\hat {H}}{{{\text{H}}}^{{ - 1}}}(r)} \right\|_{2}^{2}dr} .$

Это можно видеть в работе (Hsu, Sawhney, 1998) в задаче автоматического исправления дисторсии, вызванной кривизной линзы и движением камеры, в статье (Chen, 2002), где решалась задача проективного выравнивания изображения, созданного при помощи матрицы проекторов, и во многих других работах, например (Baltzopoulos, 1995; Stein, 1997; Mallon, 2005).

Разделим эти критерии на две группы: $\{ {{K}_{{{\text{Jaccard}}}}},{{d}_{{{\text{Hausdorff}}}}},F\} $ и $\{ {{L}_{2}},{{L}_{\infty }}\} $. Первая группа сравнивает множества Q и R, не учитывая попарные соответствия их элементов. Это приводит к тому, что существуют такие ${\hat {H}} \ne {\text{H}}$, для которых критерии возвращают значения, соответствующие максимальной точности: ${{d}_{{{\text{Hausdorff}}}}} = F = 0$, ${{K}_{{{\text{Jaccard}}}}} = 1$. Критерии второй группы учитывают попарные соответствия элементов Q и R и в случае ${\hat {H}} \ne {\text{H}}$ не могут вернуть значения, соответствующие максимальной точности: ${{L}_{2}} = {{L}_{\infty }} = 0$. В данной работе мы будем рассматривать только критерии второй группы.

КРИТЕРИИ ТОЧНОСТИ АФФИННОЙ АППРОКСИМАЦИИ ПРОЕКТИВНОГО ПРЕОБРАЗОВАНИЯ

Теперь будем считать, что преобразование H известно на практике, и вместо проективной оценки ${\hat {H}}$ проективного преобразования H будем рассматривать его аппроксимацию – аффинное преобразование A. Таким образом, мы адаптируем критерии точности проективного исправления для описания точности аффинной аппроксимации проективного преобразования:

(6)
${{L}_{2}}({\text{A}},{\text{H}};R) = \sqrt {\frac{1}{{S(R)}}\int\limits_R \left\| {r - {\text{A}}{{{\text{H}}}^{{ - 1}}}(r)} \right\|_{2}^{2}dr} ,$
(7)
${{L}_{\infty }}({\text{A}},{\text{H}};R) = \mathop {\max }\limits_{r \in R} {{\left\| {r - {\text{A}}{{{\text{H}}}^{{ - 1}}}(r)} \right\|}_{2}}.$

Зададим преобразование A матрицей $A = \left[ {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}} \end{array}} \right]$ следующим образом:

(8)
$\begin{gathered} {\text{A}}\left( {\left[ {\begin{array}{*{20}{c}} x \\ y \end{array}} \right]} \right)\;\mathop = \limits^{{\text{def}}} \;A\left[ {\begin{array}{*{20}{c}} x \\ y \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \\ 1 \end{array}} \right] = \\ = \;\left[ {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{a}_{{13}}}} \\ {{{a}_{{23}}}} \end{array}} \right]. \\ \end{gathered} $

Тогда:

(9)
$\begin{gathered} {{L}_{2}}({\text{A}},{\text{H}};R) = {{L}_{2}}(A,{\text{H}};R) = \\ = \;\sqrt {\frac{1}{{S(R)}}\int\limits_R \left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|_{2}^{2}dr} , \\ \end{gathered} $
(10)
$\begin{gathered} {{L}_{\infty }}({\text{A}},{\text{H}};R) = \\ = {{L}_{\infty }}(A,{\text{H}};R) = \mathop {\max }\limits_{r \in R} {{\left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|}_{2}}. \\ \end{gathered} $

ОПТИМАЛЬНЫЕ АФФИННЫЕ АППРОКСИМАЦИИ ПРОЕКТИВНОГО ПРЕОБРАЗОВАНИЯ

Задача поиска оптимальной в смысле ${{L}_{2}}$ аффинной аппроксимации проективного преобразования ${\text{H}}$ относительно области интереса R формулируется следующим образом:

$\begin{gathered} A_{{{{L}_{2}}}}^{*}\;\mathop = \limits^{{\text{def}}} \;\arg \;\mathop {\min }\limits_A {{L}_{2}}(A,{\text{H}};R) = \\ = \;\arg \;\mathop {\min }\limits_A \sqrt {\frac{1}{{S(R)}}\int\limits_R \left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|_{2}^{2}dr} , \\ \end{gathered} $
(11)
$A_{{{{L}_{2}}}}^{*} = \arg \;\mathop {\min }\limits_A \int\limits_R \left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|_{2}^{2}dr,$
а в смысле ${{L}_{\infty }}$ – следующим:

$A_{{{{L}_{\infty }}}}^{*}\;\mathop = \limits^{{\text{def}}} \;\arg \;\mathop {\min }\limits_A {{L}_{\infty }}(A,{\text{H}};R),$
(12)
$A_{{{{L}_{\infty }}}}^{*} = \arg \;\mathop {\min }\limits_A \mathop {\max }\limits_{r \in R} {{\left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|}_{2}}.$

Докажем выпуклость задач (11) и (12).

Теорема 1. Задача (11) – выпуклая.

Доказательство. Задача называется выпуклой, если выпуклы допустимое множество и целевая функция. Допустимое множество в нашем случае есть ${{\mathbb{R}}^{{2 \times 3}}}$, а значит, выпукло. Таким образом, осталось доказать выпуклость целевой функции по A. Выпишем ее

$\int\limits_R \left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|_{2}^{2}dr.$

При каждом значении r подынтегральная функция $\left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|_{2}^{2}$ выпукла по A, а значит, выпуклый по A и интеграл (бесконечная сумма) таких функций, что и требовалось доказать.

Теорема 2. Задача (12) – выпуклая.

Доказательство. Отличие от предыдущего доказательства состоит в том, что тут требуется доказать выпуклость другой целевой функции:

$\mathop {\max }\limits_{r \in R} {{\left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|}_{2}}.$

При каждом значении r функция ${{\left| {\left| {r - A\left[ {\begin{array}{*{20}{c}} {{{{\text{H}}}^{{ - 1}}}(r)} \\ 1 \end{array}} \right]} \right|} \right|}_{2}}$ выпукла по A, а значит, выпуклый по A и поточечный максимум таких функций, что и требовалось доказать.

Таким образом, обе задачи могут быть решены эффективно. Пример оптимальной аффинной аппроксимации проективного преобразования представлен на рис. 1.

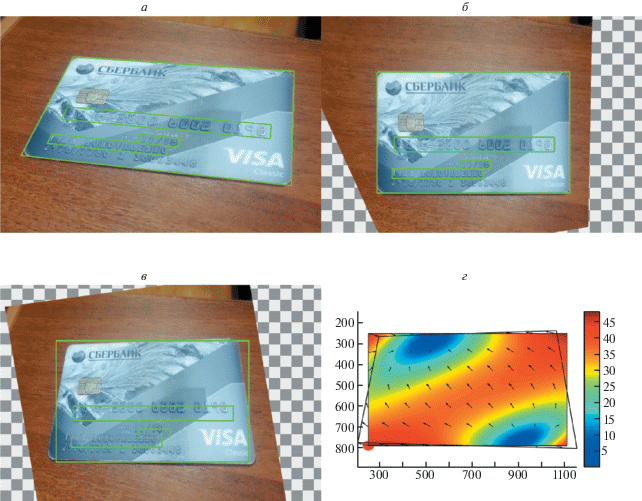
Рис. 1.

а – исходное изображение; б – исходное изображение, исправленное проективным преобразованием H; в – исходное изображение, исправленное оптимальной аффинной аппроксимацией $A_{{{{S}_{\infty }}}}^{{^{*}}}$ преобразования H; г – Область интереса R, векторное поле смещений $\left[ {\begin{array}{*{20}{c}} {A_{{{{L}_{\infty }}}}^{*}{{{\text{H}}}^{{ - 1}}}(r) - r} \end{array}} \right],$ $r \in R$ и его ${{\ell }_{2}}$ норма – невязка (показана цветом), положение максимальной невязки выделено красной точкой.

ПРИМЕНЕНИЕ АФФИННОЙ АППРОКСИМАЦИИ ПРОЕКТИВНОГО ПРЕОБРАЗОВАНИЯ ДЛЯ УЛУЧШЕНИЯ БЫСТРОДЕЙСТВИЯ

С одной стороны, известно, что применение к растровому изображению аффинного преобразования занимает значительно меньше времени, чем применение проективного, и часто выполняется качественнее. С другой стороны, заменяя проективное преобразование на его быструю аффинную аппроксимацию, мы можем сильно потерять в геометрической точности. Поэтому мы предлагаем следующий подход, параметром которого является пороговая допустимая потеря точности T в смысле $L \in \{ {{L}_{2}},{{L}_{\infty }}\} $:

• По известным H и R вычисляем ${\text{A}}_{L}^{*}$.

• Если $L({\text{A}}_{L}^{*},{\text{H}};R) \leqslant T$, то применяем к изображению преобразование ${\text{A}}_{L}^{*}$, иначе – ${\text{H}}$.

Таким образом, мы экономим вычислительные ресурсы только в тех случаях, когда проективное преобразование приближается аффинным преобразованием с высокой точностью.

ЗАКЛЮЧЕНИЕ

Показано, что для критериев точности, предложенных авторами в настоящей работе, задача оптимальной в смысле этих критериев аффинной аппроксимации является выпуклой, что делает возможным эффективный поиск глобального оптимума. Это позволяет исследовать точность возможной аппроксимации проективного преобразования аффинным и, если она достаточна, использовать вычислительно более эффективное аффинное преобразование изображения.

Исследование выполнено при частичной финансовой поддержке РФФИ в рамках научных проектов № 16-07-00616, № 17-29-03370 и № 17-29-03514.

Список литературы

  1. Балицкий А.М., Савчик А.В., Гафаров Р.Ф., Коноваленко И.А. О проективно инвариантных точках овала с выделенной внешней прямой. Проблемы передачи информации. 2017. Т. 53. № 3. С. 84–89.

  2. Березский О.Н., Березская К.М. Количественная оценка качества сегментации изображений на основе метрик. Управляющие системы и машины. 2015. № 6. С. 59–65.

  3. Болотова Ю.А., Спицын В.Г., Осина П.М. Обзор алгоритмов детектирования текстовых областей на изображениях и видеозаписях. Компьютерная оптика. 2017. Т. 41. № 3.

  4. Ефимов А.И., Новиков А.И. Алгоритм поэтапного уточнения проективного преобразования для совмещения изображений. Компьютерная оптика. 2016. Т. 40. № 2.

  5. Коноваленко И.А., Шемякина Ю.А. Анализ величин ошибки при неточном проективном преобразовании четырехугольника. Информационные технологии и нанотехнологии. 2018. С. 1251–1260.

  6. Николаев П.П. Проективно инвариантное описание неплоских гладких фигур. 1. Предварительный анализ задачи. Сенсорные системы. 2016. Т. 30. № 4. С. 290–311.

  7. Притула Н.Е., Николаев П.П., Шешкус А.В. Сравнение двух алгоритмов проективно-инвариантного распознавания плоских замкнутых контуров с единственной вогнутостью. “Информационные технологии и системы”, Сборник трудов. 2014. С. 367–373.

  8. Савчик А.В., Николаев П.П. Теорема о пересечении T-и H-поляр. Информационные процессы. 2016. Т. 16. № 4. С. 430–443.

  9. Холопов И.С. Алгоритм коррекции проективных искажений при маловысотной съёмке. Компьютерная оптика. 2017. Т. 41. № 2.

  10. Чернов Т.С., Ильин Д.А., Безматерных П.В., Фараджев И.А., Карпенко С.М. Исследование методов сегментации изображений текстовых блоков документов с помощью алгоритмов структурного анализа и машинного обучения. Вестник Российского фонда фундаментальных исследований. 2016. № 4. С. 55–71.

  11. Шемякина Ю.А. Использование точек и прямых для вычисления проективного преобразования по двум изображениям плоского объекта. Информационные технологии и вычислительные системы. 2017. № 3. С. 79–91.

  12. Шемякина Ю.А., Жуковский А.Е., Фараджев И.А. Исследование алгоритмов вычисления проективного преобразования в задаче наведения на планарный объект по особым точкам. Искусственный интеллект и принятие решений. 2017. № 1. С. 43–49.

  13. Alter T. 3D pose from 3 corresponding points under weak-perspective projection. Technical report, Massachusetts inst. of tech. cambridge artificial intelligence lab, 1992.

  14. Aradhye H., Myers G. Method and apparatus for recognition of symbols in images of three-dimensional scenes, US Patent 7,738,706. 2010.

  15. Baltzopoulos V. A videofluoroscopy method for optical distortion correction and measurement of knee-joint kinematics. Clinical Biomechanics. 1995. V. 10 (2). P. 85–92.

  16. Chen H., Sukthankar R., Wallace G., Li K. Scalable alignment of large-format multi-projector displays using camera homography trees. Proceedings of the conference on Visualization’02. 2002. P. 339–346.

  17. Darko P., Volker S., Leif K. Interactive image completion with perspective correction. The Visual Computer. 2006. V. 22 (9–11). P. 671–681.

  18. Dong-Gyu S., Oh-Kyu K., Rae-Hong P. Object matching algorithms using robust hausdorff distance measures. IEEE Transactions on image processing. 1999. V. 8 (3). P. 425–429.

  19. Dubuisson M., Jain A. A modified hausdorff distance for object matching. Proceedings of the 12th IAPR International Conference.1994. V. 1. P. 566–568.

  20. Faugeras O. What can be seen in three dimensions with an uncalibrated stereo rig? European conference on computer vision. 1992. P. 563–578.

  21. Fréchet M. Sur quelques points du calcul fonctionnel. Rendiconti del Circolo Matematico di Palermo (1884–1940). 1906. V. 22 (1). P. 1–72.

  22. Gruen A. Adaptive least squares correlation: a powerful image matching technique. South African Journal of Photogrammetry, Remote Sensing and Cartography. 1985. V. 14 (3). P. 175–187.

  23. Heckbert P. Fundamentals of texture mapping and image warping. 1989. UC Berkeley Master’s thesis. 86 p.

  24. Hsu S., Sawhney H. Influence of global constraints and lens distortion on pose and appearance recovery from a purely rotating camera. Applications of Computer Vision, 1998. WACV’98. Proceedings., Fourth IEEE Workshop. 1998. P. 154–159.

  25. Huang J., Singh A., Ahuja N. Single image super-resolution from transformed self-exemplars. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015. P. 5197–5206.

  26. Huttenlocher D., Klanderman G., Rucklidge W. Comparing images using the hausdorff distance. IEEE Transactions on pattern analysis and machine intelligence. 1993. V. 15 (9). P. 850–863.

  27. Jaccard P. Étude comparative de la distribution florale dans une portion des alpes et des jura. Bull Soc Vaudoise Sci Nat. 1901. V. 37. P. 547–579.

  28. Jesorsky O., Kirchberg K.J., Frischholz R.W. Robust face detection using the hausdorff distance. International Conference on Audio-and Video-Based Biometric Person Authentication. 2001. P. 90–95.

  29. Kadir T., Zisserman A., Brady M. An affine invariant salient region detector. European conference on computer vision. 2004. P. 228–241.

  30. Karpenko S., Konovalenko I., Miller A., Miller B., Nikolaev D. UAV control on the basis of 3d landmark bearing-only observations. Sensors. 2015. V. 15 (12). P. 29802–29820.

  31. Kutulakos K.N., Vallino J. Affine object representations for calibration-free augmented reality. Virtual Reality Annual International Symposium, 1996., Proceedings of the IEEE. 1996. P. 25–36.

  32. Lorenz H., Döllner J. Real-time piecewise perspective projections. GRAPP. 2009. P. 147–155.

  33. Mallon J., Whelan P.F. Projective rectification from the fundamental matrix. Image and Vision Computing. 2005. V. 23 (7). P. 643–650.

  34. Mikolajczyk K., Schmid C. An affine invariant interest point detector. European conference on computer vision. 2002. P. 128–142.

  35. Mikolajczyk K., Schmid C. Scale & affine invariant interest point detectors. International journal of computer vision. 2004. V. 60 (1). P. 63–86.

  36. Morel J-M., Yu G. Asift: A new framework for fully affine invariant image comparison. SIAM journal on imaging sciences. 2009. V. 2 (2). P. 438–469.

  37. Orrite C., Herrero J.E. Shape matching of partially occluded curves invariant under projective transformation. Computer Vision and Image Understanding. 2004. V. 93 (1). P. 34–64.

  38. Povolotskiy M.A., Kuznetsova E.G., Khanipov T.M. Russian license plate segmentation based on dynamic time warping. 31st European Conference on Modelling and Simulation (ECMS). 2017. P. 285–291.

  39. Skoryukina N., Chernov T., Bulatov K., Nikolaev D.P., Arlazarov V. Snapscreen: Tv-stream frame search with projectively distorted and noisy query. Ninth International Conference on Machine Vision. 2017. V. 10341. P. 103410Y.

  40. Skoryukina N., Shemiakina J., Arlazarov V., Faradjev I. Document localization algorithms based on feature points and straight lines. Tenth International Conference on Machine Vision. 2018. V. 10696. P. 106961H.

  41. Stein G.P. Lens distortion calibration using point correspondences. Computer Vision and Pattern Recognition. Proceedings. IEEE Computer Society Conference. 1997. P. 602–608.

  42. Tu-ichi O., Kiyoshi M., Toshiyuki S. Obtaining surface orientation from texels under perspective projection. IJCAI. 1981. P. 746–751.

  43. Wei H., Wang Y., Forman G., Zhu Y. Map matching by fréchet distance and global weight optimization. Technical Paper, Departement of Computer Science and Engineering. 2013. P. 19.

  44. Zhukovsky A.E., Arlazarov V.V., Postnikov V.V., Krivtsov V.E. Segments graph-based approach for smartphone document capture. Eighth International Conference on Machine Vision . 2015. V. 9875. P. 98750P.

  45. Zwicker M., Räsänen J., Botsch M., Dachsbacher C., Pauly M. Perspective accurate splatting. Proceedings of Graphics interface 2004. 2004. P. 247–254.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Сенсорные системы

Архивы выпусков Информация о журнале Отправить рукопись в журнал