Известия РАН. Теория и системы управления, 2019, № 5, стр. 32-43
АСИМПТОТИКА РЕШЕНИЯ ЗАДАЧИ МИНИМИЗАЦИИ ИНТЕГРАЛЬНОГО КВАДРАТИЧНОГО ФУНКЦИОНАЛА НА ТРАЕКТОРИЯХ КВАЗИЛИНЕЙНОЙ СИСТЕМЫ
А. И. Калинин a, *, Л. И. Лавринович a, **
a Белорусский государственный ун-т
Минск, Белоруссия
* E-mail: kalininai@bsu.by
** E-mail: lavrinovich@bsu.by
Поступила в редакцию 08.05.2018
После доработки 11.03.2019
Принята к публикации 20.04.2019
Аннотация
Рассматривается задача минимизации интегрального квадратичного функционала на траекториях квазилинейной динамической системы (содержащей малый параметр при нелинейностях) с линейными терминальными ограничениями. Строятся асимптотические приближения в виде программы и обратной связи к оптимальному управлению в этой задаче. Вычисления сводятся к решению невозмущенной линейно-квадратичной задачи, интегрированию систем линейных дифференциальных уравнений, а также к нахождению корней невырожденных линейных алгебраических систем.
Введение. Динамические системы, содержащие малые параметры при нелинейностях, принято называть квазилинейными. Задачи оптимизации таких систем в различных постановках исследовались многими авторами (см., например, [1–6]). Интерес к квазилинейным задачам вызван эффективностью асимптотических методов их решения, при применении которых исходные по существу нелинейные задачи сводятся к сравнительно несложной коррекции решений задач оптимизации линейных систем.
В статье рассматривается задача оптимального управления квазилинейной системой с интегральным квадратичным критерием качества при наличии линейных терминальных ограничений на траектории. Ее можно трактовать как задачу управления с минимальными энергетическими затратами. Целью работы является построение асимптотических приближений к оптимальному программному управлению и оптимальной обратной связи в рассмотренной задаче. Суть применяемого подхода к исследованию состоит в асимптотическом разложении по целым степеням малого параметра начальных значений сопряженных переменных и множителей Лагранжа – конечномерных элементов, соответствующих в силу принципа максимума [7] оптимальному управлению. Статья обобщает результаты, полученные в [8], где рассматривалась задача с фиксированным правым концом траекторий.
1. Постановка задачи. В классе многомерных управляющих воздействий с кусочно-непрерывными компонентами рассмотрим следующую задачу оптимизации квазилинейной системы:
(1.3)
$J(u) = \frac{1}{2}\int\limits_{{{t}_{*}}}^{t{\text{*}}} {({{x}^{{\rm T}}}Q(t)x + {{u}^{{\rm T}}}P(t)u)dt} \to \min ,$Предположение 1. Элементы матриц $A(t)$, $B(t)$, $Q(t)$, $P(t)$, $\partial f(x,t){\text{/}}\partial x$, $x \in {{R}^{n}}$, $t \in T$, принадлежат классу ${{C}^{p}}$, $p \geqslant 1$.
Управление $u(t,\mu )$, $t \in T$, с кусочно-непрерывными компонентами принято называть допустимым, если для порожденной им траектории $x(t,\mu )$, $t \in T$, системы (1.1) выполняется условие $Hx(t{\text{*}},\mu ) = g$. Допустимое управление, минимизирующее функционал J(u), называют оптимальным. Наряду с этими общеупотребительными понятиями определим то, что будет пониматься под асимптотическими приближениями к решению рассматриваемой задачи.
Определение 1. Управление ${{u}^{{(N)}}}(t,\mu )$, $t \in T$, с кусочно-непрерывными компонентами назовем (программным) асимптотически субоптимальным управлением N-го порядка ($N = 0,1,2,\; \ldots $,) в задаче (1.1)–(1.3), если оно отклоняется по критерию качества (1.3) от оптимального управления на величину $O({{{\mu }}^{{N + 1}}})$, а порожденная им траектория $x\left( {t,\mu } \right)$, $t \in T$, удовлетворяет терминальному ограничению (1.2) с точностью того же порядка малости.
Определение 2. Вектор-функцию ${{u}^{{(N)}}}(x,t,\mu )$ назовем асимптотически субоптимальной обратной связью N-го порядка, если для любого начального состояния $({{x}_{*}},{{t}_{*}})$, ${{t}_{*}} < t{\text{*}}$, имеет место ${{u}^{{(N)}}}({{x}_{*}},{{t}_{*}},\mu ) = {{u}^{{(N)}}}({{t}_{*}},\mu )$, где ${{u}^{{(N)}}}(t,\mu )$, $t \in T$, – асимптотически субоптимальное управление N-го порядка в задаче (1.1)–(1.3).
В статье предлагается алгоритм, с помощью которого для заданного числа N (N < p) можно построить асимптотически субоптимальное управление N-го порядка в рассматриваемой задаче. Алгоритм опирается на конструктивное доказательство теоремы о существовании при сделанном далее предположении оптимального управления и его асимптотических свойствах. Его суть состоит в построении полиномов Тейлора начальных значений сопряженных переменных (в момент времени ${{t}_{*}}$), которые в силу принципа максимума [7] соответствуют оптимальному управлению. Эти величины как функции малого параметра принадлежат классу Cp. В работе также построены асимптотически субоптимальные обратные связи нулевого и первого порядков.
2. Базовая задача. На первом этапе построения асимптотически субоптимальных управлений решается базовая задача
(2.2)
$Hx(t*) = g,\quad J(u) = \frac{1}{2}\int\limits_{{{t}_{*}}}^{t*} {({{x}^{{\rm T}}}Q(t)x + {{u}^{{\rm T}}}P(t)u)dt} \to \min ,$Предположение 2. Динамическая система (2.1) является управляемой на отрезке $\left[ {\tau ,\;t{\text{*}}} \right]$ относительно подпространства $Hx = 0$ при любом $\tau \in [{{t}_{*}},t{\text{*}})$ (см. [9]).
Это предположение выполняется тогда и только тогда (см., например, [10]), когда при любом $\tau \in [{{t}_{*}},t{\text{*}})$ и любом ненулевом m-векторе l имеет место соотношение
где ${{F}_{0}}(t)$, $t \in T$, – (n × n) – матричная функция, являющаяся решением начальной задачи с единичной матрицей ${{E}_{n}}$. Заметим, что условие (2.3), которое называют неявным критерием управляемости на подпространство, для стационарной динамической системы эквивалентно требованию [9]При выполнении предположения 2 в задаче (2.1), (2.2) существуют допустимые управления, а тогда эта задача имеет единственное решение (см. [11]), которое является нормальной экстремалью. Последнее означает, что принцип максимума [7] в данном случае может быть сформулирован следующим образом: пусть ${{u}^{0}}(t)$, ${{x}^{0}}(t)$, $t \in T$, – оптимальные управление и траектория в задаче (2.1), (2.2), тогда существует такой m-вектор множителей Лагранжа ${{\lambda }_{0}}$, что выполняется условие
Отсюда непосредственно получаем
После решения базовой задачи формируется матрица
(2.6)
${{I}_{0}}\left( {{{t}_{*}}} \right) = \left( {\begin{array}{*{20}{c}} {H{{F}_{{12}}}\left( {{{t}_{*}}} \right)}&{{{0}_{{m \times m}}}} \\ {{{F}_{{22}}}\left( {{{t}_{*}}} \right)}&{ - {{H}^{{\text{T}}}}} \end{array}} \right).$Здесь ${{F}_{{12}}}\left( t \right)$, ${{F}_{{22}}}\left( t \right)$, $t \in T$, – блоки размеров n × n матричной функции
(2.7)
$F = \left( {\begin{array}{*{20}{c}} {{{F}_{{11}}}}&{{{F}_{{12}}}} \\ {{{F}_{{21}}}}&{{{F}_{{22}}}} \end{array}} \right)$,(2.9)
$\bar {A}(t) = \left( {\begin{array}{*{20}{c}} {A(t)}&{B(t){{P}^{{ - 1}}}(t){{B}^{{\text{T}}}}(t)} \\ {Q(t)}&{ - {{A}^{{\text{T}}}}(t)} \end{array}} \right)$.Пусть ${{{\nu }}_{0}} = {{\psi }^{0}}({{t}_{*}})$. В [10] показано, что при выполнении предположения 2 матрица (2.6) является невырожденной при ${{t}_{*}} < t{\text{*}}$, а компоненты векторов ${{{\nu }}_{0}}$, ${{\lambda }_{0}}$ – решением следующей системы линейных алгебраических уравнений:
(2.10)
${{I}_{0}}\left( {{{t}_{*}}} \right)\left( {\begin{array}{*{20}{c}} {{{\nu }_{0}}} \\ {{{\lambda }_{0}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {g - H{{F}_{{11}}}\left( {{{t}_{*}}} \right){{x}_{*}}} \\ { - {{F}_{{21}}}\left( {{{t}_{*}}} \right){{x}_{*}}} \end{array}} \right).$3. Асимптотический анализ решения исходной задачи. Говорить об асимптотически субоптимальных управлениях можно лишь в том случае, когда исходная задача имеет решение. Убедимся, что при сделанных предположениях в задаче (1.1)–(1.3) с достаточно малым µ существует оптимальное управление. Доказательство будет конструктивным и предопределит дальнейшие вычисления при построении асимптотически субоптимальных управлений.
Рассмотрим начальную задачу
(3.1)
$\begin{gathered} \dot {x} = A(t)x + \mu f(x,t) + B(t){{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t)\psi ,\quad x({{t}_{*}}) = {{x}_{*}}, \\ \dot {\psi } = Q(t)x - {{\left( {A(t) + \mu \frac{{\partial f}}{{\partial x}}(x,t)} \right)}^{{\rm T}}}\psi ,\quad \psi ({{t}_{*}}) = v, \\ \end{gathered} $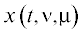 ,
, 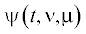 , $t \in T$, принадлежащее классу Cp, если только $\left\| {\nu - {{\nu }_{0}}} \right\| < {{{\varepsilon }}_{0}}$, $\left| {\mu } \right| < {{\mu }_{0}}$. Ниже будет показано, что ответ о существовании оптимального управления в исходной
задаче тесно связан с разрешимостью системы конечных уравнений
, $t \in T$, принадлежащее классу Cp, если только $\left\| {\nu - {{\nu }_{0}}} \right\| < {{{\varepsilon }}_{0}}$, $\left| {\mu } \right| < {{\mu }_{0}}$. Ниже будет показано, что ответ о существовании оптимального управления в исходной
задаче тесно связан с разрешимостью системы конечных уравнений
(3.2)
$Hx\left( {t*,\nu ,\mu } \right) - g = 0,\quad \psi \left( {t*,\nu ,\mu } \right) - {{H}^{{\rm T}}}\lambda = 0$(3.3)
$R\left( {\eta ,\mu } \right) = \left( {\begin{array}{*{20}{c}} {Hx\left( {t*,\nu ,\mu } \right) - g} \\ {\psi \left( {t*,\nu ,\mu } \right) - {{H}^{{\rm T}}}\lambda } \end{array}} \right),$Теорема. При выполнении предположений 1, 2 в задаче (1.1)–(1.3) с достаточно малым (по модулю) μ существует единственное оптимальное управление, которое является нормальной экстремалью и представимо в виде
(3.5)
${{u}^{0}}(t,\mu ) = {{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t)\psi (t,\nu (\mu ),\mu ),\quad t \in T.$Значение ν(µ) вектора сопряженных переменных в момент ${{t}_{*}}$ и m-вектор множителей Лагранжа λ(µ), соответствующий в силу принципа максимума оптимальному управлению, удовлетворяют уравнениям (3.2), причем $\nu (\mu ) \in {{C}^{p}}$, $\nu \left( 0 \right) = {{\nu }_{0}}$, $\lambda \left( \mu \right) \in {{C}^{p}}$, $\lambda \left( 0 \right) = {{\lambda }_{0}}$.
Доказательство. С помощью теоремы о неявной функции убедимся, что система уравнений (3.4) однозначно разрешима относительно η при достаточно малых μ. Прежде всего, заметим, что вектор-функция $R(\eta ,\mu )$, определенная в области $\left\| {\eta - {{\eta }_{0}}} \right\| < {{{\varepsilon }}_{0}}$, $\left| {\mu } \right| < {{\mu }_{0}}$, принадлежит классу Cp. Поскольку $x\left( {t,{{\nu }_{0}},0} \right) = {{x}^{0}}(t)$, $\psi \left( {t,{{\nu }_{0}},0} \right) = {{\psi }^{0}}(t)$, $t \in T$, то, как видно из (3.3), $R({{\eta }_{0}},0) = 0$. Привлекая для записи решения задачи (3.1) при μ = 0 фундаментальную матрицу, а затем дифференцируя, получаем $\partial R\left( {{{\eta }_{0}},0} \right){\text{/}}\partial \eta = {{I}_{0}}({{t}_{*}})$ (см. формулу (2.6)). Как было отмечено в предыдущем разделе, при выполнении предположения 2 эта матрица Якоби будет невырожденной. Таким образом, для системы (3.4) или, что то же самое, (3.2) выполнены условия теоремы о неявной функции. Согласно этой теореме, в некоторой окрестности нуля $\left| \mu \right| < {{\mu }_{1}}$ однозначно определена вектор-функция $\eta (\mu ) = (\nu (\mu ),\lambda (\mu ))$ из класса Cp, удовлетворяющая уравнениям (3.2) и условию $\eta (0) = {{\eta }_{0}}$ = (ν0, λ0).
Рассмотрим управление (3.5). Оно будет допустимым в исходной задаче, поскольку для порожденной им траектории ${{x}^{0}}(t,\mu ) = x(t,\nu (\mu ),\mu )$, $t \in T$, системы (1.1) выполняется терминальное ограничение $H{{x}^{0}}(t{\text{*}},\mu ) = g$. Вместе с тем это управление удовлетворяет принципу максимума [7] с вектором сопряженных переменных ${{\psi }^{0}}\left( {t,\mu } \right) = \psi \left( {t,\nu \left( \mu \right),\mu } \right)$, $t \in T$. Заметим, что управление (3.5) является нормальной экстремалью, которой соответствует m-вектор множителей Лагранжа $\lambda \left( \mu \right)$.
Покажем, что экстремаль ${{u}^{0}}(t,\mu )$, $t \in T$, будет единственным оптимальным управлением в задаче (1.1)–(1.3), если $\mu $ достаточно мало. Предположим противное, тогда существует такая последовательность ${{\mu }_{k}} \to 0$, что управление ${{u}^{0}}(t,{{\mu }_{k}})$, $t \in T$, k = 1, 2, …, либо не является оптимальным в исходной задаче с $\mu = {{\mu }_{k}}$, либо существует другое оптимальное управление. Поскольку установлено, что в задаче (1.1)–(1.3) с достаточно малым $\mu $ существует допустимое управление, то эта задача имеет решение в классе измеримых функций [11]. Решение исходной задачи с μ = μk отличное от u0(t, μk), t ∈ T, обозначим через $\bar {u}$(t, μk), t ∈ T, и пусть $\bar {x}$(t, μk), t ∈ T – соответствующая оптимальная траектория. Тогда
Опираясь на эти неравенства, можно убедиться в том, что последовательность измеримых вектор-функций $\bar {u}\left( {t,{{\mu }_{k}}} \right)$, $t \in T$, содержит подпоследовательность, сходящуюся почти всюду к ${{u}^{0}}(t)$, $t \in T$. Рассуждения, которые приводят к такому выводу, аналогичны тем, что использовались при доказательстве теоремы 8.1 из [6]. Чтобы не усложнять обозначений, будем считать, что сама последовательность $\bar {u}\left( {t,{{\mu }_{k}}} \right)$, t ∈ T, сходится почти всюду к оптимальному управлению базовой задачи. Тогда $\bar {x}\left( {t,{{\mu }_{k}}} \right) \to {{x}^{0}}(t)$ равномерно на T. Поскольку управление $\bar {u}\left( {t,{{\mu }_{k}}} \right)$, t ∈ T, является оптимальным, то для него выполняется принцип максимума, т.е. существует такой ненулевой вектор множителей Лагранжа $({{\overline \lambda }_{0}}\left( {{{\mu }_{k}}} \right),\,{{\overline \lambda }_{1}}\left( {{{\mu }_{k}}} \right),\,...,\,{{\overline \lambda }_{m}}\left( {{{\mu }_{k}}} \right)),\,({{\overline \lambda }_{0}}\left( {{{\mu }_{k}}} \right) \geqslant 0),$ что вдоль $\bar {u}\left( {t,{{\mu }_{k}}} \right)$, $\bar {x}\left( {t,{{\mu }_{k}}} \right)$ и решения ${\bar {\psi }}\left( {t,{{\mu }_{k}}} \right)$, $t \in T$, сопряженной системы
(3.6)
$\begin{gathered} \dot {\psi } = - {{\left( {A(t) + {{\mu }_{k}}\frac{{\partial f}}{{\partial x}}\left( {\bar {x}\left( {t,{{\mu }_{k}}} \right),t} \right)} \right)}^{\operatorname{T} }}\psi + {{\overline \lambda }_{0}}\left( {{{\mu }_{k}}} \right)Q(t)\bar {x}\left( {t,{{\mu }_{k}}} \right),\quad \psi \left( {t{\text{*}}} \right) = {{H}^{{\rm T}}}\bar {\lambda }\left( {{{\mu }_{k}}} \right), \\ \overline \lambda \left( {{{\mu }_{k}}} \right) = {{({{\overline \lambda }_{1}}\left( {{{\mu }_{k}}} \right),\,...,\,{{\overline \lambda }_{m}}\left( {{{\mu }_{k}}} \right))}^{{\rm T}}}, \\ \end{gathered} $(3.7)
$\begin{gathered} {{{\bar {\psi }}}^{{\text{T}}}}\left( {t,{{\mu }_{k}}} \right)B(t)\bar {u}\left( {t,{{\mu }_{k}}} \right) - \frac{{{{{\bar {\lambda }}}_{0}}\left( {{{\mu }_{k}}} \right)}}{2}{{{\bar {u}}}^{{\text{T}}}}\left( {t,{{\mu }_{k}}} \right)P(t)\bar {u}\left( {t,{{\mu }_{k}}} \right) = \\ = \mathop {\max }\limits_{u \in {{R}^{r}}} \left( {{{{\bar {\psi }}}^{{\text{T}}}}\left( {t,{{\mu }_{k}}} \right)B(t)u - \frac{{{{{\bar {\lambda }}}_{0}}\left( {{{\mu }_{k}}} \right)}}{2}{{u}^{{\text{T}}}}P(t)u} \right). \\ \end{gathered} $Поскольку вектор $({{\bar {\lambda }}_{0}}\left( {{{\mu }_{k}}} \right),\bar {\lambda }\left( {{{\mu }_{k}}} \right))$ определен с точностью до положительного множителя, то без ограничения общности можно считать, что $\left\| {\left( {{{{\bar {\lambda }}}_{0}}\left( {{{\mu }_{k}}} \right),\bar {\lambda }\left( {{{\mu }_{k}}} \right)} \right)} \right\| = \left\| {\,\left( {1,\,{{\lambda }_{0}}} \right)} \right\|$, $k = 1,2,\; \ldots $ Тогда из последовательности векторов $\left( {{{{\bar {\lambda }}}_{0}}\left( {{{\mu }_{k}}} \right),\bar {\lambda }\left( {{{\mu }_{k}}} \right)} \right)$ можно выбрать сходящуюся подпоследовательность. Чтобы не усложнять обозначений, будем считать, что сама последовательность сходится и обозначим ее предел через $({{\bar {\lambda }}_{0}},\bar {\lambda })$. Понятно, что ${{\bar {\lambda }}_{0}} \geqslant 0,$ $\left\| {\left( {{{{\bar {\lambda }}}_{0}},\bar {\lambda }} \right)} \right\| = \left\| {\,\left( {1,\,{{\lambda }_{0}}} \right)} \right\|$. Последовательность $\bar {\psi }(t,{{\mu }_{k}})$, t ∈ T, как видно из (3.6), будет равномерно сходиться к решению ${\bar {\psi }}\left( t \right)$, t ∈ T, начальной задачи
(3.8)
$\dot {\psi } = - {{A}^{{\rm T}}}(t){\psi } + {{{\lambda }}_{0}}Q(t){{x}^{0}}(t),\quad \psi \left( {t{\text{*}}} \right) = {{H}^{{\rm T}}}\bar {\lambda }.$Переходя к пределу в (3.7) при $k \to \infty $, получаем, что почти всюду на T
(3.9)
${{\bar {\psi }}^{{\text{T}}}}\left( t \right)B(t){{u}^{0}}\left( t \right) - \frac{{{{{\bar {\lambda }}}_{0}}}}{2}{{u}^{0}}^{{\text{T}}}\left( t \right)P(t){{u}^{0}}\left( t \right) = \mathop {\max }\limits_{u \in {{R}^{r}}} \left( {{{{\bar {\psi }}}^{{\text{T}}}}\left( t \right)B(t)u - \frac{{{{{\bar {\lambda }}}_{0}}}}{2}{{u}^{{\text{T}}}}P(t)u} \right).$В силу (3.8), (3.9) управление ${{u}^{0}}\left( t \right)$, $t \in T$, удовлетворяет принципу максимума с вектором множителей Лагранжа $\left( {{{{\bar {\lambda }}}_{0}},\bar {\lambda }} \right)$. В [10] показано, что при выполнении предположения 2 оптимальному управлению в задаче (2.1), (2.2) соответствует в силу принципа максимума единственный (с точностью до положительного множителя) вектор сопряженных переменных. Поэтому ${{\bar {\lambda }}_{0}} = 1,\,\,\bar {\lambda } = {{\lambda }_{0}}$ и соответственно $\bar {\psi }(t) = {{\psi }_{0}}(t)$, $t \in T$. Поскольку ${{\lambda }^{0}}\left( {{{\mu }_{k}}} \right) > 0$ для достаточно больших k, то из (3.7) следует, что почти всюду на T
Отсюда и из (1.1), (3.1), (3.6) видно, что
4. Построение асимптотически субоптимальных управлений. Продолжим изложение алгоритма построения асимптотических приближений к решению задачи (1.1)–(1.3), опираясь на утверждения теоремы. Пусть задано натуральное число N, N < p. Поскольку $\eta (\mu ) = (\nu (\mu ),\lambda (\mu ))$ принадлежит классу C p и $\eta (0) = ({{\nu }_{0}},{{\lambda }_{0}})$, то имеют место асимптотические равенства ν(μ) = ${{\nu }^{{\left( N \right)}}}(\mu ) + O({{\mu }^{{N + 1}}})$, $\lambda (\mu ) = {{\lambda }^{{\left( N \right)}}}(\mu ) + O({{\mu }^{{N + 1}}})$, где
(4.1)
${{\nu }^{{\left( N \right)}}}\left( \mu \right) = {{\nu }_{0}} + \sum\limits_{k = 1}^N {{{\mu }^{k}}{{\nu }_{k}}} ,\quad {{\lambda }^{{\left( N \right)}}}\left( \mu \right) = {{\lambda }_{0}} + \sum\limits_{k = 1}^N {{{\mu }^{k}}{{\lambda }_{k}}} $(4.2)
${{u}^{{\left( N \right)}}}(t,\mu ) = {{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t)\psi (t,{{\nu }^{{\left( N \right)}}}(\mu ),\mu ),\quad t \in T,$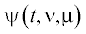 , как было отмечено, принадлежит классу Cp. Поэтому управление (4.2) отличается от оптимального по норме пространства непрерывных
вектор-функций на величину порядка $O({{\mu }^{{N + 1}}})$. По доказанному оптимальная траектория в исходной задаче представима в виде ${{x}^{0}}\left( {t,\mu } \right) = x\left( {t,\nu (\mu ),\mu } \right)$, t ∈ T, а для траектории, порожденной управлением (4.2), справедливо равенство ${{x}^{{\left( N \right)}}}\left( {t,\mu } \right) = x\left( {t,{{\nu }_{N}}(\mu ),\mu } \right)$, t ∈ T. Поскольку вектор-функция $x\left( {t,\nu ,\mu } \right)$ принадлежит классу Cp, то траектория ${{x}^{{\left( N \right)}}}\left( {t,\mu } \right)$, t ∈ T, отличается от оптимальной по норме пространства непрерывных вектор-функций на величину
порядка $O({{\mu }^{{N + 1}}})$. Из вышесказанного следует, что для достаточно малых (по модулю) µ имеют место оценки
, как было отмечено, принадлежит классу Cp. Поэтому управление (4.2) отличается от оптимального по норме пространства непрерывных
вектор-функций на величину порядка $O({{\mu }^{{N + 1}}})$. По доказанному оптимальная траектория в исходной задаче представима в виде ${{x}^{0}}\left( {t,\mu } \right) = x\left( {t,\nu (\mu ),\mu } \right)$, t ∈ T, а для траектории, порожденной управлением (4.2), справедливо равенство ${{x}^{{\left( N \right)}}}\left( {t,\mu } \right) = x\left( {t,{{\nu }_{N}}(\mu ),\mu } \right)$, t ∈ T. Поскольку вектор-функция $x\left( {t,\nu ,\mu } \right)$ принадлежит классу Cp, то траектория ${{x}^{{\left( N \right)}}}\left( {t,\mu } \right)$, t ∈ T, отличается от оптимальной по норме пространства непрерывных вектор-функций на величину
порядка $O({{\mu }^{{N + 1}}})$. Из вышесказанного следует, что для достаточно малых (по модулю) µ имеют место оценки
Для построения управления (4.2) нужно найти коэффициенты ${{\nu }_{k}}$, k = 1, 2, …, N, полинома (4.1), что можно сделать с помощью методики, изложенной в [6]. Согласно этой методике, прежде всего, нужно разложить левую часть уравнения (3.4) по степеням малого параметра. Вектор-функции $x\left( {t,\nu ,\mu } \right)$, $\psi \left( {t,\nu ,\mu } \right)$ в каждой точке области определения имеют частные производные по μ до порядка p включительно, поэтому они представимы в виде
(4.3)
$x\left( {t,\nu ,\mu } \right) = \sum\limits_{k = 0}^N {{{\mu }^{k}}{{x}_{k}}(t,\nu ) + O({{\mu }^{{N + 1}}})} ,\quad \psi \left( {t,\nu ,\mu } \right) = \sum\limits_{k = 0}^N {{{\mu }^{k}}{{\psi }_{k}}(t,\nu ) + O({{\mu }^{{N + 1}}})} $Применяя формализм Пуанкаре к системе (3.1), составим дифференциальные уравнения для функций ${{x}_{k}}(t,\nu )$, ${{\psi }_{k}}(t,\nu )$, k = 0, 1, 2, …, N, при фиксированном ν:
(4.4)
${{\dot {\psi }}_{1}} = Q(t){{x}_{1}} - {{A}^{{\rm T}}}(t){{\psi }_{1}} - \frac{{\partial h}}{{\partial x}}\left( {{{x}_{0}}(t),{{\psi }_{0}}(t),t} \right),\quad {{\psi }_{1}}({{t}_{*}}) = 0;$Как видно из (4.4), нахождение коэффициентов разложений (4.3) при заданном ν сводится к последовательному решению начальных задач для систем линейных дифференциальных уравнений.
В силу формул (3.3), (4.3) левая часть уравнения (3.3) допускает асимптотическое представление
(4.5)
${{R}_{0}}\left( \eta \right) = \left( {\begin{array}{*{20}{c}} {H{{x}_{0}}(t{\text{*}},\nu ) - g} \\ {{{\psi }_{0}}(t{\text{*}},\nu ) - {{H}^{{\rm T}}}\lambda } \end{array}} \right),\quad {{R}_{k}}\left( \eta \right) = \left( {\begin{array}{*{20}{c}} {H{{x}_{k}}(t{\text{*}},\nu )} \\ {{{\psi }_{k}}(t{\text{*}},\nu )} \end{array}} \right),\quad k = \,1,2,\, \ldots ,N.$Составим системы линейных уравнений для векторов ${{\eta }_{k}} = \left( {{{\nu }_{k}},{{\lambda }_{k}}} \right)$, k = 1, 2, …, N. В соответствии со схемой, изложенной в [6], применим для этого метод неопределенных коэффициентов, а именно разложим с помощью формулы Тейлора вектор-функцию
где ${{\eta }^{{\left( N \right)}}}\left( \mu \right) = ({{\nu }^{{\left( N \right)}}}\left( \mu \right),{{\lambda }^{{\left( N \right)}}}\left( \mu \right))$, по степеням $\mu $ до порядка N включительно и приравняем коэффициенты разложения (начиная с коэффициента при µ) к нулю. В результате с учетом того, что вектор-функции ${{R}_{k}}(\eta )$, $k = 0,1,2,\;...,\;N$, линейны по η, получим невырожденные системы линейных уравнений для последовательного нахождения векторов ${{\eta }_{k}} = \left( {{{\nu }_{k}},{{\lambda }_{k}}} \right)$, k = 1, 2, …, N:
(4.6)
${{I}_{0}}({{t}_{*}}){{\eta }_{1}} = - {{R}_{1}}\left( {{{\eta }_{0}}} \right),\quad {{I}_{0}}({{t}_{*}}){{\eta }_{2}} = - {{R}_{2}}\left( {{{\eta }_{0}}} \right) - \frac{{\partial {{R}_{1}}}}{{\partial \eta }}\left( {{{\eta }_{0}}} \right){{\eta }_{1}},...$Как видно из (4.5), чтобы сформировать правые части этих систем, необходимо знать значения функций ${{x}_{k}}(t,\nu )$, ${{\psi }_{k}}(t,\nu )$ и их частных производных по компонентам вектора ν в точке $(t*,{{\nu }_{0}})$. Значения функций находятся посредством интегрирования уравнений (4.4). Формальным дифференцированием этих уравнений получаем начальные задачи для производных. Например,
При вычислении правых частей систем (4.6) следует учитывать, что ${{x}_{0}}(t,{{\nu }_{0}}) = {{x}^{0}}(t)$, ψ0(t, ν0) = = ${{\psi }^{0}}(t)$, t ∈ T. Тогда, как видно из (4.4), (4.5),
(4.7)
$\begin{gathered} {{{\dot {x}}}_{1}} = A(t){{x}_{1}} + B(t){{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t){{\psi }_{1}} + f({{x}^{0}}(t),t),\quad {{x}_{1}}({{t}_{*}}) = 0 \\ {{{\dot {\psi }}}_{1}} = Q(t){{x}_{1}} - {{A}^{{\rm T}}}(t){{\psi }_{1}} - \frac{{\partial h}}{{\partial x}}\left( {{{x}^{0}}(t),{{\psi }^{0}}(t),t} \right),\quad {{\psi }_{1}}({{t}_{*}}) = 0. \\ \end{gathered} $Последовательно решая системы (4.6), находим векторы ${{\eta }_{k}} = \left( {{{\nu }_{k}},{{\lambda }_{k}}} \right)$, k = 1, 2, …, N, и составляем полином (4.1). Управление (4.2), как было отмечено, является асимптотически субоптимальным управлением N-го порядка в исходной задаче. Для его построения необходимо решить начальную задачу (3.1) при $\nu = {{\nu }^{{\left( N \right)}}}\left( \mu \right)$. Вместе с тем в силу (4.3) $\psi (t,{{\nu }^{{\left( N \right)}}}\left( \mu \right),\mu ) = {{\bar {\psi }}^{{\left( N \right)}}}\left( {t,\mu } \right) + O({{\mu }^{{N + 1}}})$, где
(4.8)
${{\bar {\psi }}^{{\left( N \right)}}}\left( {t,\mu } \right) = \sum\limits_{k = 0}^N {{{\mu }^{k}}{{{\bar {\psi }}}_{k}}\left( t \right)} ,\quad t \in T,$(4.9)
${{\bar {u}}^{{\left( N \right)}}}\left( {t,\mu } \right) = {{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t){{\bar {\psi }}^{{\left( N \right)}}}\left( {t,\mu } \right),\quad t \in T,$Поскольку ${{\bar {\psi }}^{{\left( 0 \right)}}}\left( {t,\mu } \right) = {{\psi }^{0}}(t)$, t ∈ T, то ${{\bar {u}}^{{\left( 0 \right)}}}\left( {t,\mu } \right) = {{u}^{0}}\left( t \right)$, t ∈ T, т.е. решение базовой задачи является асимптотически субоптимальным управлением нулевого порядка в исходной задаче. Согласно (4.8), (4.9), асимптотически субоптимальное управление первого порядка представимо в виде
(4.10)
${{\bar {u}}^{{\left( 1 \right)}}}\left( {t,\mu } \right) = {{u}^{0}}(t) + \mu {{P}^{{ - 1}}}\left( t \right){{B}^{{\rm T}}}\left( t \right){{\bar {\psi }}_{1}}\left( t \right),\quad t \in T,$(4.11)
${{\bar {\psi }}_{1}}\left( t \right) = \psi _{1}^{0}\left( t \right) + {{\Phi }_{{22}}}(t,{{t}_{*}}){{\nu }_{1}},\quad t \in T,$(4.12)
$\Phi (t,{{t}_{*}}) = \left( {\begin{array}{*{20}{c}} {{{\Phi }_{{11}}}(t,{{t}_{*}})}&{{{\Phi }_{{12}}}(t,{{t}_{*}})} \\ {{{\Phi }_{{21}}}(t,{{t}_{*}})}&{{{\Phi }_{{22}}}(t,{{t}_{*}})} \end{array}} \right),$В силу (4.11) асимптотически субоптимальное управление первого порядка (4.10) может быть представлено в виде
(4.14)
${{\bar {u}}^{{\left( 1 \right)}}}\left( {t,\mu } \right) = {{u}^{0}}(t) + \mu {{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t)(\psi _{1}^{0}(t) + {{\Phi }_{{22}}}(t,{{t}_{*}}){{\nu }_{1}}),\quad t \in T.$Заметим, что для всех $t \leqslant t{\text{*}}$ имеет место равенство $\Phi (t*,t) = F\left( t \right)$ (см. (2.7), (2.8)).
Построенные асимптотические приближения корней системы уравнений (3.4) можно использовать для точного решения этой системы, а значит, и рассмотренной задачи при заданном значении µ. Для этого нужно применить процедуру доводки [13], т.е. найти с помощью метода Ньютона корни уравнения (3.2), взяв в качестве начального приближения ${{\eta }^{{\left( N \right)}}}\left( \mu \right)$. Чтобы упростить вычисления вместо матрицы $\partial R\left( {\eta ,\mu } \right){\text{/}}\partial \eta $, можно воспользоваться ее асимптотическим приближением ${{I}_{0}}({{t}_{*}})$.
5. Асимптотически субоптимальный синтез. Коэффициенты полиномов (4.1), (4.8), которые используются при построении программных асимптотически субоптимальных управлений, разумеется, зависят от начального состояния $({{x}_{*}},{{t}_{*}})$ динамической системы. Ранее такая зависимость нами не учитывалась, поскольку начальное состояние считалось заданным. В настоящем разделе, который посвящен построению асимптотически субоптимальных обратных связей нулевого и первого порядков, нас будет интересовать в первую очередь именно эта зависимость. Она будет учтена и в обозначениях.
Рассмотрим невырожденную систему алгебраических уравнений (2.10). В [10] показано, что ${{F}_{{22}}}({{t}_{*}})$ – невырожденная матрица. Тогда, как следует из системы (2.10),
(5.1)
${{\nu }_{0}} = {{\nu }_{0}}({{x}_{*}},{{t}_{*}}) = F_{{22}}^{{ - 1}}({{t}_{*}}){{H}^{{\rm T}}}{{M}^{{ - 1}}}({{t}_{*}})(H({{F}_{{12}}}({{t}_{*}})K({{t}_{*}}) - {{F}_{{11}}}({{t}_{*}})){{x}_{*}} + g) - K({{t}_{*}}){{x}_{*}},$(5.2)
$M\left( t \right) = H{{F}_{{12}}}\left( t \right)F_{{22}}^{{ - 1}}\left( t \right){{H}^{{\rm T}}},\quad t \in T,$(5.3)
$\dot {K} = - KA\left( t \right) - {{A}^{{\rm T}}}\left( t \right)K + KB\left( t \right){{P}^{{ - 1}}}\left( t \right){{B}^{{\rm T}}}\left( t \right)K - Q\left( t \right),\quad K\left( {t{\text{*}}} \right) = 0.$Поскольку ${{u}^{0}}\left( t \right)$, t ∈ T, является асимптотически субоптимальным управлением нулевого порядка в задаче (1.1)–(1.3) и ${{u}^{0}}({{t}_{*}}) = {{P}^{{ - 1}}}({{t}_{*}}){{B}^{{\text{T}}}}({{t}_{*}}){{\nu }_{0}}$, то, как следует из формулы (5.1), вектор-функция
(5.4)
${{u}^{{\left( 0 \right)}}}\left( {x,t} \right) = {{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t)(F_{{22}}^{{ - 1}}\left( t \right){{H}^{{\rm T}}}{{M}^{{ - 1}}}(t)\left( {H\left( {{{F}_{{12}}}\left( t \right)K\left( t \right) - {{F}_{{11}}}\left( t \right)} \right)x + g} \right) - K\left( t \right)x)$Перейдем к построению асимптотически субоптимальной обратной связи первого порядка. Как видно из формулы (4.10), для асимптотически субоптимального управления первого порядка
(5.5)
${{\bar {u}}^{{\left( 1 \right)}}}({{t}_{*}},\mu ) = {{P}^{{ - 1}}}({{t}_{*}}){{B}^{{\rm T}}}({{t}_{*}})\left( {{{\nu }_{0}} + \mu {{\nu }_{1}}} \right).$Решив первую из систем (4.6), получаем
(5.6)
$\begin{gathered} {{\nu }_{1}} = {{\nu }_{1}}({{x}_{*}},{{t}_{*}}) = \\ = - F_{{22}}^{{ - 1}}({{t}_{*}})({{H}^{{\rm T}}}{{M}^{{ - 1}}}({{t}_{*}})H({{F}_{{12}}}({{t}_{*}})F_{{22}}^{{ - 1}}({{t}_{*}})\psi _{1}^{0}(t*,{{x}_{*}},{{t}_{*}}) - x_{1}^{0}(t*,{{x}_{*}},{{t}_{*}})) - \psi _{1}^{0}(t*,{{x}_{*}},{{t}_{*}})), \\ \end{gathered} $(5.7)
${{x}^{0}}(t,{{x}_{*}},{{t}_{*}}) = {{С}_{1}}(t,{{t}_{*}}){{x}_{*}} + {{C}_{2}}(t,{{t}_{*}}),\quad {{\psi }^{0}}(t,{{x}_{*}},{{t}_{*}}) = {{С}_{3}}(t,{{t}_{*}}){{x}_{*}} + {{С}_{4}}(t,{{t}_{*}}),$(5.8)
$\begin{gathered} {{С}_{1}}(t,{{t}_{*}}) = {{\Phi }_{{11}}}(t,{{t}_{*}}) + {{\Phi }_{{12}}}(t,{{t}_{*}})(F_{{22}}^{{ - 1}}({{t}_{*}}){{H}^{{\rm T}}}{{M}^{{ - 1}}}({{t}_{*}})H\left( {{{F}_{{12}}}({{t}_{*}})K({{t}_{*}}) - {{F}_{{11}}}({{t}_{*}})} \right) - K({{t}_{*}})), \\ {{С}_{2}}(t,{{t}_{*}}) = {{\Phi }_{{12}}}(t,{{t}_{*}})F_{{22}}^{{ - 1}}({{t}_{*}}){{H}^{{\rm T}}}{{M}^{{ - 1}}}({{t}_{*}})g, \\ {{С}_{3}}(t,{{t}_{*}}) = {{\Phi }_{{21}}}(t,{{t}_{*}}) + {{\Phi }_{{22}}}(t,{{t}_{*}})(F_{{22}}^{{ - 1}}({{t}_{*}}){{H}^{{\rm T}}}{{M}^{{ - 1}}}({{t}_{*}})H({{F}_{{12}}}({{t}_{*}})K({{t}_{*}}) - {{F}_{{11}}}({{t}_{*}})) - K({{t}_{*}})), \\ {{С}_{4}}(t,{{t}_{*}}) = {{\Phi }_{{22}}}(t,{{t}_{*}})F_{{22}}^{{ - 1}}({{t}_{*}}){{H}^{{\rm T}}}{{M}^{{ - 1}}}({{t}_{*}})g. \\ \end{gathered} $Из формул (5.1), (5.4)–(5.6) следует, что асимптотически субоптимальная обратная связь первого порядка представима в виде
(5.9)
${{\bar {u}}^{{\left( 1 \right)}}}\left( {x,t,\mu } \right) = {{u}^{{\left( 0 \right)}}}\left( {x,t} \right) + \mu {{u}^{{\left( 1 \right)}}}\left( {x,t} \right),$(5.10)
$\begin{gathered} {{u}^{{\left( 1 \right)}}}\left( {x,t} \right) = - {{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t)F_{{22}}^{{ - 1}}\left( t \right) \times \\ \times \;({{H}^{{\rm T}}}{{M}^{{ - 1}}}\left( t \right)H({{F}_{{12}}}\left( t \right)F_{{22}}^{{ - 1}}\left( t \right)\psi _{1}^{0}\left( {t*,x,t} \right) - x_{1}^{0}\left( {t*,x,t} \right)) - \psi _{1}^{0}\left( {t*,x,t} \right)). \\ \end{gathered} $Записав решение начальной задачи (4.7) по формуле Коши с учетом (5.7), получаем формулу, которой можно пользоваться при вычислении значений вектор-функции (5.10):
Матричные функции ${{C}_{1}}\left( {\tau ,t} \right)$, ${{C}_{2}}\left( {\tau ,t} \right)$, ${{C}_{2}}\left( {\tau ,t} \right)$, ${{C}_{4}}\left( {\tau ,t} \right)$ определены ранее формулами (5.8).
В задаче оптимального управления с закрепленным правым концом траектории, которая является частным случаем задачи (1.1)–(1.3) $\left( {H = {{E}_{n}},\;g = 0} \right)$, формулы для асимптотически субоптимальных обратных связей упрощаются. Обратная связь нулевого порядка, как легко убедиться, принимает вид ${{u}^{{\left( 0 \right)}}}\left( {х,t} \right) = - {{P}^{{ - 1}}}(t){{B}^{{\rm T}}}(t)F_{{12}}^{{ - 1}}\left( t \right){{F}_{{11}}}\left( t \right)x$ (см. также [8]). Относительная управляемость в данном случае означает полную управляемость [1].
Значительно проще строятся асимптотически субоптимальные обратные связи в задаче (1.1)–(1.3) и случае, когда $Q\left( t \right) = 0$, $t \in T$. В этом случае ${{F}_{{21}}}\left( t \right) = K\left( t \right) = 0$, ${{F}_{{11}}}\left( t \right) = {{F}_{0}}\left( t \right)$, $F_{{22}}^{{ - 1}}\left( t \right) = F_{0}^{{\rm T}}\left( t \right)$, $M\left( t \right) = C\left( t \right)$, $t \in T$. Матричная функция F0(t) является решением начальной задачи (2.4), а
6. Пример. В классе управляющих воздействий $u\left( t \right) = \left( {{{u}_{1}}(t),{{u}_{2}}(t),{{u}_{3}}\left( t \right)} \right)$, $t \in [{{t}_{*}},t*]$, $0 \leqslant {{t}_{*}} < t{\text{*}}$, с кусочно-непрерывными компонентами рассмотрим задачу
С помощью формул (2.8), (2.9) находим
Здесь и далее под ch, sh, th понимаются гиперболические косинус, синус и тангенс соответственно. Тогда согласно (5.2), (5.3) получаем
Асимптотически субоптимальная обратная связь нулевого порядка (5.4) в данном случае задается формулой
Перейдем к построению асимптотически субоптимальной обратной связи первого порядка (5.9). Для этого остается найти вектор-функцию (5.10). В данном случае
Используя равенства (5.7), (5.10), получаем
Для оценки точности построенных асимптотических приближений были найдены невязки в терминальных ограничениях на траектории, порожденные субоптимальными обратными связями нулевого и первого порядков при конкретных значениях начальных данных и малого параметра. Результаты вычислений приведены в таблице (с точностью до 10–6). В левом столбце таблицы указан порядок субоптимальных обратных связей, а в остальных столбцах приведены невязки в терминальных ограничениях для траекторий, порожденных этими связями. Судить о близости по критерию качества невозможно, поскольку неизвестно его оптимальное значение.
Заключение. В статье предложены вычислительные процедуры построения асимптотических приближений к оптимальному программному управлению и оптимальной обратной связи в рассмотренной задаче. При их использовании вычисления сводятся к решению линейно-квадратичной задачи оптимального управления, интегрированию систем линейных дифференциальных уравнений, а также к нахождению корней невырожденных линейных алгебраических систем.
Таблица.
Результаты вычислений
| ${{t}_{*}} = 0$, $t* = 3$, ${{\omega }_{1}} = - 1$, ${{\omega }_{2}} = 2$, ${{\omega }_{3}} = 1$ | μ = 0.1 | μ = 0.01 | ||
| Субоптимальные обратные связи | ${{x}_{1}}\left( {t{\text{*}}} \right)$ | ${{x}_{2}}\left( {t{\text{*}}} \right)$ | ${{x}_{1}}\left( {t{\text{*}}} \right)$ | ${{x}_{2}}\left( {t{\text{*}}} \right)$ |
| Нулевого порядка | 0.192306 | –0.078842 | 0.014561 | –0.007208 |
| Первого порядка | 0.044495 | 0.004701 | 0.000529 | –0.000129 |
| ${{t}_{*}} = 1$, $t* = 3$, ${{\omega }_{1}} = - 1$, ${{\omega }_{2}} = 2$, ${{\omega }_{3}} = 1$ | μ = 0.1 | μ = 0.01 | ||
| Субоптимальные обратные связи | ${{x}_{1}}\left( {t{\text{*}}} \right)$ | ${{x}_{2}}\left( {t{\text{*}}} \right)$ | ${{x}_{1}}\left( {t{\text{*}}} \right)$ | ${{x}_{2}}\left( {t{\text{*}}} \right)$ |
| Нулевого порядка | 0.142878 | –0.061882 | –0.012217 | –0.006050 |
| Первого порядка | 0.012584 | –0.001784 | 0.000130 | –0.000036 |
Список литературы
Красовский Н.Н. Теория управления движением. М.: Наука, 1968.
Киселев Ю.Н. Асимптотическое решение задачи оптимального быстродействия для систем управления близких к линейным // Докл. АН СССР. 1968. Т. 182. № 1. С. 31–34.
Falb P.L., Jong J.L. Some Successive Approximation Methods on Control and Oscillation Theory. N. Y., L.: Acad. Press, 1969.
Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980.
Калинин А.И. Асимптотика решений возмущенных задач оптимального управления // Изв. РАН. Техн. кибернетика. 1994. № 3. С. 104–114.
Калинин А.И. Асимптотические методы оптимизации возмущенных динамических систем. Минск: Экоперспектива, 2000.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1983.
Калинин А.И., Лавринович Л.И. Применение метода возмущений к задаче минимизации интегрального квадратичного функционала на траекториях квазилинейной системы // Изв. РАН. ТиСУ. 2014. № 2. С. 3–12.
Габасов Р., Кириллова Ф.М. Качественная теория оптимальных процессов. М.: Наука, 1971.
Калинин А.И. О проблеме синтеза оптимальных систем управления // ЖВМ и МФ. 2018. Т. 58. № 3. С. 397–402.
Мордухович Б.Ш. Существование оптимальных управлений // Итоги науки и техники. Современные проблемы математики. 1976. Т. 6.
Хартман Ф. Обыкновенные дифференциальные уравнения. М.: Мир, 1970.
Габасов Р., Кириллова Ф.М. Конструктивные методы оптимизации. Ч. 2. Задачи управления. Минск: Университетское, 1984.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления