Известия РАН. Теория и системы управления, 2019, № 5, стр. 44-55
УПРАВЛЕНИЕ ИСТОЧНИКОМ РЕСУРСА, МИНИМИЗИРУЮЩЕЕ ЕГО ПОТРЕБНУЮ ЕМКОСТЬ
В. А. Мозжечков *
ЗАО “Инженерно-технический центр “Привод”, Тульский государственный ун-т
Тула, Россия
* E-mail: itc@tulaprivod.ru
Поступила в редакцию 15.01.2018
После доработки 15.04.2019
Принята к публикации 20.05.2019
Аннотация
Предлагается метод поиска оптимального закона управления источником ограниченного ресурса. Примерами источников рассматриваемого класса являются: конденсаторные источники электроэнергии, баллонные источники газа, гидронапорные башни. Предполагается, что источник разделен на несколько секций. Искомый закон управления минимизирует потребную емкость источника на основе рационального отключения и подключения секций источника к его выходной магистрали в рассчитанные моменты времени в соответствии с известной программой потребления ресурса. Закон управления ищется в форме кусочно-постоянной вектор-функции времени, элементы значений которой равны единице или нулю. Рассмотрен пример реализации предлагаемого метода применительно к задаче управления источником газа.
Введение. В разнообразных технологических и энергетических установках применяются источники ограниченных ресурсов. Примерами таких источников являются конденсаторные и аккумуляторные источники электроэнергии, баллонные источники (хранилища) газа, гидронапорные башни, пружинные и гироскопические (инерционные) накопители энергии. Источники указанного типа могут пополняться, но при интенсивном потреблении ресурса роль линии подпитки, как правило, пренебрежимо мала, доминирующая часть ресурса к потребителям поступает из запаса, сохраненного в источнике.
Будем предполагать, что источник должен обеспечить ресурсом потребителей в соответствии с известной программой потребления, которая для каждого момента времени указывает запланированный текущий секундный расход и требуемый потенциал ресурса (электрический потенциал, давление газа или жидкости на выходе источника и т.п.). Источник ресурса конструктивно разбит на секции. Емкость каждой секции и их количество выбирают исходя из конструктивных соображений и известных затрат ресурса на реализацию программы потребления. Связи секций между собой и с выходной магистралью питания, исходящей из источника, традиционно считают стационарными.
Потребную емкость источника и запас ресурса, необходимый для реализации заданной программы потребления, можно сократить, если допустить возможность управления процессом отключения и подключения его секций к выходной магистрали в заранее запланированные моменты времени. Сокращение потребного запаса и емкости источника при этом обусловлено возможностью более полного опорожнения его секций на интервалах времени с низким уровнем запрашиваемого потенциала (т.е. запрашиваемого электрического напряжения, давления и т.п.) и сбережения высокого потенциала для соответствующих участков программы потребления только в одной или нескольких секциях источника.
Требуется определить программное управление, указывающее моменты времени отключения и подключения секций источника к его выходной магистрали, которое минимизирует потребную емкость источника. Закон управления будем искать в форме кусочно-постоянной функции времени, значением которой является двоичный вектор, i-й элемент которого указывает открыта или закрыта в данный момент времени линия, подводящая ресурс от i-й секции источника к потребителям. Минимизация потребной емкости источника эквивалентна минимизации потребного запаса ресурса, определяемого произведением емкости источника и заданного начального значения потенциала ресурса.
Разнообразные практические задачи управления ресурсами явились одним из важных стимулов становления и развития теории оптимального управления и оптимизации [1–4]. Несмотря на неутихающий и в настоящее время интерес к теме оптимального управления ресурсами [5–13], вышеизложенная задача в научной литературе не рассматривалась. В данной работе предлагается ее математическая постановка и численный метод решения.
1. Математическая постановка задачи. Считаем, что на интервале времени t ∈ [0, T] заданы функции p*(t), g*(t), определяющие программу потребления ресурса. Функция p*(t) указывает минимально необходимый потенциал (электрический потенциал, давление газа или жидкости и т.п.) в магистрали питания, исходящей из источника, а функция g*(t) – секундный расход ресурса из источника (электрический ток, секундный расход газа или жидкости и т.п.). Потребители ресурса получают его из магистрали через стабилизатор, понижающий потенциал магистрали до уровня, запрашиваемого данным потребителем или группой потребителей. Потенциал ресурса в магистрали p(t) должен быть не меньше его значения, запрашиваемого тем или иным потребителем в текущий момент времени, т.е. в каждый момент времени t ∈ [0, T] должно выполняться условие:
(1.1)
$p(t) = \sum\limits_{i = 1}^n {{{p}_{i}}(t){{u}_{i}}(t)} \geqslant p{\text{*}}(t),\quad {{u}_{i}}(t) \in \{ 0,1\} ,\quad i = \overline {1,n} ,\quad \forall t \in [0,T],$Считаем, что скорость убывания потенциала в секции пропорциональна расходу ресурса и обратно пропорциональна емкости секции (такая зависимость с учетом известных допущений соответствует, например, классическим моделям разряда конденсатора и газового баллона),
где Gi(t) = g*(t)ui(t) – расход ресурса из i-й секции, Ci – емкость i-й секции, Ci > 0, i = $\overline {1,n} $. Емкость Ci в рассматриваемой задаче считается постоянной на всем отрезке времени [0, T].В каждый момент времени к выходной магистрали источника может быть подключена не более чем одна из его секций. Это исключает бесполезное перетекание ресурса из секций с более высоким потенциалом в другие секции (указанное перетекание снижает потенциальные возможности обслуживать запросы на ресурс с высоким потенциалом). Данное требование опишем условием
Потенциал ресурса в секциях источника не может превышать заданной величины pmax:
(1.4)
${{p}_{i}}(t) \leqslant {{p}^{{{\text{max}}}}},\quad i = \overline {1,n} ,\quad \forall t \in [0,T].$Показателем качества, подлежащим минимизации, считаем суммарную емкость секций источника
минимально необходимую для реализации заданной программы потребления ресурса.Неизвестными являются: закон управления u(t), емкости секций Ci и начальные потенциалы ресурса pi(0) в каждой из них. Закон управления u(t) ищется в форме кусочно-постоянной вектор-функции времени, элементы значений которой равны 1 или 0.
Рассматриваемая задача состоит в выборе значений перечисленных неизвестных, обеспечивающих выполнение соотношений (1.1)–(1.4) и минимизирующих суммарную емкость секций источника (1.5).
2. Метод решения. Сформулированная выше задача является задачей оптимального управления. В ней требуется определить закон управления u(t), параметры объекта управления Ci и начальные значения фазовых переменных pi(0), доставляющие минимум показателю качества (1.5) с учетом ограничений (1.1)–(1.4).
Формально параметры Ci можно включить в вектор фазовых переменных, дополнив систему (1.2) уравнениями dCi(t)/dt = 0, i = $\overline {1,n} $, и, таким образом, заменить неизвестные параметры Ci неизвестными начальными значениями Ci(0) фазовых переменных Ci(t). При этом функционал (1.5), вычисляемый для момента времени T, соответствует функционалу классической задачи Майера вариационного исчисления. В таком случае в терминах оптимального управления рассматриваемая задача является задачей минимизации функционала Майера (1.5) c фиксированным временем на множестве фазовых траекторий объекта управления (1.2), стесненных ограничениями (1.1), (1.3), (1.4), на управление и фазовые переменные.
Эффективное применение известных методов оптимального управления к рассматриваемой задаче не представляется возможным в силу наличия у нее ряда особенностей, не позволяющих отнести ее к каноническим задачам теории оптимального управления. В частности, методы вариационного исчисления в данном случае не могут использоваться из-за дискретности значений искомой функции u(t). Применение метода динамического программирования [1] и принципа максимума [2] к рассматриваемой задаче неэффективно из-за сложности ограничений, накладываемых не только на управляющие (1.3) и фазовые переменные (1.4), но и на их комбинацию (1.1) в комплексе с требованием бинарности значений и с многомерностью искомой вектор-функции u(t). Такое сочетание ограничений и минимизируемого функционала выходит за рамки канонических задач, решаемых с использованием методов динамического программирования и принципа максимума.
Применение известных методов математического программирования к конечномерному аналогу рассматриваемой задачи также не представляется эффективным из-за его существенных отличий от классических задач математического программирования [3, 4].
В силу указанных причин для решения рассматриваемой задачи представляется рациональной разработка, согласно классификации, принятой в [3], прямого численного поискового метода, существенно учитывающего специфику решаемой задачи.
2.1. Описание метода. Предлагаемый метод основан на задании конечного набора моментов времени, в которые может происходить смена значений функции управления u(t). Таким образом, производится аппроксимация искомого закона управления u(t) функцией, меняющей значения в некоторые моменты времени из заданного конечного набора. При этом на остальные переменные указанная дискретизация времени не распространяется. В результате задача сводится к анализу конечного множества вариантов управлений. Значительная часть вариантов управлений исключается из последующего анализа на основе применения логического правила, изложенного ниже. Для очередного анализируемого варианта управления по найденным простым аналитическим зависимостям вычисляются оптимальные значения емкости секций и суммарная потребная емкость источника. Простые в вычислительном плане зависимости позволяют достаточно быстро анализировать большой объем возможных вариантов управлений. В итоге среди всех возможных вариантов управлений выявляется оптимальный вариант, которому соответствует минимальная потребная емкость источника.
В более детальном изложении предлагаемый метод сводится к выполнению следующих действий.
Шаг 1. Интервал времени [0, T] разбиваем на N частей Δt, далее называемых дискретами времени. Момент времени, соответствующий началу k-й дискреты времени (k = 1, … N), обозначим как tk. Для каждой дискреты времени назначаем номер секции, подключаемой к магистрали питания в момент времени tk на всем протяжении данной дискреты времени. В результате находится значение вектора s, состоящего из N компонент. В нем k-я компонента sk принимает значения из множества {$\overline {1,n} $} и указывает тем самым номер секции, подключаемой к магистрали питания на протяжении k-й дискреты времени.
Вектор s на интервале времени [0, T] задает значения компонент вектора управления согласно формуле:
(2.1)
$\begin{gathered} \forall t \in [0,T]{\text{:}}\,{{u}_{i}}(t) = 1,\quad {\text{если}}\quad i = {{s}_{k}}, \\ \forall t \in [{{t}_{k}},{{t}_{k}} + \Delta t];\quad {\text{иначе}}\quad {{u}_{i}}(t) = 0,\quad i = \overline {1,n} , \\ \end{gathered} $Таким образом, вектор s, согласно (2.1), задает дискретную аппроксимацию искомого закона управления u(t).
Множество значений вектора s конечно. В терминах комбинаторики множество всех возможных значений вектора s эквивалентно множеству размещений с повторениями n различных предметов по N различным местам. Число таких размещений равно nN. Следовательно, перебор всех возможных значений векторов s эквивалентен перебору всех целых чисел от 0 до nN – 1. Каждому целому числу из указанного диапазона взаимно однозначно соответствует единственный вектор s. Он является n-разрядным представлением целого числа из диапазона от 0 до nN – 1, если секциям присвоить номера от 0 до n – 1.
Перебрав и проанализировав все возможные значения вектора s, можно найти его оптимальное значение, определяющее оптимальный закон управления источником.
Перебор можно сократить, если учесть, что изменение названий (обозначений) секций источника не влияет на результат его работы. Например, вектор s' = (1 2 1 2) и вектор s'' = (2 1 2 1) предполагают одинаковый алгоритм работы источника: применение двух секций и смену используемой секции на каждой дискрете времени, т.е векторы s' и s'' отличаются только обозначениями компонент и указывают одинаковый алгоритм работы источника – поочередное опорожнение одной из двух секций на каждой дискрете времени. Очевидно, в рамках решаемой задачи имеет значение лишь та информация, заложенная в векторе s, которая определяет количество и последовательность задействования секций. Поэтому векторы s, указывающие одинаковое количество и последовательность (очередность) опорожнения секций, которые различаются только названиями компонент, являются эквивалентными в рамках решаемой задачи. Следовательно, достаточно анализировать только один вектор s из множества векторов, эквивалентных с точностью до обозначений компонент. Выделить единственный вектор s из множества эквивалентных позволяет следующее правило: первую применяемую секцию источника обозначаем номером 1, далее каждую вновь задействованную секцию обозначаем номером на единицу больше максимального номера секции из множества ранее задействованных секций. В формальной интерпретации это правило сводится к тому, что необходимо анализировать только такие векторы s, в которых впервые встречающиеся уникальные значения компонент монотонно возрастают на единицу с ростом их порядкового номера. Все прочие векторы s исключаются из анализа как эквивалентные тем, которые, согласно указанному правилу, подлежат анализу. Например, вектор (1 1 2 3 1 2) подлежит анализу: в нем уникальные значения компонент 1, 2, 3 монотонно возрастают на единицу с ростом порядкового номера компонент. Вектор (2 2 1 3 2 1) исключается из анализа. Он не удовлетворяет сформулированному правилу: в нем впервые встречающиеся уникальные значения компонент 2, 1, 3 не образуют монотонно возрастающей последовательности. Вектор (1 1 3 4 1 3) также исключается из анализа: в нем уникальные значения компонент 1, 3, 4 монотонно возрастают, но второе значение превышает первое более чем на единицу. Оба исключаемых вектора эквивалентны вышеприведенному вектору (1 1 2 3 1 2), поскольку отличается только обозначениями компонент и определяют такое же количество используемых секций и тот же порядок их применения. Обоснование правомерности указанного правила отсева вариантов представлено в Приложении (см. утверждение 1).
Шаг 2. Применительно к выбранному значению s формируем функции Gi(t), Pi(t), определяющие соответственно запрашиваемый расход и потенциал ресурса из i-й секции:
∀k ∈ {$\overline {1,N} $}: если sk = i, то ∀t ∈ [tk, tk + Δt]: Gi(t) = g*(t), Pi(t) = p*(t); иначе Gi(t) = 0, Pi(t) = 0, i = $\overline {1,n} $.
Шаг 3. Для анализируемого значения s вычисляем оптимальные емкости секций С$_{i}^{{\min }}$ по формулам:
(2.2)
$\begin{gathered} {{p}_{i}}(T) = \mathop {\max }\limits_{t \in [0 + \varepsilon ,T]} ([{{P}_{i}}(t) - {{p}^{{\max }}}{{q}_{i}}(t)]{\text{/}}[1 - {{q}_{i}}(t)]), \\ {{q}_{i}}(t) = {{Q}_{i}}(t){\text{/}}{{Q}_{i}}(0),\quad i = \overline {1,n} , \\ \end{gathered} $Справедливость формул (2.2) обоснована в Приложении (см. утверждение 2). Там же показано, что оптимальные начальные потенциалы ресурса в секциях одинаковы и равны максимально допустимому значению pmax, т.е. pi(0) = pmax.
Шаг 4. Используя формулы (1.5) и (2.2), вычисляем и запоминаем суммарную потребную емкость секций источника Cmin = $C_{1}^{{\min }}$ + … + $C_{n}^{{\min }}$, соответствующую анализируемому значению вектора s.
Шаг 5. По окончании перебора всех возможных значений векторов s, генерируемых на шаге 1, среди них выбирается оптимальный вариант sopt, которому соответствует минимальное значение потребной емкости среди всех значений Cmin, вычисленных на шаге 4.
В результате выполнения вышеперечисленных шагов метода находим оптимальное значение вектора s = sopt, определяющее, согласно (2.1), оптимальный закон управления u(t)opt и, согласно (1.5), (2.2), соответствующее оптимальное значение емкости источника Cmin, при этом оптимальные начальные потенциалы ресурса в секциях источника одинаковы и равны максимально допустимому значению pmax, т.е. pi(0) = pmax.
Основным фактором, от которого зависит точность решения рассматриваемой задачи, является значение Δt. Уменьшение Δt повышает точность решения. Однако соответствующее увеличение числа дискрет N (Δt = T/N) вызывает значительный рост вычислительных затрат. Поэтому для определения значения Δt, обеспечивающего приемлемый компромисс между точностью решения и трудоемкостью его поиска, разумно вначале найти решение для небольшого значения N. Затем следует увеличивать N и сравнивать получаемые решения по значению показателя качества (1.5). Увеличение N можно прекратить, когда очередное решение незначительно отличается от предшествующего. Разность решений по показателю (1.5), полученных с шагом дискретизации Δt и Δt/2, можно принять в качестве приближенной оценки погрешности решения, полученного с шагом Δt/2.
2.2. Расширение метода. Изложенный выше метод предполагает, что число секций источника n задано. Однако его можно распространить на более общий случай, когда число секций подлежит определению. В таком случае представляется рациональным последовательно увеличивать число секций источника с единицы до значения, когда дальнейшее увеличение их числа не приводит к достаточно значимому уменьшению потребной емкости источника. Таким образом достигается разумный компромисс между усложнением конструкции источника и снижением его емкости. Кроме того, следует изначально учитывать, что если исходные данные задачи соответствуют условиям утверждения 3 (см. Приложение), то никакое увеличение значения n не позволяет снизить потребную емкость источника.
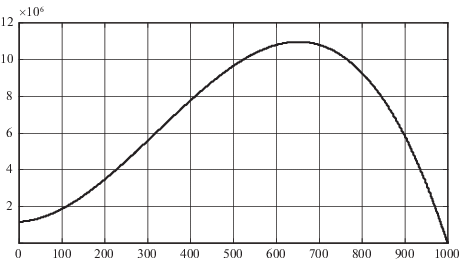
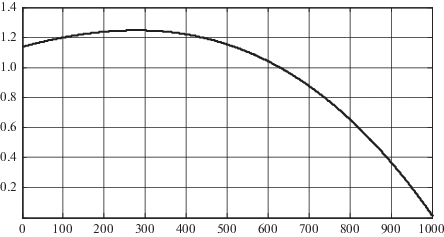
3. Пример. Рассмотрим реализацию предлагаемого метода применительно к задаче управления секционированным газобаллонным источником азота, обеспечивающим реализацию технологического процесса, который требует подачи азота в соответствии с программой потребления (рис. 1, 2). Настоящая программа для каждого момента времени указывает потребный секундный массовый расход g*(t) и потребное давление p*(t) в выходной магистрали источника газа (единицы измерения физических величин, представленных на графиках, соответствуют системе СИ). Максимально допустимое давление газа, запасаемого в источнике pmax = 150 × 105 Па.
В случае, когда источник состоит из одной секции (n = 1), множество возможных значений вектора s состоит из единственного вектора, все компоненты которого – единицы. Следовательно, производить перебор значений вектора s не требуется. Предложенный метод в данном случае сводится к следующим действиям: на этапе 1 всем компонентам вектора s присваиваем значение 1; на этапе 2 находим G1(t) ≡ g*(t), P1(t) ≡ p*(t), ∀t ∈ [0, T]; на этапе 3 по формулам (2.2) определяем минимально необходимое значение емкости источника: C = 1.960 × 10–4 м3кг/Дж. Начальное давление p1(0) = pmax = 150 × 105 Па. Емкость Ci в формуле (1.2) связана с параметрами источника газа известной [14] зависимостью Ci = Wi/(RTg), где Wi – объем i-й секции, R – газовая постоянная, Tg – температура газа. Указанная зависимость позволяет рассчитать объем баллонов, составляющих секцию источника: Wi = CiRTg. В данном примере R = 297 Дж/(кг ⋅ K), Tg = 300 K, W = 17.46 м3.
Процесс изменения давления p(t) в выходной магистрали односекционного источника, соответствующий найденному оптимальному значению его емкости, представлен на рис. 3. Свидетельством оптимальности выбранной емкости источника является наличие точки касания графиков функций p*(t) и p(t), указывающее на то, что ограничение (1.1) выполняется, но стало активным (в один из моментов времени выполняется как равенство) и, следовательно, дальнейшее уменьшение емкости источника невозможно.
Рис. 3.
График потребного давления p*(t) (штрихпунктирная линия) и давления p(t) (сплошная линия) в выходной магистрали односекционного источника

Проверка условия утверждения 3 показывает, что увеличение числа секций источника может снизить его потребную емкость.
В случаях, когда источник состоит из нескольких секций, согласно предложенному методу, интервал времени от 0 до 1000 с, на котором задана программа потребления (рис. 1, 2), разбиваем на N частей. Примем, что разбиение осуществляется на 10 равных частей (N = 10). Далее осуществляем генерацию и анализ векторов s с учетом рекомендаций, изложенных в описании рассмотренного метода.
Для двухсекционного источника (n = 2), действуя в соответствии с разработанным методом, находим оптимальное значение вектора s = (1 1 1 1 2 2 2 2 2 1), определяющее, согласно (2.1), оптимальный закон управления u(t) и, согласно (1.5), (2.2), соответствующее оптимальное (минимально необходимое) значение емкости источника C = 1.46 × 10–4 м3кг/Дж. Начальные давления в секциях источника одинаковы и равны максимально допустимому значению pmax, т.е. pi(0) = = pmax = 150 × 105 Па (это относится также к нижеследующим примерам независимо от числа секций).
Процесс изменения давления p(t) в выходной магистрали двухсекционного источника, соответствующий найденному оптимальному управлению, представлен на рис. 4.
Рис. 4.
График потребного давления p*(t) (штрихпунктирная линия) и давления p(t) (сплошная линия) в выходной магистрали двухсекционного источника

Анализируя полученное оптимальное значение вектора s, видим, что закон управления предполагает подключение к выходной магистрали источника вначале (на первых четырех дискретах времени) первой секции, затем (на следующих пяти дискретах времени) второй секции и вновь подключение первой секции источника на заключительной дискрете времени.
Сравнивая найденное минимально необходимое значение емкости односекционного и двухсекционного источника, видим, что оптимальный закон управления двухсекционным источником позволяет сократить потребную емкость источника на 25% в сравнении с односекционным вариантом.
Соприкосновение графиков функций p*(t) и p(t), как уже отмечалось в комментарии к рис. 3, указывает на то, что ограничение (1.1) стало активным и не допускает дальнейшего уменьшения емкости источника.
Увеличение числа N (т.е. увеличение размерности вектора s и соответствующее уменьшение дискреты времени Δt в аппроксимации функции управления) относительно ранее принятого значения N = 10 в рассматриваемом примере не приводит к существенному изменению получаемых результатов. Так, для N = 20 получаем значение показателя качества (1.5) C = 1.45 × × 10–4 м3 кг/Дж, что менее чем на 1%, отличается от значения, найденного в случае N = 10. Структура закона управления при этом также существенно не меняется. Для N = 20 получаем оптимальное значение вектора s = (1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 1), которое аналогично ранее найденному для N = 10 значению s = (1 1 1 1 2 2 2 2 2 1) предполагает использование первой секции, затем второй и доиспользование первой секции на заключительной дискрете времени. Увеличение числа N приводит к существенному росту трудоемкости решаемой задачи. Поэтому значение N = 10 в рассматриваемом примере является рациональным выбором, реализующим разумный компромисс между трудоемкостью и точностью получаемого решения.
В соответствии с предложенным расширением метода в ходе последовательного увеличения числа секций источника n с единицы до восьми найдены представленные в таблице оптимальные значения вектора s и емкости источника C для каждого фиксированного значения n. В колонке таблицы с заголовком Cn/Cn – 1 представлено отношение емкости источника C, указанной в данной строке, к емкости, указанной в предыдущей строке, а в колонке с заголовком Cn/Cn = 1 – отношение емкости источника C, указанной в данной строке, к оптимальной емкости односекционного источника.
Таблица.
Оптимальные значения вектора s и емкости C для фиксированных значений n
| n | s | C, м3 кг/Дж | Cn/Cn– 1 | Cn/Cn= 1 |
|---|---|---|---|---|
| 1 | 1 | 1.960 × 10–4 | 1.000 | |
| 2 | 1 1 1 1 2 2 2 2 2 1 | 1.464 × 10–4 | 0.7469 | 0.747 |
| 3 | 1 1 2 2 3 3 3 3 3 2 | 1.341 × 10–4 | 0.9160 | 0.684 |
| 4 | 1 1 2 2 3 4 4 4 4 2 | 1.298 × 10–4 | 0.9679 | 0.662 |
| 5 | 1 1 2 3 4 5 5 5 5 3 | 1.258 × 10–4 | 0.9692 | 0.642 |
| 6 | 1 2 3 4 5 6 6 6 6 4 | 1.245 × 10–4 | 0.9897 | 0.635 |
| 7 | 1 2 3 4 5 6 6 6 6 7 | 1.259 × 10–4 | 1.0112 | 0.642 |
| 8 | 1 2 3 4 5 6 7 6 7 8 | 1.296 × 10–4 | 1.0294 | 0.661 |
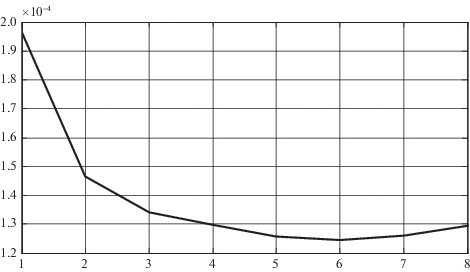
Из таблицы следует, что потребная емкость источника C монотонно уменьшается при возрастании значения n от 1 до 6, а затем при увеличении n монотонно увеличивается.
На рис. 5 представлен график зависимости минимально достаточной емкости источника от числа его секций C(n).
Анализ графика зависимости C(n) показывает, что потребная емкость источника интенсивно уменьшается при увеличении числа его секций в диапазоне от 1 до 5, после чего увеличение их числа не приводит к достаточно значимому уменьшению потребной емкости источника. Более того, увеличение числа секций сверх 6 приводит к увеличению потребной емкости источника. Таким образом, минимальное значение потребной емкости источника достигается при n = 6. Процесс изменения давления p(t) в выходной магистрали шести секционного источника, соответствующий оптимальному управлению, представлен на рис. 6.
Рис. 6.
График потребного давления p*(t) (штрихпунктирная линия) и давления p(t) (сплошная линия) в выходной магистрали шестисекционного источника
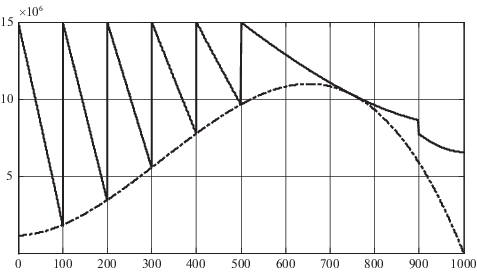
На графике рис. 6 видим, что найденный оптимальный закон управления предполагает подключение к выходной магистрали накопителя вначале на каждой очередной дискрете времени (с первой по шестую) новой секции источника, затем (с шестой дискреты времени до девятой включительно) используется шестая секция, а на заключительной (десятой) дискрете времени вновь используется четвертая.
Сравнивая минимально необходимое значение емкости односекционного и шестисекционного источника видим, что оптимальный закон управления шестисекционным источником позволяет сократить потребную емкость на 36.5% в сравнении с односекционным вариантом.
Заключение. Таким образом, разработан метод поиска оптимального закона управления источниками ограниченного ресурса. К источникам рассматриваемого класса относятся, в частности, конденсаторные источники электроэнергии, баллонные источники газа, гидронапорные башни. Предполагается, что источник разделен на несколько секций. Искомый закон управления минимизирует потребную емкость источника на основе рационального отключения и подключения секций источника к его выходной магистрали в рассчитанные моменты времени в соответствии с известной программой потребления ресурса. Сокращение потребной емкости источника достигается в результате более полного опорожнения части его секций на временных интервалах с низким уровнем запрашиваемого потенциала и сбережения высокого потенциала для предстоящих временных интервалов только в некоторой части секций источника.
Осуществлена формализация решаемой задачи. Предложенный метод ее решения основан на задании конечного набора моментов времени, в которые может происходить смена значений функции управления. Таким образом, производится аппроксимация искомого закона управления функцией, меняющей значения в некоторые моменты времени из заданного конечного набора. При этом на остальные переменные указанная дискретизация времени не распространяется. В результате задача сводится к анализу конечного множества вариантов управлений. Значительная часть вариантов управлений исключается из последующего анализа на основе применения логического правила, предложенного и обоснованного в данной статье. Для очередного анализируемого варианта управления по найденным простым аналитическим зависимостям вычисляются оптимальные значения емкости секций и суммарная потребная емкость источника. Простые в вычислительном плане зависимости и правила позволяют быстро анализировать большой объем возможных вариантов управлений. В итоге среди всех возможных вариантов управлений выявляется оптимальный вариант, которому соответствует минимальная потребная емкость источника.
Список литературы
Беллман Р. Динамическое программирование. М.: Изд-во иностр. лит., 1960. 400 с.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969. 384 с.
Моисеев Н.Н. Численные методы в теории оптимальных систем. М.: Наука, 1971. 424 с.
Гилл Ф., Мюррэй У., Райт М. Практическая оптимизация. М.: Мир, 1985. 509 с.
Вдовин П.М., Зотов И.А., Костенко В.А., Плакунов А.В., Смелянский Р.Л. Сравнение различных подходов к распределению ресурсов в центрах обработки данных // Изв. РАН. ТиСУ. 2014. № 5. С. 71–81.
Топорков В.В. Оптимизация распределения ресурсов в системах жесткого реального времени // Изв. РАН. ТиСУ. 2004. № 3. С. 61–71.
Струченков В.И. Новые алгоритмы оптимального распределения ресурса // Прикладная дискретная математика. 2010. № 4 (10). С. 73–78.
Шевченко Г.В. Численный метод решения задачи минимизации расхода ресурсов для линейных систем с постоянным запаздыванием // АиТ. 2014. № 10. С. 25–38.
Шевченко Г.В. Метод нахождения оптимального по минимуму расхода ресурсов управления для объектов специального вида // Автометрия. 2006. Т. 42. № 2. С. 49–67.
Рапопорт Э.О. Об оптимальном управлении при распределении неделимого ресурса // Дискретный анализ и исследование операций. 2009. Т. 16. № 1 (85). С. 64–79.
Kia S.S. Distributed Optimal In-network Resource Allocation Algorithm Design Via a Control Theoretic Approach // Systems & Control Letters. 2017. V. 107. P. 49–57.
Guerin F., Lefebvre D., Loisel V. Supervisory Control Design for Systems of Multiple Sources of Energy // Control Engineering Practice. 2012. V. 20. Iss. 12. P. 1310–1324.
Castelletti A., Pianosi F., Soncini-Sessa R. Integration, Participation and Optimal Control in Water Resources Planning and Management // Applied Mathematics and Computation. 2008. V. 206. Iss. 1. P. 21–33.
Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. М.: Физматлит, 2014. 544 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления