Известия РАН. Теория и системы управления, 2020, № 2, стр. 64-74
ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ МНОГОКОМПОНЕНТНЫХ ХИМИЧЕСКИХ СИСТЕМ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ ИСХОДНЫХ ДАННЫХ
О. Г. Кантор *
ФГБОУ ВО “Уфимский государственный нефтяной технический университет”
г. Уфа, Россия
* E-mail: o_kantor@mail.ru
Поступила в редакцию 19.11.2019
После доработки 20.11.2019
Принята к публикации 25.11.2019
Аннотация
Представлен метод идентификации моделей заданной спецификации, основанный на использовании предельно допустимых оценок искомых параметров, обеспечивающий проведение параметрической идентификации моделей в случае, когда априорная информация об изучаемой системе характеризуется малым числом наблюдений и не позволяет пренебречь фактором ее неопределенности. Осуществлена его апробация применительно к задаче количественного анализа многокомпонентных фуллеренсодержащих смесей, проводимого с использованием метода Фирордта.
0. Введение. Современный уровень развития информационных технологий обусловил использование математического моделирования в качестве основного метода исследования сложных химических систем как для изучения их характеристик, так и в целях разработки и обоснования алгоритмов управления протекающими в них превращениями. Одно из направлений совершенствования методов управления химическими процессами связано с планированием экспериментов, которое призвано повысить обоснованность и достоверность получаемых результатов. В частности, высокий уровень сложности химических систем требует тщательного планирования экспериментов, нацеленных на получение оптимальных или заранее заданных комбинаций веществ. В случае, если химические системы образованы изомерными структурами, их компоненты могут быть близки по строению, но принципиально отличаться по своим свойствам, в силу чего присутствие некоторых из них может быть крайне нежелательным. В этой связи для смесей с известным составом важным этапом исследования является проведение количественного анализа. Один из наиболее эффективных подходов, отвечающих целям такого анализа, основан на использовании данных ультрафиолетовой спектроскопии.
В полной мере сказанное относится к химическим системам, содержащим продукты радикальной полимеризации мономеров в присутствии фуллерена, для которых характерной является сложность проведения количественного анализа в силу присутствия большого набора соединений [1]. Для количественного анализа таких многокомпонентных смесей, как правило, применяются методы ультрафиолетовой спектроскопии в сочетании с последующей обработкой полученных данных на основе использования специфических методов, в число которых входит метод Фирордта [2]. Условия его применимости определяются двумя положениями, в соответствии с которыми для каждого компонента смеси должен выполняться закон Бугера–Ламберта–Бера, а для смеси в целом – принцип аддитивности.
Это позволяет проводить количественный анализ многокомпонентных смесей на основе системы уравнений Фирордта:
(0.1)
$\begin{gathered} {{D}^{{{{\lambda }_{1}}}}} = \varepsilon _{1}^{{{{\lambda }_{1}}}}{{с}_{1}}l + \ldots + \varepsilon _{m}^{{{{\lambda }_{1}}}}{{с}_{m}}l \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\ {{D}^{{{{\lambda }_{m}}}}} = \varepsilon _{1}^{{{{\lambda }_{m}}}}{{с}_{1}}l + \ldots + \varepsilon _{m}^{{{{\lambda }_{m}}}}{{с}_{m}}l, \\ \end{gathered} $Если ввести обозначения ${{b}_{i}} = {{D}^{{{{\lambda }_{i}}}}}$, ${{x}_{j}} = {{c}_{j}}$, ${{a}_{{ij}}} = \varepsilon _{j}^{{{{\lambda }_{i}}}}l$, $А = \left( {{{a}_{{ij}}}} \right)$, $В = \left( {{{b}_{i}}} \right)$, $\bar {x} = \left( {{{x}_{j}}} \right)$, $i,j = \overline {1,m} $, то система (0.1) запишется в виде
Известно, что молярные коэффициенты поглощения являются характеристиками компонентов смеси и не зависят от их концентраций. Оптические плотности, напротив, изменяются в зависимости от концентраций cj. Это означает, что для смесей с одинаковым компонентным составом при формировании системы (0.2) матрица А не изменится, а векторы B будут отличаться. Поэтому, зная матрицу А и измеряя оптические плотности для произвольных смесей, на основании модели (0.2) могут быть получены количественные оценки концентраций их компонентов. Это позволяет планировать и реализовывать эксперименты, нацеленные на получение смесей с определенными характеристиками, что в силу высокой востребованности производных фуллерена представляет практический интерес. Определение элементов матрицы А традиционно осуществляется на основе использования модельных смесей с известным количественным составом.
Величины ${{\lambda }_{i}}$, ${{D}^{{{{\lambda }_{i}}}}}$ и $\varepsilon _{j}^{{{{\lambda }_{i}}}}$ находятся по результатам спектрофотометрических исследований. Причем относительно погрешностей измерения длин волн и оптических плотностей достоверно известно, что они пренебрежимо малы, в то время как погрешности молярных коэффициентов поглощения могут быть существенными в силу многоэтапности процедуры их расчета. В частности, они могут приводить к кажущимся отклонениям от закона Бугера–Ламберта–Бера [2]. Поэтому задача определения достоверных значений компонентов коэффициентной матрицы системы (0.2) в рамках количественного анализа многокомпонентных фуллеренсодержащих смесей является актуальной.
1. Постановка задачи. Задача параметрической идентификации явно заданных функциональных зависимостей известной спецификации состоит в определении вектора $\bar {a}{\text{*}}$, который должен обеспечивать в некотором смысле лучшее соответствие результатов наблюдений yt и значений ${{\hat {y}}_{t}}$, рассчитанных согласно модели:
где $y \in R$, $\bar {a} \in {{R}^{p}}$ – вектор параметров, подлежащих определению, $\bar {x} \in {{R}^{n}}$ – вектор переменных модели, ${{\hat {y}}_{t}} = f\left( {\bar {a},{{{\bar {x}}}_{t}}} \right)$, ${{\bar {x}}_{t}}$ – исходные данные, t – порядковый номер наблюдений, $t = \overline {1,m} $, m – общее число наблюдений.Как правило, степень подобного соответствия оценивается с помощью критерия, для которого набор $\bar {a}{\text{*}}$ обеспечивает минимальное значение. В этой связи совершенно логичным является выбор в качестве такого критерия выпуклой по оцениваемым параметрам функции, что в хорошем или плохом приближении гарантирует существование решения задачи параметрической идентификации.
В случае достаточно большого массива исходных данных определение вектора $\bar {a}{\text{*}}$ целесообразно осуществлять методами математической статистики, представляющими на сегодняшний день мощный и наиболее распространенный инструмент прикладного анализа наблюдений [2–6]. Однако далеко не всегда на практике предоставляется возможность получения экспериментальных данных в требуемом количестве: в некоторых случаях это объясняется сложностью проведения соответствующих опытов, а в некоторых – принципиальной невозможностью. Помимо этого необходимо признать, что любые экспериментальные данные априори не являются абсолютно точными, так как содержат в себе некоторые погрешности, связанные с их измерениями. На данных большого объема такие погрешности могут быть отслежены, а их последствия нивелированы. В случае ограниченного количества исходных данных погрешности в них могут привести к существенному искажению решения. Неточность и малое число исходных данных формируют условиях неопределенности в задачах параметрической идентификации и обусловливают необходимость применения специальных методов для их решения.
По своей сути задачи параметрической идентификации являются коэффициентными обратными задачами [7], так как в них определению подлежат параметры, задающие точный вид функции, на основании некоторой информации о решении. Относительно обратных задач известно, что они, как правило, являются некорректными [8, 9], в силу чего решение $\bar {a}{\text{*}}$ может не быть единственным и может не удовлетворять условию устойчивости.
Применительно к задачам параметрической идентификации модель можно считать обладающей свойством устойчивости, если малые изменения каких-либо ее параметров (одного или нескольких), приводящие к получению пусть похожей, но все-таки новой модели, сохраняют адекватность и приемлемую точность описания исходных данных. Помимо этого оптимальный набор значений параметров $\bar {a}{\text{*}}$ должен обеспечивать устойчивость и самих решений ${{\hat {y}}_{t}}$.
Большое значение для решения обратных задач имело введенное понятие приближенного решения некорректных задач [8], что позволило перенести фокус внимания с доказательства существования решения (в практических задачах это является самостоятельной, крайне сложной, а иногда и неразрешимой задачей) на поиск устойчивых методов приближенного решения [10, 11]. Устойчивость математических методов означает возможность их применения при незначительных изменениях параметров модели, диапазонов значений переменных или начальных данных. В некоторых работах свойство устойчивости модели рассматривается как необходимое условие ее адекватности исследуемому объекту [12].
В настоящей работе применительно к задачам параметрической идентификации исследуются вопросы оценки устойчивости решений и степени неопределенности исходных данных.
2. Методы и модели. Основу представленного в работе метода параметрической идентификации составляют идеи, высказанные Л.В. Канторовичем [13], относительно целесообразности определению областей неопределенностей параметров моделей, каждый элемент которых обеспечивает достижение требуемых характеристик [14]. Ключевой посыл при этом состоит в том, чтобы по каждому оцениваемому параметру определялись интервалы его приемлемых значений с учетом всей имеющейся в распоряжении исследователя информации. Развитие данного подхода нашло отражение как в исследованиях, посвященных математической обработке экспериментальных данных в рамках отдельных научных направлениях, в частности при решении обратных задач химической кинетики [15–19], так и при разработке нового направления прикладной математики – интервального анализа [20, 21].
Будем полагать, что все требования к переменным модели формализованы в виде ограничений $G\left( {\bar {x},y} \right) \leqslant 0$. Так как все расчетные значения ${{\hat {y}}_{t}}$ зависят от параметров $\bar {a}$, введем в рассмотрение множество $\Im = \Im \left( {\bar {a}} \right) = \left\{ {\left. {{{{\hat {y}}}_{t}}} \right|G\left( {{{{\bar {x}}}_{t}},{{{\hat {y}}}_{t}}} \right) \leqslant 0} \right\}$. В качестве критерия для оценки степени соответствия расчетных и исходных значений переменной y выберем чебышевский радиус, в соответствии с которым искомые параметры должны обеспечивать минимальное значение ошибки в наихудшем случае. Расчет ошибок будем производить с использованием нормы ${{\left\| \circ \right\|}_{\infty }}$. Также будем считать, что для каждого из параметров ai, $i = \overline {1,p} $, известны диапазоны их приближенных значений ${{\underline a }_{i}} \leqslant {{a}_{i}} \leqslant {{\bar {a}}_{i}}$. Это позволяет ввести множество начальных приближений Λ0 = $\{ \left. {{{a}_{i}}} \right|{{\underline a }_{i}} \leqslant {{a}_{i}} \leqslant {{\bar {a}}_{i}}$, $i = \overline {1,p} \} $.
В сделанных предположениях выражение для чебышевского радиуса идентифицируемой зависимости (0.1) запишется в виде
(2.1)
$\xi * = \mathop {{\text{min}}}\limits_{\bar {a} \in {{\Lambda }^{0}}} \mathop {{\text{max}}}\limits_{\Im ,\;t = \overline {1,m} } \left| {{{{\hat {y}}}_{t}} - {{y}_{t}}} \right|.$Теорема 1. Если (1.1) – непрерывная на множестве $\Im $ функция по параметрам $\bar {a}$, то решение задачи (2.1) существует.
Доказательство. В силу того, что зависимость $y = f\left( {\bar {a},\bar {x}} \right)$ на множестве $\Im $ является непрерывной функцией по параметрам $\bar {a}$, функция $\left| {{{{\hat {y}}}_{t}} - {{y}_{t}}} \right|$ также будет непрерывной по параметрам $\bar {a}$ $\forall $$t = \overline {1,m} $.
Максимум непрерывных функций $\mathop {{\text{max}}}\limits_{t = \overline {1,m} } \left| {{{{\hat {y}}}_{t}} - {{y}_{t}}} \right|$ есть функция непрерывная. Поэтому для нее на компактном множестве Λ0 существует минимум (1.1) [22].
Далее будем считать функцию (1.1) непрерывной по каждому из своих аргументов. Известно, что решение задачи (2.1) может быть неединственным [23]. Обозначим через Λ* область, образованную всевозможными наборами значений параметров $\bar {a}$, обеспечивающих справедливость (2.1). Очевидно, что область Λ* может иметь нетривиальную структуру, однако ее границы совпадают с границами аппроксимирующего множества, имеющего форму многомерного параллелепипеда со сторонами, параллельными осям координат: $\bar {\Lambda }* = \{ \left. {{{a}_{i}}} \right|\underline a _{i}^{*} \leqslant {{a}_{i}} \leqslant \bar {a}_{i}^{*},\;i = \overline {1,p} \} $.
Назначение множества $\bar {\Lambda }{\text{*}}$ состоит в том, чтобы в дальнейшем на его элементах организовать вычислительный эксперимент по уточнению границ области Λ* с последующим определением лучшего набора значений параметров $\bar {a}{\text{*}}$ и анализом устойчивости полученного решения.
Определение 1. Будем называть отрезки $[\underline a _{i}^{*},\bar {a}_{i}^{*}]$, $i = \overline {1,p} $, значений параметров, определяющих множество $\bar {\Lambda }{\text{*}}$, интервалами неопределенности, а их границы – предельно допустимыми оценками соответствующих параметров.
В контексте сказанного выше расчет предельно допустимых оценок параметров предлагается осуществлять на основе модели:
Очевидно, что чем меньше множество $\bar {\Lambda }{\text{*}}$, тем меньше разнообразие вариантов для выбора окончательного вида вектора параметров $\bar {a}$, соответственно меньше и неопределенность при осуществлении такого выбора. Поэтому в качестве меры неопределенности множества потенциально приемлемых для идентификации модели (1.1) векторов будем рассматривать диаметр:
Заметим, что ${\text{diam}}\,\bar {\Lambda }{\text{*}} = {\text{diam}}\,\Lambda {\text{*}}$.
Введем обозначение для множества исходных данных: $\aleph = \{ \left( {{{{\bar {x}}}_{t}},{{y}_{t}}} \right),t = \overline {1,m} \} $.
Определение 2. Абсолютным δ-приближением множества $\aleph $ $\left( {\delta \geqslant 0} \right)$ будем называть множество ${{\aleph }^{\delta }} = \{ (\bar {x}_{t}^{\delta },y_{t}^{\delta }),t = \overline {1,m} \} $, если $\forall \,t = \overline {1,m} $ $({\text{||}}\bar {x}_{t}^{\delta } - {{\bar {x}}_{t}}{\text{|}}{{{\text{|}}}_{\infty }} \leqslant \delta )$ $ \wedge $ $({\text{|}}y_{t}^{\delta } - {{y}_{t}}{\text{|}} \leqslant \delta )$, и $(\exists {{t}_{1}} = \overline {1,m} :{\text{||}}\bar {x}_{{{{t}_{1}}}}^{\delta } - {{\bar {x}}_{{{{t}_{1}}}}}{\text{|}}{{{\text{|}}}_{\infty }}$ = = δ) $ \vee $ $(\exists {{t}_{2}} = \overline {1,m} :{\text{|}}y_{{{{t}_{2}}}}^{\delta } - {{y}_{{{{t}_{2}}}}}{\text{|}} = \delta )$.
Принятие предположения о наличии априорной неопределенности в исходных данных означает, что их истинные значения нам неизвестны, но будем полагать, что они принадлежат множеству ${{\aleph }^{\delta }}$ при некотором $\delta \geqslant 0$. (Подобная информация может быть доступна, например, на основании данных о погрешности используемых для измерения приборов.)
Недостаток абсолютного δ-приближения множества $\aleph $ состоит в том, что в случае его использования не учитывается дифференциация вклада компонентов исходных данных в результирующие показатели, характеризующие качество модели (1.1). В этой связи введем следующее определение.
Определение 3. Относительным $\delta $-приближением множества $\aleph $ $\left( {\delta \geqslant 0} \right)$ будем называть множество ${{\aleph }^{{ \propto \delta }}} = \{ (\bar {x}_{t}^{\delta },y_{t}^{\delta }),\bar {x}_{t}^{\delta } = \delta \bar {x}_{t}^{{}},y_{t}^{\delta } = \delta y_{t}^{{}},t = \overline {1,m} \} $, если $\forall \,t = \overline {1,m} $ $({\text{||}}\bar {x}_{t}^{\delta } - {{\bar {x}}_{t}}{\text{|}}{{{\text{|}}}_{\infty }} \leqslant \left| {1 - \delta } \right|{\text{||}}\bar {x}_{t}^{{}}{\text{|}}{{{\text{|}}}_{\infty }})$ $ \wedge $ $ \wedge $ $({\text{|}}y_{t}^{\delta } - {{y}_{t}}{\text{|}}$ ≤ $\left| {1 - \delta } \right|{{\left\| {{{y}_{t}}} \right\|}_{\infty }})$, и $(\exists {{t}_{1}} = \overline {1,m} \,:\;{\text{||}}\bar {x}_{{{{t}_{1}}}}^{\delta } - {{\bar {x}}_{{{{t}_{1}}}}}{\text{|}}{{{\text{|}}}_{\infty }} = \left| {1 - \delta } \right|{\text{||}}\bar {x}_{{{{t}_{1}}}}^{{}}{\text{|}}{{{\text{|}}}_{\infty }})$ $ \vee $ $(\exists {{t}_{2}} = \overline {1,m} \,:\;{\text{|}}y_{{{{t}_{2}}}}^{\delta } - {{y}_{{{{t}_{2}}}}}{\text{|}} = \left| {1 - \delta } \right|{{\left\| {{{y}_{{{{t}_{2}}}}}} \right\|}_{\infty }})$.
Общепринятый подход к анализу влияния неопределенности исходных данных состоит в том, чтобы оценить, в какой мере их возмущения сказываются на изменении результатов моделирования (будем называть его анализом прямого влияния неопределенности исходных данных). Реализация данного подхода с учетом представленного выше метода параметрической идентификации может быть сведена к следующей процедуре.
Шаг 1. Найти $\underline \xi {\text{*}} = \mathop {{\text{min}}}\limits_{\left( {{{{\bar {x}}}_{t}},{{y}_{t}}} \right) \in {{\aleph }^{\delta }}} \xi {\text{*}}$, $\bar {\xi }{\text{*}} = \mathop {{\text{min}}}\limits_{\left( {{{{\bar {x}}}_{t}},{{y}_{t}}} \right) \in {{\aleph }^{\delta }}} \xi {\text{*}}$, где $\xi {\text{*}}$ – чебышевский радиус, рассчитываемый на основе модели (2.1).
Шаг 2. Найти $\underline {\underline a } _{i}^{*} = \mathop {{\text{min}}}\limits_{\left( {{{{\bar {x}}}_{t}},{{y}_{t}}} \right) \in {{\aleph }^{\delta }}} \underline a _{i}^{*}$, $\bar {\bar {a}}_{i}^{*} = \mathop {{\text{min}}}\limits_{\left( {{{{\bar {x}}}_{t}},{{y}_{t}}} \right) \in {{\aleph }^{\delta }}} \bar {a}_{i}^{*}$, $i = \overline {1,p} $, где $\underline a _{i}^{*}$ и $\bar {a}_{i}^{*}$ определяются на основе моделей (2.2).
Шаг 3. Оценить степень неопределенности интервалов, границы которых рассчитаны на шагах 1 и 2, на основе анализа их длин: ${{\Delta }_{{\xi *}}} = \bar {\xi }{\text{*}} - \underline \xi {\text{*}}$, ${{\Delta }_{{a_{i}^{*}}}} = \bar {\bar {a}}_{i}^{*} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} } _{i}^{*}$, $i = \overline {1,p} $.
Шаг 4. Если ${{\Delta }_{{\xi {\text{*}}}}} \leqslant \Delta _{{\xi {\text{*}}}}^{0}$и ${{\Delta }_{{a_{i}^{*}}}} \leqslant \Delta _{{a_{i}^{*}}}^{0}$ $\forall \,i = \overline {1,p} $, где $\Delta _{ \circ }^{0}$ – пороговые значения для соответствующих величин, то неопределенность исходных данных считать приемлемой. Переход на шаг 6.
Шаг 5. Осуществить планирование и реализацию экспериментов, направленных на уточнение исходных данных. Переход на шаг 1.
Шаг 6. Конец.
Если же спецификация модели (1.1) обусловливает необходимость применения численных методов, то вместо шагов 1 и 2 следует использовать шаги 1а и 2а соответственно.
Шаг 1а. На множестве ${{\aleph }^{\delta }}$ ввести сетку ${{\bar {\aleph }}^{\delta }}$. В каждой узловой точке этой сетки решить задачи (2.1) и (2.2).
Шаг 2а. Сформировать интервалы неопределенности $[\underline \xi {\text{*}},\bar {\xi }{\text{*}}]$ и $[\underline {\underline a } _{i}^{*},\bar {\bar {a}}_{i}^{*}]$, $i = \overline {1,p} $, описывающие соответственно вариацию всех значений чебышевского радиуса и всех оцениваемых параметров, рассчитанных на шаге 1 ($\underline \xi * = \mathop {{\text{min}}}\limits_{{{{\bar {\aleph }}}^{\delta }}} \xi {\text{*}}$, $\bar {\xi }{\text{*}} = \mathop {{\text{min}}}\limits_{{{{\bar {\aleph }}}^{\delta }}} \xi {\text{*}}$, $\underline {\underline a } _{i}^{*} = \mathop {{\text{min}}}\limits_{{{{\bar {\aleph }}}^{\delta }}} \underline a _{i}^{*}$, $\bar {\bar {a}}_{i}^{*} = \mathop {{\text{min}}}\limits_{{{{\bar {\aleph }}}^{\delta }}} \bar {a}_{i}^{*}$, $i = \overline {1,p} $).
Аналогичным образом процедура анализа прямого влияния неопределенности исходных данных может быть сформулирована в случае использования множества относительных приближений исходных данных ${{\aleph }^{{ \propto \delta }}}$.
Очевидно, что при использовании численных методов анализ прямого влияния неопределенности исходных данных требует проведения вычислений, количество которых напрямую зависит от шага сетки ${{\bar {\aleph }}^{\delta }}$. Так, если шаг сетки на каждом из интервалов значений исходных данных, определяющих множество ${{\aleph }^{\delta }}$, будет равен 2, то с учетом размерности ${{\aleph }^{\delta }}$ количество подлежащих решению задач (2.1) составит ${{2}^{{\left( {n + 1} \right)m}}}$, а задач (2.2) – в 2p раз больше. Подобная вычислительная сложность ставит под сомнение эффективность такой процедуры.
В этой связи целесообразным может оказаться исследование влияния допустимой вариации абсолютной точности на предполагаемые изменения исходных данных.
3. Учет неопределенности исходных данных. Мерой абсолютной точности, согласно модели (2.1), является чебышевский радиус $\xi {\text{*}}$. Его допустимую вариацию зададим выражением $\lambda \xi {\text{*}}$, где $\lambda \in \left[ {0,1} \right)$ – заданный параметр. Соответствующие изменения исходных данных будем оценивать на основе анализа границ множества $\tilde {\aleph }{\text{*}}$, составленного из всех возмущенных исходных данных, обеспечивающих достижение улучшенного чебышевского радиуса.
В некотором смысле такой подход реализует процедуру, обратную той, которая осуществляется в рамках анализа прямого влияния неопределенности исходных данных, поэтому в дальнейшем, ссылаясь на него, будем использовать термин “анализ обусловленного обратного влияния неопределенности исходных данных”.
Само по себе множество $\tilde {\aleph }{\text{*}}$ может иметь сложную структуру, но его границы совпадают с аппроксимирующим множеством $\tilde {\aleph } = \{ (\bar {x}_{t}^{'},y_{t}^{'}),t = \overline {1,m} \} $: $\bar {x}_{t}^{'}$ = $\{ x_{{jt}}^{'}|x_{{jt}}^{'} = {{\gamma }_{j}}{{x}_{{jt}}},j = \overline {1,n} \} $, $y_{t}^{'} = {{\gamma }_{0}}{{y}_{t}}$ при некоторых значениях параметров ${{\gamma }_{j}} \geqslant 0$, $j = \overline {0,n} $.
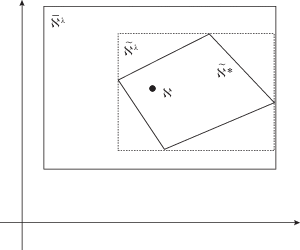
Таким образом, задача установления границ множества $\tilde {\aleph }{\text{*}}$ сводится к определению минимальных и максимальных значений параметров $\{ {{\gamma }_{j}},j = \overline {0,n} \} $. Их расчет будем проводить в два этапа: на первом определим границы вспомогательного множества ${{\tilde {\aleph }}^{\lambda }}$ (рисунок), а на втором – рассчитаем верхние и нижние оценки параметров γj (${{\bar {\gamma }}_{j}}$ и ${{\underline \gamma }_{j}}$ соответственно).
Смысл параметров γj состоит в том, что они показывают, во сколько раз должен быть изменен каждый элемент множества исходных данных (в меньшую и большую стороны) с тем, чтобы обеспечить заданное улучшенное приближение.
Для реализации первого этапа будем использовать модель:
Теорема 2. $\forall \,\lambda \in \left[ {0,1} \right)$ множество допустимых решений задачи (3.1) непусто.
Доказательство. Зафиксируем любой вектор ${{\bar {a}}^{0}} \in \Lambda {\text{*}}$ (например, тот, который получается при решении задачи (2.1)); ${{\gamma }_{j}}: = 1$, $j = \overline {1,n} $. Введем в рассмотрение функции ${\text{|}}{{\hat {y}}_{t}}({{\bar {a}}^{0}},{{\bar {x}}_{t}}) - {{\gamma }_{{0t}}}{{y}_{t}}{\text{|}}$, $\forall t = \overline {1,m} $, где ${{\gamma }_{{0t}}} \geqslant 0$ – числа. Каждая из функций ${\text{|}}{{\hat {y}}_{t}}({{\bar {a}}^{0}},{{\bar {x}}_{t}}) - {{\gamma }_{{0t}}}{{y}_{t}}{\text{|}}$ непрерывна по ${{\gamma }_{{0t}}}$ и в зависимости от этого параметра может принимать любое неотрицательное значение, в том числе $\exists \gamma _{{0t}}^{*}$: ${\text{|}}{{\hat {y}}_{t}}({{\bar {a}}^{0}},{{\bar {x}}_{t}}) - \gamma _{{0t}}^{*}{{y}_{t}}{\text{|}} = \lambda \xi {\text{*}}$. Далее
В сделанных предположениях ограничение $G(\bar {x}_{t}^{'},\hat {y}_{t}^{'}) \leqslant 0$ выполняется в силу того, что $\bar {x}_{t}^{'} = {{\bar {x}}_{t}}$, $\hat {y}_{t}^{'} = {{\hat {y}}_{t}}({{\bar {a}}^{0}},{{\bar {x}}_{t}}) \in \Im $.
Таким образом, множество допустимых решений задачи (3.1) непусто.
Доказанный факт позволяет организовывать численные эксперименты по определению оптимального значения $\zeta {\text{*}}$, которое характеризует минимальное из всех худших относительных отклонений от исходных данных.
По результатам решения задачи (3.1), по сути, будет определено относительное $\zeta {\text{*}}$-приближение исходных данных ${{\aleph }^{{ \propto \zeta *}}}$. Знание множества ${{\aleph }^{{ \propto \zeta {\text{*}}}}}$ позволяет сузить область поиска значений параметров ${{\bar {\gamma }}_{j}}$ и ${{\underline \gamma }_{j}}$ на втором этапе (см. модель (3.2)), что имеет существенное значение в том случае, если для реализации этого этапа необходимо будет применять численные методы:
Обозначим через ${{\left. {{{{\hat {y}}}_{t}}} \right|}_{{{{{\bar {\gamma }}}_{j}}}}}$ и ${{\left. {{{{\hat {y}}}_{t}}} \right|}_{{{{{\underline \gamma }}_{j}}}}}$ значения, рассчитанные, согласно модели (1.1), на каких-либо элементах множества ${{\aleph }^{{ \propto \zeta {\text{*}}}}}$, для которых ${{x}_{{jt}}} = {{\bar {\gamma }}_{j}}{{x}_{{jt}}}$ и ${{x}_{{jt}}} = {{\underline \gamma }_{j}}{{x}_{{jt}}}$ соответственно. Очевидно, что $\forall \,j = \overline {1,n} $ ${\text{|}}{{\left. {{{{\hat {y}}}_{t}}} \right|}_{{{{{\bar {\gamma }}}_{j}}}}} - {{\left. {{{{\hat {y}}}_{t}}} \right|}_{{{{{\underline \gamma }}_{j}}}}}{\text{|}} \leqslant 2\lambda \xi {\text{*}}$.
В силу
В контексте изложенного выше количественную оценку степени неопределенности исходных данных будем проводить на основе следующего определения.
Определение 4. Будем называть обусловленное обратное влияние неопределенности исходных данных устойчивым на уровне $\lambda \in \left[ {0,1} \right)$, если $\zeta {\text{*}}\mathop {{\text{max}}}\limits_t \left\{ {\left| {{{y}_{t}}} \right|,{{{\left\| {{{{\bar {x}}}_{t}}} \right\|}}_{\infty }}} \right\} \leqslant \lambda \xi {\text{*}}$, квазиустойчивым, если $\exists L$: $0 < {{L}^{0}} \leqslant L < 1$ и $L\zeta {\text{*}}\mathop {{\text{max}}}\limits_t \left\{ {\left| {{{y}_{t}}} \right|,{{{\left\| {{{{\bar {x}}}_{t}}} \right\|}}_{\infty }}} \right\} \leqslant \lambda \xi {\text{*}}$, и неустойчивым, если $\exists L$: $0 < L \leqslant {{L}^{0}}$ и $L\zeta {\text{*}}\mathop {{\text{max}}}\limits_t \left\{ {\left| {{{y}_{t}}} \right|,{{{\left\| {{{{\bar {x}}}_{t}}} \right\|}}_{\infty }}} \right\}$ ≤ λξ*.
Величина L0 – пороговый уровень, задаваемый исследователем. Определение параметра λ, устанавливающего пограничное состояние между устойчивостью и квазиустойчивостью обусловленного обратного влияния неопределенности исходных данных, может представлять самостоятельный интерес, в силу того, что с его помощью можно оценить целесообразность проведения экспериментов, направленных на уточнение исходных данных. Так, если при малых значениях λ обусловленное обратное влияние неопределенности исходных данных является только квазиустойчивым, для повышения точности модели (1.1) целесообразно проведение подобных экспериментов. Альтернатива данному способу улучшения точности состоит в рассмотрении другой спецификации модели (1.1). Если же при значимых с точки зрения исследователя вариациях параметра λ обусловленное обратное влияние неопределенности исходных данных остается устойчивым, то степень их неопределенности следует считать приемлемой.
4. Результаты расчетов и их обсуждение. Апробация представленного подхода проводилась для задачи количественного анализа 4 и 5 компонентных смесей фуллерена С60 и продуктов его замещения: моно- (I), ди- (II), три- (III) и тетра- (IV) присоединения диаллилмалонового эфира к фуллерену (табл. 1). Все модельные смеси были получены в лаборатории синтеза низкомолекулярных биорегуляторов УфИХ РАН [1].
Таблица 1.
Концентрации компонентов модельных смесей, ×10–6 моль/л
| Компоненты смеси | Номер компонента смеси, j | Векторы концентраций модельных смесей | ||
|---|---|---|---|---|
| ${{\bar {x}}^{1}}$ | ${{\bar {x}}^{2}}$ | ${{\bar {x}}^{3}}$ | ||
| С60 | 1 | – | – | 7.5 |
| I | 2 | 7.5 | 3.82 | 7.5 |
| II | 3 | 7.5 | 7.62 | 7.5 |
| III | 4 | 7.5 | 11.36 | 7.5 |
| IV | 5 | 7.5 | 14.97 | 7.5 |
По результатам обработки данных УФ-спектрометрии были определены компоненты $b_{i}^{k}$ векторов оптических плотностей ($k = \overline {1,3} $) и рассчитаны элементы ${{a}_{{ij}}}$ матрицы молярных коэффициентов поглощения A (табл. 2).
Таблица 2.
Экспериментальные значения коэффициентов системы (0.2)
| ${{\lambda }_{i}}$ | ${{a}_{{ij}}}$ | $b_{i}^{k}$ | ||||||
|---|---|---|---|---|---|---|---|---|
| соответствие компонентам смеси | обозначение векторов | |||||||
| С60 | I | II | III | IV | B1 | B2 | B3 | |
| 280 | 54 000 | 30 800 | 35 800 | 28 500 | 30 900 | 1.228 | 1.481 | 1.622 |
| 290 | 30 900 | 22 800 | 28 300 | 27 900 | 28 800 | 1.005 | 1.249 | 1.240 |
| 315 | 19 600 | 21 000 | 21 800 | 18 500 | 16 050 | 0.697 | 0.899 | 0.851 |
| 326 | 50 500 | 24 370 | 17 630 | 15 070 | 11 800 | 0.589 | 0.715 | 0.989 |
| 330 | 60 780 | 24 150 | 15 350 | 13 000 | 11 700 | – | – | 1.029 |
Обозначим через ${{A}_{r}}$ матрицу, получаемую вычеркиванием первого столбца и последней строки матрицы А.
Исходные данные таковы, что при подстановке их в модель (0.2) погрешности для $b_{i}^{k}$ варьируются в диапазонах 16.8–23.0%, 15.9–22.5% и 8.9–16.8% для 1-, 2- и 3-й модельных смесей соответственно:
Полученные несоответствия подтверждают представленный выше тезис о необходимости корректировки элементов коэффициентной матрицы А.
Введем в рассмотрение матрицу $А{\text{'}} = \left( {{{\gamma }_{{ij}}}{{a}_{{ij}}}} \right)$, где ${{\gamma }_{{ij}}}$, $i,j = \overline {1,m} $, – неотрицательные числа, которые характеризуют, во сколько раз должно быть изменено соответствующее экспериментальное значение ${{a}_{{ij}}}$. Так же, как и ранее, через $A_{r}^{'}$ будем обозначать матрицу, получаемую вычеркиванием первого столбца и последней строки матрицы $А{\text{'}}$. Коэффициенты ${{\gamma }_{{ij}}}$ по своей сути являются оценками погрешностей измерений соответствующих экспериментальных величин aij. Тогда поиск интервалов неопределенностей для aij в соответствии с моделью (2.2) может быть заменен поиском интервалов неопределенностей для ${{\gamma }_{{ij}}}$.
Зададим начальное приближение для параметров ${{\gamma }_{{ij}}}$, исходя из предположения о 40%-ной предполагаемой погрешности в элементах матрицы А: ${{\Lambda }^{0}} = \{ \left. {{{\gamma }_{{ij}}}} \right|0.6 \leqslant {{\gamma }_{{ij}}} \leqslant 1.4,\;i,j = \overline {1,5} \} $. Тогда модель (2.1) в контексте решаемой задачи примет вид:
Ее оптимальное решение: $\xi * = 2.34 \times {{10}^{{ - 9}}}$. Задачи для расчета предельно допустимых оценок параметров ${{\gamma }_{{ij}}}$ (аналог задач (2.2)) запишем как:
Результаты численных расчетов моделей (4.2) показали, что для параметров ${{\gamma }_{{11}}}$, ${{\gamma }_{{21}}}$, ${{\gamma }_{{31}}}$ и ${{\gamma }_{{41}}}$ интервалы неопределенности оказались стянутыми в одну точку, а для параметров ${{\gamma }_{{52}}}$, ${{\gamma }_{{53}}}$, ${{\gamma }_{{54}}}$ и ${{\gamma }_{{55}}}$ совпали с начальными приближениями (табл. 3).
Таблица 3.
Интервалы неопределенности $[\underline \gamma _{{ij}}^{*},\bar {\gamma }_{{ij}}^{*}]$
| i | j | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | [0.973, 0.973] | [1.333, 1.400] | [1.312, 1.400] | [1.175, 1.400] | [1.057, 1.197] |
| 2 | [1.014, 1.014] | [1.278, 1.400] | [1.250, 1.400] | [1.091, 1.400] | [0.909, 1.112] |
| 3 | [1.048, 1.048] | [0.755, 0.892] | [1.185, 1.400] | [1.272, 1.400] | [1.300, 1.400] |
| 4 | [1.056, 1.056] | [0.747, 0.904] | [1.071, 1.400] | [1.206, 1.400] | [1.232, 1.400] |
| 5 | [0.779, 1.400] | [0.600, 1.400] | [0.600, 1.400] | [0.600, 1.400] | [0.600, 1.400] |
В целях проведения анализа обусловленного обратного влияния неопределенности исходных значений коэффициентной матрицы было задано значение параметра $\lambda = 0.7$ и выписана следующая модель (аналог модели (3.1) для исследуемой задачи):
Оптимальное решение задачи (4.3) $\zeta {\text{*}} = 0.367$ означает, что заданная на уровне $\lambda \xi {\text{*}}$ = 1.64 × × 10–9 точность соответствия левых и правых частей системы (0.2) достигается за счет вариации значений элементов коэффициентной матрицы, максимальное значение из которых составляет 36.7% от исходного.
Таким образом, соотношение $L\zeta {\text{*}}{{\left\| А \right\|}_{\infty }} \leqslant 0.7\xi {\text{*}}$ будет выполняться при $0 < L \leqslant 7.34 \times {{10}^{{ - 14}}}$, из чего следует (в силу определения 4), что обусловленное обратное влияние неопределенности исходных значений коэффициентной матрицы даже с учетом порядка ее элементов является неустойчивым.
Аналогичным образом может быть осуществлен анализ обусловленного обратного влияния неопределенности исходных значений концентраций компонентов модельных смесей. Для этого при $\lambda = 0.7$ выпишем модель:
(4.4)
${{\underline \gamma }_{{ij}}} \leqslant {{\gamma }_{{ij}}} \leqslant {{\bar {\gamma }}_{{ij}}},\quad i,j = \overline {1,5} ,$Получим $\varsigma * = 1.277$ × 10–8$ \Rightarrow $ $\varsigma {\text{*}}\mathop {{\text{max}}}\limits_{k = \overline {1,3} } \{ {\text{||}}{{\bar {x}}^{k}}{\text{|}}{{{\text{|}}}_{\infty }}\} = 1.91 \times {{10}^{{ - 13}}} \leqslant 0.7\xi {\text{*}} = 1.64$ × 10–9. Согласно определению 4, обусловленное обратное влияние неопределенности исходных значений концентраций компонентов модельных смесей является устойчивым, а следовательно, возможные погрешности при вычислении концентраций не оказывают значимого влияния на точность модели (0.2).
Исследование при том же значении параметра $\lambda $ обусловленного обратного влияния неопределенности значений оптических плотностей, рассчитанных для модельных смесей, выявило их квазиустойчивость для пороговых значений ${{L}^{0}} \leqslant 0.076$.
Таким образом, по совокупности проведенных расчетов показано, что на точность системы уравнений Фирордта, выписанной для исследуемых химических систем, наибольшее влияние оказывают значения молярных коэффициентов поглощения.
Для определения окончательного вида модели (0.2) необходимо выбрать критерий, в соответствии с которым из множества Λ*, составленного из всех наборов значений параметров $\{ {{\gamma }_{{ij}}},i,j = \overline {1,5} \} $, являющихся решением задачи (4.1), будет выбран лучший.
В качестве такой характеристики примем число обусловленности матрицы:
Определение наборов значений параметров $\{ {{\gamma }_{{ij}}},i,j = \overline {1,5} \} $, обеспечивающих лучшее значение числа обусловленности коэффициентной матрицы в модели (0.2), будем проводить на основе решения задачи:
(4.5)
${\text{|}}A{\text{'}}{{\bar {x}}^{3}} - {{B}^{3}}{\text{|}} \leqslant {{\bar {\xi }}^{{*3}}},$Минимальное число обусловленности по результатам решения задачи (4.5) составило ${\text{cond}}\left( {A{\text{'}}} \right) = 49.5$ (для сравнения, ${\text{cond}}\left( A \right) = 274.6$). Рассчитанные при этом параметры $\{ \gamma _{{ij}}^{*},i,j = \overline {1,5} \} $ (табл. 4), позволили установить вид матрицы $A{\text{'}}$ и тем самым идентифицировать систему (0.2).
Таблица 4.
Оптимальные значения $\{ \gamma _{{ij}}^{*},i,j = \overline {1,5} \} $
| i | J | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0.973 | 1.400 | 1.381 | 1.224 | 1.174 |
| 2 | 1.014 | 1.389 | 1.263 | 1.400 | 0.955 |
| 3 | 1.048 | 0.766 | 1.400 | 1.327 | 1.357 |
| 4 | 1.056 | 0.864 | 1.155 | 1.400 | 1.357 |
| 5 | 1.118 | 1.019 | 1.400 | 1.195 | 0.652 |
Заключение. Представлен метод параметрической идентификации математических моделей, основанный на использовании предельно допустимых оценок искомых параметров. Метод позволяет осуществлять идентификацию моделей в условиях неопределенности исходных данных, обусловленной их неточностью и незначительностью объема выборки. Сформулированы положения, обеспечивающие проведение оценки устойчивости получаемых решений и степени неопределенности исходных данных. Представленный метод реализован применительно к задаче количественного анализа многокомпонентных фуллеренсодержащих смесей, проводимого с использованием метода Фирордта, что обеспечивает основу управления селективностью соответствующих химических реакций. Полученные результаты позволили оценить влияние неопределенности всех групп исходных данных и установить вид идентифицируемой системы уравнений, гарантирующий для модельных смесей погрешность на уровне, не превышающем $\xi * = 2.34 \times {{10}^{{ - 9}}}$. На основе этих результатов может осуществляться планирование экспериментов по уточнению информации об использованных модельных смесях, исследованию свойств химических систем идентичного состава, что в свою очередь позволяет управлять процессом получения востребованных на практике изомеров фуллерена С60.
Список литературы
Kuznetsov S.I., Yumagulova R.K., Miftakhov M.S., Kolesov S.V., Yunusova D.S., Spivak S.I., Kantor O.G. Quantitative UV Spectrophotometric Analysis of Mixtures of Substituted C60 Fullerenes // J. Applied Spectroscopy. 2015. V. 82. № 4. P. 644–652.
Берштейн И.Я., Каминский Ю.А. Спектрофотометрический анализ в органической химии. Л.: Химия, 1986. 200 с.
Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. М.: ЮНИТИ, 1998. 1022 с.
Алгоритмы и программы восстановления зависимостей / Под ред. В.Н. Вапника. М.: Наука, 1984. 816 с.
Белов В.М., Суханов В.А., Унгер Ф.Г. Обзор основных статистических методов определения параметров аппроксимирующих функций: Препринт № 46. Томск: ТНЦ СО АН СССР, 1990. 34 с.
Вапник В.Н. Восстановление зависимостей по эмпирическим данным. М.: Наука, 1979. 448 с.
Иванов В.К. Об одном типе некорректных линейных уравнений в векторных топологических пространствах // Сиб. мат. журн. 1965. Т. 4. № 4. С. 832–839.
Тихонов А.Н. О регуляризации некорректно поставленных задач // ДАН СССР. 1963. Т. 153. № 1. С. 49–52.
Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука. Физматлит, 1990. 232 с.
Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Сибирское научное изд-во, 2009. 457 с.
Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с.
Блехман И.И., Мышкис А.Д., Пановко Я.Г. Прикладная математика: предмет, логика, особенности подходов. Киев: Наук. думка, 1976. 260 с.
Канторович Л.В. О некоторых новых подходах к вычислительным методам и обработке наблюдений // Сиб. мат. журн. 1962. Т. 3. № 5. С. 701–709.
Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971. 384 с.
Кантор О.Г., Спивак С.И., Талипова Р.Р. Параметрическая идентификация математических моделей химической кинетики // Системы и средства информатики. 2017. Т. 27. № 3. С. 145–154.
Спивак С.И., Кантор О.Г., Юнусова Д.С., Кузнецов С.И., Колесов С.В. Предельно допустимые оценки расчета параметров физико-химических моделей // ДАН. 2015. Т. 464. № 4. С. 437–439.
Спивак С.И., Тимошенко В.И., Слинько М.Г. Методы построения кинетических моделей стационарных реакций // Хим. пром-сть сегодня. 1979. № 3. С. 33–36.
Pomerantsev A.L., Kutsenova A.V., Rodionova O.Y. Kinetic Analysis of Non-isothermal Solid-state Reactions: Multi-Stage Modeling Without Assumptions in the Reaction Mechanism // Physical Chemistry Chemical Physics. 2017. V. 19. № 5. P. 3606–3615.
Brereton R.G., Jansen J., Lopes J., Marini F., Pomerantsev A., Rodionova O., Roger J.M., Walczak B., Tauler R. Chemometrics in Analytical Chemistry. Pt. II. Modeling, Validation, and Applications // Analytical and Bioanalytical Chemistry. 2018. V. 410. № 26. P. 6691–6704.
Калмыков С.А., Шокин Ю.И., Юлдашев З.Х. Методы интервального анализа. Новосибирск: Наука, 1986. 223 с.
Шарый С.П. Сильная согласованность в задаче восстановления зависимостей при интервальной неопределенности данных // Вычисл. технологии. 2017. Т. 22. № 2. С. 150–172.
Ильин В.А., Позняк Э.Г. Основы математического анализа: В 2 ч. Ч. I. М.: Наука. Физматлит, 1998. 616 с.
Зуховицкий С.И., Авдеева Л.И. Линейное и выпуклое программирование. М.: Наука, 1967. 460 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления