1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 2, 2023

Известия РАН. Теория и системы управления, 2023, № 2, стр. 140-150

ОБ АВТОКОЛЕБАНИЯХ МНОГОЗВЕННОГО АЭРОДИНАМИЧЕСКОГО МАЯТНИКА

А. П. Голуб a, Л. А. Климина a, Б. Я. Локшин a, Ю. Д. Селюцкий a, *

a НИИ механики МГУ
Москва, Россия

* E-mail: seliutski@imec.msu.ru

Поступила в редакцию 09.11.2022
После доработки 23.11.2022
Принята к публикации 05.12.2022

Полный текст (PDF)

Аннотация

Рассматривается многозвенный маятник, находящийся в потоке среды. На последнем звене маятника установлено крыло, на котором сосредоточено взаимодействие с потоком. Изучается динамика этой системы как потенциального рабочего элемента ветроэнергетической установки колебательного типа. Для разных скоростей потока численно исследуются периодические режимы, возникающие при разном количестве звеньев и различных значениях внешней нагрузки. Показано, в частности, что максимальная мощность, которая может быть получена с помощью 2-звенного маятника, в широком диапазоне скоростей потока больше, чем с помощью маятников с числом звеньев больше двух. В то же время маятники с большим количеством звеньев позволяют получать заметную мощность в более широком интервале значений нагрузки, чем двухзвенный.

Введение. Маятники, состоящие из нескольких звеньев, могут рассматриваться как модели элементов различных технических систем (например, шагающих роботов, систем гашения колебаний, ветроэнергетических установок и т.п.). Это обуславливает интерес к ним как с точки зрения управления и стабилизации, так и с точки зрения анализа периодических движений, возникающих в таких системах.

Значительное количество исследований посвящено вопросам оценки частот собственных колебаний и количества периодических решений многозвенных маятников. Например, в работе [1] показано, что сумма обратных квадратов собственных частот многозвенного маятника с точечными массами не зависит от распределения масс между звеньями. Некоторые оценки собственных частот многозвенных маятников с точечными и с распределенными массами даны в [2].

В [3] получены условия, при которых для маятника с n звеньями, находящегося под действием периодической возбуждающей силы с нулевым средним, существует не менее ${{2}^{n}}$ периодических решений, период которых равен периоду возбуждающей силы. В [4, 5] найдены аналогичные условия для ситуации, когда возбуждение имеет ненулевое среднее. Вопросы устойчивости этих решений не обсуждаются.

Достаточно большое число исследований посвящено управлению движением многозвенных маятников и их стабилизации в перевернутом положении. Так, в [6] получены необходимые и достаточные условия возможности стабилизации перевернутого положения многозвенного маятника (с точечными массами) периодической силой, приложенной в точке подвеса. В [7] предложен метод управления многозвенным маятником с распределенными массами, обеспечивающий приведение системы в любое заданное положение (в предположении, что управляющие моменты приложены во всех шарнирах и ограничения на их величину отсутствуют). В [8–10] рассмотрено ограниченное управление в виде обратной связи, позволяющее привести многозвенный маятник в любое положение равновесия за конечное время с помощью только момента, приложенного в точке подвеса (или к последнему звену) из начальных условий, которые находятся вблизи этого равновесия.

Все перечисленные выше исследования посвящены маятниковым системам, движущимся в поле силы тяжести (в том числе, при наличии управления). В то же время представляет интерес изучить динамику многозвенных маятников, находящихся под действием сил другой природы. В [11] изучаются регулярные и хаотические движения двойного маятника в поле силы тяжести и магнитных сил. В [12] анализируется динамика многозвенного маятника, последнее звено которого может соударяться с опорой. При этом в ходе соударения выделяется упругая фаза, упругопластическая фаза и фаза восстановления. В [13, 14] изучается динамика 2-звенного маятника под действием следящей силы. Ряд работ (например, [15–17]) посвящен исследованию динамики 1- и 2-звенных маятников, взаимодействующих с потоком среды.

Автоколебания многозвенных маятников, возникающие под действием внешних сил, обуславливают интерес к таким маятникам как к возможным виброгасителям. Так, в работе [18] рассматриваются вопросы гашения колебаний зданий и сооружений (например, во время землетрясений) с помощью многозвенных точечных маятников. В частности, показано, что наиболее эффективно гашение колебаний осуществляется в случае, когда число звеньев маятника больше 10.

Кроме того, многозвенные маятники изучаются и как потенциальные рабочие элементы энергетических установок колебательного типа. В частности, в [19] в качестве портативного источника энергии рассматривается 2-звенный маятник, закрепленный на человеке. В [20] изучается возможность выработки энергии с помощью двойного маятника, связанного с вертикально-осевой ветротурбиной и взаимодействующего с постоянным магнитом. Следует отметить, что в этой конфигурации маятник непосредственно с потоком не взаимодействует. В [21] обсуждается применение 2-звенного аэродинамического маятника с пружиной в первом шарнире для преобразования энергии потока. Отметим, что в [15] показано, что для 1-звенных маятников периодические режимы возникают в достаточно узком диапазоне параметров (причем в отсутствие демпфирования, т.е. внешней нагрузки). Поэтому, по-видимому, использовать такие маятники для преобразования энергии потока нецелесообразно.

В работе исследуется динамика аэродинамического маятника, состоящего из нескольких (не менее двух) упругосоединенных звеньев, на последнем из которых закреплено крыло с симметричным профилем. Проводится численное исследование периодических режимов, возникающих в этой системе при разном количестве звеньев и разных значениях параметров системы. Даются оценки выходной мощности, которая может быть получена с помощью таких колебаний.

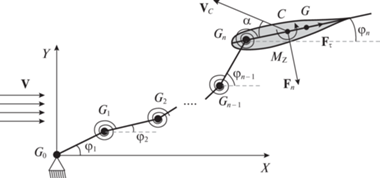
1. Постановка задачи. Рассмотрим многозвенный аэродинамический маятник, состоящий из $n$ звеньев (рис. 1), причем $n \geqslant 2$. Все звенья, кроме последнего, одинаковы, и звено с номером $i$ ($i < n$) представляет собой невесомый стержень ${{G}_{{i - 1}}}{{G}_{i}}$ длиной ${{l}_{0}}$, в конце ${{G}_{i}}$ которого находится материальная точка массы ${{m}_{0}}$. Последнее звено – стержень, на котором жестко закреплено крыло с симметричным профилем (таким образом, что хорда крыла лежит на этом стержне). Будем считать, что центр масс $G$ этого звена также лежит на указанном стержне.

Рис. 1.

Схема многозвенного аэродинамического маятника (вид сверху)

Первое звено шарнирно закреплено в точке ${{G}_{0}}$ таким образом, что оно может свободно вращаться вокруг неподвижной вертикальной оси ${{G}_{0}}Z$. Соседние звенья маятника соединены друг с другом шарнирами (их оси также будем считать вертикальными). Таким образом, маятник может совершать колебания в горизонтальной плоскости.

Во всех шарнирах (кроме первого) установлены одинаковые спиральные пружины. Будем считать, что каждая такая пружина находится в недеформированном состоянии, когда звенья, смежные с соответствующим шарниром, образуют друг с другом развернутый угол.

Пусть система помещена в горизонтальный поток среды, скорость которого на бесконечности постоянна и равна V. Введем в горизонтальной плоскости неподвижную систему координат ${{G}_{0}}XY$, ось абсцисс которой направим вдоль скорости набегающего потока.

В работах [17, 21] рассматривались 2-звенные маятники с пружиной в первом шарнире. Такому маятнику, вообще говоря, требуется дополнительное устройство, обеспечивающее поворот всей конструкции в случае изменения направления скорости ветра. Отсутствие пружины в первом шарнире в многозвенном маятнике, рассматриваемом в настоящей статье, по-видимому, позволяет обойтись без такого устройства.

В качестве обобщенных координат будем использовать углы ${{\varphi }_{i}}$, $i = \overline {1,n} $, между соответствующими звеньями и осью абсцисс.

Запишем выражение для кинетической энергии системы:

$T = \sum\limits_{i = 1}^{n - 1} {\frac{{{{m}_{0}}{v}_{i}^{2}}}{2}} + \frac{{m{v}_{G}^{2}}}{2} + \frac{{mr_{0}^{2}\dot {\varphi }_{n}^{2}}}{2}.$

Здесь введены следующие обозначения: $m$ – масса последнего звена; ${{r}_{0}}$ – радиус инерции этого звена относительно его центра масс; ${{{v}}_{G}}$ – величина скорости центра масс последнего звена; ${{{v}}_{i}}$ – величины скоростей центров масс соответствующих звеньев, которые определяются следующими формулами:

${v}_{s}^{2} = \sum\limits_{i = 1}^s {\sum\limits_{j = 1}^s {{{l}_{i}}{{l}_{j}}{{{\dot {\varphi }}}_{i}}{{{\dot {\varphi }}}_{j}}\cos \left( {{{\varphi }_{i}} - {{\varphi }_{j}}} \right)} } ,\quad {v}_{G}^{2} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{l}_{i}}{{l}_{j}}{{{\dot {\varphi }}}_{i}}{{{\dot {\varphi }}}_{j}}\cos \left( {{{\varphi }_{i}} - {{\varphi }_{j}}} \right)} } .$

Здесь ${{l}_{i}} = {{l}_{0}}$ при $1 \leqslant i \leqslant n - 1$ и ${{l}_{n}} = l$, где l – расстояние от последнего шарнира до центра масс G последнего звена.

Предположим, что поток действует только на крыло, и аэродинамическое воздействие сводится к нормальной силе ${{{\mathbf{F}}}_{n}}$ и тангенциальной силе ${{{\mathbf{F}}}_{\tau }}$, приложенным в середине C хорды крыла, а также к моменту ${{M}_{z}}$ относительно этой точки. Нормальная сила направлена перпендикулярно хорде, а тангенциальная – вдоль хорды (рис. 1). Для описания этих сил воспользуемся квазистатическим подходом, в рамках которого их модули определяются по формулам

(1.1)
${{F}_{n}} = \frac{{\rho S}}{2}V_{C}^{2}{{C}_{n}}(\alpha ),\quad {{F}_{\tau }} = \frac{{\rho S}}{2}V_{C}^{2}{{C}_{\tau }}(\alpha ),\quad {{M}_{z}} = \frac{{\rho S}}{2}bV_{C}^{2}{{C}_{m}}(\alpha ).$

Здесь $\rho $ – плотность воздуха, $S$ – площадь крыла, $b$ – длина хорды крыла, ${{{\mathbf{V}}}_{C}}$ – воздушная скорость точки $C$, т.е. скорость этой точки относительно набегающего потока, $\alpha $ – угол атаки, т.е. угол между вектором ${{{\mathbf{V}}}_{C}}$ и хордой, ${{C}_{n}}$, ${{C}_{\tau }}$, ${{C}_{m}}$ – безразмерные коэффициенты нормальной силы, тангенциальной силы и момента соответственно. Эти коэффициенты предполагаются зависящими только от угла атаки.

Нетрудно видеть, что величины воздушной скорости и угла атаки определяются следующими соотношениями:

(1.2)
$\begin{gathered} {{V}_{C}}\cos \alpha = V\cos {{\varphi }_{n}} + \sum\limits_{i = 1}^n {{{r}_{i}}{{{\dot {\varphi }}}_{i}}\sin \left( {{{\varphi }_{i}} - {{\varphi }_{n}}} \right)} , \hfill \\ {{V}_{C}}\sin \alpha = V\sin {{\varphi }_{n}} + \sum\limits_{i = 1}^n {{{r}_{i}}{{{\dot {\varphi }}}_{i}}\cos \left( {{{\varphi }_{i}} - {{\varphi }_{n}}} \right)} . \hfill \\ \end{gathered} $

Здесь ${{r}_{i}} = {{l}_{i}} = {{l}_{0}}$ при $1 \leqslant i \leqslant n - 1$ и ${{r}_{n}} = r$, где r – расстояние от последнего шарнира до середины хорды крыла.

Для того чтобы промоделировать полезную нагрузку, прикладываемую к маятнику как к элементу ветроэнергетической установки, введем в первом шарнире демпфирование с коэффициентом $\chi $. Такой способ описания полезной нагрузки использовался, в частности, в [22, 23]. В дальнейшем при анализе динамики маятников с разным числом звеньев будем считать, что увеличение количества звеньев не влияет на изменение полной массы и длины маятника.

Чтобы несколько упростить обозначения, выберем единицы измерения таким образом, чтобы сделать равными единице следующие величины: суммарную массу всех звеньев, кроме последнего, суммарную длину этих звеньев, а также коэффициенты жесткости спиральных пружин, т.е.

(1.3)
${{m}_{0}}(n - 1) = 1,\quad {{l}_{0}}(n - 1) = 1,\quad k = 1.$

Эта процедура фактически означает переход к безразмерным переменным.

С учетом вышесказанного уравнения движения системы можно записать в следующем виде:

(1.4)
$\sum\limits_{j = 1}^n {{{a}_{{ij}}}{{{\ddot {\varphi }}}_{j}}} + \sum\limits_{j = 1}^n {{{u}_{{ij}}}\dot {\varphi }_{j}^{2}} = {{Q}_{i}},\quad i = \overline {1,n} ,$
где

$\begin{gathered} {{a}_{{ij}}} = {{l}_{i}}{{l}_{j}}\left( {m + {{m}_{0}}(n - \max (i,j))} \right)\cos ({{\varphi }_{j}} - {{\varphi }_{i}}) + mr_{0}^{2}{{\delta }_{{in}}}{{\delta }_{{jn}}}, \\ {{u}_{{ij}}} = - {{l}_{i}}{{l}_{j}}\left( {m + {{m}_{0}}(n - \max (i,j))} \right)\sin ({{\varphi }_{j}} - {{\varphi }_{i}}). \\ \end{gathered} $

Здесь ${{\delta }_{{ij}}}$ – символ Кронекера.

Обобщенные силы определяются следующими соотношениями:

$\begin{gathered} {{Q}_{i}} = - ({{\varphi }_{i}} - {{\varphi }_{{i - 1}}})(1 - {{\delta }_{{1i}}}) - ({{\varphi }_{i}} - {{\varphi }_{{i + 1}}})(1 - {{\delta }_{{ni}}}) - \chi {{{\dot {\varphi }}}_{1}}{{\delta }_{{1i}}} - h({{{\dot {\varphi }}}_{i}} - {{{\dot {\varphi }}}_{{i - 1}}})(1 - {{\delta }_{{1i}}}) - \\ \, - h({{{\dot {\varphi }}}_{i}} - {{{\dot {\varphi }}}_{{i + 1}}})(1 - {{\delta }_{{ni}}}) - \mu V_{C}^{2}\left( {{{r}_{i}}{{C}_{n}}\cos ({{\varphi }_{i}} - {{\varphi }_{n}}) + {{r}_{i}}{{C}_{\tau }}\sin ({{\varphi }_{i}} - {{\varphi }_{n}}) - {{C}_{m}}b{{\delta }_{{ni}}}} \right), \\ \end{gathered} $
где $\mu = {{\rho S{{l}_{0}}} \mathord{\left/ {\vphantom {{\rho S{{l}_{0}}} {2{{m}_{0}}}}} \right. \kern-0em} {2{{m}_{0}}}}$, h – коэффициенты демпфирования пружин между звеньями. Уравнения (1.4) вместе с соотношениями (1.1) и (1.2) образуют замкнутую систему.

2. Положения равновесия. Для симметричного профиля ${{C}_{n}}(0) = {{C}_{n}}(\pi ) = 0$ и ${{C}_{m}}(0) = {{C}_{m}}(\pi ) = 0$. Поэтому ясно, что система (1.4) имеет по крайней мере два положения равновесия: φ1 = ${{\varphi }_{2}} = \ldots = {{\varphi }_{n}}$ = 0 и ${{\varphi }_{1}} = {{\varphi }_{2}} = \ldots = {{\varphi }_{n}} = \pi $. Вообще говоря, при соответствующих значениях параметров могут существовать и другие положения равновесия. Нетрудно показать, что положение, в котором все звенья маятника ориентированы навстречу потоку, всегда неустойчиво.

Проанализируем устойчивость первого равновесия – положения “по потоку”. При этом нужно заметить, что с точки зрения использования энергии потока асимптотическая устойчивость является нежелательной.

Характеристический полином системы, линеаризованной вблизи этого положения равновесия, можно записать в следующем виде:

(2.1)
${{{\mathbf{A}}}_{0}}{{\lambda }^{2}} + {{{\mathbf{B}}}_{0}}\lambda + {{{\mathbf{C}}}_{0}} = 0,$
где ${{{\mathbf{A}}}_{0}} = \left\{ {a_{{ij}}^{0}} \right\}$, ${{{\mathbf{B}}}_{0}} = \left\{ {b_{{ij}}^{0}} \right\}$, ${{{\mathbf{C}}}_{0}} = \left\{ {c_{{ij}}^{0}} \right\}$, причем

$\begin{gathered} a_{{ij}}^{0} = {{l}_{i}}{{l}_{j}}\left( {m + {{m}_{0}}(n - \max (i,j))} \right) + mr_{0}^{2}{{\delta }_{{in}}}{{\delta }_{{jn}}}, \\ b_{{ij}}^{0} = \chi {{\delta }_{{1i}}}{{\delta }_{{1j}}} + h(2 - {{\delta }_{{1i}}} - {{\delta }_{{ni}}}){{\delta }_{{ij}}} - h(1 - {{\delta }_{{1i}}}){{\delta }_{{i - 1j}}} - h(1 - {{\delta }_{{ni}}}){{\delta }_{{i + 1j}}} + \mu V{{r}_{j}}({{r}_{i}}C_{n}^{\alpha } - C_{m}^{\alpha }b{{\delta }_{{ni}}}), \\ c_{{ij}}^{0} = (2 - {{\delta }_{{1i}}} - {{\delta }_{{ni}}}){{\delta }_{{ij}}} - (1 - {{\delta }_{{1i}}}){{\delta }_{{i - 1j}}} - (1 - {{\delta }_{{ni}}}){{\delta }_{{i + 1j}}} + \mu {{V}^{2}}{{r}_{i}}{{C}_{{\tau 0}}}({{\delta }_{{ij}}} - {{\delta }_{{nj}}}) + \mu {{V}^{2}}({{r}_{i}}C_{n}^{\alpha } - C_{m}^{\alpha }b{{\delta }_{{ni}}}){{\delta }_{{nj}}}. \\ \end{gathered} $

Здесь

$C_{n}^{\alpha } = {{\left. {\frac{{d{{C}_{n}}(\alpha )}}{{d\alpha }}} \right|}_{{\alpha = 0}}},\quad C_{m}^{\alpha } = {{\left. {\frac{{d{{C}_{m}}(\alpha )}}{{d\alpha }}} \right|}_{{\alpha = 0}}},\quad {{C}_{{\tau 0}}} = {{C}_{\tau }}(0).$

Миноры Гурвица для характеристического полинома (2.1), очевидно, представляют собой полиномы некоторой степени относительно параметров (в частности, r и ${{r}_{0}}$). Для 2- и 3-звенных маятников нетрудно показать прямым вычислением, что в минорах Гурвица порядка $2n - 1$ коэффициенты при старшей степени ${{r}_{0}}$ отрицательны, если скорость потока достаточно велика и выполнено условие $C_{m}^{\alpha }b - (r + 1)C_{n}^{\alpha } < 0$. Нужно отметить, что, как показывают статические эксперименты, для тонких профилей это неравенство заведомо выполняется для всех $b \leqslant 1$. Таким образом, увеличение радиуса инерции последнего звена приводит к дестабилизации положения равновесия. С другой стороны, коэффициенты при старших степенях r во всех минорах Гурвица для указанных маятников оказываются положительными при всех физически осмысленных значениях прочих параметров. Следовательно, если расстояние от последнего шарнира до середины хорды крыла достаточно велико, то имеет место асимптотическая устойчивость.

На рис. 2 изображены границы областей неустойчивости равновесия “по потоку” на плоскости параметров $({{r}_{0}},r)$ для маятников с разным числом звеньев $n$ при разных значениях скорости $V$ потока ($V = 1.5$, 2.0, 2.5, 5, 10, 15). Области неустойчивости расположены ниже и правее соответствующих кривых. Расчеты проводились при следующих значениях параметров (в принятых безразмерных единицах (1.3)):

(2.2)
$m = 3,\quad l = 0.3,\quad b = 0.5,\quad \mu = 0.1.$
Рис. 2.

Границы областей неустойчивости равновесия “по потоку” для маятников при разных значениях параметров n и V

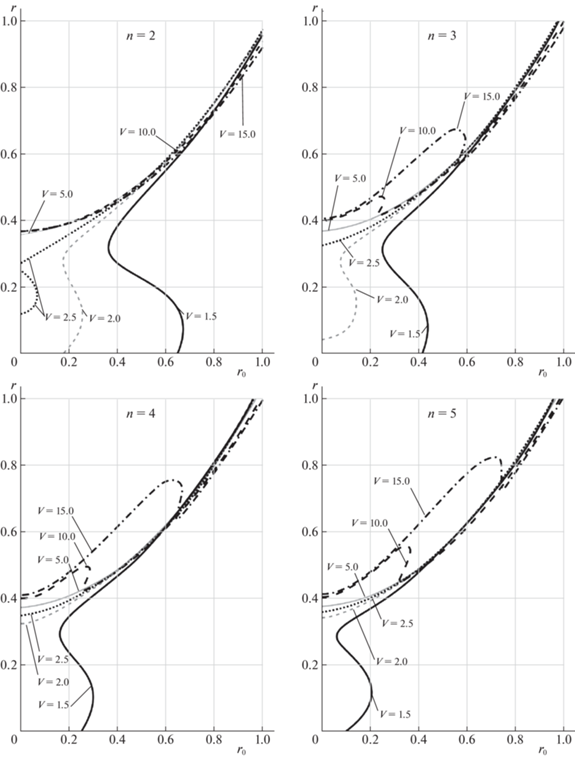
Кроме того, предполагалось, что демпфирование в шарнирах отсутствует, т.е. $\chi = 0$.

Для аэродинамических характеристик были приняты зависимости из экспериментов [24], проведенных для профиля NACA0012. При этом

$C_{n}^{\alpha } = 6.58,\quad C_{m}^{\alpha } = 1.69,\quad {{C}_{{\tau 0}}} = 0.01$.

Из рис. 2 видно, что увеличение $V$ приводит к расширению области неустойчивости равновесия “по потоку”, как и следовало ожидать. В частности, при достаточно большой скорости потока в случае, когда крыло расположено достаточно близко к шарниру (параметр r мал), неустойчивость имеет место при любых значениях радиуса инерции последнего звена.

Кроме того, область неустойчивости расширяется с увеличением числа звеньев. В частности, с ростом $n$ уменьшается величина скорости потока, при которой равновесие становится неустойчивым. Тем не менее, в области сравнительно больших значений r и ${{r}_{0}}$ границы области устойчивости для разных $n$ оказываются достаточно близкими.

Интересно, что в области малых значений ${{r}_{0}}$ значение $r$, при котором происходит потеря устойчивости, увеличивается с ростом $V$, а при относительно больших ${{r}_{0}}$ (в расчетах – близких к 1) – несколько убывает. Учитывая, что на практике увеличение радиуса инерции последнего звена может оказаться достаточно затруднительным, для расширения рабочего диапазона скоростей (т.е. уменьшения критической скорости ${{V}_{{cr}}}$, при которой положение “по потоку” теряет устойчивость) представляется целесообразным увеличивать число звеньев.

3. Периодические режимы. Исследуем периодические режимы, возникающие в системе при различных значениях параметров. При расчетах будем использовать значения параметров (2.2), а для радиуса инерции последнего звена примем ${{r}_{0}} = 0.25$. Будем варьировать величину скорости потока, значение параметра $\chi $, характеризующего нагрузку, а также количество звеньев.

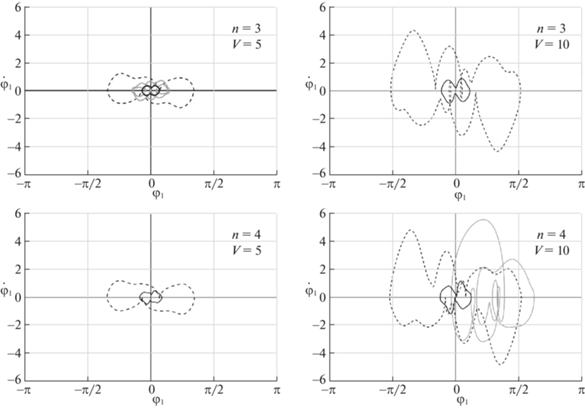
В [17] уже для 2-звенного аэродинамического маятника с пружиной в первом шарнире было показано, что в достаточно широком диапазоне параметров существуют два притягивающих периодических решения. Можно ожидать, что и для рассматриваемых конфигураций маятниковых систем будет наблюдаться неединственность притягивающих периодических решений.

На рис. 3 изображены проекции периодических траекторий на плоскость $({{\varphi }_{1}},{{\dot {\varphi }}_{1}})$ для 3- и 4‑звенного маятника при нагрузке $\chi = 0.2$ и значениях безразмерной скорости потока 5 и 10. Видно, что при некоторых значениях параметров в системе существуют три притягивающих периодических решения. Для 4-звенного маятника в случае, когда скорость $V = 10$, наблюдается решение, несимметричное относительно начала координат. В силу симметрии системы существует и другое решение, расположенное симметрично ему (оно не изображено на рис. 3). Таким образом, в системе в этом случае имеется, по крайней мере, четыре притягивающие периодические траектории. Вообще, при малых нагрузках несимметричные решения существуют для всех рассмотренных маятников.

Рис. 3.

Примеры периодических решений в проекции на плоскость $({{\varphi }_{1}},{{\dot {\varphi }}_{1}})$ при $\chi = 0.2$

С точки зрения выработки энергии основной характеристикой периодических решений является мощность $P$, развиваемая системой на соответствующих режимах. Эта величина определяется следующей формулой:

(3.1)
$P = \frac{1}{{\tau _{*}^{{}}}}\int\limits_0^{\tau _{*}^{{}}} {\chi \dot {\varphi }{{{_{1}^{2}}}_{1}}} d\tau ,$
где $\tau _{*}^{{}}$ – период колебаний.

Очевидно, что мощность $P = 0$ при $\chi = 0$. Из физических соображений ясно, что при $\chi \to \infty $ развиваемая мощность также будет стремиться к нулю. Таким образом, для маятника с заданным количеством звеньев при любой фиксированной скорости потока существует некоторое значение $\chi = {{\chi }_{m}}$, при котором достигается максимальная мощность. Эту мощность будем обозначать через Pmax.

На рис. 4 приведены рассчитанные по формуле (3.1) зависимости мощности от коэффициента нагрузки для маятников с разным числом звеньев и при различных значениях скорости потока. Крестиками обозначены данные расчетов, отвечающие 2-звенному маятнику, ромбиками – 3-звенному, косыми крестиками – 4-звенному, и квадратиками – 5-звенному.

Рис. 4.

Мощность, развиваемая на различных периодических режимах, в зависимости от нагрузки, количества звеньев и скорости потока

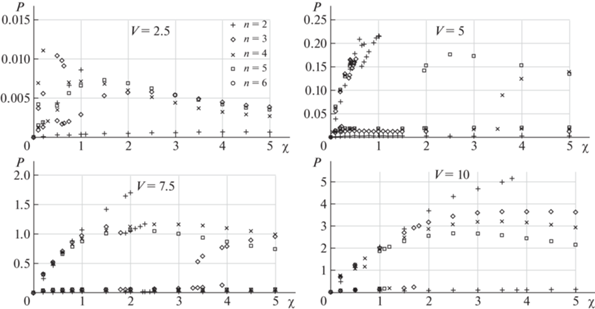
Видно, что ситуация, когда в системе одновременно существуют несколько притягивающих периодических решений с достаточно большой областью притяжения (позволяющей обнаружить такие решения при численном интегрировании), реализуется для всех рассмотренных маятников и в весьма широком диапазоне параметров.

Для 2-звенного маятника периодическое решение, на котором достигается максимальная мощность, существует при нагрузках, не превышающих некоторого критического значения ${{\chi }_{{c1}}}$. При $\chi > {{\chi }_{{c1}}}$ это решение исчезает, и остается только решение, на котором развиваемая мощность мала (следует отметить, что оно существует при всех рассмотренных значениях $\chi $). При этом величина ${{\chi }_{{c1}}}$ оказывается достаточно близкой к значению ${{\chi }_{m}}$, при котором достигается максимум мощности. Такая ситуация имеет место при всех исследованных скоростях потока. Она представляется нежелательной с практической точки зрения, поскольку незначительное увеличение нагрузки (или снижение скорости потока) может привести к существенному падению мощности.

Для 3-звенного маятника при небольших значениях $V$ имеет место аналогичная ситуация. Однако с ростом скорости потока в области нагрузок, превышающих некоторое критическое значение ${{\chi }_{{c2}}}$, появляется еще одно периодическое решение, на котором мощность достигает относительно больших значений. При скоростях $V \leqslant 7.5$ существует некоторый интервал ${{\chi }_{{c1}}} < \chi < {{\chi }_{{c2}}}$, на котором наблюдается только решение с малой мощностью. При скорости $V = 10$ этот интервал отсутствует, и то семейство решений, на котором реализуется значение Pmax, соответствующее данной скорости потока, имеется при всех рассмотренных значениях $\chi $. В то же время решение с малой мощностью наблюдается только при сравнительно малых величинах $\chi $ и исчезает с ростом нагрузки.

Для 4- и 5-звенных маятников ситуация оказывается сходной, но интервал значений $\chi $, в котором наблюдается только решение с малой мощностью, исчезает уже при скорости $V = 7.5$.

Отметим, что величины ${{\chi }_{{c1}}}$ и ${{\chi }_{{c2}}}$ уменьшаются с ростом числа $n$ звеньев. При достаточно больших скоростях 4-звенный маятник выходит на режим с большей мощностью из окрестности неустойчивого положения равновесия “по потоку”. В то же время 2-звенный маятник не выходит на такой режим из окрестности данного равновесия (для выхода требуется, чтобы начальный угол отклонения звена с крылом был достаточно велик).

4. Регулирование выходной мощности. В рамках использования аэродинамического маятника в качестве рабочего элемента ветроэнергетической установки представляется целесообразным, чтобы, с одной стороны, развиваемая мощность была максимальной, а с другой стороны, чтобы небольшие изменения параметров (скорости потока или нагрузки) не приводили к резкому падению мощности.

Для достижения первой из этих целей необходимо соответствующим образом регулировать нагрузку. Вообще, управление нагрузкой является одним из наиболее естественных способов выхода на целевой режим функционирования ветроэнергетической установки (см. [25]). В то же время достичь второй цели только путем регулирования параметра $\chi $, разумеется, невозможно.

Проанализируем влияние числа звеньев, скорости потока и нагрузки на выходную мощность. На рис. 5,а представлена зависимость величины Pmax от скорости потока для маятников с разным числом звеньев, а на рис. 5,б – зависимость величины ${{\chi }_{m}}$ от значения $V$ для этих маятников.

Рис. 5.

Зависимость максимальной мощности Pmax и соответствующей нагрузки ${{\chi }_{m}}$ от скорости потока для маятников с разным числом звеньев

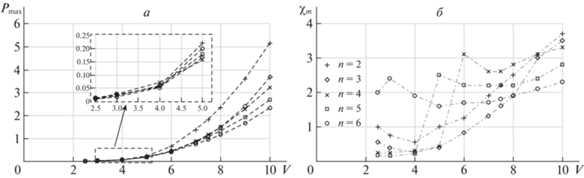
С ростом скорости величина Pmax, как и следовало ожидать, монотонно растет. В то же время ее зависимость от числа звеньев более сложная. Так, при относительно больших скоростях потока ($V \geqslant 5$) максимальная мощность монотонно убывает с ростом числа звеньев. А при значениях $V$, близких к ${{V}_{{cr}}}$, эта монотонность нарушается. В частности, при скорости $V = 2.5$ максимальная мощность (при рассмотренных значениях $n$) наблюдается для 5-звенного маятника, при $V = 3$ – для 3-звенного, а при $V = 4$ – для 4-звенного. Для 6-звенного маятника максимальная мощность меньше, чем для маятников с меньшим числом звеньев (за исключением довольно узкого интервала скоростей вблизи значения $V = 5$).

Нагрузка ${{\chi }_{m}}$, при которой достигается максимальная мощность, также немонотонно зависит от $V$. Тем не менее, при достаточно больших значениях $V$ величина ${{\chi }_{m}}$ возрастает с ростом скорости потока.

Чтобы оценить влияние “скачков” нагрузки и скорости на мощность, построим для разных скоростей потока интервалы значений $\chi $, на которых существует такой периодический режим, что $P{\text{/}}{{P}_{{\max }}} \geqslant 0.5$. На рис. 6 представлены эти интервалы для 2-звенного и 4-звенного маятников. Крестиками обозначены значения ${{\chi }_{m}}$ для соответствующих скоростей потока. Видно, при сравнительно больших скоростях потока для 4-звенного маятника диапазон нагрузки, в котором мощность менее чем в 2 раза отличается от максимальной, значительно шире, чем для 2-звенного.

Рис. 6.

Области, в которых мощность отличается от максимальной не более чем в 2 раза (крестики – нагрузка, отвечающая максимуму мощности)

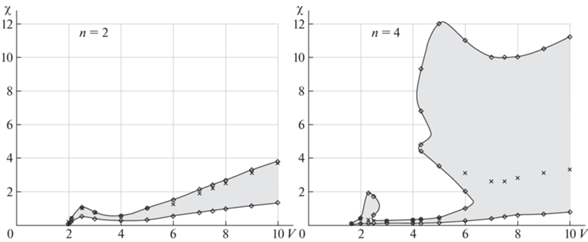
Следует отметить, что для 2-звенного маятника максимальная мощность достигается почти на верхней границе этого диапазона. Это означает, что даже небольшое увеличение нагрузки или уменьшение скорости приведут к серьезному падению мощности по сравнению с максимальной. Более того, выход за верхнюю границу диапазона по $\chi $ сопровождается исчезновением соответствующего периодического режима, так что развиваемая мощность падает сразу в несколько раз. Этот эффект сохраняется во всем рассмотренном интервале скоростей.

Для 4-звенного маятника при небольших значениях $V$ имеет место аналогичная ситуация. Однако при $V \geqslant 6$ максимум мощности достигается вдали от границ диапазона по $\chi $, так что чувствительность  к изменению нагрузки заметно снижается. Кроме того, как видно из рисунка, при таких $V$ уменьшается и чувствительность к падению скорости потока. Иными словами, величины $V$ и/или $\chi $ могут довольно сильно измениться, но при этом в системе будет существовать периодическое решение с достаточно большой (для новой скорости потока) мощностью.

Таким образом, 2-звенный маятник позволяет (при надлежащем выборе нагрузки и, вообще говоря, начальных условий) обеспечить максимальную мощность при фиксированной скорости потока. Однако это требует достаточно точного регулирования нагрузки с учетом текущей скорости потока. И если необходимо обеспечить возможность варьировать нагрузку в сравнительно широких пределах в процессе эксплуатации установки, то предпочтительно использовать маятник с числом звеньев $n > 2$.

Заключение. Проведено исследование динамики многозвенного аэродинамического маятника как рабочего элемента ветроэнергетической установки колебательного типа. Проанализировано влияние числа звеньев, скорости потока и нагрузки на выходную мощность. Показано, что увеличение числа звеньев позволяет снизить критическую скорость потока, при которой в системе возникают автоколебания. Кроме того, установлено, что максимальная мощность в широком диапазоне скоростей достигается для 2-звенного маятника. В то же время увеличение числа звеньев дает возможность существенно расширить диапазон нагрузок, при которых маятник может развивать достаточно большую мощность, и, в частности, обеспечивает эффективную работу при больших значениях нагрузки.

Список литературы

  1. Braun M. On Some Properties of the Multiple Pendulum // Archive of Applied Mechanics. 2003. V. 72. P. 899–910. https://doi.org/10.1007/s00419-002-0263-4

  2. Gupta M.K., Sinha N., Bansal K., Singh A.K. Natural Frequencies of Multiple Pendulum Systems Under Free Condition // Arch. Appl. Mech. 2016. V. 86. P. 1049–1061. https://doi.org/10.1007/s00419-015-1078-4

  3. Felmer P.L. Multiple Periodic Solutions for Lagrangian Systems in Tn // Nonlinear Analysis: Theory, Methods & Applications. 1990. V. 15. Iss. 9. P. 815–831. https://doi.org/10.1016/0362-546X(90)90095-X

  4. Tarantello G. Multiple Forced Oscillations for the N-Pendulum Equation // Commun. Math. Phys. 1990. V. 132. P. 499–517.

  5. Roselli P. A Multiplicity Result for the Periodically Forced N-Pendulum with Nonzero-Mean Valued Forcings // Nonlinear Anal. T.M.A. 2001. V. 43. P. 1019–1041. https://doi.org/10.1016/S0362-546X(99)00239-4

  6. Розенблат Г.М. О параметрической стабилизации многозвенного обращенного маятника // АиТ. 1985. № 3. С. 162–165.

  7. Udwadia F.E., Koganti P.B. Dynamics and Control of a Multi-Body Planar Pendulum // Nonlinear Dynamics. 2015. V. 81. P. 845–866. https://doi.org/10.1007/s11071-015-2362-0

  8. Анохин Н.В. Приведение многозвенного маятника в положение равновесия с помощью одного управляющего момента // Изв. РАН. ТиСУ. 2013. № 5. С. 44–53.

  9. Ананьевский И.М., Анохин Н.В. Управление пространственным движением многозвенного перевернутого маятника с помощью момента, приложенного к первому звену // ПММ. 2014. Т. 78. Вып. 6. С. 755–765.

  10. Ананьевский И.М. Управление трехзвенным перевернутым маятником в окрестности положения равновесия // ПММ. 2018. Т. 82. Вып. 2. С. 149–155.

  11. Wojna M., Wijata A., Wasilewski G., Awrejcewicz J. Numerical and Experimental Study of a Double Physical Pendulum with Magnetic Interaction // J. Sound and Vibration. 2018. V. 430. P. 214–230.https://doi.org/10.1016/j.jsv.2018.05.032

  12. Marghitu D.B., Zhao J. Impact of a Multiple Pendulum with a Non-Linear Contact Force // Mathematics. 2020. V. 8. P. 1202. https://doi.org/10.3390/math8081202

  13. Lobas L.G. Generalized Mathematical Model of an Inverted Multilink Pendulum with Follower Force // Int. Appl. Mech. 2005. V. 41. P. 566–572. https://doi.org/10.1007/s10778-005-0125-1

  14. Puzyrov V., Awrejcewicz J., Losyeva N., Savchenko N. On the Stability of the Equilibrium of the Double Pendulum with Follower Force: Some New Results // J. Sound and Vibration. 2022. V. 523. P. 116699. https://doi.org/10.1016/j.jsv.2021.116699

  15. Локшин Б.Я., Самсонов В А. Авторотационные и автоколебательные режимы движения аэродинамического маятника // ПММ. 2013. Т. 77. Вып. 4. С. 501–513.

  16. Локшин Б.Я., Самсонов В.А., Шамолин М.В. Маятниковые системы с динамической симметрией // Современная математика и ее приложения. 2016. Т. 100. С. 76–133.

  17. Selyutskiy Y.D., Holub A.P., Dosaev M.Z. Elastically Mounted Double Aerodynamic Pendulum // Int. J. Structural Stability and Dynamics. 2019. V. 19. № 5. P. 1941007. https://doi.org/10.1142/S0219455419410074

  18. Egger P., Caracoglia L. Analytical and Experimental Investigation on a Multiple-Mass-Element Pendulum Impact Damper for Vibration Mitigation // J. Sound and Vibration. 2015. V. 353. P. 38–57. https://doi.org/10.1016/j.jsv.2015.05.003

  19. Izadgoshasb I., Lim Y.Y., Tang L., Padilla R.V., Tang Z.S., Sedighi M. Improving Efficiency of Piezoelectric Based Energy Harvesting from Human Motions Using Double Pendulum System // Energy Conversion and Management. 2019. V. 184. P. 559–570. Doi: .https://doi.org/10.1016/j.enconman.2019.02.001

  20. Chen J., Bao B., Liu J., Wu Y., Wang Q. Piezoelectric Energy Harvester Featuring a Magnetic Chaotic Pendulum // Energy Conversion and Management. 2022. V. 269. P. 116155. https://doi.org/10.1016/j.enconman.2022.116155

  21. Selyutskiy Y., Dosaev M., Holub A., Ceccarelli M. Wind Power Harvester Based on an Aerodynamic Double Pendulum // Proc. Institution of Mechanical Engineers, P. C: J. Mechanical Engineering Science. 2022. V. 236. № 18. P. 10025–10032. https://doi.org/10.1177/09544062221085

  22. Dosaev M., Klimina L., Selyutskiy Y. Wind Turbine Based on Antiparallel Link Mechanism // New Trends in Mechanism and Machine Science, Mechanisms and Machine Science. V. 43. Springer International Publishing Switzerland, 2017. P. 543–550.

  23. Pigolotti L., Mannini C., Bartoli G., Thiele K. Critical and Post-Critical Behaviour of Two-Degree-of-Freedom Flutter-Based Generators // J. Sound and Vibration. 2017. V. 404. P. 116–140.https://doi.org/10.1016/j.jsv.2017.05.024

  24. Sheldahl R.E., Klimas P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections Through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines // Technical Report SAND-80-2114. Sandia National Labs. (USA), 1981. https://doi.org/10.2172/6548367

  25. Климина Л.А. Метод формирования авторотаций в управляемой механической системе с двумя степенями свободы // Изв. РАН. ТиСУ. 2020. № 6. С. 3–14.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал