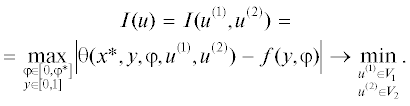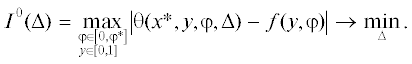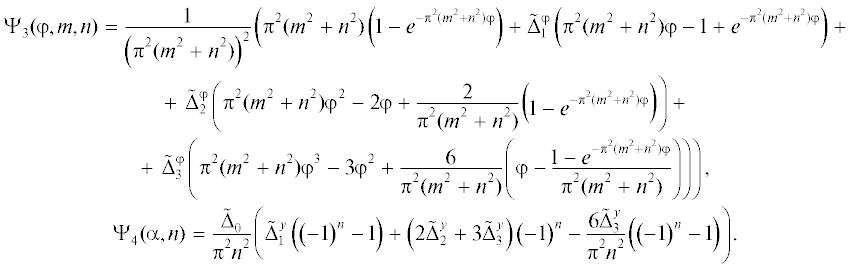Теплофизика высоких температур, 2019, T. 57, № 2, стр. 226-233
Метод минимаксной оптимизации в двумерной граничной обратной задаче теплопроводности
А. Н. Дилигенская *
Самарский государственный технический университет
г. Самара, Россия
* E-mail: adiligenskaya@mail.ru
Поступила в редакцию 31.01.2018
После доработки 10.10.2018
Принята к публикации 10.07.2018
Аннотация
Предложен метод решения двумерной обратной задачи теплопроводности по восстановлению пространственно-временнóй плотности граничного теплового потока, основанный на теории оптимального управления объектами с распределенными параметрами. Метод предусматривает ограничение множества искомых решений классом физически реализуемых функций, что позволяет установить структуру искомого воздействия в виде произведения двух функций одной переменной. На основе параметризации искомой характеристики, рассматриваемой в качестве управляющего воздействия, формулируется задача полубесконечной оптимизации, обеспечивающая минимизацию температурных невязок в равномерной метрике оценивания. Решение задачи аналитическим методом, использующим альтернансные свойства искомых оптимальных температурных отклонений, позволяет получить оптимальные значения вектора параметров.
ВВЕДЕНИЕ
Исследование нестационарных процессов теплообмена, решение задач идентификации и диагностики тепловых процессов часто основываются на решении граничных обратных задач теплопроводности (ОЗТ). На сегодняшний день существует большое число подходов к решению этой проблемы [1–4]. В литературе наиболее полно освещены подходы к решению одномерных граничных ОЗТ, методы решения двумерных и трехмерных обратных задач представлены в меньшем объеме.
Базовые постановки двумерных и трехмерных ОЗТ приведены в [1], где на примере некоторых частных обратных задач, сформулированных в экстремальной постановке, предложен метод итерационной регуляризации, который в дальнейшем получил развитие в работах [5, 6]. Численные методы с применением регуляризирующих алгоритмов использованы для решения двумерных граничных ОЗТ в линейной [7] и нелинейной постановках [8]. Регуляризирующий алгоритм, позволяющий проводить параметрическую идентификацию тепловых потоков к границам анизотропной пластины, приведен в [9]. В работе [10] предложены методика и алгоритм решения двумерной ОЗТ по восстановлению пространственно-временнóй плотности теплового потока, приложенного к внешней поверхности полого кругового цилиндра, по измерениям на его внутренней поверхности. Для решения задачи построен итерационный регуляризирующий алгоритм, использующий для минимизации функционала невязки метод сопряженных градиентов.
Другой подход к решению ОЗТ основывается на сужении множества искомых решений до множества физически реализуемых функций, представляющего собой класс корректности [1], что позволяет получить параметрическое представление искомой характеристики, вектор параметров которого определяется на последующем этапе параметрической оптимизации.
В настоящей работе для решения двумерной граничной ОЗТ применяется разработанный и успешно апробированный при решении одномерных граничных обратных задач метод минимаксной оптимизации [11, 12], базирующийся на теории оптимального управления объектами с распределенными параметрами. Этот метод использует равномерную метрику оценивания [13, 14] температурных невязок, реализует сужение множества искомых характеристик, рассматриваемых в качестве оптимального управляющего воздействия, до класса корректности и тем самым обеспечивает редукцию исходной некорректно поставленной задачи к задаче полубесконечной оптимизации, соответствующей условно-корректной постановке и сохраняющей качественные особенности процессов с распределенными параметрами. Нахождение оптимальных значений конечномерного вектора параметров, определяемого выбранной структурой управляющего воздействия, осуществляется на последующем этапе минимизации на основе метода, учитывающего альтернансные свойства оптимальных решений [14, 15].
Предложенный метод минимаксной оптимизации достаточно универсален по отношению к виду математической модели и может быть применен к задачам, использующим как аналитические, так и численные модели процесса теплообмена. В работе на его основе решена задача определения граничного теплового потока, зависящего от времени и пространственной координаты для двумерного тела канонической формы.
ПОСТАНОВКА ОБРАТНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ
Подобно [1, 8] формулируется двумерная обратная задача нестационарной теплопроводности в случае одностороннего нагрева плоского тела прямоугольной формы, с пространственными координатами x и y, когда на ограничивающих плоскостях x = 0, y = 0 и 1 теплообмен отсутствует, а вектор теплового потока q(y, φ) параллелен плоскости xy.
Рассматривается уравнение теплопроводности для температурного поля θ(x, y, φ), заданное в относительных единицах изменения временнóй φ и пространственных координат:
(1)
$\begin{gathered} \frac{{\partial \theta (x,y,\varphi )}}{{\partial \varphi }} = \frac{{{{\partial }^{2}}\theta (x,y,\varphi )}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\theta (x,y,\varphi )}}{{\partial {{y}^{2}}}}, \\ x,y \in \left( {0,1} \right),\,\,\,\,\varphi \in \left( {0,\varphi {\text{*}}} \right), \\ \end{gathered} $(3)
$\frac{{\partial \theta (0,y,\varphi )}}{{\partial x}} = \frac{{\partial \theta (x,0,\varphi )}}{{\partial y}} = \frac{{\partial \theta (x,1,\varphi )}}{{\partial y}} = 0,\,\,\,\,\varphi \in [0,{\kern 1pt} \varphi {\text{*}}],$(4)
$\frac{{\partial \theta (1,y,\varphi )}}{{\partial x}} = q(y,\varphi ),\,\,\,\,\varphi \in [0,\varphi *].$Здесь функция q(y, φ) неизвестна и является искомой величиной. Задана дополнительная информация о температуре на некоторой линии $x = x* = {\text{const}},$ $0 \leqslant x* \leqslant 1{\text{:}}$
(5)
$\theta (x*,y,\varphi ) = f(y,\varphi ),\,\,\,\,\varphi \in \left[ {0,\varphi {\text{*}}} \right].$Полагается, что пространственно-временнáя функция q(y, φ) двух переменных может быть представлена в виде произведения двух функций одной переменной
что соответствует большинству физически обоснованных ситуаций.Идентифицируемая функция q(y, φ) рассматривается в качестве управляющего воздействия u(y, φ) = q(y, φ), структура которого соответствует виду (6):
где функции ${{u}^{{(1)}}}(y)$ и ${{u}^{{(2)}}}(\varphi )$ выступают как пространственно-распределенное и сосредоточенное управляющие воздействия, подчиненные типовым ограничениям принадлежности заданным множествам V1 и V2 функций. Таким образом, искомое управление u(y, φ) представляет собой произведение (7) пространственно-распределенной и сосредоточенной составляющих.Формулируется ОЗТ в экстремальной постановке, предусматривающей минимизацию погрешности равномерного приближения модельного значения $\theta (x*,y,\varphi ),$ соответствующего искомой функции u(y, φ), к измеряемому температурному состоянию f(y, φ) на заданной области $\Omega = \left\{ {\left( {y,\varphi } \right);y \in [0,1];\varphi \in [0,\varphi *]} \right\}$ изменения пространственной переменной и временнóм интервале идентификации.
Для объекта (1)–(4) требуется определить управляющее воздействие u(y, φ), подчиненное согласно (7) ограничениям (8) и (9), обеспечивающее на заданной области изменения пространственной и временнóй переменной выполнение минимаксного соотношения
Для решения задачи производится сужение множества допустимых решений до класса корректности – физически реализуемых на заданных областях изменения соответствующих переменных функций, – осуществляемое на основе требований их достаточной гладкости [1]. Здесь в качестве класса корректности (компакта) рассматривается множество функций, непрерывных вместе со своими производными, – полиномиальных функций соответствующих переменных:
Значения N и M определяют порядки полиномов (11) и (12) и тем самым задают точную структуру искомых функций, что позволяет перейти к параметризованной форме искомых управлений. Таким образом, при фиксированных значениях N и M идентифицируемое воздействие u(y, φ) однозначно задается значениями полиномиальных коэффициентов в (11) и (12), образующих соответствующие векторы параметров ${{\Delta }^{y}} = \left( {\Delta _{0}^{y},\Delta _{1}^{y},...\Delta _{N}^{y}} \right)$ и ${{\Delta }^{\varphi }} = \left( {\Delta _{0}^{\varphi },\Delta _{1}^{\varphi },...\Delta _{M}^{\varphi }} \right).$ В результате на основе (7), (11) и (12) параметрическое представление управляющего воздействия имеет вид
(13)
$\begin{gathered} u(y,\varphi ) = {{u}^{{(1)}}}(y){{u}^{{(2)}}}(\varphi ) = \left( {\Delta _{0}^{y} + \Delta _{1}^{y}y + ... + \Delta _{N}^{y}{{y}^{N}}} \right) \times \\ \times \,\,\left( {\Delta _{0}^{\varphi } + \Delta _{1}^{\varphi }\varphi + ... + \Delta _{M}^{\varphi }{{\varphi }^{M}}} \right) = \\ = {{{\tilde {\Delta }}}_{0}}\left( {1 + \tilde {\Delta }_{1}^{y}y + ... + \tilde {\Delta }_{N}^{y}{{y}^{N}}} \right)\left( {1 + \tilde {\Delta }_{1}^{\varphi }\varphi + ... + \tilde {\Delta }_{M}^{\varphi }{{\varphi }^{M}}} \right), \\ \end{gathered} $При этом температурное поле $\theta (x*,y,\varphi ,{{u}^{{(1)}}},{{u}^{{(2)}}})$ = = $\theta (x*,y,\varphi ,\Delta )$ также является функцией рассматриваемого вектора Δ параметров и вычисляется как реакция на управляющее воздействие (13) при заданных значениях N и M и векторе Δ. Использование параметрического представления температурного поля $\theta (x*,y,\varphi ,\Delta )$ позволяет перейти от исходной некорректно поставленной обратной задачи к эквивалентной задаче параметрической оптимизации относительно вектора Δ, минимизирующей абсолютное отклонение расчетного температурного состояния от измеряемого в равномерной метрике оценивания
РЕШЕНИЕ ЗАДАЧИ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Решение полученной задачи математического программирования (14), подобно [14–16], может основываться на известных качественных свойствах оптимальных температурных распределений, обладающих при Δ = Δ0 наилучшим равномерным приближением к требуемому состоянию f(y, φ). Данные свойства фиксируют в отдельных точках ${{z}^{0}} = ({{y}^{0}},{{\varphi }^{0}})$ на всей пространственно-временнóй области идентификации достижение предельных отклонений расчетной температуры $\theta (x*,y,\varphi ,{{\Delta }^{0}})$ от заданной f(y, φ), равных ±I 0, и тем самым устанавливают конфигурацию погрешности $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ аппроксимации температурного распределения f(y, φ). Число точек, где достигаются предельно допустимые максимальные по абсолютной величине значения погрешности $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ),$ характеризуемые разными знаками, должно быть не меньше числа неизвестных оптимального процесса [14], в роли которых выступают вектор Δ параметров искомого управления и сама величина погрешности I 0. Таким образом, при поиске аппроксимирующей функции u(y, φ), заданной, согласно (13), фиксированными значениями N и M, на наблюдаемой пространственно-временнóй области Ω всегда найдутся такие R = N + M + 2 точек $z = z_{k}^{0} = (y_{k}^{0},\varphi _{k}^{0}),$ $k = \overline {1,R} ,$ для которых выполняются равенства
(15)
$\begin{gathered} \left| {\theta (x*,y_{k}^{0},\varphi _{k}^{0},{{\Delta }^{0}}) - f(y,\varphi )} \right| = {{I}^{0}}({{\Delta }^{0}}), \\ k = \overline {1,R} ;\,\,\,\,{{\Delta }^{0}} = \left( {\tilde {\Delta }_{0}^{0},\tilde {\Delta }_{1}^{{y0}},...\tilde {\Delta }_{N}^{{y0}},\tilde {\Delta }_{1}^{{\varphi 0}},...\tilde {\Delta }_{M}^{{\varphi 0}}} \right). \\ \end{gathered} $В силу замкнутости системы равенств (15) относительно всех параметров оптимального управления, ее возможно перевести в систему расчетных уравнений относительно этих параметров. Последующее решение полученной системы и окажется решением задачи полубесконечной оптимизации (14).
Специфика данной задачи по сравнению с одномерными случаями, где минимизация ошибки равномерного приближения осуществляется по одной (временнóй или пространственной) переменной, заключается в требовании достижения минимаксной погрешности ${{I}^{0}}({{\Delta }^{0}})$ = $ = {{\max }_{{\varphi ,\,y}}}\left| {\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )} \right|$ аппроксимации f(y, φ) на всей пространственно-временнóй области Ω. В связи со сложным многоэкстремальным характером зависимости $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ от искомого вектора параметров, пространственной координаты и времени в общем случае может возникать множество вариантов комбинаций расположения точек ${{z}^{0}} = ({{y}^{0}},{{\varphi }^{0}})$ с предельно допустимыми отклонениями I 0, соответствующих равенствам (15). Эти варианты различаются формой поверхности распределения $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ по переменным y и φ и координатами $({{y}^{0}},{{\varphi }^{0}})$ точек ${{z}^{0}}.$ Процедура опознавания точек z0 на плоскости (y,φ) и знаков предельных отклонений I 0 в этих точках на множестве возможных вариантов представляет основную сложность при решении двумерной задачи. Тем не менее в большинстве ситуаций, представляющих практический интерес, на основе физических закономерностей процесса теплопроводности возможно существенно уменьшить число претендентов на роль точек z0 альтернанса и среди оставшихся вариантов (если их количество больше одного), отвечающих системе равенств (15), выделить единственный вариант распределения $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ),$ обеспечивающий выполнение минимаксного соотношения (14).
С целью распространения результатов решения одномерных ОЗТ по идентификации сосредоточенного граничного воздействия q(φ) на двумерную область будем далее рассматривать конфигурацию поверхности температурной невязки как совокупность температурных кривых $\theta (x*,{{y}_{k}},\varphi ,{{\Delta }^{0}}) - f({{y}_{k}},\varphi ),$ $k = \overline {1,R} ,$ $\varphi \in \left[ {0,\varphi {\text{*}}} \right],$ характеризуемых предельно допустимыми отклонениями, достигаемыми на различных сечениях yk = = const по объему тела ${{y}_{k}} \in \left[ {0,1} \right]$. При этом число точек альтернанса на совокупности зависимостей $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ во времени $\varphi \in \left[ {0,\varphi {\text{*}}} \right]$ соотносится с количеством искомых параметров оптимального управления, но достигаются они в точках с разными координатами yk.
Методика решения двумерных граничных ОЗТ, основанная на минимаксной оптимизации погрешности аппроксимации наблюдаемого температурного поля, может быть сведена к следующей последовательности действий.
ВЫЧИСЛИТЕЛЬНАЯ ПРОЦЕДУРА
Решается последовательность задач полубесконечной оптимизации (14), ориентированных на выявление формы кривой $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ для различных значений N и M, поочередно возрастающих, начиная с N = M = 0. На каждом этапе система равенств (15) трансформируется в систему R расчетных соотношений
(16)
$\theta (x*,y_{k}^{0},\varphi _{k}^{0},{{\Delta }^{0}}) - f(y_{k}^{0},\varphi _{k}^{0}) = \pm {{I}^{0}}({{\Delta }^{0}}),\,\,\,\,k = \overline {1,R} ,$(17)
$\frac{\partial }{{\partial \varphi }}\left( {\theta (x*,y_{{{\text{ex }}i}}^{0},\varphi _{{{\text{ex }}j}}^{0},{{{\tilde {\Delta }}}^{0}}) - f(y_{{{\text{ex }}i}}^{0},\varphi _{{{\text{ex }}j}}^{0})} \right) = 0$(18)
$\frac{\partial }{{\partial y}}\left( {\theta (x*,y_{{{\text{ex }}i}}^{0},\varphi _{{{\text{ex }}j}}^{0},{{{\tilde {\Delta }}}^{0}}) - f(y_{{{\text{ex }}i}}^{0},\varphi _{{{\text{ex }}j}}^{0})} \right) = 0.$Для каждого конкретного случая, заданного значениями N и M, проблема сводится к выбору соответствующей системы (16)–(18) и вычислению ее корней. При этом на первых этапах вычислительной процедуры могут использоваться аналогии с одномерными ситуациями, позволяющими конкретизировать расположение точек альтернанса и соответствующую расчетную систему уравнений. Например, результаты решения одномерных задач [11, 17] показывают, что первыми претендентами на роль точек альтернанса являются точки на границах ${{\left. {\partial \Omega } \right|}_{\begin{subarray}{l} 0 \leqslant y \leqslant 1,\varphi = \varphi * \\ y = 1,0 \leqslant \varphi \leqslant \varphi * \end{subarray} }}$ рассматриваемой пространственно-временнóй области. В двумерном случае, для демонстрируемого ниже примера, простейший случай N = M = 0, соответствующий постоянному управлению $u(y,\varphi ) = {{\tilde {\Delta }}_{0}},$ приводит к очевидному варианту формы разности $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ с двумя точками экстремума на сечениях $y_{1}^{0} = 1$ и $y_{2}^{0} = 0$ в моменты времени $\varphi _{1}^{0} = \varphi {\text{*}}$ и $\varphi _{2}^{0} = \varphi _{{{\text{ex}}}}^{0}$ (рис. 1). При этом в точках $z_{1}^{0} = (y_{1}^{0},\varphi _{1}^{0})$ и $z_{2}^{0} = (y_{2}^{0},\varphi _{2}^{0})$ достигаются соответственно максимальное и минимальное значения температурной невязки, что согласуется с законом знакочередования предельных отклонений [14].
Рис. 1.
Конфигурация погрешности аппроксимации температурного поля $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ),$ $y \in \left[ {0,1} \right],\varphi \in \left[ {0,\varphi {\text{*}}} \right]$ (а); 1 – $y_{1}^{0} = 1$, 2 – $y_{2}^{0} = 0,$ $\varphi \in \left[ {0,\varphi {\text{*}}} \right]$ (б) при N = M = 0.
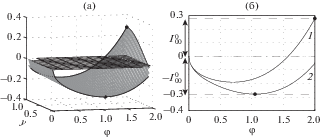
При увеличении значений N или M в расчетной конфигурации $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ появляются дополнительные точки с предельно допустимыми отклонениями ±I 0. По-прежнему, варианты y0 = 1 или y 0 = 0, в том числе соответствующие расположению в “угловых” точках $({{y}^{0}} = 1,{{\varphi }^{0}} = \varphi {\text{*}})$ или $({{y}^{0}} = 0,{{\varphi }^{0}} = \varphi {\text{*}}),$ остаются первоочередными, но при этом предельно допустимые отклонения достигаются также во внутренних точках 0 < y0 < 1, число которых возрастает с увеличением порядков N и M. Ситуация усложняется тем, что для двумерной модели температурного поля в общем случае не выполняется правило знакочередования предельных температурных отклонений, которое существенно ограничивает число вариантов конфигурации $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ).$
Таким образом, число претендентов на роль точек z0 может оказаться больше их минимально необходимого количества, равного R, и заранее выявить конкретный, зависящий от исходных данных, вариант расположения точек альтернанса из всех возможных уже не удается.
В этом случае возможно применить специальным образом организованную вычислительную процедуру, подобную [14, 18], основанную на решении ряда задач оптимизации для возрастающих с достаточно малым шагом значений очередного N + 1-го или M + 1-го параметра относительно решенной на предыдущем шаге задачи, заданной N и M параметрами.
Пусть на очередном этапе найдено решение ${{\Delta }^{0}} = \left( {\tilde {\Delta }_{0}^{0},\tilde {\Delta }_{1}^{{y0}},...\tilde {\Delta }_{{N{\text{*}}}}^{{y0}},\tilde {\Delta }_{1}^{{\varphi 0}},...\tilde {\Delta }_{{M{\text{*}}}}^{{\varphi 0}}} \right)$ минимаксной задачи (14) в классе полиномиальных функций при N = = N*, M = M*. Конфигурация $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi )$ характеризуется наличием N* + M* + 2 точек альтернанса. Пусть на следующем этапе увеличивается порядок аппроксимирующей функции u(2)(φ), т.е. N = N*, M = M* + 1, и искомый вектор параметров имеет вид ${{\Delta }^{0}} = \left( {\tilde {\Delta }_{0}^{0},\tilde {\Delta }_{1}^{{y0}},...\tilde {\Delta }_{{N{\text{*}}}}^{{y0}},\tilde {\Delta }_{1}^{{\varphi 0}},...\tilde {\Delta }_{{M*}}^{{\varphi 0}},\tilde {\Delta }_{{M* + 1}}^{{\varphi 0}}} \right).$ Решается задача оптимизации, заданная соответствующей системой расчетных уравнений (16)–(18), для ряда увеличивающихся с достаточно малым шагом значений $\tilde {\Delta }_{{M* + 1}}^{{\varphi 0}}$ до тех пор, пока абсолютное значение невязки температуры в какой-либо из вновь появляющихся точек экстремумов не сравняется со значениями невязки в других точках z0 и не станет равным $I_{{N*M* + 1}}^{0}({{\Delta }^{0}}).$ Такая ситуация соответствует наличию в форме $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ),$ $N{\text{*}} + M{\text{*}} + 3$ точек альтернанса. Начальные приближения для решения очередной задачи могут основываться на результатах решения расчетной системы на предыдущем шаге.
ПРИМЕР РЕШЕНИЯ
Решение прямой задачи теплопроводности производилось на основе двумерной модели, найденной в результате последовательного применения двух конечных интегральных преобразований [19] по пространственным аргументам x и y с ядрами, равными собственным функциям $K({{\mu }_{m}}x) = \cos {{\mu }_{m}}x$ и $K{\text{*}}({{\lambda }_{n}}y) = \cos {{\lambda }_{n}}y,$ где $\mu _{m}^{2} = {{\pi }^{2}}{{m}^{2}},$ $m = 0,1,2...$ и $\lambda _{n}^{2} = {{\pi }^{2}}{{n}^{2}},$ $n = 0,1,2...$ – собственные числа, полученные на основе решения уравнений sin μ = 0 и sin λ = 0 соответственно. Расчетное температурное поле задается в виде двумерного бесконечного ряда относительно коэффициентов (временны́х мод) $\overline \theta ({{\mu }_{m}},{{\lambda }_{n}},\varphi )$ разложения θ(x, y, φ) по $K({{\mu }_{m}}x)$ и $K{\text{*}}({{\lambda }_{n}}y)$ [19]
(19)
$\begin{gathered} \theta (x,y,\varphi ) = \int\limits_0^\varphi {{{q}_{{00}}}(\tau )d\tau } + \\ + \,\,2\sum\limits_{m = 1}^\infty {\cos \left( {{{\mu }_{m}}x} \right)} \int\limits_0^\varphi {{{q}_{{m0}}}(\tau ){{e}^{{ - \mu _{m}^{2}(\varphi - \tau )}}}d\tau } + \\ + \,\,2\sum\limits_{n = 1}^\infty {\cos \left( {{{\lambda }_{n}}y} \right)} \int\limits_0^\varphi {{{q}_{{0n}}}(\tau ){{e}^{{ - \lambda _{n}^{2}(\varphi - \tau )}}}d\tau } + \\ + \,\,4\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {\cos \left( {{{\mu }_{m}}x} \right)\cos \left( {{{\lambda }_{n}}y} \right)} } \int\limits_0^\varphi {{{q}_{{mn}}}(\tau ){{e}^{{ - (\mu _{m}^{2} + \lambda _{n}^{2})(\varphi - \tau )}}}d\tau } , \\ \end{gathered} $Искомая функция $q{\text{*}}(y,\varphi ),$ согласно (6), представлена в виде
Соотношения (19)–(21) с учетом (22) приводят к выражению для температурного поля при $\alpha \ne 1,2,...$
(23)
$\begin{gathered} \theta (x,y,\varphi ) = \frac{1}{{\pi \alpha }}\left( {1 - \cos \pi \alpha } \right)\frac{{{{e}^{{\beta \varphi }}} - \beta \varphi - 1}}{\beta } + \\ + \,\,\frac{2}{{\pi \alpha }}\left( {1 - \cos \pi \alpha } \right)\sum\limits_{m = 1}^\infty {{{{\left( { - 1} \right)}}^{m}}\cos (\pi mx){{\Psi }_{1}}(\varphi ,m,0) + } \\ + \,\,2\sum\limits_{n = 1}^\infty {\cos (\pi ny){{\Psi }_{2}}(\alpha ,n){{\Psi }_{1}}(\varphi ,0,n) + } \\ + \,\,4\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{{{\left( { - 1} \right)}}^{m}}\cos (\pi mx)\cos (\pi ny){{\Psi }_{2}}(\alpha ,n){{\Psi }_{1}}(\varphi ,m,n),} } \\ \end{gathered} $На основе выражения (23) в результате проведения вычислительного эксперимента на интервале $\,\varphi \in \left[ {0,\varphi {\text{*}}} \right]$ в точках на линии $\left( {x = x*;\,\,y \in \left[ {0,1} \right]} \right)$ были получены двумерные температурные распределения $f(y,\varphi ) = \theta (x*,y,\varphi ),$ используемые как входная информация при решении обратной задачи.
Серия ОЗТ была решена для случая возрастающих значений N и M в классе $N = \overline {0,3} ,$ $M = \overline {0,3} .$ В общем случае при N = M = 3 искомое управление имеет вид
(24)
$\begin{gathered} u(y,\varphi ) = {{{\tilde {\Delta }}}_{0}}\left( {1 + \tilde {\Delta }_{1}^{y}y + \tilde {\Delta }_{2}^{y}{{y}^{2}} + \tilde {\Delta }_{3}^{y}{{y}^{3}}} \right) \times \\ \times \,\,\left( {1 + \tilde {\Delta }_{1}^{\varphi }\varphi + \tilde {\Delta }_{2}^{\varphi }{{\varphi }^{2}} + \tilde {\Delta }_{3}^{\varphi }{{\varphi }^{3}}} \right) \\ \end{gathered} $Параметризованная форма расчетного температурного поля имеет вид
(25)
$\begin{gathered} \theta (x,y,\varphi ) = {{{\tilde {\Delta }}}_{0}}\left( {1 + \frac{{\tilde {\Delta }_{1}^{y}}}{2} + \frac{{\tilde {\Delta }_{2}^{y}}}{3} + \frac{{\tilde {\Delta }_{3}^{y}}}{4}} \right) \times \\ \times \,\,\left( {\varphi + \frac{{\tilde {\Delta }_{1}^{\varphi }}}{2}{{\varphi }^{2}} + \frac{{\tilde {\Delta }_{2}^{\varphi }}}{3}{{\varphi }^{3}} + \frac{{\tilde {\Delta }_{3}^{\varphi }}}{4}{{\varphi }^{4}}} \right) + \\ + \,\,2\sum\limits_{m = 1}^\infty {{{{\left( { - 1} \right)}}^{m}}\cos \left( {\pi mx} \right){{{\tilde {\Delta }}}_{0}}\left( {1 + \frac{{\tilde {\Delta }_{1}^{y}}}{2} + \frac{{\tilde {\Delta }_{2}^{y}}}{3} + \frac{{\tilde {\Delta }_{3}^{y}}}{4}} \right) \times } \\ \times \,\,{{\Psi }_{3}}\left( {\varphi ,m,0} \right) + 2\sum\limits_{n = 1}^\infty {\cos \left( {\pi ny} \right)} {{\Psi }_{4}}(\alpha ,n){{\Psi }_{3}}\left( {\varphi ,0,n} \right) + \\ + \,\,4\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{{{\left( { - 1} \right)}}^{m}}\cos \left( {\pi mx} \right)\cos \left( {\pi ny} \right)} } \times \\ \times \,\,{{\Psi }_{4}}(\alpha ,n){{\Psi }_{3}}\left( {\varphi ,m,n} \right), \\ \end{gathered} $Некоторые результаты решения соответствующих ОЗТ при $N = \overline {0,3} ,$ $M = \overline {0,3} $ приведены в таблице 1 и на рис. 1–4.
Таблица 1.
Точность решения задачи в зависимости от значений N и M
| N | M | Погрешность аппроксимации | |
|---|---|---|---|
| температурного распределения ${{I}^{0}}(\Delta ),$ % | искомой характеристики $\mathop {\max }\limits_{y,\varphi } \left| {u\left( {y,\varphi ,{{\Delta }^{0}}} \right) - q{\text{*}}(y,\varphi )} \right|,$ % | ||
| 0 | 0 | 27.83 | 74.94 |
| 0 | 1 | 16.52 | 68.87 |
| 1 | 1 | 3.96 | 15.74 |
| 1 | 2 | 1.72 | 15.94 |
| 2 | 2 | 0.43 | 4.39 |
| 2 | 3 | 0.16 | 2.44 |
| 3 | 3 | 0.031 | 0.32 |
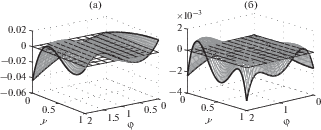
Рис. 2.
Конфигурация $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ),$ $y \in \left[ {0,1} \right],$ $\varphi \in \left[ {0,\varphi {\text{*}}} \right]$ (а); 1 – $y_{1}^{0} = 1$, 2 – $y_{2}^{0} = 0$, 3 – $y_{3}^{0} = y_{{{\text{ex}}1}}^{0}$ (б) при N = M = 2.
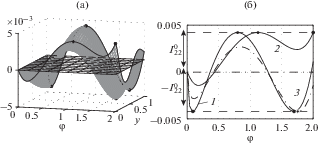
Рис. 3.
Конфигурация $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ),$ $y \in \left[ {0,1} \right],$ $\varphi \in \left[ {0,\varphi {\text{*}}} \right]$ (а); 1 – $y_{1}^{0} = 1$, 2 – $y_{2}^{0} = y_{{{\text{ex}}1}}^{0},$ 3 – $y_{3}^{0} = y_{{{\text{ex}}2}}^{0}$, 4 – $y_{4}^{0} = y_{{{\text{ex}}3}}^{0}$ (б) при N = M = 3.
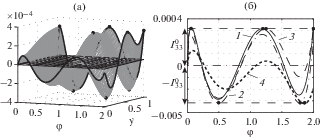
Рис. 4.
Погрешность аппроксимации идентифицируемого воздействия $u(y,\varphi ,{{\Delta }^{0}}) - q{\text{*}}(y,\varphi ),$ $y \in \left[ {0,1} \right],$ $\varphi \in \left[ {0,\varphi {\text{*}}} \right]$: (а) – N = M = 2, (б) – N = M = 3.
Как видно из представленных результатов, увеличение значений N и M приводит к уменьшению погрешности аппроксимации температурного поля, которая стремится к нулю при $N \to \infty $ и $M \to \infty .$
В подавляющем большинстве практических ситуаций на первых этапах вычислительной процедуры при малых значениях N и M величина $I_{{}}^{0}({{\Delta }^{0}})$ и соответствующее значение ошибки ${{\max }_{{y,\varphi }}}\left| {u\left( {y,\varphi ,{{\Delta }^{0}}} \right) - q{\text{*}}(y,\varphi )} \right|$ идентификации управляющего воздействия значительно превышают допустимую погрешность решения задачи. Эти этапы выполняются для того, чтобы получить решение, которое может служить начальным приближением на последующем шаге.
Например, в классе N = M = 0 постоянных управлений $u(y,\varphi ) = \tilde {\Delta }_{0}^{{}}$ конфигурация $\theta (x*,y,\varphi ,{{\Delta }^{0}})$ – ‒ $f(y,\varphi )$ характеризуется двумя точками $z_{j}^{0} = (y_{j}^{0},\varphi _{j}^{0}),j = 1,2$ с предельно допустимыми, противоположными по знаку, отклонениями $I_{{00}}^{0}({{\Delta }^{0}})$ (рис. 1) и задача (14) сводится к решению относительно единственного параметра управления $\tilde {\Delta }_{0}^{{}}$, величины $I_{{00}}^{0}$ и неизвестной координаты $\varphi _{{{\text{ex}}}}^{0}$ системы трех уравнений (система конкретизирована для рассматриваемого случая):
Далее с увеличением значений N и M в общем случае может возникать несколько вариантов конфигурации $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ),$ отвечающих системе (15). Для рассматриваемого примера (22), (23), (25) при N = M = 2 система расчетных уравнений, соответствующая конфигурации, представленной на рис. 2, имеет вид
При N = M = 3 количество сечений yk, на которых достигаются предельно допустимые отклонения, опять увеличивается, что ведет к возрастанию числа вариантов конфигурации $\theta (x*,y,\varphi ,{{\Delta }^{0}}) - f(y,\varphi ).$ Результирующая система уравнений, обеспечивающая решение задачи (14), соответствует варианту, представленному на рис. 3, и имеет вид
Погрешность ${{\max }_{{y,\varphi }}}\left| {u\left( {y,\varphi ,{{\Delta }^{0}}} \right) - q{\text{*}}(y,\varphi )} \right|$ приближения идентифицируемой функции в общем случае убывает с ростом N и M, но их взаимосвязь имеет немонотонный характер. При практической реализации поочередное увеличение значений N и M заканчивается при выполнении на очередном l-м шаге неравенства $I_{l}^{0}(\Delta ) \leqslant {{\delta }_{1}}$ или $\left| {I_{l}^{0}(\Delta ) - I_{{l - 1}}^{0}(\Delta )} \right| \leqslant {{\delta }_{2}},$ где δ1 и δ2 задаются априори. Опыт решения конкретных задач показывает, что в большинстве ситуаций при ${{\delta }_{1}} \leqslant 1\% $ обеспечивается погрешность идентификации u(y, φ) до 10%, а при ${{\delta }_{1}} \leqslant 0.1\% $ – в пределах одного процента. Максимальные отклонения наблюдаются в “угловых” точках – в последний момент времени $({{y}^{0}} = 1,{{\varphi }^{0}} = \varphi *)$ или $({{y}^{0}} = 0,{{\varphi }^{0}} = \varphi {\text{*}})$ или в начале интервала идентификации $(y_{{}}^{0} = 1,{\text{ }}{{\varphi }^{0}} = 0)$.
ЗАКЛЮЧЕНИЕ
Предложенный в работе метод решения ОЗТ на основе минимаксной оптимизации погрешности аппроксимации наблюдаемого температурного состояния позволяет получить приближенное аналитическое описание плотности теплового потока, зависящей от пространственной координаты и времени в виде произведения двух полиномиальных функций одной переменной.
Сужение класса искомых решений обеспечивает приведение исходной некорректно поставленной обратной задачи к задаче математического программирования, решение которой относительно параметров идентифицируемого воздействия осуществляется на основе специального метода, учитывающего альтернансные свойства оптимальных решений, и позволяет сохранить качественные особенности процессов с распределенными параметрами.
Работа выполнена при поддержке РФФИ (проект № 18-08-00565).
Список литературы
Алифанов О.М. Обратные задачи теплообмена. М.: Машиностроение, 1988. 280 с.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 288 с.
Бек Дж., Блакуэлл Б., Сент-Клэр Ч. мл. Некорректные обратные задачи теплопроводности. М.: Мир, 1989. 312 с.
Мацевитый Ю.М., Гайшун И.В., Борухов В.Т., Костиков А.О. Параметрическая и функциональная идентификация тепловых процессов // Пробл. машиностроения. 2011. Т. 14. № 3. С. 40.
Алифанов О.М., Егоров Ю.В. Алгоритм и результаты решения граничной обратной задачи теплопроводности в двумерной постановке // ИФЖ. 1985. Т. 48. № 4. С. 658.
Алифанов О.М., Ненарокомов А.В. Трехмерная граничная обратная задача теплопроводности // ТВТ. 1999. Т. 37. № 2. С. 231.
Guerrier B., Benard C. Two-dimensional Linear Transient Inverse Heat Conduction Problem – Boundary Condition Identification // J. Thermophys. Heat Transfer. 1993. V. 7. № 3. P. 472.
Кузин А.Я. Регуляризованное численное решение нелинейной двумерной обратной задачи теплопроводности // ПМиТФ. 1995. № 1. С. 106.
Колесник С.А., Формалев В.Ф., Кузнецова Е.Л. О граничной обратной задаче теплопроводности по восстановлению тепловых потоков к границам анизотропных тел // ТВТ. 2015. Т. 53. № 1. С. 72.
Алифанов О.М., Керов Н.В. Определение параметров внешнего теплового нагружения из решения двухмерной обратной задачи теплопроводности // ИФЖ. 1981. Т. 41. № 4. С. 581.
Рапопорт Э.Я., Плешивцева Ю.Э. Специальные методы оптимизации в обратных задачах теплопроводности // Изв. РАН. Энергетика. 2002. № 5. С. 144.
Diligenskaya A. Estimation of the Heat Flux Density During the Induction Heating Process Based on the Parametric Optimization // Int. J. Microstruct. Mater. Prop. 2016. V. 11. № 1/2. P. 5.
Коллатц Л., Крабс В. Теория приближений. Чебышевские приближения. М.: Наука, 1978. 271 с.
Рапопорт Э.Я. Альтернансный метод в прикладных задачах оптимизации. М.: Наука, 2000. 336 с.
Рапопорт Э.Я. Точный метод в задачах оптимизации нестационарных процессов теплопроводности // Изв. АН СССР. Энергетика и транспорт. 1978. № 4. С. 137.
Рапопорт Э.Я., Плешивцева Ю.Э. Алгоритмически точный метод параметрической оптимизации в краевых задачах оптимального управления системами с распределенными параметрами // Автометрия. 2009. Т. 45. № 5. С. 103.
Дилигенская А.Н., Рапопорт Э.Я. Аналитические методы параметрической оптимизации в обратных задачах теплопроводности с внутренним тепловыделением // ИФЖ. 2014. Т. 87. № 5. С. 1082.
Рапопорт Э.Я. Оптимизация процессов индукционного нагрева металла. М.: Металлургия, 1993. 278 с.
Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. М.: Наука, 1970. 712 с.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур