Теплофизика высоких температур, 2019, T. 57, № 5, стр. 694-701

ВВЕДЕНИЕ

При исследовании температурного режима твердых тел в условиях конвективного теплообмена с окружающей средой наиболее существенные результаты получены для случая постоянного относительного коэффициента теплообмена $h = {\alpha \mathord{\left/ {\vphantom {\alpha \lambda }} \right. \kern-0em} \lambda }$ (α – коэффициент теплообмена, λ – теплопроводность) [1]; считается, что $\alpha $ определяется только температурным напором. Однако, как показывают экспериментальные исследования [2], в ряде нестационарных процессов теплообмена коэффициент теплоотдачи является неравновесным и намного сильнее зависит от времени, чем от температуры, т.е. $h = h(t).$

Соответствующие задачи теплопроводности с граничными условиями вида ${{\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial n}}} \right. \kern-0em} {\partial n}}} \right)}_{{\text{Г}}}}$ = $ = h(t)\left[ {T\left| {_{{\text{Г}}}} \right. - {{T}_{{\text{C}}}}} \right],$ $t > 0$ представляют большой практический интерес, и этим случаям в аналитической теории теплопроводности традиционно уделялось повышенное внимание [2, 3]. Зависимость $h(t)$ наблюдается при формировании теплового пограничного слоя в условиях нестационарного обтекания твердых поверхностей охлаждающей жидкостью; нагреве тел пульсирующим потоком жидкости или газа; движении баллистического тела в среде с переменной плотностью и температурой; теплообмене прокатываемого металла с валками и окружающей средой; изучении явлений турбулентности при контактном измерении температуры выходных газов; нестационарном охлаждении термоэлектрических устройств; в процессах диффузии в условиях переменной температуры при изучении физической химии металлов; фазовых переходах и др. [2, 3]. Помимо технологических имеется также ряд других причин изменения коэффициента теплообмена во времени: изменение физических характеристик теплоносителя (скорости движения, степени черноты, плотности и т.п.) или изменение с течением времени состояния поверхности нагреваемого тела (окисление, засорение пылью, растрескивание и т.п.).

До настоящего времени не найдено точного решения задачи теплопроводности в замкнутой форме при произвольном законе изменения коэффициента h(t): искомая температурная функция не выражается в квадратурах и точное решение задачи имеет вид бесконечного ряда последовательных приближений. Трудность заключается в том, что невозможно, оставаясь в рамках классических методов математической физики, согласовать решение уравнения теплопроводности с граничным условием теплопроводности при переменном h(t). Объяснение этому факту достаточно простое. Для произвольной временной зависимости относительного коэффициента теплообмена собственные значения и собственные функции как решения соответствующей спектральной задачи формально зависят от времени, а это значит, что решение исходной задачи не может быть записано в виде интеграла Фурье–Ханкеля для частично ограниченной области или в виде ряда Фурье–Ханкеля для конечной области канонического типа. Последнее означает, что метод разделения переменных Фурье, лежащий в основе практически всех подходов классических дифференциальных уравнений математической физики, к цели не приводит. Характерной особенностью указанного класса задач при поиске их решений является возможность варьирования различными подходами. Это объясняется тем, что решение одной и той же тепловой задачи можно искать в различных классах функций, когда выявляются особенности структуры получаемых решений. Эти функции должны удовлетворять ряду требований: во-первых, они должны достаточно легко рассчитываться; во-вторых, обеспечивать сходимость процесса настолько хорошо, чтобы можно было сделать требуемые в задаче заключения о свойствах полученного решения; в-третьих, обеспечивать существование всех операций, допускаемых в процессе преобразований; в-четвертых, быть удобными в практическом плане при рассмотрении конкретных (частных) законов $h(t)$ после нахождения решения задачи для произвольной зависимости коэффициента теплообмена. В связи с этим на практике используются различные подходы, дающие точные (в виде бесконечного ряда) или приближенные решения такого класса задач для пластины, цилиндра, шара, полуограниченного стержня при произвольном законе $h(t)$ и его частных зависимостях: экспоненциальной, степенной, корневой, линейной, периодической, импульсной, пульсирующей и т.д.

Таковыми являются метод тепловых потенциалов, когда уравнение теплопроводности сводится к интегральному уравнению Вольтера второго рода и далее используется пикаровский процесс разложения по параметру; интегральный метод Кармана–Польгаузена из теории гидродинамического пограничного слоя; метод разложения по малому параметру (методы возмущений); операционный с использованием метода последовательных приближений; метод бичастотной передаточной функции; метод осреднения функциональных поправок; метод сведения уравнения теплопроводности к системе обыкновенных дифференциальных уравнений с использованием функции Грина; вариационный метод; метод расщепления обобщенного интегрального преобразования Фурье, дающего интегральную форму первого приближения при произвольной зависимости h(t); асимптотические методы; метод координатных функций с использованием фронта температурного возмущения и дополнительных граничных условий и др. ([2–4] (и ссылки в них). Несмотря на многообразие подходов, каждый из них в конечном счете приводит решение задачи к бесконечному ряду последовательных приближений и главной целью каждого из подходов является поиск наиболее удачного первого приближения.

РАЗЛИЧНЫЕ ФОРМЫ ПИКАРОВСКОГО ПРОЦЕССА

Рассмотрим некоторые подходы при нахождении аналитического решения задачи с переменным относительным коэффициентом теплообмена с использованием пикаровского процесса последовательных приближений. В безразмерных переменных

где $l$ – выбранная единица масштаба, имеем задачу Здесь ${\text{Bi}}\left( {{{{\text{F}}}_{{\text{0}}}}} \right)$ – непрерывно дифференцируемая неотрицательная функция. Искомое решение:

Для решения задачи применим метод расщепления обобщенного интегрального преобразования Фурье. В отличие от [5, 6], где реализованы основы этого метода, в настоящей работе дан ряд обобщений и добавлений при рассмотрении практически важных случаев. Введем интегральное преобразование

функции $T\left( {x,{{{\text{F}}}_{0}}} \right)$ с формулой обращения

Если ввести обозначения

при которых а также то изображение

Для перевода уравнения (1) в пространство изображений понадобиться еще два соотношения:

Переведем задачу (1)–(4) в пространство изображений (5):

Рассмотрим подробнее:

Раскрывая соотношение $\omega \left( {\frac{{\partial A}}{{\partial {{{\text{F}}}_{0}}}} + {{\xi }^{2}}A} \right) - {\text{Bi}}\left( {{{{\text{F}}}_{{\text{0}}}}} \right)$ с учетом (15), (16), находим

или где Таким образом, можно перейти к задаче Коши относительно функции $A\left( {\xi ,{{{\text{F}}}_{0}}} \right)$ вида Функцию $\frac{{i\psi \left( {\xi ,{{{\text{F}}}_{0}}} \right)}}{\omega } = i\frac{{\bar {\omega }}}{{{{{\left| \omega \right|}}^{2}}}}\psi \left( {\xi ,{{{\text{F}}}_{0}}} \right)$ представим как

Решение задачи Коши (19) имеет вид

и далее из (21) находим искомое изображение $\tilde {T}\left( {\xi ,{{{\text{F}}}_{{\text{0}}}}} \right)$ с учетом (20):

После упрощения выражение (22) приводится к окончательному виду

Теперь по формуле обращения (6) можно записать для искомой функции $T\left( {x,{{{\text{F}}}_{0}}} \right){\text{:}}$

Одним из доказательств справедливости найденного соотношения (24) является рассмотрение частного (классического) случая ${\text{Bi}}\left( {{{{\text{F}}}_{{\text{0}}}}} \right) = {\text{Bi*}} = {\text{const}}{\text{.}}$ Для этого случая соотношение (24) автоматически дает классическое решение

где ${\text{Ф*}}\left( z \right) = 1 - {\text{Ф}}\left( z \right),$ ${\text{Ф}}\left( z \right)$ – функция Лапласа.

Правая часть (24) зависит от неизвестной величины $T\left( {0,{{{\text{F}}}_{0}}} \right).$ Полагая в (24) $x = 0,$ приходим к интегральному уравнению Вольтера второго рода относительно $T\left( {0,{{{\text{F}}}_{0}}} \right){\text{:}}$

где

Решение уравнения (26) с использованием пикаровского процесса последовательных приближений представим в виде

где Из (28), (29) находим искомую величину $T\left( {0,{{{\text{F}}}_{0}}} \right)$ в виде бесконечного ряда последовательных приближений Покажем, что ряд (30) сходится равномерно при всех ${{{\text{F}}}_{0}} > 0$ в любом конечном промежутке изменения ${{{\text{F}}}_{0}}.$ Будем считать, что функция ${\text{Bi}}\left( {{{{\text{F}}}_{{\text{0}}}}} \right)$ ограничена на отрезке $\left[ {0,{{{\text{F}}}_{0}}} \right],$ т.е. $\left| {{\text{Bi}}\left( {{{{\text{F}}}_{{\text{0}}}}} \right)} \right| \leqslant {M \mathord{\left/ {\vphantom {M 2}} \right. \kern-0em} 2}.$ Тогда ряд, составленный из абсолютных величин членов ряда (30), будет мажорироваться рядом

Можно определить общий член этого ряда. Вычислим несколько первых интегралов

и, проверяя по индукции, замечаем, что где ${{\lambda }_{m}}$ – пока неизвестна. Для нахождения ${{\lambda }_{m}}$ сделаем в интеграле замену переменной ${{\tau }_{{n - \left( {m - 1} \right)}}}$ = $ = {{\tau }_{{n - m}}}{{\sin }^{2}}\varphi .$ Тогда получим

Отсюда

Заметим, что ${{\lambda }_{m}} \to 0$ при $m \to \infty $ и $(n + 1)$-й член ряда (31) содержит $(n + 1)$ интеграл, следовательно, он равен $\left[ {{{{{2}^{{n - 1}}}{{M}^{{n + 1}}}} \mathord{\left/ {\vphantom {{{{2}^{{n - 1}}}{{M}^{{n + 1}}}} {{{{\left( {\sqrt \pi } \right)}}^{{3n + 1}}}}}} \right. \kern-0em} {{{{\left( {\sqrt \pi } \right)}}^{{3n + 1}}}}}} \right]$ × × $\lambda {{\lambda }_{1}}{{\lambda }_{2}}.....{{\lambda }_{{n + 1}}}{{\left( {\sqrt {{{{\text{F}}}_{{\text{0}}}}} } \right)}^{{n + 1}}}.$ Вычислим коэффициенты

Таким образом, ряд (31) принимает вид Сходимость ряда (32) для всех ${{{\text{F}}}_{0}} > 0$ легко проверить по признаку Даламбера.

В качестве примеров рассмотрим случаи, представляющие интерес для процессов теплообмена прокатываемого металла с валками и окружающей средой [3]. В первом случае ${\text{Bi(}}{{{\text{F}}}_{0}}) = {\text{Bi*}} + {\text{Pd}}{{{\text{F}}}_{0}}$ (${\text{Pd}}$ – число Прандтля), во втором – ${\text{Bi}}({{F}_{0}}) = {\text{Bi*}} + \beta \exp ( - {\text{Pd}}{{{\text{F}}}_{0}}).$

На рис. 1 приведены значения приближений температурной функции (30) ${{\Psi }_{1}}({{{\text{F}}}_{0}}) = {{T}_{0}}({{{\text{F}}}_{0}}),$ ${{\Psi }_{2}}({{{\text{F}}}_{0}}) = {{T}_{0}}({{{\text{F}}}_{0}}) + ({2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi }){{T}_{1}}({{{\text{F}}}_{0}}),$ ${{\Psi }_{3}}({{{\text{F}}}_{{\text{0}}}}) = {{T}_{0}}({{{\text{F}}}_{0}})$ + $ + \,\,({2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi }){{T}_{1}}({{{\text{F}}}_{0}}) + {{({2 \mathord{\left/ {\vphantom {2 \pi }} \right. \kern-0em} \pi })}^{2}}{{T}_{2}}({{{\text{F}}}_{0}})$ для первого случая, рассчитанные в зависимости от критерия ${{{\text{F}}}_{0}}$ в сечении $x = 0.5$ при ${\text{Bi*}} = 0.5,$ ${\text{Pd}} = 1.$ Видно, что первое и второе приближения берут в вилку третье приближение, что позволяет с достаточной для практики точностью ограничиться тремя первыми приближениями.

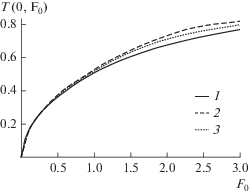
На рис. 2 приведены кривые распределения температуры $T(x,{{{\text{F}}}_{0}})$ (24) в сечении $x = 0.5$ в зависимости от ${{{\text{F}}}_{0}}$ для первого случая изменения ${\text{Bi(}}{{{\text{F}}}_{0}})$ при ${\text{Bi*}} = 0.5$ и $1$ (при трех приближениях в (30)) для ${\text{Pd}} = 0$ (классический случай (25)) и ${\text{Pd}} = 1.$ Видно, что наличие переменного во времени линейного относительного коэффициента теплообмена резко меняет картину тепловой реакции области на нагрев: температура возрастает, достигает максимума и затем убывает, заходя в отрицательную область значений (последнее, по-видимому, ограничивает область значений числа Фурье при конкретных расчетах).

На рис. 3 приведены кривые распределения температуры $T(x,{{{\text{F}}}_{0}})$ (24) в сечении $x = 0.5$ в зависимости от числа Фурье для второго случая изменения ${\text{Bi(}}{{{\text{F}}}_{0}})$ (при трех приближениях в (30)) для $\beta = 0$ (классический случай (25)) $\beta = 1,$ ${\text{Pd}} = 1.$ Видно, что в интервале практических значений числа Фурье влияние экспоненциального во времени коэффициента ${\text{Bi(}}{{{\text{F}}}_{0}})$ не существенно.

Продолжим изучение указанного класса задач теплопроводности и рассмотрим следующий подход для решения задачи:

Для простоты записи положено $a = 1,$ ${{T}_{C}} = 0,$ что не ограничивает общности рассуждения. Решение уравнения (33) записывается в виде

и на отрицательной полуоси $x$ в качестве начальной подбирается такая функция $F\left( x \right),$ чтобы (36) удовлетворяло граничному условию (35). Последнее приводит к функциональному уравнению вида где $f\left( x \right) = F\left( { - x} \right) - {{T}_{0}},$ $\gamma \left( t \right) = h\left( t \right)\sqrt {\pi t} .$ Если предположить, что функция $h\left( t \right)$ раскладывается в ряд по степеням ${{t}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ т.е. $\gamma \left( t \right) = \sum\nolimits_{n = 0}^\infty {{{\gamma }_{n}}{{t}^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0em} 2}}}}} ,$ и искать функцию $f\left( x \right)$ в виде ряда $f\left( x \right) = \sum\nolimits_{n = 0}^\infty {{{a}_{n}}{{x}^{n}}} ,$ то уравнение (37) дает для коэффициентов соотношение а вместе с этим решение $T\left( {x,t} \right)$ в виде

Метод последовательных приближений для уравнения $\frac{{\partial T}}{{\partial t}} = \frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}}$ с нулевым начальным условием (34) и граничным условием ${{\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0em} {\partial x}}} \right)}_{{x = 0}}} = h\left( t \right)\left[ {T\left( {0,t} \right) - \varphi \left( t \right)} \right]$ дает решение задачи в другом виде

Для ограниченной на отрезке $\left[ {0,t} \right]$ функции $h\left( t \right)$ ряд (39) сходится абсолютно и равномерно при всех $x > 0$ и $t > 0$ в любом конечном промежутке изменения и допускает ряд частных случаев, представляющих практический интерес. Так, для $h\left( t \right) = {{h}_{0}}{{t}^{m}},$ $\varphi \left( t \right) = {{T}_{C}}{{t}^{r}},$ где $m,$ r – действительные числа, выражение (39) принимает вид где $B\left( {c,d} \right)$ – бета-функция. Предполагается, что $\left[ {r + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} + k\left( {m + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} \right] > 0.$ При $m = - \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right),$ т.е. $h\left( t \right) = {{h}_{0}}{{t}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ и $r = 0,$ выражение (40) дает компактное решение при условии, что ${{h}_{0}}\sqrt {a\pi } < 1.$ Аналогично могут быть представлены и другие случаи.

Рассмотрим далее подход, основанный на функциональных преобразованиях Гринберга (ссылки в [2]) при решении задачи

Введем функцию $R(t) = {1 \mathord{\left/ {\vphantom {1 {h(t)}}} \right. \kern-0em} {h(t)}}$ и запишем (43) в виде

Пусть $y = {x \mathord{\left/ {\vphantom {x {R(t)}}} \right. \kern-0em} {R(t)}},$ $T(x,t) = \Theta (y,t).$ Тогда (41), (42), (44) записываются в виде Здесь $\dot {R}(t) = {{dR(t)} \mathord{\left/ {\vphantom {{dR(t)} {dt}}} \right. \kern-0em} {dt}}.$ Введем далее новую функцию с помощью преобразования что позволит записать (45)–(47) в виде Рассмотрим для (49) случаи, допускающие точное решение. Пусть ${{R}^{3}}\ddot {R} = - {{M}^{2}} = {\text{const}},$ что означает изменение $R(t)$ по закону $R(t) = \sqrt {{{{(At + B)}}^{2}} - {{A}^{2}}B} .$ Этот случай встречается при изучении нестационарного охлаждения термоэлектрических элементов (ссылки в [2]). Собственные функции задачи (49)–(51) при данном условии представляют где ${{W}_{{\nu ,\mu }}}(x)$ – функция Уиттекера. Собственные числа ${{\nu }_{n}}$ образуют дискретный спектр и удовлетворяют уравнению $\Gamma (x)$ – гамма-функция. Решение этой задачи возможно получить на основе разложения в ряд Фурье искомой функции по системе (52), (53). Если ${{M}^{2}} = 0,$ $R(t) = At \pm B,$ то собственные функции (52) переходят в тригонометрические функции, спектр собственных чисел становится непрерывным.

Рассмотрим подробно последний случай. В (49)–(51) при ${{R}^{3}}\ddot {R} = 0$ введем новые переменные

Так как величина ${1 \mathord{\left/ {\vphantom {1 {{{R}^{2}}(t)}}} \right. \kern-0em} {{{R}^{2}}(t)}} > 0,$ то $\tau $ монотонно возрастает вместе с $t$ и задача (49)–(51) записывается в виде Здесь $\varphi (\tau ) = {{T}_{0}}\sqrt {R(t)} \left| {_{{t = {{L}^{{ - 1}}}(\tau )}}} \right..$ Заметим, что размерность $\left[ \tau \right] = {c \mathord{\left/ {\vphantom {c {{{M}^{2}}}}} \right. \kern-0em} {{{M}^{2}}}}.$ Решение $U(y,\tau )$ получим, используя подход, развитый в [7]. Интегральное представление аналитического решения задачи (55)–(57) имеет вид где $G(y,y{\kern 1pt} {\text{'}},\tau - \tau {\kern 1pt} {\text{'}})$ – функция Грина: Здесь $\Phi {\text{*}}(x) = 1 - \Phi (x),$ $\Phi (x)$ = $ = {2 \mathord{\left/ {\vphantom {2 {\sqrt \pi }}} \right. \kern-0em} {\sqrt \pi }}\int_0^x {\exp ( - {{y}^{2}})dy} $ – функция Лапласа.

В качестве еще одного примера, имеющего многочисленные приложения [3], рассмотрим для (33)–(35) случай, когда условие теплообмена (35) задается в виде свертки двух функций

В пространстве изображений (по Лапласу) решение имеет вид

Тогда для оригинала можно записать

Доказательство сходимости этого ряда аналогично доказательству сходимости ряда (30).

ЗАКЛЮЧЕНИЕ

Таким образом, приведенные подходы дают разные функциональные выражения для первых слагаемых бесконечного ряда последовательных приближений и лишь для небольшого числа частных зависимостей $h\left( t \right)$ в (35) можно получить аналитическое решение задачи в замкнутой форме. Решение класса такого рода зависимостей $h\left( t \right)$ представляет собой одну из открытых проблем аналитической теории теплопроводности для краевых задач нестационарного тепло- и массопереноса с переменным во времени относительным коэффициентом теплообмена (массообмена). Дальнейшее развитие этой проблемы – переход к теории теплопроводности на основе гипотезы Максвелла–Каттанео–Лыкова–Вернотта [3].