1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 57, № 6, 2019

Теплофизика высоких температур, 2019, T. 57, № 6, стр. 886-892

Стационарное температурное поле разделительной системы с активной теплозащитой, обладающей обратной связью и анизотропным покрытием

А. В. Аттетков 1, *, П. А. Власов 1, И. К. Волков 1

1 Московский государственный технический университет им. Н.Э. Баумана (национальный исследовательский университет)
Москва, Россия

* E-mail: fn2@bmstu.ru

Поступила в редакцию 11.04.2019
После доработки 16.05.2019
Принята к публикации 16.05.2019

Полный текст (PDF)

Аннотация

Сформулирована задача об определении стационарного температурного поля системы, имитируемой стенкой, разделяющей две различные среды. С одной стороны стенка снабжена анизотропным теплозащитным покрытием, подвергаемым локальному тепловому воздействию в условиях теплообмена с внешней средой, а также термоактивной прокладкой, функционирующей по принципу обратной связи. Решение задачи получено с использованием методов интегральных преобразований в аналитически замкнутом виде.

ВВЕДЕНИЕ

В приложениях математической теории теплопроводности [1–4] важное место занимают вопросы разработки эффективных способов тепловой защиты конструкций [4–11]. Одно из перспективных направлений их технической реализации связано с использованием термоэлектрических эффектов путем применения термоактивной прокладки, являющейся средством управляемого внешнего воздействия на температурное поле объекта за счет регулирования силы тока или проявления эффекта обратной связи [12–14].

Трудности, возникающие при параметрическом анализе температурных полей конструкций с активной теплозащитой, известны [12–14]. Они усугубляются при использовании в качестве покрытий современных композиционных материалов, обладающих значимой степенью анизотропии [4, 15]. Исследования по рассматриваемому вопросу немногочисленны [16–19], а любой новый результат, полученный аналитическими методами, имеет и теоретическое, и определенное практическое значение.

Цель проведенных исследований – решить задачу об определении стационарного температурного поля системы, имитируемой разделяющей две различных среды стенкой с термоактивной прокладкой на одной из ее поверхностей, которая функционирует по принципу обратной связи, а также с анизотропным теплозащитным покрытием, подвергаемым локальному тепловому воздействию в условиях теплообмена с внешней средой.

ИСХОДНЫЕ ДОПУЩЕНИЯ И МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

При построении исходной математической модели для определения стационарного температурного поля $T\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right)$ объекта исследований в фиксированной декартовой системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ пространства ${{\mathbb{R}}^{3}}$ предполагалось следующее.

1) Объект исследований представляет собой систему, состоящую из изотропной разделительной стенки:

${{{\Omega }}_{{{\text{ст}}}}} = \left\{ {\left. {\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right] \in {{\mathbb{R}}^{3}}:~\begin{array}{*{20}{c}} { - \infty < {{x}_{1}} < + \infty } \\ {0 < {{x}_{2}} < {{h}_{{{\text{ст}}}}}} \\ { - \infty < {{x}_{3}} < + \infty } \end{array}} \right\}} \right.,$
поверхность ${{x}_{2}} = 0$ которой обладает анизотропным покрытием
${{{\Omega }}_{{\text{п}}}} = \left\{ {\left. {\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right] \in {{\mathbb{R}}^{3}}:~\begin{array}{*{20}{c}} { - \infty < {{x}_{1}} < + \infty } \\ { - \left( {{{h}_{{\text{п}}}} + {{h}_{{{\text{тп}}}}}} \right) < {{x}_{2}} < - {{h}_{{{\text{тп}}}}}} \\ { - \infty < {{x}_{3}} < + \infty } \end{array}} \right\}} \right.$
с термоактивной прокладкой [12–14]
${{{\Omega }}_{{{\text{тп}}}}} = \left\{ {\left. {\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right] \in {{\mathbb{R}}^{3}}:~\begin{array}{*{20}{c}} { - \infty < {{x}_{1}} < + \infty } \\ { - {{h}_{{{\text{тп}}}}} < {{x}_{2}} < 0} \\ { - \infty < {{x}_{3}} < + \infty } \end{array}} \right\}} \right.,$
где значения геометрических характеристик ${{h}_{{{\text{ст}}}}},$ ${{h}_{{{\text{тп}}}}},$ ${{h}_{{\text{п}}}}$ элементов объекта исследований – постоянные величины.

2) Термоактивная прокладка является ортотропной и функционирует по принципу обратной связи [14, 20, 21], т.е. в системах “анизотропное покрытие–термоактивная прокладка” и “термоактивная прокладка–изотропная разделительная стенка” для искомого температурного поля $T\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right)$ реализуются следующие условия сопряжения:

$T\left( {{{x}_{1}}, - {{h}_{{{\text{тп}}}}} - 0,{{x}_{3}}} \right) = T\left( {{{x}_{1}}, - {{h}_{{{\text{тп}}}}} + 0,{{x}_{3}}} \right),$
$\begin{gathered} {{\left. {\left[ {\lambda _{{12}}^{{\left( {\text{п}} \right)}}\frac{{\partial T}}{{\partial {{x}_{1}}}} + \lambda _{{22}}^{{\left( {\text{п}} \right)}}\frac{{\partial T}}{{\partial {{x}_{2}}}} + \lambda _{{23}}^{{\left( {\text{п}} \right)}}\frac{{\partial T}}{{\partial {{x}_{3}}}}} \right]} \right|}_{{{{x}_{2}} = - {{h}_{{{\text{тп}}}}} - 0}}} - \\ - \,\,{{\left. {\lambda _{2}^{{\left( {{\text{тп}}} \right)}}\frac{{\partial T}}{{\partial {{x}_{2}}}}} \right|}_{{{{x}_{2}} = - {{h}_{{{\text{тп}}}}} + 0}}} = - q_{{{\text{тп}}}}^{{\left( {\text{п}} \right)}}{{\left. {\left[ {T - {{T}_{0}}} \right]} \right|}_{{{{x}_{2}} = - {{h}_{{{\text{тп}}}}} + 0}}}, \\ \end{gathered} $
$T\left( {{{x}_{1}},~0 - 0,{{x}_{3}}} \right) = T\left( {{{x}_{1}},0 + 0,{{x}_{3}}} \right),$
$\begin{gathered} {{\left. {\lambda _{2}^{{\left( {{\text{тп}}} \right)}}\frac{{\partial T}}{{\partial {{x}_{2}}}}} \right|}_{{{{x}_{2}} = 0 - 0}}} - {{\left. {{{\lambda }^{{\left( {{\text{ст}}} \right)}}}\frac{{\partial T}}{{\partial {{x}_{2}}}}} \right|}_{{{{x}_{2}} = 0 + 0}}} = \\ = - q_{{{\text{тп}}}}^{{\left( {{\text{ст}}} \right)}}{{\left. {\left[ {T - {{T}_{0}}} \right]} \right|}_{{{{x}_{2}} = 0 + 0}}}, \\ \end{gathered} $
где $\left\{ {\lambda _{{ij}}^{{\left( {\text{п}} \right)}}} \right\},$ $\left\{ {\lambda _{k}^{{\left( {{\text{тп}}} \right)}}} \right\}$ и ${{\lambda }^{{\left( {{\text{ст}}} \right)}}}$ – компоненты тензоров теплопроводности анизотропного материала покрытия, ортотропного материала термоактивной прокладки при $\lambda _{1}^{{\left( {{\text{тп}}} \right)}} = \lambda _{3}^{{\left( {{\text{тп}}} \right)}}$ и изотропного материала разделительной стенки соответственно; $q_{{{\text{тп}}}}^{{\left( {\text{п}} \right)}}$ – определяющий параметр обратной связи термоактивной прокладки со стороны покрытия, а $q_{{{\text{тп}}}}^{{\left( {{\text{ст}}} \right)}}$ – со стороны стенки; ${{T}_{0}}$ – начальная температура объекта исследований, принятая постоянной.

3) Обратная связь настроена по начальной температуре ${{T}_{0}}$ объекта исследований, которая отлична от температур внешней среды $T_{{\text{с}}}^{{\left( {{\text{ст}}} \right)}}$ (при ${{x}_{2}} > {{h}_{{{\text{ст}}}}}$) и $T_{{\text{с}}}^{{\left( {\text{п}} \right)}}$ (${{x}_{2}} < - \left( {{{h}_{{\text{п}}}} + {{h}_{{{\text{тп}}}}}} \right)$), также постоянных. При этом в общем случае $T_{{\text{с}}}^{{\left( {{\text{ст}}} \right)}} \ne T_{{\text{с}}}^{{\left( {\text{п}} \right)}}.$

4) Теплообмен в системах “внешняя поверхность разделительной стенки–внешняя среда” и “внешняя поверхность анизотропного покрытия–внешняя среда” реализуется по закону Ньютона [2, 3] с коэффициентами теплоотдачи ${{\alpha }_{{\text{п}}}}$ и ${{\alpha }_{{{\text{ст}}}}}$ соответственно.

5) Внешняя поверхность анизотропного покрытия находится под воздействием не только внешней среды с $T_{{\text{с}}}^{{\left( {\text{п}} \right)}},$ отличной от ${{T}_{0}},$ но и теплового потока с плотностью $q\left( {{{x}_{1}},{{x}_{3}}} \right).$

6) Внешний тепловой поток с плотностью $q\left( {{{x}_{1}},{{x}_{3}}} \right)$ воздействует на поверхность x2 = $ = - \left( {{{h}_{{\text{п}}}} + {{h}_{{{\text{тп}}}}}} \right)$ анизотропного покрытия разделительной стенки в направлении его внутренней нормали.

7) Функция $q\left( {{{x}_{1}},{{x}_{3}}} \right)$ интегрируема с квадратом в ${{\mathbb{R}}^{2}}$ по совокупности пространственных переменных, представленных вектором ${{\left[ {{{x}_{1}},{{x}_{3}}} \right]}^{{\text{T}}}} \in {{\mathbb{R}}^{2}},$ т.е. $q\left( {{{x}_{1}},{{x}_{3}}} \right) \in {{L}^{2}}({{\mathbb{R}}^{2}})$ [22].

8) Термоактивная прокладка является “термически тонкой”, т.е. допустима реализация идеи “сосредоточенной емкости” [23], суть которой полностью определена равенствами

$T\left( {{{x}_{1}}, - {{h}_{{{\text{тп}}}}} + 0,{{x}_{3}}} \right) = \left\langle {T\left( {{{x}_{1}},{{x}_{3}}} \right)} \right\rangle = T\left( {{{x}_{1}},0 - 0,{{x}_{3}}} \right),$
$\left\langle {T\left( {{{x}_{1}},{{x}_{3}}} \right)} \right\rangle \triangleq \frac{1}{{{{h}_{{{\text{тп}}}}}}}\int\limits_{ - {{h}_{{{\text{тп}}}}}}^0 {T\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right)d{{x}_{2}}} .$

Для удобства дальнейших рассуждений целесообразно воспользоваться следующими обозначениями:

$\begin{gathered} \theta = \frac{{T - {{T}_{0}}}}{{T_{{\text{с}}}^{{\left( {\text{п}} \right)}} - {{T}_{0}}}},\,\,\,\,~x = \frac{{{{x}_{1}}}}{{l{\text{*}}}},\,\,\,\,~y = \frac{{{{x}_{2}}}}{{l{\text{*}}}}, \\ z = \frac{{{{x}_{3}}}}{{l{\text{*}}}},\,\,\,\,{{H}_{1}} = \frac{{{{h}_{{\text{п}}}}}}{{l{\text{*}}}}, \\ \end{gathered} $
$\begin{gathered} {{H}_{2}} = \frac{{{{h}_{{{\text{тп}}}}}}}{{l{\text{*}}}},\,\,\,\,{{H}_{3}} = \frac{{{{h}_{{{\text{ст}}}}}}}{{l{\text{*}}}},\,\,\,\,\left\langle \theta \right\rangle = \frac{{\left\langle T \right\rangle - {{T}_{0}}}}{{T_{{\text{с}}}^{{\left( {\text{п}} \right)}} - {{T}_{0}}}}, \\ {\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}} = \frac{{{{\alpha }_{{\text{п}}}}l{\text{*}}}}{{\lambda _{{22}}^{{\left( {\text{п}} \right)}}}}, \\ \end{gathered} $
$\begin{gathered} {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}} = \frac{{{{\alpha }_{{{\text{ст}}}}}{{l}_{{\text{*}}}}}}{{{{\lambda }^{{\left( {{\text{ст}}} \right)}}}}},\,\,\,\,{{\mu }_{k}} = \frac{{{{c}_{{\text{п}}}}{{\rho }_{{\text{п}}}}\lambda _{{22}}^{{\left( {{\text{тп}}} \right)}}}}{{{{c}_{{{\text{тп}}}}}{{\rho }_{{{\text{тп}}}}}\lambda _{{22}}^{{\left( {\text{п}} \right)}}}}, \\ {{Q}_{{\text{*}}}} = \frac{{\left( {q_{{{\text{тп}}}}^{{\left( {\text{п}} \right)}} + q_{{{\text{тп}}}}^{{\left( {{\text{ст}}} \right)}}} \right){{l}_{{\text{*}}}}}}{{\lambda _{{22}}^{{\left( {\text{п}} \right)}}}}, \\ \end{gathered} $
$\begin{gathered} {{\mu }_{{ij}}} = \frac{{\lambda _{{ij}}^{{\left( {\text{п}} \right)}}}}{{\lambda _{{22}}^{{\left( {\text{п}} \right)}}}},\,\,\,\,\mu = \frac{{{{c}_{{\text{п}}}}{{\rho }_{{\text{п}}}}{{\lambda }^{{{\text{ст}}}}}}}{{{{c}_{{{\text{ст}}}}}{{\rho }_{{{\text{ст}}}}}\lambda _{{22}}^{{\left( {\text{п}} \right)}}}}, \\ Q = \frac{{q{{l}_{{\text{*}}}}}}{{\lambda _{{22}}^{{\left( {\text{п}} \right)}}\left( {T_{{\text{с}}}^{{\left( {\text{п}} \right)}} - {{T}_{0}}} \right)}},\,\,\,\,\Delta {{\theta }_{{13}}} = \frac{{T_{{\text{с}}}^{{\left( {{\text{ст}}} \right)}} - {{T}_{0}}}}{{T_{{\text{с}}}^{{\left( {\text{п}} \right)}} - {{T}_{0}}}}, \\ \end{gathered} $
где ${{l}_{{\text{*}}}}$ – масштаб пространственных переменных, а ${{\rho }_{{\text{п}}}},$ ${{\rho }_{{{\text{тп}}}}},$ ${{\rho }_{{{\text{ст}}}}},$ $~{{c}_{{\text{п}}}},$ ${{c}_{{{\text{тп}}}}},$ ${{c}_{{{\text{ст}}}}}$ – плотности и удельные массовые теплоемкости анизотропного материала покрытия, ортотропного материала термоактивной прокладки и изотропного материала разделительной стенки соответственно. В этом случае согласно исходным допущениям, представленным выше, функция $\theta \left( {x,y,z} \right),$ определяющая искомое температурное поле, должна удовлетворять системе трех линейных дифференциальных уравнений в частных производных второго порядка эллиптического типа [2–4, 22]:
(1)
$\begin{gathered} {{\mu }_{{11}}}\frac{{{{\partial }^{2}}{\theta }}}{{\partial {{x}^{2}}}} + 2{{\mu }_{{12}}}\frac{{{{\partial }^{2}}{\theta }}}{{\partial x\partial y}} + 2{{\mu }_{{13}}}\frac{{{{\partial }^{2}}{\theta }}}{{\partial x\partial z}} + \frac{{{{\partial }^{2}}{\theta }}}{{\partial {{y}^{2}}}} + \\ + \,\,2{{\mu }_{{23}}}\frac{{{{\partial }^{2}}{\theta }}}{{\partial y\partial z}} + {{\mu }_{{33}}}\frac{{{{\partial }^{2}}{\theta }}}{{\partial {{z}^{2}}}} = 0,\,\,\,\,\left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}}, \\ - \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}},\,\,\,\,{{\mu }_{1}}\left[ {\frac{{{{\partial }^{2}}\left\langle {\theta } \right\rangle }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\left\langle {\theta } \right\rangle }}{{\partial {{z}^{2}}}}} \right] - \\ - \,\,\frac{{{{Q}_{{\text{*}}}}}}{{{{H}_{2}}}}\left\langle {\theta } \right\rangle + \frac{1}{{{{H}_{2}}}}\left\{ {\mu {{{\left. {\frac{{\partial {\theta }}}{{\partial y}}} \right|}}_{{y = 0 + 0}}} - } \right. \\ \left. { - \,\,{{{\left. {\left[ {{{\mu }_{{12}}}\frac{{\partial {\theta }}}{{\partial x}} + \frac{{\partial {\theta }}}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial {\theta }}}{{\partial z}}} \right]} \right|}}_{{y = - {{H}_{2}} - 0}}}} \right\} = 0, \\ \left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\, - {{H}_{2}} < y < 0, \\ \frac{{{{\partial }^{2}}{\theta }}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\theta }}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{\theta }}}{{\partial {{z}^{2}}}} = 0,\,\,\,\,~\left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\,0 < y < {{H}_{3}}, \\ \end{gathered} $
условиям реализуемости идеи “сосредоточенная емкость” по толщине термоактивной прокладки [23]:

(2)
$\theta \left( {x, - {{H}_{2}} - 0,z} \right) = \left\langle {\theta \left( {x,z} \right)} \right\rangle = \theta \left( {x,0 + 0,z} \right)$

и неоднородным краевым условиям [2–4]

(3)
$\begin{gathered} {{\left. { - \left[ {{{\mu }_{{12}}}\frac{{\partial {\theta }}}{{\partial x}} + \frac{{\partial {\theta }}}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial {\theta }}}{{\partial z}}} \right]} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} = \\ = {{\left. {{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}\left( {1 - {\theta }} \right)} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} + Q\left( {x,z} \right), \\ \end{gathered} $
(4)
${{\left. {\frac{{\partial \theta }}{{\partial y}}} \right|}_{{y = {{H}_{3}}}}} = {{\left. {{\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}\left( {\Delta {{\theta }_{{13}}} - \theta } \right)} \right|}_{{y = {{H}_{3}}}}}.$

Анализ формализованной исходной информации, представленной в виде незамкнутой математической модели (1)–(4), в сочетании с исходными допущениями позволяет выдвинуть гипотезу о том, что искомое стационарное температурное поле объекта исследований имеет аддитивную структуру с двумя независимыми составляющими. Первая аддитивная составляющая определяет стационарное температурное поле объекта исследований, сформированное исключительно в результате его теплообмена с разделенными средами, обладающими различной температурой, а вторая – стационарное температурное поле объекта исследований, сформированное под воздействием внешнего теплового потока и охлаждения разделенными средами с нулевой температурой. Таким образом, приходим к равенству

(5)
${\theta }\left( {x,y,z} \right) = {{{\theta }}_{1}}\left( y \right) + {{{\theta }}_{2}}\left( {x,y,z} \right),$
где функция ${{{\theta }}_{1}}\left( y \right)$ должна являться решением замкнутого варианта исходной краевой задачи (1)–(4) при нулевой плотности внешнего теплового потока, т.е. удовлетворять следующей краевой задаче для системы двух обыкновенных линейных дифференциальных уравнений второго порядка со специфическими условиями сопряжения:
(6)
$\begin{gathered} \frac{{{{d}^{2}}{{{\theta }}_{1}}}}{{d{{y}^{2}}}} = 0,\,\,\,\,~ - {\kern 1pt} \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}}, \\ \frac{{{{d}^{2}}{{{\theta }}_{1}}}}{{d{{y}^{2}}}} = 0,\,\,\,\,~0 < y < {{H}_{3}}, \\ {{\left. { - \frac{{d{{{\theta }}_{1}}}}{{dy}}} \right|}_{{y = - ({{H}_{1}} + {{H}_{2}})}}} = {{\left. {{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}\left[ {1 - {{{\theta }}_{1}}} \right]} \right|}_{{y = - ({{H}_{1}} + {{H}_{2}})}}}, \\ {{{\theta }}_{1}}\left( { - {{H}_{2}} - 0} \right) = \left\langle {{{{\theta }}_{1}}} \right\rangle = {{{\theta }}_{1}}\left( {0 + 0} \right), \\ {{\left. {\mu \frac{{d{{{\theta }}_{1}}}}{{dy}}} \right|}_{{y = 0 + 0}}} - {{\left. {\frac{{d{{{\theta }}_{1}}}}{{dy}}} \right|}_{{y = - {{H}_{2}} - 0}}} = {{Q}_{{\text{*}}}}\left\langle {{{{\theta }}_{1}}} \right\rangle , \\ {{\left. {\frac{{d{{{\theta }}_{1}}}}{{dy}}} \right|}_{{y = {{H}_{3}}}}} = {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}{{\left[ {\Delta {{\theta }_{{13}}} - {{\theta }_{1}}} \right]}_{{y = {{H}_{3}}}}}. \\ \end{gathered} $
При этом, согласно (5), исходному допущению 8 и линейности оператора интегрирования, имеем
(7)
$\begin{gathered} \left\langle {\theta \left( {x,z} \right)} \right\rangle = \left\langle {{{\theta }_{1}}} \right\rangle + \left\langle {{{\theta }_{2}}\left( {x,z} \right)} \right\rangle , \\ \left\langle {{{\theta }_{1}}} \right\rangle \equiv \frac{1}{{{{H}_{2}}}}\int\limits_{ - {{H}_{2}}}^0 {{{\theta }_{1}}\left( y \right)dy,} \\ \left\langle {{{\theta }_{2}}\left( {x,y,z} \right)} \right\rangle \equiv \frac{1}{{{{H}_{2}}}}\int\limits_{ - {{H}_{2}}}^0 {{{\theta }_{2}}\left( {x,y,z} \right)dy} .~~ \\ \end{gathered} $
Далее, согласно (1)–(7), с учетом допущения 7 приходим к математической модели для определения второй аддитивной составляющей искомого температурного поля объекта исследований, представленной функцией ${{\theta }_{2}}\left( {x,y,z} \right){\text{:}}$

$\begin{gathered} {{\mu }_{{11}}}\frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial {{x}^{2}}}} + 2{{\mu }_{{12}}}\frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial x\partial y}} + 2{{\mu }_{{13}}}\frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial x\partial z}} + \frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial {{y}^{2}}}} + \\ + \,\,2{{\mu }_{{23}}}\frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial y\partial z}} + {{\mu }_{{33}}}\frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial {{z}^{2}}}} = 0, \\ \left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\, - \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}}, \\ {{\mu }_{1}}\left[ {\frac{{{{\partial }^{2}}\left\langle {{{{\theta }}_{2}}} \right\rangle }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\left\langle {{{{\theta }}_{2}}} \right\rangle }}{{\partial {{z}^{2}}}}} \right] - \frac{{{{Q}_{{\text{*}}}}}}{{{{H}_{2}}}}\left\langle {{{{\theta }}_{2}}} \right\rangle + \frac{1}{{{{H}_{2}}}}\left\{ {\mu {{{\left. {\frac{{\partial {{{\theta }}_{2}}}}{{\partial y}}} \right|}}_{{y = 0 + 0}}} - } \right. \\ \end{gathered} $
$\begin{gathered} \left. { - \,\,{{{\left. {\left[ {{{\mu }_{{12}}}\frac{{\partial {{{\theta }}_{2}}}}{{\partial x}} + \frac{{\partial {{{\theta }}_{2}}}}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial {{{\theta }}_{2}}}}{{\partial z}}} \right]} \right|}}_{{y = - {{H}_{2}} - 0}}}} \right\} = 0, \\ \left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\, - {\kern 1pt} {{H}_{2}} < y < 0, \\ \frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{{\theta }}_{2}}}}{{\partial {{z}^{2}}}} = 0,~\,\,\,\,\left[ {\begin{array}{*{20}{c}} x \\ z \end{array}} \right] \in {{\mathbb{R}}^{2}},\,\,\,\,0 < y < {{H}_{3}}, \\ {{\left. {\left[ {{{\mu }_{{12}}}\frac{{\partial {{{\theta }}_{2}}}}{{\partial x}} + \frac{{\partial {{{\theta }}_{2}}}}{{\partial y}} + {{\mu }_{{23}}}\frac{{\partial {{{\theta }}_{2}}}}{{\partial z}}} \right]} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} = \\ = {{\left. {{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}{{{\theta }}_{2}}} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} - Q\left( {x,z} \right), \\ \end{gathered} $
$\begin{gathered} {{{\theta }}_{2}}\left( {x, - {{H}_{2}} - 0,z} \right) = \left\langle {{{{\theta }}_{2}}\left( {x,z} \right)} \right\rangle = {{{\theta }}_{2}}\left( {x,0 + 0,z} \right), \\ {{\left. {\frac{{\partial {\theta }}}{{\partial y}}} \right|}_{{y = {{H}_{3}}}}} = - {{\left. {{\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}{{{\theta }}_{2}}} \right|}_{{y = {{H}_{3}}}}},\,\,\,\,Q\left( {x,z} \right) \in {{L}^{2}}({{\mathbb{R}}^{2}}), \\ {{\left. {{{{\theta }}_{2}}\left( {x,y,z} \right)} \right|}_{{\left( {y \in \left[ { - \left( {{{H}_{1}} + {{H}_{2}}} \right),~{{H}_{3}}} \right]} \right)}}} \in {{L}^{2}}({{\mathbb{R}}^{2}}), \\ \left\langle {{{{\theta }}_{2}}\left( {x,z} \right)} \right\rangle \in {{L}^{2}}({{\mathbb{R}}^{2}}). \\ \end{gathered} $

ТЕМПЕРАТУРНОЕ ПОЛЕ

Согласно равенству (5), первая независимая аддитивная составляющая искомого стационарного температурного поля объекта исследований представлена функцией ${{\theta }_{1}}\left( y \right),$ которая полностью определена краевой задачей (6). Решение этой краевой задачи может быть найдено стандартными методами [24] и представлено в следующем виде:

${{\left. {{{{\theta }}_{1}}\left( y \right)} \right|}_{{\left( { - \left( {{{H}_{1}} + {{H}_{2}}} \right) \leqslant y \leqslant - {{H}_{2}}} \right)}}} = \left( {y + {{H}_{2}}} \right){{C}_{1}} + \left\langle {{{{\theta }}_{1}}} \right\rangle ,$
${{\left. {{{{\theta }}_{1}}\left( y \right)} \right|}_{{\left( {0 \leqslant y \leqslant {{H}_{3}}} \right)}}} = y{{C}_{2}} + \left\langle {{{{\theta }}_{1}}} \right\rangle ,$
$\left\langle {{{{\theta }}_{1}}} \right\rangle = \left( {\mu {{C}_{2}} - {{C}_{1}}} \right)Q_{*}^{{ - 1}},$
${{C}_{1}} = \left[ {\left( {\Delta {{{\theta }}_{{13}}} - 1} \right)\mu {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}} - {{Q}_{{\text{*}}}}\left( {1 + {{H}_{3}}{\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}} \right)} \right]{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}{{\Delta }^{{ - 1}}},$
$\begin{gathered} {{C}_{2}} = \left[ {\left( {\Delta {{{\theta }}_{{13}}} - 1} \right)\mu {\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}} + } \right. \\ \left. { + \,\,{{Q}_{{\text{*}}}}\left( {1 + {{H}_{1}}{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}} \right)\Delta {{{\theta }}_{{13}}}} \right]{\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}{{\Delta }^{{ - 1}}}, \\ \end{gathered} $
$\begin{gathered} \Delta = \left( {1 + {{H}_{1}}{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}} \right)\mu {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}} + \left( {1 + {{H}_{3}}{\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}} \right){\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}} + \\ + \,\,\left( {1 + {{H}_{1}}{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}} \right)\left( {1 + {{H}_{3}}{\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}} \right){{\theta }_{{\text{*}}}}{\text{.}} \\ \end{gathered} $

При идентификации второй независимой аддитивной составляющей искомого стационарного температурного поля объекта исследований воспользуемся исходными допущениями, представленными в математической модели (8), согласно которым ${{\theta }_{2}}\left( {x,y,z} \right)$ как скалярная функция пространственных переменных $x$ и $z$ является оригиналом двумерного экспоненциального интегрального преобразования Фурье [25], задаваемого парой линейных интегральных операторов:

$\begin{gathered} {\Phi }\left[ \cdot \right] \equiv \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty { \cdot \,{\text{exp}}\left( { - ipx - irz} \right)dxdz} } , \\ {{{\Phi }}^{{ - 1}}}\left[ \cdot \right] \equiv \frac{1}{{{{{\left( {2\pi } \right)}}^{2}}}}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty { \cdot \,{\text{exp}}\left( {ipx + irz} \right)dpdr} } , \\ \end{gathered} $
где $i$ – мнимая единица [2]. Полагая
$\begin{gathered} A\left( {p,y,r} \right) \triangleq {\Phi }\left[ {{{\theta }_{2}}\left( {x,y,z} \right)} \right], \\ \left\langle {A\left( {p,r} \right)} \right\rangle \triangleq {\Phi }\left[ {\left\langle {{{\theta }_{2}}\left( {x,z} \right)} \right\rangle } \right],\,\,\,\,{\Pi }\left( {p,r} \right) \triangleq {\Phi }\left[ {Q\left( {x,z} \right)} \right],~ \\ \end{gathered} $
воспользуемся стандартными свойствами [25] двумерного экспоненциального интегрального преобразования Фурье (9) и в пространстве его изображений представим исходную математическую модель (8) в следующем виде:

$\begin{gathered} \frac{{{{d}^{2}}A}}{{d{{y}^{2}}}} + 2i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)\frac{{dA}}{{dy}} - \\ - \,\,\left( {{{\mu }_{{11}}}{{p}^{2}} + 2{{\mu }_{{13}}}pr + {{\mu }_{{33}}}{{r}^{2}}} \right)A = 0, \\ ~ - {\kern 1pt} \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}}, \\ \frac{{{{d}^{2}}A}}{{d{{y}^{2}}}} - \left( {{{p}^{2}} + {{r}^{2}}} \right)A = 0,\,\,\,\, - {\kern 1pt} 0 < y < {{H}_{3}}, \\ \end{gathered} $
$\begin{gathered} {{\left. {\left[ {\frac{{dA}}{{dy}} + i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)A} \right]} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} = \\ = {{\left. {{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}A} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} - {\Pi }\left( {p,r} \right), \\ A\left( {p, - {{H}_{2}} - 0,r} \right) = \left\langle {A\left( {p,r} \right)} \right\rangle = A\left( {p,0 + 0,r} \right), \\ \end{gathered} $
$\begin{gathered} {{\left. {\mu \frac{{dA}}{{dy}}} \right|}_{{y = 0 + 0}}} - {{\left. {\left[ {\frac{{dA}}{{dy}} + i\left( {{{{\mu }}_{{12}}}p + {{{\mu }}_{{23}}}r} \right)A} \right]} \right|}_{{y = - {{H}_{2}} - 0}}} = \\ = {{\mu }_{1}}{{H}_{2}}\left( {{{p}^{2}} + {{r}^{2}}} \right)\left\langle A \right\rangle + {{Q}_{{\text{*}}}}\left\langle A \right\rangle , \\ {{\left. {\frac{{dA}}{{dy}}} \right|}_{{y = {{H}_{3}}}}} = {{\left. { - {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}A} \right|}_{{y = {{H}_{3}}}}}. \\ \end{gathered} $

Изображение (11) исходной математической модели (8) представляет собой краевую задачу для системы двух обыкновенных линейных дифференциальных уравнений второго порядка, специфика которой связана не только с нестандартными условиями сопряжения, но и с наличием комплекса $i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)$ в различных элементах этой задачи. С учетом сказанного естественно предполагать, что изображение $A\left( {p,y,r} \right)$ оригинала ${{{\theta }}_{2}}\left( {x,y,z} \right)$ обладает следующей структурой:

$A\left( {p,y,r} \right) = B\left( {p,y,r} \right){\text{exp}}\left\{ {\begin{array}{*{20}{c}} { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)\left( {y + {{H}_{2}}} \right),~\,\, - \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}}} \\ {~~~~~~~~~~~~~~0,~~~~~~~~~~~~~~~~~~~~~~~~~~~~\,~~~~~~~~~~~~~0 < y < {{H}_{3}}} \end{array}} \right\}.$

Согласно (12) и (11), функция B(p, y, r) в свою очередь должна удовлетворять соответствующему упрощенному аналогу краевой задачи (11):

$\begin{gathered} \frac{{{{d}^{2}}B}}{{d{{y}^{2}}}} - \delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)B = 0,\,\,\,\,~ - {\kern 1pt} \left( {{{H}_{1}} + {{H}_{2}}} \right) < y < - {{H}_{2}}, \\ \frac{{{{d}^{2}}B}}{{d{{y}^{2}}}} - \left( {{{p}^{2}} + {{r}^{2}}} \right)B = 0,\,\,\,\,0 < y < {{H}_{3}}, \\ {{\left. {\left[ {\frac{{dB}}{{dy}} - {\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}B} \right]} \right|}_{{y = - \left( {{{H}_{1}} + {{H}_{2}}} \right)}}} = \\ = - {\Pi }\left( {p,r} \right){\text{exp}}\left[ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right){{H}_{1}}} \right], \\ B\left( {p, - {{H}_{2}} - 0,r} \right) = \left\langle {B\left( {p,r} \right)} \right\rangle = B\left( {p,0 + 0,r} \right), \\ {{\left. {\mu \frac{{dB}}{{dy}}} \right|}_{{y = 0 + 0}}} - {{\left. {\frac{{dB}}{{dy}}} \right|}_{{y = - {{H}_{2}} - 0}}} = \left[ {{{Q}_{{\text{*}}}} + \mu {{H}_{2}}\left( {{{p}^{2}} + {{r}^{2}}} \right)} \right]\left\langle B \right\rangle , \\ {{\left. {\left[ {\frac{{dB}}{{dy}} + {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}B} \right]} \right|}_{{y = {{H}_{3}}}}} = 0, \\ \end{gathered} $
где квадратичная форма
$\begin{gathered} \delta \left( {p,r,\left\{ {{{\mu }_{{ij}}}} \right\}} \right) = \left( {{{\mu }_{{11}}} - \mu _{{12}}^{2}} \right){{p}^{2}} + \\ + \,\,2\left( {{{\mu }_{{13}}} - {{\mu }_{{12}}}{{\mu }_{{23}}}} \right)pr + \left( {{{\mu }_{{33}}} - \mu _{{32}}^{2}} \right){{r}^{2}} \\ \end{gathered} $
является положительно определенной, что проверяется использованием критерия Сильвестра [26] и свойств тензора теплопроводности второго ранга [4]. Решение краевой задачи (13), (14) может быть получено стандартными методами [25] и представлено в виде

$\begin{gathered} {{\left. {B\left( {p,y,r} \right)} \right|}_{{ - \left( {{{H}_{1}} + {{H}_{2}}} \right) \leqslant y \leqslant - {{H}_{2}}}}} = \\ = {{C}_{1}}\left( {p,r} \right){\text{sh}}\left[ {\left( {y + {{H}_{2}}} \right)\sqrt {\delta \left( {p,r,\left\{ {{{\mu }_{{ij}}}} \right\}} \right)} } \right] + \\ + \,\,\left\langle {B\left( {p,r} \right)} \right\rangle {\text{ch}}\left[ {\left( {y + {{H}_{2}}} \right)\sqrt {\delta \left( {p,r,\left\{ {{{\mu }_{{ij}}}} \right\}} \right)} } \right], \\ {{\left. {B\left( {p,y,r} \right)} \right|}_{{0 \leqslant y \leqslant {{H}_{3}}}}} = \\ = {{C}_{2}}\left( {p,r} \right){\text{sh}}\left[ {y\sqrt {{{p}^{2}} + {{r}^{2}}} } \right] + \left\langle {B\left( {p,r} \right)} \right\rangle {\text{ch}}\left[ {y\sqrt {{{p}^{2}} + {{r}^{2}}} } \right], \\ \left\langle {B\left( {p,r} \right)} \right\rangle = {{a}_{2}}\left( {p,r} \right){{C}_{2}}\left( {p,r} \right) - {{a}_{1}}\left( {p,r} \right){{C}_{1}}\left( {p,r} \right), \\ \end{gathered} $
$\begin{gathered} {{a}_{1}}\left( {p,r} \right) = \frac{{\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} }}{{{{Q}_{{\text{*}}}} + \mu {{H}_{2}}\left( {{{p}^{2}} + {{r}^{2}}} \right)}}, \\ ~{{a}_{2}}\left( {p,r} \right) = \frac{{\mu \sqrt {{{p}^{2}} + {{r}^{2}}} }}{{{{Q}_{{\text{*}}}} + {\mu }{{H}_{2}}\left( {{{p}^{2}} + {{r}^{2}}} \right)}}, \\ {{C}_{1}}\left( {p,r} \right) = {\Lambda }\left( {p,r} \right){{C}_{2}}\left( {p,r} \right), \\ {\Lambda }\left( {p,r} \right) = \frac{{{{a}_{2}}\left( {p,r} \right)}}{{{{a}_{1}}\left( {p,r} \right)}} + \\ + \,\,\frac{{\sqrt {{{p}^{2}} + {{r}^{2}}} + {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}{\text{th}}\left[ {{{H}_{2}}\sqrt {{{p}^{2}} + {{r}^{2}}} } \right]}}{{{{a}_{1}}\left( {p,r} \right)\left\{ {\sqrt {{{p}^{2}} + {{r}^{2}}} {\text{th}}\left[ {{{H}_{3}}\sqrt {{{p}^{2}} + {{r}^{2}}} } \right] + {\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}}} \right\}}}, \\ \end{gathered} $
$\begin{gathered} {{C}_{2}}\left( {p,r} \right) = \left\{ {\left[ {{{a}_{2}}\left( {p,r} \right) - {{a}_{1}}\left( {p,r} \right){\Lambda }\left( {p,r} \right)} \right] \times \sqrt {1_{{}}^{{}}} } \right. \\ \times \,\,\left\{ {\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} {\kern 1pt} {\text{sh}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right] + } \right. \\ \left. { + \,\,{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}{\text{ch}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right]} \right\} - {\Lambda }\left( {p,r} \right) \times \\ \times \,\,\left\{ {\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right.{\text{ch}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right] + \\ {{\left. {\left. { + \,\,{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}{\text{sh}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right]} \right\}} \right\}}^{{ - 1}}}{\Pi }\left( {p,r} \right) \times \\ \times \,\,{\text{exp}}\left[ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right){{H}_{1}}} \right]. \\ \end{gathered} $

Для завершения процедуры определения ${{{\theta }}_{2}}\left( {x,y,z} \right)$ в пространстве изображений двумерного экспоненциального интегрального преобразования Фурье (9) с учетом первого условия сопряжения в рассматриваемой системе, представленного в математической модели (11), достаточно воспользоваться равенствами (10), (12), (14) и (15):

$\begin{gathered} {{\left. {A\left( {p,y,r} \right)} \right|}_{{ - \left( {{{H}_{1}} + {{H}_{2}}} \right) \leqslant y \leqslant - {{H}_{2}}}}} = {{g}_{{\text{п}}}}\left( {p,y,r} \right){\Pi }\left( {p,r} \right) \times \\ \times \,\,{\text{exp}}\left[ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right)\left( {y + {{H}_{1}} + {{H}_{2}}} \right)} \right], \\ {{\left. {A\left( {p,y,r} \right)} \right|}_{{0 \leqslant y \leqslant {{H}_{3}}}}} = {{g}_{{{\text{ст}}}}}\left( {p,y,r} \right){\Pi }\left( {p,r} \right) \times \\ \times \,\,{\text{exp}}\left[ { - i\left( {{{\mu }_{{12}}}p + {{\mu }_{{23}}}r} \right){{H}_{1}}} \right], \\ \end{gathered} $
$\begin{gathered} {{g}_{{\text{п}}}}\left( {p,y,r} \right) = \left\{ {{\Lambda }\left( {p,r} \right){\text{sh}}\left[ {\left( {y + {{H}_{2}}} \right)\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right] + } \right.~ \\ + \,\,\left[ {{{a}_{2}}\left( {p,r} \right) - {{a}_{1}}\left( {p,r} \right){\Lambda }\left( {p,r} \right)} \right] \times \\ \left. { \times \,\,{\text{ch}}\left[ {\left( {y + {{H}_{2}}} \right)\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right]} \right\}{{d}^{{ - 1}}}\left( {p,r} \right), \\ {{g}_{{{\text{ст}}}}}\left( {p,y,r} \right) = \left\{ {{\text{sh}}\left[ {y\sqrt {{{p}^{2}} + {{r}^{2}}} } \right] + } \right. \\ + \,\,\left[ {{{a}_{2}}\left( {p,r} \right) - {{a}_{1}}\left( {p,r} \right){\Lambda }\left( {p,r} \right)} \right] \times \\ \left. { \times \,\,{\text{ch}}\left[ {y\sqrt {{{p}^{2}} + {{r}^{2}}} } \right]} \right\}{{d}^{{ - 1}}}\left( {p,r} \right), \\ \end{gathered} $
$\begin{gathered} d\left( {p,r} \right) = \left[ {{{a}_{2}}\left( {p,r} \right) - {{a}_{1}}\left( {p,r} \right){\Lambda }\left( {p,r} \right)} \right] \times \\ \times \,\,\left\{ {\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} {\kern 1pt} {\text{sh}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right] + } \right. \\ \left. { + \,\,{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}{\text{ch}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)} } \right]} \right\} - \\ - \,\,{\Lambda }\left( {p,r} \right)\left\{ {\sqrt {\delta \left( {p,r,\left\{ {{{\mu }_{{ij}}}} \right\}} \right)} {\kern 1pt} {\text{ch}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{\mu }_{{ij}}}} \right\}} \right)} } \right] + } \right. \\ \left. { + \,\,{\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}}{\text{sh}}\left[ {{{H}_{1}}\sqrt {\delta \left( {p,r,\left\{ {{{\mu }_{{ij}}}} \right\}} \right)} } \right]} \right\}. \\ \end{gathered} $

В общем случае для перехода в пространство оригиналов преобразования Фурье (9) воспользуемся теоремой о свертках и теоремой смещения [25]. При этом, согласно (9) (10) и (16), имеем

$\begin{gathered} {{\left. {{{{\theta }}_{2}}\left( {x,y,z} \right){\text{\;}}} \right|}_{{ - \left( {{{H}_{1}} + {{H}_{2}}} \right) \leqslant y \leqslant - {{H}_{2}}}}} = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {Q(x - {{{\mu }}_{{12}}}} } \times \\ \times \,\,\left( {y + {{H}_{1}} + {{H}_{2}}} \right) - x{\kern 1pt} ',z - {{{\mu }}_{{23}}}\left( {y + {{H}_{1}} + {{H}_{2}}} \right) - z{\kern 1pt} ') \times \\ \times \,\,{{G}_{{\text{п}}}}\left( {x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} '} \right)dx{\kern 1pt} 'dz{\kern 1pt} ',\,\,\,\,~{{G}_{{\text{п}}}}\left( {x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} '} \right) = \\ = {{{\Phi }}^{{ - 1}}}\left[ {{{g}_{{\text{п}}}}\left( {p,y,r} \right)} \right],\,\,\,\,{{\left. {{{{\theta }}_{2}}\left( {x,y,z} \right){\text{\;}}} \right|}_{{0 \leqslant y \leqslant {{H}_{3}}}}} = \\ = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {Q(x - {{{\mu }}_{{12}}}{{H}_{1}} - x{\kern 1pt} ',z - {{\mu }_{{23}}}{{H}_{1}} - z{\kern 1pt} ')} } \times \\ \times \,\,{{G}_{{{\text{ст}}}}}\left( {x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} '} \right)dx{\kern 1pt} 'dz,~ \\ {{G}_{{{\text{ст}}}}}\left( {x{\kern 1pt} ',y{\kern 1pt} ',z{\kern 1pt} '} \right) = {{{\Phi }}^{{ - 1}}}\left[ {{{g}_{{{\text{ст}}}}}\left( {p,y,r} \right)} \right]. \\ \end{gathered} $

В соответствии с (15), (16) изображения ${{g}_{{{\text{ст}}}}}\left( {p,y,r} \right),$ ${{g}_{{\text{п}}}}\left( {p,y,r} \right)$ зависят от положительно определенных квадратичных форм $({{p}^{2}} + {{r}^{2}})$ и $\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right),$ где $\delta \left( {p,r,\left\{ {{{{\mu }}_{{ij}}}} \right\}} \right)$ задана равенством (14). Поэтому во избежание известных трудностей, характерных для вычислительных экспериментов в комплексных пространствах [27] при реализации оператора ${{{\Phi }}^{{ - 1}}}\left[ \cdot \right]$ в (9) аналогично [28] целесообразно сначала воспользоваться теоремой об одновременном приведении двух квадратичных форм к диагональному виду [26], а затем – связью между экспоненциальным интегральным преобразованием Фурье и интегральным косинус-преобразованием Фурье [25].

Следует заметить, что соотношения (17), определяющие функцию ${{{\theta }}_{2}}\left( {x,y,z} \right),$ заметно упрощаются, если изображение ${\Pi }\left( {p,r} \right)$ является четной функцией по каждому из аргументов и выполнено равенство

(18)
${{\mu }_{{13}}} = {{\mu }_{{12}}}{{\mu }_{{23}}},$
так как в этом случае, согласно (14)–(16), (18), изображения ${{g}_{{\text{п}}}}\left( {p,y,r} \right){\Pi }\left( {p,r} \right),$ ${{g}_{{{\text{ст}}}}}\left( {p,y,r} \right){\Pi }\left( {p,r} \right)$ являются четными функциями по аргументам $p$ и $r.$ Как следствие, согласно (9), (10) и (16) имеем

$\begin{gathered} {{\left. {{{{\theta }}_{2}}\left( {x,y,z} \right)} \right|}_{{ - \left( {{{H}_{1}} + {{H}_{2}}} \right) \leqslant y \leqslant - {{H}_{2}}}}} = \frac{1}{{{{\pi }^{2}}}}\int\limits_0^\infty {\int\limits_0^\infty {{{g}_{{\text{п}}}}\left( {p,y,r} \right)} } \times \\ \times \,\,{\Pi }\left( {p,r} \right)\cos \left\{ {\left[ {x - {{{\mu }}_{{12}}}\left( {y + {{H}_{1}} + {{H}_{2}}} \right)} \right]p} \right\} \times \\ \times \,\,\cos \left\{ {\left[ {z - {{\mu }_{{12}}}\left( {y + {{H}_{1}} + {{H}_{2}}} \right)} \right]r} \right\}dpdr, \\ \end{gathered} $
$\begin{gathered} {{\left. {{{{\theta }}_{2}}\left( {x,y,z} \right)} \right|}_{{0 \leqslant y \leqslant {{H}_{3}}}}}{\text{\;}} = \frac{1}{{{{\pi }^{2}}}}\int\limits_0^\infty {\int\limits_0^\infty {{{g}_{{{\text{ст}}}}}\left( {p,y,r} \right)} } \times \\ \times \,\,{\Pi }\left( {p,r} \right)\cos \left\{ {\left[ {x - {{{\mu }}_{{12}}}{{H}_{1}}} \right]p} \right\}\cos \left\{ {\left[ {z - {{{\mu }}_{{12}}}{{H}_{1}}} \right]r} \right\}dpdr.~ \\ \end{gathered} $

ЗАКЛЮЧЕНИЕ

Стационарное температурное поле разделительной системы с активной теплозащитой представляет собой аддитивную композицию двух независимых составляющих, первая из которых зависит лишь от интенсивности теплового взаимодействия разделяемых сред с граничными поверхностями анализируемой системы, а вторая – от плотности мощности теплового потока, воздействующего на охлаждаемую систему с нулевыми температурами разделяемых сред.

Согласно равенству (17), в теплозащитном покрытии из композиционного материала с анизотропией свойств общего вида проявляется известный [29] эффект “сноса” температурного поля.

Механизм функционирования “термически тонкой” термоактивной прокладки, не учитывающий возможности протекания в ней теплодиффузионных процессов, качественно не искажает стационарное температурное поле анализируемой системы, но требует количественных оценок [23].

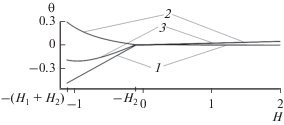
На рис. 1 частично представлены результаты вычислительных экспериментов, связанных с определением стационарного температурного поля анизотропной разделительной системы с термоактивной прокладкой, функционирующей по принципу обратной связи, при воздействии стационарного теплового потока с интенсивностью гауссовского типа [18]

$Q\left( {x,z} \right) = {{Q}_{0}}\left( {{{{{K}^{2}}} \mathord{\left/ {\vphantom {{{{K}^{2}}} \pi }} \right. \kern-0em} \pi }} \right){\text{exp}}\left\{ { - {{K}^{2}}\left( {{{x}^{2}} + {{z}^{2}}} \right)} \right\}$
в условиях теплообмена с внешней средой. Расчет выполнен при следующих безразмерных параметрах: ${{H}_{1}} = 1,$ ${{H}_{2}} = 0.1,$ ${{H}_{3}} = 2,$ ${{Q}_{0}} = 3,$ $K = 1,$ ${{Q}_{{\text{*}}}} = 10,$ ${\text{B}}{{{\text{i}}}^{{\left( 1 \right)}}} = 1,$ $~{\text{B}}{{{\text{i}}}^{{\left( 3 \right)}}} = 3,$ ${\mu } = 20,$ $~{{{\mu }}_{{11}}} = 2,$ ${{{\mu }}_{{22}}} = 1,$ ${{{\mu }}_{{33}}} = 3,$ ${{{\mu }}_{{12}}} = 0.5,$ ${{{\mu }}_{{23}}} = 0.7,$ ${{{\mu }}_{{13}}} = {{{\mu }}_{{12}}}{{{\mu }}_{{23}}} = 0.35$ и различных значениях $\Delta {{{\theta }}_{{13}}}$ – симплекса подобия начальной температуры системы и температур разделяемых сред (рис. 1а – $\Delta {{\theta }_{{13}}} = 0.25,$ рис. 1б – 2.0). При $\Delta {{\theta }_{{13}}} = 0.25$ стационарное температурное поле формируется под воздействием внешнего теплового потока и при тепловом взаимодействии среды заданной температуры $T_{{\text{с}}}^{{\left( {{\text{ст}}} \right)}} > T_{{\text{с}}}^{{\left( {\text{п}} \right)}}$ с поверхностью анизотропного покрытия в условиях охлаждения разделительной стенки анализируемой системы; в случае $\Delta {{\theta }_{{13}}} = 2.0$ – при локальном тепловом нагреве охлаждаемого анизотропного покрытия в условиях теплового взаимодействия среды с $T_{{\text{с}}}^{{\left( {{\text{ст}}} \right)}} > T_{{\text{с}}}^{{\left( {\text{п}} \right)}}$ с поверхностью разделительной стенки системы. В последнем случае проявление эффекта обратной связи при формировании стационарного температурного поля разделительной системы с активной теплозащитой является наиболее значимым (рис. 2, ${{Q}_{*}} = 0$).

Рис. 1.

Стационарный температурный профиль объекта исследований при функционирующей обратной связи термоактивной прокладки: 1 – ${{{\theta }}_{1}}\left( y \right),$ 2 – ${{{\theta }}_{2}}\left( {0,y,0} \right),$ 3 – ${\theta }\left( {0,y,0} \right).$

Рис. 2.

Стационарный температурный профиль объекта исследований при отключенной обратной связи термоактивной прокладки: 1–3 – см. рис. 1.

Список литературы

  1. Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 448 с.

  2. Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.

  3. Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М.: Высшая школа, 2001. 550 с.

  4. Формалёв В.Ф. Теплопроводность анизотропных тел. Аналитические методы решения задач. М.: Физматлит, 2014. 312 с.

  5. Полежаев Ю.В., Юревич Ф.Б. Тепловая защита. М.: Энергия, 1976. 392 с.

  6. Зарубин В.С. Расчет и оптимизация термоизоляции. М.: Энергоатомиздат, 1991. 192 с.

  7. Полежаев Ю.В., Шишков А.А. Газодинамические испытания тепловой защиты. М.: Промедак, 1992. 248 с.

  8. Галицейский Б.М., Совершенный В.Д., Формалев В.Ф. Тепловая защита лопаток турбин. М.: Изд-во МАИ, 1996. 356 с.

  9. Формалев В.Ф., Чипашвили А.А., Миканев С.В. Моделирование нового способа тепловой защиты стенок энергетических установок при высокоинтенсивном нагреве // Изв. РАН. Энергетика. 2004. № 5. С. 147.

  10. Формалев В.Ф., Колесник С.А., Чипашвили А.А. Аналитическое исследование тепломассопереноса при пленочном охлаждении тел // ТВТ. 2006. Т. 44. № 1. С. 107.

  11. Формалев В.Ф., Колесник С.А., Селин И.А., Кузнецова Е.Л. Оптимальный выбор параметров экранно-вакуумной теплоизоляции космических аппаратов // ТВТ. 2017. Т. 55. № 1. С. 108.

  12. Аттетков А.В., Волков И.К., Тверская Е.С. Термоактивная прокладка как средство управляемого воздействия на температурное поле конструкции // Изв. РАН. Энергетика. 2002. № 4. С. 131.

  13. Аттетков А.В., Волков И.К., Тверская Е.С. Базовая модель процесса теплопереноса в экранированном полупространстве с термоактивной прокладкой // Изв. РАН. Энергетика. 2009. № 2. С. 147.

  14. Волков И.К., Тверская Е.С. Оптимальная толщина экранированной стенки с термоактивной прокладкой, функционирующей по принципу обратной связи // Наука и образование. МГТУ им. Н. Э. Баумана. Электр. журн. 2012. № 5. С. 172.

  15. Формалев В.Ф. Теплоперенос в анизотропных твердых телах. Численные методы, тепловые волны, обратные задачи. М.: Физматлит, 2015. 280 с.

  16. Аттетков А.В., Волков И.К. Особенности процесса формирования температурного поля в системе с активной теплозащитой // Изв. РАН. Энергетика. 2014. № 3. С. 69.

  17. Формалев В.Ф., Колесник С.А., Кузнецова Е.Л. Нестационарный теплоперенос в пластине с анизотропией общего вида при воздействии импульсных источников теплоты // ТВТ. 2017. Т. 55. № 5. С. 778.

  18. Аттетков А.В., Власов П.А., Волков И.К. Условие существования оптимальной толщины охлаждаемой анизотропной стенки, подверженной локальному тепловому воздействию // ТВТ. 2018. Т. 56. № 3. С. 407.

  19. Аттетков А.В., Волков И.К. Влияние анизотропии свойств на оптимальную толщину покрытия охлаждаемой пластины при локальном тепловом воздействии // Изв. РАН. Энергетика. 2018. № 1. С. 78.

  20. Негойцэ К. Применение теории систем к проблемам управления. М.: Мир, 1981. 184 с.

  21. Дезоер Ч., Видьясагар М. Системы с обратной связью: вход-выходные соотношения. М.: Наука, 1983. 278 с.

  22. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. М.: Высшая школа, 1970. 712 с.

  23. Пудовкин М.А., Волков И.К. Краевые задачи математической теории теплопроводности в приложении к расчетам температурных полей в нефтяных пластах при заводнении. Казань: Изд-во Казанск. ун-та, 1978. 188 с.

  24. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969. 424 с.

  25. Снеддон И. Преобразования Фурье. М.: Изд-во иностр. лит., 1955. 668 с.

  26. Беллман Р. Введение в теорию матриц. М.: Наука, 1969. 368 с.

  27. Диткин В.А., Прудников А.П. Операционное исчисление. М.: Высшая школа, 1966. 408 с.

  28. Аттетков А.В., Волков И.К. Температурное поле анизотропного полупространства с подвижной границей, обладающей термически тонким покрытием, при его нагреве внешней средой // Тепловые процессы в технике. 2016. Т. 8. № 8. С. 378.

  29. Аттетков А.В., Волков И.К. Температурное поле анизотропной охлаждаемой пластины, находящейся под воздействием импульсно-периодического теплового потока с интенсивностью гауссовского типа // Изв. РАН. Энергетика. 2012. № 5. С. 70.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал