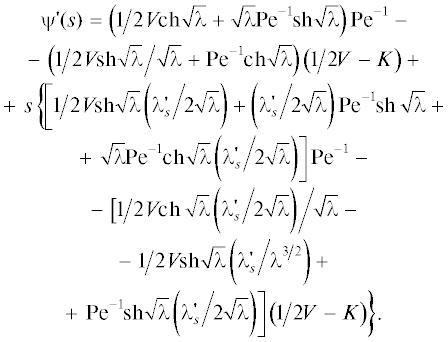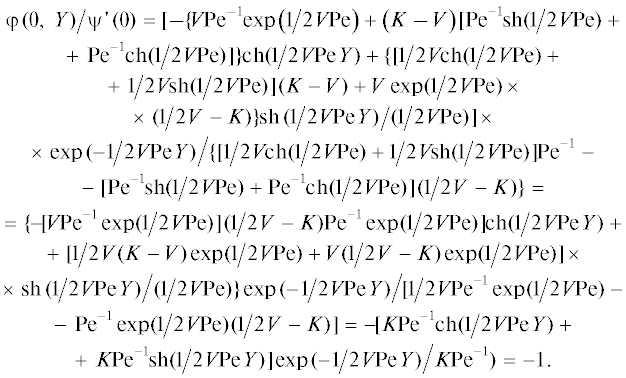Теоретические основы химической технологии, 2019, T. 53, № 1, стр. 87-101
Математическое моделирование процесса микрофильтрации в канале прямоугольного сечения
С. Т. Антипов 1, А. И. Ключников 1, *
1 Воронежский государственный университет инженерных технологий
Воронеж, Россия
* E-mail: kaivanov@mail.ru
Поступила в редакцию 09.04.2016
После доработки 19.07.2018
Принята к публикации 30.05.2017
Аннотация
Как правило, при формулировке задач физических моделей гидродинамических процессов невозможно объективно провести количественный учет большинства факторов из-за их большого многообразия и изменчивости. Также отсутствует единая и общепринятая теория массопереноса при микро- и ультрафильтрации, что является существенным сдерживающим фактором. Следует подчеркнуть особую сложность трансмембранного переноса при создании развитых гидродинамических неустойчивостей переменной интенсивности, так как любое (даже незначительное) изменение режимных параметров процессов микро- и ультрафильтрации приводит к различным условиям образования (или разрушения) поверхностного слоя, что неизбежно отражается на граничных условиях. В настоящей работе показана возможность адаптации однопараметрической диффузионной модели к мембранному процессу разделения за счет учета проницаемости одной из стенок рассматриваемого канала прямоугольного сечения. Изучена структура гидродинамического потока, позволяющая определить поведение поля концентраций растворенного вещества на поверхности мембраны и оценить эффективность применяемых мероприятий, направленных на снижение концентрационной поляризации гидродинамическими методами за счет вариаций скорости.
ВВЕДЕНИЕ
Наибольший научный интерес представляют исследования, посвященные разработке конструкций мембранных аппаратов, позволяющих в полной мере реализовать гидродинамические приемы интенсификации при решении практических задач обработки технологических жидкостей.
Дальнейшее становление теории, техники и технологии мембранных процессов связано, прежде всего, с созданием научных подходов к разработке мембранных процессов и оборудования, обеспечивающих комплексное решение задач по разделению (концентрированию) при развитых гидродинамических режимах, снижающих концентрационную поляризацию. Это направление развития мембранных процессов является актуальной проблемой.
Достаточно развернутое исследование процессов микро- и ультрафильтрации технологических жидкостей с использованием различных вариативных состояний гидродинамической картины в мембранном модуле различных типов либо отсутствует, либо представлено частным описанием. Известные научные работы отечественных и зарубежных ученых, достигнутые практические результаты отражают, преимущественно, узкое решение той или иной технологической задачи применительно к конкретной конструкции мембранного аппарата или установке.
Процессы массопереноса с участием полупроницаемых мембран сопровождаются перемещением материальных потоков обрабатываемой технологической жидкости, газа или твердой фазы. В реальных условиях процессы мембранной обработки всегда осуществляются с участием нескольких фаз, взаимодействие которых представляет повышенный научно-практический интерес. Изучение гидродинамики мембранных процессов, ввиду их высочайшей сложности и специфики, позволяет на сегодняшний день создать теоретические описание в общем виде и только для одной фазы или компонента. В этом случае приходится прибегать к использованию приближенных описаний внутренней структуры потоков, характеризующейся степенью перемешивания, определяющей поле концентраций и температуры обрабатываемой технологической жидкости. Поскольку в каналах мембранных аппаратов происходит, главным образом, только продольное и радиальное перемешивание, то наиболее удобно использовать для теоретического описания именно диффузионную математическую модель. Для ее адаптации к мембранному процессу разделения требуется учет проницаемости одной из стенок рассматриваемого канала прямоугольного сечения. Изучение структуры потоков, в конечном итоге, позволит определить поведение поля концентраций растворенного вещества на поверхности мембраны и оценить эффективность применяемых мероприятий, направленных на снижение концентрационной поляризации.
Математическим моделированием мембранных процессов в условиях концентрационной поляризации, нахождением концентрации растворенного вещества в примембранной области занимались авторы работ [1–8].
Целью данной работы являлось создание такой математической модели движения вязкой несжимаемой жидкости в мембранном канале прямоугольного сечения, которая бы позволила, с одной стороны, определить гидродинамическую составляющую для характеристики эффективности применяемых способов снижения концентрационной поляризации, а с другой – параметр, учитывающий удельную проницаемость мембраны.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
При формулировке физической модели массопереноса в процессах микро- и ультрафильтрации технологических жидкостей допускается использование математического описания линейной термодинамики необратимых процессов с использованием условий термодинамического равновесия по компонентам разделяемых смесей в примембранной области [9–11].
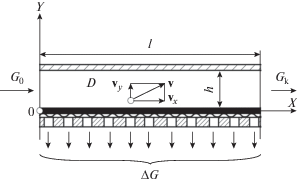
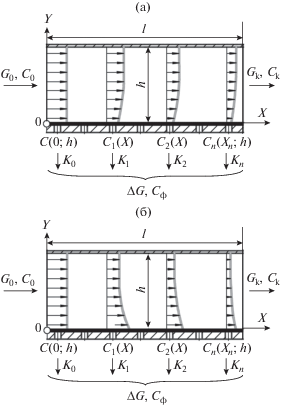
Выделим некоторый элемент мембранного канала (рис. 1), длина которого l, высота h, по которому под давлением Р движется поток разделяемой технологической жидкости с заданным расходом G0 на входе и Gк – на выходе. Поток пермеата, прошедшего через мембрану, составляет величину ∆G.
Основные допущения при создании физической модели:
1. При стационарном режиме массопереноса концентрация вещества на входе в пору мембраны всегда равна концентрации на выходе.
2. Поток пермеата ∆G вдоль поверхности рассматриваемой мембраны длиной l имеет постоянную величину.
3. Отсутствие нелинейных эффектов любой природы.
4. Расход исходной технологической жидкости G0 всегда больше расхода получаемого пермеата ∆G, т.е. G0$ \gg $ ∆G.
5. Рассматривается абсолютно плоская мембрана.
6. Исходная технологическая жидкость однородна по составу, газовая фаза отсутствует.
Запишем уравнения движения вязкой несжимаемой жидкости для элементарного объема разделяемой жидкости, движущейся вдоль поверхности мембраны в декартовой системе координат 0(x, y) со скоростью $v\,{\text{:}}$
где D – коэффициент диффузии, м2/с; с – концентрация раствора в рассматриваемом объеме, мас. %.В общем случае выражения (1) и (2) можно привести к следующей форме:
(3)
${{v}_{x}}\frac{{\partial c}}{{\partial x}} + {{v}_{y}}\frac{{\partial c}}{{\partial y}} = D\frac{{{{\partial }^{2}}c}}{{\partial {{y}^{2}}}}.$Формулировка граничных условий запишется в виде
(5)
$y = 0;\,\,\,\,{{v}_{y}}c\left( {x,0} \right) - D\frac{{\partial c\left( {x,0} \right)}}{{\partial y}} = kc\left( {x,0} \right);$(6)
$y = h;\,\,\,\,{{v}_{y}} = 0;\,\,\,\,{{v}_{y}}c\left( {x,h} \right) - D\frac{{\partial c\left( {x,h} \right)}}{{\partial y}} = 0,$Приведем уравнение (3) к безразмерному виду:
(7)
${{c}_{0}}{{v}_{x}}\frac{1}{h}\frac{{\partial \left( {\frac{c}{{{{c}_{0}}}}} \right)}}{{\partial \left( {\frac{x}{h}} \right)}} + {{c}_{0}}{{v}_{y}}\frac{1}{h}\frac{{\partial \left( {\frac{c}{{{{c}_{0}}}}} \right)}}{{\partial \left( {\frac{y}{h}} \right)}} = {{c}_{0}}D\frac{1}{{{{h}^{2}}}}\frac{{{{\partial }^{2}}\left( {\frac{c}{{{{c}_{0}}}}} \right)}}{{\partial {{{\left( {\frac{y}{h}} \right)}}^{2}}}}.$В уравнение (7) входят концентрация, скорость, коэффициент диффузии, а также параметр, характеризующий геометрию мембранного канала. Именно математическая модель с данными параметрами представляет научно-практический интерес.
Синтез уравнений модели. На основе выбранной физической модели применительно к решаемой задаче переходим к построению математической модели. Для этого полученная физическая модель процесса была подвергнута упрощению путем ввода следующих безразмерных переменных:
(8)
$\begin{gathered} X = {x \mathord{\left/ {\vphantom {x y}} \right. \kern-0em} y};\,\,\,\,Y = {y \mathord{\left/ {\vphantom {y h}} \right. \kern-0em} h};\,\,\,\,С (X,Y){\text{ }} = {{с (x,y)} \mathord{\left/ {\vphantom {{с (x,y)} {{{с }_{0}}}}} \right. \kern-0em} {{{с }_{0}}}}; \\ K = {k \mathord{\left/ {\vphantom {k {{{{\mathbf{v}}}_{x}}}}} \right. \kern-0em} {{{{\mathbf{v}}}_{x}}}};\,\,\,\,V = {{{{{\mathbf{v}}}_{y}}} \mathord{\left/ {\vphantom {{{{{\mathbf{v}}}_{y}}} {{{{\mathbf{v}}}_{x}}}}} \right. \kern-0em} {{{{\mathbf{v}}}_{x}}}},\quad \\ \end{gathered} $С учетом безразмерных переменных (8), уравнение (7) можно переписать в виде
(9)
$\frac{{\partial C\left( {X,Y} \right)}}{{\partial X}} + V\frac{{\partial C\left( {X,Y} \right)}}{{\partial Y}} = \frac{D}{{{{v}_{x}}h}}\frac{{{{\partial }^{2}}C\left( {X,Y} \right)}}{{\partial {{Y}^{2}}}},$(11)
$Y = 0;\,\,\,\,VC\left( {X,0} \right) - \frac{1}{{{\text{Pe}}}}\frac{{\partial C\left( {X,0} \right)}}{{\partial Y}} = KC\left( {X,0} \right).$(12)
$Y = 1;\,\,\,\,VC\left( {X,1} \right) - \frac{1}{{{\text{Pe}}}}\frac{{\partial C\left( {X,1} \right)}}{{\partial Y}} = 0.$В результате проведенного синтеза уравнений модели получена система дифференциальных уравнений в частных производных в безразмерном виде. В уравнениях (11) и (12) величины Ре и K являются параметрами модели.
Анализ математической модели. Введем новую переменную
тогда система дифференциальных уравнений (9)–(12) запишется в следующем виде:
(14)
$\frac{{\partial N\left( {X,Y} \right)}}{{\partial X}} + V\frac{{\partial N\left( {X,Y} \right)}}{{\partial Y}} = \frac{1}{{{\text{Pe}}}}\frac{{{{\partial }^{2}}N\left( {X,Y} \right)}}{{\partial {{Y}^{2}}}},$(16)
$\begin{gathered} Y = 0;\,\,\,\,VN\left( {X,0} \right) - \frac{1}{{{\text{Pe}}}}\frac{{\partial N\left( {X,0} \right)}}{{\partial Y}} = \\ = - V + K + KN\left( {X,0} \right). \\ \end{gathered} $(17)
$Y = 1;\,\,\,\,VN\left( {X,1} \right) - \frac{1}{{{\text{Pe}}}}\frac{{\partial N\left( {X,1} \right)}}{{\partial Y}} = - V.$Для решения уравнений (14)–(17) применим интегральное преобразование Лапласа по переменной х:
(18)
$s{{N}_{L}}\left( {s,Y} \right) + V\frac{{\partial {{N}_{L}}\left( {s,Y} \right)}}{{\partial Y}} = \frac{1}{{{\text{Pe}}}}\frac{{{{d}^{2}}{{N}_{L}}\left( {s,Y} \right)}}{{d{{Y}^{2}}}},$(19)
$V{{N}_{L}}\left( {s,1} \right) - \frac{1}{{{\text{Pe}}}}\frac{{d{{N}_{L}}\left( {s,1} \right)}}{{dY}} = - \frac{V}{s},$(20)
$\begin{gathered} V{{N}_{L}}\left( {s,0} \right) - \frac{1}{{{\text{Pe}}}}\frac{{d{{N}_{L}}\left( {s,0} \right)}}{{dY}} = \\ = \frac{{K - V}}{s} + K{{N}_{L}}\left( {s,0} \right), \\ \end{gathered} $Перепишем уравнение (18) в виде
(21)
$\begin{gathered} \frac{{{{d}^{2}}{{N}_{L}}\left( {s,Y} \right)}}{{d{{Y}^{2}}}} - V{\text{Pe}}\frac{{d{{N}_{L}}\left( {s,Y} \right)}}{{dY}} - \\ - \,\,s{\text{Pe}}{{N}_{L}}\left( {s,Y} \right) = 0. \\ \end{gathered} $Равенство (21) представляет собой линейное дифференциальное уравнение в обыкновенных производных с постоянными коэффициентами. Решим данное уравнение. Составим характеристическое уравнение вида
где λ – характеристическое число.Из уравнения (22) следует
(23)
$\begin{gathered} {{\lambda }_{1}} = V\frac{{{\text{Pe}}}}{2} + \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} ; \\ {{\lambda }_{2}} = V\frac{{{\text{Pe}}}}{2} - \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} . \\ \end{gathered} $На основании (23) общее решение уравнения (21) можно записать в виде
(24)
$\begin{gathered} {{N}_{L}}\left( {s,Y} \right) = \\ = {{C}_{1}}{\text{exp}}\left\{ {\left[ {V\frac{{{\text{Pe}}}}{2} + \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]Y} \right\} + \\ + \,\,{{C}_{2}}{\text{exp}}\left\{ {\left[ {V\frac{{{\text{Pe}}}}{2} - \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]Y} \right\}. \\ \end{gathered} $Перепишем уравнение (24) через гиперболические функции:
(25)
$\begin{gathered} {{N}_{L}}\left( {s,Y} \right) = \left\{ {{{C}_{1}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} Y} \right]} \right. + \\ \left. { + \,\,{{C}_{2}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} Y} \right]} \right\} \times \\ \times \,\,{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}Y} \right). \\ \end{gathered} $Вычислим производную по Y от решения уравнения (25):
(26)
$\begin{gathered} \frac{{d{{N}_{L}}\left( {s,Y} \right)}}{{dY}} = \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} \times \\ \times \,\,\left\{ {{{C}_{1}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} Y} \right] + } \right. \\ + \,\,\left. {{{C}_{2}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} Y} \right]} \right\}{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}Y} \right) - \\ - \,\,V\frac{{{\text{Pe}}}}{2}\left\{ {{{C}_{1}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} Y} \right]} \right. + \\ \left. { + \,\,{{C}_{2}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} Y} \right]} \right\}{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}Y} \right). \\ \end{gathered} $Найдем значения NL(s, 0), NL(s, 1), dNL(s, 0)/dY, dNL(s, 1)/dY:
(27)
$\begin{gathered} {{N}_{L}}\left( {s,0} \right) = \left\{ {{{C}_{1}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} 0} \right] + } \right. \\ + \left. {{{C}_{2}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} 0} \right]} \right\}{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}0} \right) = {{C}_{1}}; \\ \end{gathered} $(28)
$\begin{gathered} {{N}_{L}}\left( {s,1} \right) = \left\{ {{{C}_{1}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right. + \\ + \,\,\left. {{{C}_{2}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right\}{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}} \right); \\ \end{gathered} $(29)
$\frac{{d{{N}_{L}}\left( {s,0} \right)}}{{dY}} = \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} {{C}_{2}} + V\frac{{{\text{Pe}}}}{2}{{C}_{1}};$(30)
$\begin{gathered} \frac{{d{{N}_{L}}\left( {s,1} \right)}}{{dY}} = \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} \times \\ \times \,\,\left\{ {{{C}_{1}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right. + \left. {{{C}_{2}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right\} \times \\ \times \,\,{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}} \right) - V\frac{{{\text{Pe}}}}{2}\left\{ {{{C}_{1}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right. + \\ \left. { + \,\,{{C}_{2}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right\}{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}} \right). \\ \end{gathered} $Полученные выражения (27)–(30) подставим в краевые условия (19)–(20) и получим систему двух линейных уравнений для определения констант интегрирования С1 и С2. Подставим выражения (27)–(30) в уравнение (19):
(31)
$\begin{gathered} V\left\{ {{{C}_{1}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right] + {{C}_{2}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right\} \times \\ \times \,\,{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}} \right) + {\text{P}}{{{\text{e}}}^{{ - 1}}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right. \times \\ \times \,\,\left\{ {{{C}_{1}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right. + \left. {{{C}_{2}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right\} - \\ - \,\,V\frac{{{\text{Pe}}}}{2}\left\{ {{{C}_{1}}{\text{ch}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right. + \\ \left. {\left. { + \,\,{{C}_{2}}{\text{sh}}\left[ {\sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} } \right]} \right\}} \right]{\text{exp}}\left( {V\frac{{{\text{Pe}}}}{2}} \right) = - \frac{V}{S}. \\ \end{gathered} $Введем обозначения
(32)
$a = \sqrt {\frac{{{{{\left( {V{\text{Pe}}} \right)}}^{2}}}}{4} + s{\text{Pe}}} ;\,\,\,\,b = V\frac{{{\text{Pe}}}}{2}$и преобразуем выражение (31) с учетом обозначений (32):
(33)
$\begin{gathered} V\left( {{{C}_{1}}{\text{ch}}a + {{C}_{2}}{\text{sh}}a} \right){\text{exp}}b + \\ + \,\,{\text{P}}{{{\text{e}}}^{--}}^{1}[a\left( {{{C}_{1}}{\text{sh}}a{\text{ }} + {\text{ }}{{C}_{2}}{\text{ch}}a} \right) - \\ - \,\,V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2}\left( {{{C}_{1}}{\text{ch}}a{\text{ }} + {\text{ }}{{C}_{2}}{\text{sh}}a} \right)]{\text{ exp}}b = {{ - V} \mathord{\left/ {\vphantom {{ - V} s}} \right. \kern-0em} s}. \\ \end{gathered} $Сделаем перегруппировку в выражении (33):
(34)
$\begin{gathered} V({{C}_{1}}{\text{ch}}a + {{C}_{2}}{\text{sh}}a){\text{exp}}b + \\ + \,\,a{\text{P}}{{{\text{e}}}^{--}}^{1}({{C}_{1}}{\text{sh}}a + {{C}_{2}}{\text{ch}}a){\text{exp}}b-- \\ --\,\,{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}}\left( {{{C}_{1}}{\text{ch}}a{\text{ }} + {\text{ }}{{C}_{2}}{\text{sh}}a} \right){\text{exp}}b = {{--V} \mathord{\left/ {\vphantom {{--V} s}} \right. \kern-0em} s};\quad \\ \end{gathered} $(35)
$\begin{gathered} {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\left( {{{C}_{1}}{\text{ch}}a + {{C}_{2}}{\text{sh}}a} \right) + \\ + \,\,a{\text{P}}{{{\text{e}}}^{--}}^{1}\left( {{{C}_{1}}{\text{sh}}a + {{C}_{2}}{\text{ch}}a} \right) = {{ - V} \mathord{\left/ {\vphantom {{ - V} {s{\text{ex}}p\left( { - b} \right)}}} \right. \kern-0em} {s{\text{ex}}p\left( { - b} \right)}}. \\ \end{gathered} $Окончательно имеем
(36)
$\begin{gathered} \left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}}{\text{ch}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{sh}}a} \right){{C}_{1}} + \\ + \,\,\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}}{\text{sh}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{ch}}a} \right){{C}_{2}} = {{ - V} \mathord{\left/ {\vphantom {{ - V} {s{\text{exp}}\left( { - b} \right)}}} \right. \kern-0em} {s{\text{exp}}\left( { - b} \right)}}. \\ \end{gathered} $Подставим теперь (27) и (29) в (20):
(37)
$V{{C}_{1}}--{\text{P}}{{{\text{e}}}^{--}}^{1}\left( {a{{C}_{2}} + b{{C}_{1}}} \right) = {{\left( {K - V} \right)} \mathord{\left/ {\vphantom {{\left( {K - V} \right)} s}} \right. \kern-0em} s} + K{{C}_{1}};$(38)
$\left( {V - b{\text{P}}{{{\text{e}}}^{--}}^{1} - K} \right){{C}_{1}} - a{\text{P}}{{{\text{e}}}^{--}}^{1}{{C}_{2}} = {{\left( {K - V} \right)} \mathord{\left/ {\vphantom {{\left( {K - V} \right)} s}} \right. \kern-0em} s}.$Приступим к решению уравнений (36), (37) и (38) относительно С1 и С2:
(39)
$\begin{gathered} \Delta = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{sh}}a)a{\text{P}}{{{\text{e}}}^{--}}^{1} + \\ + \,\,({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{ch}}a)\left( {V - b{\text{P}}{{{\text{e}}}^{--}}^{1} - K} \right);\quad \\ \end{gathered} $(40)
$\begin{gathered} {{\Delta }_{{C1}}} = {{ - V} \mathord{\left/ {\vphantom {{ - V} {s{\text{exp}}}}} \right. \kern-0em} {s{\text{exp}}}}\left( { - b} \right)a{\text{P}}{{{\text{e}}}^{{ - 1}}} + \\ + \,\,{{\left( {K - V} \right)} \mathord{\left/ {\vphantom {{\left( {K - V} \right)} s}} \right. \kern-0em} s}\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{ch}}a} \right); \\ \end{gathered} $(41)
$\begin{gathered} {{\Delta }_{{C2}}} = - \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{sh}}a} \right){{\left( {K - V} \right)} \mathord{\left/ {\vphantom {{\left( {K - V} \right)} s}} \right. \kern-0em} s} - \\ - \,\,{V \mathord{\left/ {\vphantom {V s}} \right. \kern-0em} s}{\text{exp}}\left( { - b} \right)\left( {V - b{\text{P}}{{{\text{e}}}^{--}}^{1} - K} \right). \\ \end{gathered} $Из (39)–(41) следует
(42)
$\begin{gathered} {{C}_{1}} = {{{{\Delta }_{{C1}}}} \mathord{\left/ {\vphantom {{{{\Delta }_{{C1}}}} \Delta }} \right. \kern-0em} \Delta } = - [{V \mathord{\left/ {\vphantom {V {s{\text{exp}}}}} \right. \kern-0em} {s{\text{exp}}}}\left( { - b} \right)a{\text{P}}{{{\text{e}}}^{--}}^{1} + \\ + \,\,{{\left( {K - V} \right)} \mathord{\left/ {\vphantom {{\left( {K - V} \right)} s}} \right. \kern-0em} s}{\text{ }}({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}a{\text{ }} + {{\left. {a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{ch}}a)} \right]} \mathord{\left/ {\vphantom {{\left. {a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{ch}}a)} \right]} {\left[ {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right.}}} \right. \kern-0em} {\left[ {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right.}}V{\text{ch}}a + \\ + \,\,a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{sh}}a)a{\text{P}}{{{\text{e}}}^{--}}^{1} + \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{ch}}a} \right) \times \\ \times \,\,(V - b{\text{P}}{{{\text{e}}}^{--}}^{1} - K)]; \\ \end{gathered} $(43)
$\begin{gathered} {{C}_{2}} = {{{{\Delta }_{{C2}}}} \mathord{\left/ {\vphantom {{{{\Delta }_{{C2}}}} \Delta }} \right. \kern-0em} \Delta } = [--\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a + a{\text{P}}{{{\text{e}}}^{--}}^{1}{\text{sh}}a} \right){{\left( {K--V} \right)} \mathord{\left/ {\vphantom {{\left( {K--V} \right)} s}} \right. \kern-0em} s}-- \\ - \,\,{V \mathord{\left/ {\vphantom {V {s\exp ( - b)}}} \right. \kern-0em} {s\exp ( - b)}}{{(V - b{{{\operatorname{Re} }}^{{ - 1}}} - K)]} \mathord{\left/ {\vphantom {{(V - b{{{\operatorname{Re} }}^{{ - 1}}} - K)]} {[({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a}}} \right. \kern-0em} {[({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a}} + \\ + \,\,a{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}a)a{\text{P}}{{{\text{e}}}^{{ - 1}}} + \\ + \,\,({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}a + a{\text{P}}{{{\text{e}}}^{{{\text{ - 1}}}}}{\text{ch}}a)(V - b{\text{P}}{{{\text{e}}}^{{ - 1}}} - K)]. \\ \end{gathered} $На основании (25), (42) и (43) решение (18)–(20) имеет следующий вид:
(44)
$\begin{gathered} {{N}_{L}}\left( {s,Y} \right) = \{ - [{V \mathord{\left/ {\vphantom {V {s\exp }}} \right. \kern-0em} {s\exp }}\left( {--b} \right)a{\text{P}}{{{\text{e}}}^{--}}^{1} + {{(K - V)} \mathord{\left/ {\vphantom {{(K - V)} s}} \right. \kern-0em} s} \times \\ \times \,\,({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}a + a{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}a)]{\text{ch}}(aY) + \\ + \,\,[ - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a + a{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}a){{(K - V)} \mathord{\left/ {\vphantom {{(K - V)} s}} \right. \kern-0em} s} - \\ - \,\,{V \mathord{\left/ {\vphantom {V s}} \right. \kern-0em} s}\exp ( - b)(V - b{\text{P}}{{{\text{e}}}^{{ - 1}}} - K)]{\text{sh}}(aY)\} \times \\ \times \,\,\exp ({{ - bY)} \mathord{\left/ {\vphantom {{ - bY)} {[({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a}}} \right. \kern-0em} {[({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}a}} + a{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}a)a{\text{P}}{{{\text{e}}}^{{ - 1}}} + \\ + \,\,({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}a + a{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}a)(V - b{\text{P}}{{{\text{e}}}^{{ - 1}}} - K)]. \\ \end{gathered} $Легко показать, разделив числитель и знаменатель выражения (44) на а, что NL(s, Y) есть отношение бесконечных полиномов, причем порядок полинома в знаменателе выше, чем в числителе. В этом случае для перехода к оригиналу для выражения (44) можно воспользоваться теоремой обращения Ващенко–Захарченко. В связи с этим представим в обобщенном виде выражение (44):
(45)
${{N}_{L}}\left( {s,Y} \right) = {{\varphi \left( {s,Y} \right)} \mathord{\left/ {\vphantom {{\varphi \left( {s,Y} \right)} {\psi (s)}}} \right. \kern-0em} {\psi (s)}},$тогда
(46)
$N\left( {X,Y} \right) = \sum\limits_{n = 0}^\infty {\varphi {{\left( {{{s}_{n}},Y} \right)} \mathord{\left/ {\vphantom {{\left( {{{s}_{n}},Y} \right)} {\psi {\text{'}}}}} \right. \kern-0em} {\psi {\text{'}}}}\left( {{{s}_{n}}} \right)\exp \left( {{{s}_{n}}x} \right)} ,$Выпишем это уравнение, полагая, что
(47)
$\lambda = {{{{{(V{\text{Pe}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{(V{\text{Pe}})}}^{2}}} 4}} \right. \kern-0em} 4} + s{\text{Pe}},$имеем
(48)
$\begin{gathered} s\left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}\sqrt \lambda } \right)\sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}} \right. - \\ - \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\sqrt \lambda } \right)\left. {\left( {V - b{\text{P}}{{{\text{e}}}^{{ - 1}}} - K} \right)} \right] = 0 \\ \end{gathered} $или с учетом того, что b = VPe/2, получим
(49)
$\begin{gathered} s\left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}\sqrt \lambda } \right)\sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}} \right. - \\ - \,\,\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\sqrt \lambda } \right)\left. {\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} \right] = 0. \\ \end{gathered} $Из выражения (49) следует, что s0= 0, а остальные корни находятся из уравнения
(50)
$\begin{gathered} \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}\sqrt \lambda } \right)\sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}} - \\ - \,\,\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\sqrt \lambda } \right)\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K} \right) = 0. \\ \end{gathered} $Если иметь в виду, что левая часть выражения (50) должна быть обобщенным полиномом, то выражение (50) перепишется в виде
(51)
$\begin{gathered} \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}\sqrt \lambda } \right){\text{P}}{{{\text{e}}}^{{ - 1}}} - \\ - \,\,\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\sqrt \lambda } \right)\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K} \right) = 0. \\ \end{gathered} $Разделим выражение (51) на ${\text{ch}}\sqrt \lambda \,:$
(52)
$\begin{gathered} {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{P}}{{{\text{e}}}^{{ - 1}}} + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 2}}}{\text{th}}\sqrt \lambda - \\ - \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K} \right){\text{th}}{{\sqrt \lambda } \mathord{\left/ {\vphantom {{\sqrt \lambda } {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }} - \\ - \,\,\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right){\text{P}}{{{\text{e}}}^{{ - 1}}} = 0; \\ \end{gathered} $(53)
$\begin{gathered} \left[ {\sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 2}}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K} \right)} {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }}} \right]{\text{th}}\sqrt \lambda = \\ = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}V{\text{P}}{{{\text{e}}}^{{ - 1}}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{P}}{{{\text{e}}}^{{ - 1}}} - K{\text{P}}{{{\text{e}}}^{{ - 1}}}; \\ \end{gathered} $(54)
$\begin{gathered} {\text{th}}\sqrt \lambda = \\ = {{ - K{\text{P}}{{{\text{e}}}^{{ - 1}}}} \mathord{\left/ {\vphantom {{ - K{\text{P}}{{{\text{e}}}^{{ - 1}}}} {\left[ {\sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 2}}} - {1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}}{{\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }}} \right]}}} \right. \kern-0em} {\left[ {\sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 2}}} - {1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}}{{\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }}} \right]}}. \\ \end{gathered} $Физическому смыслу задачи отвечают только вещественные отрицательные корни sn (см. выражение (46)), при этом аргумент гиперболического тангенса может быть или вещественным,
или мнимым
В связи с этим получаем соответственно два вида характеристических уравнения:
(57)
${\text{th}}\mu = {{4K{\text{Pe}}\mu } \mathord{\left/ {\vphantom {{4K{\text{Pe}}\mu } {[V(V - 2K) - 4{{\mu }^{2}}]}}} \right. \kern-0em} {[V(V - 2K) - 4{{\mu }^{2}}]}},$(58)
${\text{th}}{{\mu }_{n}} = {{4K{\text{Pe}}{{\mu }_{n}}} \mathord{\left/ {\vphantom {{4K{\text{Pe}}{{\mu }_{n}}} {[V(V - 2K) - 4{{\mu }^{2}}]}}} \right. \kern-0em} {[V(V - 2K) - 4{{\mu }^{2}}]}}.$Исследуем уравнения (57) и (58).
1. Пусть V < 2K, тогда из уравнения (57) следует, что правая часть
(59)
$f{\text{(}}\mu ) = {{4K{\text{Pe}}\mu } \mathord{\left/ {\vphantom {{4K{\text{Pe}}\mu } {[V(V - 2K) - 4{{\mu }^{2}}]}}} \right. \kern-0em} {[V(V - 2K) - 4{{\mu }^{2}}]}} < 0,$причем
(60)
$\begin{gathered} f{\kern 1pt} '(\mu ) = \{ 4K{\text{Pe[}}V(V--2K)--4{{\mu }^{2}}]-- \\ - \,\,{{4K{\text{Pe}}\mu (--8\mu )\} } \mathord{\left/ {\vphantom {{4K{\text{Pe}}\mu (--8\mu )\} } {{{{[V(V - 2K) - 4{{\mu }^{2}}]}}^{2}}}}} \right. \kern-0em} {{{{[V(V - 2K) - 4{{\mu }^{2}}]}}^{2}}}}. \\ \end{gathered} $Числитель последнего выражения представим в виде
(62)
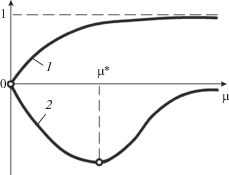
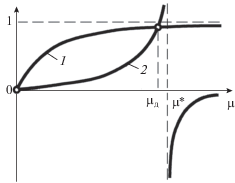
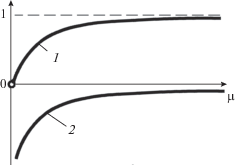
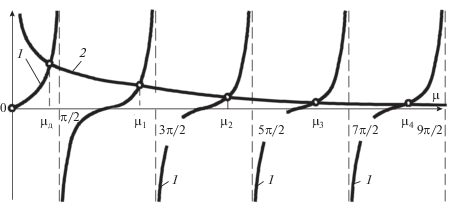
$\mu * = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sqrt {V\left( {2K - V} \right)} .$В этом случае уравнение (57) не имеет корня (рис. 2).
Рассмотрим уравнение (58) при таком же предположении, т.е. V < 2K. Правая часть уравнения (58) имеет разрыв 2-го рода в точке μ* = = ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sqrt {V\left( {2K - V} \right)} .$
Исследуем функцию
(63)
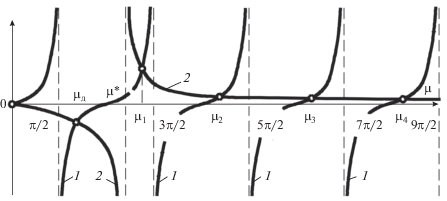
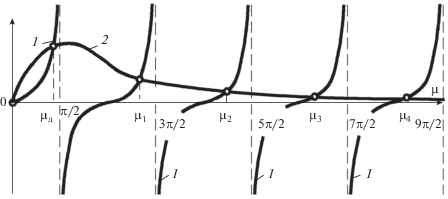
$f(\mu ) = {{4K{\text{Pe}}\mu } \mathord{\left/ {\vphantom {{4K{\text{Pe}}\mu } {[V(V - 2K) + 4{{\mu }^{2}}]}}} \right. \kern-0em} {[V(V - 2K) + 4{{\mu }^{2}}]}}.$Очевидно, что при μ < μ*f(μ) < 0, а при μ > > μ*f(μ) > 0, поэтому появляется дополнительный корень μд (рис. 3), а остальные корни находятся в интервалах
(64)
${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\pi {\text{ }}(2n--1) \leqslant {{\mu }_{n}} \leqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\pi {\text{ }}(n + 1).$В этой же связи отметим случай, когда μ* < < 1/2π (рис. 4).
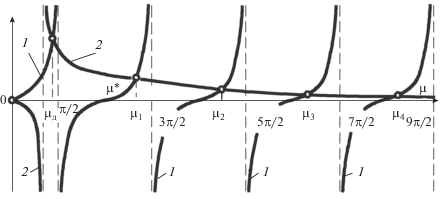
2. Пусть V > 2K. Уравнение (57) имеет дополнительный корень (рис. 5). Причем точка разрыва 2-го рода определяется из равенства нулю знаменателя правой части уравнения (57), т.е. $\mu {\text{*}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sqrt {V\left( {V - 2K} \right)} .$
Вычислим производную правой части уравнения (57):
(65)
$\begin{gathered} f{\kern 1pt} '(\mu ) = \{ 4K{\text{Pe[}}V{\text{(}}V - {\text{2}}K{\text{)}} + {\text{4}}{{\mu }^{2}}]-- \\ --\,\,{{4K{\text{Pe}}\mu 8\mu )\} } \mathord{\left/ {\vphantom {{4K{\text{Pe}}\mu 8\mu )\} } {[V(V - 2K)}}} \right. \kern-0em} {[V(V - 2K)}} - 4{{\mu }^{2}}{{]}^{2}} < 0, \\ \end{gathered} $или
(66)
$\begin{gathered} f{\kern 1pt} '(\mu ) = [4K{\text{Р e}}V(V--2K)-- \\ - \,\,{{16K{\text{Р e}}{{\mu }^{2}}]} \mathord{\left/ {\vphantom {{16K{\text{Р e}}{{\mu }^{2}}]} {{{{[V(V - 2K) + 4{{\mu }^{2}}]}}^{2}}}}} \right. \kern-0em} {{{{[V(V - 2K) + 4{{\mu }^{2}}]}}^{2}}}}. \\ \end{gathered} $Найдем значение f '(μ) при μ = 0: f'(0) = = 4KPe/[V(V – 2K)].
Легко показать, что f'(0) = 4KPe/[V(V – 2K)] и для левой части (57). Продолжая анализировать, вычислим значения производных левых частей уравнений (57) и (58):
Следовательно, рис. 5 соответствует случаю, когда
(68)
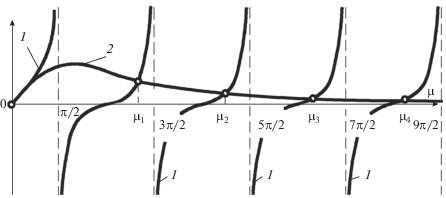
${{4K{\text{Pe}}} \mathord{\left/ {\vphantom {{4K{\text{Pe}}} {[V(V - 2K)] < 1.}}} \right. \kern-0em} {[V(V - 2K)] < 1.}}$В этом случае множество корней уравнения (57) показано на рис. 6.
В случае, когда 4KPe/[V(V – 2K)] > 1, уравнение (57) не имеет корней (рис. 7), а уравнение (58) приобретает дополнительный корень на отрезке 0 и 1/2π (рис. 8).
Если же выполняется условие 4KPe/[V(V – 2K)] = = 1, то дополнительный корень μд = 0 и, в конечном итоге, он становится корнем кратности два.
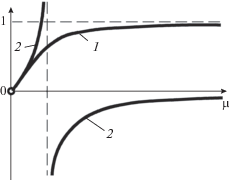
3. Пусть V = 2K. В этом случае уравнения (57) и (58) вырождаются в уравнения следующего вида:
(69)
${\text{th}}\mu = {{ - K{\text{Pe}}} \mathord{\left/ {\vphantom {{ - K{\text{Pe}}} \mu }} \right. \kern-0em} \mu },$(70)
${\text{th}}{{\mu }_{n}} = {{K{\text{Pe}}} \mathord{\left/ {\vphantom {{K{\text{Pe}}} \mu }} \right. \kern-0em} \mu }.$Уравнение (69), как видно из рис. 9, не может иметь корней ни при каких условиях, а дополнительный корень μд находится в интервале 0 < μд < < 1/2π (рис. 10).
Выяснив ситуацию с характеристическими числами решения, приступим теперь к выяснению окончательного вида структуры решения (46).
Итак, выпишем вновь вид ψ(sn):
(71)
$\begin{gathered} \varphi (s) = s\left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}\sqrt \lambda } \right){\text{P}}{{{\text{e}}}^{{ - 1}}} - } \right. \\ - \,\,\left. {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{V{\text{sh}}\sqrt \lambda } \mathord{\left/ {\vphantom {{V{\text{sh}}\sqrt \lambda } {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }} + {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\sqrt \lambda } \right)\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} \right]. \\ \end{gathered} $Вычислим ψ'(s):
Поскольку λ = 1/4(VPe)2 + Pes, то $\lambda _{s}^{'}$ = Pe, поэтому (72) примет следующий вид:
(73)
$\begin{gathered} \psi {\text{'}}(s) = \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}\sqrt \lambda } \right){\text{P}}{{{\text{e}}}^{{ - 1}}} - \\ - \,\,{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}\sqrt \lambda } \right.} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}\sqrt \lambda } \right.} {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }} + \left. {{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\sqrt \lambda } \right)\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right) + \\ + \,\,s\left[ {\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}}\,{\text{sh}}} \right.} \right.{{\sqrt \lambda } \mathord{\left/ {\vphantom {{\sqrt \lambda } {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{sh}}{{\sqrt \lambda } \mathord{\left/ {\vphantom {{\sqrt \lambda } {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }} + \\ + \,\,\left. {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{ch}}\sqrt \lambda } \right){\text{P}}{{{\text{e}}}^{{ - 1}}} - {{\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}}\,{\text{ch}}\sqrt \lambda } \right.} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}}\,{\text{ch}}\sqrt \lambda } \right.} \lambda }} \right. \kern-0em} \lambda } - \\ \left. { - \,\,\left. {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{Pe}}\,{\text{sh}}{{\sqrt \lambda } \mathord{\left/ {\vphantom {{\sqrt \lambda } {\lambda \sqrt \lambda }}} \right. \kern-0em} {\lambda \sqrt \lambda }} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{sh}}{{\sqrt \lambda } \mathord{\left/ {\vphantom {{\sqrt \lambda } {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }}} \right)\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} \right]. \\ \end{gathered} $Выпишем теперь φ(s, Y):
(74)
$\begin{gathered} \varphi \left( {s,Y} \right) = \left\{ { - \left[ {V{\text{P}}{{{\text{e}}}^{{ - 1}}}\left( {V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2}} \right) + \left( {K - V} \right)} \right.} \right. \times \\ \times \,\,\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}{{\sqrt \lambda } \mathord{\left/ {\vphantom {{\sqrt \lambda } {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }} + } \right.\left. {\left. {{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\sqrt \lambda } \right)} \right]{\text{ch}}\left( {\sqrt \lambda Y} \right) + \\ + \,\,\left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\sqrt \lambda + \sqrt \lambda {\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{sh}}\sqrt \lambda } \right) \times } \right. \\ \times \,\,\left. {\left( {K - V} \right) + V\exp \left( {V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2}} \right)\left( {{1 \mathord{\left/ {\vphantom {1 {2V}}} \right. \kern-0em} {2V}} - K} \right)} \right] \times \\ \times \,\,\left. {{\text{sh}}{{\left( {\sqrt \lambda Y} \right)} \mathord{\left/ {\vphantom {{\left( {\sqrt \lambda Y} \right)} {\sqrt \lambda }}} \right. \kern-0em} {\sqrt \lambda }}} \right\}\exp \left( {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}V{\text{Pe}}Y} \right). \\ \end{gathered} $Найдем
Запишем выражение (73) и (74) для случаев:
при $\sqrt \lambda = \mu $
(76)
$\begin{gathered} \psi {\kern 1pt} '(\mu ) = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\mu + {\text{P}}{{{\text{e}}}^{{--1}}}\mu {\text{sh}}\mu ){\text{P}}{{{\text{e}}}^{{--1}}}--({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{{V{\text{sh}}\mu } \mathord{\left/ {\vphantom {{V{\text{sh}}\mu } \mu }} \right. \kern-0em} \mu } + \\ + \,\,{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\mu )({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K) + {\text{P}}{{{\text{e}}}^{{ - 1}}}[\mu - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{{(V{\text{Pe}})}^{2}}][{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}} \cdot {\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } + \\ + \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{ch}}\mu ){\text{P}}{{{\text{e}}}^{{ - 1}}} - ({1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{\text{Pe}}\,{\text{ch}}{\mu \mathord{\left/ {\vphantom {\mu {{{\mu }^{2}}}}} \right. \kern-0em} {{{\mu }^{2}}}} - \\ - \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{Pe}}\,{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu {{{\mu }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{\mu }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu })({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)], \\ \end{gathered} $(77)
$\begin{gathered} \varphi (\mu ,Y) = \{ --[V{\text{P}}{{{\text{e}}}^{{--1}}}{\text{exp}}\left( {V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2}} \right) + \left( {K--V} \right)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } + \\ + \,\,{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{ch}}\mu )]{\text{ch}}(\mu Y) + [({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\mu + {\text{P}}{{{\text{e}}}^{{ - 1}}}\mu {\text{sh}}\mu ) \times \\ \times \,\,(K - V) + \exp (V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]{\text{sh}}{{(\mu Y)} \mathord{\left/ {\vphantom {{(\mu Y)} \mu }} \right. \kern-0em} \mu }\} \exp ({{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}V{\text{Pe}}Y); \\ \end{gathered} $при $\sqrt \lambda = \lambda i$
(78)
$\begin{gathered} \psi {\kern 1pt} '({{\mu }_{n}}) = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\cos {{\mu }_{n}} - {\text{P}}{{{\text{e}}}^{{ - 1}}}{{\mu }_{n}}\sin {{\mu }_{n}}){\text{P}}{{{\text{e}}}^{{--1}}}--({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sin }}{{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + \\ + \,\,{\text{P}}{{{\text{e}}}^{{ - 1}}}\cos {{\mu }_{n}}({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K) - {\text{P}}{{{\text{e}}}^{{ - 1}}}[\mu _{n}^{2} + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{{(V{\text{Pe}})}^{2}}][{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}}\,\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + \\ + \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\cos {{\mu }_{n}}){\text{P}}{{{\text{e}}}^{{ - 1}}} + ({1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{\text{Pe}}\,\cos \mu _{n}^{2} - \\ - \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{Pe}}\,\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}}\sqrt {{{\mu }_{n}}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)], \\ \end{gathered} $(79)
$\begin{gathered} \varphi ({{\mu }_{n}},Y) = \{ --[V{\text{P}}{{{\text{e}}}^{{--1}}}{\text{exp(}}V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2}) + (K--V)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sin}}{{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + \\ + \,\,{\text{P}}{{{\text{e}}}^{{ - 1}}}\cos {{\mu }_{n}})]\cos ({{\mu }_{n}}Y) + [({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\cos {{\mu }_{n}} - {\text{P}}{{{\text{e}}}^{{ - 1}}}{{\mu }_{n}}\sin {{\mu }_{n}}) \times \\ \times \,\,(K - V) + V\exp (V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K]\sin {{({{\mu }_{n}}Y)} \mathord{\left/ {\vphantom {{({{\mu }_{n}}Y)} {{{\mu }_{n}}]\} \exp ({{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \right. \kern-0em} {{{\mu }_{n}}]\} \exp ({{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}V{\text{Pe}}Y). \\ \end{gathered} $На основании проведенного анализа математической модели запишем окончательно решение поставленной задачи:
(80)
$\begin{gathered} C\left( {X,Y} \right) = F\left( {X,Y} \right) + \\ + \,\,\sum\limits_{n = 1}^\infty {R_{n}^{{ - 1}}\left[ {{{P}_{n}}\cos \left( {{{\mu }_{n}}Y} \right) + {{Q}_{n}}\sin \left( {{{\mu }_{n}}Y} \right)} \right]} \times \\ \times \,\,\exp \left\{ {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}V{\text{Pe}}Y - {\text{P}}{{{\text{e}}}^{{ - 1}}}\left[ {\mu _{n}^{2} + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{{{\left( {V{\text{Pe}}} \right)}}^{2}}} \right]X} \right\} \\ \end{gathered} $при V ≤ 2K: F(X, Y) = 0;
при V > 2K и 4KPe/[V(V – 2K)] > 1: F(X, Y) = 0;
при V > 2K и 4KPe/[V(V – 2K)] < 1;
(81)
$\begin{gathered} F(X,Y) = {{R}^{{--1}}}[P\cos (\mu Y) + Q\sin (\mu Y)] \times \\ \times \,\,\exp \{ {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}V{\text{Pe}}Y + \\ + \,\,{\text{P}}{{{\text{e}}}^{{ - 1}}}[{{\mu }^{2}} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{{(V{\text{Pe}})}^{2}}X\} , \\ \end{gathered} $(82)
$\begin{gathered} R = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\mu + {\text{P}}{{{\text{e}}}^{{--1}}}\mu {\text{sh}}\mu ){\text{P}}{{{\text{e}}}^{{--1}}}--({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } + {\text{P}}{{{\text{e}}}^{{--1}}}{\text{ch}}\mu ) \times \\ \times \,\,({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K) + {\text{P}}{{{\text{e}}}^{{ - 1}}}[\mu - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{{(V{\text{Pe}})}^{2}}][{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}}\,{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } + \\ + \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{ch}}\mu ){\text{P}}{{{\text{e}}}^{{ - 1}}} - ({1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{\text{Pe}}\,{\text{ch}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } - \\ - \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{Pe}}\,{\text{sh}}{{{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu }}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu })({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)], \\ \end{gathered} $(83)
$\begin{gathered} P = --[V{\text{P}}{{{\text{e}}}^{{--1}}}{\text{exp(}}V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2}) + \\ + \,\,(K--V)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{sh}}{\mu \mathord{\left/ {\vphantom {\mu \mu }} \right. \kern-0em} \mu } + {\text{P}}{{{\text{e}}}^{{--1}}}{\text{ch}}\mu )], \\ \end{gathered} $(84)
$\begin{gathered} Q = [({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{ch}}\mu + {\text{P}}{{{\text{e}}}^{{ - 1}}}\mu {\text{sh}}\mu )(K - V) + \\ + \,\,{{V\exp (V{{Pe} \mathord{\left/ {\vphantom {{Pe} {2)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]}}} \right. \kern-0em} {2)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]}}} \mathord{\left/ {\vphantom {{V\exp (V{{Pe} \mathord{\left/ {\vphantom {{Pe} {2)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]}}} \right. \kern-0em} {2)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]}}} \mu }} \right. \kern-0em} \mu }, \\ \end{gathered} $(85)
${\text{th}}\mu = {{4K{\text{Pe}}\mu } \mathord{\left/ {\vphantom {{4K{\text{Pe}}\mu } {[V(V - 2K) - 4{{\mu }^{2}}]}}} \right. \kern-0em} {[V(V - 2K) - 4{{\mu }^{2}}]}};$(86)
$\begin{gathered} {{R}_{n}} = ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\cos {{\mu }_{n}} - {\text{P}}{{{\text{e}}}^{{ - 1}}}{{\mu }_{n}}\sin {{\mu }_{n}}){\text{P}}{{{\text{e}}}^{{ - 1}}} - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + \\ + \,\,{\text{P}}{{{\text{e}}}^{{ - 1}}}\cos {{\mu }_{n}})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K) - {\text{P}}{{{\text{e}}}^{{ - 1}}}[(\mu _{n}^{2} + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{{(V{\text{Pe}})}^{2}}][{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}}\,\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + \\ + \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\cos {{\mu }_{n}}){\text{P}}{{{\text{e}}}^{{ - 1}}} + ({1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}V{\text{Pe}}\,\cos {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {\mu _{n}^{2}}}} \right. \kern-0em} {\mu _{n}^{2}}} - \\ - \,\,{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V{\text{Pe}}\,\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]; \\ \end{gathered} $(87)
$\begin{gathered} {{P}_{n}} = --[V{\text{P}}{{{\text{e}}}^{{ - 1}}}{\text{exp(}}V{{{\text{Pe}}} \mathord{\left/ {\vphantom {{{\text{Pe}}} 2}} \right. \kern-0em} 2}) + \\ + \,\,(K - V)({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\sin {{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {{{\mu }_{n}}}}} \right. \kern-0em} {{{\mu }_{n}}}} + {\text{P}}{{{\text{e}}}^{{ - 1}}}\cos {{\mu }_{n}})]; \\ \end{gathered} $(88)
$\begin{gathered} {{Q}_{n}} = [{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V\cos {{\mu }_{n}} - P{{e}^{{ - 1}}}{{\mu }_{n}}\sin {{\mu }_{n}})(K - V) + \\ + \,\,{{V\exp ({{V{\text{Pe}}} \mathord{\left/ {\vphantom {{V{\text{Pe}}} 2}} \right. \kern-0em} 2})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]} \mathord{\left/ {\vphantom {{V\exp ({{V{\text{Pe}}} \mathord{\left/ {\vphantom {{V{\text{Pe}}} 2}} \right. \kern-0em} 2})({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}V - K)]} \mu }} \right. \kern-0em} \mu }, \\ \end{gathered} $(89)
${\text{tg}}{{\mu }_{n}} = 4K{\text{Pe}}{{{{\mu }_{n}}} \mathord{\left/ {\vphantom {{{{\mu }_{n}}} {[V(V - 2K) + 4\mu _{n}^{2}].}}} \right. \kern-0em} {[V(V - 2K) + 4\mu _{n}^{2}].}}$Графическая интерпретация результатов расчета профилей концентраций разделяемого раствора в мембранном канале прямоугольного сечения при различных входных параметрах K, V, Pe представлена на рис. 11.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Исследования процесса микрофильтрации пива нефильтрованного непастеризованного осуществляли на экспериментальной установке (рис. 12), состоящей из баллона 1 со сжатой пищевой газовой смесью “BIOGON”, емкости 2 с фильтруемым пивом, манометров 3, насоса 4, плоскорамного мембранного модуля 5 (рис. 13), приемной емкости 6 осветленного продукта, коммуникаций с вентилями, стеклянной трубки с делениями для измерения скорости процесса, мерного цилиндра с колпаком для осветленного пива (на рисунке не показаны).
Рис. 12.
Экспериментальная установка для исследования проточной микрофильтрации: 1 – баллон со сжатой пищевой газовой смесью “BIOGON”; 2 – емкость с фильтруемым пивом; 3 – манометр; 4 – насос; 5 – плоскорамный мембранный модуль; 6 – приемная емкость осветленного продукта.
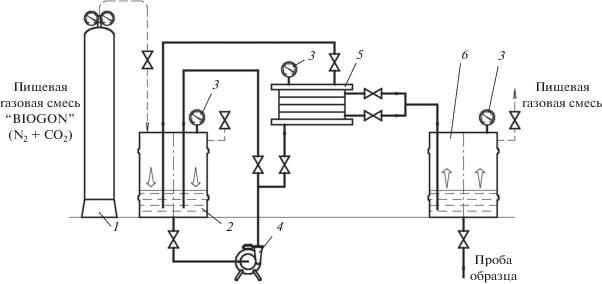
Организация экспериментальных исследований проточной микрофильтрации пива сводилась к следующей последовательности. Вначале мембранный модуль заполняли стерильной водой для полного вытеснения из системы воздуха через патрубки отвода пермеата и ретентата. Затем из расходной емкости насосом подавали нефильтрованное пиво, вытесняя им воду. Затем краном на линии отвода концентрата, на основании показаний манометра, устанавливали необходимый перепад давлений. Удельная проницаемость ядерного фильтра оценивалась по объему пермеата в стеклянной трубке, получаемого за определенный период времени.
Микрофильтрация пива при проточном режиме организации процесса проводилась при следующих технологических параметрах: температура 2–6°С, рабочее давление 0.08–0.25 МПа, скорость разделяемого потока над поверхностью мембраны 2–3 м/с.
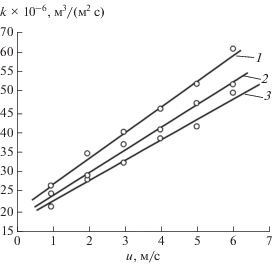
С увеличением скорости разделяемого потока над мембраной можно показать линейный рост проницаемости ядерного фильтра с разрешающей способностью 0.90 мкм (рис. 14). При достижении скоростей потока до величин 3.5–4.5 м/с проницаемость мембран достигала значений 45.6 × 10–6 (кривая 3), 48.7 × 10–6 (кривая 2) и 52.3 × × 10–6 м/с (кривая 1) для высот мембранного канала 2.7, 1.47 и 0.5 мм соответственно. При выбранном диапазоне тангенциальной скорости 3.5–4.5 м/с и правильной организации гидравлической системы мембранной установки можно предотвратить оседание частиц белковых взвесей, дрожжей и бактерий на ядерном фильтре. Величина потерь давления для плоскорамного мембранного модуля составит не более 0.2–0.3 МПа.
Рис. 14.
Зависимость удельной скорости микрофильтрации пива на трековой мембране с размером пор 0.90 мкм от величины тангенциальной скорости в мембранном канале различной высоты, мм: 1 – 0.5; 2 – 1.45; 3 – 2.7.
Превышение диапазона тангенциальной скорости сопровождается существенными потерями давления до 0.6–0.8 МПа, что нерационально по причине увеличивающихся энергетических затрат. Следует подчеркнуть, что проведение экспериментов при тангенциальной скорости свыше 5 м/с сопровождалось существенным увеличением объема образующего концентрата, с большим количеством целевого компонента. Концентрат для более глубокой очистки вынуждены были возвращать в циркуляционный контур, что приводило к ухудшению качества разделяемого продукта.
Для того чтобы изменить высоту мембранного канала плоскорамного мембранного модуля, использовали комплект прокладок высотой 0.5, 1.45 и 2.7 мм. Анализ полученной зависимости (рис. 15) говорит о существенном влиянии высоты мембранного канала в момент формирования слоя высокой концентрации на ядерном фильтре.
Рис. 15.
Зависимость удельной скорости микрофильтрации пива на трековой мембране с размером пор 0.90 мкм от продолжительности процесса в мембранном канале различной высоты, мм: 1 – 0.5; 2 – 1.45; 3 – 2.7.
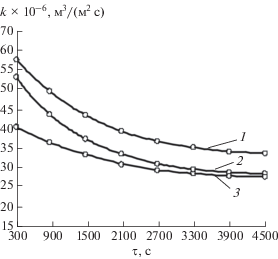
Таблица 1.
Параметры, определяемые на основании результатов эксперимента
| Линейная скорость, м/с | Re | Re–0.25 | Коэффициент сопротивления Блазиуса | Re0.125 | Pe | Коэффициент продольного перемешивания, м2/с |
|---|---|---|---|---|---|---|
| 2.5 | 2717 | 0.1385 | 0.0437 | 2.68 | 2.04 | 0.183 |
| 3 | 3260 | 0.1323 | 0.0418 | 2.74 | 2.08 | 0.215 |
| 3.5 | 3804 | 0.1273 | 0.0402 | 2.80 | 2.12 | 0.246 |
| 4 | 4347 | 0.1231 | 0.0389 | 2.84 | 2.16 | 0.277 |
Через 5–10 мин ведения процесса проницаемость ядерного фильтра составляла (55–58) × × 10–6 м/с в мембранном канале высотой 0.5 мм (кривая 1). Как показывает кинетическая зависимость, кривые 1–3 проницаемости постепенно выходят на постоянный уровень, что свидетельствует о малозначащем влиянии высоты мембранного канала по истечении определенного времени. Режим движения жидкости в мембранном канале напрямую влияет на слой высокой концентрации, т.е. с увеличением высоты канала уменьшается величина тангенциальной скорости, число Рейнольдса также уменьшается и, как следствие, падает проницаемость мембраны из-за образования слоя высокой концентрации на ее поверхности [12–14].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Полученные в результате вычислений профили концентраций растворенного вещества позволяют сделать вывод о характере гидродинамических условий в канале мембранного аппарата. Для более объективной картины расчеты проводили при числе Ре = 2. При этом случай, при котором величины безразмерной проницаемости K = 1.5 и безразмерной скорости V = 0.2, является наиболее предпочтительным для изучаемого мембранного процесса микрофильтрации, так как характер поведения профилей концентраций предполагает создание таких гидродинамических условий, при которых обеспечивается и проницаемость мембраны, и снижение концентрации растворенного вещества на ее поверхности по длине рассматриваемого канала. Такие результаты говорят об эффективности проводимых мероприятий по снижению концентрационной поляризации на поверхности мембраны при помощи гидродинамических методов воздействия на слой высокой концентрации, например, за счет вариаций скорости разделяемого потока.
Важнейшей характеристикой гидродинамической структуры потока является коэффициент продольного перемешивания, который можно вычислить через статистические параметры дифференциальной функции распределения времени пребывания индикатора в канале мембранного аппарата, получаемой экспериментально с помощью импульсного метода. Однако экспериментальный мембранный модуль имел небольшие геометрические размеры (длина мембранного канала l = 0.15 м; высота мембранного канала h = = 2.7 × 10–3 м), а при скорости движения 2.5–3.5 м/с разделяемый поток находился в мембранном канале менее 1.0–1.5 с, поэтому выполнить достоверные измерения концентрации индикатора на выходе из мембранного модуля не представлялось возможным. Также практически невозможно определить существующими инструментальными методами характер распределения поля концентраций растворенного вещества по высоте и длине мембранного канала с данными геометрическими размерами.
Поэтому определение практических значений числа Pe с целью его сравнения с результатами, полученными по математической модели, осуществляли на основании экспериментальных значений тангенциальной скорости потока.
Исходные данные для расчета: плотность пива ρ = 1018.6 кг/м3; динамическая вязкость пива при температуре микрофильтрации (t = 2°С) ξ = 2.816 × × 10–3 Па с.
Для приближенного расчета коэффициента турбулентного перемешивания Ре использовали уравнения Тейлора [15]. Результаты вычислительного эксперимента удовлетворительно согласуются с экспериментальными данными для скорости потока 2.5 м/с и мембранного канала высотой 2.7 мм. В таблице приведены параметры, определяемые на основании результатов эксперимента.
ЗАКЛЮЧЕНИЕ
В настоящей работе показана возможность адаптации однопараметрической диффузионной модели к мембранному процессу разделения за счет учета проницаемости одной из стенок рассматриваемого канала прямоугольного сечения. Изучена структура гидродинамического потока, позволяющая определить поведение поля концентраций растворенного вещества на поверхности мембраны и оценить эффективность применяемых мероприятий, направленных на снижение концентрационной поляризации гидродинамическими методами за счет вариаций скорости. Ввиду практических сложностей вычисления характера распределения поля концентраций растворенного вещества по высоте и длине мембранного канала существующими инструментальными методами, показана возможность оценки коэффициента эффективного перемешивания Ре с помощью уравнений Тейлора по практическим значениям тангенциальных скоростей разделяемого потока.
ОБОЗНАЧЕНИЯ
| С(X, Y) | безразмерная величина, характеризующая отношение текущей концентрации разделяемого раствора с(x, y) к концентрации на входе в мембранный канал с0 |
| С1, С2 | константы интегрирования |
| с | концентрация раствора в рассматриваемом объеме, мас. % |
| c(x, y), c0 | соответственно текущая и при входе в мембранный канал концентрации разделяемого раствора, мас. % |
| D | коэффициент диффузии, м2/с |
| G0 | расход разделяемой технологической жидкости на входе в мембранный канал, м3/с |
| Gк | расход разделяемой технологической жидкости на выходе из мембранного канала, м3/с |
| ∆G | расход пермеата, прошедшего через мембрану, м3/с |
| h | высота мембранного канала, м |
| K | безразмерная величина, характеризующая проницаемость мембраны вдоль оси абсцисс X |
| k | проницаемость мембраны по длине канала, м3/(м2 с) |
| l | длина мембранного канала, м |
| Р | давление потока разделяемой технологической жидкости, Па |
| s, NL(s, Y) | изображения X и N(X, Y) по Лапласу |
| sn | корни уравнения ψ(s) = 0 |
| V | безразмерная величина, характеризующая отношение скоростей разделяемого потока вдоль осей ординат Y и абсцисс Х |
| ${{{\mathbf{v}}}_{x}},{{{\mathbf{v}}}_{y}}$ | скорости разделяемого продукта в канале, м/с |
| X, Y | безразмерные продольная и поперечная координаты, отчитываемые от нижней кромки мембранного канала высотой h |
| x, y | продольная и поперечная координаты, отчитываемые от нижней кромки мембранного канала высотой h |
| λ | характеристическое число |
| μ, μn, μд, μ* | корни уравнения |
| ξ | динамическая вязкость пива при температуре микрофильтрации, Па с |
| ρ | плотность пива, кг/м3 |
| Pe–1 = = D/(${{{\mathbf{v}}}_{x}}$h) | диффузионный критерий Пекле |
| Re = ${{{\mathbf{v}}}_{x}}$l/ξ | число Рейнольдса |
ИНДЕКСЫ
Список литературы
Akhmadiev F.G., Farakhov M.I., Bekbulatov I.G., Isyanov Ch.Kh. Mathematical modeling of filtering process of two-phase suspensions in tubular filters under nonisothermal conditions // Theor. Found. Chem. Eng. 2016. V. 50. № 1. P. 41. [Ахмадиев Ф.Г., Фарахов М.И., Бекбулатов И.Г., Исянов Ч.Х. Математическое моделирование процесса фильтрования двухфазных суспензий в трубчатых фильтрах в неизотермических условиях // Теорет. основы хим. технологии. 2016. Т. 50. № 1. С. 44.]
Gan Q., Howell J.A., Field R.W., England R., Bird M.R., O’Shaughnessy C.L., McKechinie M.T. Beer clarification by microfiltration – product quality control and fractionation of particles and macromolecules // Journal of Membrane Science. 2001. V. 194. P. 185.
Hunt J.W., Brouchaert C.J., Raal J.D., Treffry-Goatley K., Buckley C.A. The unsteady-state modeling of cross-flow microfiltration // Desalination. 1987. V. 64. P. 431.
Бабёнышев С.П., Чернов П.С., Мамай Д.С. Моделирование процесса мембранной фильтрации жидких систем // Научный журнал КубГАУ. 2012. № 76 (02). С. 1.
Баженов В.И., Устюжанин А.В. Математическая модель биологической очистки сточных вод с учетом гидродинамических и нестационарных условий // Вестник ИрГТУ. 2014. № 11 (94). С. 128.
Горбунова Ю.А., Тимкин В.А. Гидродинамика процессов микро- и ультрафильтрационного разделения молока и творожного калье // Аграрный вестник Урала. 2016. № 06 (148). С. 70.
Лобасенко Б.А., Павский В.А. Определение концентрации растворенных веществ в пограничном слое на поверхности мембраны // Известия вузов. Пищевая технология. 2001. № 2–3. С. 68.
Семенов А.Г. Развития гелевого загрязнения мембраны при тангенциальной ультрафильтрации раствора высокомолекулярного соединения // Техника и технология пищевых производств. 2011. № 1 (20). С. 1.
Беккер В.Ф. Моделирование химико-технологических объектов управления: учеб. пособ. 2-е изд., перераб. и доп. М.: РИОР: ИНФРА–М, 2014.
Тимашев С.Ф. Физикохимия мембранных процессов. М.: Химия, 1998.
Брык М.Т. Ультрафильтрация. Киев: Наук. думка, 1989.
Schmitz P., Houi D., Wandelt B. Hydrodynamic aspects of crossflow microfiltration. Analysis of particle deposition at the membrane surface // Journal of Membrane Science. 1992. V. 71. P. 29.
Антипов С.Т., Кретов И.Т., Шахов С.В., Ключников А.И. Концентрационная поляризация в процессе осветления пива // Пиво и напитки. 2001. № 3. С. 18.
Антипов С.Т., Шахов С.В., Рязанов А.Н., Ключников А.И., Бляхман Д.А., Васильченко А.Н. Мембранный аппарат с изменяющейся высотой каналов. Пат. 2147459 РФ // Б. И. 2000. № 11.
Лаптев А.Г., Лаптева Е.А. Определение коэффициентов турбулентного перемешивания в одно- и двухфазных средах по модели Тейлора // Фундаментальные исследования. 2015. № 2. С. 2810.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии