Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 83-90
Теоретическое прогнозирование процесса электромембранного разделения медьсодержащих растворов гальванических производств
С. И. Лазарев a, О. А. Абоносимов a, Д. Н. Протасов a, К. В. Шестаков a, *
a Тамбовский государственный технический университет
Тамбов, Россия
* E-mail: geometry@mail.nnn.tstu.ru
Поступила в редакцию 20.06.2018
После доработки 16.11.2018
Принята к публикации 30.11.2018
Аннотация
Работа посвящена теоретическому прогнозированию процесса электромембранного разделения медьсодержащих растворов в медно-гальваническом производстве с помощью математической модели, основанной на решении уравнений Нернста–Планка и Пуассона–Больцмана. Модель отслеживает изменения объемных потоков пермеата и концентрации раствора от времени проведения электромембранного процесса. Математическая модель позволяет рассчитывать концентрацию на выходе из электромембранного аппарата, удельный выходной поток растворителя и расход энергии на мембранное разделение растворов. Уравнения модели при расчете учитывают явления массопереноса и гидродинамику течения раствора в межмембранном канале. Выполнена проверка адекватности математической модели путем сравнения расчетных и экспериментально полученных данных по изменению концентрации целевого вещества в ретентате относительно давления при постоянной плотности тока.
ВВЕДЕНИЕ
Научное решение реальных прикладных задач в различных сферах промышленности играет важную роль, этому посвящается большое количество научных трудов. Не является исключением и гальваническое производство, в работах [1–6] рассматриваются различные задачи. Рассматриваемая работа пытается решить проблему, относящуюся к очистным мероприятиям, исследованию и прогнозированию кинетики таких процессов с помощью математических моделей.
Прежде всего, нужно отметить, что в этом случае при решении прикладных задач удобно рассматривать процессы в установившемся режиме. Определенный интерес вызывает модель, предложенная в компании Dow Chemical [7]. Модель связывает расход разделяемого раствора с числом и площадью мембранных элементов, проницаемостью растворителя через мембрану, температурой процесса, загрязнением мембраны, трансмембранным давлением, осмотическим давлением раствора, концентрациями разделяемого раствора и коэффициентом задержания мембраны, но не учитывает диффузионные процессы.
Важной особенностью модели является оценка вклада эффектов загрязнения мембраны и концентрационной поляризации на мембранное разделение растворов. Например, автор работы [8], предлагая модель комплексного загрязнения мембраны, связывает динамику гелеобразования с фильтрационной скоростью, которая, в свою очередь, уже учитывает площадь сечений открытых пор. Однако если в основе эффекта концентрационной поляризации лежит увеличение концентрации растворенного вещества в примембранном слое, то загрязнение мембраны и снижение площади сечения открытых пор связаны с непосредственным оседанием вещества в порах. В модели неравномерного осаждения частиц внутри пор полупроницаемой мембраны, в ее приближенном аналитическом решении, а также в модели совместного неравномерного осаждения частиц на внешней и внутренней поверхности мембран, процессы осаждения рассматриваются раздельно [9].
Авторы работы [10], например, отдельно рассматривают закупоривание применительно к отдельной поре и к участку мембраны в целом. При разработке математической модели рассматривается динамика процесса и учитывается, что кроме потока пермеата может образовываться поток фильтрата за счет образования осадка на поверхности половолоконной мембраны. Слабым местом использования модели [11] является наличие в уравнениях показателя проницаемости пермеата через мембрану, его зависимость определена авторами только для мембранных элементов серии BW. Хотя величина проницаемости пермеата может быть определена и по другим уравнениям, возможность использования этих значений при расчетах по исходной модели не проверена на практике.
Расчет проницаемости мембраны, состоящей из совокупности пористых сферических частиц, рассмотрен в модели, приведенной в работе [12]. В расчетах использован ячеечный метод, граничные условия на поверхности ячейки – Хаппеля, Кувабары, Квашнина и др. Течение раствора в модели описано уравнением Бринкмана. Получено решение задачи об обтекании одиночной сферической частицы, покрытой пористым слоем, однородным потоком вязкой несжимаемой жидкости, но при этом не затрагивается динамика процесса проницания веществ через пористую среду. Свое дальнейшее развитие эта модель получила в работе [13], где рассматривается пористая среда, образованная цилиндрическими волокнами, несущими пористый адсорбционный слой.
В работе [14] предложена модель расчета массопереноса через асимметричные мембраны, которая учитывает физико-химические свойства их слоев. В модели показано, что разность эффективных плотностей фиксированных зарядов в слоях мембраны является главным фактором, определяющим степень асимметрии диффузионной проницаемости, но ее слабым звеном является неучет других процессов динамики, например, осмотических. Так, в работе [15] рассмотрены вопросы математического описания транспортных характеристик пермеата и оценка влияния модификаторов (краун-эфиры) на перенос воды через полиамидные и полисульфоновые мембраны, но не затрагиваются процессы концентрационной поляризации и диффузии.
В работе [16] авторы рассматривают гидродинамику термоперварационного проточного мембранного модуля с цилиндрическими турбулизаторами, при этом в основном учитывается влияние испарения на перенос компонентов в области низких трансмембранных давлений. Авторы работы [17] исследуют в основном массоперенос в поперечном потоке в модельной гексагональной системе половолоконных мембран, не затрагивая вопросы исследования гидродинамики, позволяющей перемешивать раствор в пограничном слое мембраны.
Авторы работ [18–21] останавливаются на проблемах мембранного разделения растворов и его математического описания, уходя от вопросов рассмотрения явлений переноса веществ. В работе [22] авторы исследуют проницаемость мембраны, морфологию поверхности с полиэфирсульфоновым покрытием на ультрафильтрационных мембранах, не затрагивая вопросы изменения структуры и скорости течения потока. Авторы работы [23] сравнивают гидродинамическую проницаемость пористых мембран с полностью пористыми частицами или частицами с пористой оболочкой. Для расчета потока раствора внутри пористого слоя мембраны применяется уравнение Бринкмана, но оно исключает влияние структуры и скорости течения потока в межмембранном канале.
Выполненный обзор математических моделей и рассмотренные вопросы математического описания массопереноса в работах [7–23] показали, что не полностью учитывается динамика мембранного процесса, включающая диффузионные, осмотические и гидродинамические процессы. А в случае электромембранных процессов учету не подлежат электродиффузионный и электроосмотический переносы. Универсальный подход, учитывающий динамику процесса, позволит наиболее точно, с позиции физики мембранного процесса, описать математически электромембранные процессы и проверить их адекватность на реальных химических процессах. Поэтому целью данной работы является разработка математической модели, основанной на решении уравнений Нернста–Планка и Пуассона–Больцмана, учитывающей не только диффузионные, осмотические, гидродинамические процессы, но и электродиффузионные и электроосмотические переносы вещества, которая позволит решить одну или несколько существующих реальных задач по очистке.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Рассмотрим задачу массопереноса через мембраны при наложении трансмембранного давления и электрического потенциала при течении раствора в плоском межмембранном канале. При этом примем следующие допущения: скорость электродных реакций намного ниже скорости массопереноса; рабочая плотность тока намного ниже критической; насос обеспечивает постоянство подачи; микропотоки растворителя и растворенного вещества учитываются через коэффициент задержания и удельный выходной поток пермеата; режим стационарный; течение раствора в мембранном канале – ламинарное [24, 25].
Рассмотрим математическую запись задачи [26]:
(1)
$\nabla [\eta (\nabla {\mathbf{u}} + {{(\nabla {\mathbf{u}})}^{T}})] + \rho ({\mathbf{u}}\nabla ){\mathbf{u}} + \nabla P = 0,$Рассмотрим задачу гидродинамики: для ламинарного, стационарного, установившегося течения уравнения движения жидкости имеют вид
(5)
$\frac{{{{\partial }^{2}}{\mathbf{u}}(x,y)}}{{\partial {{y}^{2}}}} = \frac{1}{\mu }\left( {\frac{{\partial P(x,y)}}{{\partial x}} - \frac{{\partial \pi (x,y)}}{{\partial x}}} \right).$Определяем граничные условия:
Поскольку давление меняется только вдоль оси канала, то можно записать уравнение (5) в виде
(8)
$\frac{{{{\partial }^{2}}{\mathbf{u}}}}{{\partial {{y}^{2}}}} = \frac{1}{\mu }\left( {\frac{{\partial P}}{{\partial x}} - \frac{{\partial \pi }}{{\partial x}}} \right).$Проинтегрируем уравнение (8) по переменной $y$, соответствующей направлению вдоль оси канала:
(9)
$\frac{{d{\mathbf{u}}}}{{dy}} = \frac{1}{\mu }\left( {\frac{{dP}}{{dx}} - \frac{{d\pi }}{{dx}}} \right)y + {{C}_{1}},$(10)
${\mathbf{u}}(x,y) = \frac{1}{{2\mu }} = \frac{1}{{2\mu }}\left( {\frac{{dP}}{{dx}} - \frac{{d\pi }}{{dx}}} \right){{y}^{2}} + {{C}_{1}}y + {{C}_{2}}.$Здесь C1, C2 – постоянные интегрирования. Найдем C1 и C2 из уравнений (6) и (7):
(11)
${\mathbf{u}}(x,Y) = \frac{1}{{2\mu }}\left( {\frac{{dP}}{{dx}} - \frac{{d\pi }}{{dx}}} \right){{Y}^{2}} + {{C}_{1}}Y + {{C}_{2}} = 0,$(12)
${\mathbf{u}}(x, - Y) = \frac{1}{{2\mu }}\left( {\frac{{dP}}{{dx}} - \frac{{d\pi }}{{dx}}} \right){{Y}^{2}} - {{C}_{1}}Y + {{C}_{2}} = 0.$Таким образом, имеем решение в виде
Расход жидкости через канал определяем по формуле
Электроосмотический поток, как возникающий в результате электроосмотического давления, можно записать как
Приведем дифференциальное уравнение для проницаемости
Отсюда получаем
Знак “–” из-за того, что расход в канале убывает.
Учитывая приведенные выше преобразования, получим
Уравнение для случая оттока под действием трансмембранного давления представляем как
(20)
$ - \frac{{2b{{Y}^{3}}}}{{3\mu }}\left( {\frac{{{{d}^{2}}P(x)}}{{d{{x}^{2}}}}} \right)dx = - 2bkP(x)dx.$Обозначив $\lambda = \frac{{3\mu k}}{{{{R}^{3}}}},$ где $\lambda > 0,$ так как $\mu > 0,$ $k > 0,$ $R > 0,$ получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
Решение дифференциального уравнения (21) принимает вид $P(x) = {{С}_{1}}{{e}^{{\sqrt \lambda x}}} + {{С}_{2}}{{e}^{{ - \sqrt \lambda x}}}.$ Определив постоянные интегрирования C1 и C2 с учетом граничных условий, получим
(22)
$P(x) = \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - \sqrt {\lambda L} }}}}}{{{{e}^{{\sqrt {\lambda L} }}} - {{e}^{{ - \sqrt {\lambda L} }}}}}{{e}^{{\sqrt {\lambda x} }}} + \frac{{{{P}_{{{\text{in}}}}}{{e}^{{\sqrt {\lambda L} }}} - {{P}_{{\text{f}}}}}}{{{{e}^{{\sqrt {\lambda L} }}} - {{e}^{{ - \sqrt {\lambda L} }}}}}{{e}^{{ - \sqrt {\lambda x} }}}.$В результате проведенных преобразований и расчетов можно сделать вывод, что первая производная гидродинамического давления будет равна соответственно
(23)
$\frac{{dP(x)}}{{dx}} = \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}}A - \frac{{{{P}_{{{\text{in}}}}}{{e}^{{ - AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}A,$Для случая оттока под действием электроосмотического давления имеем
(24)
$ - \frac{{2b{{Y}^{3}}}}{{3\mu }}\left( {\frac{{{{d}^{2}}{{\pi }_{{\text{e}}}}(x)}}{{d{{x}^{2}}}}} \right)dx = - 2bk{{\pi }_{{\text{e}}}}(x)dx.$Проведя аналогичные преобразования для электроосмотического давления, получим
(25)
$\frac{{d{{\pi }_{{\text{e}}}}(x)}}{{dx}} = \frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}}A - \frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}A.$Таким образом, с учетом (21), (23) можно записать
(26)
$\begin{gathered} {\mathbf{u}}(x,y) = - \frac{1}{{2\mu }}\left( \begin{gathered} \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}}A - \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}A \hfill \\ - \,\,\frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}}A - \frac{{{{\pi }_{{{\text{ef}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}A \hfill \\ \end{gathered} \right)({{Y}^{2}} - {{y}^{2}}) = \\ = \,\,\frac{A}{{2\mu }}\left( {\frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}} - \frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{\pi }_{{{\text{ein}}}}}{{A}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}} \right)({{Y}^{2}} - {{y}^{2}}). \\ \end{gathered} $Проницаемость мембраны с учетом электроосмотического давления определяем как
(27)
$v = k(\Delta P - \Delta \pi ) = k({{P}_{{{\text{in}}}}} - P(x) - {{\pi }_{{\text{e}}}}(x) + {{\pi }_{{{\text{ein}}}}}).$Подставив выражения для составляющих давления в уравнение проницаемости (27), получим
(28)
$\begin{gathered} v(x,y) = k\left( {{{P}_{{{\text{in}}}}} - \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}} \right. - \\ - \,\,\left. {\frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}} + {{\pi }_{{{\text{ein}}}}}} \right). \\ \end{gathered} $Подставляем полученные выражения для продольной и поперечной скорости в уравнение (3) и решаем его совместно с уравнением (4) численным методом, находим распределение концентрации анионов по длине и высоте канала.
Уравнение Нернста–Планка имеет вид
(29)
$\begin{gathered} \nabla ( - D\nabla c(x,y) - z\upsilon F\nabla U(x,y)) \\ = \,\, - \left( {{\mathbf{u}}(x,y)\frac{{\partial c(x,y)}}{{\partial x}} + v(x,y)\frac{{\partial c(x,y)}}{{\partial y}}} \right). \\ \end{gathered} $Граничные условия:
(31)
$\begin{gathered} Rv(x, - R)c(x, - R) = D\nabla c(x, - Y) + \\ + \,\,z\upsilon Fc(x, - Y)\nabla U(x, - Y), \\ \end{gathered} $(32)
$\begin{gathered} Rv(x,Y)c(x,Y) = \\ = \,\,D\nabla c(x,Y) + z\upsilon Fc(x,Y)\nabla U(x,Y). \\ \end{gathered} $Уравнение Пуассона–Больцмана имеет вид
(33)
$ - \nabla {{\varepsilon }_{{{\text{vac}}}}}{{\varepsilon }_{{\text{r}}}}\nabla U(x,y) = \theta .$Граничные условия:
При расчетах используются основные кинетические характеристики электромембранного процесса, полученные при экспериментальных исследованиях разделения модельных медно-гальванических растворов.
Расход энергии на процесс концентрирования водного раствора в электромембранном процессе:
Проницаемость на границе мембраны можно записать как
(39)
$\begin{gathered} v(x) = k\left( {{{P}_{{{\text{in}}}}} - \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}} \right. - \\ - \,\,\left. {\frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}} \right). \\ \end{gathered} $Для упрощения записей и расчетов определим промежуточную величину
(40)
$\begin{gathered} \int\limits_0^L {v(x)dx} = \int\limits_0^L k \left( {{{P}_{{{\text{in}}}}} - \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}} \right. - \left. {\frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{Ax}}} - \frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}{{e}^{{ - Ax}}}} \right)dx = \\ = \,\,k({{P}_{{{\text{in}}}}} + {{\pi }_{{{\text{ein}}}}})\int\limits_0^L {dx - k} \left( {\frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}} + \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}} \right)\int\limits_0^L {{{e}^{{Ax}}}} dx - k\left( {\frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}} + \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}} \right)\int\limits_0^L {{{e}^{{ - Ax}}}} dx = \\ = \,\,\left. {k({{P}_{{{\text{in}}}}} + {{\pi }_{{{\text{ein}}}}})x} \right|_{0}^{L} - \frac{k}{A}\left. {\left( {\frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}} + \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}} \right){{e}^{{Ax}}}} \right|_{0}^{L} - \frac{k}{A}\left. {\left( {\frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}} + \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}} \right){{e}^{{ - Ax}}}} \right|_{0}^{L} = \\ = \,\,k({{P}_{{{\text{in}}}}} + {{\pi }_{{{\text{ein}}}}})L - \frac{k}{A}\left( {\frac{{{{\pi }_{{{\text{ef}}}}} - {{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}} + \frac{{{{P}_{{\text{f}}}} - {{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}} \right)({{e}^{{Ax}}} - 1) + \frac{k}{A}\left( {\frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}} - {{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}} + \frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}} - {{P}_{{\text{f}}}}}}{{{{e}^{{AL}}} - {{e}^{{ - AL}}}}}} \right)({{e}^{{Ax}}} - 1). \\ \end{gathered} $Количество трубок в аппарате определяется как
Количество секций в каскаде:
Из уравнений материального баланса запишем выражение, позволяющее найти концентрацию на выходе из секции:
(43)
$\begin{gathered} {{c}_{{\text{f}}}} = {{c}_{{{\text{in}}}}}\frac{{{{Q}_{{{\text{in}}}}} - (1 - k)n\frac{S}{L}\int\limits_0^L {\gamma (x)dx} }}{{{{Q}_{{{\text{in}}}}} - n\frac{S}{L}\int\limits_0^L {\gamma (x)dx} }} = {{c}_{{{\text{in}}}}}\frac{{{{Q}_{{{\text{in}}}}} - n\frac{S}{L}\int\limits_0^L {(x)dx + kn\frac{S}{L}\int\limits_0^L {\gamma (x)dx} } }}{{{{Q}_{{{\text{in}}}}} - n\frac{S}{L}\int\limits_0^L {\gamma (x)dx} }} = {{c}_{{{\text{in}}}}}\left( {1 + \frac{{kn\frac{S}{L}\int\limits_0^L {\gamma (x)dx} }}{{{{Q}_{{{\text{in}}}}} - n\frac{S}{L}\int\limits_0^L {\gamma (x)dx} }}} \right) = \\ = {\kern 1pt} {\kern 1pt} {{c}_{{{\text{in}}}}}\left( {1\, + \,\frac{{kn\frac{S}{L}\left( {\int\limits_0^L {k({{P}_{{{\text{in}}}}}{\kern 1pt} + \,{{\pi }_{{{\text{ein}}}}})L\, - \,\frac{k}{A}\left( {\frac{{{{\pi }_{{{\text{ef}}}}}{\kern 1pt} - \,{{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{\text{f}}}}{\kern 1pt} - \,{{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{AL}}}{\kern 1pt} - \,1)\, + \,\frac{k}{A}\left( {\frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}}{\kern 1pt} - \,{{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}}{\kern 1pt} - \,{{P}_{{\text{f}}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{ - AL}}}{\kern 1pt} - \,1)} } \right)}}{{{{Q}_{{{\text{in}}}}}{\kern 1pt} - \,n\frac{S}{L}\left( {k({{P}_{{{\text{in}}}}}{\kern 1pt} + \,{{\pi }_{{{\text{ein}}}}})L\, - \,\frac{k}{A}\left( {\frac{{{{\pi }_{{{\text{ef}}}}}{\kern 1pt} - \,{{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{\text{f}}}}{\kern 1pt} - \,{{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{AL}}}{\kern 1pt} - \,1)\, + \,\frac{k}{A}\left( {\frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}}{\kern 1pt} - \,{{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}}{\kern 1pt} - \,{{P}_{{\text{f}}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{ - AL}}}{\kern 1pt} - \,1)} \right)}}} \right){\kern 1pt} . \\ \end{gathered} $Видим, что на выходе концентрация увеличивается на величину
(44)
$\begin{gathered} \Delta c = \\ = \,{{c}_{{{\text{in}}}}}{\kern 1pt} \left( {\frac{{kn\frac{S}{L}{\kern 1pt} \left( {({{P}_{{{\text{in}}}}}{\kern 1pt} + \,{{\pi }_{{{\text{ein}}}}})L\, - \,\frac{k}{A}{\kern 1pt} \left( {\frac{{{{\pi }_{{{\text{ef}}}}}{\kern 1pt} - \,{{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}\, - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{\text{f}}}}\, - \,{{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}\, - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{AL}}}{\kern 1pt} - \,1)\, + \,\frac{k}{A}{\kern 1pt} \left( {\frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}}\, - \,{{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}}\, - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}}\, - \,{{P}_{{\text{f}}}}}}{{{{e}^{{AL}}}\, - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{ - AL}}}{\kern 1pt} - \,1)} \right)}}{{{{Q}_{{{\text{in}}}}}{\kern 1pt} - \,n{\kern 1pt} \frac{S}{L}{\kern 1pt} \left( {k({{P}_{{{\text{in}}}}}{\kern 1pt} + \,{{\pi }_{{{\text{ein}}}}})L\, - \,\frac{k}{A}{\kern 1pt} \left( {\frac{{{{\pi }_{{{\text{ef}}}}}{\kern 1pt} - \,{{\pi }_{{{\text{ein}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{\text{f}}}}{\kern 1pt} - \,{{P}_{{{\text{in}}}}}{{e}^{{ - AL}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{AL}}}{\kern 1pt} - \,1)\, + \,\frac{k}{A}{\kern 1pt} \left( {\frac{{{{\pi }_{{{\text{ein}}}}}{{e}^{{AL}}}{\kern 1pt} - \,{{\pi }_{{{\text{ef}}}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}\, + \,\frac{{{{P}_{{{\text{in}}}}}{{e}^{{AL}}}{\kern 1pt} - \,{{P}_{{\text{f}}}}}}{{{{e}^{{AL}}}{\kern 1pt} - \,{{e}^{{ - AL}}}}}} \right){\kern 1pt} ({{e}^{{ - AL}}}{\kern 1pt} - \,1)} \right)}}} \right). \\ \end{gathered} $Расчет ведется методом последовательных приближений, задавая различные длины и выходя на заданную концентрацию, а проверка адекватности математической модели проводится путем сравнения расчетных и экспериментальных данных. Сравнение проводилось по величине концентрации целевого компонента в ретентате.
Экспериментальные исследования проводили на электробаромембранной установке плоскокамерного типа. Ее конструкция и принцип действия описаны в работах [27, 28]. В качестве объектов исследования были выбраны пористая ацетатцеллюлозная мембрана МГА-95, рабочие характеристики которой представлены в табл. 1, и модельные водные растворы CuSO4 ⋅ 5H2O с исходной концентрацией меди в них 0.03 и 0.06 кг/м3. Показания концентрации меди в ретентате снимались при рабочем давлении в 1, 2, 3 и 4 МПа.
Таблица 1.
Рабочие характеристики пористой ацетатцеллюлозной мембраны МГА-95
| Рабочие параметры | МГА-95 |
|---|---|
| P, МПа | 5.0 |
| J, м3/(м2 с) | 1.11× 10–5 |
| K по 0.15% NaCl | не менее 0.95 |
| рН | 3–8 |
| B, м | 1.2× 10–3 |
| Тmax, °C | 50 |
Рабочие параметры, которые были получены при проведении экспериментов с разной концентрацией целевого компонента, в дальнейшем применены при теоретическом расчете процесса разделения и приведены в Теоретически рассчитанные данные были проанализированы и сравнены с экспериментальными данными, полученными при аналогичных рабочих параметрах. Все данные приведены на рис. 1 и 2.
Рис. 1.
Зависимость концентрации меди в ретентате Срет от давления Р при исходной концентрации Сисх = = 0.03 кг/м3. Линия – эксперимент, точки – расчет.
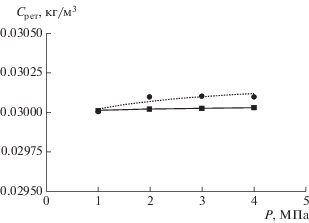
Рис. 2.
Зависимость концентрации меди в ретентате Срет от давления Р при исходной концентрации Сисх = = 0.06 кг/м3. Линия – эксперимент, точки – расчет.
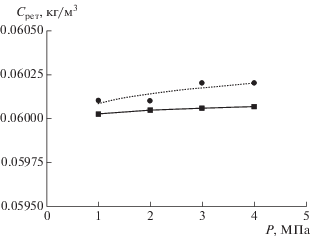
Отклонение расчета от эксперимента не превышает 5% для обеих концентраций исходных растворов, что свидетельствует о достаточно высокой точности расчета по представленной математической модели.
Таблица 2.
Рабочие параметры теоретического расчета
| Рабочий параметр | Значение | |||
|---|---|---|---|---|
| 1 МПа | 2 МПа | 3 МПа | 4 МПа | |
| L, м | 0.9 | 0.9 | 0.9 | 0.9 |
| R, м | 1 × 10–3 | 1 × 10–3 | 1 × 10–3 | 1 × 10–3 |
| μ, Па с | 9.5 × 10–4 | 9.5 × 10–4 | 9.5 × 10–4 | 9.5 × 10–4 |
| k | 4.62 × 10–12 | 4.62 × 10–12 | 4.62 × 10–12 | 4.62 × 10–12 |
| D, м2/c | 1 × 10–9 | 1 × 10–9 | 1 × 10–9 | 1 × 10–9 |
| Pin, Па | 4 × 106 | 3 × 106 | 2 × 106 | 1 × 106 |
| Pf, Па | 3.99 × 106 | 2.99 × 106 | 1.99 × 106 | 0.99 × 106 |
| K | 0.859 | 0.859 | 0.859 | 0.859 |
| is, А/м2 | 57.5 | 57.5 | 57.5 | 57.5 |
ЗАКЛЮЧЕНИЕ
Разработанная математическая модель электромембранного процесса, основанная на решении уравнений Нернста–Планка и Пуассона–Больцмана с учетом принятых допущений и граничных условий, и учитывающая влияние на мембранный процесс двух движущих сил – трансмембранного давления и градиента электрического потенциала, решает одну из реальных задач, позволяя рассчитывать концентрации по растворенному веществу на выходе из мембранного аппарата в ретентате и в пермеате, находить среднюю величину удельного выходного потока пермеата при разделении технологических растворов электролитов химического процесса меднения. Возможность извлечения целевых металлов, в частности меди, используя результаты теоретического прогнозирования электромембранного разделения растворов по предлагаемой математической модели, позволит значительно сократить производственные издержки предприятий, сократить загрязнение водоемов. Кроме того, результаты расчета по представленной математической модели могут быть использованы при проектировании электромембранных аппаратов с необходимыми очистными характеристиками.
Проверка на адекватность математической модели проведена путем сравнения рассчитанных и экспериментально полученных данных по изменению концентрации целевого вещества в ретентате относительно давления при постоянной плотности тока в процессе электромембранного разделения технологических растворов химического процесса меднения.
ОБОЗНАЧЕНИЯ
| B | толщина мембраны, м |
| b | ширина канала, м |
| C | постоянная интегрирования |
| c | параметр, характеризующий концентрации растворенного вещества в растворе, кг/м3 |
| D | коэффициент диффузии, м2/с |
| F | постоянная Фарадея, Кл/моль |
| i | плотность тока, А/м2 |
| J | удельный поток растворителя, м3/(м2 c) |
| K | среднее значение коэффициента задержания |
| k | параметр, характеризующий коэффициент задержания растворенного вещества в мембранах |
| L | длина мембранного канала в трубчатом элементе, м |
| l | длина секций, позволяющих получить заданную концентрацию на выходе, м |
| N | количество секций в каскаде |
| n | количество мембран в модуле |
| P | трансмембранное давление, Па |
| Q | расход жидкости, м3/с |
| R | радиус трубчатой мембраны, м |
| S | площадь одной мембраны, м2 |
| T | температура, К |
| U | продольная скорость течения раствора в трубчатом элементе, м/с |
| u | вектор поля скоростей |
| V | объем пермеата, м3 |
| W | расход энергии, кВт ч |
| Y | параметр по полувысоте межмембранного канала, м |
| z | валентность |
| γ | поперечная скорость течения раствора в трубчатом элементе, м/с |
| ε | диэлектрическая постоянная |
| η | выход по току |
| θ | плотность электрического заряда, Кл/м3 |
| λ | теплопроводность раствора, Вт/(м К) |
| μ | коэффициент динамической вязкости раствора, Па |
| ν | проницаемость мембраны, м3/(м2 с) |
| π | осмотическое давление, Па |
| ρ | плотность раствора, кг/м3 |
| υ | подвижность ионов, м2/(В с) |
ИНДЕКСЫ
Список литературы
Шевченко Т.Ю., Соловьева Н.Д. Электроосаждение композиционных электрохимических покрытий на основе цинка в реверсивном режиме электролиза // Вестн. Сарат. гос. тех. унив. 2011. Т. 4. № 1(59). С. 121.
Кругликов С.С., Тураев Д.Ю., Бузикова А.М. Регенерация раствора травления меди в производстве печатных плат методом мембранного электролиза // Гальванотех. обраб. поверхн. 2009. Т. 17. № 1. С. 59.
Тураев Д.Ю. Применение метода мембранного электролиза для извлечения ионов тяжелых металлов // Журн. прикл. хим. 2007. Т. 80. № 1. С. 84.
Тураев Д.Ю., Кругликов С.С., Парфенова А.В. Изучение процесса регенерации травильного раствора на основе хлорида меди с помощью мембранного электролиза // Журн. прикл. хим. 2005. Т. 78. С. 1469.
Шиблева Т.Г., Поветкин В.В., Молданова Н.А. Кинетика электроосаждения и свойства висмута из омагниченного электролита // Вестн. Тюмен. гос. унив. Экол. природопольз. 2014. № 5. С. 81.
Тураев Д.Ю., Кругликов С.С. Регенерация раствора химического осаждения меди // Журн. прикл. хим. 2005. Т. 78. С. 586.
FILMTEC Reverse Osmosis Membranes. Technical Manual. Dow Chemical Company, 2004.
Семенов А.Г. Совершенствование технологии переработки молочного сырья на основе интенсификации мембранных процессов. Дис. … док. техн. наук. Кемерово, 2014.
Поляков Ю.С. Неравномерное осаждение частиц на внешней и внутренней поверхности полупроницаемых мембран. Дис. … док. физ.-мат. наук. М., 2007.
Поляков Ю.С. Ультра- и микрофильтрация в половолоконных аппаратах с образованием осадка на поверхности мембран. Дис. … канд. тех. наук. М., 2004.
Шоботов С.С., Квитка А.А., Френдж Ф. Математическое моделирование процесса обратноосмотической деминерализации воды // Вост.-Евр. Журн. передовых технол. 2010. Т. 2. № 10(44). С. 55.
Vasin S.I., Filippov A.N. Permeability of complex porous media // Colloid J. 2009. V. 71. № 1. P. 31. [Васин С.И., Филиппов А.Н. Проницаемость сложнопористых сред // Коллоидн. журн. 2009. Т. 71. № 1. С. 32.]
Vasin S.I., Sherysheva E.E., Filippov A.N. Permeability of medium composed of cylindrical fibers with fractal porous adlayer // Colloid J. 2011. V. 73. № 2. P. 167. [Васин С.И., Шерышева Е.Е., Филиппов А.Н. Проницаемость среды, образованной цилиндрическими волокнами с фрактальным пористым адслоем // Коллоидн. ж. 2011. Т. 73. № 2. С. 164.]
Filippov A.N., Iksanov R.Kh., Kononenko N.A., Bere-zina N.P., Falina I.V. Theoretical and experimental study of asymmetry of diffusion permeability of composite membranes // Colloid J. 2010. V. 72. № 2. P. 243. [Филиппов А.Н., Иксанов Р.Х., Кононенко Н.А., Березина Н.П., Фалина И.В. Теоретическое и экспериментальное исследование асимметрии диффузионной проницаемости композитных мембран // Коллоидн. ж. 2010. Т. 72. № 2. С. 238.]
Ochkina K.A., Kulov N.N., Fomichev S.V. Transport properties of reverse-osmosis polyamide and polysulfone membranes modified with crown ethers // Theor. Found. Chem. Eng. 1998. V. 32. № 1. P. 44. [Очкина К.А., Кулов Н.Н., Фомичев С.В. Транспортные характеристики полиамидных и полисуль- фоновых обратноосмотических мембран, модифицированных краун-эфирами // Теор. осн. хим. технол. 1998. Т. 32. № 1. С. 51.]
Kirsh V.A., Borisov I.L., Volkov V.V. Hydrodynamics of a thermopervaporation flow membrane module with cylindrical spacers // Pet. Chem. 2013. V. 53. № 8. P. 578. [Кирш В.А., Борисов И.Л., Волков В.В. Гидродинамика термопервапорационного проточного мембранного модуля с цилиндрическими турбулизаторами // Мембр. мембр. технол. 2013. Т. 3. № 4. С. 269.]
Kirsh V.A., Roldugin V.I., Bazhenov S.D., Bildukevich A.V. Cross-flow mass transfer in a model hexagonal system of hollow fiber membranes // Pet. Chem. 2015. V. 55. № 5. P. 339. [Кирш В.А., Ролдугин В.И., Баженов С.Д., Бильдюкевич А.В. Массоперенос в поперечном потоке в модельной гексагональной системе половолоконных мембран // Мембр. мембр. технол. 2015. Т. 5. № 2. С. 269.]
Al-Jeshi S., Neville A. An experimental evaluation of reverse osmosis membrane performance // Desalination. 2008. V. 22L8. № 1–3. P. 287.
Kumar R.U., Muthukrishnan M., Guha B.K. Tertiary treatment of distillery wastewater by nanofiltration // Desalination. 2008. V. 230. № 1–3. P. 70.
Lipp P., Baldauf G. Stand der membrantechnik in der trinkwasseraufbereitung in Deutschland // DVGW ENERG. Wasser-Prax. 2008. № 4. P. 60.
Khayet M., Matsuura T. Membrane Distillation: Principles and Applications. Amsterdam: Elsevier, 2011.
Cheng C., Li S., Zhao W., Wei Q., Nie S., Sun S., Zhao C. The hydrodynamic permeability and surface property of polyethersulfone ultrafiltration membranes with mussel-inspired polydopamine coatings // J. Membr. Sci. 2012. V. 417–418. № 1. P. 228.
Filippov A.N., Vasin S.I., Starov V.M. Mathematical modeling of the hydrodynamic permeability of a membrane built up from porous particles with a permeable shell // Colloids Surf., A. 2006. V. 282–283. P. 272.
Чепеняк П.А. Кинетика электрохимической мембранной очистки фосфатсодержащих сточных вод. Дис. … канд. техн. наук. Тамбов, 2011.
Лазарев С.И., Богомолов В.Ю., Арзамасцев А.А., Полянский К.К., Вязовов С.А., Левин А.А. Эмпирическая модель ультрафильтрационного концентрирования белка в подсырной сыворотке // Вестн. Тамбов. унив. Сер.: естеств. тех. науки. 2016. Т. 21. № 2. С. 655.
Головашин В.Л. Математическая модель совместного электротепломассопереноса в электробаромембранных системах // Вестн. Тамбов. гос. тех. унив. 2014. № 4. С. 734.
Лазарев С.И., Ковалев С.В., Казаков В.Г. Исследования кинетических и структурных характеристик электробаромембранной очистки промывных вод производства 2,2'-дибензтиазолилдисульфида // Изв. высш. учебн. завед. Хим. хим. технол. 2016. Т. 59. № 2. С. 34.
Ковалева О.А., Лазарев С.И Исследование процесса обратноосмотического разделения технологических растворов производств кукурузного крахмала // Тех. технол. пищ. производ. 2016. № 4 (43). С. 110.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


