Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 636-642

Математическое моделирование скорости осаждения частиц с учетом динамической релаксации

В. Б. Пономарев^a, *, И. П. Фесун^a

^a Уральский федеральный университет
Екатеринбург, Россия

Поступила в редакцию 02.12.2019
После доработки 11.02.2020
Принята к публикации 14.02.2020

DOI: 10.31857/S0040357120040119

Аннотация

Показано, что при расчете траекторий движения полидисперсных твердых частиц в двухфазных потоках необходимо учитывать время их динамической релаксации. Получена универсальная зависимость времени релаксации для скорости осаждения частицы от ее размера и плотности, а также от параметров дисперсионной среды. Проведен анализ относительных погрешностей аппроксимации табличных данных кривой Рэлея формулами Адамова и Розенбаум–Тодеса, который показал среднее отклонение аппроксимаций 7–9%. Предложены новые формулы с оптимизированными эмпирическими коэффициентами, показывающие среднюю относительную погрешность менее 1%. Проанализировано влияние скорости вертикального потока среды на время динамической релаксации твердых частиц. Отмечено, что для частиц, движущихся в областях скоростей, близких к скорости витания, их время релаксации стремится к нулю. Предложено для движущегося дисперсного потока строить обобщающий график относительного времени от относительной скорости и из него находить время динамической релаксации частиц.

Ключевые слова: время релаксации, скорость осаждения, частица, дисперсионная среда, твердая фаза, двухфазный поток, траектория, кривая Рэлея, эксперимент

ВВЕДЕНИЕ

В основе расчетов процессов переноса твердых частиц в двухфазных потоках (гравитационная классификация, сушка в кипящем слое, пылеулавливание, пневматический транспорт и др.) лежит определение скоростей их движения [1–5]. Довольно часто модели этих процессов основываются на квазистационарности скоростей частиц дисперсной среды, в то время как в зависимости от размера зерен, плотности и вязкости дисперсионной среды время, в течение которого частица начинает двигаться с постоянной скоростью, может превышать время самого процесса [6–8]. В ряде работ [9, 10] практикуется применение формулы для времени динамической релаксации, рассчитанной для ламинарного режима, в переходной или турбулентной области движения частиц, что не совсем корректно.

Целью данной работы является получение аналитического описания времени релаксации скоростей осаждения и транспортирования твердых шарообразных частиц в неподвижной и движущейся дисперсионной среде.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Временем релаксации частицы в потоке газа принято считать время, в течение которого частица перейдет в стационарное состояние и начнет двигаться с постоянной скоростью [11, 12].

В работе [13] предлагается определять время динамической релаксации следующим образом. Сила инерции приближенно определяется как произведение скорости относительного движения частицы на ее массу, отнесенную к времени ее релаксации:

(1)

$F = \frac{{\left| u \right|m}}{\tau }.$

Для процесса осаждения частиц относительная скорость |u| = |v_dep|.

Если приравнять силу инерции к силе потока (силе аэродинамического сопротивления)

(2)

$\lambda S\frac{{{{{\left| {{{v}_{{{\text{dep}}}}}} \right|}}^{2}}}}{2}\Delta = \frac{{\left| {{{v}_{{{\text{dep}}}}}} \right|m}}{\tau },$

нетрудно определить величину времени релаксации

(3)

$\tau = \frac{{2m}}{{\left| {{{v}_{{{\text{dep}}}}}} \right|\lambda S\Delta }}.$

Для сферических круглых частиц в области Стокса (Re < 0.4 и λ = 24/Re) выражение примет вид

(4)

$\tau = \frac{{\rho {{d}^{2}}}}{{18\mu }},$

для автомодельной области (Re > 1000 и λ = 0.44)

(5)

$\tau = \frac{{3d\rho }}{{\left| {{{v}_{{{\text{dep}}}}}} \right|\Delta }}.$

Для переходной области нужно знать величину коэффициента аэродинамического сопротивления.

Коэффициент аэродинамического сопротивления λ для промежуточной области Re можно определить по ряду общеизвестных формул [14–17], например по выражению Адамова [18]

(6)

$\lambda = \frac{{24}}{{\operatorname{Re} }}{{\left( {1 + 0.065{{{\operatorname{Re} }}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$

Имея табличные данные кривой Рэлея [19], нетрудно оценить среднюю относительную погрешность применения формулы (6), в диапазоне Re = 0.4–1000 она равна около 9%.

После компьютерной оптимизации эмпирических коэффициентов отклонение расчетных и табличных данных составило 1.0%, а формула приобрела следующий вид:

(7)

$\lambda = \frac{{24}}{{\operatorname{Re} }}{{\left( {0.92 + 0.147{{{\operatorname{Re} }}^{{0.55}}}} \right)}^{{1.45}}}.$

После преобразований время динамической релаксации для переходной области можно вычислить как

(8)

$\tau = \frac{{\rho {{d}^{2}}}}{{18\mu {{{\left( {0.92 + 0.147\operatorname{Re} _{{{\text{dep}}}}^{{0.55}}} \right)}}^{{1.45}}}}}.$

Здесь

(9)

${{\operatorname{Re} }_{{{\text{dep}}}}} = \frac{{{{v}_{{{\text{dep}}}}}d\Delta }}{\mu }.$

Для области Стокса [17] конечная скорость осаждения

(10)

${{v}_{{{\text{dep}}}}} = \frac{{g{{d}^{2}}\left( {\rho - \Delta } \right)}}{{18\mu }};$

для автомодельного режима

(11)

${{v}_{{{\text{dep}}}}} = \sqrt {\frac{{3gd\left( {\rho - \Delta } \right)}}{\Delta }} .$

Одним из способов определения стационарной скорости осаждения для переходной области чисел Рейнольдса является решение критериального уравнения [17]

(12)

$\lambda {{\operatorname{Re} }^{2}} = \frac{4}{3}{\text{Ar,}}$

например, с использованием формулы Розенбаум–Тодеса [9, 17]

(13)

$\operatorname{Re} = \frac{{{\text{Ar}}}}{{18 + 0.6\sqrt {{\text{Ar}}} }}.$

При сравнении формулы (11) с модифицированными данными кривой Рэлея [19] средняя относительная погрешность ее применения в диапазоне Re = 0.4–1000 составила около 7%.

После оптимизации эмпирических коэффициентов удалось снизить погрешность до 0.6%. Зависимость с новыми коэффициентами выглядит следующим образом:

(14)

${{\operatorname{Re} }_{{{\text{dep}}}}} = \frac{{{\text{Ar}}}}{{15 + 1.35{\text{A}}{{{\text{r}}}^{{0.43}}}}},$

а скорость осаждения определяется как

(15)

${{v}_{{{\text{dep}}}}} = \frac{{{\text{Ar}}}}{{15 + 1.35{\text{A}}{{{\text{r}}}^{{0.43}}}}}\frac{\mu }{{d\Delta }}.$

КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ

Осаждение твердых частиц в неподвижной среде. Для оценки правильности рассуждений решим дифференциальное уравнение осаждения частицы [17] в поле сил тяжести, Архимеда и аэродинамического сопротивления среды:

(16)

$\frac{{dv}}{{dt}} = \lambda \frac{3}{4}\frac{{{{v}^{2}}}}{{\rho d}}\Delta - g\left( {1 - \frac{\Delta }{\rho }} \right).$

Так как при гравитационной классификации, пылеулавливании, пневматическом транспорте и подобных процессах участвуют частицы крупнодисперсной и зернистой твердой фазы, будем рассматривать размеры частиц от 10 до 1000 мкм с плотностью от 1000 до 8000 кг/м³.

Решая уравнение (16) методом Рунге–Кутты 4-го порядка с начальными условиями v = v₀ = 0; t = t₀ = 0, можно найти значение v_n _{+ 1} при t_{n +} ₁= t_n + + δt по итерационной формуле

(17)

${{v}_{{n + 1}}} = {{v}_{n}} + \frac{1}{6}\left( {{{k}_{1}} + 2{{k}_{2}} + 2{{k}_{3}} + {{k}_{4}}} \right),$

где

$\begin{gathered} {{v}_{n}} = \lambda \frac{3}{4}\frac{{{{v}^{2}}}}{{\rho d}}\Delta - g\left( {1 - \frac{\Delta }{\rho }} \right);\,\,\,\,{{k}_{1}} = dt{{v}_{n}}; \\ {{k}_{2}} = dt({{v}_{n}} + {{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} 2}} \right. \kern-0em} 2});\,\,\,\,{{k}_{3}} = dt({{v}_{n}} + {{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} 2}} \right. \kern-0em} 2}); \\ \end{gathered} $

k₄ = δt(v_n + k₃); δt – величина шага сетки по t.

На каждом шаге дифференцирования фиксировалось время процесса и текущая скорость частицы. Вычисления прекращались при выполнении условия $\left| {\frac{{{{v}_{{n + 1}}} - {{v}_{{{\text{dep}}}}}}}{{{{v}_{{{\text{dep}}}}}}}} \right| \leqslant 0.01$, т.е. при остаточной погрешности приближения к теоретической скорости осаждения по формулам (12), (13), (15) менее 1%.

Движение твердых частиц в вертикальном восходящем потоке. В отличие от неподвижной среды, в движущемся потоке необходимо решать два дифференциальных уравнения движения частиц – в случае, когда вектор начальной скорости частицы противоположен вектору скорости потока:

(18)

$\frac{{dv}}{{dt}} = \lambda \frac{3}{4}\frac{{{{{\left( {w - v} \right)}}^{2}}}}{{\rho d}}\Delta - g\left( {1 - \frac{\Delta }{\rho }} \right)$

и когда векторы начальной скорости частицы и потока совпадают по направлению:

(19)

$\frac{{dv}}{{dt}} = \lambda \frac{3}{4}\frac{{{{{\left( {w - v} \right)}}^{2}}}}{{\rho d}}\Delta + g\left( {1 - \frac{\Delta }{\rho }} \right),$

при этом скорость движения частиц через определенное время должна приблизиться либо к стационарной скорости осаждения или транспортирования, либо к смене направления ее вектора и дальнейшему движению согласно уравнению (18).

При решении методом Рунге–Кутты уравнения (17) скорость частицы будет вычисляться как

${{v}_{n}} = \lambda \frac{3}{4}\frac{{{{{\left( {w - v} \right)}}^{2}}}}{{\rho d}}\Delta - g\left( {1 - \frac{\Delta }{\rho }} \right)$ при движении по уравнению (18);

${{v}_{n}} = \lambda \frac{3}{4}\frac{{{{{\left( {w - v} \right)}}^{2}}}}{{\rho d}}\Delta + g\left( {1 - \frac{\Delta }{\rho }} \right)$ при движении по уравнению (19).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Осаждение твердых частиц в неподвижной среде. В табл. 1 приведены теоретические значения времени динамической релаксации с учетом числа Re по формулам (4), (5), (8) и результаты численного решения.

Таблица 1.

Время релаксации скорости осаждении частиц в неподвижной среде

d, мкм	ρ = 1000 кг/м³		ρ = 2700 кг/м³		ρ = 5000 кг/м³		ρ = 7800 кг/м³
d, мкм	τ_th	τ_cal	τ_th	τ_cal	τ_th	τ_cal	τ_th	τ_cal
10	0.000	0.001	0.001	0.004	0.002	0.006	0.002	0.010
20	0.001	0.004	0.003	0.012	0.006	0.027	0.010	0.041
30	0.003	0.011	0.008	0.031	0.014	0.061	0.021	0.093
50	0.008	0.032	0.020	0.075	0.035	0.123	0.051	0.170
75	0.016	0.062	0.039	0.132	0.067	0.216	0.096	0.306
100	0.026	0.080	0.061	0.192	0.102	0.318	0.144	0.450
150	0.049	0.150	0.108	0.336	0.174	0.540	0.240	0.730
200	0.074	0.232	0.156	0.496	0.243	0.750	0.331	0.960
300	0.122	0.380	0.246	0.740	0.373	1.125	0.500	1.400
500	0.213	0.645	0.407	1.200	0.602	1.640	0.793	2.000
750	0.314	0.901	0.582	1.590	0.848	2.160	1.109	2.700
1000	0.405	1.120	0.739	1.960	1.068	2.640	1.391	3.440

Из таблицы видно, что имеется существенное отличие расчетных данных от теоретических, причем с уменьшением размера частиц это различие увеличивается. Можно предположить, что τ_dep = Cτ.

Нетрудно найти аппроксимационный коэффициент, приближающий теоретические и расчетные данные, представленные в табл. 1:

(20)

$C = {{d}^{{ - 0.13}}}.$

С учетом этого время динамической релаксации скорости осаждения частиц можно определить как

(21)

${{\tau }_{{{\text{dep}}}}} = \left\{ \begin{gathered} \begin{array}{*{20}{c}} {\frac{{\rho {{d}^{{1.87}}}}}{{18\mu }}}&{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\operatorname{Re} \leqslant 0.4} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\frac{{\rho {{d}^{{1.87}}}}}{{18\mu {{{\left( {0.92 + \frac{{{\text{A}}{{{\text{r}}}^{{0.55}}}}}{{30.17 + 8.02{\text{A}}{{{\text{r}}}^{{0.2365}}}}}} \right)}}^{{1.45}}}}}}&{\,\,\operatorname{Re} = 0.4 - 1000} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\sqrt {\frac{{3{{d}^{{0.74}}}{{\rho }^{2}}}}{{g\left( {\rho - \Delta } \right)\Delta }}} }&{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\operatorname{Re} = 1000 - 200\,000} \end{array} \hfill \\ \end{gathered} \right..$

В работе [20] был использован другой подход к вычислению времени релаксации, которое определяется по конечной скорости осаждения v_dep частиц:

(22)

${{\tau }_{{{\text{dep}}}}} = \frac{{2.5{{v}_{{{\text{dep}}}}}\rho }}{{\left( {\rho - \Delta } \right)g}}.$

На рис. 1 представлены данные компьютерного эксперимента и графики, полученные по зависимостям (21), (22).

Рис. 1.

Изменение времени релаксации скорости осаждении частиц в воздухе в зависимости от их размера: точки – данные компьютерного эксперимента при ρ = 1000 (1), 2700 (2), 5000 (3) и 7800 (4) кг/м³; пунктирная линия – формула (12); сплошная линия – формула (13).

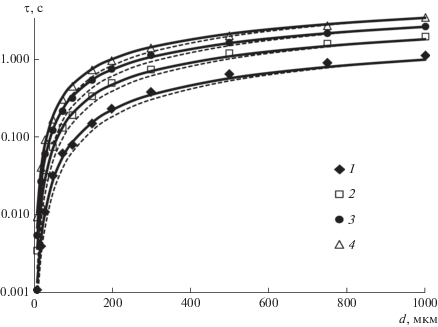
Из рис. 1 следует, что полученная аппроксимация (21) хорошо согласуется с компьютерным экспериментом, а формула (22) показывает некоторую погрешность в переходной области чисел Рейнольдса.

Движение твердых частиц в вертикальном восходящем потоке. При вводе частицы в несущий вертикальный поток возможны три варианта ее движения.

1. При начальной скорости движения частицы, имеющей направление противоположное скорости потока, она начнет опускаться или подниматься, в зависимости от того если ее конечная скорость осаждения больше или меньше скорости потока. В этом случае через промежуток времени τ ее относительная скорость будет равна v = = w – v_dep.

2. При начальной скорости движения частицы, имеющей направление, совпадающее со скоростью потока, она начнет замедляться и через промежуток времени τ ее скорость также примет значение v = w – v_dep.

3. Если конечная скорость осаждения частицы равна скорости потока (скорости витания), она теоретически будет находиться в состоянии покоя v = 0, при этом время релаксации τ = 0.

На рис. 2 показана зависимость времени динамической релаксации частиц плотностью 2700 кг/м³ от скорости восходящего воздушного потока.

Рис. 2.

Зависимость времени динамической релаксации от скорости воздушного потока и размеров частиц: 1 – d = 200 мкм; 2 – 500; 3 – 1000; 4 – d = 3000 мкм.

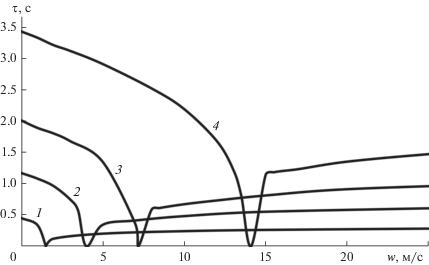
Если в качестве абсциссы принять относительную скорость v_rel = w/v_dep, а за ординату – относительное время релаксации τ_rel = τ/τ_dep, можно построить обобщающий график.

На рис. 3 показан такой график для частиц плотностью 7800 кг/м³, при этом зависимость времени динамической релаксации от относительной скорости потока можно аппроксимировать, например, как

(29)

$\tau = \left\{ \begin{gathered} \begin{array}{*{20}{c}} {{{\tau }_{{{\text{dep}}}}}\left( {1 - {{{\left( {\frac{w}{{{{v}_{{{\text{dep}}}}}}}} \right)}}^{{4.1}}}} \right)}&{{\text{при}}\,\,\,\,\frac{w}{{{{v}_{{{\text{dep}}}}}}} \leqslant 1} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{{\tau }_{{{\text{dep}}}}}\frac{{0.096{{{\left( {\frac{w}{{{{v}_{{{\text{dep}}}}}}}} \right)}}^{{10}}}}}{{1 + 0.2{{{\left( {\frac{w}{{{{v}_{{{\text{dep}}}}}}}} \right)}}^{{10}}}}}}&{{\text{при}}\,\,\,\,\frac{w}{{{{v}_{{{\text{dep}}}}}}} \geqslant 1} \end{array} \hfill \\ \end{gathered} \right..$

Рис. 3.

Зависимость относительного времени динамической релаксации от относительной скорости потока для частиц плотностью 7800 кг/м³ в воздухе.

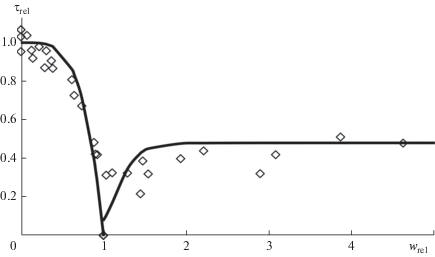
Для частиц с плотностью 2700 кг/м³ эта зависимость приобретает следующий вид:

(30)

$\tau = \left\{ \begin{gathered} \begin{array}{*{20}{c}} {{{\tau }_{{{\text{dep}}}}}\left( {1 - {{{\left( {\frac{w}{{{{v}_{{{\text{dep}}}}}}}} \right)}}^{{5.46}}}} \right)}&{{\text{при}}\,\,\,\,\frac{w}{{{{v}_{{{\text{dep}}}}}}} \leqslant 1} \end{array} \hfill \\ \begin{array}{*{20}{c}} {{{\tau }_{{{\text{dep}}}}}\frac{{0.104{{{\left( {\frac{w}{{{{v}_{{{\text{dep}}}}}}}} \right)}}^{{20}}}}}{{1 + 0.2{{{\left( {\frac{w}{{{{v}_{{{\text{dep}}}}}}}} \right)}}^{{20}}}}}}&{{\text{при}}\,\,\,\,\frac{w}{{{{v}_{{{\text{dep}}}}}}} \geqslant 1} \end{array} \hfill \\ \end{gathered} \right..$

Рассмотрим для примера процесс фракционирования частиц полевого шпата в многорядном воздушном классификаторе [21]. В данной работе ставилась задача удалить из исходного материала фракцию менее 0.125 мм.

Высота разделяющих колонок классификатора составляла около 2 м, скорость воздушного потока через аппарат 1 м/с. Принимая кажущуюся плотность шпата 2700 кг/м³ и плотность воздушного потока 1.2 кг/м³, число Архимеда для частиц размером 0.125 мм составит Ar = 188. Скорость осаждения по уравнению (15) v_dep = 0.81 м/с, при этом число Re_dep = 14900.

Применяя выражение (21), для неподвижной среды получим τ_dep = 0.93 с. При скорости воздушного потока в классификаторе 1 м/с частицы шпата размером 0.125 мм перейдут в стационарный режим согласно уравнению (30) через τ = 0.45 с.

Относительная скорость этих частиц w – v = = 0.19 м/с. Соответственно, за время τ они пройдут расстояние около 85 мм, что значительно меньше высоты колонны классификатора, и процесс разделения для этих частиц происходит в стационарном режиме. Это позволяет использовать существующие методики расчета, не принимая во внимание нестационарность процесса.

Однако при выходе из классификатора частицы попадают в транспортный воздуховод и систему пылеулавливания. Рекомендуемая скорость воздушного потока в аспирационных трубопроводах не менее 15 м/с. Время релаксации частиц 0.125 мм для такой скорости составит по уравнению (30) τ = 0.49 с.

Так как относительная скорость движения частиц w – v = 14.19 м/с, до выхода на стационарный режим они пролетят расстояние 6.9 м. С учетом рекомендаций монтажа пылеулавливающих агрегатов по возможности ближе к классификатору, такие частицы будут транспортироваться практически в нестационарном режиме. Действительная скорость их движения не совпадает с расчетной, что требует корректировки расчетов диаметра транспортирующего воздуховода.

ЗАКЛЮЧЕНИЕ

Из опыта проектирования воздушных гравитационных классификаторов и пылеулавливающего оборудования время пребывания твердой фазы в этих процессах составляет от 0.2 до 5 с. Проведенные компьютерные исследования показывают, что при такой продолжительности процессов в нестационарном режиме движения могут находиться частицы уже крупнее 50 мкм. Это нужно учитывать при расчете траекторий их движения и проектировании оборудования.

Понимание динамики изменения времени динамической релаксации позволяет находить более простые решения расчета движения двухфазных сред. Например, при гравитационном фракционировании сыпучих материалов для расчета границы разделения можно не учитывать время динамической релаксации для частиц, движущихся в областях, близких к скоростям витания.

Оригинальность данной работы заключается в разработке методики оценки времени релаксации частиц сыпучего материала в двухфазных потоках и новых, более точных формул расчета коэффициентов сопротивления шарообразных частиц и скоростей их осаждения.

Считаем, что проведенные исследования будут полезны специалистам, разрабатывающим процессы движения крупнодисперсных и зернистых материалов в дисперсионных средах.

ОБОЗНАЧЕНИЯ

A	дополнительная переменная
C	эмпирическая переменная
F	сила инерции частиц, Н
g	ускорение свободного падения, м/с²
k	члены уравнения Рунге–Кутты
m	масса частицы, кг
S	площадь миделевого сечения частицы, м²
t	время, с
δt	временной интервал, шаг сетки в уравнении Рунге–Кутты
u	относительная скорость движения частицы в потоке, м/с
v	скорость движения частицы, м/с
w	скорость движения среды, м/с
Δ	плотность среды, кг/м³
λ	коэффициент динамического сопротивления частицы
μ	динамическая вязкость среды, Па с
ρ	истинная плотность частицы, кг/м³
τ	время динамической релаксации частицы, с
Ar	число Архимеда
Re	число Рейнольдса

ИНДЕКСЫ

0	начальное значение
cal	расчетный
dep	осаждение
n	номер шага итерации
q	квазистационарный
rel	относительный
th	теоретический

Список литературы

Amanbaev T.R. Simulation of hindered sedimentation of the coarse fraction of a bidisperse suspension in the presence of interfractional coagulation // Theor. Found. Chem. Eng. 2018. V. 52. № 4. P. 533. [Аманбаев Т.Р. Моделирование стесненного осаждения крупной фракции бидисперсной суспензии при наличии межфракционной коагуляции // Теор. осн. хим. технол. 2018. Т. 52. № 4. С. 431.]
Tarasov V.P., Mukhopad K.A. A Theory on the Operation of a Single-Tube Pneumatic Conveyor // Theor. Found. Chem. Eng. 2019. V. 53. № 3. P. 443. [Тарасов В.П., Мухопад К.А. Развитие теории работы однотрубной пневмотранспортной установки // Теор. осн. хим. технол. 2019. Т. 53. № 3. С. 349.]
Трушин А.М., Равичев Л.В., Яшин В.Е., Носов М.А., Комляшев Р.Б. Полуэмпирический метод определения скорости стесненного медленного движения // Теор. осн. хим. технол. 2019. Т. 53. № 6. С. 617.
Ni P., Jonsson L.T.I., Ersson M., Jönsson P.G. Deposition of particles in liquid flows in horizontal straight channels // Int. J. Heat Fluid Flow. 2016. V. 62. P. 166.
Казаков Ю.Б., Мизонов В.Е., Баранцева Е.А., Филиппов В.А. Механика сепарации частиц из концентрированной взвеси при неоднородной массовой силе // Вестн. Иванов. гос. энерг. унив. 2011. № 3. С. 1.
Новоселов А.Г., Гуляева Ю.Н., Дужий А.Б. Процессы и аппараты пищевых производств. Ч. 1. Гидромеханические процессы разделения. СПб.: Университет ИТМО, 2016.
Водопьянов И.С., Петров А.Г., Шундерюк М.М. О нестационарном осаждении сферической твердой частицы в вязкой жидкости // Изв. Акад. наук. Мех. жидк. газа. 2010. № 2. С. 97.
Park W.C., Klausner J.F., Mei R. Unsteady forces on spherical bubbles // Exp. Fluids. 1995. V. 19. P. 167.
Иваненко А.Ю., Яблокова М.А., Георгиевский Н.В., Некрасов В.А. Газодинамика полидисперсной системы частиц мелочи нефтяного кокса в вертикальной пневмотранспортной трубе // Фундам. исслед. 2017. № 10. С. 212.
Ivanenko A.Yu., Yablokova M.A. A Mathematical Simulation of the Vertical Pneumatic Transport of a Polydisperse Material // Theor. Found. Chem. Eng. 2019. V. 53. № 3. P. 432. [Иваненко А.Ю., Яблокова М.А. Математическое моделирование вертикального пневмотранспорта полидисперсного материала // Теор. осн. хим. технол. 2019. Т. 53. № 3. С. 338.]
Райст П. Аэрозоли. Введение в теорию. М.: Мир, 1987.
Lu H., Lu L., Jiang Y. Numerical study of monodispersed particle deposition rates in variable-section ducts with different expanding or contracting ratios // Appl. Therm. Eng. 2017. V. 110. P. 150.
Василевский М.В., Романдин В.И., Зыков Е.Г. Транспортировка и осаждение частиц в технологиях переработки дисперсных материалов: монография. Томск: Томский политехнический университет, 2013.
Kelbaliyev G.I. Drag coefficients of variously shaped solid particles, drops, and bubbles // Theor. Found. Chem. Eng. 2011. V. 45. № 3. P. 265. [Келбалиев Г.И. Коэффициенты сопротивления твердых частиц, капель и пузырей различной формы // Теор. осн. хим. технол. 2011. Т. 45. № 3. С. 264.]
Arkhipov V.A., Usanina A.S. Gravity Sedimentation of a Set of Solid Spherical Particles in the Regime of a Partially Blown Cloud // J. Eng. Phys. Thermophys. 2017. V. 90. № 5. P. 1061.
Cheng N.-S. Comparison of formulas for drag coefficient and settling velocity of spherical particles // Powder Technol. 2009. V. 189. № 3. P. 395.
Архипов В.А., Усанина А.С. Движение частиц дисперсной фазы в несущей среде. Томск: Томский государственный университет, 2014.
Адамов Г.А. Общая формула сопротивления при относительном движении частиц и среды // Изв. Акад. наук СССР. Отд. тех. наук. Металл. топл. 1961. № 6. С. 317.
Разумов И.М. Псевдоожижение и пневмотранспорт сыпучих материалов. М.: Химия, 1972.
Шохин В.Н., Лопатин А.Г. Гравитационные методы обогащения. М.: Недра, 1993.
Пономарев В.Б., Шишкин С.Ф., Дзюзер В.Я., Катаев А.В. Установка пневматической классификации шпата // Огнеупоры тех. керам. 2010. № 10. С. 28.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал