Теоретические основы химической технологии, 2021, T. 55, № 2, стр. 210-215

Линейные концентрационные и температурные законы сохранения в открытом безградиентном химическом реакторе

Н. И. Кольцов^*

Чувашский государственный университет им. И.Н. Ульянова
Чебоксары, Россия

Поступила в редакцию 25.05.2020
После доработки 25.11.2020
Принята к публикации 27.11.2020

DOI: 10.31857/S0040357121020032

Аннотация

Найдены новые линейные концентрационные и температурные законы сохранения для химических реакций, протекающих по нелинейным механизмам в открытом неизотермическом реакторе идеального смешения. Такие законы связывают нестационарные значения концентраций и температуры с начальными условиями и тепловыми эффектами реакций и могут использоваться для идентификации механизмов химических реакций.

Ключевые слова: химическая кинетика, неизотермический безградиентный реактор, линейные концентрационные и температурные законы сохранения

ВВЕДЕНИЕ

Линейные законы сохранения (ЛЗС) представляют собой комбинации нестационарных значений концентраций реагентов, температуры и других параметров реакции, сохраняющие постоянные значения в течение всей реакции (автономные инварианты). К настоящему времени известно [1–6], что в закрытом неизотермическом реакторе идеального смешения (НРИС) всегда выполняются концентрационные стехиометрические ЛЗС (ЛСЗС), число которых равно числу различных (независимых) атомов реагентов. Кроме ЛСЗС, в закрытом реакторе могут выполняться и более сложные концентрационные кинетические ЛЗС (ЛКЗС), зависящие от особенностей кинетики химической реакции. В закрытых системах могут выполняться и температурные ЛЗС (ЛТЗС). В открытых идеальных системах, из-за переменного потока реагентов, эти закономерности нарушаются и ЛЗС могут вообще отсутствовать. Поэтому, обнаружить ЛЗС, в особенности – температурные, в открытых системах сложнее и в настоящее время механизмы их формирования и методы установления не известны. В связи с этим целью данной работы является разработка метода установления концентрационных и температурных ЛЗС в сложных химических реакциях, протекающих по линейным и нелинейным механизмам в открытом НРИС. Идея метода состоит в использовании двух или более дифференциальных соотношений, которые являются обобщением аналогичных ЛЗС в закрытых системах. Эти соотношения представляют собой обыкновенные линейные дифференциальные уравнения, которые интегрируются аналитически и позволяют получать новые концентрационные и температурные законы сохранения.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Пусть химическая реакция протекает через нелинейные стадии вида

(1)

${{\Sigma }_{j}}{{a}_{{ij}}}{{{\text{А}}}_{j}} \Leftrightarrow {{\Sigma }_{j}}{{a}_{{ - ij}}}{{{\text{А}}}_{j}},\,\,\,i = 1, \ldots ,\,s,$

где a_ij, a_−ij – стехиометрические коэффициенты реагентов А_j, j = 1, …, n в левых и правых частях стадии i. Динамика такой реакции в открытом и закрытом неизотермическом реакторе идеального смешения в рамках закона действующих масс описывается системой нелинейных обыкновенных дифференциальных уравнений (ОДУ) [7–12]:

(2)

$\begin{gathered} A_{j}^{'} = {{\Sigma }_{i}}({{a}_{{ - ij}}} - {{a}_{{ij}}})({{r}_{i}} - {{r}_{{ - i}}}) + {{q}_{0}}{{A}_{{0j}}}--q{{A}_{j}},\,\,j = 1,\, \ldots ,\,n, \\ T{\kern 1pt} ' = \beta {{\Sigma }_{i}}({{r}_{{i~}}} - {{r}_{{ - i}}})Q_{i}^{*} + \alpha \left( {{{T}_{x}}--T} \right) + {{q}_{0}}{{T}_{0}}--qT, \\ \end{gathered} $

где A_j = A_j(t) – концентрации реагентов, мол. доли; t – время, с; T – температура реакционной смеси, К; T_x – температура стенки реактора, К; r_i = = ${{k}_{i}}{{\Pi }_{j}}A_{k}^{{aij}},$ r_−i = ${{k}_{{ - i}}}{{\Pi }_{j}}A_{k}^{{a - ij}}$ – скорости стадий в прямом и обратном направлениях, 1/с; k_i = = k_i0exp(–E_i/RT), k_−i = k_−i0exp(–E_−i/RT) − константы скоростей стадий, 1/с; k_i0, k_−i0 – предэкспоненты, 1/с; R ≈ 8.314, Дж/(моль К); E_i, E_−i − энергии активации стадий, Дж/моль; A_j0, T₀ – начальные условия (н. у.); q₀, q – начальная и текущая скорости потока реакционной смеси в реакторе, 1/с; $Q_{i}^{*}$ – тепловые эффекты стадий, Дж/моль; β ≡ 1/C_p, моль К/Дж; С_р – удельная теплоемкость реакционной смеси, Дж/(моль К); α ≡ βγSM/(ρV), 1/с; γ – коэффициент теплопередачи, Дж/(с м² К); S – площадь поверхности теплообмена, м²; M – молекулярная масса, кг/моль; ρ – плотность реакционной смеси, кг/м³; V – объем реактора, м³. Перепишем эту систему в безразмерном виде (аналог классических моделей [7–10]):

(3)

$\begin{gathered} A_{j}^{'} = {{\Sigma }_{i}}({{a}_{{ - ij}}} - {{a}_{{ij}}})({{r}_{i}} - {{r}_{{ - i}}}) + {{q}_{0}}{{A}_{{0j}}}--q{{A}_{j}},\,\,j = 1,\, \ldots ,\,n, \\ \theta {\kern 1pt} ' = {{\Sigma }_{i}}({{r}_{i}}--{{r}_{{ - i}}}){{Q}_{i}} + \alpha ({{\theta }_{x}}--\theta ) + {{q}_{0}}{{\theta }_{0}}--q\theta , \\ \end{gathered} $

здесь θ = T/T₀ – безразмерная температура; r_i = = k_i0exp(–E_i/RθT₀)${{\Pi }_{j}}A_{k}^{{aij}},$ r_−i = k_−i0exp(–E_−i/RθT₀) × × ${{\Pi }_{j}}A_{k}^{{a - ij}}$ – скорости стадий; θ_x = T_x/T₀; θ₀ = 1; Q_i = = ${{\beta Q_{i}^{*}} \mathord{\left/ {\vphantom {{\beta Q_{i}^{*}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}.$ При q = q₀ = 0 эти уравнения описывают закрытый НРИС и позволяют найти точное число независимых концентрационных ЛЗС для закрытых систем N = n – P [1–4] и их конкретный вид [5, 6]:

(4)

${{\Sigma }_{j}}{{\alpha }_{{mj}}}{{A}_{j}}_{{}} = {{C}_{m}},\,\,\,m = 1,{\text{ }}2,\,\, \ldots ,\,\,N,$

где P – ранг матрицы стехиометрических коэффициентов (a_−ij – a_ij); α_mj – константы, зависящие от стехиометрии стадий; C_m – константы нормирования. Если при этом и α = 0 (идеальный закрытый НРИС), то могут также выполняться и независимые температурные ЛЗС вида

(5)

${{\Sigma }_{j}}{{\beta }_{{kj}}}{{A}_{j}}_{{}} + \theta = {{C}_{k}},\,\,\,k = 1,{\text{ }}2,\,\, \ldots ,$

где β_kj – константы, зависящие от температурных параметров стадий реакции; C_k – константы нормирования.

При q ≠ q₀уравнения (1)–(3) перестают описывать закрытый НРИС, и алгебраические ЛЗС вида (4)–(5) не выполняются и замещаются более общими дифференциальными соотношениями

(6)

${{\Sigma }_{j}}{{\alpha }_{{mj}}}A_{j}^{'} = {{q}_{0}}{{\Sigma }_{j}}{{\alpha }_{{mj}}}{{A}_{{0j}}} - q{{\Sigma }_{j}}{{\alpha }_{{mj}}}{{A}_{j}},\,\,\,{{m}_{j}} = 1,\,\,2,\,\, \ldots ,$

(7)

$\begin{gathered} {{\Sigma }_{j}}{{\beta }_{{kj}}}A_{j}^{'} + \theta {\kern 1pt} ' = {{q}_{0}}({{\Sigma }_{j}}{{\beta }_{{kj}}}{{A}_{{0j}}} + {{\theta }_{0}}) - \hfill \\ - \,\,q({{\Sigma }_{j}}{{\beta }_{{kj}}}{{A}_{j}} + \theta ),\,\,\,{{k}_{j}} = 1,2, \ldots \,\,. \hfill \\ \end{gathered} $

Эти соотношения являются линейными ОДУ относительно комбинаций реагентов и температуры, и, поэтому, интегрируются аналитически

(8)

$\begin{gathered} q{{\Sigma }_{j}}{{\alpha }_{{mj}}}{{A}_{j}} = {{\Sigma }_{j}}{{\alpha }_{{mj}}}{{A}_{{0j}}} \times \\ \times \,\,[{{q}_{0}} + (q--{{q}_{0}})\exp (--qt)],\,\,\,{{m}_{j}} = 1,2,\,\, \ldots , \\ \end{gathered} $

(9)

$\begin{gathered} q({{\Sigma }_{j}}{{\beta }_{{kj}}}{{A}_{j}} + \theta ) = ({{\Sigma }_{j}}{{\beta }_{{kj}}}{{A}_{{0j}}} + {{\theta }_{0}}) \times \\ \times \,\,[{{q}_{0}} + (q--{{q}_{0}})\exp (--qt)],\,\,\,{{k}_{j}} = 1,\,\,2,\,\, \ldots \,\,. \\ \end{gathered} $

Эти равенства, рассмотренные попарно (обозначим номера этих пар индексами m_j1, m_j2), позволяют исключить из них время и получить не зависящие от времени новые концентрационные и температурные ЛЗС для открытого реактора

(10)

$\begin{gathered} {{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{j1}}}{{\Sigma }_{{j2}}}{{\alpha }_{{mj2}}}{{A}_{{0j2}}} = \\ = \,\,{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{0j1}}}{{\Sigma }_{{j2}}}{{a}_{{mj2}}}{{A}_{{j2}}},{{m}_{{j1}}},\,\,\,{{m}_{{j2}}} = 1,\,\,2,\,\, \ldots , \\ \end{gathered} $

(11)

$\begin{gathered} {{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{j1}}}({{\Sigma }_{{j2}}}{{\beta }_{{kj2}}}{{A}_{{0j2}}} + {{\theta }_{0}}) = \\ = \,\,{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{0j1}}}({{\Sigma }_{{j2}}}{{\beta }_{{kj2}}}{{A}_{{j2}}} + \theta ),\,\,\,{{m}_{{j1}}},\,\,\,{{m}_{{j2}}} = 1,2,\,\, \ldots \,\,. \\ \end{gathered} $

Эти ЛЗС зависят только от стехиометрии и тепловых эффектов стадий, концентраций реагентов и температуры, но не зависят от констант скоростей стадий. Это позволяет использовать их для решения обратных задач по идентификации механизмов химических реакций [13–19].

На практике ЛЗС (10)–(11) удобнее использовать в следующем эквивалентном виде (с постоянными правыми частями)

(12)

$\begin{gathered} {{K}_{m}}(t) \equiv {{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{{{{{A}_{{j1}}}} \mathord{\left/ {\vphantom {{{{A}_{{j1}}}} \Sigma }} \right. \kern-0em} \Sigma }}_{{j2}}}{{\alpha }_{{mj2}}}{{A}_{{j2}}} = \\ = \,\,{{{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{0j1}}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{0j1}}}} {{{\Sigma }_{{j2}}}}}} \right. \kern-0em} {{{\Sigma }_{{j2}}}}}{{\alpha }_{{mj2}}}{{A}_{{0j2}}},\,\,\,m = 1,\,\,2,\,\, \ldots , \\ \end{gathered} $

(13)

$\begin{gathered} {{L}_{k}}(t) \equiv {{{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{j1}}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{j1}}}} {({{\Sigma }_{j}}_{2}{{\beta }_{{kj}}}_{2}{{A}_{j}}_{2} + \theta )}}} \right. \kern-0em} {({{\Sigma }_{j}}_{2}{{\beta }_{{kj}}}_{2}{{A}_{j}}_{2} + \theta )}} = \\ = \,\,{{{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{0j1}}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{{j1}}}{{\alpha }_{{mj1}}}{{A}_{{0j1}}}} {({{\Sigma }_{{j2}}}{{\beta }_{{kj2}}}{{A}_{{0j2}}} + {{\theta }_{0}})}}} \right. \kern-0em} {({{\Sigma }_{{j2}}}{{\beta }_{{kj2}}}{{A}_{{0j2}}} + {{\theta }_{0}})}},\,\,\,k = 1,\,\,2,\,\, \ldots \,\,. \\ \end{gathered} $

Для экспериментальной проверки этих ЛЗС достаточно измерить значения нестационарных концентраций реагентов и температуры в различные моменты времени и подставить их в выражения (12)–(13). Если при этом будут получены тождества (с учетом ошибок измерений), то предполагаемый механизм реакции может быть принят как возможный.

ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

Применим приведенные выше результаты к конкретным реакциям.

Пример 1. Пусть реакция А ⇔ С + D протекает по схеме

(1.1)

$1)\,\,\,{\text{A}} \Leftrightarrow {\text{B}},\,\,\,2)\,\,\,{\text{B}} \Leftrightarrow {\text{C}} + {\text{D}}.$

Найдем ЛЗС вида (12)–(13) для этой реакции в открытом НРИС. Запишем для нее модель (3):

(1.2)

$\begin{gathered} A' = --{{r}_{1}} + {{r}_{{ - 1}}} + {{q}_{0}}{{A}_{0}}--qA, \\ B' = {{r}_{1}}--{{r}_{{ - 1}}}--{{r}_{2}} + {\text{ }}{{r}_{{ - 2}}} + {{q}_{0}}{{B}_{0}}--qB, \\ \end{gathered} $

(1.3)

$\begin{gathered} C' = {{r}_{2}}--{{r}_{{ - 2}}} + {{q}_{0}}{{C}_{0}}--qC, \\ D' = {{r}_{2}}--{{r}_{{ - 2}}} + {{q}_{0}}{{D}_{0}}--qD, \\ \end{gathered} $

(1.4)

$\begin{gathered} \theta ' = {{Q}_{1}}({{r}_{1}}--{{r}_{ - }}_{1}) + {{Q}_{2}}({{r}_{2}}--{{r}_{ - }}_{2}) + \\ + \,\,\alpha ({{\theta }_{x}}--\theta ) + {{q}_{0}}{{\theta }_{0}}--q\theta , \\ \end{gathered} $

где r₁ = k₁A, r₋₁ = k₋₁B, r₂ = k₂B, r₋₂ = k₋₂CD, k_i = = k_i0exp(–E_i/RθT₀), k_−i = k_−i0exp(–E_−i/RθT₀). Отсюда следует, что в закрытом НРИС (q = q₀ = 0) выполняются два независимых концентрационных стехиометрических ЛЗС вида (4):

(1.5)

$A + B + C = {\text{ }}1,\,\,\,C--D = 0.$

Если при этом α = 0 (идеальный закрытый НРИС), то выполняется еще один независимый температурный ЛЗС вида (5):

(1.6)

${{Q}_{1}}A--{{Q}_{2}}C + \theta = 1.$

В открытом НРИС (q ≠ q₀) ЛЗС (1.5)–(1.6) нарушаются, но выполняются более общие дифференциальные соотношения вида (6)–(7):

(1.7)

$\begin{gathered} A' + B'\,\, + С' = \\ = \,\,{{q}_{0}}({{A}_{0}} + {{B}_{0}} + {{С}_{0}})--q(A + B + С), \\ \end{gathered} $

(1.8)

$C'\,\,--D' = {{q}_{0}}({{С}_{0}}--{{D}_{0}})--q(С--D),$

(1.9)

$\begin{gathered} {{Q}_{1}}A'\,\,--{{Q}_{2}}C'\,\, + q' = \\ = \,\,{{q}_{0}}({{Q}_{1}}{{A}_{0}}--{{Q}_{2}}{{C}_{0}} + {{q}_{0}})--q({{Q}_{1}}A--{{Q}_{2}}C + \theta ). \\ \end{gathered} $

Проинтегрируем эти уравнения и получим соответственно

(1.10)

$\begin{gathered} q(A + B + С) = {{q}_{0}}({{A}_{0}} + {{B}_{0}} + {{С}_{0}}) + \hfill \\ + \,\,\left( {q--{{q}_{0}}} \right)({{A}_{0}} + {{B}_{0}} + {{С}_{0}})\exp \left( {--qt} \right), \hfill \\ \end{gathered} $

(1.11)

$\begin{gathered} q(С--D) = {{q}_{0}}\left( {{{C}_{0}}--{{D}_{0}}} \right) + \\ + \,\,\left( {q--{{q}_{0}}} \right)\left( {{{C}_{0}}--{{D}_{0}}} \right)\exp \left( {--qt} \right), \\ \end{gathered} $

(1.12)

$\begin{gathered} q({{Q}_{1}}A--{{Q}_{2}}C + \theta ) = {{q}_{0}}({{Q}_{1}}{{A}_{0}}--{{Q}_{2}}{{C}_{0}} + {{\theta }_{0}}) + \\ + \,\,\left( {q--{{q}_{0}}} \right)({{Q}_{1}}{{A}_{0}}--{{Q}_{2}}{{C}_{0}} + {{\theta }_{0}})\exp \left( {--qt} \right). \\ \end{gathered} $

Исключим из (1.10)–(1.12) время t и получим один независимый концентрационный ЛЗС в форме (10):

(1.13)

$\begin{gathered} (A + B + С)({{C}_{0}}--{{D}_{0}}) = \\ = \,\,(С--D)({{A}_{0}} + {{B}_{0}} + {{С}_{0}}), \\ \end{gathered} $

и один независимый температурный ЛЗС в форме (11):

(1.14)

$\begin{gathered} (A + B + С)({{Q}_{1}}{{A}_{0}}--{{Q}_{2}}{{C}_{0}} + {{\theta }_{0}}) = \\ = \,\,({{Q}_{1}}A--{{Q}_{2}}C + \theta )({{A}_{0}} + {{B}_{0}} + {{С}_{0}}). \\ \end{gathered} $

Эти же ЛЗС удобно переписать в форме (12)–(13):

(1.15)

$\begin{gathered} K\left( t \right) \equiv {{(С--D)} \mathord{\left/ {\vphantom {{(С--D)} {(A + B + С)}}} \right. \kern-0em} {(A + B + С)}} = \\ = \,\,{{\left( {{{C}_{0}}--{{D}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{C}_{0}}--{{D}_{0}}} \right)} {({{A}_{0}} + {{B}_{0}} + {{С}_{0}})}}} \right. \kern-0em} {({{A}_{0}} + {{B}_{0}} + {{С}_{0}})}}, \\ \end{gathered} $

(1.16)

$\begin{gathered} L\left( t \right) \equiv {{({{Q}_{1}}A--{{Q}_{2}}C + \theta )} \mathord{\left/ {\vphantom {{({{Q}_{1}}A--{{Q}_{2}}C + \theta )} {(A + B + С)}}} \right. \kern-0em} {(A + B + С)}} = \\ = \,\,{{({{Q}_{1}}{{A}_{0}}--{{Q}_{2}}{{C}_{0}} + {{\theta }_{0}})} \mathord{\left/ {\vphantom {{({{Q}_{1}}{{A}_{0}}--{{Q}_{2}}{{C}_{0}} + {{\theta }_{0}})} {({{A}_{0}} + {{B}_{0}} + {{С}_{0}})}}} \right. \kern-0em} {({{A}_{0}} + {{B}_{0}} + {{С}_{0}})}}. \\ \end{gathered} $

Графическая иллюстрация этих ЛЗС при q₀ = 1, q = 0.9, A₀ = 1, B₀ = 0, C₀ = 0, D₀ = 0, T₀ = 300, T_x = T₀, R = 8.314, $Q_{1}^{*}$ = 10000, $Q_{2}^{*}$ = 20000, E₁ = 10000, E₋₁ = = 20 000, E₂ = 10 000, E₋₂ = 30 000, α = 0, β = 0.03 приведена на рис. 1.

Рис. 1.

Концентрационный и температурный ЛЗС, зависимости концентраций реагентов и температуры от времени для реакции (1.1): 1 – K(t), 2 – L(t), 3 – A(t), 4 – C(t), 5 – T(t)/T₀.

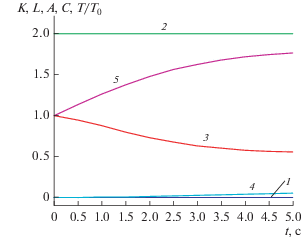
Покажем, как можно использовать эти ЛЗС для решения обратных задач. Предположим, что для реакции, протекающей по схеме (1.1) , в моменты времени, например, t = 0.5, 1 и 1.5 по рис. 1 с погрешностью ε = 0.05 (5%) определены нестационарные концентрации реагентов A = (0.95, 0.90, 0.80), B = (0.10, 0.20, 0.30), C = (0.00, 0.00, 0.01), D = (0.03, 0.08, 0.01) и соответствующие температуры θ = (1.15, 1.30, 1.40). Подставим эти данные в (1.15)–(1.16) и найдем расчетные значения концентрационного K_расч = (–0.03, –0.07, 0.00) и температурного L_расч = (2.00, 2.00, 1.96) ЛЗС. Поэлементно сравним их с соответствующими теоретическими (точными) значениями K = (0.00, 0.00, 0.00) и L = (2.00, 2.00, 2.00). Поскольку |K – K_расч| ≤ 0.07, |L – L_расч| ≤ 0.04, то механизм (1.1) согласуется с концентрационным и температурным ЛЗС с ошибками 7% и 4% соответственно.

Рассмотрим для реакции А ⇔ С + D альтернативный механизм

$1)\,\,\,{\text{A}} \Leftrightarrow B + С,\,\,\,\,2)\,\,\,{\text{B}} \Leftrightarrow {\text{D}}.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1.1*)$

Запишем для него модель (3):

$\begin{array}{*{20}{c}} {A' = --{{r}_{1}} + {{r}_{{ - 1}}} + {{q}_{0}}{{A}_{0}}--qA,} \\ {B' = {{r}_{1}}--{{r}_{{ - 1}}}--{{r}_{2}} + {\text{ }}{{r}_{{ - 2}}} + {{q}_{0}}{{B}_{0}}--qB.} \end{array}\,\,\,\,\,\,\,\,(1.2*)$

$\begin{array}{*{20}{c}} {C' = {{r}_{1}}--{{r}_{{ - 1}}} + {{q}_{0}}{{C}_{0}}--qC,} \\ {D' = {{r}_{2}}--{{r}_{{ - 2}}} + {{q}_{0}}{{D}_{0}}--qD.} \end{array}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1.3*)$

$\begin{array}{*{20}{c}} {\theta ' = {{Q}_{1}}({{r}_{1}}--{{r}_{ - }}_{1}){\text{ }} + {{Q}_{2}}({{r}_{2}}--{{r}_{ - }}_{2}) + } \\ { + \,\,\alpha ({{\theta }_{x}}--\theta ) + {{q}_{0}}{{\theta }_{0}}--q\theta ,} \end{array}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1.4*)$

где r₁ = k₁A, r₋₁ = k₋₁BС, r₂ = k₂B, r₋₂ = k₋₂D. Проинтегрируем эти уравнения численно и примем результаты интегрирования за экспериментальные данные. “Измерим” в любые моменты времени, например, те же t = 0.5, 1 и 1.5 с той же погрешностью ε = 0.05 (5%) концентрации A = (0.90, 0.84, 0.75), B = (0.05, 0.15, 0.22), C = (0.05, 0.15, 0.25), D = = (0.00, 0.00, 0.01) и температуру θ = (1.15, 1.30, 1.40). Подставим эти данные в (1.15)–(1.16) и найдем K_расч = (0.05, 0.13, 0.20) и L_расч = (1.95, 1.61, 1.35). Поэлементно сравним их с теоретическими значениями K = (0.00, 0.00, 0.00) и L = (2.00, 2.00, 2.00) и получим |K – K_расч| ≤ 0.20, |L – L_расч| ≤ 0.65. Следовательно, механизм (1.1*) согласуется с концентрационным и температурным ЛСЗ (1.15)–(1.16) с ошибками 20 и 65% соответственно. Поскольку эти ошибки значительно больше, чем для механизма (1.1), то альтернативный механизм (1.1*) должен быть отвергнут.

Пример 2. Реакция H₂ + 1/2O₂ ⇔ H₂O протекающая по схеме

(2.1)

$\begin{gathered} 1)\,\,\,{{{\text{H}}}_{2}} \Leftrightarrow 2{\text{H}}*,\,\,\,\,2)\,\,\,{{{\text{O}}}_{2}} \Leftrightarrow 2{\text{O}}*, \\ 3)\,\,\,2{\text{H}}* + \,\,{\text{O}}* \Leftrightarrow {{{\text{H}}}_{{\text{2}}}}{\text{O}}, \\ \end{gathered} $

в открытом НРИС описывается системой ОДУ (3):

(2.2)

$\begin{gathered} A' = --{{r}_{1}} + {{r}_{ - }}_{1} + {{q}_{0}}{{A}_{0}}--qA, \\ B' = --{{r}_{2}} + {{r}_{{ - 2}}} + {{q}_{0}}{{B}_{0}}--qB, \\ \end{gathered} $

(2.3)

$\begin{gathered} C' = {{r}_{3}}--{{r}_{{ - 3}}} + {{q}_{0}}{{C}_{0}}--qC, \\ D' = 2{{r}_{1}}--2{{r}_{ - }}_{1}--2{{r}_{3}} + 2{{r}_{{ - 3}}} + {{q}_{0}}{{D}_{0}}--qD, \\ \end{gathered} $

(2.4)

$E' = 2{{r}_{2}}--2{{r}_{{ - 2}}}--{{r}_{3}} + {{r}_{{ - 3}}} + {{q}_{0}}{{E}_{0}}--qE,$

(2.5)

$\begin{gathered} \theta ' = {{Q}_{1}}({{r}_{1}}--{{r}_{ - }}_{1}) + {{Q}_{2}}({{r}_{2}}--{{r}_{ - }}_{2}) + \\ + \,\,{{Q}_{3}}({{r}_{3}}--{{r}_{ - }}_{3}) + a({{\theta }_{x}}--\theta ) + {{q}_{0}}{{\theta }_{0}}--q\theta , \\ \end{gathered} $

где A = [H₂], B = [O₂], C = [H₂O], D = [H*], E = [O*] – концентрации реагентов; r₁ = k₁A, r₋₁ = k₋₁D², r₂ = k₂B, r₋₂ = k₋₂E², r₃ = k₃D²E, r₋₃ = k₋₃C, k_i = = k_i0exp(–E_i/RθT₀), k_−i = k_−i0exp(–E_−i/RθT₀). Отсюда следует, что в закрытом НРИС выполняются два концентрационных ЛСЗС вида (4):

(2.6)

$2A + 2С + D = 1,\,\,\,2B + С + E = 1.$

В идеальном закрытом НРИС выполняется и температурный ЛЗС вида (5):

(2.7)

${{Q}_{1}}A + {{Q}_{2}}B--{{Q}_{3}}C + \theta = 1.$

В открытом НРИС выполняются соотношения вида (6)–(7):

(2.8)

$\begin{gathered} 2B'\,\, + C' + E' = \\ = \,\,{{q}_{0}}\left( {2{{B}_{0}} + {{C}_{0}} + {{E}_{0}}} \right)--q\left( {2B + C + E} \right), \\ \end{gathered} $

(2.9)

$\begin{gathered} 2A'\,\, + 2C' + D' = \\ = \,\,{{q}_{0}}\left( {2{{A}_{0}} + 2{{C}_{0}} + {{D}_{0}}} \right)--q\left( {2A + 2C + D} \right), \\ \end{gathered} $

(2.10)

$\begin{gathered} {{Q}_{1}}A'\,\, + {{Q}_{2}}B'\,\,--{{Q}_{3}}C'\,\, + \theta ' = \\ = \,\,{{q}_{0}}({{Q}_{1}}{{A}_{0}} + {{Q}_{2}}{{B}_{0}}--{{Q}_{3}}{{C}_{0}} + {{\theta }_{0}})-- \\ - \,\,q({{Q}_{1}}A + {{Q}_{2}}B--{{Q}_{3}}C + \theta ). \\ \end{gathered} $

Проинтегрируем эти уравнения и получим соответственно

(2.11)

$\begin{gathered} q(2A + 2С + D) = \\ = \,\,(2{{A}_{0}} + 2{{С}_{0}} + {{D}_{0}})\left[ {{{q}_{0}} + \left( {q--{{q}_{0}}} \right)\exp \left( {--qt} \right)} \right], \\ \end{gathered} $

(2.12)

$\begin{gathered} q\left( {2B + C + E} \right) = \left( {2{{B}_{0}} + {{C}_{0}} + {{E}_{0}}} \right) \times \\ \times \,\,\left[ {{{q}_{0}} + \left( {q--{{q}_{0}}} \right)\exp \left( {--qt} \right)} \right], \\ \end{gathered} $

(2.13)

$\begin{gathered} q({{Q}_{1}}A + {{Q}_{2}}B--{{Q}_{3}}C + \theta ) = \\ = \,\,({{Q}_{1}}{{A}_{0}} + {{Q}_{2}}{{B}_{0}}--{{Q}_{3}}{{C}_{0}} + {{\theta }_{0}}) \times \\ \times \,\,\left[ {{{q}_{0}} + \left( {q--{{q}_{0}}} \right)\exp \left( {--qt} \right)} \right]. \\ \end{gathered} $

Исключим время t из уравнений (2.11)–(2.13) и найдем концентрационный и температурный ЛЗС

(2.14)

$\begin{gathered} \left( {2A + 2C + D} \right)\left( {2{{B}_{0}} + {{C}_{0}} + {{E}_{0}}} \right) = \\ = \,\,\left( {2B + C + E} \right)\left( {2{{A}_{0}} + 2{{C}_{0}} + {{D}_{0}}} \right), \\ \end{gathered} $

(2.15)

$\begin{gathered} \left( {2A + 2C + D} \right)({{Q}_{1}}{{A}_{0}} + {{Q}_{2}}{{B}_{0}}--{{Q}_{3}}{{C}_{0}} + {{\theta }_{0}}) = \\ = \,\,({{Q}_{1}}A + {{Q}_{2}}B--{{Q}_{3}}C + \theta )(2{{A}_{0}} + 2{{С}_{0}} + {{D}_{0}}). \\ \end{gathered} $

Запишем эти ЛЗС в форме (12)–(13):

(2.16)

$\begin{gathered} K\left( t \right) \equiv {{\left( {2A + 2C + D} \right)} \mathord{\left/ {\vphantom {{\left( {2A + 2C + D} \right)} {}}} \right. \kern-0em} {}}\left( {2B + C + E} \right) = \\ = \,\,{{\left( {2{{A}_{0}} + 2{{C}_{0}} + {{D}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {2{{A}_{0}} + 2{{C}_{0}} + {{D}_{0}}} \right)} {\left( {2{{B}_{0}} + {{C}_{0}} + {{E}_{0}}} \right)}}} \right. \kern-0em} {\left( {2{{B}_{0}} + {{C}_{0}} + {{E}_{0}}} \right)}}, \\ \end{gathered} $

(2.17)

$\begin{gathered} L\left( t \right) \equiv {{(2A{\text{ }} + 2C + D)} \mathord{\left/ {\vphantom {{(2A{\text{ }} + 2C + D)} {({{Q}_{1}}A + {{Q}_{2}}B - {{Q}_{3}}C + \theta )}}} \right. \kern-0em} {({{Q}_{1}}A + {{Q}_{2}}B - {{Q}_{3}}C + \theta )}} = \\ = \,\,{{(2{{A}_{0}} + 2{{С}_{0}} + {{D}_{0}})} \mathord{\left/ {\vphantom {{(2{{A}_{0}} + 2{{С}_{0}} + {{D}_{0}})} {({{Q}_{1}}{{A}_{0}} + {{Q}_{2}}{{B}_{0}} - {{Q}_{3}}{{C}_{0}} + {{\theta }_{0}})}}} \right. \kern-0em} {({{Q}_{1}}{{A}_{0}} + {{Q}_{2}}{{B}_{0}} - {{Q}_{3}}{{C}_{0}} + {{\theta }_{0}})}}. \\ \end{gathered} $

Эти ЛЗС при q₀ = 1, q = 0.9, A₀ = 0.5, B₀ = 0.5, C₀ = 0, D₀ = 0, E₀ = 0, T₀ = 300, T_x = T₀, R = 8.314, $Q_{{\text{1}}}^{*}$ = 10 000, $Q_{{\text{2}}}^{*}$ = 10 000, $Q_{{\text{3}}}^{*}$ = 10 000, E₁ = 10 000, E₋₁ = 20 000, E₂ = 10 000, E₋₂ = 20 000, E₃ = 10 000, E₋₃ = 20 000, α = 0, β = 0.03 приведены на рис. 2.

Рис. 2.

Концентрационный и температурный ЛЗС, зависимости концентраций реагентов и температуры от времени для реакции (2.1): 1 – K(t), 2 – L(t), 3 – A(t), 4 – B(t), 5 – C(t), 6 – T(t)/T₀.

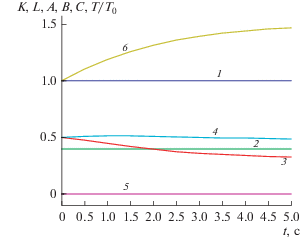
Применим ЛЗС (2.16)–(2.17) и данные рис. 2 для решения обратной задачи. Определим в моменты времени, например, t = 0.5, 1.0 и 1.5 с погрешностью ε = 0.1 (10%) значения концентраций реагентов A = (0.50, 0.45 и 0.40), B = (0.50, 0.50 и 0.50), C = (0.00, 0.00 и 0.01), D = (0.10, 0.20 и 0.25), E = (0.00, 0.05 и 0.10) и температуру θ = (1.10, 1.20 и 1.30). Подставим эти значения в (2.16)–(2.17) и найдем расчетные значения концентрационного K_расч = (1.10, 1.0476, 0.9640) и температурного L_расч = (0.4151, 0.4000, 0.3863) ЛЗС. Поэлементно сравним их с теоретическими значениями K = = (1.00, 1.00, 1.00) и L = (0.40, 0.40, 0.40) и получим |K – K_расч| ≤ 0.10, |L – L_расч| ≤ 0.02. Следовательно, механизм (2.1) согласуется с концентрационным и температурным ЛЗС (2.16)–(2.17) с ошибками 10 и 2% соответственно.

Рассмотрим для той же реакции H₂ + 1/2O₂ ⇔ ⇔ H₂O альтернативный необратимый механизм

$\begin{array}{*{20}{c}} {1)\,\,\,{{{\text{H}}}_{2}} \Rightarrow 2{\text{H}}*,\,\,\,\,2)\,\,\,{{{\text{O}}}_{2}} \Rightarrow 2{\text{O}}*,} \\ {3)\,\,\,2{\text{H}}{\kern 1pt} * + \,\,{\text{O}}* \Rightarrow {{{\text{H}}}_{{\text{2}}}}{\text{O}}{\text{.}}} \end{array}\,\,\,\,\,\,\,(2.1*)$

Динамика этой реакции описывается уравнениями (2.2)–(2.5) при r₋₁ = r₋₂ = r₋₃ = 0. Проинтегрируем эти уравнения численно и примем их решения за экспериментальные данные. “Измерим” в моменты времени t = 0.5, 1 и 1.5 с погрешностью ε = 0.01 (10%) концентрации A = (0.50, 0.45, 0.40), B = (0.50, 0.50, 0.50), C = (0.00, 0.00, 0.00), D = = (0.10, 0.20, 0.25)), E = (0.00, 0.05, 0.10) и температуру θ = (1.10, 1.20, 1.30). Подставим эти данные в (2.16)–(2.17) и найдем K_расч = (1.09, 1.04, 0.95) и L_расч = (0.41, 0.41, 0.39). Поэлементно сравним их с теоретическими значениями K = (1.00, 1.00, 1.00) и L = (0.40, 0.40, 0.40) и получим |K – K_расч| ≤ ≤ 0.09 (9%), |L – L_расч| ≤ 0.01 (1%). Следовательно, механизм (2.1*) лучше согласуется с концентрационным и температурным ЛСЗ (2.16)–(2.17), чем механизм (2.1).

ЗАКЛЮЧЕНИЕ

Приведен метод определения новых типов линейных концентрационных и температурных законов сохранения химических реакций, которые можно наблюдать в открытом реакторе идеального смешения. Методы установления и исследования таких законов для открытых систем в литературе не описаны. Новизна предлагаемого в данной статье метода состоит в возможности получения точных аналитических выражений для линейных концентрационных и температурных законов сохранения химических реакций. Нахождение таких законов позволяет априори получать новую информацию о нестационарных характеристиках изучаемого процесса, которая может быть проверена экспериментально. Найденные с помощью предложенного в работе метода законы сохранения зависят только от стехиометрических и тепловых, но не зависят от кинетических параметров реакции. Полученные результаты расширяют набор инвариантных и релаксационных характеристик реакций и могут быть использованы при решении обратных задач химической кинетики, связанных с идентификацией механизмов химических реакций.

Автор выражает благодарность В.Х. Федотову за обсуждение работы.

ОБОЗНАЧЕНИЯ

A_j	концентрации реагентов, мол. д.
$A_{j}^{0}$	концентрации реагентов на входе реактора, мол. д.
a_ij	безразмерные стехиометрические коэффициенты прямых стадий
a_−ij	безразмерные стехиометрические коэффициенты обратных стадий
C_m, C_k	безразмерные константы нормирования
С_р	удельная теплоемкость реакционной смеси, Дж/(моль К)
E_i	энергии активации прямых стадий, Дж/моль
E_−i	энергии активации обратных стадий, Дж/моль
K_m	безразмерные концентрационные ЛЗС
k_i	константы скоростей прямых стадий, 1/с
k_−i	константы скоростей обратных стадий, 1/с
k_i0	предэкспоненты констант скоростей прямых стадий, 1/с
k_−i0	предэкспоненты констант скоростей обратных стадий, 1/с
L_k	безразмерные температурные ЛЗС
M	молекулярная масса, кг/моль
N	число независимых реагентов
n	число реагентов
P	ранг матрицы стехиометрических коэффициентов
Q_i	тепловые эффекты стадий, Дж/моль
q	скорость потока реакционной смеси, 1/c
R	газовая постоянная, Дж/(моль К)
r_i	скорости прямых стадий, 1/с
r_−i	скорости обратных стадий, 1/с
S	площадь поверхности теплообмена, м²
T	температура реакционной смеси, К
T_x	температура стенки реактора, К
t	время, с
V	объем реактора, м³
α ≡ ≡ βγSM/(ρV)	комбинированный параметр, 1/с
α_mj	безразмерные константы, зависящие от стехиометрии стадий
β	величина, равная 1/C_p, (моль К)/Дж
β_kj	безразмерные константы, зависящие от температурных параметров стадий реакции
γ	коэффициент теплопередачи через стенку реактора, Дж/(с м² К)
ε	погрешность измерений
θ	безразмерная температура реакционной смеси
θ_x	безразмерная температура стенки реактора
ρ	плотность реакционной смеси, кг/м³

ИНДЕКСЫ

0	начальное значение
i	номер стадии
j	номер реагента
k	номер температурного ЛЗС
m	номер концентрационного ЛЗС

Список литературы

Гиббс Дж. Термодинамические работы. М.: ГИТЛ, 1950.
Корзухин М.Д. Линейные законы сохранения в химической кинетике // Журн. физ. хим. 1972. Т. 46. № 7. С. 1845.
Вольперт А.И., Худяев С.И. Анализ в классах разрывных функций и уравнения математической физики. М.: Наука, 1975.
Яблонский Г.С., Быков В.И., Горбань А.Н. Кинетические модели реакций. Новосибирск: Наука, 1983.
Алексеев Б.В., Кольцов Н.И., Федотов В.Х. Линейные инварианты в формальной кинетике химических реакций // Журн. физ. хим. 1992. Т. 66. № 12. С. 3219.
Кольцов Н.И. Математическое моделирование каталитических реакций. Чебоксары: Чувашский университет, 2007.
Арис Р. Анализ процессов в химических реакторах. Л.: Химия, 1967.
Вольтер Б.В., Сальников И.Е. Устойчивость режимов работы химических реакторов. М.: Химия, 1981.
Франк-Каменецкий Д.А. Основы макрокинетики. Диффузия и теплопередача в химической кинетике. М.: Интеллект, 2008.
Быков В.И., Цыбенова С.Б. Нелинейные модели химической кинетики. М.: URSS, 2011.
Островский Г.М., Зиятдинов Н.Н., Лаптева Т.В. Оптимизация технических систем. М.: КНОРУС, 2012.
Ziyatdinov N.N. Modeling and Optimization of Chemical-Technological Processes and Systems // Theor. Found. Chem. Eng. 2017. V. 51. № 5. P. 889. [Зиятдинов Н.Н. Моделирование и оптимизация химико-технологических процессов и систем // Теор. осн. хим. технол. 2017. Т. 51. № 5. С. 546.]
Исмагилова А.С., Спивак С.И. Обратные задачи химической кинетики, Saarbrücken: Lambert Academic, 2013.
Aster R.C., Borchers B., Thurber C.H. Parameter estimation and inverse problems. N.Y.: Elsevier, 2013.
Pisarenko E.V., Pisarenko V.N. Analysis and simulation of the nonlinear kinetics of reacting chemical systems // Theor. Found. Chem. Eng. 2013. V. 47. № 2. P. 128. [Писаренко Е.В., Писаренко В.Н. Анализ и моделирование нелинейной кинетики химических реагирующих систем // Теор. осн. хим. технол. 2013. Т. 47. № 2. С. 173.]
Shatalov M.Yu., Fedotov S.I., Shatalov Yu.M. New methods of determination of kinetic parameters of theoretical models from experimental data // Theor. Found. Chem. Eng. 2013. V. 47. № 3. P. 207. [Шаталов М.Ю., Федотов С.И., Шаталов Ю.М. Новый метод определения кинетических параметров теоретических моделей на основе экспериментальных данных // Теор. осн. хим. технол. 2013. Т. 47. № 3. С. 260.]
Katsman E.A., Sokolova I.V., Temkin O.N. Solution of the reverse kinetic problem for oscillatory reactions // Theor. Found. Chem. Eng. 2014. V. 48. № 2. P. 175. [Кацман Е.А., Соколова И.В., Темкин О.Н. Решение обратной кинетической задачи для колебательных реакций // Теор. осн. хим. технол. 2014. Т. 48. № 2. С. 190.]
Shatalov M.Yu., Demidov A.S., Fedotov I.A. Estimating the parameters of chemical kinetics equations from the partial information about their solution // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 148. [Шаталов М.Ю., Демидов А.С., Федотов И.А. Оценка параметров уравнений химической кинетики по частичной информации об их решении // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 153.]
Sahibgareeva M.V. Interval algorithm for the global search of uncertainty domains in simulating the kinetics of complex chemical reactions // Theor. Found. Chem. Eng. 2019. V. 53. № 3. P. 389. [Сахибгареева М.В. Интервальный алгоритм глобального поиска областей неопределенности при моделировании кинетики сложных химических реакций // Теор. осн. хим. технол. 2019. Т. 53. № 3. С. 302.]

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал