Теоретические основы химической технологии, 2021, T. 55, № 3, стр. 375-389
Влияние избытка титана в реакционной смеси Ti–Si на синтез композита в волне горения
Ю. А. Чумаков a, *, А. Г. Князева a, Г. А. Прибытков a
a Институт физики прочности и материаловедения СО РАН
Томск, Россия
* E-mail: chya@ispms.tsc.ru
Поступила в редакцию 30.03.2020
После доработки 21.12.2020
Принята к публикации 14.01.2021
Аннотация
На основе классических представлений теории твердофазного горения впервые численно реализована модель с детальной схемой химических реакции, учитывающая зависимость свойств от состава и стадию поджигания воспламенителя. Представлено теоретическое обоснование нетеплового характера прекращения реакции после ее инициирования при достижении массовой доли избытка титана в продуктах реакции более 50%. Обнаружено, что, как и при моделировании, так и в эксперименте основными продуктами СВС в исследованном концентрационном интервале являются силицид титана Ti5Si3 и титан. Расчет показали, что в реакционных смесях с целевым составом продуктов СВС Ti5Si3 + 20% Ti горение происходит в колебательном режиме с возрастающей амплитудой колебания скорости горения в процессе распространения волны по реакционной смеси, что может быть причиной появления неустойчивых силицидов в СВС материалах. Полученные теоретические результаты не противоречат данным эксперимента.
ВВЕДЕНИЕ
Силициды титана являются одними из перспективных материалов для применения в современной микроэлектронике и нагревательной технике. Тонкие пленки дисилицида титана (TiSi2) широко используют в качестве омических контактов, управляющих электродов, барьера Шотки и межкомпонентных соединений в цепях электрических микросхемах [1], а также в качестве материалов для нагревателей, благодаря их исключительно коррозионной стойкости, в интервале температур 1300–1700°С [2]. Дисилицид титана TiSi2 является весьма привлекательным материалом для применения в качестве фотокатализатора в солнечной энергетике при разложении воды [3].
Из всего разнообразия способов получения силицидов титана самораспространяющийся высокотемпературный синтез (СВС) привлекает исследователей своей высокой энергоэффективностью по сравнению с другими технологиями (методы порошковой металлургии, горячее прессование, механическое сплавление, реакционной спекания и т.п.) [4, 5]. Суть метода заключается в том, что после локального инициирования внешним тепловым источником тепла происходит распространение волны реакции по гетерогенной смеси реагентов [6] в самоподдерживающемся режиме.
Закономерности горения в системе титан–кремний впервые были исследованы в [7, 8]. В работах изучалось влияние параметров процесса (давления инертного газа, диаметра образцов, размера частиц металла, соотношения компонентов в исходной шихте) на скорость горения, химический и фазовый состав продуктов горения. В [7] было показано, что стационарный режим горения в системе Ti–Si реализуется при массовом содержании кремния от 15.3 до 42%; при меньших концентрациях кремния наблюдается затухание волны, а при бόльших – система горит в автоколебательном (пульсирующем) режиме. При добавлении в исходную смесь Ti + 0.6Si разбавителя в виде готового продукта Ti5Si3 было обнаружено [7], что при содержании Ti5Si3 > 30% происходит смена режима горения из устойчивого стационарного в ярко выраженный автоколебательный режим. В продуктах реакции авторы обнаружили всего два вида силицидов: Ti5Si3 и TiSi2. Исследования [8] показали, что в зависимости от соотношения металла и неметалла (коэффициент α) в исходной смеси при горении в системе “титан–кремний” происходит следующее: при α = 0.6 продукт горения состоит из однофазного силицида Ti5Si3; при α < 0.6 конечным продуктом является Ti5Si3, однако остается непрореагировавший титан; при α > 0.6 в процессе горения образуется три фазы: Ti5Si3, TiSi, TiSi2. На основании экспериментальных данных определен вид кинетической функции взаимодействия титана с кремнием и определена энергия активации для реакции 5Ti + 3Si → Ti5Si3 (Ea = 30 ккал/моль). Дальнейшие работы по СВ-синтезу силицидов титана были посвящены изучению влиянию различных добавок в исходную смесь порошков титана и кремния с целью улучшения коррозионной стойкости, повышению прочности и температуры плавления полученных композитов [9–12]. Например, авторы [9] исследовали СВ-синтез силицида титана на воздухе (смесь Ti + 0.6Si) с 15 мас. % SiC, в образцах были обнаружены фазы: Ti5Si3, TiSi, Ti5Si4, Ti2O, свободный Si и SiO2, а TiSi2 – отсутствовал. Карбид кремния (SiC) является инертным компонентом в реакции, который приводит к потерям тепла, накопленного в этой реакции и, как следствие, к уменьшению температуры процесса и скорости распространения фронта, но увеличивает прочность и трещиностойкость композита. Добавка железа (Fe) в систему Ti–Si значительно усложняет фазовый состав СВС продуктов реакции [10] (кроме Ti5Si3 в стехиометрической смеси Ti–Si и Fe образуются переходные фазы Fe2Ti и FeSi). В отличие от инертного карбида кремния SiC, железо Fe активно участвует в экзотермической реакции, является “источником” жидкой фазы для образования Ti5Si3 в процессе СВС процесса, изменяет микроструктуру и морфологию продуктов реакции, а также является связующим агентом для частиц Ti5Si3. В [11] исследовали влияния добавки TiH2 на синтез композитов Ti5Si3/TiAl из элементарных порошков (Ti, Si, Al) методом СВС. Авторы показали, что добавка TiH2 от 1.25 до 6.25% на моль приводит к уменьшению температуры реакции на 200°С (экзотермичность реакции снижается), что, в свою очередь, приводит к падению скорости распространения фронта реакции в 2 раза (с 30 до 15 мм/c) и к увеличению пористости синтезированных монолитов Ti5Si3 (с 34 до 60%).
Механизм фазообразования Ti5Si3, TiSi2 в процессе СВС был подробно исследован в [12]. Было показано, что образование Ti5Si3 из стехиометрической смеси порошков Ti : Si = 5 : 3 происходит по “твердо-жидкому” механизму, который включает в себя полное растворение реагентов и выделение жидких продуктов, в результате чего в продуктах обнаружена только одна фаза Ti5Si3. Для второй системы (TiSi2) в стехиометрической смеси Ti + 2Si взаимодействие реагентов происходит по твердофазному механизму вследствие низких реакционных температур (ниже эвтектической 1300°С). В последнем случае в продуктах реакции, помимо TiSi2, обнаружена фаза TiSi и чистый Si. В этой работе также показано, что скорость распространения фронта реакции в системе Ti + 2Si в 10 раз меньше чем для 5Ti + 3Si. В следующей работе Yeh и др. [13] осуществили сравнительное исследование синтеза различных силицидов титана (Ti5Si3, TiSi2, Ti3Si, Ti5Si4, TiSi) СВС методом в системе Ti–Si, а также изучили влияние исходной стехиометрии на характеристики и фазовый состав продуктов реакции. Показано, что для составов Ti : Si = 5 : 4 и 1 : 1 в продуктах реакции образуются, в основном, две силицидные фазы: Ti5Si4 и TiSi, а также присутствует небольшое количество силицида TiSi2 и титан Ti, не вступивший в реакцию. Для состава Ti : Si = 5 : 3, как и в [12], образуется единственная фаза Ti5Si3. Для Ti : Si = 1 : 2 в продуктах реакции присутствует основная фаза TiSi2 и небольшое количество непрореагировавшего кремния. Только при соотношении Ti : Si = = 3 : 1 фаза Ti3Si не образуется; вместо этого в продуктах реакции присутствует Ti5Si3 и большое количество непрореагировавшего титана. Самая высокая скорость распространения фронта реакции для составов Ti : Si = 5 : 4 и 5 : 3 достигала 50 мм/c, самая низкая скорость имела место для соотношения Ti : Si = 1 : 2 и составляла 2.6–3 мм/c.
Последние два десятка лет при изучении синтеза горением многих исследователей привлекает внимание влияние механической активации порошковых реагентов в шаровых мельницах на процесс СВ-синтеза, в том числе и силицидов титана [14]. Механическая активация играет роль в увеличении площади контакта между реагентами за счет измельчения порошков и (или) образования композиционной структуры из тонких чередующихся слоев разнородных компонентов. В зависимости от длительности активации порошков титана и кремния в мельнице для получения активных реагентов наблюдают следующее: во-первых, непосредственное образование силицида титана Ti5Si3 в процессе механообработки порошков за счет механического инициирования самоподдерживающейся реакции в смеси (наблюдается спонтанное горение) [15]. Во-вторых, при увеличении времени перемешивания порошков в мельнице уменьшается энергия активации, необходимая для инициирования реакции. Например, в [14] было показано, что при механической активации порошков в соотношении Ti : Si = 5 : 3 в течение 240 мин энергия активации суммарной самораспространяющейся реакции в СВС режиме составляет 155 кДж/моль, что значительно меньше энергии активации для неактивированного состава Ea = 205.2 кДж/моль [13]. В-третьих, механическая активация порошков приводит к повышению температуры процесса и скорости распространения фронта реакции, а также к стабилизации распространения волны горения, но усложняет фазовый состав продуктов реакции (в эксперименте обнаруживается разнообразие фазового состава) [14].
Наряду с активными экспериментальными исследованиями механизма формирования продукта в системах типа “титан–неметалл”, в макрокинетике большая роль отводится математическому моделированию [16]. Однако единой точки зрения на необходимость учета в моделях тех или иных физических явлений до сих пор нет. Одной из последних работ, посвященных теоретическому и экспериментальному изучению синтеза силицидов титана методом СВС, является [17]. Авторы исследовали режим распространения волны горения в стехиометрической смеси Ti : Si = 5 : 3 с исходной пористостью от 50 до 60%. Для расчета профиля температуры и скорости распространения волны горения была использована простейшая модель, предложенная еще в начале 1980-х годов [18]. В модели рассматривается простейшая суммарная реакционная схема 5Ti + 3Si → Ti5Si3 (считается, что реакция протекает по первому порядку), а все теплофизические и кинетические параметры считаются постоянными. Из сопоставления экспериментальных термограмм и численного решения авторы находят значения энергии активации Ea = 193 кДж/моль и предэкспонента в законе Аррениуса k0 = 3 × 109 c–1. Однако вследствие неравновесности самого процесса СВ-синтеза предсказать состав продуктов синтеза на основе моделей с суммарными реакциями не представляется возможным.
Цель настоящей работы состоит в исследовании особенностей синтеза силицидов титана в режиме горения в лабораторном эксперименте, реализующем инициирование реакции в нестехиометрической смеси волной горения. Предложенная в работе модель, в отличие от известных моделей, учитывает детальную реакционную кинетику процесса и зависимость свойств от состава.
МОДЕЛИРОВАНИЕ СИНТЕЗА КОМПОЗИТА В РЕЖИМЕ ГОРЕНИЯ
Постановка задачи. Математическую модель процесса инициирования реакции в порошковой смеси титан–кремний и последующего распространения зоны реакции рассмотрим в следующей постановке. Рассмотрим образец, который представляет собой цилиндр радиуса R (рис. 1), состоящий из двух слоев порошковых насыпок. Полагаем, что слой 1 (воспламенитель) представляет собой стехиометрическую смесь порошков титана и кремния, толщина насыпки равна l (т.е. η0(Ti) = 73.9 мас. % η0(Si) 26.1 мас. % или Ti/Si = = 5/3 (в ат. %)), что соответствует суммарной реакции
Второй слой толщиной L (поджигаемая смесь) имеет аналогичный состав, но смесь не является стехиометрической. Полагаем, что титан во второй смеси представлен в избытке, так что он полностью не расходуется в реакции. Результат процесса формирования силицидов титана предварительно можно оценить, основываясь на термодинамическом анализе возможных реакций в системе кремний–титан. Согласно фазовой диаграмме Ti–Si, в системе можно ожидать появление следующих промежуточных и конечных фаз: TiSi, TiSi2, Ti3Si, Ti5Si3, Ti5Si4. Предполагаемые химические реакции (для первого и второго слоя ограничиваемся десятью реакциями) представлены во втором столбце табл. 1. Таким образом, в общем случае в системе одновременно могут присутствовать свободные титан и кремний, а также пять силицидов титана. Для их массовых концентраций введем следующие обозначения:
Таблица 1.
Кинетические параметры реакции
| № | Реакция | Q, Дж/см3 | k0, с–1 | Ea, Дж/моль | Кинетические функции |
|---|---|---|---|---|---|
| 1 | Ti + Si → TiSi | 6879 | 0.363 × 1014 | 236 145 | ${{\varphi }_{1}}(\eta ) = {{k}_{1}}{{\eta }_{1}}{{\eta }_{2}}$ |
| 2 | Ti + 2Si → TiSi2 | 5418 | 0.146 × 1014 | 196 935 | ${{\varphi }_{2}}(\eta ) = {{k}_{2}}{{\eta }_{1}}\eta _{2}^{2}$ |
| 3 | TiSi2 + Ti → 2TiSi | 6497 | 0.573 × 1014 | 299 065 | ${{\varphi }_{3}}(\eta ) = {{k}_{3}}{{\eta }_{1}}{{\eta }_{4}}$ |
| 4 | 3Ti + Si → Ti3Si | 8280 | 0.342 × 1015 | 193 169 | ${{\varphi }_{4}}(\eta ) = {{k}_{4}}\eta _{1}^{3}{{\eta }_{2}}$ |
| 5 | 2Ti + TiSi → Ti3Si | 5018 | 0.638 × 1015 | 210 644 | ${{\varphi }_{5}}(\eta ) = {{k}_{5}}\eta _{1}^{2}{{\eta }_{3}}$ |
| 6 | 5Ti + 3Si → Ti5Si3 | 7685 | 0.374 × 1015 | 151 187 | ${{\varphi }_{6}}(\eta ) = {{k}_{6}}\eta _{1}^{5}\eta _{2}^{3}$ |
| 7 | 5Ti + 4Si → Ti5Si4 | 7071 | 0.583 × 1012 | 279 997 | ${{\varphi }_{7}}(\eta ) = {{k}_{7}}\eta _{1}^{5}\eta _{2}^{4}$ |
| 8 | 2TiSi + Ti3Si → Ti5Si3 | –131.29 | 0.287 × 1015 | 146 115 | ${{\varphi }_{9}}(\eta ) = {{k}_{9}}\eta _{3}^{2}{{\eta }_{5}}$ |
| 9 | 3Ti5Si4 + 5Ti → 4Ti5Si3 | 7108 | 0.546 × 1023 | 526 753 | ${{\varphi }_{{10}}}(\eta ) = {{k}_{{10}}}\eta _{1}^{5}\eta _{7}^{2}$ |
| 10 | 4TiSi + Ti → Ti5Si4 | 789.44 | 0.705 × 1013 | 181 557 | ${{\varphi }_{{11}}}(\eta ) = {{k}_{{11}}}{{\eta }_{1}}\eta _{3}^{4}$ |
а ρ – плотность смеси.
Математическая модель будет включать уравнения теплопроводности для слоев и систему уравнений химической кинетики.
В уравнении теплопроводности учитываем тепловыделение вследствие химических реакций, теплопотери в окружающую среду за счет конвекции (если синтез осуществляется в атмосфере инертного газа) и за счет теплового излучения (что преобладает при синтезе в вакууме). Таким образом, уравнения теплопроводности принимают вид
(1)
$\begin{gathered} {{\left( {c\rho } \right)}_{{{\text{eff}},i}}}\frac{{\partial {{T}_{i}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {{{\lambda }_{{{\text{eff}},i}}}\frac{{\partial {{T}_{i}}}}{{\partial x}}} \right) + \sum\limits_{j = 1}^{10} {{{Q}_{j}}{{\Phi }_{j}}\left( {{{\eta }_{k}},{{T}_{i}}} \right)} - \\ - \,\,\frac{{2\alpha }}{R}\left( {{{T}_{i}} - {{T}_{0}}} \right) - \frac{{2\varepsilon {{\sigma }_{0}}}}{R}\left( {T_{i}^{4} - T_{0}^{4}} \right), \\ \end{gathered} $Заметим, что каждую из 10 выписанных в табл. 1 реакций в общем случае нельзя рассматривать как элементарную. Тем не менее для записи кинетических законов полагаем, что скорости реакций зависят от концентраций в соответствии с законом действующих масс, а от температуры по закону Аррениуса. Поскольку реакции в системе Ti–Si могут протекать как в жидкой, так и в твердой фазах, учтем следующие обстоятельства. Если температура лежит в пределах 1687–1941°С, в результате взаимодействия расплавленного кремния с титаном могут образоваться четыре тугоплавких соединения, последовательность появления которых в неравновесных условиях может и не совпадать с последовательностью их расположения на диаграмме состояния. Если температура выше температуры плавления титана, все реакции идут в жидкой фазе. Тугоплавкими продуктами могут быть Ti5Si3 и Ti5Si4. В реакциях с образованием тугоплавкого продукта скорость реакции замедляется вследствие затруднения подвода реагентов друг к другу. Торможение реакции растущим слоем твердофазного продукта конкурирует с ее тепловым ускорением [19]. Учтем это следующим образом:
где k0k – предэкспоненты; Eak – энергии активации реакций; Rg – универсальная газовая постоянная; b – параметр торможения, $k = \overline {1,10} ,$ зависящие от конкретной реакции и величины температуры. Такая форма кинетических функций соответствует сильному торможению реакций слоем продукта [4] и использована, например, при описании процесса синтеза на подложке с учетом детальной реакционной кинетики в [20], что позволило установить качественные закономерности, близкие к экспериментально наблюдаемым. Кинетические функции для всех реакций φk(ηj) представлены в последнем столбце табл. 1.
В результате система кинетических уравнений примет следующий вид:
(2)
$\begin{gathered} \frac{{d{{\eta }_{1}}}}{{dt}} = - {{K}_{1}}\left( {{{\Phi }_{1}} + {{\Phi }_{2}} + 2{{\Phi }_{3}} + 3{{\Phi }_{4}} + 2{{\Phi }_{5}} + 5{{\Phi }_{6}} + } \right. \\ \left. { + \,\,5{{\Phi }_{7}} + 5{{\Phi }_{9}} + {{\Phi }_{{10}}}} \right);\,\,\,\,\frac{{d{{\eta }_{2}}}}{{dt}} = - {{K}_{2}}\left( {{{\Phi }_{1}} + 2{{\Phi }_{2}} + {{\Phi }_{4}} + } \right. \\ \left. { + \,\,3{{\Phi }_{6}} + 4{{\Phi }_{7}}} \right);\,\,\,\,\frac{{d{{\eta }_{3}}}}{{dt}} = {{K}_{3}}({{\Phi }_{1}} + 2{{\Phi }_{3}} - {{\Phi }_{5}} - 2{{\Phi }_{8}} - \\ - \,\,4{{\Phi }_{{10}}});\,\,\,\,\frac{{d{{\eta }_{4}}}}{{dt}} = {{K}_{4}}\left( {{{\Phi }_{2}} - {{\Phi }_{3}}} \right);\,\,\,\,\frac{{d{{\eta }_{5}}}}{{dt}} = \\ = {{K}_{5}}\left( {{{\Phi }_{4}} + {{\Phi }_{5}} - {{\Phi }_{8}}} \right);\,\,\,\,\frac{{d{{\eta }_{6}}}}{{dt}} = {{K}_{6}}\left( {{{\Phi }_{6}} + {{\Phi }_{8}} + 4{{\Phi }_{9}}} \right); \\ \frac{{d{{\eta }_{7}}}}{{dt}} = {{K}_{7}}\left( {{{\Phi }_{7}} + {{\Phi }_{{10}}} - 3{{\Phi }_{9}}} \right); \\ \end{gathered} $Полагаем, что между слоями имеет место идеальный тепловой контакт:
(3)
$x = l{\text{:}}\,\,\left\{ \begin{gathered} {{\lambda }_{1}}\frac{{\partial {{T}_{1}}}}{{\partial x}} = {{\lambda }_{2}}\frac{{\partial {{T}_{2}}}}{{\partial x}}, \hfill \\ {{T}_{1}} = {{T}_{2}} \hfill \\ \end{gathered} \right..$Инициирование реакции в воспламенителе осуществляется искрой, что отражает граничное условие
(4)
$x = 0{\text{:}}\,\,{{\lambda }_{1}}\frac{{\partial {{T}_{1}}}}{{\partial x}} = {{q}_{0}}\delta \left( t \right),$На удалении от границы раздела слоев имеет место условие адиабатичности:
В начальный момент времени имеем
(6)
$t = 0{\text{:}}\,\,{{T}_{1}} = {{T}_{2}} = {{T}_{0}},\,\,\,\,{{\eta }_{1}} = {{\eta }_{1}}_{0},\,\,\,\,{{\eta }_{2}} = {{\eta }_{{20}}}.$Поскольку исходная прессовка реагентов пористая, а при нагреве структура и свойства порошковой системы изменяются и в произвольный момент времени неизвестны, то в расчетах используем эффективные (эквивалентные или осредненные по составу) свойства. Так, для расчета объемной теплоемкости и теплопроводности в зависимости от состава используем правило смеси; для учета зависимости свойств от пористости используем соотношения, полученные в теории спекания [21]:
(6)
$\begin{gathered} {{\left( {c\rho } \right)}_{{{\text{eff}}}}} = \sum\limits_{i = 1}^7 {{{c}_{i}}{{\rho }_{{{\text{i}}0}}}{{\eta }_{i}}} \left( {1 - {{\varepsilon }_{{\text{p}}}}} \right),\,\,\,\,{{\lambda }_{{{\text{eff}}}}} = \sum\limits_{i = 1}^7 {{{\lambda }_{i}}{{\eta }_{i}}} \times \\ \times \,\,\left( {\frac{{1 - {{\varepsilon }_{{\text{p}}}}}}{{1 + 11{{\varepsilon }_{{\text{p}}}}}}} \right),\,\,\,\,\rho = {{\rho }_{0}}\left( {1 - {{\varepsilon }_{{\text{p}}}}} \right), \\ \end{gathered} $Используем кинетическое уравнение для эволюции пористости, полученное в теории спекания [21] для случая действия только капиллярных сил:
(7)
$\frac{{d{{\varepsilon }_{{\text{p}}}}}}{{dt}} = - \frac{9}{4}\frac{{{{\varepsilon }_{{\text{p}}}}\gamma {{{\left( {1 - {{\varepsilon }_{{\text{p}}}}} \right)}}^{2}}}}{{\mu {{r}_{0}}}},$Собственно затраты тепла на плавление учтем в простейшем приближении. Температуры плавления реагентов и силицидов лежат в пределах от 1443 до 2193 К (табл. 2), причем самую низкую температуру плавления имеет силицид Ti3Si – один из продуктов. Поскольку реакции активно ускоряются при появлении жидкой фазы; примем, что эффективная теплоемкость изменяется в окрестности температуры плавления кремния следующим образом:
Таблица 2.
Теплофизические свойства
| Вещество | M, г/моль | ρ, кг/м3 | λ, Вт/(м2 К) | c, Дж/(кг К) | Тph, K |
|---|---|---|---|---|---|
| Ti | 47.88 | 4540 | 22 | 498 | 1941 |
| Si | 28.08 | 2330 | 150 | 690 | 1687 |
| TiSi | 75.97 | 4030 | 16.8 | 365 | 1843 |
| TiSi2 | 104.05 | 4210 | 45.9 | 518 | 1773 |
| Ti3Si | 171.73 | 4310 | 20 | 400 | 1443 |
| Ti5Si3 | 323.66 | 4320 | 26.8 | 430 | 2403 |
| Ti5Si4 | 351.74 | 4260 | 30 | 310 | 2193 |
Более строго, такую формулу следует записать для каждого компонента смеси в первом соотношении (6).
Свойства, параметры и алгоритм решения. Значения кинетических параметров суммарных реакций, с которыми проводились расчеты, представлены в табл. 3 [12, 17, 22].
Таблица 3.
Состав реакционных смесей
| Целевой состав СВС продукта | Состав реакционных смесей, мас. % | Теоретическая плотность реакционных смесей, г/см3 | |
|---|---|---|---|
| Ti | Si | ||
| Ti5Si3 | 73.97 | 26.03 | 3.6262 |
| Ti5Si3 + 10%Ti | 76.71 | 23.29 | 3.704 |
| Ti5Si3 + 20%Ti | 79.39 | 20.61 | 3.781 |
| Ti5Si3 + 30%Ti | 82.04 | 17.96 | 3.861 |
| Ti5Si3 + 40%Ti | 84.68 | 15.32 | 3.944 |
Экспериментальные данные по значениям предэкспонент k0k, как правило, неизвестны. Значения k0 существенно зависят от условий эксперимента, структуры реагентов и многих микроскопических факторов, которые плохо контролируются; эти величины отличаются на порядки у разных авторов. Поэтому предэкспоненты, как и другие кинетические параметры реакций, предварительно оценивали на основе подхода, опирающегося на химическую термодинамику и стандартные таблицы термодинамических свойств веществ [23] (табл. 1):
Для других параметров использованы справочные данные [22]. Теплофизические свойства титана, кремния и различных силицидов титана представлены в табл. 2. В расчетах принято: l = 0.5 см, L = 2 см, R = 1.2 см, α = 103 Вт/(м2 К), σ = 5.67 × × 10–8 Вт/(К4 м2), остальные параметры варьировались.
Задачу решали численно. Дифференциальные уравнения аппроксимировали разностными по четырехточечной неявной схеме; получившуюся систему алгебраических уравнений решали методом прогонки. Уравнения кинетики аппроксимировали явной схемой Эйлера. В расчетах находили поле температуры и распределения концентрации компонентов в различные моменты времени. Поскольку в задаче присутствует несколько характерных масштабов и характерных температур, требуется тщательный выбор параметров разностной сетки и тестирование сходимости при экстраполяции на нулевой шаг.
Типичное распределение температуры и концентрации титана для стационарного режима для двух моментов времени показано на рис. 2а, 2б. При уменьшении шага по времени (dt = 5, 10, 15 мс, что соответствует числу точек разностной сетки N = = 1500, 1000, 500). Из рисунка видна достаточно хорошая сходимость при изменении шагов по координате и времени.
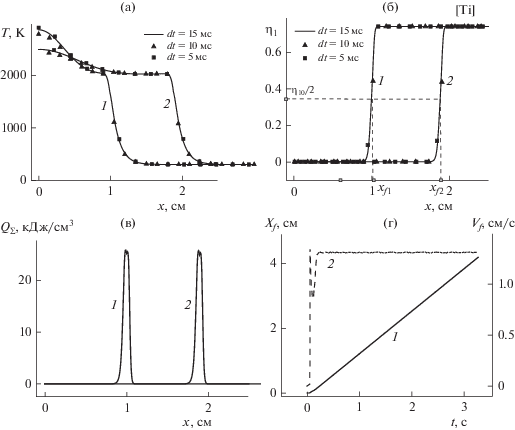
Рис. 2.
Температура реакционной смеси (а), концентрация титана (б) (при различных шагах по времени), суммарное тепловыделение (в), координата (сплошная линия – 1) и скорость фронта (пунктирная – 2) (г). Начальная массовая доля в обоих слоях [Ti] = 73.9%, кремния [Si] = 26.1%, q0 = 1.5 кВт/см2, b = 2, εp = 0.5, 1 – t = 1; 2 – t = 2 с.
Чтобы проанализировать возможные режимы распространения волны горения ведем понятия интегральной концентрации компонентов (реагентов и продуктов реакции) ζk и суммарный тепловой эффект реакций Qs следующим образом:
Суммарное тепловыделение в реакциях, соответствующее кривым на рис. 2а, 2б, показано на рис. 2в.
Координату фронта реакции Xf (рис. 2г) определяли по значению концентрации титана, равному половине начальной η(x) = η10/2, скорость фронта Vf получали численным дифференцированием:
Способ проиллюстрирован на рис. 2б. Рядом представлен пример расчета координаты и скорости распространения фронта реакции для стехиометрической смеси. Видим, что выход на стационарный режим происходит после небольшого нестационарного участка, где скорость сначала резко возрастает, затем падает (что связано с исчерпанием реагентов), и только потом устанавливается стационарное значение скорости.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Материалы, методики и результаты эксперимента. Для приготовления реакционных смесей использовали порошки титана (марка ТПП-8; <160 мкм; 99.4%) и кремния (марка Кр-00; <40 мкм; 99.45%). Порошки смешивали 4 ч всухую и прессовали до получения пористости 32–36%. Двухкомпонентные реакционные смеси содержали от 15.32 до 23.29 мас. % кремния, что соответствовало расчетному объемному содержанию титановой связки в продуктах синтеза (несвязанный титан) от 10 до 40%, в предположении, что при синтезе образуется единственный силицид – Ti5Si3. Это предположение основано на экспериментальных данных более ранних исследований других авторов, согласно которым фаза Ti3Si при синтезе в составах богатых титаном не образуется [8]. Составы реакционных смесей приведены в табл. 3.
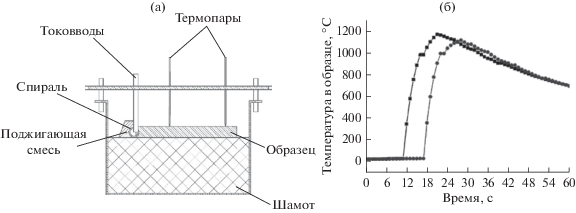
Для синтеза готовили цилиндрические прессовки диаметром 24 мм и высотой 20 мм из смеси порошков титана и кремния. Исходная пористость прессовок колебалась в пределах 33–38%. Для инициирования реакции синтеза сверху на прессовку насыпали поджигающую смесь, горение которой инициировали пропусканием тока через спираль из молибденовой проволоки. Состав поджигающей смеси из порошков титана и кремния соответствовал составу силицида Ti5Si3. Реакция синтеза во всем исследованном концентрационном интервале проходила в стационарном волновом режиме. Максимальные температуры на фронте реакции Tc, были измерены термопарным методом. Спай термопары ВР5–ВР20 помещали в геометрический центр цилиндрического образца в глухое отверстие, просверленное с боковой поверхности цилиндрической прессовки. Для изготовления термопар использовали термопарную проволоку диаметром 100 мкм. Термопарный метод более точный и надежный по сравнению с бесконтактным пирометрическим методом измерения температуры, при котором измеряется температура на поверхности образца.
Скорости горения рассчитывали по времени прохождения фронта реакции вдоль спрессованного из реакционной смеси образца размерами 90 × 19 × 10 мм. Изменение температуры во времени в двух точках образца с расстоянием 50 мм между ними автоматически регистрировали с помощью двух термопар, спаи которых помещали в глухие отверстия, засверленные на половину толщины образца. Для того чтобы устранить влияние теплового импульса от поджигающей смеси на регистрируемую температуру, расстояние от торца с поджигающей смесью до ближайшей термопары увеличили до 30 мм.
На рис. 3 приведен эскиз устройства для измерения скорости горения (а) и типичные термограммы (б), по которым рассчитывали среднюю скорость горения делением 50 мм на временной интервал между двумя пиками на термограммах.
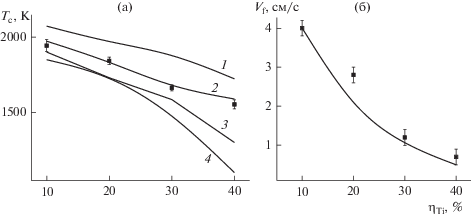
Результаты измерения максимальных температур на фронте реакции Tc и скоростей движений фронта Vf реакции представлены на рис. 4. Монотонное уменьшение температуры и скорости горения по мере увеличения содержания титанового порошка в реакционных смесях объясняется тем, что непрореагировавший титан является инертной добавкой в реакционных смесях титана и кремния, понижающей температуру горения. Подобная монотонная зависимость температуры горения от содержания инертных в тепловом отношении добавок в реакционные смеси является типичной для реакций СВС.
Рис. 4.
Зависимость температуры (а) и скорости (б) горения от целевого содержания титановой связки в СВС композитах. Символы – данные эксперимента. Разные кривые получены при разных значениях параметра торможения: 1 – b = 0; 2 – 1; 3 – 2; 4 – b = 4.
Фазовый состав продуктов синтеза (табл. 4) определяли методом рентгеноструктурного анализа (дифрактометр XRD-6000, CuKα-излучение). Для идентификации фаз и определения их относительного содержания использовали картотеку рентгеновских данных PDF 4+ и программу POWDER CELL 2.4. Экспериментально определенное содержание силицида в СВС продуктах № 2–4 оказалось завышенным по сравнению с расчетным, что объясняется методическими причинами. Для синтеза был использован полидисперсный порошок титана (<160 мкм). На поверхности крупных частиц титана при взаимодействии с кремнием образовывался слой силицида в виде “скорлупы”, внутри которой оставалась сердцевина из непрореагировавшего титана. Толщина силицидной оболочки была больше оцененной нами толщины отражающего слоя, формирующего дифракционную картину. Таким образом, титан из сердцевины крупных частиц не давал отражений, что привело к занижению его содержания по сравнению с фактическим.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Для выбора неизвестных заранее параметров торможения реакции продуктами построены зависимости максимальной температуры в волне горения во втором слое от избыточной доли титана при различных значениях b, одинаковых для всех реакций (рис. 4). Полученные численно результаты сопоставлены с экспериментальными данными. Наилучшее согласие получаем для b = 1.
В модели присутствует еще один параметр, который требует согласования. Это связано с тем, что предэкспоненциальные множители, определенные экспериментально, соответствуют только конкретным условиям эксперимента, а рассчитанные теоретически – идеальным условиям, когда все компоненты реакционной смеси перемешаны на молекулярном уровне. В реальной ситуации на величину предэкспонент оказывают влияние факторы, которые очень сложно или практически невозможно учесть в макроскопической модели. К ним относятся размер частиц всех реагентов, распределение частиц по размерам; форма поверхностей частиц, наличие дефектов и их влияние на скорость каждой реакции и т.п. Величины предэкспонент оказывают влияние на время завершения реакций. Как правило, в теоретических работах ограничиваются суммарной реакцией и переходят к безразмерным переменным, что позволяет “спрятать” описанную проблему. В моделях типа (1)–(6) корректным является следующий подход [23–26]: домножим скорости всех реакций (все предэкспоненты) на один и тот же множитель Z, который выберем из условия, что за время завершения реакции для смеси Ti–Si (состава: 76.71 мас. % Ti, 23.29 мас. % Si) скорость распространения волны реакции составляет 4.0 ± ± 0.2 см/c, а максимальная температура 1943 ± 45 К, что соответствует эксперименту. В нашей модели множитель оказался равным Z = 0.03. Как видно из рис. 3б, при выбранных b и Z значения скорости горения, рассчитанные численно, достаточно хорошо согласуются с экспериментальными.
Все расчеты, описанные далее, были направлены на исследование влияния на процесс синтеза доли избыточного титана в продуктах реакции, которая рассчитывалась в предположении, что реакция пройдет до конца по схеме 5Ti + 3Si → → Ti5Si3, а какая-то часть титана ηe[Ti], не вступившего в реакцию, будет играть роль матрицы в получившемся продукте реакции.
Распределения температуры и концентраций компонентов для разных составов реакционных смесей показаны на рис. 5. Расчеты показали, что для случая стехиометрического состава смеси реагентов (слева на рис. 5) максимальная температура в волне горения примерно равна температуре плавления титана (около 1950 К). Исходные реагенты реакционной смеси практически полностью превращаются в продукты. Состав продуктов реакции в этом случае: около 85% Ti5Si3, около 7% Ti3Si, содержание остальных фаз менее 1% (рис. 5, кривые 1). Если используется теоретически рассчитанный целевой состав полученного композита Ti5Si3 + 50% Ti (справа на рис. 5), что соответствует большому избыточному содержанию титана в исходной реакционной смеси, то горение происходит неустойчиво, переходя в колебательный режим. В этом случае в полученном композите присутствует непрореагировавший титан (около 37%). Содержание Ti3Si около 7%, а Ti5Si3 около 55% в полученном композите (рис. 6, кривые 3). Содержание остальных фаз менее 1%. Также наблюдается падение на порядок скорости распространения волны с 4.4 см/c для стехиометрической смеси до 0.2 см/c для ηe[Ti] = 0.5 (справа на рис. 5, кривые “сближаются”), что приводит к остановке реакций до момента достижение волны нижней границы прессовки, что также наблюдается в эксперименте.
Рис. 5.
Распределение температуры и массовой концентрации компонентов для двух различных исходных составов реакционной смеси. Слева – стехиометрическая смесь в обоих слоях η01[Ti] = 73.9%, η02[Si] = 26.1%, 1 – t = 0.2; 2 – 0.4; 3 – 0.6; 4 – t = 0.8. Справа – доля избыточного титана во втором слое ηe0[Ti] = 50% (η01[Ti] = 88.3%, η02[Si] = 11.7%), 1 – t = 1; 2 – 2; 3 – 3; 4 – t = 4 с.
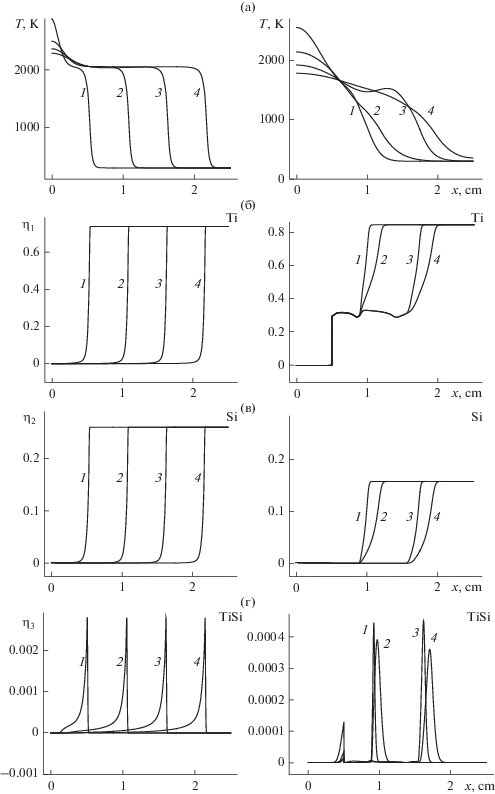
Рис. 5.
Окончание
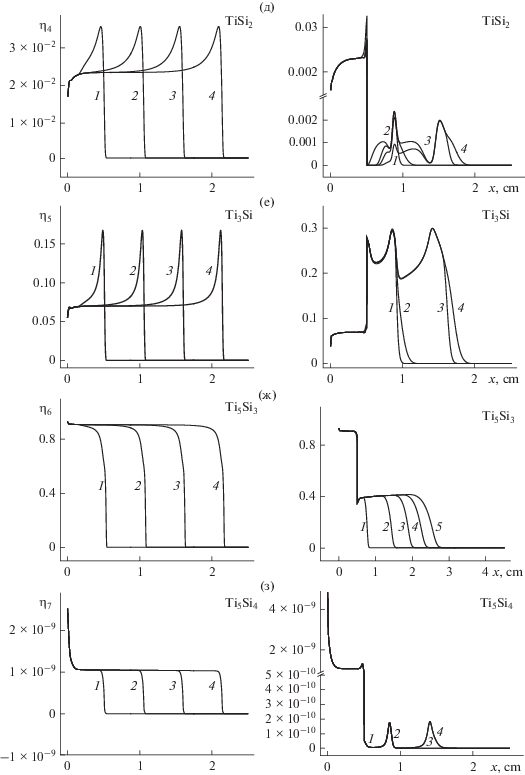
Рис. 6.
Изменение суммарной концентрации компонентов во времени в зависимости от доли избыточного титана в продуктах q0 = 300 Вт/см2, εp = 0.5: 1 – ηe0[Ti] = 0.1; 2 – 0.2; 3 – 0.3; 4 – 0.4; 5 – ηe0[Ti] = 0.5.
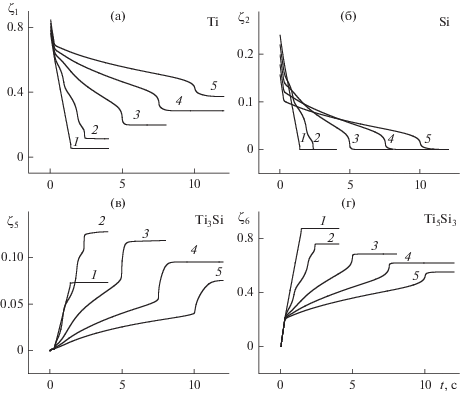
На рис. 6 представлено изменение суммарной концентрации компонентов смеси во времени. Как уже отмечалось выше, при увеличении доли избыточного титана в смеси горение переходит в колебательный режим, что отражается на профилях концентраций компонентов (кривые 3). В продуктах всегда есть небольшая доля титана, не вступившего в реакцию: для стехиометрической смеси около 1–2%, для ηe0[Ti] = 0.3 она составляет 20%, а для ηe0[Ti] = 0.5, около 38%. Кремний практически всегда полностью расходуется и в продуктах реакции не присутствует. Из анализа рис. 6 стоит отметить достаточно хорошее согласие между расчетными и экспериментальными данными по титану в связке, не вступившему реакцию (табл. 4). Отсутствие более полного согласия суммарного процентного содержания фаз в полученном численно композите с экспериментальными результатами говорит о неполном наборе реакций, входящих в рассматриваемую систему, либо о недостаточно точных кинетических параметрах. На данном этапе исследований установить более точные данные не представляется возможным, а литературные данные на эту тему практически отсутствуют.
На рис. 7 представлена скорость распространения фронта реакции и суммарного тепловыделения при различном содержании избыточного титана ηe[Ti]. Для стехиометрической смеси (рис. 7, кривые 1) после инициирования реакции (воздействия резкого теплового импульса) практически сразу формируется волна, распространяющаяся с постоянной скоростью. Для всех остальных случаев волна, сформировавшаяся в воспламенителе, дойдя до границы “воспламенитель–реакционная смесь”, изменяет скорость. Это обнаруживалось, например, в модели горения [18]. Найдено, что горение при ηe[Ti] = 0.2 происходит в колебательном режиме с возрастающей амплитудой колебания скорости в процессе распространения волны горения по реакционной смеси. При дальнейшем увеличение доли избытка титана в связке скорость либо сразу (кривые 3), либо через несколько колебаний (кривые 4) устанавливается, и волна продолжает перемещаться с постоянной скоростью.
Рис. 7.
Скорость распространения фронта реакции и суммарное тепловыделение во времени для различных значений массовой доли избыточного титана при l = 0.5 см, L = 4.5 см, q0 = 300 Вт/см2, εp = 0.5: 1 – ηe0[Ti] = 0.0; 2 – 0.2; 3 – 0.3; 4 – ηe0[Ti] = 0.5.
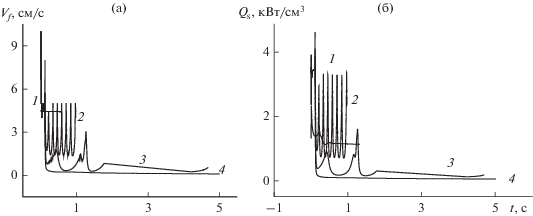
С суммарным тепловыделением наблюдается обратная ситуация (рис. 7б): если для стехиометрической смеси все понятно и никаких колебаний не наблюдается, то для остальных случаев наблюдается резкое уменьшение суммарного тепловыделения на границе “воспламенитель-реагент”. Минимум тем больше, чем больше ηe[Ti], а при ηe[Ti] = 50% наблюдается практически прекращение тепловыделения от реакций и, как следствие, затухание реакций. Часть тепла, выделившаяся в реакциях в воспламенителе, тратится на нагрев компонента, не вступающего в реакцию, суммарная доля реагентов, с которыми связано тепловыделение, уменьшается, что и приводит к понижению температуры в волне горения (ηe[Ti] = 50%; рис. 7, кривые 4). В этом случае наблюдается затухание реакции и остановка волны, а тепло, накопленное в воспламенителе, постепенно за счет теплопроводности уходит в окружающую среду (т.е. имеются теплопотери) и распространяется по всему реагенту, практически не вызывая значительных химических превращений. Расчеты показали, что для колебательного режима (Ti5Si3 + 20% Ti; рис. 7, кривая 2), наряду с осцилляцией скорости и максимальной температуры горения также наблюдаются колебания тепловыделения от химических реакций с резким возрастанием и падением.
ЗАКЛЮЧЕНИЕ
В работе представлены экспериментальные и численные исследования синтеза горением силицида титана из элементной порошковой смеси титана и кремния (с избытком титана). Экспериментальные исследования (рентгенофазовый анализ) показали, что в двухкомпонентных реакционных смесях с содержанием от 15.32 до 23.29 мас. % кремния в составе СВС материала всегда образуются только Ti5Si3 и непрореагировавший титан. Максимальная температура падает с 1670 до 1279°С, а скорость горения изменяется с 4 до 0.7 см/c с увеличением доли избыточного титана в продуктах синтеза c 10 до 40%.
На основе классических представлений теории твердофазного горения с детальной реакционной схемой численно реализована модель, учитывающая нестехиометрический состав исходной смеси, торможение реакции слоем продукта и зависимость свойств от состава. В модели обнаруживаются все режимы превращения, наблюдаемые экспериментально. Значения температуры во фронте горения и содержание основных фаз, полученные численно, соответствуют данным эксперимента.
Работа выполнена при финансовой поддержке Российского научного фонда (грант № 17-19-01425-П).
ОБОЗНАЧЕНИЯ
| b | параметр торможения |
| сeff | эффективная теплоемкость, Дж/(кг · К) |
| Ea | энергии активации реакций, Дж/моль |
| e | число Эйлера |
| h | постоянная Планка, Дж · с |
| K | отношение молярных масс компонентов к плотности смеси, ${{K}_{i}} = \frac{{{{M}_{i}}}}{{\left( {{{M}_{1}} + {{M}_{2}}} \right)\rho }}$ м3/кг |
| k0 | предэкспоненциальный множитель, с–1 |
| l, L | толщина первого и второго слоя цилиндра соответственно, м |
| М | молярная масса реагентов и продуктов реакции, кг/моль |
| m | масса реагентов и продуктов реакции, кг |
| Na | число Авогадро, моль–1 |
| Q | тепловые эффекты суммарных реакций, Дж/м3 |
| Qph | теплота фазового перехода, Дж/(кг К) |
| Qs | суммарный тепловой эффект, Дж/м3 |
| q0 | плотность мощности источника, Вт/см2 |
| R | радиус цилиндра, м |
| Rg | универсальная газовая постоянная, Дж/(моль · K) |
| r0 | радиус частиц, м |
| S | энтальпии реакции, Дж/К |
| T | температура, К |
| Tc | температура горения, К |
| Tph | температура плавления, К |
| t | время, с |
| Vf | скорость координата фронта реакции, м/c |
| Xf | координата фронта реакции, м |
| Xf | координата фронта реакции, м |
| x | пространственная координата, м |
| α | коэффициент теплоотдачи в окружающую среду, Вт/(м2 К) |
| γ | коэффициент поверхностного натяжения, Н/м |
| δ(t) | дельта-функция Дирака |
| ε0 | степень черноты |
| εp | пористость |
| ζ | интегральная концентрация компонентов |
| η | доля реагентов |
| μ | вязкость, кг/(м · с) |
| ρeff | эффективная плотность, кг/м3 |
| σ0 | постоянная Стефана–Больцмана, Вт/(К4 м2) |
| φ | кинетическая функция, моль/(м3с) |
ИНДЕКСЫ
Список литературы
Murarka S.P. Silicide thin films and their applications in microelectronics // Intermetallics. 1995. V. 3. № 3. P. 173.
Zhang L., Wu J. Ti5Si3 and Ti5Si3-based alloys: alloying behavior, microstructure and mechanical property evaluation // Acta Mater. 1998. V. 46. № 10. P. 3535.
Ritterskamp P., Kuklya A., Wustkamp M. A, Kerpen K, Weidenthaler C., Demuth M. A Titanium Disilicide De-rived Semiconducting Catalyst for Water Splitting under Solar Radiation – Reversible Storage of Oxygen and Hydrogen // Angew. Chem., Int. Ed. 2007. V. 46. № 41. P. 7770.
Merzhanov A.G. Combustion processes that synthesize materials // J. Mater. Process. Technol. 1996. V. 56, № 1–4. P. 222.
Stel’makh L.S., Stolin A.M., Stel’makh E.B. Role of the scaling factor in the process of SHS extrusion based on the example of a TiC + Co system // Theor. Found. Chem. Eng. 2017. V. 51. № 5. P. 686. [Стельмах Л.С., Столин А.М., Стельмах Э.В. Роль масштабного фактора в процессе СВС-экструзии (на примере системы TiC + CO) // Теор. осн. хим. технол. 2017. Т. 51. № 5. С. 538.]
Varma A., Rogachev A.S. Mukasyan A.S. Hwang S. Combustion Synthesis of Advanced Materials: Principles and Applications // Adv. Chem. Eng. 1998. V. 24. P. 79.
Sarkisyan A.R., Dolukhanyan S.K., Borovinskaya I.P., Merzhanov A.G. Laws of the combustion of mixtures of transition metals with silicon and the synthesis of silicides // Combust., Explos., Shock Waves. 1978. V. 14. № 3. P. 310.
Azatyan T.S., Mal’tsev V.M., Merzhanov A.G., Seleznev V.A. Some principles of combustion of titanium-silicon mixtures // Combust., Explos., Shock Waves. 1979. V. 15. № 1. P. 35.
Bhattacharya A.K. Effect of Silicon Carbide Reinforcement on the Properties of Combustion-Synthesized Titanium Silicide // J. Am. Ceram. Soc. 1991. V. 74. № 10. P. 2707.
Guan Q.L., Wang H.Y., Li S.L., Zhang W.N., Lu S.J., Jiang Q.C. Effect of Fe addition on self-propagating high-temperature synthesis of Ti5Si3 in Fe–Ti–Si system // J. Alloys Compd. 2008. V. 456. № 1–2. P. 79.
Yeh C.L., Sun W.E. Use of TiH2 as a reactant in combustion synthesis of porous Ti5Si3 and Ti5Si3/TiAl intermetallics // J. Alloys Compd. 2016. V. 669. № 1–2. P. 66.
Yeh C.L., Chen, W.H. Hsu C.C. Formation of titanium silicides Ti5Si3 and TiSi2 by self-propagating combustion synthesis// J. Alloys Compd. 2007. V. 432. № 1–2. P. 90.
Yeh C.L., Chen, W.H. Wang H.J. A comparative study on combustion synthesis of Ti–Si compounds // J. Alloys Compd. 2008. V. 450. № 1–2. P. 200.
Maglia F., Anselmi-Tamburini U., Cocco G., Monagheddu M., Bertolino N., Munir Z. Combustion synthesis of mechanically activated powders in the Ti–Si system // J. Mater. Res. 2001. V. 16. № 4. P. 1074.
Yen B.K., Aizawa T., Kihara J. Reaction Synthesis of Titanium Silicides via Self-Propagating Reaction Kinetics // J. Am. Ceram. Soc. 1998. V. 81. № 7. P. 1953.
Markov A.A., Filimonov I.A., Martirosyan K.S. Modeling of submicron complex oxides synthesis // Theor. Found. Chem. Eng. 2017. V. 51. № 1. P. 27.
Yeh C.L., Hwang P.W., Chen W.H., Hsu C.C. Formation of Ti5Si3 and V5Si3 by self-propagating high-temperature synthesis and evaluation of combustion wave kinetics // J. Alloys Compd. 2017. V. 714. P. 567.
Strunina A.G., Firsov A.N., Kostin S.V. Transition modes in the combustion of heterogeneous systems with solid-phase products // Combust., Explos., Shock Waves. 1981. V. 17. № 5. P. 500.
Liu G., Li J., Chen K. Combustion synthesis of refractory and hard materials: A review // Int. J. Refract. Met. Hard Mater. 2013. V. 39. P. 90.
Sorokova S.N., Knyazeva A.G. Simulation of coating phase structure formation in solid phase synthesis assisted by electron-beam treatment // Theor. Found. Chem. Eng. 2008. V. 42. № 4. P. 443.
Скороход В.В. Реологические основы теории спекания. Киев: Наукова думка, 1972.
Бабичев А.П., Бабушкина Н.А., Братковский А.М. и др. Физические величины: справочник. М.: Энергоатомиздат, 1991.
Knyazeva A.G., Kryukova O.N. Simulation of the synthesis of multiphase composites on a substrate, taking into account the staging of chemical reactions // Appl. Solid State Chem. 2019. № 1. P. 11.
Knyazeva A.G., Kryukova O.N., Sorokova S.N., Shanin S.A. Coupling Models of New Material Synthesis in Modern Technologies // Handbook of Mechanics of Materials. Singapore: Springer, 2018. P. 1.
Knyazeva A.G., Kryukova O.N. Modeling Ti–Al–C-composite synthesis on a substrate under control of electron beam // J. Cryst. Growth. 2020. V. 531. P. 125349.
Bakinovskii A.A., Knyazeva A.G., Krinitcyn M.G., Kryukova O.N., Pobol I.L., Fedorov V.V., Rajczyk J. Electron Beam Assisted Deposition of Ni–Al Coating on to Steel Substrate // Int. J. Self-Propag. High-Temp. Synth. 2019. V. 28. № 4. P. 245.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии