Теоретические основы химической технологии, 2023, T. 57, № 3, стр. 325-334

Прогнозирование нанофильтрационной очистки промышленных растворов от ионов металлов на основе теорий конвективной диффузии и гидродинамики

С. И. Лазарев^a, Д. Н. Протасов^a, О. А. Абоносимов^a, Д. С. Лазарев^a, К. В. Шестаков^a, *

^a Тамбовский государственный технический университет
Тамбов, Россия

Поступила в редакцию 26.02.2023
После доработки 24.03.2023
Принята к публикации 30.03.2023

EDN: RPFWXZ
DOI: 10.31857/S0040357123030090

Аннотация

В работе проанализировано состояние проблемы теоретического прогнозирования коэффициента задержания и удельного выходного потока для очистки или концентрирования промышленных растворов во всем в цикле нанофильтрационного разделения промышленных растворов, содержащих ионы металлов. Для прогнозирования нанофильтрационного процесса разработана математическая модель, основанная на решении уравнений конвективной диффузии, уравнения Навье–Стокса и уравнения неразрывности потока с применением полярной системы координат. Теоретические результаты, полученные в результате решения системы уравнений позволяют оценить качество и производительность нанофильтрационного разделения, путем расчета концентраций в трактах пермеата и ретентата и объема пермеата. Оценка адекватности разработаного метода производилась путем сравнения рассчитанных по модели данных с экспериментальными, полученными на нанофильтрационной установке при разделении растворов, содержащих катионы Cr³⁺ и Zn²⁺, с применением полупроницаемых мембран ОПМН-П и АМН-П.

Ключевые слова: нанофильтрация, прогнозирование, мембрана, математическая модель, ионы металлов

ВВЕДЕНИЕ

В гальванических и химических производствах образуется значительное количество промышленных растворов, которые необходимо очищать и утилизировать. С промышленными растворами, например, гальванических производств, безвозвратно уносится до 70% содержащихся в них металлов, которые являются дорогостоящими. В нашей стране общий уровень извлечения из отработанных промышленных растворов цветных металлов, по последним данным, не превышает 15% от возможного [1–4].

Среди множества методов очистки широкое распространение получили мембранные процессы, в частности, нанофильтрация, где затраты энергии расходуются только на разрыв межмолекулярных связей [5–9]. Как и другие мембранные методы очистки промышленных растворов, нанофильтрация имеет свои преимущества и недостатки. Существенное недостатком является невозможность теоретического прогнозирования коэффициента задержания и удельного выходного потока очистки или концентрирования промышленных растворов для всего цикла нанофильтрационного разделения. На процесс нанофильтрации через полупроницаемую мембрану с течением времени оказывает влияние такие факторы как гидродинамика течения раствора в межмембранном канале и образование диффузионного пограничного слоя. Определяющими кинетическими характеристиками рассматриваемого процесса являются коэффициент задержания и удельный выходной поток нанофильтрационного разделения. Таким образом, кинетические характеристики, получаемые в результате нанофильтрационной очистки, зависят от концентрации, трансмембранного давления, диффузионных явлений в пограничном слое и гидродинамической обстановки:

$R = f(D,\Delta C),$

$J = f(\Delta P,{{R}_{e}}).$

где R – коэффициент задержания, J – удельный выходной поток м³/м² с.

Теоретический расчет нанофильтрационных процессов и аппаратов проводят, основываясь на явлениях массопереноса растворенного вещества через полупроницаемую мембрану. Авторы работы [5] проанализировали некоторые методы теоретического описания эффектов асимметрии транспортных характеристик при использовании композиционных мембран и предложили новый метод расчета массопереноса через асимметричные мембраны, который будет учитывать физико-химические свойства отдельных слоев композиционных мембран и осуществляться рамках модели однородной “тонкопористой мембраны”. В работе [10] рассмотрена возможность оценки селективной проницаемости мембран на основе данных по кажущемуся коэффициенту диффузии. Методами спектроскопии определяли характеристики коэффициента диффузии малых молекул растворителей в полимерных мембранах. Авторами работы [11] представлены результаты исследования активного слоя композиционных мембран, состоящего из неоднородной запутанной полимерной сетки, пронизанной извилистыми трансмембранными “туннелями” и нанопорами, заполненными водой. Авторами [12] показано использование керамической нанофильтрационной мембраны для контроля органических и неорганических загрязнений. Показано применение комбинированного раствора NH₄HCO₃ и Na₂SO₄, который обеспечивает удовлетворительную степень задерживания иона аммония на уровне 88.7%, что объясняется присутствием в данном растворе анионов более высокой валентности (${\text{SO}}_{4}^{{2 - }}$). Авторами в [13] выполнены экспериментальные исследования по электрохимическим и транспортным параметрам на мембранах ОПМН-П, ОФАМ-К при разделении растворов, содержащих нитрат аммония и сульфат калия, методом электронанофильтрации. Показано, что на электрохимические характеристики оказывают влияние дросселирование раствора в электрохимической ячейке и его разогрев. Исследования, проведенные в работе [14], позволили оценить степень влияния температуры, солесодержания и скорости циркуляции раствора на поток пермеата и его компонентный состав. Была выявлена зависимость производительности и времени ресурсной эксплуатации мембраны от концентрационной поляризации и осадкообразования. Кроме того, был исследован такой важный параметр, как чувствительность полимера, из которого изготовлена мембрана, к температурному воздействию при обработке растворов с температурой 20–40°С. Авторами работы [15], предложен усовершенствованный подход к определению кинетических характеристик электрохимического баромембранного разделения растворов, основанный на фрикционной теории Шпиглера с учетом суммарного воздействия химического и электрохимического потенциалов. На примере процесса электрохимического баромембранного разделения водных растворов CuSO₄, Ni(NO₃)₂ и Fe(NO₃)₃ с концентрациями 1 × 10^–2, 2 × 10^–3 и 1 × 10^–5 моль/л соответственно с помощью мембран МГА-95 и МГА-100 получены численные величины фрикционных коэффициентов взаимодействия систем растворитель–мембрана f_ωm, растворенное вещество (катионы)–мембрана f_+m, растворенное вещество (катионы)–растворитель f_+ω, а также найдены эмпирические коэффициенты для определения аппроксимирующих кривых.

Проведенный анализ работ [1–15] по применению нанофильтрационного разделения и оценке селективных и проницаемых свойств полупроницаемых мембран физическими методами, позволил оценить влияние гидродинамики течения раствора и диффузии растворенных веществ на качество и производительность нанофильтрационного разделения растворов содержащих ионы тяжелых металлов. Поэтому, целью данной работы стало прогнозирование процесса нанофильтрационной очистки и концентрирования промышленных растворов от ионов металлов на полупроницаемых мембранах ОПМН-П и АМН-П типа на основе теории гидродинамики и конвективной диффузии.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Большинство математических моделей, направленных на описание массопереноса в процессах баромембранного разделения, основаны на уравнениях гидродинамики движения раствора и конвективной диффузии вещества в мембранном канале [16–18]. При этом следует отметить, что создание математической модели рассматриваемого объекта аналитическим методом проходит в несколько стадий, включая выбор рассчитываемых характеристик, ввод допущений модели и ряд других этапов.

В качестве примера можно привести расчет нанофильтрационных аппаратов и установок. Перед их проектированием необходимо проанализировать сведения по основным характеристикам рассчитываемого модуля. Обычно особое внимание уделяется длине и ширине канала разделения в мембранном модуле, скорость потока растворителя вдоль и поперек (проницание через мембрану) данного канала, коэффициент задержания, а также степень концентрирования или концентрацию растворенного вещества в ретентате на выходе из мембранного модуля.

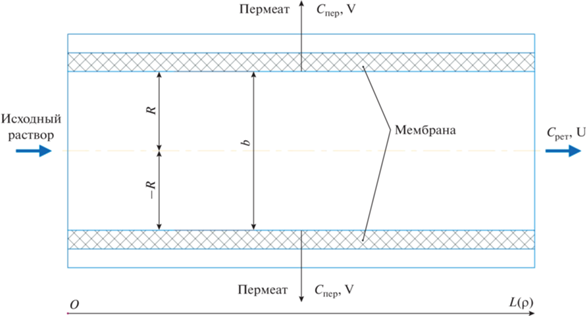
Для более полного понимания массопереноса в плоском канале, представим его структурную схему на рис. 1. Канал с двух сторон ограничен мембранами и рассматривается вместе с ними как одно звено.

Рис. 1.

Схема основных потоков в нанофильтрационном аппарате трубчатого типа.

Помимо структурной схемы необходимо ввести ряд допущений, которые облегчат процесс решения системы уравнений:

• в момент начала работы нанофильтрационного аппарата концентрация на входе в межмембранный канал равна концентрации на выходе из него;

• поток жидкости стационарен, а режим течения – ламинарный;

• насос обеспечивает беспрерывную подачу разделяемого раствора в межмембранный канал;

• силы трения между ионами и молекулами растворителя малы, что ими можно пренебречь.

Рассмотрим систему выражений, основанную на решении уравнений конвективной диффузии, уравнения Навье–Стокса и уравнения неразрывности потока, которые имеют вид:

(1)

$\frac{{\partial U}}{{\partial x}} + \frac{{\partial V}}{{\partial y}} = 0,$

(2)

$\frac{{\partial U}}{{\partial \tau }} + U\frac{{\partial U}}{{\partial x}} + V\frac{{\partial U}}{{\partial y}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + v\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}}} \right),$

(3)

$\frac{{\partial V}}{{\partial {{\tau }}}} + U\frac{{\partial V}}{{\partial x}} + V\frac{{\partial V}}{{\partial y}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial y}} + v\left( {\frac{{{{\partial }^{2}}V}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}V}}{{\partial {{y}^{2}}}}} \right),$

(4)

$U\frac{{\partial C}}{{\partial x}} + V\frac{{\partial C}}{{\partial y}} = D\frac{{{{\partial }^{2}}C}}{{\partial {{y}^{2}}}}.$

Перейдем к полярной системе координат, тогда:

$U(x,y) = u\left( {\rho \cos \varphi ,\rho \sin \varphi } \right) = \bar {u}(\varphi ,\rho ),$

$V(x,y) = \nu \left( {\rho \cos \varphi ,\rho \sin \varphi } \right) = \bar {\nu }(\varphi ,\rho ),$

$C(x,y) = c\left( {\rho \cos \varphi ,\rho \sin \varphi } \right) = \bar {c}(\varphi ,\rho ).$

Математическая запись задачи примет вид:

(5)

$\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos \varphi - \frac{{\partial{ \bar {u}}}}{{\partial \varphi }}\frac{{\sin \varphi }}{\rho } + \frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin \varphi + \frac{{\partial{ \bar {v}}}}{{\partial \varphi }}\frac{{\cos \varphi }}{\rho } = 0,$

(6)

$\begin{gathered} \frac{{\partial U}}{{\partial {{\tau }}}} + \bar {u}\left( {\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos {{\varphi }} - \frac{{\partial{ \bar {u}}}}{{\partial {{\varphi }}}}\frac{{\sin {{\varphi }}}}{\rho }} \right) + \\ + \,\,\bar {v}\left( {\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\sin {{\varphi }} + \frac{{\partial{ \bar {u}}}}{{\partial {{\varphi }}}}\frac{{\cos {{\varphi }}}}{\rho }} \right) = \\ = - \frac{1}{\rho }\left( {\frac{{\partial P}}{{\partial \rho }}\cos {{\varphi }} - \frac{{\partial P}}{{\partial {{\varphi }}}}\frac{{\sin {{\varphi }}}}{\rho }} \right) + \\ + \,\,v\left( {\frac{{{{\partial }^{2}}\bar {u}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {u}}}}{{\partial \rho }} + \frac{1}{{{{\rho }^{2}}}}\frac{{{{\partial }^{2}}\bar {u}}}{{\partial {{{{\varphi }}}^{2}}}}} \right); \\ \end{gathered} $

(7)

$\begin{gathered} \frac{{\partial V}}{{\partial {{\tau }}}} + \bar {u}\left( {\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\cos {{\varphi }} - \frac{{\partial{ \bar {v}}}}{{\partial {{\varphi }}}}\frac{{\sin {{\varphi }}}}{\rho }} \right) + \\ + \,\,\bar {v}\left( {\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin {{\varphi }} + \frac{{\partial{ \bar {v}}}}{{\partial {{\varphi }}}}\frac{{\cos {{\varphi }}}}{\rho }} \right) = \\ = - \frac{1}{\rho }\left( {\frac{{\partial P}}{{\partial \rho }}\sin {{\varphi }} + \frac{{\partial P}}{{\partial {{\varphi }}}}\frac{{\cos {{\varphi }}}}{\rho }} \right) + \\ + \,\,v\left( {\frac{{{{\partial }^{2}}\bar {v}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {v}}}}{{\partial \rho }} + \frac{1}{{{{\rho }^{2}}}}\frac{{{{\partial }^{2}}\bar {v}}}{{\partial {{{{\varphi }}}^{2}}}}} \right); \\ \end{gathered} $

(8)

$\begin{gathered} \bar {U}\left( {\frac{{\partial{ \bar {c}}}}{{\partial \rho }}\cos {{\varphi }} - \frac{{\partial{ \bar {c}}}}{{\partial {{\varphi }}}}\frac{{\sin {{\varphi }}}}{\rho }} \right) + \\ + \,\,\bar {V}\left( {\frac{{\partial{ \bar {c}}}}{{\partial \rho }}\sin {{\varphi }} + \frac{{\partial{ \bar {c}}}}{{\partial {{\varphi }}}}\frac{{\cos {{\varphi }}}}{\rho }} \right) = \\ = \bar {D}\left( {\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{\rho }^{2}}}}{{{\sin }}^{2}}{{\varphi }} + 2\frac{{{{\partial }^{2}}\bar {c}}}{{\partial \varphi \partial \rho }}\frac{{\cos {{\varphi }}\sin {{\varphi }}}}{\rho }} \right. - \\ - \,\,\frac{{\partial{ \bar {c}}}}{{\partial {{\varphi }}}}\frac{{\cos {{\varphi }}\sin {{\varphi }}}}{{{{\rho }^{2}}}} + \frac{{\partial{ \bar {c}}}}{{\partial \rho }}\frac{{{{{\cos }}^{2}}{{\varphi }}}}{\rho } + \\ \left. { + \,\,\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{{{\varphi }}}^{2}}}}\frac{{{{{\cos }}^{2}}{{\varphi }}}}{{{{\rho }^{2}}}} - \frac{{\partial{ \bar {c}}}}{{\partial {{\varphi }}}}\frac{{\sin {{\varphi }}\cos {{\varphi }}}}{{{{\rho }^{2}}}}} \right). \\ \end{gathered} $

Так как поток не вихревой, закручивания потока нет, то $\frac{{\partial{ \bar {u}}}}{{\partial {{\varphi }}}} = 0$, $\frac{{\partial{ \bar {v}}}}{{\partial {{\varphi }}}} = 0$, $\frac{{\partial{ \bar {c}}}}{{\partial {{\varphi }}}} = 0$ и уравнения (5)–(8) примут вид:

(9)

$\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos {{\varphi }} + \frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin {{\varphi }} = 0,$

(10)

$\begin{gathered} \frac{{\partial U}}{{\partial \tau }} + \bar {u}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos \varphi + \bar {v}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\sin \varphi = \\ = - \frac{1}{\rho }\frac{{\partial P}}{{\partial \rho }}\cos \varphi + v\left( {\frac{{{{\partial }^{2}}\bar {u}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {u}}}}{{\partial \rho }}} \right), \\ \end{gathered} $

(11)

$\begin{gathered} \frac{{\partial V}}{{\partial {{\tau }}}} + \bar {u}\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\cos {{\varphi }} + \bar {v}\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin {{\varphi }} = \\ = - \frac{1}{\rho }\frac{{\partial P}}{{\partial \rho }}\sin \varphi + v\left( {\frac{{{{\partial }^{2}}\bar {v}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {v}}}}{{\partial \rho }}} \right), \\ \end{gathered} $

(12)

$\begin{gathered} \bar {U}\frac{{\partial{ \bar {c}}}}{{\partial \rho }}\cos {{\varphi }} + \bar {V}\frac{{\partial{ \bar {c}}}}{{\partial \rho }}\sin {{\varphi }} = \\ = \bar {D}\left( {\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{\rho }^{2}}}}{{{\sin }}^{2}}{{\varphi }} + \frac{{\partial{ \bar {c}}}}{{\partial \rho }}\frac{{{{{\cos }}^{2}}{{\varphi }}}}{\rho }} \right). \\ \end{gathered} $

Граничные условия для уравнений гидродинамики будут следующими:

(13)

$\bar {U}\left( {\frac{\pi }{2},R} \right) = 0,\,\,\,\,\bar {U}\left( { - \frac{\pi }{2},R} \right) = 0.$

Аналитическим решением получены формулы для скорости фильтрации с учетом модифицированного выражения для уравнения конвективной диффузии и граничных условий, и которые можно рассчитать по следующим зависимостям:

(14)

$\begin{gathered} {{\left( {1 + \left( {\frac{1}{{{{k}_{1}}{{\varepsilon }}}} - 1} \right)\left[ {1 - \exp \left( { - \frac{{{{k}_{2}}}}{{{{D}_{\partial }}}} - {{k}_{3}}} \right)} \right]} \right)}^{{ - 1}}} \times \\ \times \,\,\bar {C}({{\rho }},{{\varphi }})\bar {V}(\rho ,{{\varphi }}) = D\frac{{\partial{ \bar {C}}(R,{{\varphi }})}}{{\partial \rho }}\sin {{\varphi ,}} \\ \end{gathered} $

(15)

$\begin{gathered} {{\left( {1 + \left( {\frac{1}{{{{k}_{1}}{{\varepsilon }}}} - 1} \right)\left[ {1 - \exp \left( { - \frac{{{{k}_{2}}}}{{{{D}_{\partial }}}} - {{k}_{3}}} \right)} \right]} \right)}^{{ - 1}}} \times \\ \times \,\,\bar {C}(\rho ,{{\varphi }})\bar {V}(\rho ,{{\varphi }}) = D\frac{{\partial{ \bar {C}}( - R,{{\varphi }})}}{{\partial \rho }}\sin {{\varphi }}{\text{.}} \\ \end{gathered} $

Рассмотрим решения уравнений гидродинамики:

(16)

$\begin{gathered} \frac{{\partial U}}{{\partial \tau }} + \bar {u}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos {{\varphi }} + \bar {v}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\sin {{\varphi }} = \\ = - \frac{1}{\rho }\frac{{\partial P}}{{\partial \rho }}\cos {{\varphi }} + v\left( {\frac{{{{\partial }^{2}}\bar {u}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {u}}}}{{\partial \rho }}} \right), \\ \end{gathered} $

(17)

$\begin{gathered} \frac{{\partial V}}{{\partial \tau }} + \bar {u}\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\cos {{\varphi }} + \bar {v}\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin {{\varphi }} = \\ = - \frac{1}{\rho }\frac{{\partial P}}{{\partial \rho }}\sin {{\varphi }} + v\left( {\frac{{{{\partial }^{2}}\bar {v}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {v}}}}{{\partial \rho }}} \right), \\ \end{gathered} $

(18)

$\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos {{\varphi }} + \frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin {{\varphi }} = 0.$

С учетом того, что по введенным ранее допущениям рассматриваемый процесс является стационарным, то $\frac{{\partial U}}{{\partial \tau }} + \frac{{\partial V}}{{\partial \tau }} = 0$ и система уравнений (16)–(18) преобразуется к виду:

(19)

$\begin{gathered} \bar {u}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos {{\varphi }} + \bar {v}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\sin {{\varphi }} = \\ = - \frac{1}{\rho }\frac{{\partial P}}{{\partial \rho }}\cos {{\varphi }} + v\left( {\frac{{{{\partial }^{2}}\bar {u}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {u}}}}{{\partial \rho }}} \right), \\ \end{gathered} $

(20)

$\begin{gathered} \bar {u}\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\cos {{\varphi }} + \bar {v}\frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin {{\varphi }} = \\ = - \frac{1}{\rho }\frac{{\partial P}}{{\partial \rho }}\sin {{\varphi }} + v\left( {\frac{{{{\partial }^{2}}\bar {v}}}{{\partial {{\rho }^{2}}}} + \frac{1}{\rho }\frac{{\partial{ \bar {v}}}}{{\partial \rho }}} \right), \\ \end{gathered} $

(21)

$\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos {{\varphi }} + \frac{{\partial{ \bar {v}}}}{{\partial \rho }}\sin {{\varphi }} = 0.$

По высоте в сечении канала давление не изменяется, тогда:

(22)

$\frac{{\partial P}}{{\partial \varphi }} = 0.$

Уравнение гидродинамики $v\frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}} = \frac{1}{\rho }\frac{{\partial P}}{{\partial x}}$ примет вид:

(23)

$\bar {\nu }\left( {\frac{{{{\partial }^{2}}\bar {u}}}{{\partial {{\rho }^{2}}}}{{{\sin }}^{2}}\varphi + \frac{{\partial{ \bar {u}}}}{{\partial \rho }}\frac{{{{{\cos }}^{2}}\varphi }}{\rho }} \right) = \frac{1}{\rho }\frac{{\partial{ \bar {P}}}}{{\partial \rho }}\cos \varphi .$

При граничных условиях:

(24)

$\begin{gathered} U(x,R) = \bar {U}\left( {\frac{\pi }{2},R} \right) = 0, \\ U(x, - R) = \bar {U}\left( { - \frac{\pi }{2},R} \right) = 0. \\ \end{gathered} $

Решать данное уравнение будем относительно $P = f(x)$, т.к. давление изменяется только вдоль канала.

Учитывая, что $\mu = \nu \rho $, получим следующие выражения:

(25)

$\frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}} = \frac{1}{\mu }\frac{{\partial P}}{{\partial x}},$

(26)

$\frac{{\partial U}}{{\partial y}} = \frac{1}{\mu }\left( {\frac{{\partial P}}{{\partial x}}} \right)y + {{C}_{1}},$

(27)

$U = \frac{1}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right){{y}^{2}} + {{C}_{1}}y + {{C}_{2}},$

где ${{С}_{1}}$ и ${{С}_{2}}$ – постоянные интегрирования.

Найдем ${{С}_{1}}$ и ${{С}_{2}}$ из условия (24):

(28)

$U(x,R) = \frac{1}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}} + {{C}_{1}}R + {{C}_{2}},$

(29)

$U(x,R) = \frac{1}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}} + {{C}_{1}}R + {{C}_{2}} = 0,$

(30)

$U(x, - R) = \frac{1}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}} - {{C}_{1}}R + {{C}_{2}} = 0,$

(31)

$\frac{1}{\mu }\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}} + 2{{C}_{2}} = 0;$

(32)

${{С}_{2}} = - \frac{1}{{2\mu }}\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}},$

(33)

$ - \frac{1}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}} + \frac{1}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}} + {{С}_{1}}R = 0,\,\,\,\,{{С}_{1}} = 0.$

Интегрируя по $dy$ и подставляя значения граничных условий $U(x,R) = 0$, $U(x, - R) = 0$ получим решение данного дифференциального уравнения (27) в виде:

(34)

$U(x,R) = \frac{1}{{2\mu }}\left( {\frac{{\partial P}}{{\partial x}}} \right){{R}^{2}} - \frac{1}{{2\mu }}\left( {\frac{{\partial P}}{{\partial x}}} \right){{y}^{2}},$

(35)

${\text{или}}\,\,\,\,U(x,R) = \frac{1}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right)\left( {{{R}^{2}} - {{y}^{2}}} \right).$

Далее определим расход жидкости через канал как:

(36)

$\begin{gathered} Q = b\int\limits_{ - R}^R {U(x,R)} dy = - b\int\limits_{ - R}^R {\frac{1}{{2\mu }}\left( {\frac{{\partial P}}{{\partial x}}} \right)\left( {{{R}^{2}} - {{y}^{2}}} \right)} dy = \\ = - \frac{b}{{2\mu }}\left( {\frac{{\partial P}}{{\partial x}}} \right)\int\limits_{ - R}^R {\left( {{{R}^{2}} - {{y}^{2}}} \right)} dy, \\ \end{gathered} $

(37)

$\begin{gathered} Q = \frac{b}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right)\left. {\left( {{{R}^{2}}y - \frac{{{{y}^{3}}}}{3}} \right)} \right|_{{ - R}}^{{ + R}} = \\ = - \frac{b}{{2{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right)\left[ {{{R}^{3}} - \frac{{{{R}^{3}}}}{3} + {{R}^{3}} - \frac{{{{R}^{3}}}}{3}} \right], \\ \end{gathered} $

(38)

$Q = - \frac{{2b{{R}^{3}}}}{{3{{\mu }}}}\left( {\frac{{\partial P}}{{\partial x}}} \right).$

Рассматриваем дифференциальное уравнение для водопроницаемости с учетом осмотического потока, тогда:

(39)

$J = k(\Delta P - \Delta \pi ) = k({{P}_{0}} - P(x) - \Delta \pi ).$

Тогда дифференциальное уравнение для изменения расхода межмембранном канале с учетом осмотического потока:

(40)

${{Q}_{{x + dx}}} - {{Q}_{x}} = dQ = bJdx.$

Отсюда получаем:

(41)

$\frac{{\partial Q}}{{\partial x}} = - bJ.$

Приравняем уравнения для расходов (38) и (41) получим:

(42)

$ - \frac{{2b{{R}^{3}}}}{{3\mu }}\left( {\frac{{{{\partial }^{2}}P}}{{\partial {{x}^{2}}}}} \right) = - bJ.$

Граничные условия:

(43)

$\Delta P(0) = {{P}_{0}},$

(44)

$\Delta P(L) = {{P}_{k}}.$

Далее, обозначив ${{3{{\mu }}} \mathord{\left/ {\vphantom {{3{{\mu }}} {2{{R}^{3}}}}} \right. \kern-0em} {2{{R}^{3}}}} = a$ и ${{3{{\mu }}J} \mathord{\left/ {\vphantom {{3{{\mu }}J} {2{{R}^{3}}}}} \right. \kern-0em} {2{{R}^{3}}}} = \varpi $, получим дифференциальное уравнение для перепада давления в виде:

$\begin{gathered} \frac{{\partial \Delta P}}{{\partial x}} = \frac{{\partial \Delta P}}{{\partial \rho }}\frac{{\partial \rho }}{{\partial x}} + \frac{{\partial \Delta P}}{{\partial {{\varphi }}}}\frac{{\partial {{\varphi }}}}{{\partial x}} = \\ = \frac{{\partial \Delta P}}{{\partial \rho }}\cos {{\varphi }} - \frac{{\partial \Delta P}}{{\partial {{\varphi }}}}\frac{{\sin \varphi }}{\rho }, \\ \end{gathered} $

$\begin{gathered} \frac{{{{\partial }^{2}}\Delta P}}{{\partial {{x}^{2}}}} = \frac{{{{\partial }^{2}}\Delta P}}{{\partial {{\rho }^{2}}}}{{\cos }^{2}}\phi + \frac{{\partial \Delta P}}{{\partial \phi }}\frac{{\sin \phi \cos \phi }}{{{{\rho }^{2}}}} - \\ - \,\,\frac{{{{\partial }^{2}}\Delta P}}{{\partial \phi \partial \rho }}\frac{{\sin \phi \cos \phi }}{\rho } + \frac{{\partial \Delta P}}{{\partial \rho }}\frac{{{{{\sin }}^{2}}{{\varphi }}}}{{{\rho }}} + \\ + \,\,\frac{{{{\partial }^{2}}\Delta P}}{{\partial {{{{\varphi }}}^{2}}}}\frac{{{{{\sin }}^{2}}{{\varphi }}}}{{{{\rho }^{2}}}} + \frac{{\partial \Delta P}}{{\partial {{\varphi }}}}\frac{{\sin {{\varphi }}\cos {{\varphi }}}}{{{{\rho }^{2}}}} = \\ = \frac{{{{\partial }^{2}}\Delta P}}{{\partial {{\rho }^{2}}}}{{\cos }^{2}}{{\varphi }} - 2\frac{{{{\partial }^{2}}\Delta P}}{{\partial \varphi \partial \rho }}\frac{{\sin {{\varphi }}\cos {{\varphi }}}}{\rho } + \\ + \,\,2\frac{{\partial \Delta P}}{{\partial {{\varphi }}}}\frac{{\sin {{\varphi }}\cos {{\varphi }}}}{{{{\rho }^{2}}}} + \frac{{\partial \Delta P}}{{\partial \rho }}\frac{{{{{\sin }}^{2}}{{\varphi }}}}{\rho } + \\ + \,\,\frac{{{{\partial }^{2}}\Delta P}}{{\partial {{{{\varphi }}}^{2}}}}\frac{{{{{\sin }}^{2}}{{\varphi }}}}{{{{\rho }^{2}}}}. \\ \end{gathered} $

Рассмотрим дифференциальное уравнение для гидростатического давления, приведенное в работе [19] $\frac{{{{\partial }^{2}}\Delta P}}{{\partial {{x}^{2}}}} + a\Delta P + \varpi = 0$, принимающее вид:

(45)

$\begin{gathered} \frac{{{{\partial }^{2}}\Delta P}}{{\partial {{{{\rho }}}^{2}}}}{{\cos }^{2}}\varphi - 2\frac{{{{\partial }^{2}}\Delta P}}{{\partial \varphi \partial \rho }}\frac{{\sin \varphi \cos \varphi }}{\rho } + \\ + \,\,2\frac{{\partial \Delta P}}{{\partial \varphi }}\frac{{\sin \varphi \cos \varphi }}{{{{\rho }^{2}}}} + \frac{{\partial \Delta P}}{{\partial \rho }}\frac{{{{{\sin }}^{2}}\varphi }}{\rho } + \\ + \,\,\frac{{{{\partial }^{2}}\Delta P}}{{\partial {{{{\varphi }}}^{2}}}}\frac{{{{{\sin }}^{2}}\varphi }}{{{{\rho }^{2}}}} - a\Delta P + \varpi = 0, \\ \frac{{{{\partial }^{2}}\Delta P}}{{\partial {{{{\rho }}}^{2}}}}{{\cos }^{2}}\varphi + \frac{{\partial \Delta P}}{{\partial \rho }}\frac{{{{{\sin }}^{2}}\varphi }}{\rho } - a\Delta P + \varpi = 0, \\ \frac{{{{\partial }^{2}}\Delta P}}{{\partial {{\rho }^{2}}}} + \frac{{\partial \Delta P}}{{\partial \rho }}\frac{{{{{\sin }}^{2}}\varphi }}{{\rho {{{\cos }}^{2}}\varphi }} - \frac{{a\Delta P}}{{{{{\cos }}^{2}}\varphi }} = \frac{{ - \varpi }}{{{{{\cos }}^{2}}{{\varphi }}}}. \\ \end{gathered} $

Решение данного дифференциального уравнения в общем виде будет:

(46)

$\Delta P({{\rho }}) = {{С}_{1}}{{e}^{{\sqrt a \rho \cos {{\varphi }}}}} + {{С}_{2}}{{e}^{{ - \sqrt a {{\rho }}\cos {{\varphi }}}}} + \frac{\varpi }{a}.$

Найдем постоянные интегрирования C₁ и C₂ в начальный момент $\Delta P\left( {\frac{\pi }{2},0} \right) = {{P}_{0}}$ и конечный момент $\Delta P\left( {\frac{\pi }{2},L} \right) = {{P}_{k}}$:

(47)

${{P}_{0}} = {{C}_{1}}{{e}^{0}} + {{С}_{2}}{{e}^{0}} + \frac{\varpi }{a},$

(48)

${{P}_{0}} = {{C}_{1}} + {{С}_{2}} + \frac{\varpi }{a},$

(49)

${{С}_{2}} = {{P}_{0}} - {{С}_{1}} - \frac{\varpi }{a},$

(50)

${{P}_{{\text{к}}}} = {{C}_{1}}{{e}^{{\sqrt а L}}} + {{С}_{2}}{{e}^{{ - \sqrt а L}}} + \frac{\varpi }{a},$

(51)

${{P}_{{\text{к}}}} = {{C}_{1}}{{e}^{{\sqrt а L}}} + \left( {{{P}_{0}} - {{С}_{1}} - \frac{\varpi }{a}} \right){{e}^{{ - \sqrt а L}}} + \frac{\varpi }{a},$

(52)

${{C}_{1}} = \frac{{{{P}_{K}} - {{P}_{0}}{{е}^{{ - \sqrt а L}}} - \frac{\varpi }{a}}}{{{{е}^{{\sqrt а L}}} - {{е}^{{ - \sqrt а L}}}}},$

(53)

${{С}_{2}} = {{P}_{0}} - \frac{{{{P}_{K}} - {{P}_{Н}}{{е}^{{\sqrt а L}}} + \frac{\varpi }{a}{{е}^{{ - \sqrt а L}}}}}{{{{е}^{{\sqrt а L}}}{{e}^{{ - \sqrt а L}}}}} - \frac{\varpi }{a}.$

Подставим найденные C₁ и C₂ в (47) и получим выражение для расчета давления по длине канала:

(54)

$\begin{gathered} P\frac{{{{P}_{К}} - {{P}_{0}}{{е}^{{ - \sqrt а L}}} - \frac{\varpi }{a}}}{{{{е}^{{\sqrt а L}}} - {{е}^{{ - \sqrt а L}}}}}{{е}^{{\sqrt а {{\rho }}\cos {{\varphi }}}}} + \\ + \,\,\left( {{{P}_{0}} - \frac{{{{P}_{К}} - {{P}_{Н}}{{е}^{{\sqrt а L}}} + \frac{\varpi }{a}{{е}^{{ - \sqrt а L}}}}}{{{{е}^{{\sqrt а L}}}{{e}^{{ - \sqrt а L}}}}} - \frac{\varpi }{a}} \right){{e}^{{ - \sqrt а {{\rho }}\cos {{\varphi }}}}} + \frac{\varpi }{a}. \\ \end{gathered} $

Аналогично дифференциальное уравнение для электроосмотического давления $\frac{{{{\partial }^{2}}\Delta \pi }}{{\partial {{x}^{2}}}} + a\Delta \pi + \varpi = 0$, приведенное в работе [19] и принимающее вид:

(55)

$\frac{{{{\partial }^{2}}\Delta \pi }}{{\partial {{\rho }^{2}}}} + \frac{{\partial \Delta \pi }}{{\partial \rho }}\frac{{{{{\sin }}^{2}}\varphi }}{{\rho {{{\cos }}^{2}}\varphi }} - \frac{{a\Delta \pi }}{{{{{\cos }}^{2}}\varphi }} = \frac{{ - \varpi }}{{{{{\cos }}^{2}}\varphi }}.$

Решение данного дифференциального уравнения в общем виде будет:

(56)

$\Delta \pi (\rho ) = {{С}_{1}}{{e}^{{\sqrt a \rho \cos \phi }}} + {{С}_{2}}{{e}^{{ - \sqrt a \rho \cos \phi }}} + \frac{\varpi }{a}.$

Подставим найденные C₁ и C₂ из начального момента $\Delta \pi \left( {\frac{\pi }{2},0} \right) = {{\pi }_{0}}$ и конечный момент $\Delta \pi \left( {\frac{\pi }{2},L} \right) = {{\pi }_{k}}$ условия в (56) и получим выражение для расчета электроосмотического давления по длине канала:

(57)

$\begin{gathered} \Delta \pi (\varphi ,\rho ) = \frac{{{{\pi }_{К}} - {{\pi }_{0}}{{е}^{{ - \sqrt а L}}} - \frac{\varpi }{a}}}{{{{е}^{{\sqrt а L}}} - {{е}^{{ - \sqrt а L}}}}}{{е}^{{\sqrt а \rho \cos \varphi }}} + \\ + \,\,\left( {{{\pi }_{0}} - \frac{{{{\pi }_{К}} - {{\pi }_{Н}}{{е}^{{\sqrt а L}}} + \frac{\varpi }{a}{{е}^{{ - \sqrt а L}}}}}{{{{е}^{{\sqrt а L}}}{{e}^{{ - \sqrt а L}}}}} - \frac{\varpi }{a}} \right){{e}^{{ - \sqrt а \rho \cos \varphi }}} + \frac{\varpi }{a}. \\ \end{gathered} $

После определения значений давления в межмембранном канале подставляем их в формулы для проницаемости мембран и определяем значение продольной составляющей скорости потока.

Подставим найденные значения P = f(x) (54) в уравнения для определения поперечного потока (39) и продольной скоростей (35), обозначив ${{f}_{1}}(x) = k(\Delta P - \Delta \pi )$ и, ${{f}_{2}}(x,y) = \frac{1}{{2\mu }}\frac{{\partial P}}{{\partial x}}\left( {{{R}^{2}} - {{y}^{2}}} \right)$ = $ = \frac{1}{{2\mu }}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos \varphi \left( {{{R}^{2}} - {{\rho }^{2}}{{{\sin }}^{2}}\varphi } \right)$, перейдя в полярную систему координат, получим следующее уравнение, решением которой является распределение поля концентрации вещества в межмембранном канале:

(58)

$\begin{gathered} {{f}_{2}}\left( {x,y} \right)\frac{{\partial C}}{{\partial x}} + {{f}_{1}}\left( x \right)\frac{{\partial C}}{{\partial y}} = D\frac{{{{\partial }^{2}}C}}{{\partial {{y}^{2}}}}, \\ \frac{1}{{2\mu }}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos {{\varphi }}\left( {{{R}^{2}} - {{\rho }^{2}}{{{\sin }}^{2}}\varphi } \right) \times \\ \times \,\,\left( {\frac{{\partial{ \bar {c}}}}{{\partial \rho }}\cos {{\varphi }} - \frac{{\partial{ \bar {c}}}}{{\partial \varphi }}\frac{{\sin \varphi }}{\rho }} \right) + k(\Delta P - \Delta \pi ) \times \\ \times \,\,\left( {\frac{{\partial{ \bar {c}}}}{{\partial \rho }}\sin {{\varphi }} + \frac{{\partial{ \bar {c}}}}{{\partial {{\varphi }}}}\frac{{\cos \varphi }}{\rho }} \right) = \\ = \bar {D}\left( {\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{\rho }^{2}}}}{{{\sin }}^{2}}{{\varphi }} + 2\frac{{{{\partial }^{2}}\bar {c}}}{{\partial \varphi \partial \rho }}\frac{{\cos \varphi \sin \varphi }}{\rho }} \right. - \\ - \,\,\frac{{\partial{ \bar {c}}}}{{\partial \varphi }}\frac{{\cos \varphi \sin \varphi }}{{{{\rho }^{2}}}} + \frac{{\partial{ \bar {c}}}}{{\partial \rho }}\frac{{{{{\cos }}^{2}}\varphi }}{\rho } + \\ \left. { + \,\,\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{\varphi }^{2}}}}\frac{{{{{\cos }}^{2}}\varphi }}{{{{\rho }^{2}}}} - \frac{{\partial{ \bar {c}}}}{{\partial \varphi }}\frac{{\sin \varphi \cos \varphi }}{{{{\rho }^{2}}}}} \right). \\ \end{gathered} $

Так как поток не вихревой, то $\frac{{\partial{ \bar {c}}}}{{\partial \phi }} = 0$ и уравнение (58) примет вид:

(59)

$\begin{gathered} \frac{1}{{2\mu }}\frac{{\partial{ \bar {u}}}}{{\partial \rho }}\cos \varphi \left( {{{R}^{2}} - {{\rho }^{2}}{{{\sin }}^{2}}\varphi } \right)\frac{{\partial{ \bar {с}}}}{{\partial \rho }}\cos \varphi + \\ + \,\,k(\Delta P - \Delta \pi )\frac{{\partial{ \bar {c}}}}{{\partial \rho }}\sin \varphi = \\ = \bar {D}\left( {\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{\rho }^{2}}}}{{{\sin }}^{2}}\varphi + \frac{{\partial{ \bar {c}}}}{{\partial \rho }}\frac{{{{{\cos }}^{2}}\varphi }}{\rho }} \right). \\ \end{gathered} $

Учитывая начальные условия, имеющие вид $С(0,y) = \bar {C}\left( {\frac{\pi }{2},\rho } \right) = {{C}_{{{\text{исх}}}}}$, концентрацию в межмембранном канале можно вычислить по формуле:

(60)

$\bar {C}({{\varphi }},{{\rho }}) = {{C}_{{{\text{исх}}}}}\exp \left( {{{\bar {V}(\varphi ,\rho )\rho } \mathord{\left/ {\vphantom {{\bar {V}(\varphi ,\rho )\rho } {D\sin {{\varphi }}\left( {1 + \left( {\frac{1}{{{{k}_{1}}\varepsilon }} - 1} \right)\left[ {1 - \exp \left( { - \frac{{{{k}_{2}}}}{{{{D}_{\partial }}}} - {{k}_{3}}} \right)} \right]} \right)}}} \right. \kern-0em} {D\sin {{\varphi }}\left( {1 + \left( {\frac{1}{{{{k}_{1}}\varepsilon }} - 1} \right)\left[ {1 - \exp \left( { - \frac{{{{k}_{2}}}}{{{{D}_{\partial }}}} - {{k}_{3}}} \right)} \right]} \right)}}} \right).$

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Один из этапов данного исследования был направлен на получение экспериментальных данных по очистке технологических растворов от катионов Cr³⁺ и Zn²⁺ на нанофильтрационной установке с применением мембран ОПМН-П и АМН-П. Исходная концентрация Cr³⁺ и Zn²⁺ в исследуемых технологических растворах составляла 0.278 и 0.4 мг/л соответственно. Рабочее давление нанофильтрационной установки варьировалось от 1 до 1.6 МПа. Время проведения каждого эксперимента – 5 ч. Габаритные размеры камеры разделения – 0.13 × 0.06 × 0.06 м.

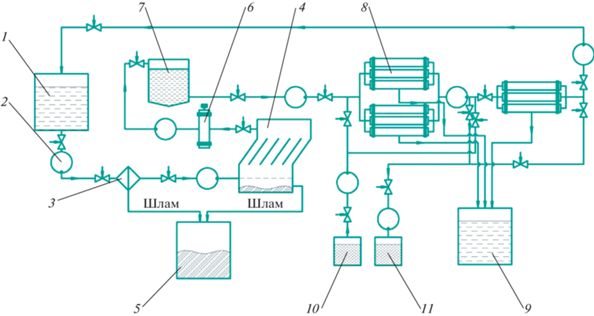
На рис. 2 приведена технологическая схема очистки сточных вод гальванического производства с последующим сбросом очищенной воды в систему канализации, либо повторной подачей на установку нанофильтрационного вида при создании оборотного водоснабжения предприятия [20]. Данная система промышленной очистки воды рекомендуется для использования при проектировании новых очистных сооружений, либо реконструкции действующих систем очистки сточных вод для повышения их экологической безопасности и экономической эффективности.

Рис. 2.

Технологическая схема очистки сточных вод методом нанофильтрации: 1 – исходная емкость со сточными водами; 2 – насос; 3 – фильтр грубой очистки; 4 – тонкослойный отстойник; 5 – шламосборник; 6 – установка корректировки рН; 7 – накопитель осветленных вод; 8 – нанофильтрационный аппарат; 9 – емкость сбора фильтрата; 10 – емкость с чистящими реагентами; 11 – емкость сбора отработанных чистящих реагентов.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Полученные экспериментальные данные по удельному потоку растворителя, коэффициенту задержания мембраны и другим кинетическим характеристикам процесса разделения при нанофильтрационной очистке технологических растворов, содержащих катионы Cr³⁺ и Zn²⁺, были использованы для теоретического расчета концентрации каждого вида катионов в ретентате в зависимости от длины канала камеры разделения и величины трансмембранного давления ΔР при разделении мембранами ОПМН-П и АМН-П.

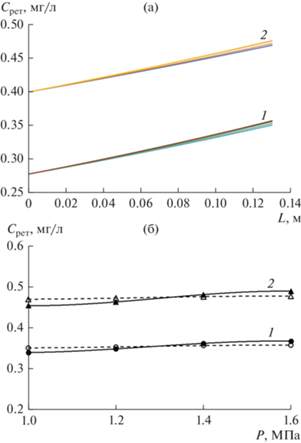
На рис. 3а представлены результаты расчета концентрации катионов Cr³⁺ и Zn²⁺ в ретентате в зависимости от длины канала в процессе нанофильтрации при использовании мембраны ОПМН-П. По полученным данным можно сделать вывод, что увеличение концентрации растворенного вещества в ретентате по мере движения по межмембранному каналу разделения происходит линейно для всех исследуемых значений трансмембранного давления ΔР (от 1 до 1.6 МПа) и свойственно обоим видам катионов. Рассчитанное значение концентрации катионов Cr³⁺ и Zn²⁺ на выходе из канала разделения хорошо коррелируется с экспериментально полученными данными по концентрации катионов Cr³⁺ в ретентате после пятичасового процесса нанофильтрационного разделения [21]. Расхождение теоретически рассчитанных и экспериментальных данных не превышает 5%, что подтверждается предсталенным на рис. 3б графиком.

Рис. 3.

Изменение концентрации ионов Cr³⁺ и Zn²⁺ в ретентате в зависимости от длины канала камеры разделения (а), величины трансмембранного давления Р (б) при разделении мембраной ОПМН-П (на рис. 3б сплошная линия – эксперимент, пунктирная линия – расчет).

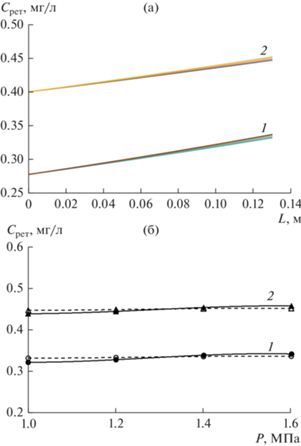
Данные по нанофильтрационной очистке технологического раствора от катионов Cr³⁺ и Zn²⁺ с применением мембраны АПМ-П (рис. 4а) аналогичны тем, что были получены с мембраной ОПМН-П. В данном случае так же зафиксировано увеличение концентрации растворенных веществ в ретентате. Однако значения концентрации катионов Cr³⁺ и Zn²⁺ в ретентате на выходе из канала разделения ниже, чем при использовании мембраны ОПМН-П. Это согласуется с экспериментальными данными [21]. Сравнение экспериментальных и расчетных данных, представленных на рис. 4б, позволяет сделать вывод, что они хорошо коррелируют между собой – расхождение так же не превышает 5%.

Рис. 4.

Изменение концентрации ионов Cr³⁺ и Zn²⁺ в ретентате в зависимости от длины канала камеры разделения (а), величины трансмембранного давления Р (б) при разделении мембраной АМН-П (на рис. 4б сплошная линия – эксперимент, пунктирная линия – расчет).

ЗАКЛЮЧЕНИЕ

1. В работе математически описан процесс прогнозирования нанофильтрационного разделения растворов, содержащих катионы Cr³⁺ и Zn²⁺, с применением мембран ОПМН-П и АПМ-П на основе решения уравнений конвективной диффузии, уравнения Навье–Стокса и уравнения неразрывности потока с применением полярной системы координат.

2. Выполнены экспериментальные исследования по нанофильтрационному разделению растворов, содержащих катионы Cr³⁺ и Zn²⁺. По модели произведен расчет изменения концентрации в ретентате. Выполнена проверка адекватности предлагаемого метода путем сравнения экспериментальных и расчетных данных. Максимальное расхождение между расчетными и экспериментальными значениями не превышает 5%.

БЛАГОДАРНОСТИ

Работа выполнена при финансовой поддержке гранта Президента РФ для поддержки молодых российских ученых – кандидатов наук № МК-4774.2022.4.

ОБОЗНАЧЕНИЯ

А	эмпирический коэффициент, К
b	ширина канала, м
C	концентрация целевого вещества, кг/м³
С₁, С₂	постоянные интегрирования
D	коэффициент диффузии в растворе, м²/с
D_д	коэффициент диффузии в мембране, м²/с
J	поток фильтрата через мембрану, м³/с
k, k₁, k₂, k₃	эмпирические коэффициенты
L	длина канала, м
ΔP	трансмембранное давление, Па
R	полувысота канала разделения, м
t	время, с
U	величина скорости потока растворителя вдоль межмембранного канала, м/с
V	величина скорости проницания потока растворителя чрез мембрану, м/с
ΔV_P	удельный поток растворителя за счет перепада давления до и после мембраны, м³/(м² с)
ε	диэлектрическая постоянная, Ф/м
ν	кинематическая вязкость раствора, м²/c
Δπ	осмотическое давление, Па;
ρ	радиус в полярной системе координат, м
φ	угол в полярной системе координат, рад

ИНДЕКС

0	начальное значение
к	конечное значение
исх	в исходном растворе
пер	в пермеате
рет	в ретентате
м	в мембране

Список литературы

Кузнецова Е.Ю., Акулова А., Мотовилов А.В. Проблемы и решения переработки и утилизации сточных вод гальванических производств // Евразийский Союз Ученых. 2016. № 3–4(24). С. 109.
Мосталыгина Л.В., Костин А.В., Шерстобитов Г.С., Прокопьева Е.А., Мосталыгин А.Г., Бирюков М.Ф. Изучение качественного состава гальванического отхода от очистки гальванической ванны и возможностей его обезвреживания // Вестник КГУ. 2014. № 2(33). С. 88.
Белогородская М.Ю., Игнаткина Д.О., Юрьев Ю.Ю., Тимофеев А.Г., Нестерчук А.В. Повышение качества очистки сточных вод машиностроительных предприятий, использующих хромовый ангидрид // Инженерно-строительный вестник Прикаспия. 2021. № 4(38). С. 33.
Первов А.Г., Спицов Д.В. Разделение высокоминерализованных стоков установок ионного обмена с применением нанофильтрационных мембран // Системные технологии. 2021. № 2(39). С. 34.
Filippov A.N., Iksanov R.H., Kononenko N.A., Berezina N.P., Falina I.V. Theoretical and experimental study of asymmetry of diffusion permeability of composite membranes // Colloid. J. 2010. 72(2). P. 243.
Кисель А.В. Опреснение морской воды черного, азовского и каспийского морей методами мембранных технологий // Вестник науки. 2019. № 2(11). С. 79.
Бурдо О.Г., Терзиев С.Г., Мордынский В.П., Сиротюк И.В., Фатеева Я.А., Молчанов М.Ю. Разработка низкотемпературной установки блочного типа для деминерализации морской воды // Проблемы региональной энергетики. 2022. № 2(54). С. 13.
Винницкий В.А., Чугунов А.С., Ершов М.В. Влияние расхода ретентата на мембранное разделение бинарных растворов хлоридов натрия, магния и кальция // Изв. вузов. Химия и хим. технология. 2021. № 10. С. 46.
Антипова Л.В., Титов С.А., Жданов В.Н., Карпак А.Н. Использование измерений внутреннего трения для исследования ультра- и нанофильтрации модифицированной творожной сыворотки // Вестник ВГУИТ. 2018. № 4(78). С. 298.
Sloan J.M. Following multicomponent diffusion in polymers by FT-IR-ATR. The Pittsburgh Conference on Analytical Chemistry and Applied Spectroscopy “Science for 21st Century”, March 12–17, 2000. NewOrleans, LA, 2000. P. 1784.
Ridgway H.F., Orbell G., Gray S. Molecular simulations of polyamide membrane materials used in desalination and water reuse applications: Recent developments and future prospects // J. Membrane Science. 2017. V. 524. P. 436.
Cha M., Boo C., Park C. Simultaneous retention of organic and inorganic contaminants by a ceramic nanofiltration membrane for the treatment of semiconductor wastewater // Process Safety and Environmental Protection. 2022. V. 159. P. 525.
Лазарев С.И., Ковалев С.В., Коновалов Д.Н., Луа П. Электрохимические и транспортные характеристики мембранных систем при электронанофильтрационном разделении растворов, содержащих нитрат аммония и сульфат калия // Электрохимия. 2021. Т. 57. № 6. С. 355. [Lazarev S.I., Kovalev S.V., Konovalov D.N., Lua P. Electrochemical and transport characteristics of membrane systems in the electronanofiltration separation of solutions containing ammonium nitrate and potassium sulfate // Russian Journal of Electrochemistry. 2021. V. 57. № 6. P. 607.]
Goosen M.F.A., Sablani S.S., Al-Maskari S.S., Al-Belushi R.H., Wilf M. Effect of feed temperature on permeate flux and mass transfer coefficient in spiral-wound reverse osmosis systems // Desalination. 2002. V. 144. № 1–3. P. 367.
Шестаков К.В., Лазарев С.И., Хохлов П.А., Полянский К.К. Прогнозирование процесса электрохимического баромембранного разделения промышленных растворов на основе фрикционной теории // Теор. Основы Хим. Техн. 2021. Т. 55. № 6. С. 754 [Shestakov K.V., Lazarev S.I., Khokhlov P.A., Polyanskii K.K. Predicting the electrochemical pressure-driven membrane separation of industrial solutions using friction theory // Theoretical Foundations of Chemical Engineering. 2021. V. 55. № 6. P. 1221.]
Байков В.И., Зновец П.К. Ультрафильтрация в плоском канале с одной проницаемой поверхностью // ИФЖ. 1999. Т. 72. № 1. С. 32. [Baikov V.I., Znovets P.K. Ultrafiltration in a Plane Channell with One Permeable Surface // Journal of engineering physics and thermophysics. 1999. V. 72. № 1. P. 32.]
Муравьев Л.Л. Моделирование работы обратноосмотических установок с рулонными фильтрующими элементами // Химия и технология воды. 1989. Т. 11. № 1. С. 107.
Абоносимов О.А., Лазарев С.И., Ковалев С.В., Рябинский М.А. К вопросу математического моделирования массопереноса в баромембранных аппаратах рулонного типа // Изв. вузов. Химия и хим. технология. 2007. Т. 50. № 8. С. 64.
Родионов Д.А., Лазарев С.И., Протасов Д.Н., Абоносимов О.А., Полянский К.К. Математическая модель процесса ультрафильтрационного концентрирования вторичного молочного сырья в трубчатом мембранных аппаратах с фильтрующими элементами типа БТУ 05/2. // Вестник Воронежского государственного университета инженерных технологий. 2021. Т. 83. № 1(87). С. 36–43.
Кругликов С.С., Архипов Е.А., Жирухин Д.А., Смирнов К.Н., Ваграмян Т.А., Колесников В.А., Филатова Е.А. Повышение эффективности электромембранных процессов на участке электрохимического кадмирования // Теор. основы хим. техн. 2021. Т. 55. № 3. С. 286 [Kruglikov S.S., Arkhipov E.A., Zhirukhin D.A., Smirnov K.N., Vagramyan T.A., Kolesnikov V.A., Filatova E.A. Increasing the efficiency of electromembrane processes in the area of electrochemical cadmium plating // Theoretical Foundations of Chemical Engineering. 2021. V. 55. № 3. P. 359].
Лазарев С.И., Ковалева О.А., Попов Р.В., Ковалев С.В., Игнатов Н.Н. Электромембранная очистка сточных вод химических производств от ионов Cr⁶⁺, Zn²⁺, ${\text{SO}}_{4}^{{2 - }}$, Сl^– // Изв. вузов. Химия и хим. технология. 2018. Т. 61. Вып. 4–5. С. 119–125.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал