Водные ресурсы, 2022, T. 49, № 2, стр. 196-203

ВВЕДЕНИЕ

Поверхностным слоем атмосферы называют тонкий слой воздуха порядка $100\;{\text{м}}$, прилегающий к подстилающей поверхности суши или водной поверхности. В ситуации, когда воздух нагревается потоком тепла, поступающим в атмосферу с нижней границы, поверхностный слой называют конвективным поверхностным слоем.

Классическая теория подобия поверхностного слоя атмосферы впервые представлена в [4, 5] для аппроксимации первых турбулентных моментов скорости и температуры. В рамках теории Монина–Обухова высота поверхностного слоя $h$ считается бесконечной, так как $h$ не входит в число определяющих параметров подобия.

Пусть $z$ – высота уровня над подстилающей поверхностью; ${{L}_{*}} < 0$ – параметр длины Монина–Обухова [6]. Введем безразмерную высоту $\xi = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}$. Тогда вертикальная протяженность конвективного поверхностного слоя определяется неравенствами $0 \leqslant \xi = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $.

Заметим, что $\left| {{{L}_{*}}} \right| = 0$ в случае отсутствия ветра и положительного потока тепла $H > 0$ на подстилающей поверхности [6]. Поэтому область $\xi \gg 1$ соответствует режиму свободной конвекции. Известно, что в области $\xi \gg 1$ теория подобия Монина–Обухова позволяет найти также турбулентные моменты более высокого порядка. В частности, аппроксимации турбулентных моментов второго порядка приведены в работах [13, 21]. Аппроксимации турбулентных моментов поверхностного слоя, соответствующие случаю $\xi = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} = \infty $, называют свободно-конвективными пределами.

В настоящей работе в конвективном поверхностном слое атмосферы выделена верхняя часть области ${{\xi }_{0}} \leqslant \xi = {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $ с фиксированной нижней границей ${{\xi }_{0}} \approx 6 \times {{10}^{{ - 2}}}$. Следуя подходу [3], для аппроксимации турбулентных моментов в области ${{\xi }_{0}} \leqslant \xi < \infty $ использованы универсальные “линейные“ формы, состоящие из двух слагаемых. Первые слагаемые “линейных“ аппроксимаций соответствуют свободно-конвективным пределам в области $\xi \gg 1$. Вторые слагаемые “линейных“ аппроксимаций получены разложением универсальных функций в ряд Тейлора по параметру ${{\xi }^{{ - 1}}}$ и включают ветер. Поэтому выделенная область ${{\xi }_{0}} \leqslant \xi < \infty $ соответствует ярусу вынужденной конвекции.

Рассмотрим семейство турбулентных моментов, в котором индекс $i~$ характеризует выбранный турбулентный момент. Предложенные линейные аппроксимации позволяют определить для вертикального профиля $i$-го турбулентного момента точку экстремума ${{\xi }_{{0i}}}$. Существование яруса вынужденной конвекции с фиксированной нижней границей означает, что экстремальные точки всех турбулентных профилей совпадают, т. е. ${{\xi }_{{0i}}} = {{\xi }_{0}}$. Заметим, что в области $0 < \xi < {{\xi }_{0}}$ “линейные“ аппроксимации моментов не соответствуют экспериментальным данным и теряют физический смысл. Поэтому экстремальную точку ${{\xi }_{0}}$ следует рассматривать как нижнюю границу яруса вынужденной конвекции.

Существование параметра ${{\xi }_{0}}$, общего для всех турбулентных профилей, значительно уменьшает количество неопределенных коэффициентов в “линейных” аппроксимациях. Можно показать, что априорное задание экстремальной точки ${{\xi }_{0}}$ позволяет вычислить все неопределенные коэффициенты “линейных“ аппроксимаций. Иными словами, понятие яруса вынужденной конвекции с фиксированной границей приводит к построению однопараметрического семейства аппроксимаций, зависящего от неопределенного параметра ${{\xi }_{0}}$. Априорное значение ${{\xi }_{0}}$ следует задавать так, чтобы реализовать условие приемлемого соответствия экспериментальным данным. Величина ${{\xi }_{0}} \approx 6 \times {{10}^{{ - 2}}}$ реализует это условие.

Аналитическое построение универсального однопараметрического семейства “линейных” аппроксимаций, соответствующих натурным измерениям вторых турбулентных моментов яруса вынужденной конвекции, является основным результатом представленной работы.

ЛОКАЛЬНЫЕ ПАРАМЕТРЫ ДИНАМИЧЕСКОЙ СКОРОСТИ, ПОТОКА ПЛАВУЧЕСТИ

Пусть $t$ – время; $x$, $y$, $z$ – декартова системы координат, расположенная на подстилающей поверхности $z = 0$, при этом ось $z$ направлена противоположено ускорению силы тяжести $~{\text{g}}$.

Допустим, что $u = u\left( {x,y,z,t} \right)$, ${v} = {v}\left( {x,y,z,t} \right)$ и $w = w\left( {x,y,z,t} \right)$ – компоненты вектора скорости вдоль осей x, y и z соответственно. Предположим, что $\bar {u} = \bar {u}\left( z \right)$ – средняя величина горизонтальной скорости вдоль оси x; ${\bar {v}} = 0$ и $\bar {w} = 0$ – средние значения горизонтальной и вертикальной скорости вдоль осей y и z соответственно. Равенство $\bar {w} = 0$ следует из уравнения неразрывности системы теории конвекции [1, 19] и условий периодичности на вертикальных границах области. Тогда $u{\kern 1pt} '\left( {x,y,z,t} \right) = u\left( {x,y,z,t} \right) - \bar {u}\left( z \right)$, ${v}{\kern 1pt} ' = {v}\left( {x,y,z,t} \right)$ и $w{\kern 1pt} ' = w\left( {x,y,z,t} \right)$ – представляют возмущения скорости вдоль осей x, y и z соответственно.

Будем считать, что $T = T\left( {x,y,z,t} \right)$ – температура воздуха; $p = p\left( {x,y,z,t} \right)$ – давление; p₀ = $ = {{10}^{5}}\,\,{\text{Па}}$ – стандартное давление воздуха на подстилающей поверхности; ${{R}_{d}}$ и ${{c}_{P}}$ – соответственно газовая постоянная и удельная теплоемкость сухого воздуха. Пусть ${{\Theta }} = T{{({p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}})}^{{ - {{{{R}_{d}}} \mathord{\left/ {\vphantom {{{{R}_{d}}} {{{c}_{P}}}}} \right. \kern-0em} {{{c}_{P}}}}}}}$ – потенциальная температура воздуха; ${{{{\Theta }}}_{0}} = {\text{const}}$ – постоянное значение средней потенциальной температуры на верхней границе поверхностного слоя [19]. Пульсацию потенциальной температуры ${{\Theta }}_{a}^{{\text{'}}}\left( {x,y,z,t} \right) = {{\Theta }}\left( {x,y,z,t} \right) - {{{{\Theta }}}_{0}}$ и безразмерную пульсацию потенциальной температуры ${{\theta }_{a}}\left( {x,y,z,t} \right)$ = ${{{{\Theta }}_{a}^{{\text{'}}}\left( {x,y,z,t} \right)} \mathord{\left/ {\vphantom {{{{\Theta }}_{a}^{{\text{'}}}\left( {x,y,z,t} \right)} {{{{{\Theta }}}_{0}}}}} \right. \kern-0em} {{{{{\Theta }}}_{0}}}}$ определим в соответствии с [19]. Эти величины близки к флуктуациям и безразмерным флуктуациям температуры $T$. Величину ${\text{g}}{{\theta }_{a}}\left( {x,y,z,t} \right)$ будем называть локальной “адиабатической” плавучестью [22].

В классической теории Монина–Обухова скорость трения ${{U}_{*}} > 0$ задана соотношением

где ${{U}_{*}}$ имеет размерность $\left[ {{{U}_{*}}} \right] = {{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$. Определение (1) согласовано с уравнением турбулентной кинетической энергии в одномерном потоке (например, [11]).

Введем параметр “адиабатического“ потока плавучести на подстилающей поверхности ${\text{g}}{{S}_{\theta }} > 0$ и параметр турбулентной плавучести ${\text{g}}{{{{\Theta }}}_{*}} < 0$, полагая, что

${\text{g}}{{S}_{\theta }}$ и ${\text{g}}{{{{\Theta }}}_{*}}$ имеют размерности $\left[ {{\text{g}}{{S}_{\theta }}} \right] = {{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{с}}}^{3}}}}} \right. \kern-0em} {{{{\text{с}}}^{3}}}}$ и $\left[ {{\text{g}}{{\Theta }_{*}}} \right] = {{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {{{{\text{с}}}^{2}}}}} \right. \kern-0em} {{{{\text{с}}}^{2}}}}$.

Пусть $H$ – средний поток тепла, поступающий в атмосферу с подстилающей поверхности; ${{\rho }_{0}}$ – средняя плотность воздуха на подстилающей поверхности; ${{T}_{*}} < 0$ – температурный параметр теории Монина–Обухова. Тогда с учетом (2) получим

Равенства (3) указывают на пропорциональность определяющих параметров ${\text{g}}{{S}_{\theta }}$ и ${\text{g}}{{{{\Theta }}}_{*}}$ традиционным параметрам теории подобия Монина–Обухова $H$ и ${{T}_{*}}$.

В работе [3] показано, что использование параметров ${\text{g}}{{S}_{\theta }}$ и ${\text{g}}{{{{\Theta }}}_{*}}$ вместо параметров $H$ и ${{T}_{*}}$ более эффективно теоретически и не влияет на обработку и использование экспериментальных данных. Поэтому далее для описания поверхностного слоя сухого воздуха теория подобия использует три базовых параметра: $z$, ${\text{g}}{{S}_{\theta }}$ и ${{U}_{*}}$. Параметр высоты $z$ – переменный, параметры потока плавучести ${\text{g}}{{S}_{\theta }}$ и динамической скорости ${{U}_{*}}$ – постоянные.

Рассмотрим поверхностный слой влажной атмосферы. Пусть $q = q\left( {x,y,z,t} \right)$ – влажность воздуха; $\bar {q} = \bar {q}\left( z \right)$ – средняя величина влажности. Следуя [5] и [18], введем также флуктуацию влажности: $q{\kern 1pt} '\left( {x,y,z,t} \right) = q\left( {x,y,z,t} \right) - \bar {q}\left( z \right)$.

Опираясь на аналогию с соотношениями (1), (2), введем параметр модифицированного потока влажности на подстилающей поверхности ${\text{g}}{{S}_{q}}$ и модифицированный параметр влажности ${\text{g}}{{q}_{*}}$. Тогда получим:

Здесь ${\text{g}}{{S}_{q}}$ и ${\text{g}}{{q}_{*}}$ имеют размерности $\left[ {{\text{g}}{{S}_{q}}} \right] = {{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{с}}}^{3}}}}} \right. \kern-0em} {{{{\text{с}}}^{3}}}}$ и $\left[ {{\text{g}}{{q}_{*}}} \right] = {{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {{{{\text{с}}}^{2}}}}} \right. \kern-0em} {{{{\text{с}}}^{2}}}}$.

Из определения (4) следует, что безразмерный параметр ${{q}_{*}}$ идентичен параметру влажности классической теории подобия Монина–Обухова, определенному, например, согласно [18].

Параметры ${\text{g}}{{S}_{\theta }} > 0$, ${\text{g}}{{S}_{q}} \geqslant 0$ и ${{U}_{*}} > 0$ позволяют ввести постоянный параметр длины для влажной атмосферы $L_{*}^{{v}} < 0$. Тогда, следуя, например, [10] и [18], получим

${{k}_{{v}}} = 0.4$ – постоянная Кармана.

Далее будет использовано приближение малого модифицированного потока влажности $0 \leqslant {\text{g}}{{S}_{q}} \ll 1.64 \times {\text{g}}{{S}_{\theta }}$. Это приближение справедливо:

а) над достаточно сухими участками суши с интенсивным конвективным потоком тепла и малым испарением;

б) над водными поверхностями в условиях, когда поток плавучести определяется в основном испарением.

В самом деле, пусть ${{L}_{W}} = 2260$ кДж/кг – удельная теплота испарения воды, ${{c}_{p}} = 1.005 \times $ × 10³ Дж/(кг К) – удельная теплоемкость сухого воздуха, ${{\Theta }_{0}} \approx 300\,{\text{K}}$ – среднее значение потенциальной температуры, тогда ${{{{L}_{W}}} \mathord{\left/ {\vphantom {{{{L}_{W}}} {\left( {{{c}_{P}}{{\Theta }_{0}}} \right)}}} \right. \kern-0em} {\left( {{{c}_{P}}{{\Theta }_{0}}} \right)}} \approx 7.5$. Поэтому можно считать, что $0 \leqslant {\text{g}}{{S}_{q}} \ll $ $ \ll {{1.64~{{L}_{W}}} \mathord{\left/ {\vphantom {{1.64~{{L}_{W}}} {\left( {{{c}_{P}}{{{{\Theta }}}_{0}}} \right){\text{g}}{{S}_{q}}}}} \right. \kern-0em} {\left( {{{c}_{P}}{{{{\Theta }}}_{0}}} \right){\text{g}}{{S}_{q}}}} \approx 1.64{\text{\;g}}{{S}_{\theta }}$. Полученное неравенство доказывает справедливость сделанного предположения.

В приближении $0 \leqslant {\text{g}}{{S}_{q}} \ll 1.64~{\text{g}}{{S}_{\theta }}$ модифицированный поток влажности ${\text{g}}{{S}_{q}}$ не входит в определение параметра длины (5), так что $L_{*}^{{v}} = {{L}_{*}}$, где

Соотношение (6) определяет классический параметр длины Монина–Обухова ${{L}_{*}}$ для сухой атмосферы.

Тем не менее приближение (6) для описания турбулентности влажной атмосферы использовано, например, в работе [9].

Приложение теории подобия для описания конвективного поверхностного слоя влажного воздуха предполагает использование четырех базовых параметров: $z$, ${\text{g}}{{S}_{\theta }}$, ${\text{g}}{{S}_{q}}$ и ${{U}_{*}}$. Параметр высоты $z$ – переменный, параметры потоков плавучести и влажности ${\text{g}}{{S}_{\theta }}$, ${\text{g}}{{S}_{q}}$, а также параметр динамической скорости ${{U}_{*}}$ – постоянные.

Существенно, что в приближении $0 \leqslant {\text{g}}{{S}_{q}} \ll $ $ \ll 1.64{\text{g}}{{S}_{\theta }}$ поток влажности ${\text{g}}{{S}_{q}}$ как базовый параметр подобия не влияет на вычисление турбулентных моментов, существующих в сухой атмосфере при ${\text{g}}{{S}_{q}} = 0$, и должен быть учтен только при вычислении турбулентных моментов влажности $q$.

ТЕОРИЯ ПОДОБИЯ МОНИНА–ОБУХОВА И СВОБОДНО-КОНВЕКТИВНЫЕ ПРЕДЕЛЫ ПОВЕРХНОСТНОГО СЛОЯ

Рассмотрим конвективный поверхностный слой сухой атмосферы в условиях свободной конвекции ${\text{g}}{{S}_{\theta }} > 0$, ${{U}_{*}} = 0$. В этом случае существуют только два определяющих параметра – ${\text{g}}{{S}_{\theta }}$ и $z$.

В соответствии с [21] выражения для вторых моментов вертикальной скорости и плавучести имеют следующий вид:

где ${{\lambda }_{{ww}}}$ и ${{\lambda }_{{\theta \theta }}}$ – постоянные коэффициенты.

Над поверхностью суши со слабой растительностью и водной поверхностью будем использовать коэффициенты ${{\lambda }_{{ww}}} = 1.8$ и ${{\lambda }_{{\theta \theta }}} = 1.8$. Эти значения получены по данным измерений как над прериями Миннесоты [14], так и над Восточно-Китайским морем [16].

Построение соотношений (7) с использованием статистической модели ансамбля спонтанных конвективных струй приведено в работах [2, 23, 24].

Рассмотрим конвективный поверхностный слой сухой атмосферы в условиях слабого ветра: $0 \ne {{U}_{*}} \ll 1$. В этом случае существуют базовые параметры $z$, ${\text{g}}{{S}_{\theta }}$ и ${{U}_{*}}$.

Для построения свободно конвективных пределов теории Монина–Обухова будем считать, что моменты вертикальной скорости и плавучести в условиях слабого ветра – $0 \ne {{U}_{*}} \ll 1$ – такие же, как и при его отсутствии – ${{U}_{*}} = 0$.

Пусть ${{\sigma }_{w}}$, ${{\sigma }_{\theta }}$ – дисперсии вертикальной скорости и флуктуации потенциальной температуры. Тогда преобразование (7) с учетом (2), (6) приводит к равенствам

Здесь $\alpha _{{ww}}^{2} = k_{{v}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}{{\lambda }_{{ww}}}$, $\alpha _{{\theta \theta }}^{2} = k_{{v}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}{{\lambda }_{{\theta \theta }}}$ – положительные постоянные [25].

Над поверхностью суши со слабой растительностью и водной поверхностью ${{\lambda }_{{ww}}} = 1.8$, ${{\lambda }_{{\theta \theta }}} = 1.8$ и ${{k}_{{v}}} = 0.4$, поэтому значения постоянных составляют ${{\alpha }_{{ww}}} = 1.82$ и ${{\alpha }_{{\theta \theta }}} = 0.99$, независимо от типа подстилающей поверхности.

Рассмотрим конвективный поверхностный слой влажной атмосферы. В этом случае существуют базовые параметры $z$, ${\text{g}}{{S}_{\theta }}$, ${\text{g}}{{S}_{q}}~$и ${{U}_{*}}$. Очевидно, что в приближении $0 \leqslant {\text{g}}{{S}_{q}} \ll 1.64 \times {\text{g}}{{S}_{\theta }}$ соотношения для моментов (7), (8) справедливы и в условиях влажного воздуха.

Известно, что перенос влажности и перенос потенциальной температуры подчиняются одному и тому же динамическому уравнению. Это обстоятельство приводит к предположению подобия профилей моментов потенциальной температуры и влажности [8]. Тогда для второго турбулентного момента флуктуации влажности справедливо соотношение, аналогичное аппроксимации момента плавучести (8):

Здесь ${{\sigma }_{q}}$ – дисперсия флуктуации влажности; ${{\alpha }_{{qq}}} \approx {{\alpha }_{{\theta \theta }}}~$ – положительная постоянная.

Зависимости (8), (9) представляют свободно-конвективные пределы вертикальной скорости, плавучести и влажности. Будем считать далее, что над водной поверхностью и поверхностью суши со слабой растительностью значения постоянных параметров в асимптотических соотношениях (8), (9) составляют ${{\alpha }_{{ww}}} = 1.8$, ${{\alpha }_{{\theta \theta }}} = 1.0$ и ${{\alpha }_{{qq}}} = 1.2$.

ЛИНЕЙНЫЕ АППРОКСИМАЦИИ ВТОРЫХ ТУРБУЛЕНТНЫХ МОМЕНТОВ СКОРОСТИ, ФЛУКТУАЦИИ ТЕМПЕРАТУРЫ И ФЛУКТУАЦИИ ВЛАЖНОСТИ В ЯРУСЕ ВЫНУЖДЕННОЙ КОНВЕКЦИИ

Рассмотрим универсальные функции турбулентных моментов в подслое вынужденной конвекции: ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $, ${{\xi }_{0}} \approx 6 \times {{10}^{{ - 2}}}.$

Без ограничения общности можно считать, что уравнения для вторых моментов вертикальной скорости, ”адиабатической” плавучести и влажности в слое вынужденной конвекции ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {{{L}_{*}}}}} \right. \kern-0em} {{{L}_{*}}}} < \infty $, ${{\xi }_{0}} \approx 6 \times {{10}^{{ - 2}}}$ могут быть записаны в форме

Здесь $F_{{ww}}^{2}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$, $F_{{\theta \theta }}^{2}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$, $F_{{qq}}^{2}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$ – гладкие функции; $\alpha _{{ww}}^{2}$, $\alpha _{{\theta \theta }}^{2}$, $\alpha _{{qq}}^{2}$ – постоянные коэффициенты.

Следуя [3], будем раскладывать функции ${{F}_{{ww}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$, ${{F}_{{\theta \theta }}}\left( {{z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}}} \right)$ и ${{F}_{{qq}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$ в ряд Тейлора по параметру ${{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}^{{ - 1}}}$. Ограничимся линейным разложением Тейлора функций ${{F}_{{ww}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$, ${{F}_{{\theta \theta }}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$, ${{F}_{{qq}}}({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})$ по параметру ${{({z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}})}^{{ - 1}}}$. Тогда дисперсии ${{\sigma }_{w}}$, ${{\sigma }_{\theta }}$ и ${{\sigma }_{q}}$ примут форму

Безразмерные параметры ${{\zeta }_{{ww}}}$, ${{\zeta }_{{\theta \theta }}}$ и ${{\zeta }_{{qq}}}$ обозначают границы яруса вынужденной конвекции для профилей вертикальной скорости, флуктуаций потенциальной температуры и флуктуаций влажности. Безразмерные параметры ${{\alpha }_{{ww}}} > 0$, ${{\alpha }_{{\theta \theta }}} > 0$ и ${{\alpha }_{{qq}}} > 0$ соответствуют предельным значениям при свободной конвекции и считаются известными. Безразмерные параметры ${{\beta }_{{ww}}} > 0$, ${{\beta }_{{\theta \theta }}} > 0$ и ${{\beta }_{{qq}}} > 0$ характеризуют линейные разложения и являются неопределенными.

Существование яруса вынужденной конвекции с фиксированной границей ${{\zeta }_{0}}$, соответствующей точке экстремума профилей, приводит к соотношениям

При априорно заданном параметре ${{\zeta }_{0}}$ уравнения системы (12) позволяют вычислить коэффициенты ${{\zeta }_{{ww}}}$, ${{\zeta }_{{\theta \theta }}}$, ${{\zeta }_{{qq}}}$ и ${{\beta }_{{ww}}}$, ${{\beta }_{{\theta \theta }}}$, ${{\beta }_{{qq}}}$. Поэтому аппроксимации (11), (12) образуют однопараметрическое семейство аналитических аппроксимаций, зависящее от ${{\zeta }_{0}}$.

Далее над поверхностью суши со слабой растительностью и над водной поверхностью будем использовать следующие коэффициенты: ${{\alpha }_{{ww}}} = 1.8$, ${{\beta }_{{ww}}} = 0.03$; ${{\alpha }_{{\theta \theta }}} = 0.97$, ${{\beta }_{{\theta \theta }}} = 0.016$ и ${{\alpha }_{{qq}}} = 1.2$, ${{\beta }_{{qq}}} = 0.016$.

СОПОСТАВЛЕНИЕ “ЛИНЕЙНЫХ” АППРОКСИМАЦИЙ ДИСПЕРСИЙ ВЕРТИКАЛЬНОЙ СКОРОСТИ, ПЛАВУЧЕСТИ И ВЛАЖНОСТИ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

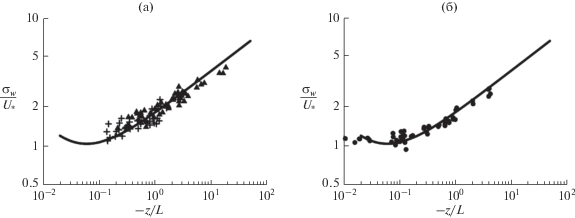
Сопоставление “линейной“ аппроксимации дисперсии вертикальной скорости (11) с параметрами ${{\alpha }_{{ww}}} = 1.8$, ${{\beta }_{{ww}}} = 0.03$ и данных измерений над океаном [12, 15] в области ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $, ${{\zeta }_{0}} = 6 \times {{10}^{{ - 2}}}$ представлено на рис. 1a. Сопоставление “линейной” аппроксимации дисперсии вертикальной скорости (11) с параметрами ${{\alpha }_{{ww}}} = 1.8$, ${{\beta }_{{ww}}} = 0.03$ и данных измерений над сушей [7] в области ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $, ${{\zeta }_{0}} = 6 \times {{10}^{{ - 2}}}$ представлено на рис. 1б.

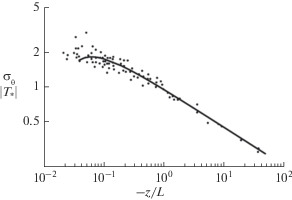
Сопоставление линейной аппроксимации безразмерной дисперсии пульсации потенциальной температуры ${{{{\sigma }_{\theta }}} \mathord{\left/ {\vphantom {{{{\sigma }_{\theta }}} {{{T}_{*}}}}} \right. \kern-0em} {{{T}_{*}}}}$ в форме (11) при $\alpha _{{\theta \theta }}^{2} = 0.95$, ${{\beta }_{{\theta \theta }}} = 0.016$ с натурными данными [17] представлено на рис. 2.

Сопоставление “линейной” аппроксимации дисперсии флуктуации влажности (11) с параметрами ${{\alpha }_{{qq}}} = 1.2$, ${{\beta }_{{qq}}} = 0.016$ и данных измерений над океаном [12, 15] в области ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $ представлено на рис. 3a. Сопоставление “линейной” аппроксимации дисперсии флуктуации влажности (11) с параметрами ${{\alpha }_{{qq}}} = 1.2$, ${{\beta }_{{qq}}} = 0.016$ и данных измерений над сушей [17, 20] в области ${{\zeta }_{0}} < {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $, ${{\zeta }_{0}} = 6 \times {{10}^{{ - 2}}}~$ показано на рис. 3б.

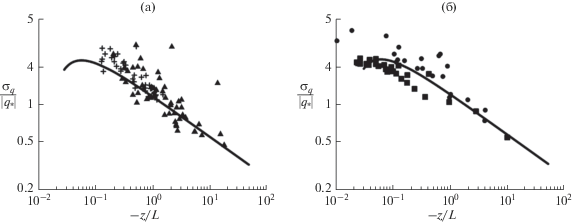
Результаты сравнения, представленные на рис. 1–3, указывают на существование мощного яруса вынужденной конвекции в области ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $, ${{\zeta }_{0}} = 6 \times {{10}^{{ - 2}}}$.

“ЛИНЕЙНАЯ“ АППРОКСИМАЦИЯ ВТОРОГО ТУРБУЛЕНТНОГО МОМЕНТА ФЛУКТУАЦИИ КОНЦЕНТРАЦИИ НЕЙТРАЛЬНОГО ГАЗА В ЯРУСЕ ВЫНУЖДЕННОЙ КОНВЕКЦИИ

Допустим, что с подстилающей поверхности в поверхностный слой атмосферы равномерно поступает некоторый нейтральный газ, не вступающий в химические реакции с воздухом, например углекислый газ.

Опираясь на аналогию с соотношениями (4), введем параметр модифицированного потока концентрации на подстилающей поверхности ${\text{g}}{{S}_{c}}$ и модифицированный параметр концентрации ${\text{g}}{{c}_{*}}$. Тогда получим

Здесь ${\text{g}}{{S}_{c}}$ и ${\text{g}}{{c}_{*}}$ имеют размерности $\left[ {{\text{g}}{{S}_{c}}} \right] = {{{{{\text{м}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{2}}} {{{{\text{с}}}^{3}}}}} \right. \kern-0em} {{{{\text{с}}}^{3}}}}$ и $\left[ {{\text{g}}{{c}_{*}}} \right] = {{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {{{{\text{с}}}^{2}}}}} \right. \kern-0em} {{{{\text{с}}}^{2}}}}$.

Пусть ${{\sigma }_{c}}$ – дисперсия флуктуации концентрации нейтрального газа, тогда по аналогии с (11) получим

Неопределенный безразмерный параметр ${{\zeta }_{{cc}}}$ означает границу яруса вынужденной конвекции для профиля флуктуации концентрации углекислого газа. Безразмерный параметр ${{\alpha }_{{сс}}} > 0$ характеризует свободно конвективный предел и считается известным. Неопределенный безразмерный параметр ${{\beta }_{{cc}}} > 0$ характеризует линейное разложение. Значения коэффициентов ${{\zeta }_{{cc}}}$ и ${{\beta }_{{cc}}}$ могут быть вычислены на основе (12), откуда следует, что ${{\zeta }_{{cc}}} = {{\zeta }_{0}}$ и ${{\beta }_{{cc}}} = {{\beta }_{{\theta \theta }}} = {{\beta }_{{qq}}}$.

Сравним ”линейную” аппроксимацию для дисперсии флуктуации концентрации углекислого газа (14) с известными данными наблюдений. Сопоставление (14) с параметрами ${{\alpha }_{{cc}}} = {{\alpha }_{{qq}}} = 1.2$, ${{\beta }_{{cc}}} = {{\beta }_{{qq}}} = 0.016$ и данных измерений [20] в области ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $, ${{\zeta }_{0}} = 6 \times {{10}^{{ - 2}}}$ представлено на рис. 4.

Результаты сравнения, представленные на рис. 4, указывают на существование мощного яруса вынужденной конвекции в области ${{\zeta }_{0}} \leqslant {z \mathord{\left/ {\vphantom {z {\left| {{{L}_{*}}} \right|}}} \right. \kern-0em} {\left| {{{L}_{*}}} \right|}} < \infty $, ${{\zeta }_{0}} = 6 \times {{10}^{{ - 2}}}$. Очевидно, что аппроксимация (14) дополняет однопараметрическое семейство аппроксимаций (11), (12).

ЗАКЛЮЧЕНИЕ

Анализ экспериментальных данных [12, 15, 17] показывает, что в конвективном поверхностном слое (как над морем, так и над сушей) существует мощный ярус вынужденной конвекции с фиксированной нижней границей.

Сопоставление аппроксимаций с данными наблюдений показывает, что ”линейные” аппроксимации (11), (12), (14) убедительно соответствуют известным экспериментальным данным о дисперсиях вертикальной скорости, флуктуаций потенциальной температуры, влажности и концентрации углекислого газа.

Ярус вынужденной конвекции может быть выделен в наблюдаемых профилях вторых турбулентных моментов вертикальной скорости, флуктуации потенциальной температуры, влажности и концентрации углекислого газа.

Профили дисперсий флуктуаций потенциальной температуры, влажности и концентрации углекислого газа являются подобными.

Граница яруса вынужденной конвекции ${{\zeta }_{0}}$ не зависит от выбора турбулентного момента и является одной и той же для моментов вертикальной скорости, флуктуации потенциальной температуры, влажности и концентрации углекислого газа. Кроме того, величина ${{\zeta }_{0}}$ не зависит от выбора подстилающей поверхности, и она одна и та же как над сушей, так и над водной поверхностью.