Журнал вычислительной математики и математической физики, 2019, T. 59, № 2, стр. 301-312

1. ВВЕДЕНИЕ

В ряде работ (см. [1]–[4]) было показано, что так называемые геометрические потоки дают определенную информацию о строении многообразия. Кроме потоков, учитывающих внутреннюю геометрию многообразия (см. [5]–[7]) (Риччи, Калаби-Яу), также интерес представляют потоки, определенные внешней геометрией, например, учитывающие кривизну вложения многообразия в евклидово пространство (см. [8], [9]). Простейшим из таковых является поток средней кривизны. Дадим необходимые определения.

Пусть ${{M}^{n}}$ – замкнутое многообразие размерности $n\; \geqslant \;1$. Потоком средней кривизны называется семейство вложений ${{f}_{t}}:{{M}^{n}} \to {{\mathbb{R}}^{{n + 1}}}$, гладко зависящее от $t$, которое удовлетворяет уравнению

где $\bar {x}$ – точка многообразия, ${\mathbf{n}}(\bar {x},t)$ и $H(\bar {x},t)$ – нормаль к вложению и средняя кривизна поверхности ${{M}^{n}}$ относительно вложения ${{f}_{t}}$ в точке $f(\bar {x},t)$ соответственно; здесь $f(\bar {x},t) = {{f}_{t}}(\bar {x})$. Отображения ${{f}_{t}}$ задают семейство вложенных многообразий ${{M}_{t}} \subset {{\mathbb{R}}^{{n + 1}}}$.

Уравнение (1) можно переписать в виде

где ${{\Delta }_{{LB}}}(t)$ – оператор Лапласа–Бельтрами, вычисленный в индуцированной вложением ${{f}_{t}}$ метрике на $M_{t}^{n}$. С геометрической точки зрения поток средней кривизны стремится “стянуть” выпуклые области $M_{t}^{n}$, причем скорость стягивания тем выше, чем больше значение средней кривизны ${{H}_{t}}(\bar {x})$. Это наглядное свойство является общим для потока Риччи и для потока средней кривизны.

Помимо семейства вложений ${{f}_{t}}(\bar {x})$, удовлетворяющего уравнению (2), удобно рассматривать так называемый нормализованный поток средней кривизны ${{\tilde {f}}_{t}}(\bar {x})$. Оба семейства определены при $t \in [0,T)$ и пропорциональны друг другу с коэффициентом $\psi (t)$

таким, что объемы многообразий, заданных семейством вложений ${{\tilde {f}}_{t}}(\bar {x})$, равны объему многообразия $M_{0}^{n}$ для всех $t$.

Выберем новый параметр времени $\tilde {t}(t) = \int_0^t \,{{\psi }^{2}}(\tau )d\tau $; тогда можно показать, что ${{\tilde {f}}_{{\tilde {t}}}}$ удовлетворяет уравнению

где

есть усредненное значение квадрата средней кривизны для ${{\tilde {M}}_{{\tilde {t}}}}$.

Теорема 1 (см. [4]). Пусть ${{f}_{0}}$ – вложение гладкого замкнутого многообразия ${{M}^{n}}$ в ${{\mathbb{R}}^{{n + 1}}}$. Пусть известно, что собственные значения второй квадратичной формы подмногообразия $M_{0}^{n}$ строго больше нуля для всех $\bar {x} \in M_{0}^{n}$. Тогда уравнение (2) с начальным условием $f(\bar {x},0) = {{f}_{0}}(\bar {x})$ имеет гладкое решение на конечном интервале времени $0\;\leqslant \;t < T$, стягивая поверхность $M_{t}^{n}$ в некоторую точку $O$ при $t \to T$. При этом уравнение (3) с начальным условием $\tilde {f}(\bar {x},0) = {{\tilde {f}}_{0}}(\bar {x})$ имеет гладкое решение при $\tilde {t} \to \infty $, при этом ${{\tilde {M}}_{{\tilde {t}}}}$ стремится принять форму сферы площади $\left| {{{M}_{0}}} \right|$. Подмногообразие ${{\tilde {M}}_{{\tilde {t}}}}$ получается из ${{M}_{t}}$ гомотетией с центром в точке $O$.

В этой работе мы приводим новый алгоритм численного решения уравнения потока средней кривизны для поверхности вращения. Он позволяет визуализировать два качественно различных сценария поведения потока средней кривизны в зависимости от начального вложения $\mathop {\tilde {f}}\nolimits_0 $. В первом случае для начального вложения $\mathop {\tilde {f}}\nolimits_0 $ со строго положительными главными кривизнами применима теорема 1, так что под действием потока средней кривизны поверхность деформируется в сферу. С другой стороны, среди вложений, не удовлетворяющих условиям теоремы 1, есть примеры, в которых предельное многообразие существует, более того, как и в первом случае, является сферой, и есть примеры, в которых под действием потока средней кривизны на конечное время развивается особенность [10].

2. ДИСКРЕТИЗАЦИЯ ПОТОКА СРЕДНЕЙ КРИВИЗНЫ

Будем строить дискретный аналог уравнения (2) для $M = {{S}^{2}}$ методом конечных элементов (см. [11]). Зададим базисные функции ${{L}_{i}},i = 1,2,...,N,$ на вершинах триангуляции, где $N$ – их количество, следующим образом:

Кроме того, потребуем, чтобы все ${{L}_{i}}$ были линейны на каждом двумерном симплексе. Уравнение (2) будем решать в слабом смысле. Это значит, что мы ищем функцию ${{f}_{t}}(x)$ такую, что для любой функции ${{g}_{t}}(x)$ выполняется условие Перепишем (7) в виде

Заменим функции ${{f}_{t}}(x)$, ${{g}_{t}}(x)$ их дискретными аналогами:

где ${{f}_{i}}(t)$, ${{g}_{i}}(t)$ – значения функций $f$ и $g$ в $i$-й вершине триангуляции соответственно. Подставляя эти выражения в уравнение (8), получаем откуда

Дискретизация данного уравнения по времени имеет вид

здесь и далее по тексту $n$ – номер шага по времени. Рассмотрим матрицы ${{A}^{n}} = \left( {\left\langle {{{L}_{i}},{{L}_{j}}} \right\rangle } \right)_{{i,j = 1}}^{N}$, ${{B}^{n}} = \left( {\left\langle {\nabla {{L}_{i}},\nabla {{L}_{j}}} \right\rangle } \right)_{{i,j = 1}}^{N}$, а также вектор-столбцы ${{F}^{{n - 1}}} = (f_{i}^{{n - 1}})_{{i = 1}}^{N}$, ${{F}^{n}} = (f_{i}^{n})_{{i = 1}}^{N}$. Тогда уравнение (11) можно переписать в виде откуда

Элементы матрицы ${{A}^{n}}$ вычисляются в явном виде:

Здесь $\left| \Delta \right|$ – площадь грани $\Delta $, причем ${{\Delta }_{1}}$, ${{\Delta }_{2}}$ – грани, смежные по ребру, соединяющему вершины ${{v}_{i}}$, ${{v}_{j}}$, а ${{\Delta }_{k}}$ пробегает набор граней, имеющих ${{v}_{i}} = {{v}_{j}}$ вершиной. Элементы матрицы ${{B}^{n}}$ тоже могут быть вычислены явно: где ${{\gamma }_{{i,qp}}}$ – угол при вершине ${{v}_{i}}$ грани ${{\Delta }_{{iqp}}}$, а ${{l}_{{pq}}}$ – длина ребра, соединяющего вершины ${{v}_{p}}$ и ${{v}_{q}}$.

Явная схема, заданная соотношением (13), неустойчива, и поэтому предпочтительнее воспользоваться неявной схемой

где ${{C}^{n}} = {{A}^{n}} - \tau \sigma {{B}^{n}}$.

Как и в случае непрерывного времени удобно вместо (16) рассматривать нормализованное уравнение. Определим дискретный аналог ${{\xi }_{n}}$ коэффициента $\psi (t)$ соотношением

где $S_{\Delta }^{n}$ и $S_{\Delta }^{{n - 1}}$ – площади триангулированной поверхности в текущий и предыдущий моменты времени, и нормализуем уравнение (16):

С учетом нормировочного коэффициента общая площадь триангулированной поверхности под действием потока (18) не меняется.

3. ЗАМКНУТАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ

Зададим хорошую с комбинаторной точки зрения триангуляцию сферы, такая триангуляция легко строится, измельчается и кодируется. Рассмотрим единичную сферу и вписанный в нее правильный икосаэдр. Выберем декартовы координаты так, чтобы ось $Oz$ проходила через две вершины икосаэдра, будем называть их полюсами: $(0,0, - 1)$ – южный, $(0,0,1)$ – северный. Шаг измельчения состоит в следующем: в каждой грани проведем средние линии. Проделаем нужное количество шагов, и обозначим через $V = \{ {{v}_{1}},{{v}_{2}},\;...,\;{{v}_{N}}\} $ множество всех вершин триангуляции, $E = \{ {{l}_{{ij}}}{\text{|}}{{v}_{i}}{{v}_{j}} - {\text{р е б р о }}\} $ – множество всех ее ребер , а 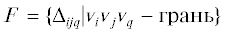– множество граней. Заметим, что после $k$-го шага измельчения икосаэдра количество вершин, ребер, граней триангуляции равно $\left| V \right| = 2 + 10 \times {{2}^{{2k}}}$, $\left| E \right| = 30 \times {{4}^{k}}$, $\left| F \right| = 20 \times {{2}^{{2k}}}$ соответственно. Назовем уровнем вершины триангуляции наименьшее количество звеньев ломаной, составленной из ребер триангуляции и соединяющей вершину с южным полюсом. Тогда уровни вершин принимают значения от $0$ до $3 \times {{2}^{k}}$, где $k$ – количество шагов измельчения исходной икосаэдральной сетки. Рассмотрим любую трехзвенную ломаную, составленную из ребер исходного икосаэдра, которая соединяет его северный и южный полюса. После нужного числа шагов разбиения такая ломаная будет состоять из $3 \times {{2}^{k}}$ звеньев и будет содержать в точности по одной вершине каждого уровня. Будем называть такие ломаные характеристическими.

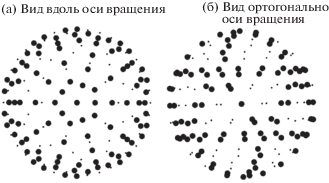
Теперь опишем триангуляцию исходной поверхности вращения на примере сферы. Вершины одного уровня измельченного икосаэдра лежат в одной плоскости, ортогональной общей оси $Oz$. Спроецировав их вдоль лучей, лежащих в плоскости данного набора на окружность радиуса $1{\text{/}}\sqrt {1 - z_{i}^{2}} $ с центром на оси $Oz$, мы получим вершины на поверхности сферы. Иными словами, вершины измельченного икосаэдра $({{x}_{i}},{{y}_{i}},{{z}_{i}})$ дают на сфере точки с координатами (см. фиг. 1)

Для поверхности вращения заданной профильной функцией $\beta (z),\beta ( - 1) = \beta (1) = 0$, $ - 1\;\leqslant \;z\;\leqslant \;1$, $\beta (z) > 0$ при $z \ne \pm 1$, поступим следующим образом: вершине измельченного икосаэдра $({{x}_{i}},{{y}_{i}},{{z}_{i}})$ ставим в соответствие вершину на поверхности вращения

Комбинаторика триангуляции остается прежней. В общем случае, когда профильная функция $\beta (z)$ поверхности вращения определена на некотором отрезке $[a,b]$, ее триангуляция подходящими сдвигом и растяжением сводится к вышеописанной.

4. ПЕРЕРАСПРЕДЕЛЕНИЕ ВЕРШИН ТРИАНГУЛИРОВАННОЙ ПОВЕРХНОСТИ ВРАЩЕНИЯ

Из геометрических соображений следует, что длины ребер нашей триангулированной поверхности под действием потока средней кривизны изменяются быстрее вблизи вершин, в которых больше абсолютное значение средней кривизны. В результате этого вершины триангулированной поверхности вращения, которая в “полярной шапочке” имеет локальный максимум кривизны, скапливаются у ее оси. В качестве примера на фиг. 2 показана эволюция триангулированного эллипсоида вращения с начальным значением полуосей $a = b = 1$, $c = 3$ под действием дискретного (для $\sigma = 1{\text{/}}2$) потока средней кривизны (17). Видно, что вершины триангуляции скапливаются к полюсам, что в конечном итоге приводит к неустойчивости разностной схемы. Более того, эволюция триангулированной сферы единичного радиуса под действием потока средней кривизны, показанная на фиг. 3, демонстрирует неустойчивость схемы даже в случае, когда кривизна исходной поверхности постоянна.

Явный вид элементов матриц ${{A}^{n}}$ и ${{B}^{n}}$ (см. формулы (14), (15)) показывает, что элементы этих матриц определяются значениями углов при вершинах триангуляции и длинами ее ребер. Если в процессе эволюции отношение максимальной площади грани триангуляции к минимальной стремится к бесконечности, то число обусловленности матрицы C_n неограниченно возрастает и поэтому схема (18) оказывается неустойчивой (типичное поведение потока показано на фиг. 2). Чтобы сохранить число обусловленности вблизи $1$, мы воспользуемся следующей идеей, происходящей из геометрии и комбинаторики рассматриваемой триангуляции. Идея состоит в перераспределении вершин триангуляции по поверхности так, чтобы уровни вершин не менялись и звенья характеристической ломаной имели одинаковую длину.

Алгоритм перераспределения вершин триангулированной поверхности использует следующие векторы:

${{R}^{n}}$ – состоит из расстояний от вершин триангулированной поверхности ${{v}_{i}}$ до оси вращения, $\{ r_{i}^{n} \in {{R}^{n}}\,{\text{|}}\,r_{i}^{n} = \sqrt {{{{(x_{i}^{n})}}^{2}} + {{{(y_{i}^{n})}}^{2}}} ;\;1\;\leqslant \;i\;\leqslant \;N\} $;

${{H}^{n}}$ – состоит из значений проекции вершин триангулированной поверхности на ось вращения, $\{ h_{i}^{n} \in {{H}^{n}}\,{\text{|}}\,h_{i}^{n} = z_{i}^{n};\;1\;\leqslant \;i\;\leqslant \;N\} $;

${{\Phi }^{n}}$ – состоит из значений полярных углов при вершинах триангулированной поверхности и определяется соотношениями: $\{ x_{i}^{n} = r_{i}^{n}cos\phi _{i}^{n},\;y_{i}^{n} = r_{i}^{n}cos\phi _{i}^{n};\;1\;\leqslant \;i\;\leqslant \;N\} $.

Кроме того, вспомогательный вектор $P = \{ {{p}_{{i(m)}}}{\text{|}}{{p}_{{i(m)}}} = i(m){\text{/}}(3 \times {{2}^{k}}),\;0\;\leqslant \;m\;\leqslant \;3 \times {{2}^{k}}\} $ нужен в качестве параметризации вектора $L_{0}^{n}$. Также используется вектор расстояний вдоль характеристической ломаной от ее вершин до южного полюса: $L_{0}^{n} = \left\{ {l_{j}^{n}\,{\text{|}}\,l_{j}^{n} = \sum\nolimits_{m = 1}^j \,d_{m}^{n};\;j = [0;3 \times {{2}^{k}}]} \right\}$, где $d_{m}^{n} = \sqrt {{{{(\Delta x_{{i(m)}}^{n})}}^{2}} + {{{(\Delta y_{{i(m)}}^{n})}}^{2}} + {{{(\Delta z_{{i(m)}}^{n})}}^{2}}} $ – расстояние между $m$-й и $(m - 1)$-й вершинами характеристической ломаной $(m = 1,...,3 \times {{2}^{k}})$, а $i(m)$ – номер вершины уровня $m$ характеристической ломаной в списке всех вершин триангуляции, полагаем $l_{0}^{n} = 0$, ${{\hat {L}}^{n}} = \left\{ {\hat {l}_{m}^{n} = \tfrac{m}{{3 \times {{2}^{k}}}}l_{{3 \cdot {{2}^{k}}}}^{n};\;m = 0,\;...,\;3 \times {{2}^{k}}} \right\}$.

${{\Lambda }^{n}}$ – вектор, содержащий изменения полярных углов вершин характеристической ломаной за один шаг по времени, $\{ \lambda _{{i(m)}}^{n} \in {{\Lambda }^{n}}\,{\text{|}}\,\lambda _{{i(m)}}^{n} = \phi _{{i(m)}}^{n} - \phi _{{i(m)}}^{{n - 1}},0\;\leqslant \;m\;\leqslant \;3 \times {{2}^{k}})\} $.

С помощью сплайновой аппроксимации вычислим вектор ${{\hat {P}}^{n}}$ такой, что соответствия $P \to L_{0}^{n}$ и ${{\hat {P}}^{n}} \to {{\hat {L}}^{n}}$ задают одну функцию, затем с помощью сплайновой аппроксимации, вычисляя новые векторы ${{\hat {R}}^{n}}$ и ${{\hat {H}}^{n}}$, как значения функций ${{\hat {P}}^{n}} \to {{\hat {R}}^{n}}$, ${{\hat {P}}^{n}} \to {{\hat {H}}^{n}}$ в точках вектора ${{\hat {P}}^{n}}$ соответственно. Результатом перераспределения служат точки с координатами ${{\hat {x}}_{i}} = {{\hat {r}}_{i}}cos\phi _{i}^{n}$; ${{\hat {y}}_{i}} = {{r}_{i}}sin\phi _{i}^{n}$; ${{z}_{i}} = {{\hat {h}}_{i}}$.

Общий алгоритм описывается следующим образом.

Aлгоритм

Шаг 1. Определить и создать глобальные данные: векторы ${{\Phi }^{n}},\;{{R}^{n}},\;{{H}^{n}}$.

Шаг 2. Проделать итерацию метода конечных элементов.

Шаг 3. Создать локальный вектор ${{\Lambda }^{n}}$, элементы которого содержат угол поворота вершин характеристической ломаной в горизонтальной плоскости.

Шаг 4. Перераспределить вершины характеристической ломаной равномерно по ее длине и определить координаты ее вершин.

Шаг 5. Определить координаты вершин множества $V$ триангулированной поверхности для каждого набора вершин одного уровня с учетом поворота вершин характеристической ломаной в горизонтальной плоскости.

5. ПРИМЕРЫ

Представленные в работе вычисления выполнены на персональном компьютере с процессором i5 2,4 GHz. Код программы написан на языке программирования “C++11”, с использованием библиотеки “Eigen”(eigen.tuxfamily.org).

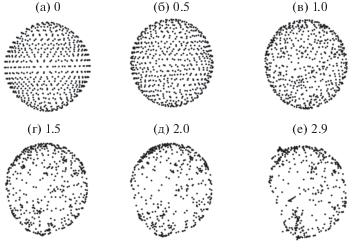
Эволюция триангулированной сферы единичного радиуса под действием потока средней кривизны с перераспределением ее вершин показана на фиг. 4. Соответствующий ей график значения числа обусловленности $\mu ({{C}^{n}})$ показывает, что при $t = \tau n > 8.0$ численное решение перестает соответствовать точному (см. фиг. 5).

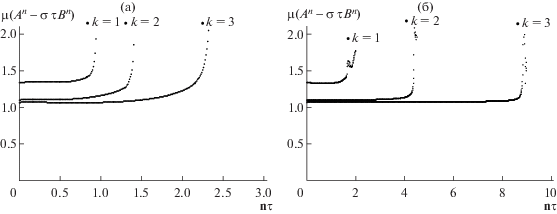
Эволюция эллипсоида вращения с полуосями $a = b = 1$, $c = 3$ под действием нормализованного дискретного потока средней кривизны показана на фиг. 6, здесь $k = 3$. При этом используется перераспределение вершин. Соответствующая зависимость числа обусловленности $\mu ({{C}^{n}})$ от времени показана на фиг. 7. Численное моделирование потока средней кривизны в этом случае, как и в случае сферы, находится в полном согласии с теоремой 1.

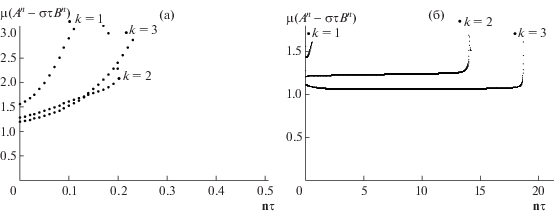
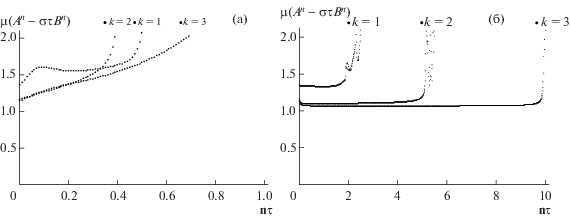
Под действием потока средней кривизны поверхность вращения, имеющая вначале форму гантели, может эволюционировать по двум различным сценариям, в зависимости от формы профильной кривой. Рассмотрим два типа поверхностей, имеющих форму гантели. В первом случае поверхность стягивается к сфере (см. фиг. 8). Во втором случае поток формирует сингулярность (см. фиг. 10). Поведение числа обусловленности $\mu ({{C}^{n}})$ в этих двух случаях показано на фиг. 9 и 11. Отметим, что к этим поверхностям теорема 1 не применима.

Для каждой из вышеописанных триангулированных поверхностей на фиг. 5, 7, 9, 11 показано, как меняется число обусловленности $\mu ({{C}^{n}})$ в процессе эволюции поверхности под действием дискретного потока средней кривизны, если применить алгоритм перераспределения вершин. Из графиков видно, что увеличение числа шагов разбиения $k$ увеличивает устойчивость численного решения для выпуклых поверхностей, замедляя рост числа обусловленности. Применение алгоритма перераспределения влечет за собой ограничение роста числа обусловленности в окрестности значения $1.5$ на значительный промежуток времени для выпуклых поверхностей. В случае невыпуклых поверхностей зависимость числа обусловленности от шага разбиения $k$ выглядит иначе. Отметим, что для гантели второго типа увеличение числа шагов разбиений $k$ увеличивает скорость роста числа обусловленности $\mu ({{C}^{n}})$ в процессе эволюции гантели под действием дискретного потока средней кривизны с перераспределением в силу формирования особенности.

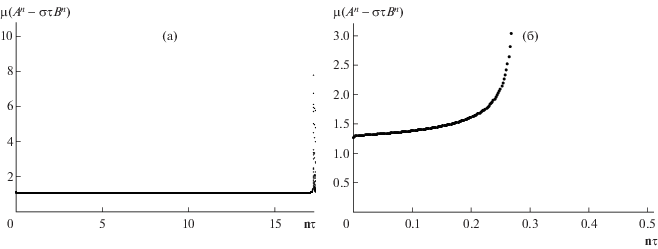
Наконец, приведем результаты расчетов для двух типов “гантелей” при $k = 4$, которые лучше приближают точное решение потока средней кривизны, чем для $k = 1,2,3$. Использование более мощного компьютера позволит в дальнейшем увеличить число шагов разбиения $k$.

Автор выражает благодарность своему научному руководителю Попеленскому Фёдору Юрьевичу за ценные обсуждения, советы и рекомендации по оформлению статьи.