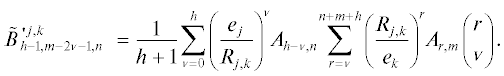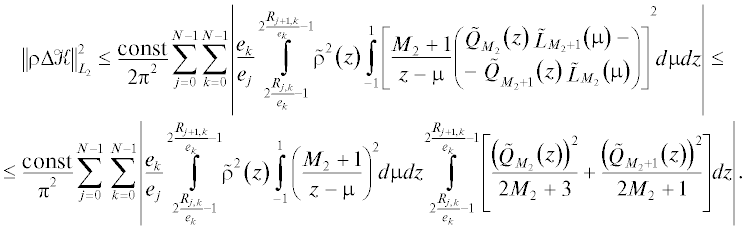Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 391-408

1. ВВЕДЕНИЕ

Основной этап барицентрического метода [1], применяемого в приближении вариационных методов И.Г. Бубнова, Б.Г. Галеркина и В. Ритца при численном решении дифференциальных уравнений теории упругости [2], дифференциальных уравнений электродинамики [3], [4], сингулярных интегральных уравнений [5], [6] в задачах дифракции электромагнитных волн на проводящих тонких экранах [7], связан с определением барицентрических координат [8]–[10] для односвязной замкнутой области с кусочно-линейной границей. Барицентрические координаты (БК) введены Мёбиусом в 1827 г. с заданием методов их определения для симплексов в ${{\mathbb{R}}^{2}}$, ${{\mathbb{R}}^{3}}$. Обобщения БК на выпуклые многоугольники предложены значительно позднее в XX веке (начиная с 1961 г.) в работах таких ученых, как J.A. Kalman, E.L. Wachspress, W.J. Gordon, J.A. Wixom, M.S. Floater и в основном связаны с введением Wachspress (WP) координат [8]. В последующих работах в XXI веке учеными M. Meyer, M.S. Floater, J. Warren, K. Hormann, N. Sukumar, Tao Ju, S. Schaefe, A. Belyaev, P. Liepa, Y. Lipman, D. Levin, O. Weber, M. Ben-Chen, C. Gotsman, R. Rustamov, A. Guessab, Xian-Ying Li, Shi-Min Hu и др. разработан ряд методов определения БК для произвольных многоугольников и многогранников, основные из которых связаны с координатами: Mean value coordinates (MVC), Gordon-Wixom (GP), Maximum entropy coordinates (MCE), Moving least squares coordinates (MLSC), Poisson coordinates (PC), Complex barycentric coordinates (CBC). Краткий обзор существующих методов определения БК с представлением дополнительных решений по обобщению задачи ${{\mathbb{R}}^{2}}$ в ${{\mathbb{R}}^{3}}$ представлен в [1], [9], [10] с указанием основного недостатка – они позволяют в лучшем случае определять псевдогармонические БК для выпуклой области. Последнее приводит к ограничению барицентрического метода [1] при решении задач математической физики для сложных относительно геометрической формы структур. Метод по определению гармонических БК для односвязной замкнутой области с кусочно-линейной границей предложен в [11]. Его недостатки связаны с необходимостью дополнительного решения обратной задачи конформного отображения анализируемой области на каноническую [12], [13] и вычислению интеграла при определении БК для вогнутых многоугольников. Последнее снижает универсальность и относительную простоту программной реализации барицентрического метода [1] в сравнении с наиболее распространенным в современных САПР методом решения краевых и начальной краевых задач математической физики – методом конечных элементов.

Целью настоящей статьи является устранение указанного недостатка путем задания относительно простого аналитического соотношения (составляется из конечных и простых математических операций и функций), позволяющего с заданной точностью определять гармонические БК для произвольных многоугольников.

2. ПОСТАНОВКА ЗАДАЧИ

Для удобства математической записи определим постановку задачи на комплексной плоскости $\mathbb{C}$. Построим односвязную область $\Omega \subset \mathbb{C}$, ограниченную замкнутой ломаной линией $\Gamma $ без самопересечений при

где ${{\Gamma }_{i}}$ – прямолинейный отрезок, соединяющий точки ${{P}_{i}}$ и ${{P}_{{i + 1}}}$ (вершины $\Omega $ при $i = \overline {0,N - 1} $, ${{P}_{N}} = {{P}_{0}}$) и допускающий следующее параметрическое представление:

С учетом известных из [2], [11] свойств и определений БК для задания гармонических барицентрических координат ${{\zeta }_{i}}$ рассмотрим следующую краевую задачу:

Решение задачи Дирихле (1) выполним известным методом Фредгольма [14] при представлении функции ${{\zeta }_{i}}$ в виде логарифмического потенциала двойного слоя (см. [15]):

где $\tfrac{\partial }{{\partial {{n}_{y}}}}$ обозначает частную производную по внутренней нормали к $\Gamma $ в точке $y$; $d{{l}_{y}}$ – дифференциал кривой $\Gamma $; ${{\Phi }_{i}}\left( y \right)$ – неизвестная плотность на границе $y \in \Gamma $ области $\Omega $, однозначно определяемая из интегрального уравнения Фредгольма II рода (см. [16]): где через ${{U}_{i}}\left( x \right)$ обозначены заданные в (1) значения ${{\zeta }_{i}}\left( x \right)$ на $\Gamma $.

Учитывая параметризацию $\Gamma $ и граничные условия из (1), интегральное уравнение (3) запишем в виде

где $\varphi _{j}^{i}\left( t \right) = {{\Phi }_{i}}\left( {{{x}_{j}}\left( t \right)} \right)$; $u_{j}^{i}\left( t \right) = 2{{U}_{i}}\left( {{{x}_{j}}\left( t \right)} \right)$; $j = \overline {0,N - 1} $; ${{K}_{{j,k}}}\left( {t,s} \right)$ – ядро интегрального уравнения (4), которое с учетом [14], [17] при $t,s \in \left[ {0,1} \right]$ определяется соотношением

В выражении (5) введены обозначения ${{e}_{k}} = {{P}_{{k + 1}}} - {{P}_{k}}$; ${{e}_{j}} = {{P}_{{j + 1}}} - {{P}_{j}}$.

Решение интегрального уравнения (4) относительно $\varphi _{j}^{i}\left( t \right)$ позволяет задать ${{\zeta }_{i}}$ при вычислении интеграла:

где

3. МЕТОД ОПРЕДЕЛЕНИЯ ГАРМОНИЧЕСКИХ БАРИЦЕНТРИЧЕСКИХ КООРДИНАТ

С учетом заданной постановки задачи определим приближение (6) при решении (4), используя следующие утверждения.

Лемма 1. Ядро ${{K}_{{j,k}}}\left( {t,s} \right)$ интегрального уравнения (4) допускает разложение вида

В выражении (8) ${{R}_{{j,k}}} = {{P}_{j}} - {{P}_{k}}$; ${{L}_{n}}\left( s \right)$ – сдвинутый на интервале ортогональности $\left[ {0,1} \right]$ многочлен Лежандра; ${{W}_{n}}\left( s \right)$ – вспомогательная функция (см. [18]):

Доказательство. Определим разложение ядра ${{K}_{{j,k}}}\left( {t,s} \right)$ интегрального уравнения (4) в системе многочленов ${{L}_{n}}\left( s \right)$

где $\tilde {\lambda }_{n}^{{j,k}}\left( t \right)$ с учетом $\int_0^1 {{{L}_{n}}\left( s \right){{L}_{m}}\left( s \right)ds} = \tfrac{{{{\delta }_{{nm}}}}}{{2n + 1}}$ задается интегралом:

В случае $j = k$ интеграл (11) вычисляется тривиально $\tilde {\lambda }_{n}^{{j,k}}\left( t \right) = 0$. Рассмотрим случай $j \ne k$ и, подставив в (11) определение ${{K}_{{j,k}}}\left( {t,s} \right)$ из (5), получим

Приняв обозначения $s = \tfrac{{l - {{P}_{k}}}}{{{{e}_{k}}}}$, $z = {{e}_{j}}t + {{P}_{j}}$, с применением формулы замены переменной приведем определенный интеграл в (12) к виду

Из [19] известно, что при $\left| {arg\left( {z - 1} \right)} \right| < \pi $ справедливо ${{\tilde {Q}}_{n}}\left( z \right) = \tfrac{1}{2}\int_{ - 1}^1 {\tfrac{{{{{\tilde {L}}}_{n}}\left( l \right)}}{{z - l}}dl} $, где ${{\tilde {L}}_{n}}\left( l \right)$ и ${{\tilde {Q}}_{n}}\left( z \right)$ – многочлены Лежандра I и II рода соответственно при ${{\tilde {Q}}_{n}}\left( z \right) = \tfrac{1}{2}{{\tilde {L}}_{n}}\left( z \right)ln\left( {\tfrac{{z + 1}}{{z - 1}}} \right)\; - $ $ - \;{{\tilde {W}}_{{n - 1}}}\left( z \right)$; ${{\tilde {W}}_{{n - 1}}}\left( z \right)$ определяется с учетом (9) через ${{\tilde {L}}_{n}}\left( z \right)$. Для указанного тождества, применяя аффинное преобразование при определении сдвинутых многочленов Лежандра на интервале ортогональности $\left[ {\tfrac{{ - {{P}_{k}}}}{{{{e}_{k}}}},\tfrac{{1 - {{P}_{k}}}}{{{{e}_{k}}}}} \right]$ с учетом (9), определим (13) в виде

Подставив (14) в (12), при обратной замене $z = {{e}_{j}}t + {{P}_{j}}$ получим

Из (15) следует $\tilde {\lambda }_{n}^{{j,k}}\left( t \right) = \sqrt {2n + 1} \lambda _{n}^{{j,k}}\left( t \right)$, что с учетом (10) доказывает справедливость (8).

Из формулировки и доказательства леммы 1 для заданной постановки задачи следует наличие особенностей при определении функции $\lambda _{n}^{{j,k}}\left( t \right)$ для $t \in \left[ {0,1} \right]$, $j,k \in \left\{ {\overline {0,N - 1} } \right\}$.

Лемма 2. Пусть $j \ne k$, $j + 1 \ne k$ и $j \ne k + 1$, тогда для $m,n \in \left\{ {0,\mathbb{N}} \right\}$ имеет место тождество

где

В выражении (17) принято обозначение

где ${{A}_{{h,n}}} = \prod\nolimits_{v = 0}^{h - 1} {\left( {v - n} \right)\left( {n + 1 + v} \right)\mathop {\left( {v + 1} \right)}\nolimits^{ - 2} } $, ${{A}_{{0,n}}} \equiv 1.$

В выражении (18) коэффициенты $\tilde {B}_{{h,m,n}}^{{j,k}}$ определяются аналогично соотношению (19) при том, что суммирование по индексу $r$ производится на интервале $\left[ {v;n + m + h} \right]$, а суммирование по индексу $v$ выполняется для мнимой части стоящего за знаком суммы выражения.

Доказательство. В интеграл выражения (16) подставим определение $\lambda _{m}^{{j,k}}\left( t \right)$ из (8) при $j \ne k$ и с учетом свойств логарифма получим сумму трех интегралов:

Заметим, что составной частью всех подынтегральных выражений (20) является произведение многочленов Лежандра ${{L}_{m}}\left( {\tfrac{{{{e}_{j}}t + {{R}_{{j,k}}}}}{{{{e}_{k}}}}} \right){{L}_{n}}\left( t \right)$. С учетом отмеченного и [20] зададим равенство

где $F\left( {a,b,c,d} \right)$ – гипергеометрическая функция [19], вычисляемая, к примеру, для $a = - m$; $b = m + 1$; $c = 1$; $d = \tfrac{{{{e}_{j}}t + {{R}_{{j,k}}}}}{{{{e}_{k}}}}$ следующим образом:

Преобразуя функцию $f\left( t \right) = \sum\nolimits_{h = 1}^\infty {\left[ {{{A}_{{h,m}}}\mathop {\left( {\tfrac{{{{e}_{j}}}}{{{{e}_{k}}}}t + \tfrac{{{{R}_{{j,k}}}}}{{{{e}_{k}}}}} \right)}\nolimits^h } \right]} $ при разложении в ряд Тейлора в окрестности точки $t = 0$ перепишем выражение (22) в виде

Используя аналогичное (22) представление для $F\left( { - n,n + 1,1,t} \right)$, с учетом (23), того, что ${{A}_{{h,m}}} = 0$ при $h \ne 0 \wedge h > m$, ${{A}_{{v,n}}} = 0$ при $v \ne 0 \wedge v > n$, равенства [19] $\int_0^1 {{{t}^{h}}{{L}_{n}}\left( t \right)dt = 0} $ при $h < n$ определим интеграл (21) следующим соотношением:

С учетом (24) и равенства

преобразуем первый интеграл в правой части выражения (20) к виду

С учетом свойств степенных рядов [21] и (19) представим (25) в виде

Выполняя аналогичные (25), (26) преобразования для второго интеграла в правой части выражения (20), определим, что

Заметим, что мнимая составляющая правой части равенства (27) эквивалентна соотношению (16), т.е.

Учитывая определение (9) функции ${{W}_{n}}\left( s \right)$ через многочлены Лежандра ${{L}_{n}}\left( s \right)$, свойства интегралов по сферическим функциям из [19] и используя (24), несложно вычислить третий слагаемый интеграл в правой части выражения(20) для $m > n$ соотношением

где

В остальных случаях $\left( {m \leqslant n} \right)$ с учетом [19] третий слагаемый интеграл в правой части выражения (20) вычисляется тривиально $\int_0^1 {{{W}_{{m - 1}}}} \left( {\tfrac{{{{e}_{j}}t + {{R}_{{j,k}}}}}{{{{e}_{k}}}}} \right){{L}_{n}}\left( t \right)dt = 0$, что для (29), (30) и (18) при 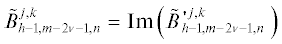определяет справедливость равенства

Доказанные тождества (28), (31) для (20) определяют справедливость (16).

Лемма 3. Пусть $j \ne k$, $j + 1 \ne k$ и $j = k + 1$, тогда для $m,n \in \left\{ {0,\mathbb{N}} \right\}$ имеет место тождество

где

Доказательство. Справедливость (32) следует из доказательства леммы 2 с учетом того, что возникает особенность в (27) при определении $ln\left( {\tfrac{{{{R}_{{j + 1,k + 1}}}}}{{{{R}_{{j,k + 1}}}}}} \right)$ и $\tfrac{{ - {{e}_{j}}}}{{{{R}_{{j,k + 1}}}}}$. Для ее устранения с применением правил интегрирования по частям с учетом (24) зададим первый интеграл из правой части выражения (20) в виде

С учетом свойств гипергеометрических функций [19], ${{R}_{{j,k + 1}}} = 0$ и (24) определим интеграл в правой части соотношения (34) в виде

Подставив (35) в (25) с учетом $j = k + 1$, (20) и (27) определим справедливость (33), (32).

Лемма 4. Пусть $j \ne k$, $j + 1 = k$ и $j \ne k + 1$, тогда для $m,n \in \left\{ {0,\mathbb{N}} \right\}$ имеет место тождество

где

Доказательство. Справедливость (36) следует из доказательства леммы 2 с учетом того, что при вычислении интеграла по правилу (27) возникает особенность при определении $ln\left( {\tfrac{{{{R}_{{j + 1,k + 1}}}}}{{{{R}_{{j + 1,k}}}}}} \right)$ и $ln\left( {\tfrac{{{{R}_{{j + 1,k}}}}}{{{{R}_{{j,k}}}}}} \right)$. Для ее устранения с учетом ${{R}_{{j,k}}} = - {{e}_{j}}$ при $j + 1 = k$ зададим разложение $ln\left( {{{e}_{j}}t + {{R}_{{j,k}}}} \right)$ в ряд Тейлора в окрестности $t = 0$:

С учетом (38) вычислим второй слагаемый интеграл в правой части выражения (20) в виде

Заметим, что [19]: $\sum\nolimits_{v = 1}^\infty {\tfrac{1}{{v\left( {h + v} \right)}} = \tfrac{1}{h}\sum\nolimits_{v = 1}^h {\tfrac{1}{v}} } $, тогда для (24) перепишем (39) в виде

Принимая во внимание (40) при вычислении (27) с учетом $j + 1 = k$ и (20), определим справедливость (37), (36).

Таким образом, полученные результаты (леммы 2–4) с учетом леммы 1 позволяют выделить особенности функции $\lambda _{n}^{{j,k}}\left( t \right)$ для $t \in \left[ {0,1} \right]$, $j,k \in \left\{ {\overline {0,N - 1} } \right\}$, и перейти к непосредственному решению задач (4), (6) нахождения гармонических БК (1).

Теорема 1. Барицентрические координаты ${{\zeta }_{i}}\left( x \right)$, удовлетворяющие условиям (1), определяются соотношением

где

В выражении (42) $D_{{n,m}}^{{j,k}}$ и $C_{{n,m}}^{{j,k}}$ вычисляются соотношениями (18) и (17), (33), (37) соответственно с учетом выделенных особенностей для $\lambda _{m}^{{j,k}}\left( t \right)$; $S_{{k,m}}^{i}$ – коэффициенты, определяемые из решения системы линейных уравнений:

где ${\mathbf{T}}$ – блочная матрица, составленная из элементов $t_{{m,n}}^{{j,k}} = \tfrac{{\mathop {\left( { - 1} \right)}\nolimits^{n + m} }}{\pi }\sqrt {2n + 1} \sqrt {2m + 1} \left( {C_{{m,n}}^{{j,k}} + D_{{m,n}}^{{j,k}}} \right)$; ${{S}^{i}}$ – блочный вектор неизвестных элементов $S_{{k,m}}^{i}$; ${{U}^{i}}$ – блочный вектор, составленный из элементов:

Доказательство. Подставив разложение (8) ядра ${{K}_{{j,k}}}\left( {t,s} \right)$ в интегральное уравнение (4), получим

Для (44) применим известный метод вырожденных ядер для решения интегральных уравнений II рода с постоянными пределами интегрирования [16]. Пусть неизвестная функция $\varphi _{j}^{i}\left( t \right)$ определяется выражением

где

Тогда при подстановке (45) в (44) в силу ортогональности функций ${{L}_{m}}\left( s \right)$, независимости $\varphi _{j}^{i}\left( t \right)$, $\varphi _{{j + 1}}^{i}\left( t \right)$ для $j = \left\{ {\overline {0,N - 1} } \right\}$ и их гладкости всюду на ${{\Gamma }_{j}}$, ${{\Gamma }_{{j + 1}}}$ соответственно кроме, быть может, угловых точек (в ${{P}_{j}}$ допускаются особенности вида [17]: $\mathop {\left( {x - {{P}_{j}}} \right)}\nolimits^\theta $, $0 < \theta < 1$) для определенных в (8) многочленов $\lambda _{m}^{{j,k}}\left( t \right)$ сведем интегральное уравнение (4) к системе линейных уравнений (43). Решение ${{S}^{i}} = \mathop {\left( {{\mathbf{E}} + {\mathbf{T}}} \right)}\nolimits^{ - 1} {{U}^{i}},$ уравнения (43) позволяет определить с учетом (45) неизвестную функцию плотности $\varphi _{j}^{i}\left( t \right)$, подстановка которой в (6) позволяет определить гармонический БК выражением

Первый интеграл в правой части выражения (47) с учетом (7) и граничных условий из (1) несложно вычислить, представив результат в виде

Второй интеграл в правой части выражения (47) вычислим, определив разложение ${{K}_{j}}\left( {t,x} \right)$ в системе многочленов ${{L}_{n}}\left( t \right)$:

где $\lambda _{{j,n}}^{'}\left( x \right)$ с учетом $\int_0^1 {{{L}_{n}}\left( s \right)} {{L}_{m}}\left( s \right)ds = \tfrac{{{{\delta }_{{nm}}}}}{{2n + 1}}$ задается интегралом:

С учетом доказательства леммы 1 при задании (12)–(15) нетрудно определить справедливость вычисления интеграла (50) в виде (42).

Подставив разложение (49) во второй интеграл (47), получим

С учетом того, что $C_{{m,n}}^{{j,k}} = D_{{m,n}}^{{j,k}} = 0$ при $j = k$, подставив (51) и (48) в (47), получим (41), что и требовалось доказать.

Таким образом, полученные соотношения (41), (42) при замене бесконечных сумм по индексам $n$ и $m$ конечными с ограничением числа слагаемых до ${{M}_{1}}$ и ${{M}_{2}}$ соответственно позволяют задать приближенно-аналитическое определение гармонических БК для $\Omega $:

4. ОЦЕНКА СХОДИМОСТИ И ТОЧНОСТИ МЕТОДА, ТЕСТОВЫЕ ПРИМЕРЫ

Заданное решение по определению гармонических БК с учетом введенных правил (17), (18), (33), (37) вычисления для $\Omega $ вызывает дополнительный интерес к оценке сходимости и точности (52) от ${{M}_{1}}$, ${{M}_{2}}$. Для этого покажем, что последовательность функций $\left\{ {\varphi _{{{{M}_{2}}}}^{i}\left( t \right) = \mathop {\left( {\varphi _{{j,{{M}_{2}}}}^{i}\left( t \right)} \right)}\nolimits_{N - 1} } \right\}$ в (44) сходится по норме к решению уравнения (4) при ${{M}_{2}} \to \infty $ и $\tilde {\zeta }_{{{{M}_{1}},{{M}_{2}}}}^{i}\left( {x)} \right.$ сходится по норме к (6) при ${{M}_{1}} \to \infty $, ${{M}_{2}} \to \infty $. Дополнительно рассмотрим возможность упрощения выражения (52) при определении $\tilde {\zeta }_{M}^{i}\left( {x)} \right.$ для ${{M}_{1}} = {{M}_{2}} = M$.

Для формирования оценок введем следующие представления. Перепишем уравнение (4) в операторной форме:

где $\mathop \varphi \nolimits^i = \mathop {\left( {\varphi _{j}^{i}} \right)}\nolimits_{N - 1} $; ${{u}^{i}} = \mathop {\left( {u_{j}^{i}} \right)}\nolimits_{N - 1} $; $\mathcal{K} = \mathop {\left( {{{\mathcal{K}}_{{j,k}}}} \right)}\nolimits_{N - 1 \times N - 1} $ – матричный оператор; $\mathcal{K}{{\varphi }^{i}} = \sum\nolimits_{k = 0}^{N - 1} {{{\mathcal{K}}_{{j,k}}}\varphi _{k}^{i}} $; $\left( {{{\mathcal{K}}_{{j,k}}}\varphi _{k}^{i}} \right)\left( t \right) \equiv \int_0^1 {{{K}_{{j,k}}}} \left( {t,s} \right)\varphi _{k}^{i}\left( s \right)ds$ – линейный ограниченный оператор на пространстве функций из $C\left( {\left[ {0,1} \right]} \right)$.

По аналогии с (53) для (44) определим уравнение

при введении в рассмотрение линейного ограниченного оператора

При определении оценок приближения векторной функции $\varphi $ будем использовать нормы в пространствах $C\left( {\left[ {0,1} \right]} \right)$ и ${{L}_{2}}\left( {\left[ {0,1} \right]} \right)$ [23], [24]:

Теорема 2. $\exists M \in \mathbb{N}:\forall {{M}_{2}} \geqslant M$ решение $\varphi _{{{{M}_{2}}}}^{i}$ уравнения (54) существует и единственно, при этом справедливы оценки

где ${\text{const}}$ положительна и не зависит от ${{M}_{2}}$.

В выражении (55), см. [17]

Доказательство. Из свойств ограниченного линейного оператора $\mathcal{K}$ следует наличие обратного оператора $\mathop {\left( {I + \mathcal{K}} \right)}\nolimits^{ - 1} $, обеспечивающего разрешимость уравнения ${{\varphi }^{i}} = \mathop {\left( {I + \mathcal{K}} \right)}\nolimits^{ - 1} {{u}^{i}}$. Для получения оценок погрешности в $C\left( {\left[ {0,1} \right]} \right)$ и ${{L}_{2}}\left( {\left[ {0,1} \right]} \right)$ функцию ${{\varphi }^{i}}$ представим в виде ${{\varphi }^{i}} = \rho \mathop \psi \nolimits^i $, где $\mathop \psi \nolimits^i $ – новая искомая функция в (53), а $\rho = \rho (t) = 2\sqrt {t - {{t}^{2}}} $ [25] – весовая функция [18]. Обозначим разность $\Delta \mathcal{K} = \mathcal{K} - {{\mathcal{K}}^{{{{M}_{2}}}}}$ и с учетом (8), свойств ортогональных многочленов [18] определим оценку

С учетом (5), тождества ${\text{Im}}\mathop {\left( z \right)}\nolimits^2 = 0,5\left[ {\left| {{{z}^{2}}} \right| - {\text{Re}}\left( {{{z}^{2}}} \right)} \right]$ и выделенных в доказательствах лемм 2–4 особенностей ядра ${{K}_{{j,k}}}\left( {t,s} \right)$ вычислим следующий интеграл из (56) при $j \ne k$:

В случае $k = j$ интеграл (57) равен 0. В выражениях (57) приняты обозначения ${{z}_{{j,k}}}\left( t \right) = {{e}_{j}}t + {{R}_{{j,k}}}$; ${{z}_{{j,k + 1}}}\left( t \right) = {{e}_{j}}t + {{R}_{{j,k + 1}}}$.

Из определения интеграла (57) следует, что при $j = k + 1$, $t \to 0$ и $j = k - 1$, $t \to 1$ возникает особенность $f\left( t \right) = \int_0^1 {\mathop {\left[ {{{K}_{{j,k}}}\left( {t,s} \right)} \right]}\nolimits^2 } ds \to \infty $. В этой связи для вычисления верхней границы оценки (56) определим асимптотическое поведение функций $f\left( t \right)$ и ${{\tilde {f}}_{{{{M}_{2}}}}}\left( t \right) = \sum\nolimits_{n = 0}^{{{M}_{2}}} {\left( {2n + 1} \right)} \mathop {\left[ {\lambda _{n}^{{j,k}}\left( t \right)} \right]}\nolimits^2 $ при $j = k + 1$, $t \to 0$. Для этого на $\mathbb{C}$ построим треугольник ${{\Delta }_{t}}$ с вершинами в ${{e}_{j}}t + {{P}_{j}}$, ${{P}_{k}}$, ${{P}_{{k + 1}}}$, углами $\tilde {\alpha }$, $\tilde {\beta }$, $\tilde {\gamma }$ при соответствующих вершинах и сторонами $a = \left| {{{e}_{k}}} \right|$, $b = \left| {{{z}_{{j,k + 1}}}\left( t \right)} \right|$, $c = \left| {{{z}_{{j,k}}}\left( t \right)} \right|$. Заметим, что для заданного представления ${{\Delta }_{t}}$ и выражений (57), (8) функции $f\left( t \right)$, ${{\tilde {f}}_{{{{M}_{2}}}}}\left( t \right)$ можно вычислить соотношениями

Из определения ${{\Delta }_{t}}$ следует, что при $j = k + 1$, $t \to 0$ треугольник вырождается в прямую ${{P}_{k}}{{P}_{{k + 1}}}$ при $c \to a$, $b \to 0$, $\tilde {\alpha } \to \pi - {{\alpha }_{j}}$, $\tilde {\beta } \to 0$, $\tilde {\gamma } \to {{\alpha }_{j}}$, где ${{\alpha }_{j}}$ – внутренний угол $\Omega $ при вершине ${{P}_{j}}$. Для заданных представлений с учетом известных правил раскрытия неопределенностей и свойств конечных сумм [19] сведем соотношения (58), (59) к виду

Аналогично изложенному, рассматривая асимптотическое поведение функций $f\left( t \right)$ и ${{\tilde {f}}_{{{{M}_{2}}}}}\left( t \right)$ при $j = k - 1$, $t \to 1$, с учетом свойств функции $\rho \left( t \right)$ для $t \in \left[ {0,1} \right]$ и (56) получаем оценку

Заметим, что из свойств ортогональных многочленов следует справедливость неравенства $\mathop {\left\| {\mathop {\left[ {\rho \left( {I + \mathcal{K}} \right)} \right]}\nolimits^{ - 1} } \right\|}\nolimits_C \mathop {\left\| {\rho \Delta \mathcal{K}} \right\|}\nolimits_C < 1$, в котором $\mathop {\left\| {\mathop {\left[ {\rho \left( {I + \mathcal{K}} \right)} \right]}\nolimits^{ - 1} } \right\|}\nolimits_C \leqslant \mathop {max}\limits_{j \in \left\{ {\overline {0,N - 1} } \right\}} \left\{ {\operatorname{const} \varpi _{j}^{{ - 1}}} \right\}$. Тогда, следуя [23], с учетом принятых обозначений в (56), (62) и неравенства Коши–Буняковского справедлива оценка в $C\left( {\left[ {0,1} \right]} \right)$:

С учетом (5) и (8), принимая замену переменных $z = 2\tfrac{{{{e}_{j}}t + {{R}_{{j,k}}}}}{{{{e}_{k}}}} - 1$ и $s = \tfrac{{\mu + 1}}{2}$, при обозначении $\tilde {\rho }\left( z \right) = \rho \left( {\tfrac{{{{e}_{k}}\left( {1 + z} \right) - 2{{R}_{{j,k}}}}}{{2{{e}_{j}}}}} \right)$ сформируем следующую оценку для $\Delta \mathcal{K}$ в ${{L}_{2}}\left( {\left[ {0,1} \right]} \right)$:

где ${\text{const}}$ не зависит от ${{M}_{2}}$.

С учетом формулы Кристоффеля [26], неравенства Коши–Буняковского и свойств ортогональных многочленов [18] сведем оценку (64) к виду

Для определения оценки (65), учитывая соотношения между ортогональными многочленами Лежандра II рода [26]

тождество

при $n \ne m$ из [20] для интеграла, содержащего функции Лежандра на разрезе, вычислим $\int_a^b {\mathop {\left( {{{{\tilde {Q}}}_{n}}\left( z \right)} \right)}\nolimits^2 dz} $ соотношением

где

Принимая во внимание равенство [19]

выражения (65), (66) при асимптотическом представлении и учитывая тождество для гамма-функции $\Gamma \left( n \right)\Gamma \left( {n + \tfrac{1}{2}} \right) = {{2}^{{1 - 2n}}}\sqrt \pi \Gamma \left( {2n} \right)$ и формулу Стирлинга $n! \approx \sqrt {2\pi n} \mathop {\left( {\tfrac{n}{e}} \right)}\nolimits^n $, окончательно определим оценку (64) в следующем виде:

Аналогично (63) при $\mathop {\left\| {\mathop {\left[ {\rho \left( {I + \mathcal{K}} \right)} \right]}\nolimits^{ - 1} } \right\|}\nolimits_{{{L}_{2}}} \leqslant \operatorname{const} \sum\nolimits_{j = 0}^{N - 1} {\varpi _{j}^{{ - 1}}} $ и, следуя [23], справедлива оценка в ${{L}_{2}}\left( {\left[ {0,1} \right]} \right)$:

Таким образом, условие существования и единственности решения $\varphi _{{{{M}_{2}}}}^{i}$ уравнения (54) обеспечивает существование предела $\mathop {lim}\limits_{{{M}_{2}} \to \infty } \left\| {\mathcal{K} - {{\mathcal{K}}^{{{{M}_{2}}}}}} \right\| = 0$, определяемого с учетом (5) и (8) при замене переменных $z = 2\tfrac{{{{e}_{j}}t + {{R}_{{j,k}}}}}{{{{e}_{k}}}} - 1$ и $s = \tfrac{{\mu + 1}}{2}$ из известной формулы Гейне [20], а полученные в $C\left( {\left[ {0,1} \right]} \right)$ и ${{L}_{2}}\left( {\left[ {0,1} \right]} \right)$ оценки (63) и (68) соответственно характеризуют справедливость (55), что и требовалось доказать.

Теорема 3. $\exists M \in \mathbb{N}:\forall {{M}_{1}} \geqslant M$, $\forall {{M}_{2}} \geqslant M$ решение $\tilde {\zeta }_{{{{M}_{1}},{{M}_{2}}}}^{i}$ (52) задачи Дирихле (1) существует и единственно, при этом справедлива оценка

где $\mathop {{\text{const}}}\nolimits_{1,2} $ положительны и не зависят от ${{M}_{1}}$, ${{M}_{2}}$.

Доказательство. Учитывая (6), неравенство треугольника и, принимая обозначения $\left( {\mathcal{K}{{\varphi }^{i}}} \right)\left( x \right) \equiv \sum\nolimits_{j = 0}^{N - 1} {\int_0^1 {\varphi _{j}^{i}\left( t \right)} } \int\limits_0^1 \,{{K}_{j}}\left( {t,x} \right)dt$, $\left( {{{\mathcal{K}}^{{{{M}_{1}}}}}\varphi _{{{{M}_{2}}}}^{i}} \right)\left( x \right)$ ≡ $\sum\nolimits_{j = 0}^{N - 1} {\int_0^1 {\varphi _{{j,{{M}_{2}}}}^{i}} } \left( t \right)\sum\nolimits_{n = 0}^{{{M}_{1}}} {\left( {2n + 1} \right)} \lambda _{{j,n}}^{'}\left( x \right){{L}_{n}}\left( t \right)dt,$ определим оценку БК в $C\left( {\left[ {0,1]} \right)} \right.$ в следующем виде:

Принимая во внимание (1), (42), (52), (55) и свойства БК [1], [11] $({{\zeta }_{i}}\left( x \right) \geqslant 0:\forall x \in \Omega $; $\mathop {max}\limits_{x \in \Omega } \left\{ {{{\zeta }_{i}}\left( x \right)} \right\} = 1$; $\mathop {{\text{argmax}}}\limits_{x \in \Omega } \left\{ {{{\zeta }_{i}}\left( x \right)} \right\} = {{P}_{i}})$ при $\mathop {\left\| \mathcal{K} \right\|}\nolimits_C = 2\pi $ сведем оценку (70) к виду

Таким образом, условие существования и единственности решения $\tilde {\zeta }_{{{{M}_{1}},{{M}_{2}}}}^{i}$ (52) задачи Дирихле (1) с учетом (6) и результатов лемм 1–4 и теоремы 1 обеспечивается предыдущим доказательством существования и единственности решения $\vec {\varphi }_{{{{M}_{2}}}}^{i}$ уравнения (54). При этом полученная оценка (71) соответствует исходной (69), что и требовалось доказать.

Из результатов теорем 2, 3 и соотношений (6), (42), (45), (52) вытекает

Следствие 1. $\exists \tilde {M} \in \mathbb{N}:\forall M \geqslant \tilde {M}$ решение

задачи Дирихле (1) существует и единственно, при этом справедлива оценка где ${\text{const}}$ положительна и не зависит от $M$.

Заданное соотношение (72) предлагается рассматривать как основное выражение определения гармонических БК для произвольных $\Omega $.

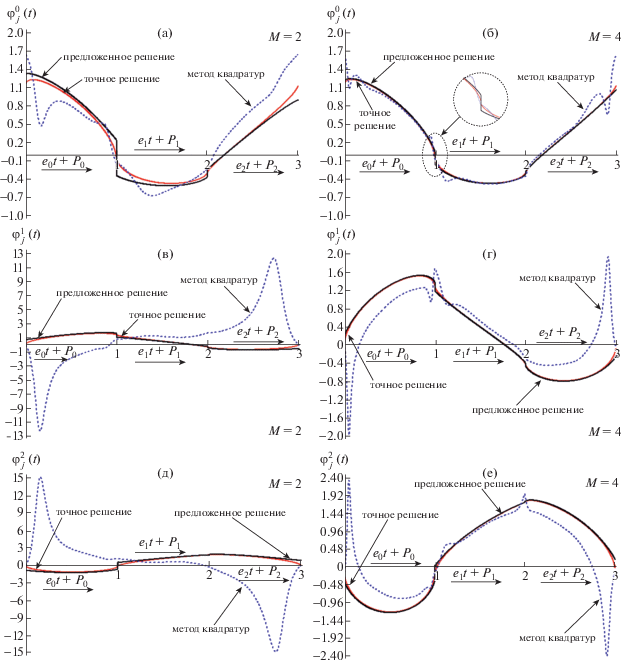
Для наглядной демонстрации предпочтительности предложенного решения в сравнении с известными [17], [22] (метод квадратур) в САПР MathCad и Matlab проведены тестовые расчеты ${{\varphi }^{i}}$ и ${{\zeta }_{i}}$ для канонических областей и областей сложной формы (вогнутые многоугольники). Ввиду известного решения по определению БК через отношение площадей в качестве канонической области выбран треугольник. Положение его вершин задано следующими координатами в $\mathbb{C}$: ${{P}_{0}} = 5 + i$; ${{P}_{1}} = - 4 + 4i$; ${{P}_{2}} = - 2 - i$. На фиг. 1 приведены сравнительные результаты расчета функций плотности ${{\vec {\varphi }}^{i}}$ на ребрах ${{e}_{j}}$ треугольника при приближенном решении интегрального уравнения (4) разработанным методом и методом квадратур для различных порядков аппроксимации $M$.

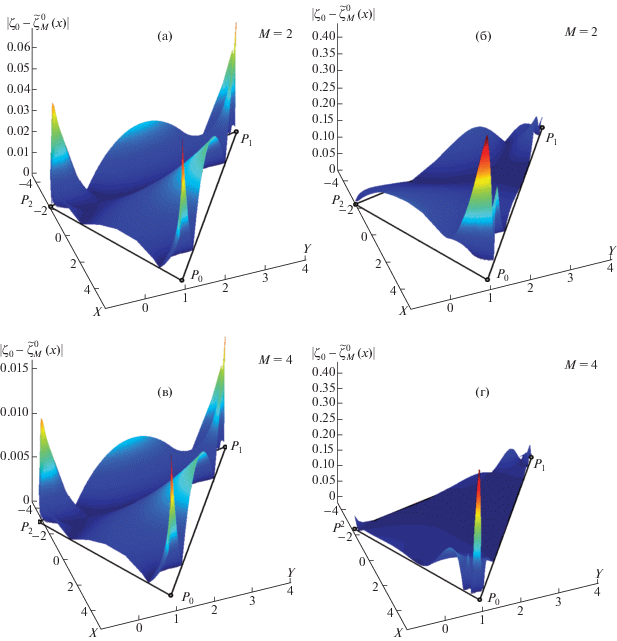
На фиг. 2 приведены распределения ошибки приближенно-аналитического решения задачи (1) для треугольника при $i = 0$. Указанные решения выполнены разработанным методом по правилу (72) и при непосредственном численном интегрировании (6) (погрешность интегрирования задана ${{10}^{{ - 10}}}$) с подстановкой в $\varphi _{j}^{i}\left( t \right)$ результата, полученного методом квадратур.

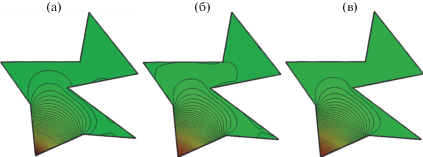
На фиг. 3 приведены расчеты БК по правилу (72) для вогнутого девятиугольника при различных порядках аппроксимации $M$.

На фиг. 4 приведены расчеты БК по правилу (72) для вогнутого многоугольника из 32 вершин при различных значениях $M$.

5. ЗАКЛЮЧЕНИЕ

Полученное соотношение (72) позволяет с экспоненциальной скоростью сходимости формировать решение по определению гармонических БК для произвольных многоугольников. Оценки (55), (69), (73) и результаты моделирования (фиг. 1–4) свидетельствуют о предпочтительности предложенного приближенно-аналитического решения задач (1) и (4) в сравнении с известными. Предложенный метод при наименьших вычислительных затратах в сравнении с известными (метод квадратур) позволяет повысить точность решения задачи (1) до 7 раз вблизи угловых точек и до 3.6 раз по всей области анализа (см. фиг. 2). Высокая точность решения обеспечивается уже при небольших $M$ (даже для достаточно сложных по форме многоугольных областей порядок аппроксимации достаточно выбирать на интервале $M \in \left[ {5;8} \right]$, см. фиг. 3, 4).

В целом в результате проведенных исследований получено относительно простое аналитическое соотношение (72), позволяющее эффективно определять гармонические БК для произвольных многоугольников. Недостаток разработанного метода состоит в необходимости решения системы линейных уравнений (43) при определении коэффициентов $S_{{k,m}}^{i}$. Принимая во внимание высокую точность метода, указанный недостаток является несущественным, поскольку: 1) неизвестные коэффициенты $S_{{k,m}}^{i}$ не зависят от $x \in \Omega $, а определяются формой $\Omega $ и требуют пересчета лишь при ее изменении; 2) количество уравнений и переменных в системе (43) с учетом рекомендации $M \in \left[ {5;8} \right]$ измеряется единицами.