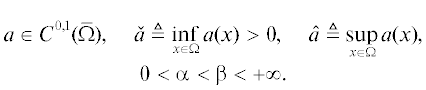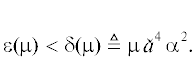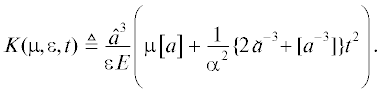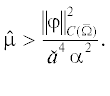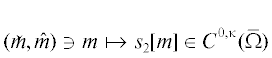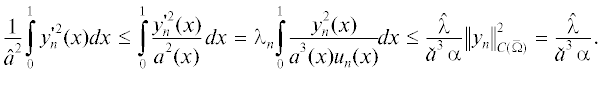Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 465-480
Минимизация массы тонкого прямого крыла при ограничении по скорости дивергенции
В. Ю. Гончаров 1, *, Л. А. Муравей 1, **
1 МАИ
125993 Москва, Волоколамское ш. 4, Россия
* E-mail: fulu.happy@gmail.com
** E-mail: l_muravey@mail.ru
Поступила в редакцию 03.07.2018
Аннотация
Рассматривается задача определения оптимального распределения толщины обшивки тонкого прямого крыла, удовлетворяющего заданному ограничению на скорость дивергенции (т.е. скорость, при превышении которой происходит закручивание крыла вплоть до разрушения), при котором достигается наименьшее возможное значение массы обшивки. Математическая формулировка задачи имеет следующий вид: минимизировать линейный функционал на некотором множестве существенно ограниченных измеримых функций, для которых наименьшее собственное значение задачи Штурма–Лиувилля не меньше заданного значения. Доказывается, что эта задача обладает единственным решением. Поскольку только кусочно-гладкие распределения толщины удовлетворяют требованиям приложений, изучается вопрос о регулярности оптимального решения. Оказывается, что оптимальное решение является непрерывной по Липшицу функцией. Кроме того, показывается, что решение непрерывно зависит от параметра, определяющего наименьшее возможное значение скорости дивергенции, т.е. рассматриваемая задача является корректной в смысле Адамара. Наконец, предлагается итерационный метод, позволяющий строить минимизирующие последовательности, сходящиеся к оптимальному решению в пространствах Гёльдера, а также приводятся и обсуждаются результаты численных расчетов. Библ. 21. Фиг. 4.
ВВЕДЕНИЕ
Рассмотрим задачу о дивергенции тонкого прямого крыла (см. [1]). Основное уравнение и граничные условия, записанные в безразмерной форме, имеют вид (см. [2], [3]):
(1)
$({{a}^{3}}u\theta {\kern 1pt} {\text{'}}){\kern 1pt} {\text{'}}(x) + \lambda ({{a}^{2}}\theta )(x) = 0,\quad x \in \Omega \triangleq (0,1),$Пусть
Введем множество(EVP1)
$\int\limits_0^1 {{{a}^{3}}(x)u(x)\theta {\kern 1pt} {\text{'}}(x)\varphi {\kern 1pt} {\text{'}}(x)dx = \lambda } \int\limits_0^1 {{{a}^{2}}(x)\theta (x)\varphi (x)dx} ,\quad \varphi \in V,$(VC1)
$\begin{gathered} {{\lambda }_{1}}[u] = \mathop {min}\limits_{\varphi \in V{\backslash }\{ \vartheta \} } \Phi (u,\varphi ), \\ \Phi (u,\varphi ) \triangleq \int\limits_0^1 {{{a}^{3}}(x)u(x)\mathop {\varphi {\kern 1pt} {\text{'}}}\nolimits^2 (x)dx} {\text{/}}\int\limits_0^1 {{{a}^{2}}(x){{\varphi }^{2}}(x)dx.} \\ \end{gathered} $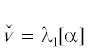 , $\hat {v} = {{\lambda }_{1}}[\beta ]$. Для
, $\hat {v} = {{\lambda }_{1}}[\beta ]$. Для  введем множество
состоящее из допустимых распределений толщины обшивки крыла, для каждого из которых
скорость дивергенции не меньше заданного значения $v$. Для $u \in U$ безразмерная масса обшивки крыла $M[u]$ определяется формулой
Поскольку крыло закручивается вплоть до разрушения при скорости, превышающей соответствующую
ему скорость дивергенции, необходимо принимать во внимание данное явление при проектировании
крыла. Одним из параметров проектирования, оказывающих влияние на скорость дивергенции,
является масса крыла. Однако увеличение массы крыла не только приводит к увеличению
скорости дивергенции, но также делает его более дорогим с точки зрения производства
и, кроме того, повышает расход топлива во время полета. Поэтому представляет интерес
рассмотреть задачу минимизации массы обшивки крыла на множестве $U(v)$: найти элемент $w \in U(v)$ такой, что
введем множество
состоящее из допустимых распределений толщины обшивки крыла, для каждого из которых
скорость дивергенции не меньше заданного значения $v$. Для $u \in U$ безразмерная масса обшивки крыла $M[u]$ определяется формулой
Поскольку крыло закручивается вплоть до разрушения при скорости, превышающей соответствующую
ему скорость дивергенции, необходимо принимать во внимание данное явление при проектировании
крыла. Одним из параметров проектирования, оказывающих влияние на скорость дивергенции,
является масса крыла. Однако увеличение массы крыла не только приводит к увеличению
скорости дивергенции, но также делает его более дорогим с точки зрения производства
и, кроме того, повышает расход топлива во время полета. Поэтому представляет интерес
рассмотреть задачу минимизации массы обшивки крыла на множестве $U(v)$: найти элемент $w \in U(v)$ такой, что
Подобные задачи для крыльев летательных аппаратов рассматривались только в нескольких работах. Близкая к (𝒫1) задача была поставлена Макинтошем и Истепом в работе [2], в которой рассмотрена задача минимизации массы обшивки крыла при заданном значении скорости дивергенции и получено решение в случае линейного распределения хорды. Их подход был обобщен Н.В. Баничуком в [5] на случай переменных параметров крыла и более общего типа краевых условий. Интересный факт состоит в том, что в [2], [5] на распределения толщины обшивки крыла не накладываются никакие ограничения и, как следствие, полученные там оптимальные решения обращаются в нуль в точке, соответствующей свободному концу крыла. Поэтому случай наличия положительной нижней грани для значений толщины обшивки крыла имеет гораздо большую практическую важность по сравнению со случаем без ограничений. Задача минимизации массы обшивки прямоугольного крыла при заданном значении скорости дивергенции была рассмотрена Ж.-Л. Арманом и В. Дж. Витте в [6], где рассмотрен как случай без ограничений, так и случай общей положительной нижней грани для значений толщины, а также дан вывод аналитических решений. Кроме того, следует отметить работу Ю.А. Арутюнова и А.П. Сейраняна [3], в которой рассмотрена задача минимизации массы обшивки крыла при различных дополнительных интегральных ограничениях. Для численного решения в [3], [6] применялся алгоритм переходной матрицы, подробно описанный в [7]. Что касается непосредственно задачи (𝒫1), то отметим, что она является выпуклой, и поэтому может достаточно эффективно решаться различными методами оптимизации [8].
Цель данной статьи – представить достаточно полное исследование экстремальной задачи (𝒫1). Доказывается, что существует единственное решение задачи (𝒫1), причем имеет место непрерывная зависимость решения этой задачи от параметра $v$, т.е. задача (𝒫1) является корректной в смысле Адамара. Поскольку допустимые управления принадлежат классу существенно ограниченных измеримых функций, оптимальное решение может не представлять практического интереса. Таким образом, возникает необходимость исследования вопроса регулярности оптимального решения. Вместе с тем существует ряд задач оптимального управления (см. [9]), связанных с уравнениями математической физики, в которых необходимость рассмотрения более “узкого” класса допустимых управлений обусловливается зависимостью функционала от управляющей переменной и ее местом в уравнении состояния. При рассмотрении задачи (𝒫1) мы не будем следовать этому подходу и покажем, что истинные свойства оптимального решения вполне согласуются с естественным требованием гладкости поверхности оптимального крыла. В действительности мы покажем, что оптимальное решение задачи (𝒫1) принадлежит пространству равномерно непрерывных по Липшицу на $\Omega $ функций. Кроме того, предлагается метод, который строит последовательности, сходящиеся к оптимальному решению в пространствах Гёльдера ${{C}^{{0,\alpha }}}(\bar {\Omega })$ для $\alpha \in (0,1)$, при условии, что удается найти решение некоторой вспомогательной экстремальной задачи. Насколько известно авторам, в настоящее время в литературе по данной теме нет исследований, посвященных как вопросу регулярности оптимальных решений, так и вопросу строгого обоснования методов, которые позволяют строить последовательности, сходящиеся к оптимальным решениям.
Упомянутые выше результаты естественным образом следуют из аналогичных свойств следующей экстремальной задачи: для фиксированного значения $m$ массы обшивки крыла найти элемент
такой, что(𝒫2)
${{\lambda }_{1}}[w] = {{v}_{{{\text{max}}}}}(m) \triangleq \mathop {sup}\limits_{u \in \mathcal{U}(m)} {{\lambda }_{1}}[u].$Статья имеет следующую структуру. Задача (𝒫2) рассматривается в разд. 1. В разд. 2 устанавливается взаимосвязь между задачами (𝒫1) и (𝒫2), а также показывается, что все полученные в разд. 1 результаты формируют основу для эффективного численного решения задачи (𝒫1). В разд. 3 обсуждается метод решения задачи (𝒫1). Результаты проведенных вычислительных экспериментов приводятся в разд. 4.
1. ОПТИМАЛЬНОЕ ПРОЕКТИРОВАНИЕ КРЫЛЬЕВ ПРОТИВ ДИВЕРГЕНЦИИ
Из (VC1) легко получаем следующее утверждение.
Лемма 1. Существуют такие  для всех $u \in U$.
для всех $u \in U$.
Функционал ${{\lambda }_{1}}[ \cdot ]$ имеет еще одно представление. Рассмотрим следующую задачу на собственные значения: найти пару $(\lambda ,y) \in \mathbb{R} \times (W{\backslash }\{ \vartheta \} )$ такую, что
(EVP2)
$\int\limits_0^1 {\frac{{y{\kern 1pt} '(x)z{\kern 1pt} '(x)}}{{{{a}^{2}}(x)}}} {\kern 1pt} dx = \lambda \int\limits_0^1 {\frac{{y(x)z(x)}}{{{{a}^{3}}(x)u(x)}}} {\kern 1pt} dx,\quad z \in W \triangleq \{ \varphi \in {{H}^{1}}(\Omega ):\varphi (1) = 0\} .$Множество собственных элементов, соответствующих первому собственному значению задачи (EVP$_{i}$), будем обозначать через ${{\mathcal{E}}_{i}}[u]$. В дальнейшем нам понадобится следующая техническая
Лемма 2. Справедливы следующие утверждения.
(i) ${{\lambda }_{1}}[u]$ является первым собственным значением задачи (EVP2).
(ii) Если $f \in {{\mathcal{E}}_{i}}[u]$ и $f(x) > 0$ на $\Omega $, то ${{( - 1)}^{{i - 1}}}f{\kern 1pt} '(x) > 0$ для п. в. $x \in \Omega $.
(iii) Пусть $y \in {{\mathcal{E}}_{2}}[u]$. Тогда существует положительная постоянная $B$ такая, что
Доказательство. Из (EVP1) получаем, что ${{a}^{3}}u\theta {\kern 1pt} ' \in {{H}^{1}}(\Omega )$,
(3)
$({{a}^{3}}u\theta {\kern 1pt} '){\kern 1pt} '(x) + \lambda ({{a}^{2}}\theta )(x) = 0\quad {\text{п }}.\;{\text{в }}.\;{\text{н а }}\;\Omega .$(6)
$({{a}^{{ - 2}}}y{\kern 1pt} '){\kern 1pt} '(x) + \lambda \frac{{y(x)}}{{{{a}^{3}}(x)u(x)}} = 0\quad {\text{п }}.\;{\text{в }}.\;{\text{н а }}\;\Omega .$Пусть теперь $\theta \in {{\mathcal{E}}_{1}}[u]$, $\theta (x) > 0$ на $\Omega $. Из (5), (7) получаем, что
Известно (см. [4]), что первое собственное значение задачи (EVP2) является простым, а соответствующие ему собственные элементы сохраняют знак на $\Omega $. Кроме того, собственные функции задачи (EVP2), соответствующие различным собственным значениям, являются ортогональными относительно билинейной формыИз (5) также следует, что $y{\kern 1pt} '(x) < 0$ на $\Omega $. Из (3), (4) получаем, что
Принимая во внимание (6), получаем, что
Таким образом, справедливо следующее вариационное представление:
(VC2)
${{\lambda }_{1}}[u] = \mathop {min}\limits_{y \in W{\backslash }\{ \vartheta \} } \Lambda (u,y),\quad \Lambda (u,y) \triangleq \int\limits_0^1 {\frac{{\mathop {y{\kern 1pt} '}\nolimits^2 (x)}}{{{{a}^{2}}(x)}}} {\kern 1pt} dx{\text{/}}\int\limits_0^1 {\frac{{{{y}^{2}}(x)}}{{{{a}^{3}}(x)u(x)}}} {\kern 1pt} dx.$Пусть 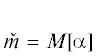 , $\hat {m} = M[\beta ]$,
, $\hat {m} = M[\beta ]$, 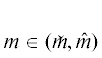 .
.
Предложение 1. Справедливы следующие утверждения.
(i) Функционал ${{\lambda }_{1}}[ \cdot ]$ является вогнутым на $U$ и строго вогнутым на $\mathcal{U}(m)$.
(ii) Функционал $1{\text{/}}{{\lambda }_{1}}[ \cdot ]$ является строго выпуклым на $U$.
Доказательство. Пусть
(9)
${{a}^{3}}(x)({{u}_{1}}(x) - {{u}_{2}}(x))\varphi _{t}^{'}(x) = ({{\lambda }_{1}}[{{u}_{1}}] - {{\lambda }_{1}}[{{u}_{2}}])\int\limits_x^1 {{{a}^{2}}(\xi ){{\varphi }_{t}}(\xi )d\xi } .$Утверждение (ii) получаем из следующих неравенств:
Из предложения 1 и [16, Теорема 2.1] следует, что существует единственное решение задачи (𝒫2). В дальнейшем это решение будем обозначать через ${{s}_{2}}[m]$.
Введем множество
Предложение 2. ПустьДоказательство. Задача (10), как нетрудно видеть, эквивалентна задаче
(11)
$\mathop {inf}\limits_{u \in \mathcal{V}(m)} \mathcal{F}[u],\quad \mathcal{F}[u] \triangleq \int\limits_0^1 {\frac{{{{\varphi }^{2}}(x)}}{{{{a}^{3}}(x)u(x)}}dx} .$Пусть $I = [\alpha ,\beta ]$. Введем функцию
определенную на $I \times \Omega \times \mathbb{R} \times {{\mathbb{R}}_{{ \geqslant 0}}}$. Зафиксируем пару $(x,\mu ) \in \Omega \times {{\mathbb{R}}_{{ \geqslant 0}}}$ и рассмотрим следующую задачу оптимизации: Поскольку $\varphi (x) > 0$ при $x \in \Omega $, то отображение $\Psi ( \cdot ,x,\varphi (x),\mu )$ является сильно выпуклым на множестве $I$. Следовательно, для $x \in \Omega $ задача (12) обладает единственным решением, которое обозначим через ${{u}_{\mu }}(x)$. Очевидно, что если $\mu = 0$, то ${{u}_{\mu }}(x) \equiv \beta $. Пусть теперь $\mu > 0$. Выберем число $\varepsilon (\mu ) > 0$ так, чтобы Пусть Легко проверить, что Таким образом, если $x \in G(\varepsilon (\mu ))$, то ${{u}_{\mu }}(x) = \alpha $. Пусть $F(\varepsilon (\mu )) = \Omega {\backslash }G(\varepsilon (\mu ))$. Так как функция $f(\xi ) = 1{\text{/}}\xi $ является сильно выпуклой на $I$, то найдется постоянная $E > 0$ такая, что(13)
$\frac{{\varepsilon (\mu )E}}{{\mathop {\hat {a}}\nolimits^3 }}{\text{|}}{{u}_{\mu }}(x{\kern 1pt} '') - {{u}_{\mu }}(x{\kern 1pt} '){\text{|}} \leqslant \mathop {sup}\limits_{\theta \in [0,1]} \left| {\Psi _{\xi }^{'}({{u}_{{\mu ,\theta }}}(x{\kern 1pt} ',x{\kern 1pt} ''),x{\kern 1pt} '',\varphi (x{\kern 1pt} ''),\mu ) - \Psi _{\xi }^{'}({{u}_{{\mu ,\theta }}}(x{\kern 1pt} ',x{\kern 1pt} ''),x{\kern 1pt} ',\varphi (x{\kern 1pt} '),\mu )} \right|,$(15)
$\begin{gathered} \frac{{\left| {{{u}_{\mu }}(x{\kern 1pt} '') - {{u}_{\mu }}(x{\kern 1pt} ')} \right|}}{{\left| {x{\kern 1pt} {\text{''}} - x{\kern 1pt} '{\kern 1pt} } \right|}} \leqslant K\left( {\mu ,\varepsilon (\mu ),{{{\left\| \varphi \right\|}}_{{{{C}^{{0,1}}}(\bar {\Omega })}}}} \right),\quad x{\kern 1pt} ' \in F(\varepsilon (\mu )),\quad x{\kern 1pt} '' \in \Omega ,\quad x{\kern 1pt} ' \ne x{\kern 1pt} ''; \\ \left| {{{u}_{\mu }}(x{\kern 1pt} '') - {{u}_{\mu }}(x{\kern 1pt} ')} \right| = 0,\quad x{\kern 1pt} ',x{\kern 1pt} '' \in G(\varepsilon (\mu )), \\ \end{gathered} $Рассмотрим отображение
В соответствии с [18, Следствие 1] задача (𝒫2) эквивалентна поиску седловой точки функционала $\Lambda ( \cdot , \cdot )$ на множестве $\mathcal{U}(m) \times (W{\backslash }\{ \vartheta \} )$. Точнее говоря, $(\hat {w},\hat {y})$ является седловой точкой функционала $\Lambda ( \cdot , \cdot )$ на $\mathcal{U}(m) \times (W{\backslash }\{ \vartheta \} )$, т.е. выполняются неравенства
(SP)
$\Lambda (u,\hat {y}) \leqslant \Lambda (\hat {w},\hat {y}) \leqslant \Lambda (\hat {w},y),\quad (u,y) \in \mathcal{U}(m) \times (W{\backslash }\{ \vartheta \} ),$(IP)
$\begin{gathered} {{y}_{n}} \in \mathop {\arg \min }\limits_{y \in S} \Lambda ({{u}_{n}},y),\quad S \triangleq \left. {\left\{ {y \in W:{{{\left\| y \right\|}}_{{C(\bar {\Omega })}}} = 1,} \right.\;y(x) > 0\;{\text{н а }}\;\Omega } \right\}, \\ {{u}_{{n + 1}}} \in \mathop {\arg \max }\limits_{u \in \mathcal{U}(m)} \Lambda (u,{{y}_{n}}). \\ \end{gathered} $Теперь мы можем сформулировать основной результат этого раздела, играющий ключевую роль в последующем изложении.
Теорема 1. Справедливы следующие утверждения.
(i) ${{s}_{2}}[m] \in {{C}^{{0,1}}}(\bar {\Omega })$.
(ii) Отображение
является непрерывным для $0 < \kappa < 1$, т.е. задача (𝒫2) является корректной в смысле Адамара относительно параметра $m$.(iii) Для фиксированного элемента ${{u}_{0}} \in \mathcal{U}(m)$ рассмотрим последовательность ${{\{ {{u}_{n}}\} }_{{n \in \mathbb{N}}}}$, определяемую итерационной процедурой (IP). Если
(17)
$\frac{1}{{{{u}_{n}}}}\;\mathop \rightharpoonup \limits^ * \;\frac{1}{{{{u}_{ * }}}}\quad в \quad \mathcal{U}(m),$Доказательство. Пусть $y \in {{\mathcal{E}}_{2}}[{{s}_{2}}[m]]$. Лемма 2 (iii) и неравенство Морри
(18)
${{\left\| z \right\|}_{{{{C}^{{1,1/2}}}(\bar {\Omega })}}} \leqslant C{{\left\| z \right\|}_{{{{H}^{2}}(\Omega )}}},\quad z \in {{H}^{2}}(\Omega ),\quad C > 0,$Пусть ${{m}_{n}} \to m$ в  , ${{u}_{n}} = {{s}_{2}}[{{m}_{n}}]$, ${{y}_{n}} \in S \cap {{\mathcal{E}}_{2}}[{{u}_{n}}]$, ${{\lambda }_{n}} = {{\lambda }_{1}}[{{u}_{n}}]$. Из леммы 1 следует, что последовательность $\{ {{\lambda }_{n}}\} $ является ограниченной. Кроме того,
, ${{u}_{n}} = {{s}_{2}}[{{m}_{n}}]$, ${{y}_{n}} \in S \cap {{\mathcal{E}}_{2}}[{{u}_{n}}]$, ${{\lambda }_{n}} = {{\lambda }_{1}}[{{u}_{n}}]$. Из леммы 1 следует, что последовательность $\{ {{\lambda }_{n}}\} $ является ограниченной. Кроме того,
(20)
$\frac{1}{{{{u}_{n}}}}\;\mathop \rightharpoonup \limits^ * \;\frac{1}{{{{u}_{ * }}}}\quad {\text{в }}\quad {{L}^{\infty }}(\Omega ),\quad {{y}_{n}} \to {{y}_{ * }}\quad {\text{в }}\quad {{C}^{1}}(\bar {\Omega }),\quad {{\lambda }_{n}} \to {{\lambda }_{ * }}.$${{v}_{n}}(x) = \left\{ {\begin{array}{*{20}{c}} {min\{ {{\tau }_{n}},u(x)\} ,\;\,{{m}_{n}} < m,} \\ {\max \{ {{\tau }_{n}},u(x)\} ,\;\,{{m}_{n}} \geqslant m,} \end{array}} \right.$
где ${{\tau }_{n}} \in I$ выбрано так, чтобы ${{v}_{n}} \in \mathcal{U}({{m}_{n}})$. Очевидно, ${{v}_{n}}(x) \to u(x)$ для п. в. $x \in \Omega $. Тогда
Доказательство (ii) будет завершено, если мы покажем, что ${{u}_{n}} \to {{u}_{ * }}$ в ${{C}^{{0,\kappa }}}(\bar {\Omega })$ для $0 < \kappa < 1$. Пусть 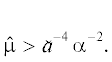 Из предложения 2 следует, что существует последовательность $\{ {{\mu }_{n}}\} \subset (0,\hat {\mu })$ такая, что для $x \in \Omega $
Из предложения 2 следует, что существует последовательность $\{ {{\mu }_{n}}\} \subset (0,\hat {\mu })$ такая, что для $x \in \Omega $
Аналогично докажем справедливость (iii). Пусть ${{y}_{n}} \in S \cap {{\mathcal{E}}_{2}}[{{u}_{n}}]$, ${{\lambda }_{n}} = {{\lambda }_{1}}[{{u}_{n}}]$. Принимая во внимание (17), (похожими рассуждениями) получаем, что последовательность $\{ {{y}_{n}}\} $ имеет единственный предел, который обозначим через ${{y}_{ * }}$. Очевидно, ${{y}_{ * }} \in S \cap {{\mathcal{E}}_{2}}[{{u}_{ * }}]$. Кроме того, ${{\lambda }_{n}} \to {{\lambda }_{1}}[{{u}_{ * }}]$. Из (IP) следует, что
Тогда2. ПРОЕКТИРОВАНИЕ КРЫЛЬЕВ МИНИМАЛЬНОГО ВЕСА
Следующее предложение устанавливает связь между задачами (𝒫1) и (𝒫2).
Предложение 3. Пусть 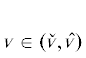 . Справедливы следующие утверждения.
. Справедливы следующие утверждения.
(i) Задача (𝒫1) обладает единственным решением $w$, причем $w \in {{C}^{{0,1}}}(\bar {\Omega })$, ${{\lambda }_{1}}[w] = v$.
(ii) Элемент $w$ является решением задачи (𝒫2) при $m = M[w]$.
(iii) Если $w$ – решение задачи (𝒫2), то $w$ также является решением задачи (𝒫1) с $v = {{v}_{{{\text{max}}}}}(m)$.
Доказательство. Существование решений задачи (𝒫1) следует из [16]. Пусть $w$ – решение этой задачи. Предположим, что ${{\lambda }_{1}}[w] > v$. Поскольку функционал ${{\lambda }_{1}}[ \cdot ]$ является непрерывным на множестве $U$ относительно сильной сходимости в ${{L}^{\infty }}(\Omega )$, то для достаточно малого числа $\delta > 0$ найдется элемент $u \in U$ такой, что
Пусть $m = M[w]$. Предположим, что существует элемент ${{u}_{ * }} \in \mathcal{V}(m)$ такой, что ${{\lambda }_{1}}[{{u}_{ * }}] > v$. Поскольку ${{u}_{ * }} \in U(v) \cap \mathcal{V}(m)$, то
Полученное противоречие показывает, что Следовательно, $w$ является решением задачи (𝒫2). Из предложения 1 и теоремы 1 теперь следует, что $w$ – единственное решение задачи (𝒫1), причем $w \in {{C}^{{0,1}}}(\bar {\Omega })$. Утверждение (iii) доказывается аналогично. Предложение доказано.В дальнейшем ${{s}_{1}}[v]$ будет обозначать решение задачи (𝒫1). Предложение 3 позволяет заменить задачу (𝒫1) задачей нахождения решения уравнения
на интервале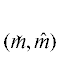 и последующим решением задачи (𝒫2) с $m = {{m}_{ * }}$ для определения оптимального решения. Поэтому крайне полезно выяснить, какими свойствами
обладает функция ${{v}_{{{\text{max}}}}}( \cdot )$. Это приводит нас к следующему предложению.
и последующим решением задачи (𝒫2) с $m = {{m}_{ * }}$ для определения оптимального решения. Поэтому крайне полезно выяснить, какими свойствами
обладает функция ${{v}_{{{\text{max}}}}}( \cdot )$. Это приводит нас к следующему предложению.
Предложение 4. Справедливы следующие утверждения.
(i) Функция  является непрерывной, возрастающей и строго вогнутой.
является непрерывной, возрастающей и строго вогнутой.
(ii) Функция $1{\text{/}}{{v}_{{{\text{max}}}}}( \cdot )$ является строго выпуклой.
Доказательство. Так как
то т.е. функция ${{v}_{{{\text{max}}}}}( \cdot )$ является возрастающей. Из предложения 3 следует, что функция ${{v}_{{{\text{max}}}}}( \cdot )$ является сюръективной. Таким образом, функция ${{v}_{{{\text{max}}}}}( \cdot )$ непрерывна на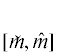 .
.
Пусть
Поскольку $t{{u}_{1}} + (1 - t){{u}_{2}} \in \mathcal{V}({{m}_{3}})$, тоНепосредственно из предложения 1 получаем, что
Теперь понятно, что свойства функции ${{v}_{{{\text{max}}}}}( \cdot )$ позволяют построить последовательность $\{ {{m}_{n}}\} $, сходящуюся к решению задачи (22) (например, с помощью метода деления отрезка пополам или метода Брента). Кроме того, утверждение (ii) теоремы 1 гарантирует, что соответствующая последовательность $\{ {{s}_{2}}[{{m}_{n}}]\} $ сходится к ${{s}_{2}}[{{m}_{ * }}]$ в ${{C}^{{0,\kappa }}}(\bar {\Omega })$ при $0 < \kappa < 1$.
Единственный вопрос, требующий ответа, заключается в следующем: является ли задача (𝒫1) корректной в смысле Адамара? Следующее утверждение дает на него ответ.
Предложение 5. Если ${{v}_{n}} \to {{v}_{ * }}$ в 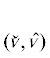 , то ${{s}_{1}}[{{v}_{n}}] \to {{s}_{1}}[{{v}_{ * }}]$ в ${{C}^{{0,\kappa }}}(\bar {\Omega })$ при $0 < \kappa < 1$.
, то ${{s}_{1}}[{{v}_{n}}] \to {{s}_{1}}[{{v}_{ * }}]$ в ${{C}^{{0,\kappa }}}(\bar {\Omega })$ при $0 < \kappa < 1$.
Доказательство. Поскольку функция ${{v}_{{{\text{max}}}}}( \cdot )$ является обратимой, то решение ${{s}_{1}}[v]$ задачи (𝒫1) в действительности может быть записано в виде ${{s}_{2}}\left[ {v_{{{\text{max}}}}^{{ - 1}}(v)} \right]$. Желаемый результат теперь следует из теоремы 1 и предложения 4.
3. ЧИСЛЕННЫЙ МЕТОД
Численный метод решения задачи (𝒫1), который мы использовали для получения численных результатов, приводимых в следующем
разделе, состоит из трех частей: (i) блок решения прямой задачи (EVP2), который численно определяет собственную пару, отвечающую наименьшему собственному
значению этой задачи; (ii) блок решения задачи (𝒫2), который находит приближенное решение $w$ этой задачи и значение ${{\lambda }_{1}}[w]$; (iii) определение значения 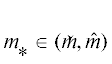 , для которого выполняется (22). Поскольку часть (iii) не должна вызывать вопросов,
мы рассмотрим оставшиеся.
, для которого выполняется (22). Поскольку часть (iii) не должна вызывать вопросов,
мы рассмотрим оставшиеся.
Перейдем к краткому описанию блока решения задачи (EVP2). Нами применяется стандартный метод последовательных приближений, состоящий в построении последовательностей $\{ {{\lambda }_{i}}\} $, $\{ {{y}_{i}}\} $, элементы которых определяются формулами
(23)
$\begin{gathered} ({{a}^{{ - 2}}}y_{{i + 1}}^{'}){\kern 1pt} '(x) + \frac{{{{y}_{i}}(x)}}{{{{a}^{3}}(x)u(x)}} = 0\quad {\text{н а }}\quad \Omega ,\quad y_{{i + 1}}^{'}(0) = 0,\quad {{y}_{{i + 1}}}(1) = 0, \\ {{\lambda }_{{i + 1}}} = \Lambda (u,{{y}_{{i + 1}}}), \\ \end{gathered} $Задачу (23) заменим конечно-разностной схемой. С этой целью определим равномерную сетку с шагом $h = 1{\text{/}}N$ на интервале $\Omega $. Далее, будем представлять функции $a$, $u$, ${{y}_{i}}$ их значениями в узлах сетки
В дальнейшем через $y_{{i + 1}}^{j}$ будем обозначать численное решение задачи (23) в узле сетки ${{x}_{j}}$, а также писать ${{a}_{j}}$, ${{u}_{j}}$ вместо $a({{x}_{j}})$, $u({{x}_{j}})$ соответственно. Конечно-разностное представление уравнения в (23) может быть записано в виде следующей системы линейных уравнений:(DEj)
$\frac{{{{p}_{{j + 1}}}}}{h}y_{{i + 1}}^{{j + 1}} - \frac{{{{p}_{{j + 1}}} + {{p}_{j}}}}{h}y_{{i + 1}}^{j} + \frac{{{{p}_{j}}}}{h}y_{{i + 1}}^{{j - 1}} = {{f}_{j}} \triangleq - \frac{{y_{i}^{j}}}{{a_{j}^{3}{{u}_{j}}}},$Блок решения задачи (𝒫2) полностью основан на итерационной процедуре (IP) и состоит из следующих шагов.
1. Задается $\varepsilon > 0$, 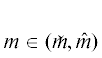 и начальное приближение ${{u}_{0}} \in \mathcal{U}(m) \cap C(\bar {\Omega })$.
и начальное приближение ${{u}_{0}} \in \mathcal{U}(m) \cap C(\bar {\Omega })$.
2. Вычисляется ${{y}_{n}} \in {{\mathcal{E}}_{2}}[{{u}_{n}}] \cap S$ и ${{\lambda }_{1}}[{{u}_{n}}]$, где $n = 0$.
3. Численно находится корень ${{\mu }_{ * }}$ уравнения
${{\mathcal{H}}_{m}}(\mu ) = 0\quad {\text{н а }}\quad [0,\hat {\mu }]$
и определяется функция ${{u}_{{{{\mu }_{ * }}}}}$, которая выступает в качестве нового приближения ${{u}_{{n + 1}}}$.
4. Для имеющегося приближения ${{u}_{{n + 1}}}$ вычисляется ${{y}_{{n + 1}}} \in {{\mathcal{E}}_{2}}[{{u}_{{n + 1}}}] \cap S$ и ${{\lambda }_{1}}[{{u}_{{n + 1}}}]$.
5. Если $\left| {{{\lambda }_{1}}[{{u}_{{n + 1}}}] - {{\lambda }_{1}}[{{u}_{n}}]} \right| < \varepsilon $ и ${{\left\| {{{u}_{{n + 1}}} - {{u}_{n}}} \right\|}_{{C(\bar {\Omega })}}} < \varepsilon $, то ${{u}_{{n + 1}}}$ берется в качестве приближенного решения задачи (𝒫2). В противном случае осуществляется переход к шагу 3 с $n: = n + 1$.
Дадим несколько поясняющих замечаний. Для того чтобы вычислить значение функции ${{\mathcal{H}}_{m}}( \cdot )$ в заданной точке $\mu $, необходимо сначала решить задачу (12) с $\varphi = {{y}_{n}}$, чтобы определить ${{u}_{\mu }}(x)$ в точках $x = {{x}_{j}}$. Таким образом, функция ${{\mathcal{H}}_{m}}( \cdot )$ неявно зависит от ${{y}_{n}}$ на каждой итерации в описанном алгоритме. Решение задачи (12) с $\varphi = {{y}_{n}}$ требует нахождения корня ${{\xi }_{ * }}(x)$ уравнения
который определяется формулой Тогда, как легко видеть,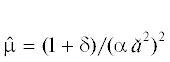 , где $\delta > 0$.
, где $\delta > 0$.
Это завершает описание метода, используемого для численного решения задачи (𝒫1).
4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
Рассмотрим численные результаты для различных значений параметра $v$ в случае прямоугольных ($a(x) \equiv 1$) и трапециевидных ($a(x) \equiv 1 - x{\text{/}}2$) крыльев.
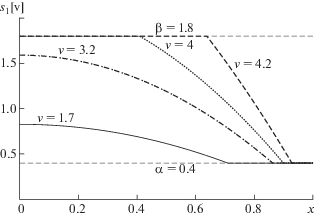
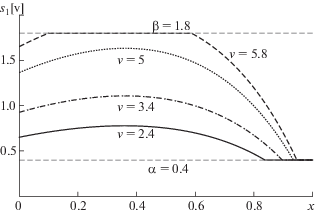
На фиг. 1 представлены оптимальные распределения толщины обшивки прямоугольного крыла ($\alpha = 0.4$, $\beta = 1.8$, $a(x) \equiv 1$), отвечающие значениям параметра $v \in \{ 1.7,3.2,4,4.2\} $, полученные с помощью численного метода, описанного в разд. 3. Качественное поведение оптимальных решений для $v \in \{ 1.7,3.2\} $ хорошо сочетается с численными результатами работы [6], где исследовался случай $\beta = + \infty $. На фиг. 2 изображены оптимальные распределения толщины обшивки трапециевидного крыла ($\alpha = 0.4$, $\beta = 1.8$, $a(x) = 1 - x{\text{/}}2$), отвечающие значениям параметра $v \in \{ 2.4,3.4,5,5.8\} $. Как мы видим, в отличие от прямоугольных крыльев здесь максимальное значение толщины обшивки смещено от точки закрепления крыла ($x = 0$). Необходимо отметить, что при выполнении всех вычислительных экспериментов последовательность приближений, получаемая с помощью процедуры (IP), демонстрировала поточечную сходимость.
Фиг. 2.
Оптимальные распределения толщины обшивки трапециевидного крыла ($a(x) \equiv 1 - x{\text{/}}2$).
Наконец, представляет интерес рассмотреть поведение функции ${{v}_{{{\text{max}}}}}( \cdot )$. Ее график для прямоугольных и трапециевидных крыльев изображен на фиг. 3 и фиг. 4 соответственно.
Фиг. 3.
Зависимость экстремального значения скорости дивергенции ${{v}_{{{\text{max}}}}}( \cdot )$ от $m$ при $\alpha = 0.4$, $\beta = 1.8$, $a(x) \equiv 1$.
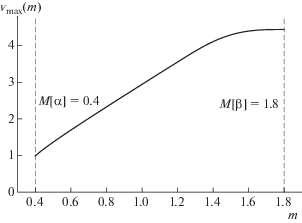
Фиг. 4.
Зависимость экстремального значения скорости дивергенции ${{v}_{{{\text{max}}}}}( \cdot )$ от $m$ при $\alpha = 0.4$, $\beta = 1.8$, $a(x) \equiv 1 - x{\text{/}}2$.
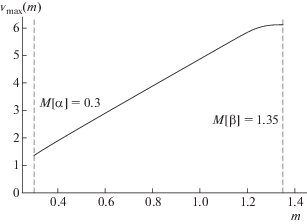
Как мы видим из фиг. 3, эта зависимость является “почти линейной” на отрезке $[0.4,1.4]$ по переменной $m$ (напомним, что функция ${{v}_{{{\text{max}}}}}( \cdot )$ является строго вогнутой в соответствии с предложением 4). На отрезке $[1.4,1.8]$ по переменной $m$ (фиг. 3) оптимизация менее “эффективна”, так как незначительный прирост параметра $v$ приводит к существенному увеличению массы обшивки оптимального крыла. Необходимо подчеркнуть, что описанное поведение функции ${{v}_{{{\text{max}}}}}( \cdot )$ характерно для всех проведенных нами вычислительных экспериментов – исходный отрезок разбивается на две части: в первой функция ${{v}_{{{\text{max}}}}}( \cdot )$ близка к линейной; во второй ее рост значительно замедляется.
ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В этой работе мы рассмотрели задачу определения оптимального распределения толщины обшивки тонкого прямого крыла, которое минимизирует массу обшивки крыла при условии, что выполняется ограничение на скорость дивергенции. Как уже упоминалось в разд. 2, эта экстремальная задача сводится к определению значения ${{m}_{ * }}$, для которого выполняется соотношение (22). Это означает, что исходная задача может быть заменена последовательностью вспомогательных задач оптимизации вида (𝒫2). В соответствии с [18] задача (𝒫2), в свою очередь, эквивалентна задаче нахождения седловой точки функционала $\Lambda ( \cdot , \cdot )$. Поэтому вполне естественно использовать итерационную процедуру (IP) для решения задачи (𝒫2). Как нам известно из разд. 1 и разд. 2, для получения нового приближения управляющей переменной в рамках этой процедуры, можно просто применить тот или иной метод отыскания корня. Интересно заметить, что предложенный нами алгоритм для решения задачи (𝒫1) в действительности не использует каких-либо методов оптимизации. Результаты этой работы позволили свести исходную экстремальную задачу к задаче нахождения корня некоторой непрерывной функции.
Разумеется, введенный в этой работе подход имеет несколько обобщений в различных направлениях. Во-первых, хотя мы концентрировали наше внимание только на случае тонких прямых крыльев, нетрудно адаптировать полученные результаты на ситуацию, когда рассматривается более общая краевая задача. Такая задача, вовлекающая большее число параметров проектирования, рассмотрена в [5]. Во-вторых, очевидно, что подобно тому, как это сделано в разд. 1, можно исследовать случай линейных эллиптических операторов в дивергентной форме, который будет рассмотрен в последующей работе. Наконец, стоит отметить, что подход, предложенный в этой работе, без труда может быть применен к аналогичным задачам оптимального проектирования для шарнирно опертых колонн, а также колонн, у которых один конец защемлен, а другой свободен. Постановка соответствующих задач оптимизации в случае без ограничений приводится в [21].
Список литературы
Бисплингхофф Р.Л., Эшли Х., Халфмэн Р.Л. Аэроупругость. М.: Изд-во иностр. лит., 1958.
McIntosh S.C., Eastep F.E. Design of minimum-mass structures with specified stiffness properties // AIAA Journal. 1968. T. 6. № 5. C. 962–964.
Арутюнов Ю.А., Сейранян А.П. Применение принципа максимума к задаче минимизации веса крыла летательного аппарата // Уч. зап. ЦАГИ. 1973. Т. 4. № 1. С. 55–70.
Шубин М.A. Лекции об уравнениях математической физики. М.: МЦНМО, 2003.
Баничук Н.В. Минимизация веса крыла при ограничении по скорости дивергенции // Уч. зап. ЦАГИ. 1978. Т. 9. № 5. С. 97–103.
Armand J.-L., Vitte W.J. Foundations of aeroelastic optimization and some applications to continuous systems. Stanford: Stanford University, 1970.
Брайсон А.Е. Прикладная теория оптимального управления. М.: Мир, 1972.
Васильев Ф.П. Методы оптимизации. М.: Факториал Пресс, 2002.
Муравей Л.А., Петров В.М., Романенков А.М. Оптимальное управление нелинейными процессами в задачах математической физики. М.: МАИ, 2018.
Баничук Н.В. Оптимизация форм упругих тел. М.: Наука, 1980.
Henrot A. Extremum problems for eigenvalues of elliptic operators. Basel–Boston–Berlin: Birkhäuser Verlag, 2006.
Troesch B.A. An isoperimetric sloshing problem // Communications on Pure and Applied Math. 1965. T. 18. C. 319–338.
Bandle C. Extremal problems for eigenvalues of the Sturm–Liouville type // General Inequalities 5. 1987. C. 319–336.
Егоров Ю.В., Кондратьев В.А. Об оценках первого собственного значения в некоторых задачах Штурма–Лиувилля // Успехи матем. наук. 1996. Т. 51. № 3. С. 73–144.
Крейн М.Г. О некоторых задачах на максимум и минимум для характеристических чисел и о ляпуновских зонах устойчивости // Прикл. матем. и механ. 1951. Т. 15. № 3. С. 323–348.
Goncharov V.Yu. Existence criteria in some extremum problems involving eigenvalues of elliptic operators // J. Sib. Fed. Univ. Math. Phys. 2016. T. 9. № 1. C. 37–47.
Измаилов А.Ф. Чувствительность в оптимизации. М.: Физматлит, 2006.
Гончаров В.Ю. Задачи максимизации собственных значений линейных эллиптических операторов // Сиб. электрон. матем. изв. 2017. Т. 14. С. 1349–1372.
Коллатц Л. Функциональный анализ и вычислительная математика. М.: Мир, 1969.
Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.
Tadjbakhsh I., Keller J.B. Strongest columns and isoperimetric inequalities for eigenvalues // J. Appl. Mech. 1962. T. 29. C. 159–164.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики