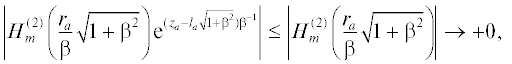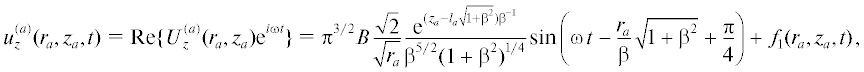Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 597-610

1. ПОСТАНОВКА ЗАДАЧИ. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ

Пусть упругая среда занимает полупространство. В случае малых относительных перемещений уравнения Ламэ имеют вид

Здесь $u$ – вектор перемещения, $\lambda $, $\mu $, $\rho $ – соответственно параметры Ламэ и плотность упругой среды. Пусть к свободной поверхности $S$ упругой среды приложена внешняя нагрузка $np$, где $n$ – вектор внешней нормали к $S$. Следуя [1], граничные условия на свободной поверхности зададим в виде где $g$ – ускорение силы тяжести (вектор силы тяжести противоположен вектору $n$). Считаем, что $p$ зависит от точки свободной поверхности и времени.

Согласно теории предельного перехода будем считать, что коэффициент Пуассона $\nu = \frac{\lambda }{{2(\lambda + \mu )}} \to \frac{1}{2} - 0$, а модуль Юнга $E = (3\lambda + 2\mu )(1 - 2\nu ) \to + 0$ так, что отношение $\frac{E}{{1 - 2\nu }}$ остается конечным, не равным нулю. Тем самым $\mu = \frac{E}{{2(1 + \nu )}} \to + 0$, что означает отсутствие в упругой среде волн сдвига. Тогда уравнения для перемещений и граничные условия на $S$ примут соответственно вид

Представим вектор перемещений в виде $u = grad\varphi $ и введем цилиндрическую систему координат $(r,\theta ,z)$, для которой поверхность $S$ совпадает с плоскостью $z = 0$ и орт оси $z$ сонаправлен с вектором $n$. Считая, что внешняя нагрузка имеет вид $p(r,t) = {{p}_{0}}f(r)cos\omega t$, где $f(r)$ –заданная функция, допускающая разложение в интеграл Фурье–Бесселя, а ${{p}_{0}}$, $\omega $ – заданные постоянные величины, получаем скалярную задачу

которая должна быть дополнена граничными условиями на бесконечности. А именно, потребуем, чтобы функция $\varphi $ описывала уходящую в бесконечность волну и $\left| \varphi \right| \to + 0$ при ${{({{r}^{2}} + {{z}^{2}})}^{{1/2}}} \to + \infty $.

Так как нагрузка не зависит от угловой переменной $\theta $, то периодическое по времени решение будем искать в виде

Для комплексной амплитуды $\Phi (r,z)$ получим Величина ${{k}_{R}}$ носит название размерного полюса Рэлея.

Далее считаем, что функция $f(r)$ имеет вид

Введем безразмерные переменные и безразмерную комплексную амплитуду по формулам

Обозначим Тогда для ${{\Phi }^{{(a)}}}$ получим задачу где Заметим, что для образа Фурье–Бесселя данной функции имеет место формула [2] Поэтому будем искать решение задачи (1) в виде комплексного интеграла где $L$ – кривая, состоящая из отрезка ${{\gamma }^{{(u)}}}$: $[0,1 - {{\rho }_{1}}]$ на верхнем берегу разреза $[ - 1,1]$, отрезка ${{\gamma }_{3}}$: $[1 + {{\rho }_{1}},{{\kappa }_{R}} - {{\rho }_{2}}]$, луча ${{\gamma }_{5}}$: $[{{\kappa }_{R}} + {{\rho }_{2}}, + \infty )$ и полуокружностей ${{C}_{1}}$: $\kappa = 1 + {{\rho }_{1}}{{{\text{e}}}^{{is}}}$, ${{C}_{2}}$: $\kappa = {{\kappa }_{R}} + {{\rho }_{2}}{{{\text{e}}}^{{is}}}$, $s \in [0,\pi ]$, пробегаемых по часовой стрелке, ${{J}_{0}}(\kappa {{r}_{a}})$ – функция Бесселя нулевого индекса аргумента $\kappa {{r}_{a}}$, а под $\sqrt {{{\kappa }^{2}} - 1} : = y(\kappa )$ понимается однозначная аналитическая ветвь двузначной функции $\sqrt {{{\kappa }^{2}} - 1} $, определенная на всей комплексной плоскости с разрезом $[ - 1,1]$ и положительная при действительном $\kappa > 1$. На ${{\gamma }^{{(u)}}}$ функция $y(\kappa )$ доопределена своими предельными значениями.

Покажем, что интеграл (2) удовлетворяет уравнению в (1) и граничному условию при $z = 0$. Для этого убедимся, что данный интеграл можно дважды дифференцировать по параметрам ${{r}_{a}}$ и ${{z}_{a}}$ под знаком интеграла. Представим данный интеграл в виде суммы пяти интегралов: по отрезкам, лучу и полуокружностям. Рассмотрим сначала интеграл по лучу ${{\gamma }_{5}}$ ($\kappa = x \geqslant {{\kappa }_{R}} + {{\rho }_{2}}$). Подынтегральная функция

непрерывна по совокупности переменных $({{r}_{a}},x)$ при фиксированном ${{z}_{a}}$ и по $({{z}_{a}},x)$ при фиксированном ${{r}_{a}}$ вместе с частными производными $\frac{{\partial h}}{{\partial {{r}_{a}}}}$, $\frac{{\partial h}}{{\partial {{z}_{a}}}}$, $\frac{{{{\partial }^{2}}h}}{{\partial r_{a}^{2}}}$, $\frac{{{{\partial }^{2}}h}}{{\partial z_{a}^{2}}}$. Интеграл вдоль ${{\gamma }_{5}}$ от $h({{r}_{a}},{{z}_{a}},x)$ сходится при любом фиксированном ${{r}_{a}} > 0$ по признаку сравнения Интегралы вдоль ${{\gamma }_{5}}$ от $\frac{{\partial h}}{{\partial {{r}_{a}}}}$, $\frac{{\partial h}}{{\partial {{z}_{a}}}}$ сходятся равномерно соответственно по ${{r}_{a}} > 0$, ${{z}_{a}} \leqslant 0$ по признаку Вейерштрасса. Это следует из оценок

Покажем, что интегралы от $\frac{{{{\partial }^{2}}h}}{{\partial r_{a}^{2}}}$, $\frac{{{{\partial }^{2}}h}}{{\partial z_{a}^{2}}}$ вдоль ${{\gamma }_{5}}$ сходятся равномерно соответственно по ${{r}_{a}} \geqslant \delta $, ${{z}_{a}} \leqslant 0$, где $\delta $ – любое положительное число. Имеем

Мы воспользовались соотношениями [2] $J_{0}^{'}(x) = - {{J}_{1}}(x)$, $J_{1}^{'}(x) = {{J}_{0}}(x) - \frac{1}{x}{{J}_{1}}(x)$.

Таким образом, интеграл вдоль ${{\gamma }_{5}}$ от $h({{r}_{a}},{{z}_{a}},x)$ имеет непрерывные частные производные по ${{r}_{a}}$, ${{z}_{a}}$ первого и второго порядков и они равны интегралам от соответствующих частных производных функции $h({{r}_{a}},{{z}_{a}},x)$.

Рассмотрим функцию трех комплексных переменных

где $\tilde {r}$, $\tilde {z}$ изменяются на всей комплексной плоскости $С $, а $\kappa \in C_{k}^{ - }$ $(k = 1,2)$ (индекс $a$ для краткости опускаем). Она аналитична по переменной $\tilde {r}$ на всей комплексной плоскости при фиксированных $\tilde {z} \in \mathbb{C}$, $\kappa \in C_{k}^{ - }$ и по переменной $\tilde {z}$ на всей комплексной плоскости при фиксированных $\tilde {r} \in \mathbb{C}$, $\kappa \in C_{k}^{ - }$. То же самое относится к частным производным $\frac{{\partial h}}{{\partial{ \tilde {r}}}}$, $\frac{{\partial h}}{{\partial{ \tilde {z}}}}$, $\frac{{{{\partial }^{2}}h}}{{\partial {{{\tilde {r}}}^{2}}}}$, $\frac{{{{\partial }^{2}}h}}{{\partial {{{\tilde {z}}}^{2}}}}$. Кроме того, и сама функция $h(\tilde {r},\tilde {z},\kappa )$ и ее указанные частные производные непрерывны по совокупности двух переменных $(\tilde {r},\kappa )$, $(\tilde {z},\kappa )$ при фиксированной третьей. Поэтому интегралы вдоль $C_{k}^{ - }$ от $h(\tilde {r},\tilde {z},\kappa )$ аналитичны на всей комплексной плоскости по переменным $\tilde {r}$ и $\tilde {z}$, а частные производные первого и второго порядков от указанных интегралов равны интегралам от частных производных функции $h(\tilde {r},\tilde {z},\kappa )$ всюду на $\mathbb{C}$, а стало быть и при $\tilde {r} = {{r}_{a}} > 0$, $\tilde {z} = {{z}_{a}} \leqslant 0$.

Аналогичным образом доказывается, что интегралы вдоль ${{\gamma }^{{(u)}}}$, ${{\gamma }_{3}}$ также можно дифференцировать два раза по параметрам ${{r}_{a}} > 0$ и ${{z}_{a}} \leqslant 0$ под знаком интеграла. Таким образом,

т.е. $\Delta {{\Phi }^{{(a)}}} + {{\Phi }^{{(a)}}} = 0$.

Покажем, что граничное условие при ${{z}_{a}} = 0$ $({{r}_{a}} > 0)$ также удовлетворяется. Имеем

Мы заменили интегралы по $C_{1}^{ - }$, $C_{2}^{ - }$ интегралами по отрезкам $[1 - {{\rho }_{1}},\;1 + {{\rho }_{1}}]$, $[{{\kappa }_{R}} - {{\rho }_{2}},\;{{\kappa }_{R}} + {{\rho }_{2}}]$ соответственно в силу аналитичности функции ${{J}_{0}}(\kappa {{r}_{a}})\kappa {{{\text{e}}}^{{ - {{l}_{a}}\kappa }}}$ по переменной $\kappa $, а затем воспользовались соотношением [2]

Для безразмерных комплексных амплитуд перемещений $U_{z}^{{(a)}}({{r}_{a}},{{z}_{a}})$ и $U_{r}^{{(a)}}({{r}_{a}},{{z}_{a}})$ получаем выражения

Заметим, что формальное интегральное представление решения задачи Лэмба в случае распределенной нагрузки для $0 < \nu < 1{\text{/}}2$ получено в [3]. Там же проведено сравнение аналитического и численного решений. В работе [4] начально-краевая задача Лэмба для полупространства решалась методом конечных элементов.

2. АСИМПТОТИЧЕСКИЕ ОЦЕНКИ ДЛЯ КОМПЛЕКСНЫХ АМПЛИТУД

Функция $y(\kappa )$ положительна при $\kappa = x > 1$. Тогда для ее значений при $\kappa = \pm i\sigma $, $\sigma > 0$, и на берегах разреза $[ - 1,1]$, т.е. при $\kappa = x \pm i0$, $ - 1 < x < 1$, будем соответственно иметь

Проведем на комплексной плоскости $\kappa $ дополнительный разрез по лучу $( - \infty , - 1]$. Функции Бесселя в подынтегральных выражениях в (2) и (3) представим в виде полусуммы функций Ханкеля I и II рода под которыми понимаем такие однозначные аналитические в области $ - \pi < arg\kappa < \pi $ функции, что при $\kappa = x > 0$ их полусумма действительна. Итак, подынтегральные функции комплексной переменной $\kappa $ мы будем рассматривать на всей комплексной плоскости с разрезом вдоль луча $( - \infty ,1]$. Это подобласть области определения функции $y(\kappa )$. Заметим, что значения функции $H_{m}^{{(n)}}(\kappa {{r}_{a}})$, $m = 0,\;1$, $n = 1,\;2$, при $\kappa = x \pm i0$, $0 < x < 1$ совпадают в силу ее аналитичности в области $ - \pi < arg\kappa < \pi $.

Обозначим через ${{C}_{R}}$ и $C_{R}^{'}$ дуги окружностей $\kappa = R{{{\text{e}}}^{{is}}}$, $s \in [0,\pi {\text{/}}2]$ и $\kappa = R{{{\text{e}}}^{{is}}}$, $s \in [ - \pi {\text{/}}2,0]$, через ${{l}_{R}}$, $l_{R}^{'}$, ${{\gamma }_{R}}$ отрезки $[i{{\rho }_{3}},iR]$, $[ - iR, - i{{\rho }_{4}}]$, $[{{\kappa }_{R}} + {{\rho }_{2}},R]$ соответственно через $\gamma _{1}^{{(u)}}$, $\gamma _{2}^{{(u)}}$ отрезки $[{{\rho }_{3}},\;1 - {{\rho }_{1}}]$, $[1 - {{\rho }_{1}},\;1 - {{\rho }_{5}}]$ (${{\rho }_{5}} < {{\rho }_{1}}$) на верхнем берегу разреза $( - \infty ,1]$ соответственно через $\gamma _{4}^{{(l)}}$ отрезок $[{{\rho }_{4}},\;1 - {{\rho }_{5}}]$ на нижнем берегу разреза $( - \infty ,1]$, проходимый справа налево, через ${{C}_{3}}$ и ${{C}_{4}}$ дуги окружностей $\kappa = {{\rho }_{3}}{{{\text{e}}}^{{is}}}$, $s \in [0,\pi {\text{/}}2]$ и $\kappa = {{\rho }_{4}}{{{\text{e}}}^{{is}}}$, $s \in [ - \pi {\text{/}}2,0]$ и через ${{C}_{5}}$ окружность $\kappa = 1 + {{\rho }_{5}}{{{\text{e}}}^{{is}}}$, $s \in [ - \pi ,\pi ]$.

Введем также обозначения

Интегралы от $h_{m}^{{(n)}}$ и ${{h}^{{(n)}}}(\kappa )$ вдоль $L$ будем понимать как предел при $R \to + \infty $, ${{\rho }_{3}} \to + 0$ интегралов Пусть ${{\Gamma }_{1}}$ – замкнутая кусочно гладкая кривая вида ${{\Gamma }_{1}} = {{L}_{1}} \cup {{C}_{R}} \cup l_{R}^{ - }$, проходимая против часовой стрелки. По теореме Коши имеем Покажем, что Пусть $\kappa = R{{{\text{e}}}^{{is}}}$, $s \in [0,\pi {\text{/}}2]$. Тогда Для достаточно большого $R$ и любого $s \in [0,\pi {\text{/}}2]$ справедливы неравенства Мы учли, что $\arg (\sqrt {{{R}^{2}}{{{\text{e}}}^{{2is}}} - 1} )$ изменяется на сегменте $[0,\pi ]$. Поэтому Считая, что $R \gg 1$, воспользуемся асимптотикой функции Ханкеля [2]. Вместо (6) будем иметь ${{A}_{2}}$ – некоторое положительное число, не зависящее от $R$, $A = {{A}_{1}} + {{A}_{2}}$. Интеграл в правой части (7) оценивается также, как при доказательстве леммы Жордана [5] Отсюда т.е. ${{I}_{{Rm}}} \to + 0$ при $R \to + \infty $.

Покажем, что

Пусть $\kappa = {{\rho }_{3}}{{{\text{e}}}^{{is}}}$, $s \in [0,\pi {\text{/}}2]$. Тогда Для ${{\rho }_{3}} \in (0,1)$ и любого $s \in [0,\pi {\text{/}}2]$ справедливы неравенства Оценим $\beta \sqrt {\rho _{3}^{2}{{{\text{e}}}^{{2is}}} - 1} - 1$ при достаточно малом ${{\rho }_{3}}$ и любом $s \in [0,\pi {\text{/}}2]$. Для абсолютной величины будем иметь где Следовательно, Отметим, что правая часть (8) стремится к ${{({{\beta }^{2}} - \beta + 1)}^{{1/2}}} > 0$ при ${{\rho }_{3}} \to + 0$.

Представим функции Ханкеля в виде

где ${{N}_{m}}(\kappa )$ – функция Неймана индекса $m$. Известно [2], что при $arg\kappa \in ( - \pi ,\pi )$где $f(\kappa )$, $g(\kappa )$ – целые функции, $ln\kappa = ln\left| \kappa \right| + iarg\kappa $, а $C$ – постоянная Эйлера. Тогда для достаточно малого ${{\rho }_{3}}$ и всех $s \in [0,\pi {\text{/}}2]$ где ${{C}_{1}}({{r}_{a}})$, ${{C}_{2}}({{r}_{a}})$ не зависят от ${{\rho }_{3}}$. Мы воспользовались тем, что функции ${{J}_{m}}(\kappa {{r}_{a}})$, $f(\kappa {{r}_{a}})$, $g(\kappa {{r}_{a}})$ ограничены в окрестности точки $\kappa = 0$ при любом фиксированном ${{r}_{a}}$. Следовательно, т.е. ${{I}_{{3m}}} \to + 0$ при ${{\rho }_{3}} \to + 0$. Аналогичным образом доказывается, что интегралы по ${{C}_{R}}$ $C_{3}^{ - }$ от ${{h}^{{(1)}}}(\kappa )$ также стремятся к нулю. Перейдем в (4) к пределу при $R \to + \infty $, ${{\rho }_{3}} \to + 0$. Тогда где $I_{z}^{{(1)}}$, $I_{r}^{{(1)}}$, ${{I}^{{(1)}}}$ есть интегралы по неотрицательной части мнимой оси. Они имеют вид ${{K}_{0}}({{r}_{a}}\sigma )$, ${{K}_{1}}({{r}_{a}}\sigma )$ – функции Макдональда нулевого и первого индексов. Мы воспользовались соотношениями [2]

Интегралы от $h_{m}^{{(2)}}(\kappa )$ вдоль ${{L}_{1}}$ представим в виде суммы интегралов вдоль ${{L}_{2}} = C_{3}^{ - } \cup \gamma _{1}^{{(u)}}$ и ${{L}_{3}} = C_{1}^{ - } \cup {{\gamma }_{3}} \cup C_{2}^{ - } \cup {{\gamma }_{R}}$. Пусть ${{\Gamma }_{2}}$ – замкнутая кусочно гладкая кривая вида ${{\Gamma }_{2}} = \gamma _{2}^{{(u)}} \cup C_{5}^{ - } \cup \gamma _{4}^{{(l)}} \cup $ $ \cup \;C_{4}^{ - } \cup l_{R}^{'} \cup C_{R}^{'} \cup L_{3}^{ - }$, проходимая против часовой стрелки. По основной теореме теории вычетов

Подобно тому, как это было сделано выше, можно показать, что

Покажем, что Пусть $\kappa = 1 + {{\rho }_{5}}{{{\text{e}}}^{{is}}}$, $s \in [ - \pi ,\pi ]$. Тогда имеем Для достаточно малого ${{\rho }_{5}}$ и любого $s \in [ - \pi ,\pi ]$ справедливы неравенства

Функции $H_{m}^{{(2)}}({{r}_{a}}\kappa )$ аналитичны в окрестности точки $\kappa = 1$, а следовательно, ограничены там, т.е. для любого $s \in [ - \pi ,\pi ]$, любого достаточно малого ${{\rho }_{5}}$ и фиксированного ${{r}_{a}}$

Поэтому где $C{\text{'}}({{r}_{a}}) = max\left\{ {{{C}_{{20}}}({{r}_{a}}),{{C}_{{21}}}({{r}_{a}})} \right\}$, т.е. ${{I}_{{5m}}} \to + 0$ при ${{\rho }_{5}} \to + 0$. Точно также доказывается, что интеграл по ${{C}_{5}}$ от ${{h}^{{(2)}}}(\kappa )$ стремится к нулю.

Перейдем в равенствах (10) к пределу при $R \to + \infty $, ${{\rho }_{4}} \to + 0$, ${{\rho }_{5}} \to + 0$. Учитывая, что

окончательно получаем где $I_{z}^{{(2)}}$, $I_{r}^{{(2)}}$, ${{I}^{{(2)}}}$ – интегралы по неположительной мнимой оси, ${{I}_{{z(u)}}}$, ${{I}_{{z(l)}}}$, ${{I}_{{r(u)}}}$, ${{I}_{{r(l)}}}$, ${{I}_{{(u)}}}$, ${{I}_{{(l)}}}$ – интегралы по отрезкам на берегах разреза. Указанные интегралы имеют вид ${{K}_{0}}({{r}_{a}}\sigma )$, ${{K}_{1}}({{r}_{a}}\sigma )$ – функции Макдональда нулевого и первого индексов. Мы воспользовались соотношениями [2] в виде Отметим, что интегралы по отрезкам $[0,\;1 - {{\rho }_{1}}]$ и $[1 - {{\rho }_{1}},\;1]$ на верхнем берегу разреза мы объединили в один по отрезку $[0,1]$. Для комплексных амплитуд получаем формулы

Покажем, что при ${{r}_{a}} \gg 1$ интегралы в правых частях (11), (12) асимптотически малы по сравнению с вычетами в полюсе Рэлея ${{\kappa }_{R}}$.

Оценим сначала интегралы $I_{z}^{{(m)}}$, $I_{r}^{{(m)}}$, ${{I}^{{(m)}}}$ ($m = 1,2$). При любых ${{r}_{a}} > 0$, ${{z}_{a}} \leqslant 0$ имеем

Мы воспользовались формулой [2] в виде при $\nu = 0$, $\mu = 1,2$ и при $\nu = 1$, $\mu = 2$. Отсюда получаем, что при любых ${{r}_{a}} > 0$, ${{z}_{a}} \leqslant 0$, а следовательно, при ${{r}_{a}} \gg 1$ и любом ${{z}_{a}} \leqslant 0$. Оценим интегралы по берегам разреза. Рассмотрим, например, интеграл ${{I}_{{z(u)}}}$. Представим его в виде Тогда Последнее неравенство справа имеет место, поскольку для непрерывной на сегменте $[0,\sqrt {{{r}_{a}}} ]$ функции $\left| {H_{0}^{{(2)}}(s)} \right|s$

На сегменте $[1{\text{/}}\sqrt {{{r}_{a}}} ,\;1]$ при ${{r}_{a}} \gg 1$ значение аргумента $x{{r}_{a}}$ функции Ханкеля $H_{0}^{{(2)}}(x{{r}_{a}})$ также много больше единицы. Поэтому для всех $x$ из указанного сегмента функцию Ханкеля можно представить асимптотической формулой [2]. Для ${{I}_{2}}$ будем иметь

где Интегралы в (13) оцениваются однотипно. Рассмотрим, например, первый, обозначив его через ${{I}_{{21}}}$. Имеем где Отметим, что функции ${{g}_{1}}(x)$, ${{g}_{2}}(x)$ непрерывны на $[0,1]$ и непрерывно дифференцируемы соответственно на $(0,1)$ и $(0,1]$. Кроме того, производные $g_{k}^{'}(x)$, $k = 1,2$ абсолютно интегрируемы на $[0,1]$, поскольку при $x \in (0,1)$ имеют место оценки Поэтому для ${{I}_{{21}}}$ справедлива формула интегрирования по частям. Тогда вместо (14) будем иметь Так как функции ${{g}_{k}}(x)$, $k = 1,2,$ непрерывны на сегменте $[0,1]$, то ограничены на нем, а следовательно, равномерно ограничены на сегменте $[1{\text{/}}\sqrt {{{r}_{a}}} ,\;1]$, т.е. $\left| {{{g}_{k}}(x)} \right| \leqslant {{C}_{3}}$ для любого $x \in [1{\text{/}}\sqrt {{{r}_{a}}} ,\;1]$ и любого ${{r}_{a}} > 1$. Отсюда с учетом (15) имеем Мы воспользовались оценками (15).

Рассуждая аналогичным образом, получаем, что четвертый интеграл в (13) имеет такую же оценку, как и ${{I}_{{21}}}$, а второй и третий, обозначим их ${{I}_{{2k}}}$, $k = 2,3$, оценку

где ${{C}_{5}}$ – постоянная, которая равномерно ограничивает функции Тем самым имеем т.е. ${{I}_{{z(u)}}} = O(1{\text{/}}r_{a}^{{5/4}})$ при ${{r}_{a}} \gg 1$ и любом фиксированном ${{z}_{a}} \leqslant 0$. Точно также можно показать, что ${{I}_{{z(l)}}} = O(1{\text{/}}r_{a}^{{5/4}})$, ${{I}_{{(u)}}} = O(1{\text{/}}r_{a}^{{5/4}})$, ${{I}_{{(l)}}} = O(1{\text{/}}r_{a}^{{5/4}})$ при тех же ${{r}_{a}}$ и ${{z}_{a}}$.

Оценим интегралы ${{I}_{{r(u)}}}$, ${{I}_{{r(l)}}}$. При этом подробных пояснений делать не будем. Представим ${{I}_{{r(u)}}}$ в виде

Откуда имеем так как верно Далее имеем где Интегралы в (16) оцениваются также, как в (13). Приведем конечный результат: а $C_{3}^{'}$, $C_{5}^{'}$ – постоянные, которыми при $x \in [0,1]$ равномерно ограничены соответственно функции

Окончательная оценка для ${{I}_{{r(u)}}}$ имеет вид

т.е. ${{I}_{{r(u)}}} = O(1{\text{/}}r_{a}^{{3/2}})$ при ${{r}_{a}} \gg 1$ и любом фиксированном ${{z}_{a}} \leqslant 0$. Аналогичная оценка имеет место для ${{I}_{{r(l)}}}$ при тех же ${{r}_{a}}$ и ${{z}_{a}}$. Рассуждая так же, как и выше, можно получить, что ${{I}_{{(u)}}} = O(1{\text{/}}r_{a}^{{5/4}})$, ${{I}_{{(u)}}} = O(1{\text{/}}r_{a}^{{5/4}})$, где ${{r}_{a}} \gg 1$ и ${{z}_{a}} \leqslant 0$ фиксировано.

В силу полученных ранее равномерных по ${{r}_{a}} > 0$, ${{z}_{a}} \leqslant 0$ оценок интегралы $I_{z}^{{(m)}}$, $I_{r}^{{(m)}}$, ${{I}^{{(m)}}}$ стремятся к нулю при ${{(r_{a}^{2} + z_{a}^{2})}^{{1/2}}} \to + \infty $. Покажем, что все интегралы по берегам разреза также стремятся к нулю при ${{(r_{a}^{2} + z_{a}^{2})}^{{1/2}}} \to + \infty $. Для них полученные ранее оценки уже неприменимы, так как они неравномерны относительно ${{z}_{a}}$. Получим равномерные. Например, для ${{I}_{{z(u)}}}$ имеем

Аналогичным образом доказывается, что и остальные интегралы по берегам разреза равномерно стремятся к нулю. Вычисляя вычеты в (11), (12), для ${{\Phi }^{{(a)}}}({{r}_{a}},{{z}_{a}})$, $U_{z}^{{(a)}}({{r}_{a}},{{z}_{a}})$ и $U_{r}^{{(a)}}({{r}_{a}},{{z}_{a}})$ будем иметь

Заметим, что

при ${{(r_{a}^{2} + z_{a}^{2})}^{{1/2}}} \to + \infty $. Отсюда и из доказанного выше следует, что $\left| {{{\Phi }^{{(a)}}}({{r}_{a}},{{z}_{a}})} \right| \to + 0$ при ${{(r_{a}^{2} + z_{a}^{2})}^{{1/2}}} \to + \infty $.

Используя асимптотику функций Ханкеля на бесконечности [2], получаем

Поэтому третье условие (1) также выполняется. Таким образом, доказана следующая

Теорема. Интеграл (2) является решением задачи (1) при ${{r}_{a}} > 0$, ${{z}_{a}} \leqslant 0$.

Для действительных безразмерных перемещений при ${{r}_{a}} \gg 1$ будем иметь следующие выражения:

где $\left| {{{f}_{1}}({{r}_{a}},{{z}_{a}},t)} \right| \leqslant {{C}_{1}}{\text{/}}r_{a}^{{5/4}}$, $\left| {{{f}_{2}}({{r}_{a}},{{z}_{a}},t)} \right| \leqslant {{C}_{2}}{\text{/}}r_{a}^{{3/2}}$ для любого $t > 0$ и любого фиксированного ${{z}_{a}} \leqslant 0$.

Возвращаясь к размерным переменным, получаем

где ${{g}_{k}}(r,z,t)$ имеют ту же оценку по переменной $r$, что и ${{f}_{k}}({{r}_{a}},{{z}_{a}},t)$ по переменной ${{r}_{a}}$ $(k = 1,2)$.