Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 684-698

1. ВВЕДЕНИЕ

Задачи дифракции в нелинейных средах изучаются в течение нескольких десятилетий [1]–[5]. В последнее время был разработан математический аппарат для исследования таких задач [6]–[11]. В данной статье будут рассмотрены некоторые новые свойства задач дифракции на нелинейном слое: задача дифракции ТЕ-волны на открытом слое, заполненном нелинейной диэлектрической средой. Выбрано два типа нелинейности [12]: нелинейность с насыщением и нелинейность Керра. Керровская нелинейность более распространена, однако, такая нелинейность зависит от интенсивности поля и неограниченно возрастает при возрастании интенсивности. Нелинейность с насыщением этим свойством не обладает. Она используется для описания механизмов воздействия сильного электромагнитного поля на диэлектрическую проницаемость среды. Нелинейность с насыщением также зависит от интенсивности поля, но ограничена при возрастании интенсивности.

Сначала рассмотрена нелинейность с насыщением. Для этого случая получены аналитические результаты о разрешимости задачи дифракции. А именно, условия, при которых задача имеет единственное решение. Доказательство единственности решения основано на применении метода возмущений [6]–[8]. Отметим, что численные расчеты показывают, что при некоторых условиях имеет место неединственность решения задачи дифракции. Что, вообще говоря, не согласуется с физическими свойствами исследуемой задачи.

Далее в работе рассмотрена задача дифракции ТЕ-волны на открытом слое, заполненном диэлектрической средой с керровской нелинейностью. В этом случае задача дифракции всегда имеет неединственное решение. Дано математическое обоснование данного факта. Для доказательства использован метод интегральных дисперсионных уравнений [9]–[11]. Неединственность решения показывает, что, с физической точки зрения, предпочтительно рассматривать нелинейность с насыщением, так как результат в случае нелинейности с насыщением соответствует физическим свойствам явления.

Также приведены численные результаты, иллюстрирующие теоретические выводы.

2. ПОСТАНОВКА ЗАДАЧИ

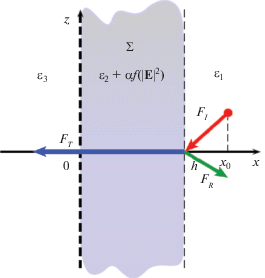
Пусть $\Sigma = \{ (x,y,z):0 \leqslant x \leqslant h,\;(y,z) \in {{\mathbb{R}}^{2}}\} $ ($h > 0$) – слой в ${{\mathbb{R}}^{3}}$. Диэлектрическая проницаемость во всем пространстве имеет вид $\varepsilon = \tilde {\varepsilon }{{\varepsilon }_{0}}$, где

${{\varepsilon }_{1}}$, ${{\varepsilon }_{2}}$, ${{\varepsilon }_{3}}$, $\tilde {\alpha } > 0$ – вещественные постоянные, ${{\varepsilon }_{0}} > 0$ – диэлектрическая проницаемость вакуума. Считаем, что ${{\varepsilon }_{2}} > max\left\{ {{{\varepsilon }_{1}},{{\varepsilon }_{3}}} \right\}$, $min\left\{ {{{\varepsilon }_{1}},{{\varepsilon }_{3}}} \right\} \geqslant {{\varepsilon }_{0}}$.

В пространстве в точке $x = {{x}_{0}} > h$ расположен источник ${{\tilde {j}}^{{{\text{с т }}}}} = {{{\mathbf{j}}}^{{{\text{с т }}}}}{{e}^{{ - i\omega t}}}$, где $\omega $ – круговая частота, ${{{\mathbf{j}}}^{{{\text{с т }}}}} = {{e}_{y}}iA{{e}^{{i\gamma z}}}\delta (x - {{x}_{0}})$, ${{\mu }_{0}}$ – магнитная проницаемость вакуума, $A$ – известная вещественная амплитуда источника, ${{x}_{0}}$ – известная вещественная постоянная, характеризующая положение источника (см. фиг. 1).

Рассмотрим задачу дифракции электромагнитной волны $({\mathbf{E}},{\mathbf{H}}){{e}^{{ - i\omega t}}}$ на слое $\Sigma $. Поле $({\mathbf{E}},{\mathbf{H}})$ должно удовлетворять уравнениям Максвелла в полупространстве $x > h$ вида

в слое $\Sigma $ и в полупространстве $x < 0$ вида

Комплексные амплитуды [13] монохроматической ТЕ-волны $({\mathbf{E}},{\mathbf{H}})$ имеют вид

Решение ищем в виде

где $\gamma $ – известная вещественная постоянная, ${{E}_{y}}$, ${{H}_{x}}$, ${{H}_{z}}$ – неизвестные функции.

Задача дифракции: требуется найти поле $({\mathbf{E}},{\mathbf{H}})$, удовлетворяющее (3), (4), уравнениям Максвелла (1) в полупространстве $x > h$, (2) в слое $\Sigma $ и в полупространстве $x < 0$, условиям непрерывности касательных компонент

и экспоненциально затухающее при $\left| x \right| \to \infty $ в полупространствах $x < 0$ и $x > h$.

Подставляя комплексные амплитуды (3) с компонентами (4) в уравнения Максвелла (1), получаем

где $({\kern 1pt} \cdot {\kern 1pt} ){\text{'}} \equiv {{\partial }_{x}}$. Из системы (6), получаем

Используя (7), находим

где $k_{0}^{2} = {{\omega }^{2}}{{\mu }_{0}}{{\varepsilon }_{0}}$.

Учитывая условия на бесконечности, получаем решение уравнения (8) в виде

где $\kappa _{1}^{2} = {{\gamma }^{2}} - k_{0}^{2}{{\varepsilon }_{1}} > 0$. Таким образом, касательная составляющая электрического поля и ее производная в точке $x = h$ будут иметь вид где ${{F}_{R}}$ – амплитуда отраженного поля, ${{F}_{I}} = A\omega {{\mu }_{0}}{{(2{{\kappa }_{1}})}^{{ - 1}}}{{e}^{{ - {{\kappa }_{1}}({{x}_{0}} - h)}}}$ – амплитуда падающего поля в точке $x = h$. Заметим, что ${{F}_{I}}$ является известной величиной, поскольку все параметры, входящие в определение ${{F}_{I}}$, известны.

Подставляя комплексные амплитуды с компонентами (4) уравнения Максвелла (2), получаем

Из системы (10) получаем выражения для ${{H}_{x}}$ и ${{H}_{z}}$ вида (7).

Используя (7), находим

В полупространстве $x \leqslant 0$ уравнение (11) будет иметь вид

где $\kappa _{3}^{2} = {{\gamma }^{2}} - k_{0}^{2}{{\varepsilon }_{3}} > 0$.

Учитывая условия на бесконечности, получаем решение уравнения (12) в виде

Таким образом, касательная составляющая электрического поля и ее производная в точке $x = 0$ будут иметь вид где ${{F}_{T}}$ – амплитуда прошедшего поля.

Сформулируем задачу дифракции для вещественной функции $u: = {{E}_{y}}$, в слое $\Sigma $ уравнение (11) можно представить в виде

где $\kappa _{2}^{2} = k_{0}^{2}{{\varepsilon }_{2}} - {{\gamma }^{2}}$, $\alpha = k_{0}^{2}\tilde {\alpha }$.

Так как касательные компоненты ${{E}_{y}}$, ${{H}_{y}}$ непрерывны на границах $x = 0$, $x = h$, функция $u(x)$ будет удовлетворять условиям сопряжения

где $\mathop {\left. {[\text{v}]} \right|}\nolimits_{x = {{x}_{0}}} = li{{m}_{{x \to {{x}_{0}} - 0}}}\text{v}(x) - li{{m}_{{x \to {{x}_{0}} + 0}}}\text{v}(x)$. Следовательно, для функции $u(x)$ будут справедливы следующие граничные условия:

Задача $P$. Найти $($вещественную$)$ функцию $u(x) \in {{C}^{1}}( - \infty , + \infty ) \cap {{C}^{2}}( - \infty ,0) \cap {{C}^{2}}(0,h) \cap {{C}^{2}}(h, + \infty )$, которая в полупространстве $x < 0$ определяется формулой

в полупространстве $x > h$ – формулой а в слое $0 < x < h$ является решением уравнения (14) и удовлетворяет условиям сопряжения (15), ${{F}_{I}}$ – известная вещественная величина, ${{F}_{T}}$ и ${{F}_{R}}$ – неизвестные вещественные величины.

После нахождения функции $u(x)$ можно определить амплитуды отраженного ${{F}_{R}}$ и прошедшего ${{F}_{T}}$ полей при заданном значении амплитуды падающего поля ${{F}_{I}}$ из (18), (19).

Вопрос о единственности (или неединственности) решения задачи $P$ будет рассмотрен в разд. 3, 4.

Утверждение 1. Функция $u(x)$ является решением задачи $P$ тогда и только тогда, когда ${{E}_{y}}$ удовлетворяет условиям исходной задачи дифракции.

Доказательство. Легко проверить, что если функция $u(x)$ – решение задачи $P$, то ${{E}_{y}}$, а также ${{H}_{x}}$, ${{H}_{z}}$ в соответствии с (7), в полупространстве $x > h$ являются решением системы (1), а в слое $\Sigma $ и в полупространстве $x < 0$ являются решением системы (2). Обратное следует из вывода уравнений (14), (18), (19).

Таким образом, задача дифракции эквивалентно сводится к задаче $P$.

Замечание 1. Если функция $u$ является решением задачи $P$, то функция $ - u$ так же является решением этой задачи. Поэтому для определенности (единственности решения) будем считать, что ${{F}_{T}} > 0$.

3. НЕЛИНЕЙНОСТЬ С НАСЫЩЕНИЕМ

Рассмотрим случай нелинейности с насыщением, когда $f({{u}^{2}}) = \tfrac{{{{u}^{2}}}}{{1 + \beta {{u}^{2}}}}$. Задачу $P$ с такой нелинейностью будем обозначать через ${{P}_{s}}$. Докажем, что в случае нелинейности с насыщением при некотором условии задача дифракции имеет единственное решение.

Перепишем уравнение (14) в виде

где Построим функцию Грина для краевой задачи Она будет иметь вид

Используя вторую формулу Грина, получаем

Отсюда, а также из (9), (13) и (20), находим

Исключим ${{F}_{R}}$ и ${{F}_{T}}$ из представления (22) функции $u$.

Пусть $s = h$, тогда из последней формулы получаем

где

Пусть $s = 0$, тогда из формулы (22) получаем

где

Используя формулы (23) и (24), получаем следующие выражения:

где

Подставляя (25), (26) в уравнение (22), получаем

где в (27) функция $u$ уже не зависит явно от ${{F}_{R}}$ и ${{F}_{T}}$.

Утверждение 2. Пусть заданы $\alpha > 0$, $\beta > 0$, $h > 0$, ${{F}_{I}}$. Функция $u(x)$ является решением уравнения (27) тогда и только тогда, когда она удовлетворяет условиям задачи ${{P}_{s}}$.

Доказательство. Выше было получено, что если функция $u(x)$ удовлетворяет условиям задачи ${{P}_{s}}$, то она является решением уравнения (27). Обратно, прямой проверкой нетрудно убедиться в том, что $u(s)$ (определенное по формуле (27)) удовлетворяет всем условиям задачи ${{P}_{s}}$.

Для уравнения (27) справедливо следующее

Утверждение 3. Пусть $\alpha > 0$, $\beta > 0$ и $q = \tfrac{{3\alpha }}{{2\beta }}M < 1$, где

Тогда уравнение (27) имеет единственное решение $u \in C[0,h]$.

Доказательство. Легко проверить следующую оценку:

Перепишем уравнение (27) в операторной форме: В соответствии с (28) получаем и, следовательно, где $M = ma{{x}_{{0 \leqslant s \leqslant h}}}\int_0^h \left| {{{Q}_{1}}(x,s)} \right|dx$ и $\left\| u \right\| = ma{{x}_{{0 \leqslant s \leqslant h}}}\left| u \right|$. Тогда для $q = \tfrac{{3\alpha }}{{2\beta }}M < 1$ отображение ${{Q}_{1}}$ является сжатием. Выберем значение $r > 0$ из условия $\left\| {{{q}_{2}}} \right\| \leqslant (1 - q)r$. В соответствии со следствием 2 (см. [14]) сжатие ${{Q}_{1}}$ действует из шара ${{B}_{r}}(0)$ в тот же шар в $C[0,h]$, где ${{B}_{r}}(0) = \left\{ {x \in \mathbb{R}:\left\| x \right\| < r} \right\}$. Таким образом, уравнение (29) имеет единственное решение $u \in {{B}_{r}}(0) \subset C[0,h]$. Так как $r$ может быть выбрано сколь угодно большим, утверждение выполняется.

Из утверждений 1, 2, 3 получаем следующую

Теорема 1 (О единственности). Пусть $\alpha > 0$, $\beta > 0$ и $\tfrac{{3\alpha }}{{2\beta }}M < 1$, где

Тогда задача дифракции (а также задача ${{P}_{s}}$) имеет единственное решение в случае нелинейности с насыщением.

4. КЕРРОВСКАЯ НЕЛИНЕЙНОСТЬ

Рассмотрим случай нелинейности Керра, когда $f({{u}^{2}}) = {{u}^{2}}$. Задачу $P$ с такой нелинейностью будем обозначать через ${{P}_{k}}$. Докажем, что в случае нелинейности Керра при некотором условии задача дифракции имеет бесконечное число решений.

Для анализа задачи дифракции будем использовать метод интегральных дисперсионных уравнений [11].

Первый интеграл уравнения (14) будет иметь вид

Используя граничные условия (16), (17), получаем систему

Из системы (31) можно найти выражение $F_{T}^{2}$ через ${{F}_{R}}$ и ${{F}_{I}}$: где Учитывая замечание 1, получаем где $C$ выражается формулой (32).

Введем новые переменные

Уравнение (14) может быть записано в виде

Первый интеграл (30) принимает вид

Разрешая (36) относительно $\tau $, учитывая, что $\tau \geqslant 0$, и подставляя результат во второе уравнение системы (35), получаем

где подкоренное выражение, очевидно, положительно для всех вещественных $\eta $ и $\gamma $, $\alpha C > 0$.

Используя условия сопряжения на границах $x = 0$, $x = h$, получаем

Так как $\eta {\text{'}} < 0$, функция $\eta $ монотонно убывает при $x \in \left[ {0,h} \right]$. Однако нельзя исключить из рассмотрения случай, когда $\eta $ имеет разрывы. В общем случае, функция $u(x)$ имеет нули при $x \in \left( {0,h} \right)$. Это означает, как видно из (34), что $\eta $ имеет разрывы. Допустим, что имеется $n$ точек разрыва ${{x}_{1}},\; \ldots ,\;{{x}_{n}} \in \left( {0,h} \right)$. Если $n = 0$, то функция $\eta $ непрерывна на отрезке $x \in \left[ {0,h} \right]$, а функция $u(x)$ не обращается в $0$ на этом же отрезке. Очевидно, что $u{\text{'}}({{x}_{i}}) \ne 0$ для всех $i = \overline {1,n} $. Отсюда, принимая во внимание формулу (37), получаем, что

Введем обозначение

где $w \equiv w(s;C)$.

Используя метод интегральных дисперсионных уравнений [11], находим

где $n = 0,1,2,\; \ldots $.

Замечание 2. Если $\eta (h) \geqslant \eta (0)$, то $n = 1,2,3\; \ldots $ .

Таким образом, получили уравнение (41) такое, что пара ${{F}_{I}}$, ${{F}_{R}}$ удовлетворяет данному уравнению, только если она удовлетворяет условиям задачи ${{P}_{k}}$.

В дальнейшем нам понадобится (см. [15])

Утверждение 4. Задача Коши для уравнения (14) с начальными условиями (16), где ${{F}_{T}} > 0$ и ${{\kappa }_{3}} = \sqrt {{{\gamma }^{2}} - k_{0}^{2}{{\varepsilon }_{3}}} > 0$ – постоянные, имеет единственное решение $u \equiv u(x;\gamma )$, определенное глобально на $[0,h]$. Это решение непрерывно зависит от $\gamma $ при всех ${{\gamma }^{2}} > k_{0}^{2}{{\varepsilon }_{3}}$.

Имеет место следующее

Утверждение 5. Пусть $\alpha > 0$, $h > 0$ и ${{F}_{I}}$ известны. Пара ${{F}_{I}}$, ${{F}_{R}}$ удовлетворяет уравнению (41) тогда и только тогда, когда она удовлетворяет условиям задачи ${{P}_{k}}$.

Доказательство. Выше было доказано, что если пара ${{F}_{I}}$, ${{F}_{R}}$ удовлетворяет условиям задачи ${{P}_{k}}$, то она удовлетворяет уравнению (41) для некоторого $\gamma $. Теперь докажем обратное.

Пусть для заданных значений параметров пара ${{F}_{I}}$, ${{F}_{R}}: = {{\tilde {F}}_{R}}$ удовлетворяет уравнению (41).

Рассмотрим задачу Коши для уравнения (14) с начальными условиями

где ${{\tilde {F}}_{T}}$ определяется в соответствии с формулами (33), (32). Решение такой задачи $u(x)$, определенное при $x \in [0,h]$, существует и единственно (см. утверждение 4). На этом этапе требовать выполнения условия $\tfrac{{u{\text{'}}(h)}}{{u(h)}} = - {{\kappa }_{1}}\tfrac{{{{{\tilde {F}}}_{R}} + {{F}_{I}}}}{{{{{\tilde {F}}}_{R}} - {{F}_{I}}}}$ мы не можем. Используя найденное решение $u$, построим по формулам (34) функции $\tau $ и $\eta $. Ясно, что $\tau (0) = \tilde {F}_{T}^{2}$, $\eta (0) = {{\kappa }_{3}}$.

Пусть $\eta (h) = p < - {{\kappa }_{1}}\tfrac{{{{{\tilde {F}}}_{R}} + {{F}_{I}}}}{{{{{\tilde {F}}}_{R}} - {{F}_{I}}}}$. Используя построенные $\tau $ и $\eta $, получаем соотношение

аналогичное уравнению (41).

Последнее соотношение перепишем в виде

В уравнении (41) и в соотношении (42) подынтегральные выражения совпадают. Вычтем из (42) уравнение (41) при ${{F}_{R}} = {{\tilde {F}}_{R}}$, получим

В силу очевидной оценки (см. (40))

получаем, что (43) выполняется только если $p = - {{\kappa }_{1}}\tfrac{{{{{\tilde {F}}}_{R}} + {{F}_{I}}}}{{{{{\tilde {F}}}_{R}} - {{F}_{I}}}}$.

Отсюда получаем, что условие $\eta (h) = p < - {{\kappa }_{1}}\tfrac{{{{{\tilde {F}}}_{R}} + {{F}_{I}}}}{{{{{\tilde {F}}}_{R}} - {{F}_{I}}}}$ неверно. Аналогично можно показать, что неверно и условие $\eta (h) = p > - {{\kappa }_{1}}\tfrac{{{{{\tilde {F}}}_{R}} + {{F}_{I}}}}{{{{{\tilde {F}}}_{R}} - {{F}_{I}}}}$. По этой причине остается единственная возможность

Следовательно, пара ${{F}_{I}}$, ${{\tilde {F}}_{R}}$ удовлетворяет условиям задачи ${{P}_{k}}$.

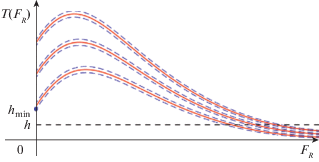
Утверждение 6. Пусть $\alpha > 0$ и ${{F}_{I}}$ известны. Если $h \leqslant {{h}_{{min}}}$

где

$\widetilde \theta = \sqrt {\left| {\kappa _{2}^{2}} \right| + \sqrt {2\alpha {{C}_{0}}} } $,    ${{\tilde {\theta }}_{1}} = \sqrt { - \left| {\kappa _{2}^{2}} \right| + \sqrt {2\alpha {{C}_{0}}} } $,    $\mathop {\widetilde \theta }\nolimits_2 = \sqrt {\left| {\kappa _{2}^{2}} \right| - \sqrt {2\alpha {{C}_{0}}} } $   и   ${{C}_{0}} = ({{\varepsilon }_{2}} - {{\varepsilon }_{1}})F_{I}^{2} + \tfrac{1}{2}\alpha F_{I}^{4},$

то для любого целого $n \geqslant 0$ найдется $F_{R}^{{(n)}}$ такое, что пара $F_{R}^{{(n)}}$ и ${{F}_{I}}$ будeт удовлетворять уравнению (41).

Доказательство. Имеем следующие оценки:

где $n = 0,1,2,\; \ldots $ и $T = \int_{ - \infty }^{ + \infty } wds$. Теперь необходимо оценить $T$. Легко проверяемые неравенства ($a > 0$, $b > 0$) дают где $T* = \int_{ - \infty }^{ + \infty } {{\left( {\left| {{{s}^{2}} + \kappa _{2}^{2}} \right| + \sqrt {2\alpha C} } \right)}^{{ - 1}}}ds$. Интеграл $T{\text{*}}$ ниже вычисляется явно.

При ${{\gamma }^{2}} < {{\omega }^{2}}{{\mu }_{0}}{{\varepsilon }_{2}}$ величина ${{s}^{2}} + \kappa _{2}^{2} > 0$ и, следовательно, имеем

Теперь пусть ${{\gamma }^{2}} \geqslant {{\omega }^{2}}{{\mu }_{0}}{{\varepsilon }_{2}}$. Обозначим $\sqrt {{{\gamma }^{2}} - {{\omega }^{2}}{{\mu }_{0}}{{\varepsilon }_{2}}} $ через ${{\tilde {\kappa }}_{2}}$, тогда получим

Очевидно, что в ${{I}_{1}}$ знаменатель всегда положителен. Действительно, максимальное значение $s = {{\tilde {\kappa }}_{2}}$. Подстановка этого значения в знаменатель дает $\tilde {\kappa }_{2}^{2} + \sqrt {2\alpha C} - \tilde {\kappa }_{2}^{2} = \sqrt {2\alpha C} > 0$.

Вычисляя ${{I}_{1}}$, получаем

В знаменателе интеграла ${{I}_{2}}$ возможны два случая. В первом случае имеем $\sqrt {2\alpha C} - \tilde {\kappa }_{2}^{2} \leqslant 0$, то есть $\sqrt {2\alpha C} \leqslant \tilde {\kappa }_{2}^{2}$, тогда

Во втором случае имеем $\sqrt {2\alpha C} - \tilde {\kappa }_{2}^{2} > 0$, откуда получаем, что $\sqrt {2\alpha C} > \tilde {\kappa }_{2}^{2}$. Тогда верно следующее:

Объединяя результаты, окончательно получаем

где

$\theta = \sqrt {\left| {\kappa _{2}^{2}} \right| + \sqrt {2\alpha C} } $,    ${{\theta }_{1}} = \sqrt { - \left| {\kappa _{2}^{2}} \right| + \sqrt {2\alpha C} } $   и   ${{\theta }_{2}} = \sqrt {\left| {\kappa _{2}^{2}} \right| - \sqrt {2\alpha C} } .$

Величина интеграла $T{\text{*}}$ зависит от значения $C$, которое определено системой (31). Введем следующую замену: $2\alpha C = 2\alpha \kappa _{1}^{2}{{({{F}_{R}} + {{F}_{I}})}^{2}} + 2\alpha \kappa _{2}^{2}{{({{F}_{R}} - {{F}_{I}})}^{2}} + {{\alpha }^{2}}{{({{F}_{R}} - {{F}_{I}})}^{4}}$.

Используя следующие разложения:

которые справедливы при $\left| x \right| \to 0$, где $q$ – любое вещественное число, отличное от $0$, получаем

Из последней формулы ясно, что $li{{m}_{{{{F}_{R}} \to \infty }}}T* = 0$. Это означает, что для любого целого $n \geqslant 0$ и для $h \leqslant \mathop {\left. {T{\text{*}}} \right|}\nolimits_{{{F}_{R}} = 0} $ уравнение (41) будет иметь, по крайней мере, одно решение $F_{R}^{n}$.

Далее удобнее исключить $C$ из уравнения (40). Это можно сделать, используя уравнение (32):

где $n = 0,1,2,\; \ldots \,{\kern 1pt} {\kern 1pt} .$

Найдем значение $T{\text{*}}$ при ${{F}_{R}} = 0$. При ${{\gamma }^{2}} < {{\omega }^{2}}{{\mu }_{0}}{{\varepsilon }_{2}}$ получаем

Если ${{\gamma }^{2}} \geqslant {{\omega }^{2}}{{\mu }_{0}}\varepsilon $, $\sqrt {2\alpha C} > \tilde {\kappa }_{2}^{2}$, то верно следующее:

Если ${{\gamma }^{2}} \geqslant {{\omega }^{2}}{{\mu }_{0}}\varepsilon $, $\sqrt {2\alpha C} \leqslant \tilde {\kappa }_{2}^{2}$, то имеем

Сформулируем основные результаты этого раздела.

Утверждение 7. Пусть $\alpha > 0$, $h$ и ${{F}_{I}}$ известны и выполняется (44). Задача ${{P}_{k}}$ имеет бесконечное число решений.

Доказательство. Для некоторого целого $n \geqslant 0$ найдется значение $F_{R}^{{(n)}}$ такое, что оно будет удовлетворять уравнению (41).

Каждая пара $F_{R}^{{(n)}}$ и ${{F}_{I}}$ определяет значение $F_{T}^{{(n)}}$ в соответствии с формулами (33), (32). Из утверждения 4 (см. [15]) следует, что задача Коши для дифференциального уравнения (14) с начальными условиями

имеет единственное решение.

Докажем, что $F_{R}^{{(n)}} \ne F_{R}^{{(m)}}$ при $n \ne m$. Предположим противное, пусть $F_{R}^{{(n)}} = F_{R}^{{(m)}}$ при $n \ne m$. Рассмотрим следующую разность:

Из последнего получаем равенство Так как $w > 0$, то $n = m$.

Из утверждений 1, 5, 7 получаем, что справедлива

Теорема 2. Пусть $\alpha > 0$, $h$ и ${{F}_{I}}$ известны и выполняется (44). Тогда задача дифракции имеет бесконечное число решений в случае нелинейности Керра.

Замечание 3. Если условие $h \leqslant {{h}_{{min}}}$ не выполняется, то найдется такое $n{\text{*}}$, что задача дифракции (и соответственно задача ${{P}_{k}}$) будет иметь бесконечное множество решений для всех $n \geqslant n{\text{*}}$.

5. ЧИСЛОВЫЕ РЕЗУЛЬТАТЫ

Для численного решения задачи $P$ предложен метод, основанный на решении вспомогательной задачи Коши [16], что позволяет, в частности, определить и построить зависимость амплитуды отраженного поля ${{F}_{R}}$ от амплитуды падающего поля ${{F}_{I}}$.

При построении использовались следующие параметры: $h = 3$ мм, ${{x}_{0}} = 4$ мм, $\omega = 1$ ГГц, ${{\mu }_{0}} = 1$, ${{\varepsilon }_{1}} = 1$, ${{\varepsilon }_{2}} = 3$, ${{\varepsilon }_{3}} = 1$, $\alpha = 0.01$ В^–2.

Графики построены для двух широко используемых типов нелинейностей. Кроме того, представлено сравнение нелинейного и линейного случаев для каждого типа нелинейности.

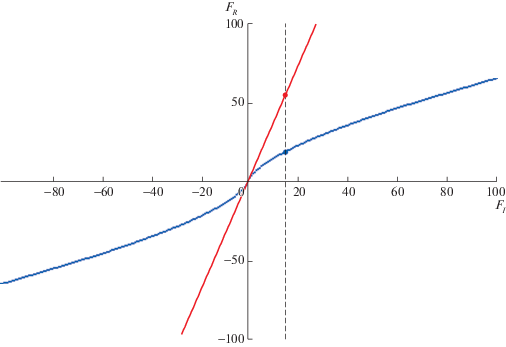
На фиг. 3–5 построена зависимость амплитуды отраженного поля ${{F}_{R}}$ от амплитуды падающего поля ${{F}_{I}}$. Наклонная линия на фиг. 3–5 соответствует линейному случаю, кривые – нелинейным. Вертикальная пунктирная прямая соответствует ${{F}_{I}} = 15$. Точки пересечения пунктирной прямой с кривыми соответствуют амплитудам отраженного поля в нелинейных случаях, а пересечение пунктирной прямой с наклонной линией соответствует амплитуде отраженного поля в линейном случае.

На фиг. 3, 4 представлены случаи нелинейности с насыщением вида $f({{u}^{2}}) = \tfrac{{{{u}^{2}}}}{{1 + \beta {{u}^{2}}}}$. Для фиг. 3 значение $\beta = 0.005$ В^–2 и условие теоремы 1 на коэффициенты нелинейности $\alpha $ и $\beta $ выполняется. На фиг. 3 видно, что каждому фиксированному значению ${{F}_{I}}$ соответствует единственное значение ${{F}_{R}}$. Для фиг. 4 значение $\beta = 0.0005$ В^–2 и условие теоремы 1 на коэффициенты нелинейности $\alpha $ и $\beta $ не выполняется. В данном случае на фиг. 4 видно, что фиксированному значению ${{F}_{I}} = 15$ соответствует несколько значений ${{F}_{R}}$, некоторые из них можно видеть на фиг. 4.

На фиг. 5 представлен случай нелинейности Керра вида $f({{\left| {\mathbf{u}} \right|}^{2}}) = {{\left| {\mathbf{u}} \right|}^{2}}$. Видно, что фиксированному значению ${{F}_{I}} = 15$ соответствует множество значений ${{F}_{R}}$ (вообще говоря, бесконечное по теореме 2), часть из них можно видеть на фиг. 5.

6. ЗАКЛЮЧЕНИЕ

В данной работе исследована задача дифракции поляризованной электромагнитной волны на нелинейном слое. Проведено качественное сравнение разрешимости задач дифракции в случаях нелинейности с насыщением и нелинейности Керра. Доказана единственность решений в задаче дифракции электромагнитной ТЕ-волны на слое, заполненной средой с нелинейностью с насыщением. А также доказано бесконечное множество решений в задаче дифракции электромагнитной ТЕ-волны на нелинейном слое в случае нелинейности Керра.

Из вышесказанного можно сделать вывод о том, что для анализа задач дифракции на нелинейном слое с сильными полями предпочтительно использовать модель нелинейности с насыщением.