Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 699-706

Решение контактной задачи теории упругости с жестким включением

Р. В. Намм^1, 2, *, Г. И. Цой^1, **

¹ ВЦ ДВО РАН
680000 Хабаровск, ул. Ким Ю Чена, 65, Россия

² Гос. ун-т
680035 Хабаровск, ул. Тихоокеанская, 136, Россия

^* E-mail: rnamm@yandex.ru
^** E-mail: tsoy.dv@mail.ru

Поступила в редакцию 24.11.2017
После доработки 14.11.2018
Принята к публикации 14.11.2018

DOI: 10.1134/S0044466919040136

Полный текст (PDF)

Аннотация

Рассматривается решение задачи о равновесии упругого тела, содержащего жесткое включение. На одном из участков границы включения и упругого тела имеется трещина отслоения. На берегах трещины задаются условия взаимного непроникания берегов друг в друга. Приводится метод решения, основанный на возможности рассмотрения задачи с жестким включением в качестве предельной для семейства задач с трещиной. Также предлагается численный метод решения задачи, который основан на модифицированной схеме двойственности и алгоритме Удзавы. Приводятся результаты численного счета с помощью МКЭ. Библ. 16. Фиг. 3. Табл. 1.

Ключевые слова: условие непроникания, жесткое включение, трещина, схема двойственности, модифицированный функционал Лагранжа, обобщенный метод Ньютона.

ВВЕДЕНИЕ

В связи с широким применением композиционных материалов в инженерной практике, исследования краевых задач равновесия упругих тел, содержащих жесткие включения, являются важной актуальной проблемой.

В результате эксплуатации композита включения могут отслаиваться от упругого тела, тем самым образуя трещины. Классические постановки задачи теории упругости с трещиной предполагают, как правило, что напряжение на берегах трещины равно нулю [1]. Но равенство нулю напряжения на берегах трещины не исключает возможность проникновения берегов трещины друг в друга, что является неестественным с точки зрения механики. В последнее время в работах по теории трещин рассматриваются модели с нелинейными краевыми условиями на берегах трещины [2]–[4]. Отметим также работы [5], [6], в которых рассматриваются методы решения задачи с трещиной и задачи с тонким жестким включением. Указанные краевые условия записываются в виде неравенств и обеспечивают взаимное непроникновение берегов трещины. Такие модели более предпочтительны в сравнении с их классическими аналогами.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим задачу о равновесии упругого тела, содержащего жесткое включение, на границе которого расположена трещина. Предполагаем, что на берегах трещины заданы краевые условия взаимного непроникания берегов.

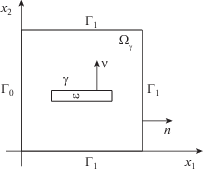
Пусть $\Omega \subset {{R}^{2}}$ – ограниченная область с достаточно регулярной границей $\Gamma = {{\Gamma }_{0}} \cup {{\Gamma }_{1}}$, $\omega \subset \Omega $ – подобласть с достаточно регулярной границей $\Sigma $ такая, что $\bar {\omega } \cap \Gamma = \emptyset $ (см. фиг. 1). Предположим, что $\Sigma $ состоит из двух частей $\gamma $ и $\Sigma {\backslash }\gamma $, $\operatorname{meas} \left( {\Sigma {\backslash }\gamma } \right) > 0$, где $\gamma $ – гладкая линия, без самопересечений.

Фиг. 1.

Упругое тело с отслоившимся жестким включением.

Обозначим через $\nu = ({{\nu }_{1}},{{\nu }_{2}})$ единичный вектор внешней нормали к $\Sigma $. Подобласть $\omega $ будет соответствовать жесткому включению, а линия $\gamma $ – трещине, расположенной на поверхности этого включения. Область $\Omega \backslash \bar {\omega }$ соответствует упругой части тела.

Термин “жесткое включение” означает, что перемещения точек подобласти $\omega $ являются элементами пространства $R(\omega )$ инфинитезимальных жестких перемещений, которое определяется следующим образом:

$\begin{gathered} R(\omega ) = \left\{ {\rho = ({{\rho }_{1}},{{\rho }_{2}}):\rho (x) = Bx + C,\;x \in \omega } \right\}, \\ B = \left( {\begin{array}{*{20}{c}} 0&b \\ { - b}&0 \end{array}} \right),\quad C = ({{c}^{1}},{{c}^{2}});\quad b,{{c}^{1}},{{c}^{2}} - {\text{п р о и з в о л ь н ы е }}\;{\text{п о с т о я н н ы е }}. \\ \end{gathered} $

Обозначим ${{\Omega }_{\gamma }} = \Omega {\backslash }\bar {\gamma }$.

Для вектора перемещений $\text{v} = ({{\text{v}}_{1}},{{\text{v}}_{2}})$ определим тензор деформаций

${{\varepsilon }_{{ij}}}(\text{v}) = \frac{1}{2}\left( {\frac{{\partial {{\text{v}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{\text{v}}_{j}}}}{{\partial {{x}_{i}}}}} \right),\quad i,j = 1,2,$

и тензор напряжений, связанный с ним по линейному закону Гука

${{\sigma }_{{ij}}}(\text{v}) = {{c}_{{ijkm}}}{{\varepsilon }_{{km}}}(\text{v}),$

где ${{c}_{{ijkm}}} = {{c}_{{jimk}}} = {{c}_{{kmij}}}$, $i,j,k,m = 1,2$, и по повторяющимся индексам ведeтся суммирование.

Пусть $\Gamma = {{\Gamma }_{0}} \cup {{\Gamma }_{1}}$, где ${{\Gamma }_{0}}$, ${{\Gamma }_{1}}$ – непустые открытые попарно непересекающиеся подмножества $\Gamma $. Кроме того, пусть заданы вектор функции $f = ({{f}_{1}},{{f}_{2}})$ и $p = ({{p}_{1}},{{p}_{2}})$ объемных и поверхностных сил соответственно.

Краевая постановка задачи о равновесии упругого тела, содержащего жесткое включение $\omega $ и трещину $\gamma $, формулируется следующим образом. В области ${{\Omega }_{\gamma }}$ требуется найти функцию $u = ({{u}_{1}},{{u}_{2}})$, $u = {{\rho }_{0}}$ на $\omega $, ${{\rho }_{0}} \in R(\omega )$ такую, что

$\begin{gathered} - \frac{{\partial {{\sigma }_{{ij}}}}}{{\partial {{x}_{j}}}} = {{f}_{i}}\quad {\text{в }}\quad \Omega {\backslash }\bar {\omega }, \\ {{\sigma }_{{ij}}} = {{c}_{{ijkm}}}{{\varepsilon }_{{km}}}\quad {\text{в }}\quad \Omega {\backslash }\bar {\omega }, \\ u = 0\quad {\text{н а }}\quad {{\Gamma }_{0}}, \\ \end{gathered} $

(1.1)

$\begin{gathered} {{\sigma }_{{ij}}}{{n}_{j}} = {{p}_{i}}\quad {\text{н а }}\quad {{\Gamma }_{1}},\quad i = 1,2, \\ (u - {{\rho }_{0}})\nu \geqslant 0\quad {\text{н а }}\quad {{\gamma }^{ + }}, \\ \\ \end{gathered} $

$\begin{gathered} {{\sigma }_{\nu }}(u) \leqslant 0,\quad {{\sigma }_{\tau }}(u) = 0\quad {\text{н а }}\quad {{\gamma }^{ + }}, \\ {{\sigma }_{\nu }} \cdot (u - {{\rho }_{0}})\nu = 0\quad {\text{н а }}\quad {{\gamma }^{ + }}, \\ - \int\limits_\Sigma \,\sigma \nu \cdot \rho d\Gamma = \int\limits_\omega \,f\rho d\Omega \quad \forall \rho \in R(\omega ). \\ \end{gathered} $

Здесь $n = ({{n}_{1}},{{n}_{2}})$ – вектор единичной внешней нормали к $\Gamma $, ${{\gamma }^{ + }}$ – положительный берег трещины $\gamma $, ${{\sigma }_{\nu }}(u) = {{\sigma }_{{ij}}}(u){{\nu }_{i}}{{\nu }_{j}}$, ${{\sigma }_{\tau }}(u) = \sigma (u) - {{\sigma }_{\nu }} \cdot \nu $, где $\sigma (u) = ({{\sigma }_{1}}(u),{{\sigma }_{2}}(u))$, ${{\sigma }_{i}}(u) = {{\sigma }_{{ij}}}(u){{\nu }_{j}}$, $i = 1,2$. Последнее интегральное равенство соответствует условию равновесия на жестком включении.

Приведем вариационную постановку задачи (1.1). Введем пространство

$H_{{{{\Gamma }_{0}}}}^{{1,\omega }} = \left\{ {\text{v} = ({{\text{v}}_{1}},{{\text{v}}_{2}}) \in {{{[{{H}^{1}}({{\Omega }_{\gamma }})]}}^{2}}:\text{v} = \rho \;{\text{н а }}\;\omega ;\;\rho \in R(\omega );\;\text{v} = 0\;{\text{н а }}\;{{\Gamma }_{0}}} \right\},$

и определим множество допустимых перемещений

${{K}_{\omega }} = \left\{ {\text{v} \in H_{{{{\Gamma }_{0}}}}^{{1,\omega }}:(\text{v} - \rho )\text{v} \geqslant 0\;{\text{н а }}\;{{\gamma }^{ + }}} \right\}.$

Вариационная постановка задачи о равновесии упругого тела, содержащего жесткое включение $\omega $ и трещину $\gamma $ имеет вид (см. [2])

(1.2)

$J(\text{v}) \to \min ,\quad \text{v} \in {{K}_{\omega }},$

в которой выпуклый функционал потенциальной энергии $J(\text{v})$ имеет вид

$\begin{gathered} J(\text{v}) = \tfrac{1}{2}\int\limits_{\Omega \backslash \bar {\omega }} {{\sigma }_{{ij}}}(\text{v}){{\varepsilon }_{{ij}}}(\text{v})d\Omega - \int\limits_{{{\Omega }_{\gamma }}} {{f}_{i}}{{\text{v}}_{i}}d\Omega - \int\limits_{{{\Gamma }_{1}}} {{p}_{i}}{{\text{v}}_{i}}d\Gamma , \\ f \in {{[{{L}_{2}}({{\Omega }_{\gamma }})]}^{2}},\quad p \in {{[{{L}_{2}}({{\Gamma }_{1}})]}^{2}}. \\ \end{gathered} $

При условии, что тензор модулей упругости $C = \left\{ {{{c}_{{ijkl}}}} \right\}$ обладает свойством положительной определенности и ${{c}_{{ijkl}}} \in {{L}^{\infty }}(\Omega )$, задача (1.2) имеет решение $u$, которое одновременно удовлетворяет вариационному неравенству

$u \in {{K}_{\omega }}:\int\limits_{\Omega \backslash \bar {\omega }} {{\sigma }_{{ij}}}(u){{\varepsilon }_{{ij}}}(\text{v} - u)d\Omega - \int\limits_{{{\Omega }_{\gamma }}} {{f}_{i}}({{\text{v}}_{i}} - {{u}_{i}})d\Omega - \int\limits_{{{\Gamma }_{1}}} {{p}_{i}}({{\text{v}}_{i}} - {{u}_{i}})d\Gamma \geqslant 0\quad \forall \text{v} \in {{K}_{\omega }}.$

Нетрудно показать, что решение $u$ единственное.

2. МЕТОД РЕШЕНИЯ

Предлагаемый метод решения основан на том, что задачу о равновесии упругого тела, содержащего жесткое включение, на границе которого расположена трещина, оказывается, можно рассматривать как предельную для семейства задач о равновесии упругих тел с трещиной, сформулированных в области ${{\Omega }_{\gamma }}$ [2]. Для упругих пластин данный метод изучен в [7]–[9]. Это означает, что можно построить семейство задач с положительным параметром $\lambda $ таких, что для любого фиксированного $\lambda > 0$ задача описывает равновесие упругого тела, занимающего область ${{\Omega }_{\gamma }}$ с трещиной $\gamma $. При этом, при $\lambda \to 0$ мы получим жесткое включение $\omega $, так что каждая точка $x \in \omega $ имеет перемещение ${{\rho }_{0}}(x),\;{{\rho }_{0}} \in R(\omega )$ [2, с. 81]. Дадим необходимое пояснение к сказанному.

Введем тензор ${{C}^{\lambda }} = \{ c_{{ijkl}}^{\lambda }\} $, $i,j,k,l = 1,2$:

$c_{{ijkl}}^{\lambda } = \left\{ \begin{gathered} {{c}_{{ijkl}}}\quad {\text{в }}\quad \Omega {\backslash }\bar {\omega }, \hfill \\ {{\lambda }^{{ - 1}}}{{c}_{{ijkl}}}\quad {\text{в }}\quad \omega \hfill \\ \end{gathered} \right.$

и рассмотрим следующее семейство задач. В области ${{\Omega }_{\gamma }}$ найти функции ${{u}^{\lambda }} = (u_{1}^{\lambda },u_{2}^{\lambda })$, ${{\sigma }^{\lambda }} = \{ \sigma _{{ij}}^{\lambda }\} $, $i,j = 1,2$ такие, что

$\begin{gathered} - \frac{{\partial \sigma _{{ij}}^{\lambda }}}{{\partial {{x}_{j}}}} = {{f}_{i}}\quad {\text{в }}\quad {{\Omega }_{\gamma }},\quad i = 1,2, \\ \sigma _{{ij}}^{\lambda } = c_{{ijkm}}^{\lambda }{{\varepsilon }_{{km}}}({{u}^{\lambda }})\quad {\text{в }}\quad {{\Omega }_{\gamma }}, \\ \end{gathered} $

(2.1)

$\begin{gathered} {{u}^{\lambda }} = 0\quad {\text{н а }}\quad {{\Gamma }_{0}}, \\ \sigma _{{ij}}^{\lambda }{{n}_{j}} = {{p}_{i}}\quad {\text{н а }}\quad {{\Gamma }_{1}},\quad i = 1,2, \\ \end{gathered} $

$\begin{gathered} [{{u}^{\lambda }}]\nu \geqslant 0,\quad [\sigma _{\nu }^{\lambda }] = 0,\quad \sigma _{\nu }^{\lambda } \times [{{u}^{\lambda }}]\nu = 0,\quad {\text{н а }}\quad \gamma , \\ \sigma _{\nu }^{\lambda } \leqslant 0,\quad \sigma _{\tau }^{\lambda } = 0\quad {\text{н а }}\quad {{\gamma }^{ \pm }}. \\ \end{gathered} $

Здесь $[\text{v}] = {{\text{v}}^{ + }} - {{\text{v}}^{ - }}$ – скачок функции $\text{v}$ на $\gamma $, где знаки $ \pm $ соответствуют положительному и отрицательному берегам ${{\gamma }^{ \pm }}$ по отношению к нормали $\nu $.

Введем множество допустимых перемещений

$K = \left\{ {\text{v} \in W: - [\text{v}]\nu \leqslant 0\;{\text{н а }}\;\gamma } \right\},$

где

$W = \left\{ {\text{v} = ({{\text{v}}_{1}},{{\text{v}}_{2}}) \in {{{[{{H}^{1}}({{\Omega }_{\gamma }})]}}^{2}}:\text{v} = 0\;{\text{н а }}\;{{\Gamma }_{0}}} \right\}.$

Вариационная постановка задачи (2.1) имеет вид

${{J}^{\lambda }}(\text{v}) \to \min ,\quad \text{v} \in K,$

где

${{J}^{\lambda }}(\text{v}) = \tfrac{1}{2}\int\limits_{{{\Omega }_{\gamma }}} \sigma _{{ij}}^{\lambda }(\text{v}){{\varepsilon }_{{ij}}}(\text{v})d\Omega - \int\limits_{{{\Omega }_{\gamma }}} {{f}_{i}}{{\text{v}}_{i}}d\Omega - \int\limits_{{{\Gamma }_{1}}} {{p}_{i}}{{\text{v}}_{i}}d\Gamma .$

Решение ${{u}^{\lambda }}$ задачи (2.2) удовлетворяет вариационному неравенству

${{u}^{\lambda }} \in K:\int\limits_{{{\Omega }_{\gamma }}} \sigma _{{ij}}^{\lambda }({{u}^{\lambda }}){{\varepsilon }_{{ij}}}(\text{v} - {{u}^{\lambda }})d\Omega - \int\limits_{{{\Omega }_{\gamma }}} {{f}_{i}}({{\text{v}}_{i}} - u_{i}^{\lambda })d\Omega - \int\limits_{{{\Gamma }_{1}}} {{p}_{i}}({{\text{v}}_{i}} - u_{i}^{\lambda })d\Gamma \geqslant 0\quad \forall \text{v} \in K.$

В [2] доказывается, что решения ${{u}^{\lambda }}$ при $\lambda \to 0$ слабо сходятся в $W$ к решению $u$ задачи (1.2).

Лемма. Имеет место предельное соотношение

$\mathop {lim}\limits_{\lambda \to 0} {{J}^{\lambda }}({{u}^{\lambda }}) = J(u).$

Доказательство. Отметим, что функционал

$J(\text{v}) = \frac{1}{2}\int\limits_{\Omega \backslash \bar {\omega }} {{\sigma }_{{ij}}}(\text{v}){{\varepsilon }_{{ij}}}(\text{v})d\Omega - \int\limits_{{{\Omega }_{\gamma }}} {{f}_{i}}{{\text{v}}_{i}}d\Omega - \int\limits_{{{\Gamma }_{1}}} {{p}_{i}}{{\text{v}}_{i}}d\Gamma $

является выпуклым и непрерывным в $W$ функционалом. Имеем

${{J}^{\lambda }}({{u}^{\lambda }}) = J({{u}^{\lambda }}) + \frac{1}{{2\lambda }}\int\limits_\omega {{\sigma }_{{ij}}}({{u}^{\lambda }}){{\varepsilon }_{{ij}}}({{u}^{\lambda }})d\Omega .$

Так как $\int_{\Omega \backslash \bar {\omega }} {{{\sigma }_{{ij}}}({{u}^{\lambda }})} {{\varepsilon }_{{ij}}}({{u}^{\lambda }})d\Omega \geqslant 0$, то

$\mathop {\underline {lim} }\limits_{\lambda \to 0} {{J}^{\lambda }}({{u}^{\lambda }}) \geqslant \mathop {\underline {lim} }\limits_{\lambda \to 0} J({{u}^{\lambda }}) \geqslant J(u).$

Последнее неравенство следует из слабой сходимости ${{u}^{\lambda }}$ к $u$. С другой стороны, для $\lambda > 0$ и любого $\text{v} \in {{K}_{\omega }}$ справедливо

${{J}^{\lambda }}({{u}^{\lambda }}) \leqslant {{J}^{\lambda }}(\text{v}) = J(\text{v}).$

Поэтому имеем

$\overline {\mathop {lim}\limits_{\lambda \to 0} } \,{{J}^{\lambda }}({{u}^{\lambda }}) \leqslant {{J}^{\lambda }}(u).$

Следовательно,

$\overline {\mathop {lim}\limits_{\lambda \to 0} } \,{{J}^{\lambda }}({{u}^{\lambda }}) \leqslant {{J}^{\lambda }}(u) \leqslant \mathop {\underline {lim} }\limits_{\lambda \to 0} {{J}^{\lambda }}({{u}^{\lambda }}),$

то есть существует

$\mathop {lim}\limits_{\lambda \to 0} {{J}^{\lambda }}({{u}^{\lambda }}) = J(u).$

3. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ

Результаты разд. 2 дают основание представить решение упругой задачи с жестким включением как предел при $\lambda \to 0$ на области ${{\Omega }_{\gamma }}$ решений задач с трещиной вида (2.2).

Для задачи (2.2) с фиксированным $\lambda $ составим двойственную задачу [10], [11]:

(3.1)

$\underline M (l) - \sup ,\quad l \in {{L}_{2}}(\gamma ),$

где

$\underline M (l) = \mathop {inf}\limits_{\text{v} \in W} M(\text{v},l) = \mathop {inf}\limits_{\text{v} \in W} \left\{ {{{J}^{\lambda }}(\text{v}) + \tfrac{1}{{2r}}\int\limits_\gamma \{ {{{[{{{(l - r[{{\text{v}}_{\nu }}])}}^{ + }}]}}^{2}} - {{l}^{2}}\} d\Gamma } \right\},$

и ${{(l - r[{{\text{v}}_{\nu }}])}^{ + }} \equiv \max \left\{ {0,l - r[{{\text{v}}_{\nu }}]} \right\}$, $r > 0$ – const.

В [12] было доказано соотношение двойственности

$\mathop {sup}\limits_{l \in {{L}_{2}}(\gamma )} \underline M (l) = \mathop {inf}\limits_{\text{v} \in K} {{J}^{\lambda }}(\text{v}).$

Для решения двойственной задачи рассмотрен градиентный метод, порождающий следующий алгоритм Удзавы решения задачи (3.1).

Шаг 1. На начальном шаге $k = 0$ задается произвольная функция ${{l}^{0}} \in {{L}_{2}}(\gamma )$.

Шаг 2. Для каждого $k = 0,1,2,\; \ldots $ последовательно вычисляются (см. [13])

(3.2)

${{u}^{{k + 1}}} = \mathop {argmin}\limits_{\text{v} \in W} \left\{ {{{J}^{\lambda }}(\text{v}) + \frac{1}{{2r}}\int\limits_\gamma \{ {{{[{{{({{l}^{k}} - r[{{\text{v}}_{\nu }}])}}^{ + }}]}}^{2}} - {{{({{l}^{k}})}}^{2}}\} d\Gamma } \right\};$

(3.3)

${{l}^{{k + 1}}} = {{({{l}^{k}} - r[u_{\nu }^{{k + 1}}])}^{ + }}.$

Область $\Omega $ выбиралась в виде единичного квадрата с границей $\Gamma $, где включение занимает область $\omega = \left\{ {0.2 < {{x}_{1}} < 0.8,\;0.48 < {{x}_{2}} < 0.5} \right\}$ и трещина отслоения $\gamma = \left\{ {0.2 < {{x}_{1}} < 0.8,\;{{x}_{2}} = 0.5} \right\}$.

Для численного решения задачи (3.2) воспользуемся методом конечных элементов. На фиг. 2 представлено разбиение области $\Omega $ с помощью триангуляции Делоне. В качестве базисных возьмем кусочно-линейные функции ${{\varphi }_{i}}(x,y)$ для P1-элементов ($i = \overline {1,N} $), где $N$ – это количество узлов триангуляции области $\Omega $.

Фиг. 2.

Триангуляция области $\Omega $.

Введем следующие обозначения: $h = 0.01$ – шаг сетки на $\gamma $, ${{N}_{\gamma }}$ – количество узлов триангуляции на $\gamma $, ${{W}_{h}}$ – линейная оболочка базисных функций ${{\varphi }_{i}}(x,y)$, ${{u}_{h}} = (u_{1}^{h},u_{2}^{h}) \in {{W}_{h}}$ – конечно-элементное решение:

$u_{1}^{h}(x,y) = \sum\limits_{j = 1}^N \,{{t}_{j}}{{\varphi }_{j}}(x,y),\quad u_{2}^{h}(x,y) = \sum\limits_{j = N + 1}^{2N} \,{{t}_{j}}{{\varphi }_{{j - N}}}(x,y),\quad {\text{д л я }}\quad {{t}_{j}} \in R.$

Так как $\Omega $ – многоугольник, обеспечено вложение ${{W}_{h}} \subset W$. Таким образом, заменим задачу (3.2) конечно-элементной задачей:

(3.4)

${{u}^{{k + 1}}} = \mathop {argmin}\limits_{\text{v} \in {{W}_{h}}} M(\text{v},{{l}^{k}}).$

Для решения задачи (3.4) в конечно-элементном приближении аппроксимируем граничный интеграл по $\gamma $ с помощью квадратурной формулы трапеций. Для узлов на нижнем берегу трещины делаем замену переменных: $t_{j}^{ - } = t_{j}^{ + } + {{\theta }_{j}}$, где ${{\theta }_{j}} = - [{{t}_{j}}] = - (t_{j}^{ + } - t_{j}^{ - })$. Пусть $t = ({{t}_{1}},{{t}_{2}},\; \ldots ,\;{{\theta }_{{{{i}_{1}}}}},{{\theta }_{{{{i}_{2}}}}},\; \ldots ,\;{{\theta }_{{{{i}_{{{{N}_{\gamma }}}}}}}},\; \ldots ,\;{{t}_{{2N}}})$, тогда задача минимизации (3.4) сводится к нахождению оптимальных значений компонент вектора $t$. Так как конечномерный функционал в (3.4) является сильно выпуклым и непрерывно дифференцируемым функционалом, в [12] для этого используется метод покоординатного спуска.

Однако для задачи с жестким включением данный метод показал плохую сходимость. При уменьшении параметра $\lambda $ растет число обусловленности матрицы жесткости, что влечет за собой большое количество итераций.

Для преодоления этого затруднения в работе был применен обобщенный метод Ньютона [14]–[16]. Пусть заданы матрица жесткости $A = ({{a}_{{ij}}}) \in {{R}^{{2N \times 2N}}}$ и вектор правой части $F$. Определим вектор ${{\alpha }^{k}} = (\alpha _{1}^{k}, \ldots ,\;\alpha _{{{{N}_{\gamma }}}}^{k})$ – приближенное значение двойственной переменной ${{l}^{k}}$ в узлах на трещине, $\theta = ({{\theta }_{{{{i}_{1}}}}},\; \ldots ,\;{{\theta }_{{{{i}_{{{{N}_{\gamma }}}}}}}})$ и градиент конечномерного функционала $g(t)$:

$g(t) = At + h{{({{\alpha }^{k}} + r\theta )}^{ + }} - F,$

где ${{({{\alpha }^{k}} + r\theta )}^{ + }} \in {{R}^{{2N}}}$ – вектор с отличными от нуля компонентами только в узлах сетки, лежащих на трещине $\gamma $.

Тогда обобщенный метод Ньютона будет выглядеть следующим образом.

1. На начальном шаге задаем ${{t}^{0}}$.

2. Для каждого $n = 0,1,2, \ldots $ вычисляем

${{t}^{{n + 1}}} = {{t}^{n}} - {{(\partial g({{t}^{n}}))}^{{ - 1}}} \cdot g({{t}^{n}}).$

3. Проверяем

$\mathop {\left\| {{{t}^{{n + 1}}} - {{t}^{n}}} \right\|}\nolimits_\infty < {{\varepsilon }_{t}},\quad {{\varepsilon }_{t}} = {{10}^{{ - 12}}}.$

Здесь $\partial g(t)$ – обобщенный Якобиан функции $g(t)$, который определяется в виде

$\partial g(t) = A + D,$

$D = \operatorname{diag} (0,0,\; \ldots ,\;{{d}_{{{{i}_{1}}}}},{{d}_{{{{i}_{2}}}}},\; \ldots ,\;{{d}_{{{{i}_{{{{N}_{\gamma }}}}}}}},\; \ldots ,\;0),$

${{d}_{{{{i}_{j}}}}} = \left\{ \begin{gathered} rh,\quad {\text{е с л и }}\quad \alpha _{j}^{k} + r{{\theta }_{j}} > 0, \hfill \\ 0,\quad {\text{в }}\;{\text{п р о т и в н о м }}\;{\text{с л у ч а е }}. \hfill \\ \end{gathered} \right.$

На шаге (3.3) вычисляем компоненты двойственной переменной по формуле

$\alpha _{i}^{{k + 1}} = \mathop {(\alpha _{i}^{k} + r\theta _{i}^{{k + 1}})}\nolimits^ + ,\quad i = \overline {1,{{N}_{\gamma }}} .$

Для метода Удзавы условие останова имеет вид

$\mathop {\left\| {{{\alpha }^{{k + 1}}} - {{\alpha }^{k}}} \right\|}\nolimits_\infty < {{\varepsilon }_{\alpha }},\quad {{\varepsilon }_{\alpha }} = {{10}^{{ - 8}}}.$

Приведем результаты численного решения поставленной задачи. Значения параметров брались следующими: $f = ({{f}_{1}},{{f}_{2}}) = (0,0)$, поверхностное усилие с правой $\mathop {\left. {{{p}_{1}}} \right|}\nolimits_{{{\Gamma }_{1}}} = g\left( {1 - 2\left| {{{x}_{2}}} \right|} \right)$, $\mathop {\left. {{{p}_{2}}} \right|}\nolimits_{{{\Gamma }_{1}}} = 0$ МПа, верхней $\mathop {\left. {{{p}_{1}}} \right|}\nolimits_{{{\Gamma }_{1}}} = 0$ МПа, $\mathop {\left. {{{p}_{2}}} \right|}\nolimits_{{{\Gamma }_{1}}} = - 1$ МПа и нижней $\mathop {\left. {{{p}_{1}}} \right|}\nolimits_{{{\Gamma }_{1}}} = 0$ МПа, $\mathop {\left. {{{p}_{2}}} \right|}\nolimits_{{{\Gamma }_{1}}} = 1$ МПа сторон, модуль упругости Юнга $E = 73\,000$ МПа, коэффициент Пуассона $\mu = 0.34$, константа $r = {{10}^{{10}}}$, $g = 27$ МПа.

Для выполнения расчетов были использованы вычислительные ресурсы ЦКП “Центр данных ДВО РАН” [17]. Численные эксперименты были проведены на гибридном вычислительном кластере на базе архитектуры OpenPOWER. Вариант с использованием метода покоординатного спуска считался на процессоре IBM POWER8 4.023 GHz, так как данный метод плохо поддается распараллеливанию. В свою очередь обобщенный метод Ньютона легко и хорошо распараллеливается, поэтому расчеты для него проводились на NVIDIA Tesla P100 GPU c использованием библиотеки cuBLAS. Это дало существенный прирост в скорости выполнения счета.

В таблице представлены результаты численного решения двойственной задачи с использованием разных методов минимизации на шаге (3.2). Из нее видно, что обобщенный метод Ньютона сходится за небольшое количество итераций, причем разница между полученными решениями оказалась порядка ${{10}^{{ - 9}}}$, ${{10}^{{ - 10}}}$. Это говорит о близости полученных решений. Однако, в отличие от метода покоординатного спуска, для обобщенного метода Ньютона не удается показать теоретическую сходимость к решению рассматриваемой задачи.

Таблица.

Результаты счета метода Удзавы

λ	Метод покоординатного спуска*		Обобщенный метод Ньютона**		Δ
λ	Число итераций по t	Число итераций по α	Число итераций по t	Число итераций по α	$\mathop {\left\\| {\theta {\kern 1pt} {\text{}}{\kern 1pt} {\text{}} - \theta {\kern 1pt} *} \right\\|}\nolimits_\infty $
0.1	61 851	5	4	5	1 × 10^–10
0.01	136 054	8	5	8	2.9 × 10^–10
0.001	916 501	22	5	22	2.3 × 10^–9

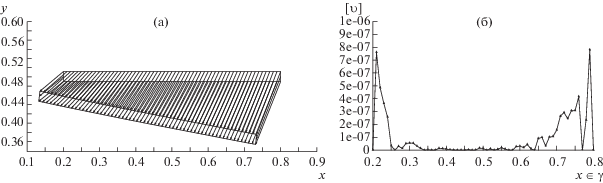
На фиг. 3 представлены перемещения $u \times 1000$ включения $\omega $ и скачок $[u]$ на трещине при $\lambda = 0.001$.

Фиг. 3.

Перемещение $\omega $ и $[u]$ при $\lambda = 0.001$.

На фиг. 3 видно, что с уменьшением параметра $\lambda $ область $\omega $ ведет себя как жесткое включение. Также скачок на трещине везде неотрицательный, т.е. не происходит взаимное проникание берегов трещины друг в друга.

Численные результаты показали, что предложенный метод эффективен при решении задач теории упругости с жестким включением. Отметим, что для решения методом Удзавы двойственной задачи (3.1) в обеих задачах потребовалось сделать небольшое число шагов (3.3). Данное обстоятельство можно объяснить хорошими дифференциальными свойствами двойственного функционала $\underline M (l)$ (см. [12, теор. 4]).

Список литературы

Морозов Н.Ф. Математические вопросы теории трещин. М.: Наука, 1984.
Хлуднев А.М. Задачи теории упругости в негладких областях. М.: Физматлит, 2010.
Khludnev A.M., Kovtunenko V.A. Analysis of crack in solids. Southhampton-Boston: WIT Press, 2000.
Hintermuller M., Kovtunenko V.A., Kunisch K. The primal-dual active set method for a crack problem with non-penetration // IMA J. Appl. Math. 2004. T. 69. № 1. C. 1–26.
Рудой Е.М. Метод декомпозиции области для модельной задачи теории трещин с возможным контактом берегов // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 2. С. 305–316.
Рудой Е.М. Численное решение задачи о равновесии упругого тела с отслоившимся тонким жестким включением // Сиб. журнал индустр. матем. 2016. Т. 19. № 2. С. 74–87.
Неустроева Н.В. Задача о равновесии упругой пластины, содержащей наклонную трещину на границе жесткого включения // Сиб. журнал индустр. матем. 2015. Т. 18. № 2. С. 74–84.
Фанкина И.В. Контактная задача для упругой пластины с тонким жестким включением // Сиб. журнал индустр. матем. 2016. Т. 19. № 3. С. 90–98.
Lazarev N.P. An Equilibrium Problem for the Timoshenko-Type Plate Containing a Crack on the Boundary of a Rigid Inclusion // J. Siberian Federal Univ. Math. Phys. 2013. V. 6. № 1. P. 53–62.
Вихтенко Э.М., Максимова Н.Н., Намм Р.В. Функционалы чувствительности в вариационных неравенствах механики и их приложение к схемам двойственности // Сиб. журн. вычисл. математики. 2014. Т. 17. № 1. С. 43–52.
Вихтенко Э.М., Намм Р.В. О методе двойственности для решения модельной задачи с трещиной // Тр. ИММ УрО РАН. 2016. Т. 22. № 1. С. 36–43.
Намм Р.В., Цой Г.И. Модифицированная схема двойственности для решения упругой задачи с трещиной // Сиб. журнал вычисл. матем. 2017. Т. 20. № 1. С. 47–58.
Вихтенко Э.М., Ву Г., Намм Р.В. Методы решения полукоэрцитивных вариационных неравенств механики на основе модифицированных функционалов Лагранжа // Дальневосточный матем. журн. 2014. Т. 14. № 1. С. 6–17.
Mangasarian O.L. A Newton Method for Linear Programming // J. Optimizat. Theory and Appl. 2004. V. 121. P. 1–18.
Голиков А.И., Евтушенко Ю.Г., Моллаверди Н. Применение метода Ньютона к решению задач линейного программирования большой размерности // Ж. вычисл. матем. и матем. физ. 2004. Т. 44. № 9. С. 1564–1573.
Гаранжа В.А., Голиков А.И., Евтушенко Ю.Г., Нгуен M.Х. Параллельная реализация метода Ньютона для решения больших задач линейного программирования // Ж. вычисл. матем. и матем. физ. 2009. Т. 49. № 8. С. 1369–1384.
Сорокин А.А., Макогонов С.В., Королев С.П. Информационная инфраструктура для коллективной работы ученых Дальнего Востока России // Научно-техническая информация. Серия 1: Организация и методика информационной работы. 2017. № 12. С. 14–16.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал