1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 4, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 4, стр. 687-699

О линейной неустойчивости состояния покоя для несжимаемой полимерной жидкости при наличии сильного разрыва

А. М. Блохин 1, 2, *, Р. Е. Семенко 1, 2, **

1 Новосибирский государственный университет
630090 Новосибирск, ул. Пирогова, 1, Россия

2 Ин-т матем. СО РАН
630090 Новосибирск, пр-т Акад. Коптюга, 4, Россия

* E-mail: blokhin@math.nsc.ru
** E-mail: r.semenko@g.nsu.ru

Поступила в редакцию 14.11.2019
После доработки 14.11.2019
Принята к публикации 16.12.2019

Полный текст (PDF)

Аннотация

Сформулирована линейная задача о малых возмущениях течения несмешиваемых полимерных жидкостей в плоском канале. Исследован вопрос о существовании у такой задачи неограниченно растущих по времени решений, наличие которых означает линейную неустойчивость состояния покоя полимерной жидкости с сильным разрывом. Библ. 8. Фиг. 5.

Ключевые слова: полимерная жидкость, состояние покоя, сильный разрыв.

ВВЕДЕНИЕ

Широкое применение полимерных материалов в самых разных областях современной промышленности вызывает необходимость в создании и изучении подробных математических моделей полимерных сред. Отдельный интерес представляют соединения нескольких несмешиваемых жидких полимеров, широко использующихся для получения материалов определенных свойств. Но нужно отметить, что математическое моделирование динамики полимеров представляет собой масштабную проблему, которую на данный момент нельзя считать решенной, несмотря на большое количество различных реологических моделей, предложенных за последние полвека. Сложность заключается в комплексной анизотропной структуре полимеров, состоящих из очень длинных перепутанных макромолекул. Это накладывает на модели ряд противоречивых требований, связанных как с молекулярной структурой вещества, так и макроскопическими свойствами, которые невозможно учесть в рамках одной модели. Более того, существующие на сегодняшний день известные модели динамики жидких полимеров достаточно слабо изучены математически.

В рамках данной работы мы будем рассматривать сравнительно недавно предложенную обобщенную реологическую модель Покровского-Виноградова [1], которая использует мезоскопический подход, представляющий собой определенный компромисс между статистическими моделями, сфокусированными на микроструктуре вещества [2], и феноменологическими моделями, отталкивающимися от эмпирически полученных макроскопических соотношений [3]. Для этой модели был получен ряд математических результатов (например, [4]–[6]), но в целом ее свойства требуют дальнейшего изучения. Так, в данной работе мы предлагаем анализ классического течения несмешиваемых вязких жидкостей в плоском канале в рамках рассматриваемой модели. Поставленная задача является обобщением задачи, рассматриваемой в [5], на случай, когда жидкости могут иметь разные плотности. Мы формулируем начально-краевую задачу о течении двух несмешиваемых вязкоупругих несжимаемых полимерных жидкостей с границей раздела, на которой мы выводим условия разрыва. Для линеаризованной на состоянии покоя задачи мы ищем частные решения, неограниченно растущие со временем. Наличие таких решений означает неустойчивость состояния покоя в данной постановке.

1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ

Следуя [1], сформулируем обобщенную реологическую модель Покровского-Виноградова, которая описывает течения несжимаемой вязкоупругой полимерной жидкости (например, в плоском канале, см. фиг. 1). В безразмерной форме (сам процесс обезразмеривания подробно описан в [4]) эта математическая модель имеет следующий вид:

$\begin{gathered} {{\rho }_{t}} + {\text{div}}(\rho {\mathbf{u}}) = 0, \\ \frac{{{\text{d}}(\rho {\mathbf{u}})}}{{{\text{d}}t}} + \rho \left( {\nabla p - \frac{1}{{{\text{Re}}}}\operatorname{div} \Pi } \right) = 0, \\ \end{gathered} $
(1.1)
$\rho \left( {\frac{{{\text{d}}{{a}_{{11}}}}}{{{\text{d}}t}} - 2{{A}_{1}}{{u}_{x}} - 2{{a}_{{12}}}{{u}_{y}}} \right) + \rho {{\mathbb{L}}_{{11}}} = 0,$
$\begin{gathered} \rho \left( {\frac{{{\text{d}}{{a}_{{12}}}}}{{{\text{d}}t}} - {{A}_{1}}{{{v}}_{x}} - {{A}_{2}}{{u}_{y}}} \right) + \rho {{{\tilde {K}}}_{I}}{{a}_{{12}}} = 0, \\ \rho \left( {\frac{{d{{a}_{{22}}}}}{{dt}} - 2{{a}_{{12}}}{{{v}}_{x}} - 2{{A}_{2}}{{v}_{y}}} \right) + \rho {{L}_{{22}}} = 0. \\ \end{gathered} $
Здесь $t$ – время, $u$, ${v}$ – компоненты вектора скорости ${\mathbf{u}}$ в декартовой системе координат $x$, $y$; $p$ – давление, ${{a}_{{ij}}},$ $i,j = 1,2$ – компоненты симметрического тензора анизотропии $\Pi $ второго ранга; ${{{\mathbf{\sigma }}}_{1}}$, ${{{\mathbf{\sigma }}}_{2}}$ – столбцы симметрической матрицы $\Pi = ({{a}_{{ij}}}) = ({{{\mathbf{\sigma }}}_{1}},{{{\mathbf{\sigma }}}_{2}})$; ${{L}_{{ii}}} = {{K}_{I}}{{a}_{{ii}}} + \beta {{\left\| {{{{\mathbf{\sigma }}}_{i}}} \right\|}^{2}}$, $i,j = 1,2$; ${{\left\| {{{{\mathbf{\sigma }}}_{i}}} \right\|}^{2}} = ({{{\mathbf{\sigma }}}_{i}},{{{\mathbf{\sigma }}}_{i}})$, $i = 1,2$; $\operatorname{div} \Pi = {{(\operatorname{div} {{{\mathbf{\sigma }}}_{1}},\operatorname{div} {{{\mathbf{\sigma }}}_{2}})}^{{\text{т}}}}$,
${{K}_{I}} = {{{\text{W}}}^{{ - 1}}} + \frac{{\bar {k}}}{3}I,\quad I = {{a}_{{11}}} + {{a}_{{22}}},\quad \bar {k} = k - \beta ;\quad {{\tilde {K}}_{I}} = {{K}_{I}} + \beta I;$
$k$, $\beta $ ($0 < \beta < 1$) – феноменологические параметры, характеризующие вклады, связанные с анизотропией (см. [1]); ${\text{Re}} = \rho {{u}_{H}}l{\text{/}}{{\eta }_{0}}$ – число Рейнольдса, $\rho $ – плотность среды, ${\text{W}} = {{\tau }_{0}}{{u}_{H}}{\text{/}}l$ – число Вайсенберга; ${{\eta }_{0}}$, ${{\tau }_{0}}$ – начальные значения сдвиговой вязкости и времени релаксации; $l$ – характерная длина (см. фиг. 1), ${{u}_{H}}$ – характерная скорость, ${{A}_{i}} = {{{\text{W}}}^{{ - 1}}} + {{a}_{{ii}}}$, $i = 1,2$;
$\frac{d}{{dt}} = \frac{\partial }{{\partial t}} + ({\mathbf{u}},\nabla ).$
В системе (1.1) время $t$, координаты $x$, $y$, компоненты вектора скорости $u$, ${v}$, давление $p$ отнесены к $l{\text{/}}{{u}_{H}},$ $l$, ${{u}_{H}}$, $\rho u_{H}^{2}$ соответственно.

Фиг. 1.

Плоский канал.

Замечание 1. Исходная математическая модель (1.1) может быть переписана в так называемом “дивергентном” виде:

$\begin{gathered} {{\rho }_{t}} + {{(\rho u)}_{x}} + {{(\rho {v})}_{y}} = 0, \\ {{(\rho u)}_{t}} + {{(\rho ({{u}^{2}} + p - {{\alpha }_{1}}))}_{x}} + {{(\rho (u{v} - {{\alpha }_{{12}}}))}_{y}} = 0, \\ \end{gathered} $
(1.2)
$\begin{gathered} {{(\rho {v})}_{t}} + {{(\rho (u{v} - {{\alpha }_{{12}}}))}_{x}} + {{(\rho ({{{v}}^{2}} + p - {{\alpha }_{2}}))}_{y}} = 0, \\ {{(\rho ({{u}^{2}} + {{\alpha }_{1}}))}_{t}} + {{(\rho u({{u}^{2}} - {{\alpha }_{1}}))}_{x}} + {{(\rho {v}({{u}^{2}} + {{\alpha }_{1}}) - 2u{{\alpha }_{{12}}}\rho )}_{y}} + 2\rho u{{p}_{x}} + \rho \frac{{{{L}_{{11}}}}}{{{\text{Re}}}} = 0, \\ \end{gathered} $
$\begin{gathered} {{(\rho ({{{v}}^{2}} + {{\alpha }_{2}}))}_{t}} + {{(\rho u({{{v}}^{2}} + {{\alpha }_{2}}) - 2\rho {v}{{\alpha }_{{12}}})}_{x}} + {{(\rho {v}({{{v}}^{2}} - {{\alpha }_{2}}))}_{y}} + 2\rho {v}{{p}_{y}} + \rho \frac{{{{L}_{{22}}}}}{{{\text{Re}}}} = 0, \\ {{(\rho (u{v} + {{\alpha }_{{12}}}))}_{t}} + {{(\rho {v}({{u}^{2}} - {{\alpha }_{1}}))}_{x}} + {{(\rho u({{{v}}^{2}} - {{\alpha }_{2}}))}_{y}} + \rho {v}{{p}_{x}} + \rho u{{p}_{y}} + \rho {{{\tilde {K}}}_{I}}{{\alpha }_{{12}}} = 0, \\ \end{gathered} $
где

${{\alpha }_{i}} = \frac{{{{A}_{i}}}}{{{\text{Re}}}} = {{\alpha }_{{ii}}} + {{\kappa }^{2}},\quad i = 1,2;\quad {{\alpha }_{{ij}}} = \frac{{{{a}_{{ij}}}}}{{{\text{Re}}}},\quad i,j = 1,2;\quad {{\kappa }^{2}} = \frac{1}{{{\text{ReW}}}}.$

Следуя [2], на стенках плоского канала (см. фиг. 1) мы должны поставить следующие краевые условия:

(1.3)
$u = {v} = 0,\quad {{p}_{y}} = ({{({{\alpha }_{{12}}})}_{x}} + {{({{\alpha }_{{22}}})}_{y}})\quad {\text{при}}\quad y = 0,1.$

В отличие от работы [5], далее будем рассматривать более общую ситуацию, когда в плоском канале мы имеем течение двух несмешивающихся несжимаемых полимерных жидкостей, занимающих области $H(t),$ ${{H}_{\infty }}(t)$ с границей раздела $S$ (см. фиг. 1) и имеющих разные постоянные плотности $\rho $ и ${{\rho }_{\infty }}$ $(\rho \ne {{\rho }_{\infty }})$.

Уравнение границы $S$ возьмем в виде

$\begin{gathered} \tilde {f}(t,x,y) = f(t,x) - y = 0, \\ 0 < f(t,x) < 1. \\ \end{gathered} $
Тогда единичный вектор нормали ${\mathbf{N}}$ определяется так:
${\mathbf{N}} = \frac{1}{{\left| {\nabla \tilde {f}} \right|}}({{f}_{x}}, - 1),\quad {{\left| {\nabla \tilde {f}} \right|}^{2}} = 1 + f_{x}^{2},$
а скорость точек сильного разрыва $S$ в направлении нормали ${\mathbf{N}}$ находится следующим образом (см. [6], [7]):
(1.4)
${{D}_{N}} = - \frac{{{{f}_{t}}}}{{\left| {\nabla \tilde {f}} \right|}}.$
Из (1.4) следует
${{D}_{N}} = {{u}_{N}} = ({\mathbf{u}},{\mathbf{N}}) = {{({{u}_{\infty }})}_{N}} = ({{{\mathbf{u}}}_{\infty }},{\mathbf{N}}),$
т.е.
(1.5)
${{f}_{t}} + {{f}_{x}}u - {v} = {{f}_{t}} + {{f}_{x}}{{u}_{\infty }} - {{{v}}_{\infty }} = 0\quad {\text{на}}\quad S.$
Здесь ${{u}_{\infty }},$ ${{{v}}_{\infty }}$ – значения компонент вектора скорости при $\tilde {f} \to + 0$; $u,$ ${v}$ – при $\tilde {f} \to - 0$.

Как известно (см. [6], [8]), на сильном разрыве $S$ должны выполняться определенные соотношения. Вывод условий на сильном разрыве для полимерной жидкости подробно описан в [4] (см. также [6]). Выпишем эти условия (см. систему (1.2)):

$\begin{gathered} {{f}_{t}}[\rho ] + {{f}_{x}}[\rho u] - [\rho {v}] = 0, \\ {{f}_{t}}[\rho u] + {{f}_{x}}[\rho ({{u}^{2}} + p - {{\alpha }_{1}})] - [\rho (u{v} - {{\alpha }_{{12}}})] = 0, \\ \end{gathered} $
(1.6)
$\begin{gathered} {{f}_{t}}[\rho {v}] + {{f}_{x}}\left[ {\rho (u{v} - {{\alpha }_{{12}}})} \right] - [\rho ({{{v}}^{2}} + p - {{\alpha }_{2}})] = 0, \\ {{f}_{t}}[\rho ({{u}^{2}} + {{\alpha }_{1}})] + {{f}_{x}}[\rho u({{u}^{2}} - {{\alpha }_{1}})] - [\rho {v}({{u}^{2}} + {{\alpha }_{1}}) - 2\rho u{{\alpha }_{{12}}}] = 0, \\ \end{gathered} $
$\begin{gathered} {{f}_{t}}[\rho ({{{v}}^{2}} + {{\alpha }_{2}})] + {{f}_{x}}[\rho u({{{v}}^{2}} + {{\alpha }_{2}}) - 2\rho {v}{{\alpha }_{{12}}}] - [\rho {v}({{{v}}^{2}} - {{\alpha }_{2}})] = 0, \\ {{f}_{t}}[\rho (u{v} + {{\alpha }_{{12}}})] + {{f}_{x}}[\rho {v}({{u}^{2}} - {{\alpha }_{1}})] - [\rho u({{{v}}^{2}} - {{\alpha }_{2}})] = 0. \\ \end{gathered} $
Здесь $[\varphi ] = \varphi - {{\varphi }_{\infty }}$ на $S$, где $\varphi $, ${{\varphi }_{\infty }}$ – значения функции $\varphi (t,x,y)$ сверху $(\tilde {f} \to + 0)$ и снизу $(\tilde {f} \to - 0)$ от сильного разрыва $S$.

Замечание 2. В силу (1.5) (см. также [6]) справедливо соотношение

(1.7)
${{f}_{t}}[\varphi ] + {{f}_{x}}[u\varphi ] - [{v}\varphi ] = {{\varphi }_{\infty }}({{f}_{x}}[u] - [{v}]) = 0,$
где $\varphi (t,x,y)$ – некоторая скалярная функция. С учетом (1.7), из (1.6) окончательно получаем
$\begin{gathered} {{f}_{x}}[u] - [{v}] = 0, \\ {{f}_{x}}[\rho (p - {{\alpha }_{1}})] + [\rho {{\alpha }_{{12}}}] = 0, \\ \end{gathered} $
(1.8)
$\begin{gathered} {{f}_{x}}[\rho {{\alpha }_{{12}}}] + [\rho (\Omega - {{\kappa }^{2}})] = 0, \\ {{f}_{x}}[\rho u{{\alpha }_{1}}] - [\rho u{{\alpha }_{{12}}}] = 0, \\ \end{gathered} $
$\begin{gathered} {{f}_{x}}[\rho ({{\alpha }_{1}}{v} + {{\alpha }_{{12}}}u)] - [\rho (u{{\alpha }_{2}} + {v}{{\alpha }_{{12}}})] = 0, \\ {{f}_{x}}[\rho {v}{{\alpha }_{{12}}}] - [\rho {v}{{\alpha }_{2}})] = 0. \\ \end{gathered} $
Здесь $\Omega = p - {{\alpha }_{{22}}}$.

В качестве основного стационарного решения мы возьмем далее состояние покоя (механическое равновесие):

(1.9)
$\begin{gathered} u = {v} = {{a}_{{11}}} = {{a}_{{12}}} = {{a}_{{22}}} = 0,\quad p = \hat {p} = {\text{const}}\quad {\text{в}}\quad \hat {H}, \\ {{u}_{\infty }} = {{{v}}_{\infty }} = {{a}_{{11\infty }}} = {{a}_{{12\infty }}} = {{a}_{{22\infty }}} = 0,\quad {{p}_{\infty }} = \mathop {\hat {p}}\nolimits_\infty = {\text{const}}\quad {\text{в}}\quad \mathop {\hat {H}}\nolimits_\infty , \\ f = 1{\text{/}}2; \\ \end{gathered} $
здесь
$\hat {H} = \left( {(x,y)\,|\,\left| x \right| < \infty ,\frac{1}{2} < y < 1} \right),\quad {{\hat {H}}_{\infty }} = \left( {(x,y)\,|\,\left| x \right| < \infty ,0 < y < \frac{1}{2}} \right).$
В силу (1.7), для (1.9) имеем
$\hat {p} = \theta {{\hat {p}}_{\infty }} + {{\kappa }^{2}} - \theta \kappa _{\infty }^{2}.$
Здесь

${{\kappa }^{2}} = \frac{1}{{{\text{WRe}}}},\quad \kappa _{\infty }^{2} = \frac{1}{{{{{\text{W}}}_{\infty }}{\text{R}}{{{\text{e}}}_{\infty }}}},\quad \theta = \frac{{{{\rho }_{\infty }}}}{\rho }.$

2. ЗАДАЧА НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

В [4] была сконструирована линейная система, полученная линеаризацией системы (1.1) относительно ее стационарных решений, аналогичных решениям Пуазейля для системы уравнений Навье–Стокса. Если в качестве стационарного решения взять состояние покоя (1.9), то линейная система будет иметь следующий вид:

(2.1)
$\begin{gathered} {{{\mathbf{U}}}_{t}} + B({{\kappa }^{2}}){{{\mathbf{U}}}_{x}} + C({{\kappa }^{2}}){{{\mathbf{U}}}_{y}} + R({\text{W}}){\mathbf{U}} + {\mathbf{F}} = 0, \\ {{\Delta }_{{x,y}}}\Omega = 2({{({{\alpha }_{{12}}})}_{{xy}}} - {{({{\alpha }_{{22}}})}_{{xx}}}), \\ t > 0,\quad (x,y) \in \hat {H}; \\ \end{gathered} $
(2.2)
$\begin{gathered} {{({{{\mathbf{U}}}_{\infty }})}_{t}} + B(\kappa _{\infty }^{2}){{({{{\mathbf{U}}}_{\infty }})}_{x}} + C(\kappa _{\infty }^{2}){{({{{\mathbf{U}}}_{\infty }})}_{y}} + R({{{\text{W}}}_{\infty }}){{{\mathbf{U}}}_{\infty }} + {{{\mathbf{F}}}_{\infty }} = 0, \\ {{\Delta }_{{x,y}}}{{\Omega }_{\infty }} = 2({{({{\alpha }_{{12\infty }}})}_{{xy}}} - {{({{\alpha }_{{22\infty }}})}_{{xx}}}), \\ t > 0,\quad (x,y) \in {{{\hat {H}}}_{\infty }}. \\ \end{gathered} $
Здесь
${\mathbf{U}} = \left( {\begin{array}{*{20}{c}} u \\ {v} \\ {{{\alpha }_{{12}}}} \\ {{{\alpha }_{{22}}}} \end{array}} \right),\quad {{{\mathbf{U}}}_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{u}_{\infty }}} \\ {{{{v}}_{\infty }}} \\ {{{\alpha }_{{12\infty }}}} \\ {{{\alpha }_{{22\infty }}}} \end{array}} \right),\quad {\mathbf{F}} = \left( {\begin{array}{*{20}{c}} {{{\Omega }_{x}}} \\ {{{\Omega }_{y}}} \\ 0 \\ 0 \end{array}} \right),\quad {{{\mathbf{F}}}_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{{({{\Omega }_{\infty }})}}_{x}}} \\ {{{{({{\Omega }_{\infty }})}}_{y}}} \\ 0 \\ 0 \end{array}} \right),$
$R({\text{W}}) = {{{\text{W}}}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} {{{\mathbb{O}}_{2}}}&\vline & {{{\mathbb{O}}_{2}}} \\ \hline {{{\mathbb{O}}_{2}}}&\vline & {{{I}_{2}}} \end{array}} \right),\quad B({{\kappa }^{2}}) = \left( {\begin{array}{*{20}{c}} {{{\mathbb{O}}_{2}}}&\vline & {\begin{array}{*{20}{c}} 0&2 \\ { - 1}&0 \end{array}} \\ \hline {\begin{array}{*{20}{c}} 0&{ - {{\kappa }^{2}}} \\ 0&0 \end{array}}&\vline & {{{\mathbb{O}}_{2}}} \end{array}} \right),$
$C({{\kappa }^{2}}) = C = \left( {\begin{array}{*{20}{c}} {{{\mathbb{O}}_{2}}}&\vline & {\begin{array}{*{20}{c}} { - 1}&0 \\ 0&0 \end{array}} \\ \hline {\begin{array}{*{20}{c}} { - {{\kappa }^{2}}}&0 \\ 0&{ - 2{{\kappa }^{2}}} \end{array}}&\vline & {{{\mathbb{O}}_{2}}} \end{array}} \right),$
$u,{v}((x,y) \in \hat {H})$); ${{u}_{\infty }}$, ${{{v}}_{\infty }}$($(x,y) \in {{\hat {H}}_{\infty }}$) – малые возмущения компонент вектора скорости; ${{a}_{{11}}}$($ = - {{a}_{{22}}}$), ${{a}_{{12}}}$, ${{a}_{{22}}}$ ($(x,y) \in \hat {H}$); ${{a}_{{11\infty }}}$($ = - {{a}_{{22\infty }}}$), ${{a}_{{12\infty }}}$, ${{a}_{{22\infty }}}$ ($(x,y) \in {{\hat {H}}_{\infty }}$) – малые возмущения компонент симметрического тензора анизотропии; ${{\alpha }_{{ij\infty }}} = {{a}_{{ij\infty }}}{\text{/R}}{{{\text{e}}}_{\infty }}$, $i,j = 1,2$; ${{\Omega }_{\infty }} = {{p}_{\infty }} - {{\alpha }_{{22\infty }}}$, $p$ ($(x,y) \in \hat {H}$), ${{p}_{\infty }}$ ($(x,y) \in {{\hat {H}}_{\infty }}$) – малые возмущения давления; ${{\Delta }_{{x,y}}} = {{\partial }^{2}}{\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{y}^{2}}$ – оператор Лапласа, ${{I}_{2}}$ – единичная матрица порядка 2, ${{\mathbb{O}}_{2}}$ – нулевая матрица порядка 2.

К (2.1), (2.2) надо добавить начальные данные:

(2.3)
$\begin{gathered} {{\left. {\mathbf{U}} \right|}_{{t = 0}}} = {{{\mathbf{U}}}^{{(0)}}}(x,y),\quad {{\left. \Omega \right|}_{{t = 0}}} = {{\Omega }^{{(0)}}}(x,y),(x,y) \in \hat {H}, \\ {{\left. {{{{\mathbf{U}}}_{\infty }}} \right|}_{{t = 0}}} = {\mathbf{U}}_{\infty }^{{(0)}}(x,y),\quad {{\left. {{{\Omega }_{\infty }}} \right|}_{{t = 0}}} = \Omega _{\infty }^{{(0)}}(x,y),(x,y) \in {{{\hat {H}}}_{\infty }} \\ \end{gathered} $
и граничные условия (см. (1.3), (1.5), (1.8)):
(2.4)
$\begin{gathered} u = {v} = 0,\quad {{\Omega }_{y}} = {{({{\alpha }_{{12}}})}_{x}}\quad {\text{при}}\quad y = 1,\quad x \in {{\mathbb{R}}^{1}},\quad t > 0, \\ {{u}_{\infty }} = {{{v}}_{\infty }} = 0,\quad {{({{\Omega }_{\infty }})}_{y}} = {{({{\alpha }_{{12\infty }}})}_{x}}\quad {\text{при}}\quad y = 0,\quad x \in {{\mathbb{R}}^{1}},\quad t > 0, \\ \end{gathered} $
(2.5)
$\begin{gathered} {{f}_{t}} = {v} = {{{v}}_{\infty }}, \\ [u] = [{v}] = 0,\quad {{\kappa }^{2}} = \theta \kappa _{\infty }^{2},\quad {{\alpha }_{{12}}} = \theta {{\alpha }_{{12\infty }}},\quad \Omega = \theta {{\Omega }_{\infty }}, \\ {{\Omega }_{y}} = \theta {{({{\Omega }_{\infty }})}_{y}} + (\theta - 1){{({{{v}}_{\infty }})}_{t}}\quad {\text{при}}\quad y = \frac{1}{2},\quad x \in {{\mathbb{R}}^{1}},\quad t > 0. \\ \end{gathered} $
Здесь $f = f(t,x)$ – малое возмущение границы раздела $S$.

При этом начальные условия (2.3) должны удовлетворять условию несжимаемости (см. (1.1)):

(2.6)
$\operatorname{div} {\mathbf{u}} = 0,\quad \operatorname{div} {{{\mathbf{u}}}_{\infty }} = 0,\quad {\mathbf{u}} = (u,{v}),\quad {{{\mathbf{u}}}_{\infty }} = ({{u}_{\infty }},{{{v}}_{\infty }}).$

Следуя работе [5], заметим, что справедливо представление

$D = {{T}^{{ - 1}}}({{\kappa }^{2}})C({{\kappa }^{2}})T({{\kappa }^{2}}) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&1 \\ 0&0 \end{array}}&\vline & {{{\mathbb{O}}_{2}}} \\ \hline {{{\mathbb{O}}_{2}}}&\vline & {\begin{array}{*{20}{c}} \kappa &0 \\ 0&{ - \kappa } \end{array}} \end{array}} \right),$
где

$T({{\kappa }^{2}}) = \left( {\begin{array}{*{20}{c}} 0&0&{ - 1{\text{/}}\kappa }&{1{\text{/}}\kappa } \\ 0&{ - 1{\text{/2}}{{\kappa }^{2}}}&0&0 \\ 0&0&1&1 \\ 1&0&0&0 \end{array}} \right),\quad {{T}^{{ - 1}}}({{\kappa }^{2}}) = \left( {\begin{array}{*{20}{c}} 0&0&0&1 \\ 0&{ - 2{{\kappa }^{2}}}&0&0 \\ { - \kappa {\text{/2}}}&0&{1{\text{/2}}}&0 \\ {\kappa {\text{/2}}}&0&{1{\text{/2}}}&0 \end{array}} \right).$

После замены

${\mathbf{U}} = T{\mathbf{Z}},\quad {{{\mathbf{U}}}_{\infty }} = {{T}_{\infty }}{{{\mathbf{Z}}}_{\infty }},\quad {\mathbf{Z}} = \left( {\begin{array}{*{20}{c}} {{{Z}_{1}}} \\ {{{Z}_{2}}} \\ {{{Z}_{3}}} \\ {{{Z}_{4}}} \end{array}} \right),\quad {{{\mathbf{Z}}}_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{Z}_{{1\infty }}}} \\ {{{Z}_{{2\infty }}}} \\ {{{Z}_{{3\infty }}}} \\ {{{Z}_{{4\infty }}}} \end{array}} \right),$
$T = T({{\kappa }^{2}}),\quad {{T}_{\infty }} = T(\kappa _{\infty }^{2}),$
$u = \frac{{{{Z}_{4}} - {{Z}_{3}}}}{\kappa } = \frac{\nu }{\kappa },\quad {{u}_{\infty }} = \frac{{{{Z}_{{4\infty }}} - {{Z}_{{3\infty }}}}}{{{{\kappa }_{\infty }}}} = \frac{{{{\nu }_{\infty }}}}{{{{\kappa }_{\infty }}}},$
${v} = - \frac{{{{Z}_{2}}}}{{2{{\kappa }^{2}}}},\quad {{{v}}_{\infty }} = - \frac{{{{Z}_{{2\infty }}}}}{{2\kappa _{\infty }^{2}}},\quad {{\alpha }_{{22}}} = {{Z}_{1}},\quad {{\alpha }_{{22\infty }}} = {{Z}_{{1\infty }}},$
${{\alpha }_{{12}}} = \sigma = {{Z}_{3}} + {{Z}_{4}},\quad {{\alpha }_{{12\infty }}} = {{\sigma }_{\infty }} = {{Z}_{{3\infty }}} + {{Z}_{{4\infty }}},$
системы (2.1), (2.2), краевые условия (2.4), (2.5) можно переписать в виде
(2.7)
$\begin{gathered} {{{\mathbf{Z}}}_{t}} + D{{{\mathbf{Z}}}_{y}} + \Lambda {{{\mathbf{Z}}}_{x}} + \tilde {R}{\mathbf{Z}} + \Gamma = 0, \\ {{\Delta }_{{x,y}}}\Omega = 2({{\sigma }_{{xy}}} - {{({{Z}_{1}})}_{{xx}}}), \\ t > 0,\quad (x,y) \in \hat {H}; \\ \end{gathered} $
(2.8)
$\begin{gathered} {{({{{\mathbf{Z}}}_{\infty }})}_{t}} + {{D}_{\infty }}{{({{{\mathbf{Z}}}_{\infty }})}_{y}} + {{\Lambda }_{\infty }}{{({{{\mathbf{Z}}}_{\infty }})}_{x}} + {{{\tilde {R}}}_{\infty }}{{{\mathbf{Z}}}_{\infty }} + {{\Gamma }_{\infty }} = 0, \\ {{\Delta }_{{x,y}}}{{\Omega }_{\infty }} = 2({{({{\sigma }_{\infty }})}_{{xy}}} - {{({{Z}_{{1\infty }}})}_{{xx}}}), \\ t > 0,\quad (x,y) \in {{{\hat {H}}}_{\infty }}; \\ \end{gathered} $
(2.9)
$\begin{gathered} {{Z}_{3}} = {{Z}_{4}},\quad {{Z}_{2}} = 0,\quad {{\Omega }_{y}} = {{\sigma }_{x}}\quad {\text{при}}\quad y = 1,\quad x \in {{\mathbb{R}}^{1}},\quad t > 0, \\ {{Z}_{{3\infty }}} = {{Z}_{{4\infty }}},\quad {{Z}_{{2\infty }}} = 0,\quad {{({{\Omega }_{\infty }})}_{y}} = {{({{\sigma }_{\infty }})}_{x}}\quad {\text{при}}\quad y = 0,\quad x \in {{\mathbb{R}}^{1}},\quad t > 0; \\ \end{gathered} $
(2.10)
$\begin{gathered} 2{{\kappa }^{2}}{{f}_{t}} + {{Z}_{2}} = 2\kappa _{\infty }^{2}{{f}_{t}} + {{Z}_{{2\infty }}} = 0, \\ \nu = \frac{\kappa }{{{{\kappa }_{\infty }}}}{{\nu }_{\infty }},\quad \sigma = \theta {{\sigma }_{\infty }},\quad \Omega = \theta {{\Omega }_{\infty }}, \\ {{\Omega }_{y}} - \frac{{{{{({{Z}_{2}})}}_{t}}}}{{2{{\kappa }^{2}}}} = {{({{\Omega }_{\infty }})}_{y}} - \frac{{\theta {{{({{Z}_{{2\infty }}})}}_{t}}}}{{2\kappa _{\infty }^{2}}}\quad {\text{при}}\quad y = \frac{1}{2},\quad x \in {{\mathbb{R}}^{1}},\quad t > 0; \\ \end{gathered} $
здесь $D = D({{\kappa }^{2}})$, ${{D}_{\infty }} = D(\kappa _{\infty }^{2})$,

$\Lambda = \left( {\begin{array}{*{20}{c}} {{{\mathbb{O}}_{2}}}&\vline & {\begin{array}{*{20}{c}} 0&0 \\ {2{{\kappa }^{2}}}&{2{{\kappa }^{2}}} \end{array}} \\ \hline { - \chi }&\vline & {{{\mathbb{O}}_{2}}} \end{array}} \right),\quad {{\Lambda }_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{\mathbb{O}}_{2}}}&\vline & {\begin{array}{*{20}{c}} 0&0 \\ {2\kappa _{\infty }^{2}}&{2\kappa _{\infty }^{2}} \end{array}} \\ \hline { - {{\chi }_{\infty }}}&\vline & {{{\mathbb{O}}_{2}}} \end{array}} \right),$
$\tilde {R} = {{{\text{W}}}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}}&\vline & {{{\mathbb{O}}_{2}}} \\ \hline {{{\mathbb{O}}_{2}}}&\vline & {L{\text{/}}2} \end{array}} \right),\quad {{\tilde {R}}_{\infty }} = \tfrac{{\text{W}}}{{{{{\text{W}}}_{\infty }}}}\tilde {R},$
${\mathbf{\Gamma }} = \left( {\begin{array}{*{20}{c}} 0 \\ { - 2{{\kappa }^{2}}{{\Omega }_{y}}} \\ { - \kappa {{\Omega }_{x}}/2} \\ {\kappa {{\Omega }_{x}}{\text{/}}2} \end{array}} \right),\quad {{{\mathbf{\Gamma }}}_{\infty }} = \left( {\begin{array}{*{20}{c}} 0 \\ { - 2\kappa _{\infty }^{2}{{{({{\Omega }_{\infty }})}}_{y}}} \\ { - {{\kappa }_{\infty }}{{{({{\Omega }_{\infty }})}}_{x}}/2} \\ {{{\kappa }_{\infty }}{{{({{\Omega }_{\infty }})}}_{x}}{\text{/}}2} \end{array}} \right),$
$\chi = \left( {\begin{array}{*{20}{c}} \kappa &{ - 1{\text{/}}4} \\ { - \kappa }&{ - 1{\text{/}}4} \end{array}} \right),\quad {{\chi }_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{\kappa }_{\infty }}}&{ - 1/4} \\ { - {{\kappa }_{\infty }}}&{ - 1/4} \end{array}} \right),\quad L = \left( {\begin{array}{*{20}{c}} 1&1 \\ 1&1 \end{array}} \right).$

Будем искать у задачи (2.7)–(2.10) решения специального вида:

(2.11)
$\begin{gathered} {\mathbf{Z}}(t,x,y) = {\mathbf{\hat {Z}}}(y){\text{exp\{ }}\lambda t + i\omega x{\text{\} }}, \\ \Omega (t,x,y) = \hat {\Omega }(y){\text{exp\{ }}\lambda t + i\omega x{\text{\} }}, \\ {{{\mathbf{Z}}}_{\infty }}(t,x,y) = {{{{\mathbf{\hat {Z}}}}}_{\infty }}(y){\text{exp\{ }}\lambda t + i\omega x{\text{\} }}, \\ {{\Omega }_{\infty }}(t,x,y) = {{{\hat {\Omega }}}_{\infty }}(y){\text{exp\{ }}\lambda t + i\omega x{\text{\} }}, \\ f(t,x) = \hat {f}{\text{exp\{ }}\lambda t + i\omega x{\text{\} }}, \\ \end{gathered} $
где $\lambda = \eta + i{{\omega }_{0}}$; ${{\omega }_{0}}$, $\omega \in {{\mathbb{R}}^{1}}$, $\hat {f}$ – постоянная.

Далее крышку над искомыми переменными в (2.11) опускаем. После подстановки (2.11), из (2.7)–(2.10) следует

(2.12)
$\begin{gathered} (\lambda {{I}_{4}} + \tilde {R} + i\omega \Lambda ){\mathbf{Z}} + D{\mathbf{Z}}{\text{'}} + \Gamma = 0, \\ \Omega {\text{''}} - {{\omega }^{2}}\Omega = 2(i\omega \sigma {\text{'}} + {{\omega }^{2}}{{Z}_{1}}),\quad \frac{1}{2} < y < 1; \\ \end{gathered} $
(2.13)
$\begin{gathered} (\lambda {{I}_{4}} + {{{\tilde {R}}}_{\infty }} + i\omega {{\Lambda }_{\infty }}){{{\mathbf{Z}}}_{\infty }} + {{D}_{\infty }}{\mathbf{Z}}_{\infty }^{'} + {{\Gamma }_{\infty }} = 0, \\ \Omega _{\infty }^{{''}} - {{\omega }^{2}}{{\Omega }_{\infty }} = 2(i\omega \sigma _{\infty }^{'} + {{\omega }^{2}}{{Z}_{{1\infty }}}),\quad 0 < y < \frac{1}{2}; \\ \end{gathered} $
(2.14)
$\begin{gathered} {{Z}_{3}} = {{Z}_{4}},\quad {{Z}_{2}} = 0,\quad \Omega {\text{'}} = i\omega \sigma \quad {\text{при}}\quad y = 1, \\ {{Z}_{{3\infty }}} = {{Z}_{{4\infty }}},\quad {{Z}_{{2\infty }}} = 0,\quad \Omega _{\infty }^{'} = i\omega {{\sigma }_{\infty }}\quad {\text{при}}\quad y = 0, \\ f = - \frac{{{{Z}_{2}}}}{{2{{\kappa }^{2}}\lambda }},\quad \nu = \frac{\kappa }{{{{\kappa }_{\infty }}}}{{\nu }_{\infty }},\quad {{Z}_{2}} = \theta {{Z}_{{2\infty }}},\quad \sigma = \theta {{\sigma }_{\infty }}, \\ \Omega = \theta {{\Omega }_{\infty }},\quad \Omega {\text{'}} - \frac{{\lambda {{Z}_{2}}}}{{2{{\kappa }^{2}}}} = \Omega _{\infty }^{'} - \frac{{\lambda {{Z}_{{2\infty }}}\theta }}{{2\kappa _{\infty }^{2}}}\quad {\text{при}}\quad y = \frac{1}{2}. \\ \end{gathered} $
Здесь

${\mathbf{\Gamma }} = \left( {\begin{array}{*{20}{c}} 0 \\ { - 2{{\kappa }^{2}}\Omega {\text{'}}} \\ { - \kappa i\omega \Omega {\text{/}}2} \\ {\kappa i\omega \Omega {\text{/}}2} \end{array}} \right),\quad {{{\mathbf{\Gamma }}}_{\infty }} = \left( {\begin{array}{*{20}{c}} 0 \\ { - 2\kappa _{\infty }^{2}\Omega _{\infty }^{'}} \\ { - {{\kappa }_{\infty }}i\omega {{\Omega }_{\infty }}/2} \\ {{{\kappa }_{\infty }}i\omega {{\Omega }_{\infty }}{\text{/}}2} \end{array}} \right).$

Положим $\Omega = i\omega Q$, $\Omega = i\omega {{Q}_{\infty }}$. Тогда для агрегатов $Q$, ${{Q}_{\infty }}$ будем иметь такие задачи: (см. (2.13), (2.14)):

$\begin{gathered} Q{\text{''}} - {{\omega }^{2}}Q = 2(\sigma {\text{'}} - i\omega {{Z}_{1}}),\quad \frac{1}{2} < y < 1, \\ Q{\text{'}}(1) = \sigma (1), \\ \end{gathered} $
(2.15)
$Q_{\infty }^{{''}} - {{\omega }^{2}}{{Q}_{\infty }} = 2(\sigma _{\infty }^{'} - i\omega {{Z}_{{1\infty }}}),\quad 0 < y < \frac{1}{2},$
$\begin{gathered} Q_{\infty }^{'}(0) = {{\sigma }_{\infty }}(0), \\ Q\left( {\frac{1}{2}} \right) = \theta {{Q}_{\infty }}\left( {\frac{1}{2}} \right),\quad Q{\text{'}}\left( {\frac{1}{2}} \right) + i\lambda {{Z}_{2}}{{\left( {\frac{1}{2}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{1}{2}} \right)} {(2{{\kappa }^{2}})}}} \right. \kern-0em} {(2{{\kappa }^{2}})}} = Q_{\infty }^{'}\left( {\frac{1}{2}} \right) + i\lambda \theta {{Z}_{{2\infty }}}{{\left( {\frac{1}{2}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{1}{2}} \right)} {(2\kappa _{\infty }^{2})}}} \right. \kern-0em} {(2\kappa _{\infty }^{2})}}. \\ \end{gathered} $

Из (2.12), (2.13), (2.6) следует

(2.16)
$\begin{gathered} {{Z}_{1}} = - {{\rho }^{{(0)}}}i\omega \nu ,\quad {{Z}_{2}} = - {{\rho }_{1}}i\omega (\sigma - Q{\text{'}}),\quad Z_{2}^{'} = 2\kappa i\omega \nu , \\ {{Z}_{{1\infty }}} = - \rho _{\infty }^{{(0)}}i\omega {{\nu }_{\infty }},\quad {{Z}_{{2\infty }}} = - {{\rho }_{{1\infty }}}i\omega ({{\sigma }_{\infty }} - Q_{\infty }^{'}),\quad Z_{{2\infty }}^{'} = 2{{\kappa }_{\infty }}i\omega {{\nu }_{\infty }}, \\ \end{gathered} $
где

${{\rho }^{{(0)}}} = \frac{{2\kappa }}{{\lambda + {{{\text{W}}}^{{ - 1}}}}},\quad {{\rho }_{1}} = \frac{{2{{\kappa }^{2}}}}{\lambda },\quad \rho _{\infty }^{{(0)}} = \frac{{2{{\kappa }_{\infty }}}}{{\lambda + {\text{W}}_{\infty }^{{ - 1}}}},\quad {{\rho }_{{1\infty }}} = \frac{{2\kappa _{\infty }^{2}}}{\lambda }.$

С учетом (2.16) для векторов ${\mathbf{u}} = \left( {\begin{array}{*{20}{c}} {{{Z}_{3}}} \\ {{{Z}_{4}}} \end{array}} \right)$, ${{{\mathbf{u}}}_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{Z}_{{3\infty }}}} \\ {{{Z}_{{4\infty }}}} \end{array}} \right)$ получаем следующие системы:

(2.17)
${\mathbf{u}}{\text{'}} + \frac{1}{\kappa }\left( {\lambda {{\Delta }_{0}} + \frac{1}{{2{\text{W}}}}{{\Delta }_{0}}L - {{\omega }^{2}}{{\Delta }_{0}}\chi {{\Delta }_{1}}} \right){\mathbf{u}} + \frac{{{{\omega }^{2}}}}{\kappa }(Q{{\Delta }_{0}}\gamma + Q{\text{'}}{{\Delta }_{0}}\chi {{\gamma }_{1}}) = 0,$
(2.18)
$({{{\mathbf{u}}}_{\infty }}){\text{'}} + \frac{1}{{{{\kappa }_{\infty }}}}\left( {\lambda {{\Delta }_{0}} + \frac{1}{{2{{{\text{W}}}_{\infty }}}}{{\Delta }_{0}}L - {{\omega }^{2}}{{\Delta }_{0}}\chi {{\Delta }_{{1\infty }}}} \right){{{\mathbf{u}}}_{\infty }} + \frac{{{{\omega }^{2}}}}{{{{\kappa }_{\infty }}}}({{Q}_{\infty }}{{\Delta }_{0}}{{\gamma }_{\infty }} + Q_{\infty }^{'}{{\Delta }_{0}}\chi {{\gamma }_{{1\infty }}}) = 0.$
Здесь
${{\Delta }_{0}} = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right),\quad {{\Delta }_{0}}L = \left( {\begin{array}{*{20}{c}} 1&1 \\ { - 1}&{ - 1} \end{array}} \right),\quad {{\Delta }_{1}} = \left( {\begin{array}{*{20}{c}} { - {{\rho }^{{(0)}}}}&{{{\rho }^{{(0)}}}} \\ {{{\rho }_{1}}}&{{{\rho }_{1}}} \end{array}} \right),$
${{\Delta }_{{1\infty }}} = \left( {\begin{array}{*{20}{c}} { - \rho _{\infty }^{{(0)}}}&{\rho _{\infty }^{{(0)}}} \\ {{{\rho }_{{1\infty }}}}&{{{\rho }_{{1\infty }}}} \end{array}} \right),\quad \gamma = \frac{\kappa }{2}\left( {\begin{array}{*{20}{c}} 1 \\ { - 1} \end{array}} \right),\quad {{\gamma }_{1}} = {{\rho }_{1}}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right),$
${{\Delta }_{0}}\chi {{\Delta }_{1}} = \left( {\begin{array}{*{20}{c}} { - {{l}_{1}}}&{{{l}_{2}}} \\ { - {{l}_{2}}}&{{{l}_{1}}} \end{array}} \right),\quad {{l}_{1}} = \kappa {{\rho }^{{(0)}}} + \frac{1}{4}{{\rho }_{1}},\quad {{l}_{2}} = {{\rho }^{{(0)}}}\kappa - \frac{1}{4}{{\rho }_{1}},$
${{\Delta }_{0}}\chi {{\Delta }_{{1\infty }}} = \left( {\begin{array}{*{20}{c}} { - {{l}_{{1\infty }}}}&{{{l}_{{2\infty }}}} \\ { - {{l}_{{2\infty }}}}&{{{l}_{{1\infty }}}} \end{array}} \right),\quad {{l}_{{1\infty }}} = {{\kappa }_{\infty }}\rho _{\infty }^{{(0)}} + \frac{1}{4}{{\rho }_{{1\infty }}},\quad {{l}_{{2\infty }}} = \rho _{\infty }^{{(0)}}{{\kappa }_{\infty }} - \frac{1}{4}{{\rho }_{{1\infty }}},$
${{\Delta }_{0}}\gamma = \frac{\kappa }{2}\left( {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right),\quad {{\Delta }_{0}}\chi {{\gamma }_{1}} = \frac{{{{\rho }_{1}}}}{4}\left( {\begin{array}{*{20}{c}} { - 1} \\ 1 \end{array}} \right),$
${{\Delta }_{0}}{{\gamma }_{\infty }} = \frac{{{{\kappa }_{\infty }}}}{2}\left( {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right),\quad {{\Delta }_{0}}\chi {{\gamma }_{{1\infty }}} = \frac{{{{\rho }_{{1\infty }}}}}{4}\left( {\begin{array}{*{20}{c}} { - 1} \\ 1 \end{array}} \right).$
Поскольку
$\tilde {T}{{\Delta }_{0}}{{\tilde {T}}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right),\quad \tilde {T} = {{t}_{3}}\left( {\begin{array}{*{20}{c}} 1&{ - 1} \\ 1&1 \end{array}} \right),\quad {{\tilde {T}}^{{ - 1}}} = \frac{1}{{2{{t}_{3}}}}\left( {\begin{array}{*{20}{c}} 1&1 \\ { - 1}&1 \end{array}} \right),$
где ${{t}_{3}} \ne 0$ – постоянная, то
$\tilde {T}({{\Delta }_{0}}\chi {{\Delta }_{1}}){{\tilde {T}}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} 0&{ - {{\rho }_{1}}{\text{/}}2} \\ { - 2\kappa {{\rho }^{{(0)}}}}&0 \end{array}} \right),\quad \tilde {T}({{\Delta }_{0}}\chi {{\Delta }_{{1\infty }}}){{\tilde {T}}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} 0&{ - {{\rho }_{{1\infty }}}{\text{/}}2} \\ { - 2{{\kappa }_{\infty }}\rho _{\infty }^{{(0)}}}&0 \end{array}} \right),$
$\tilde {T}({{\Delta }_{0}}\gamma ) = \kappa {{t}_{3}}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right),\quad \tilde {T}({{\Delta }_{0}}\chi {{\gamma }_{1}}) = \frac{{{{\rho }_{1}}{{t}_{3}}}}{2}\left( {\begin{array}{*{20}{c}} { - 1} \\ 0 \end{array}} \right),$
$\tilde {T}({{\Delta }_{0}}{{\gamma }_{\infty }}) = {{\kappa }_{\infty }}{{t}_{3}}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right),\quad \tilde {T}({{\Delta }_{0}}\chi {{\gamma }_{{1\infty }}}) = \frac{{{{\rho }_{{1\infty }}}{{t}_{3}}}}{2}\left( {\begin{array}{*{20}{c}} { - 1} \\ 0 \end{array}} \right).$
Следовательно, после замен
${\mathbf{u}} = {{\tilde {T}}^{{ - 1}}}{\mathbf{v}},\quad {{{\mathbf{u}}}_{\infty }} = {{\tilde {T}}^{{ - 1}}}{{{\mathbf{v}}}_{\infty }},\quad {\mathbf{v}} = \left( {\begin{array}{*{20}{c}} {{{{v}}_{3}}} \\ {{{{v}}_{4}}} \end{array}} \right),\quad {{{\mathbf{v}}}_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{{v}}_{{3\infty }}}} \\ {{{{v}}_{{4\infty }}}} \end{array}} \right),$
${{Z}_{3}} = \frac{{{{{v}}_{3}} + {{{v}}_{4}}}}{{2{{t}_{3}}}},\quad {{Z}_{4}} = \frac{{{{{v}}_{4}} - {{{v}}_{3}}}}{{2{{t}_{3}}}},\quad \sigma = \frac{{{{{v}}_{4}}}}{{{{t}_{3}}}},\quad \nu = - \frac{{{{{v}}_{3}}}}{{{{t}_{3}}}},$
${{Z}_{{3\infty }}} = \frac{{{{{v}}_{{3\infty }}} + {{{v}}_{{4\infty }}}}}{{2{{t}_{3}}}},\quad {{Z}_{{4\infty }}} = \frac{{{{{v}}_{{4\infty }}} - {{{v}}_{{3\infty }}}}}{{2{{t}_{3}}}},\quad {{\sigma }_{\infty }} = \frac{{{{{v}}_{{4\infty }}}}}{{{{t}_{3}}}},\quad {{\nu }_{\infty }} = - \frac{{{{{v}}_{{3\infty }}}}}{{{{t}_{3}}}},$
системы (2.17), (2.18) примут следующий вид:
(2.19)
${\mathbf{v}}{\text{'}} + \left\{ {\frac{\lambda }{\kappa }\left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right) + \frac{1}{{\kappa {\text{W}}}}\left( {\begin{array}{*{20}{c}} 0&1 \\ 0&0 \end{array}} \right) + {{\omega }^{2}}\left( {\begin{array}{*{20}{c}} 0&{{{\rho }_{1}}{\text{/}}(2\kappa )} \\ {2{{\rho }^{{(0)}}}}&0 \end{array}} \right)} \right\}v + {{\omega }^{2}}{{t}_{3}}Q\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right) - {{\omega }^{2}}\frac{{{{\rho }_{1}}{{t}_{3}}}}{{2\kappa }}Q{\text{'}}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right) = 0,$
(2.20)
${\mathbf{v}}_{\infty }^{'} + \left\{ {\frac{\lambda }{{{{\kappa }_{\infty }}}}\left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right) + \frac{1}{{{{\kappa }_{\infty }}{{{\text{W}}}_{\infty }}}}\left( {\begin{array}{*{20}{c}} 0&1 \\ 0&0 \end{array}} \right) + {{\omega }^{2}}\left( {\begin{array}{*{20}{c}} 0&{{{\rho }_{{1\infty }}}{\text{/}}(2{{\kappa }_{\infty }})} \\ {2\rho _{\infty }^{{(0)}}}&0 \end{array}} \right)} \right\}{{{\mathbf{v}}}_{\infty }} + {{\omega }^{2}}{{t}_{3}}{{Q}_{\infty }}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right) - {{\omega }^{2}}\frac{{{{\rho }_{{1\infty }}}{{t}_{3}}}}{{2{{\kappa }_{\infty }}}}Q_{\infty }^{'}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right) = 0.$
В покомпонентной записи (2.19), (2.20) перепишутся в виде
(2.21)
$\begin{gathered} {v}_{3}^{'} + {{d}^{{(0)}}}{{{v}}_{4}} = mQ{\text{'}},\quad {{d}^{{(0)}}} = \frac{\lambda }{\kappa } + \frac{1}{{\kappa {\text{W}}}} + {{\omega }^{2}}\frac{{{{\rho }_{1}}}}{{2\kappa }},\quad m = \frac{{{{\omega }^{2}}{{\rho }_{1}}{{t}_{3}}}}{{2\kappa }}, \\ {v}_{4}^{'} + {{d}^{{(1)}}}{{{v}}_{3}} + {{\omega }^{2}}{{t}_{3}}Q = 0,\quad {{d}^{{(1)}}} = \frac{\lambda }{\kappa } + 2{{\rho }^{{(0)}}}{{\omega }^{2}}; \\ \end{gathered} $
(2.22)
$\begin{gathered} {v}_{{3\infty }}^{'} + d_{\infty }^{{(0)}}{{{v}}_{{4\infty }}} = {{m}_{\infty }}Q_{\infty }^{'}, \\ d_{\infty }^{{(0)}} = \frac{\lambda }{{{{\kappa }_{\infty }}}} + \frac{1}{{{{\kappa }_{\infty }}{{{\text{W}}}_{\infty }}}} + {{\omega }^{2}}\frac{{{{\rho }_{{1\infty }}}}}{{2{{\kappa }_{\infty }}}},\quad {{m}_{\infty }} = \frac{{{{\omega }^{2}}{{\rho }_{{1\infty }}}{{t}_{3}}}}{{2{{\kappa }_{\infty }}}}, \\ {v}{{_{4}^{'}}_{\infty }} + d_{\infty }^{{(1)}}{{{v}}_{{3\infty }}} + {{\omega }^{2}}{{t}_{3}}{{Q}_{\infty }} = 0,\quad d_{\infty }^{{(1)}} = \frac{\lambda }{{{{\kappa }_{\infty }}}} + 2\rho _{\infty }^{{(0)}}{{\omega }^{2}}; \\ \end{gathered} $
а задачи (2.15) примут вид
(2.23)
$\begin{gathered} Q{\text{''}} + {{\omega }^{2}}Q = n{{{v}}_{3}},\quad \frac{1}{2} < y < 1,\quad Q{\text{'}}(1) - \frac{{{{{v}}_{4}}(1)}}{{{{t}_{3}}}} = 0, \\ Q_{\infty }^{{''}} + {{\omega }^{2}}{{Q}_{\infty }} = {{n}_{\infty }}{{{v}}_{{3\infty }}},\quad 0 < y < \frac{1}{2},\quad Q_{\infty }^{'}(0) - \frac{{{{{v}}_{{4\infty }}}(0)}}{{{{t}_{3}}}} = 0, \\ Q\left( {\frac{1}{2}} \right) = \theta {{Q}_{\infty }}\left( {\frac{1}{2}} \right),\quad (1 - \omega )Q{\text{'}}\left( {\frac{1}{2}} \right) = (1 - \omega \theta )Q_{\infty }^{'}\left( {\frac{1}{2}} \right). \\ \end{gathered} $
Здесь $n = 2({{\rho }^{{(0)}}}{{\omega }^{2}} - {{d}^{{(1)}}}){\text{/}}{{t}_{3}}$, ${{n}_{\infty }} = 2(\rho _{\infty }^{{(0)}}{{\omega }^{2}} - d_{\infty }^{{(1)}}){\text{/}}{{t}_{3}}$. Кроме этого, если ввести в рассмотрение агрегаты
${{{\tilde {v}}}_{4}} = {{{v}}_{4}} - \frac{m}{{{{d}^{{(0)}}}}}Q{\text{'}},$
${{{\tilde {v}}}_{{4\infty }}} = {{{v}}_{{4\infty }}} - \frac{{{{m}_{\infty }}}}{{d_{\infty }^{{(0)}}}}Q_{\infty }^{'},$
то системы (2.21), (2.22) можно еще переписать в виде
(2.24)
$\begin{gathered} {v}_{3}^{'} + {{d}^{{(0)}}}{{{{\tilde {v}}}}_{4}} = 0, \\ {\tilde {v}}_{4}^{'} + {{{\tilde {d}}}^{{(1)}}}{{{v}}_{3}} + \tilde {m}{{\omega }^{2}}Q = 0; \\ \end{gathered} $
(2.25)
$\begin{gathered} {v}_{{3\infty }}^{'} + d_{\infty }^{{(0)}}{{{{\tilde {v}}}}_{{4\infty }}} = 0, \\ {\tilde {v}}_{{4\infty }}^{'} + \tilde {d}_{\infty }^{{(1)}}{{{v}}_{{3\infty }}} + {{{\tilde {m}}}_{\infty }}{{\omega }^{2}}{{Q}_{\infty }} = 0, \\ \end{gathered} $
где

${{\tilde {d}}^{{(1)}}} = \frac{{mn}}{{{{d}^{{(0)}}}}} + {{d}^{{(1)}}},\quad \tilde {d}_{\infty }^{{(1)}} = \frac{{m{{n}_{\infty }}}}{{d_{\infty }^{{(0)}}}} + d_{\infty }^{{(1)}},\quad \tilde {m} = {{t}_{3}} - \frac{m}{{{{d}^{{(0)}}}}},\quad \mathop {\tilde {m}}\nolimits_\infty = {{t}_{3}} - \frac{{{{m}_{\infty }}}}{{d_{\infty }^{{(0)}}}}.$

Объединяя (2.23), (2.24), (2.25) получаем

(2.26)
$\begin{gathered} {\mathbf{G}}_{\infty }^{'} = {{\mathcal{A}}_{\infty }}{{{\mathbf{G}}}_{\infty }},\quad 0 < y < \frac{1}{2},\quad {{\mathcal{L}}_{\infty }}{{{\mathbf{G}}}_{\infty }}(0) = 0; \\ {\mathbf{G}}{\text{'}} = \mathcal{A}{\mathbf{G}},\quad \frac{1}{2} < y < 1,\quad \mathcal{L}{\mathbf{G}}(1) = 0; \\ {{{\mathbf{G}}}_{\infty }}\left( {\frac{1}{2}} \right) - \mathcal{R}{\mathbf{G}}\left( {\frac{1}{2}} \right) = 0. \\ \end{gathered} $
Здесь
${{{\mathbf{G}}}_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{Q}_{\infty }}} \\ {Q_{\infty }^{'}} \\ {{{{v}}_{{3\infty }}}} \\ {{{{{\tilde {v}}}}_{{4\infty }}}} \end{array}} \right),\quad {\mathbf{G}} = \left( {\begin{array}{*{20}{c}} Q \\ {Q{\text{'}}} \\ {{{{v}}_{3}}} \\ {{{{{\tilde {v}}}}_{4}}} \end{array}} \right),\quad {{\mathcal{A}}_{\infty }} = \left( {\begin{array}{*{20}{c}} 0&1&0&0 \\ { - {{\omega }^{2}}}&0&{{{n}_{\infty }}}&0 \\ 0&0&0&{ - d_{\infty }^{{(0)}}} \\ { - {{{\tilde {m}}}_{\infty }}{{\omega }^{2}}}&0&{ - \tilde {d}_{\infty }^{{(1)}}}&0 \end{array}} \right),$
${{\mathcal{L}}_{\infty }} = \left( {\begin{array}{*{20}{c}} 0&{{{{\tilde {m}}}_{\infty }}}&0&{ - 1} \\ 0&0&1&0 \end{array}} \right),\quad \mathcal{A} = \left( {\begin{array}{*{20}{c}} 0&1&0&0 \\ { - {{\omega }^{2}}}&0&n&0 \\ 0&0&0&{ - {{d}^{{(0)}}}} \\ { - \tilde {m}{{\omega }^{2}}}&0&{ - {{{\tilde {d}}}^{{(1)}}}}&0 \end{array}} \right),$
$\mathcal{L} = \left( {\begin{array}{*{20}{c}} 0&{\tilde {m}}&0&{ - 1} \\ 0&0&1&0 \end{array}} \right),\quad \mathcal{R} = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }^{2}}}&0&0&0 \\ 0&{{{\varepsilon }_{1}}}&0&0 \\ 0&0&\varepsilon &0 \\ 0&{\hat {m}}&0&{{{\varepsilon }^{2}}} \end{array}} \right),$
$\hat {m} = \frac{m}{{{{d}^{{(0)}}}\theta }} - \frac{{{{m}_{\infty }}}}{{d_{\infty }^{{(0)}}}}\frac{{1 - \omega }}{{1 - \omega \theta }},\quad {{\varepsilon }^{2}} = \frac{1}{\theta },\quad {{\varepsilon }_{1}} = \frac{{1 - \omega }}{{1 - \omega \theta }}.$
Ищем решение (2.26) в виде
${{{\mathbf{G}}}_{\infty }}(y) = exp(y{{\mathcal{A}}_{\infty }}){{{\mathbf{G}}}_{\infty }}(0),\quad {\mathbf{G}}(y) = exp((y - 1)\mathcal{A}){\mathbf{G}}(1),$
где вектора ${{{\mathbf{G}}}_{\infty }}(0)$, ${\mathbf{G}}(1)$ находятся как нетривиальное решение линейной системы
(2.27)
$\left( {\begin{array}{*{20}{c}} {{{\mathcal{L}}_{\infty }}}&\vline & {{{\mathbb{O}}_{{24}}}} \\ \hline {{{\mathbb{O}}_{{24}}}}&\vline & \mathcal{L} \\ \hline {\exp ({{\mathcal{A}}_{\infty }}{\text{/}}2)}&\vline & { - \mathcal{R}\exp ( - \mathcal{A}{\text{/}}2)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{{\mathbf{G}}}_{\infty }}(0)} \\ {{\mathbf{G}}(1)} \end{array}} \right) = 0.$
Здесь ${{\mathbb{O}}_{{24}}}$ – прямоугольная ($2 \times 4$) нулевая матрица.

Поскольку (см. [5])

${{\mathcal{A}}_{\infty }} = {{\Sigma }_{\infty }}\operatorname{diag} ({{k}_{{1\infty }}},{{k}_{{2\infty }}},{{k}_{{3\infty }}},{{k}_{{4\infty }}})\Sigma _{\infty }^{{ - 1}} = {{\Sigma }_{\infty }}{{\mathcal{P}}_{\infty }}\Sigma _{\infty }^{{ - 1}},$
$\mathcal{A} = \Sigma \operatorname{diag} ({{k}_{1}},{{k}_{2}},{{k}_{3}},{{k}_{4}}){{\Sigma }^{{ - 1}}} = \Sigma \mathcal{P}{{\Sigma }^{{ - 1}}},$
где
${{k}_{1}} = {{K}^{ + }} = \sqrt {{{A}^{ - }} + \sqrt {{{{({{A}^{ + }})}}^{2}} + {{\omega }^{2}}{{d}^{{(0)}}}n\tilde {m}} } ,\quad {{k}_{2}} = - {{K}^{ + }},$
${{k}_{3}} = {{K}^{ - }} = \sqrt {{{A}^{ - }} - \sqrt {{{{({{A}^{ + }})}}^{2}} + {{\omega }^{2}}{{d}^{{(0)}}}n\tilde {m}} } ,\quad {{k}_{4}} = - {{K}^{ - }},$
$\Sigma = \left( {\begin{array}{*{20}{c}} n&n&n&n \\ {n{{K}^{ + }}}&{ - n{{K}^{ + }}}&{n{{K}^{ - }}}&{ - n{{K}^{ - }}} \\ {{{\sigma }_{9}}}&{{{\sigma }_{9}}}&{{{\sigma }_{{11}}}}&{{{\sigma }_{{11}}}} \\ { - {{K}^{ + }}{{\sigma }_{9}}/{{d}^{{(0)}}}}&{{{K}^{ + }}{{\sigma }_{9}}/{{d}^{{(0)}}}}&{ - {{K}^{ - }}{{\sigma }_{{11}}}/{{d}^{{(0)}}}}&{{{K}^{ - }}{{\sigma }_{{11}}}/{{d}^{{(0)}}}} \end{array}} \right),$
${{\sigma }_{9}} = {{({{K}^{ + }})}^{2}} + {{\omega }^{2}} = {{A}^{ + }} + \sqrt {{{{({{A}^{ + }})}}^{2}} + {{\omega }^{2}}{{d}^{{(0)}}}n\tilde {m}} ,$
${{\sigma }_{{11}}} = {{({{K}^{ - }})}^{2}} + {{\omega }^{2}} = {{A}^{ + }} - \sqrt {{{{({{A}^{ + }})}}^{2}} + {{\omega }^{2}}{{d}^{{(0)}}}n\tilde {m}} ,$
${{A}^{ \pm }} = ({{d}^{{(0)}}}{{\tilde {d}}^{{(1)}}} \pm {{\omega }^{2}}){\text{/}}2,$
${{k}_{{1\infty }}} = K_{\infty }^{ + } = \sqrt {A_{\infty }^{ - } + \sqrt {{{{(A_{\infty }^{ + })}}^{2}} + {{\omega }^{2}}d_{\infty }^{{(0)}}{{n}_{\infty }}{{{\tilde {m}}}_{\infty }}} } ,\quad {{k}_{{2\infty }}} = - K_{\infty }^{ + },$
${{k}_{{3\infty }}} = K_{\infty }^{ - } = \sqrt {A_{\infty }^{ - } - \sqrt {{{{(A_{\infty }^{ + })}}^{2}} + {{\omega }^{2}}d_{\infty }^{{(0)}}{{n}_{\infty }}{{{\tilde {m}}}_{\infty }}} } ,\quad {{k}_{{4\infty }}} = - K_{\infty }^{ - },$
${{\Sigma }_{\infty }} = \left( {\begin{array}{*{20}{c}} {{{n}_{\infty }}}&{{{n}_{\infty }}}&{{{n}_{\infty }}}&{{{n}_{\infty }}} \\ {{{n}_{\infty }}K_{\infty }^{ + }}&{ - {{n}_{\infty }}K_{\infty }^{ + }}&{{{n}_{\infty }}K_{\infty }^{ - }}&{ - {{n}_{\infty }}K_{\infty }^{ - }} \\ {{{\sigma }_{{9\infty }}}}&{{{\sigma }_{{9\infty }}}}&{{{\sigma }_{{11\infty }}}}&{{{\sigma }_{{11\infty }}}} \\ { - K_{\infty }^{ + }{{\sigma }_{{9\infty }}}/d_{\infty }^{{(0)}}}&{K_{\infty }^{ + }{{\sigma }_{{9\infty }}}/d_{\infty }^{{(0)}}}&{ - K_{\infty }^{ - }{{\sigma }_{{11\infty }}}/d_{\infty }^{{(0)}}}&{K_{\infty }^{ - }{{\sigma }_{{11\infty }}}/d_{\infty }^{{(0)}}} \end{array}} \right),$
${{\sigma }_{{9\infty }}} = {{(K_{\infty }^{ + })}^{2}} + {{\omega }^{2}} = A_{\infty }^{ + } + \sqrt {{{{(A_{\infty }^{ + })}}^{2}} + {{\omega }^{2}}d_{\infty }^{{(0)}}{{n}_{\infty }}{{{\tilde {m}}}_{\infty }}} ,$
${{\sigma }_{{11\infty }}} = {{(K_{\infty }^{ - })}^{2}} + {{\omega }^{2}} = A_{\infty }^{ + } - \sqrt {{{{(A_{\infty }^{ + })}}^{2}} + {{\omega }^{2}}d_{\infty }^{{(0)}}{{n}_{\infty }}{{{\tilde {m}}}_{\infty }}} ,$
$A_{\infty }^{ \pm } = (d_{\infty }^{{(0)}}\tilde {d}_{\infty }^{{(1)}} \pm {{\omega }^{2}}){\text{/}}2;$
при этом
$\det \Sigma = - 4{{n}^{2}}\frac{{{{K}_{ - }}{{K}_{ + }}}}{{{{d}_{0}}}}{{({{({{K}^{ + }})}^{2}} - {{({{K}^{ - }})}^{2}})}^{2}} \ne 0,$
$\det {{\Sigma }_{\infty }} = - 4n_{\infty }^{2}\frac{{K_{\infty }^{ - }K_{\infty }^{ + }}}{{d_{\infty }^{{(0)}}}}{{({{(K_{\infty }^{ + })}^{2}} - {{(K_{\infty }^{ - })}^{2}})}^{2}} \ne 0,$
то условие существования нетривиального решения (2.27) примет вид:

(2.28)
$F(\lambda ) = det\left( {\begin{array}{*{20}{c}} {{{\mathcal{L}}_{\infty }}{{\Sigma }_{\infty }}}&\vline & {{{\mathbb{Q}}_{{24}}}} \\ \hline {{{\mathbb{Q}}_{{24}}}}&\vline & {\mathcal{L}\Sigma } \\ \hline {{{\Sigma }_{\infty }}exp({{\mathcal{P}}_{\infty }}{\text{/}}2)}&\vline & { - \mathcal{R}\Sigma exp( - \mathcal{P}{\text{/}}2)} \end{array}} \right) = 0.$

При заданных ${\text{Re}}$, ${\text{W}}$, ${{{\text{W}}}_{\infty }}$, $\theta $, $\omega $, ${{t}_{3}}$ формула (2.28) представляет собой уравнение для нахождения $\lambda $, поскольку все остальные величины, входящие в определитель, однозначно выражаются через указанные. Приведем далее результаты численных расчетов, в которых мы будем искать корни уравнения (2.28) в предположении, что $\lambda $ – вещественное положительное число. Во всех примерах взяты значения ${\text{Re}} = 1$, ${\text{W}} = 1$, ${{{\text{W}}}_{\infty }} = 0.1$. Значения оставшихся параметров указаны в подписях к рисункам. На фиг. 2 показаны значения определителя (2.28) в зависимости от $\lambda $ для значений параметров, при которых вещественный корень присутствует, и при которых его не наблюдается. Отметим, что на фиг. 2а график полностью находится в отрицательной области, хоть и подходит близко к нулю при малых $\lambda $.

Фиг. 2.

Графики функции $F(\lambda )$. Здесь $\omega = 0.8$; $\theta = 0.8$ для (а) и $\theta = 1$ для (б).

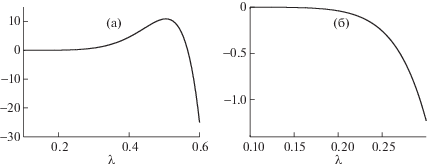
На фиг. 3 проиллюстрированы дисперсионные соотношения между вещественными величинами $\lambda $ и $\omega $ для случаев, когда плотности жидкостей различаются как в одну, так и в другую сторону ($\theta < 1$ и $\theta > 1$). Обрывы графиков означают, что в смежной области корней уравнения (2.28) не существует.

Фиг. 3.

Соотношение между $\lambda $ и $\omega $. Здесь $\theta = 0.5$ для (а) и $\theta = 10$ для (б).

Фигура 4 показывает зависимость корней $\lambda $ от соотношения плотностей $\theta $ для низкочастотных и высокочастотных колебаний.

Фиг. 4.

Зависимость собственных значений $\lambda $ от отношения плотностей $\theta $. Здесь $\omega = 0.5$ для (а) и $\omega = 2$ для (б).

Приведем также на фиг. 5 график функции $F(\lambda )$ для более высокой частоты колебаний ($\omega = 50$). Впрочем, стоит заметить, что в этом случае скачки значений функции при численном расчете становятся очень резкими, и подтвердить точность этих вычислений мы не можем.

Фиг. 5.

График функции $F(\lambda )$. Здесь $\omega = 50$; $\theta = 0.8$.

Отметим, что отсутствие у уравнения (2.28) вещественных положительных корней, вообще говоря, не означает отсутствия у задачи растущих по времени решений. У уравнения (2.28) также могут существовать комплекснозначные корни с положительной действительной частью. Однако численный поиск таких корней затруднен в связи с большой амплитудой значений определителя (2.28) в зависимости от $\lambda $.

ЗАКЛЮЧЕНИЕ

В работе предложена модель течения двух вязкоупругих несмешиваемых жидкостей в плоском канале, являющаяся обобщением модели, рассмотренной в [5], и исследована устойчивость состояния покоя для данной модели. Мы сформулировали линейную задачу на собственные значения и численно продемонстрировали наличие вещественнозначных собственных значений, что означает линейную неустойчивость состояния покоя, по крайней мере, при некоторых значениях параметров задачи. Для более тщательного анализа спектра задачи необходимо исследовать всю комплексную плоскость, что потребует дальнейшего изучения.

Список литературы

  1. Алтухов Ю.А., Гусев А.С., Пышнограй Г.В. Введение в мезоскопическую теорию текучих полимерных систем. Барнаул: Изд-во АлтГПА. 2012. 121 с.

  2. Doi M., Edwards S.F. The Theory of Polymer Dynamics. Clarendon: Oxford, 1986. 391 p.

  3. Oldroyd J.G. On the formulation of rheological equations of state // Proc. R. Soc. 1950. V. 200. № 1063. P. 523–541.

  4. Блохин А.М., Бамбаева Н.В. Стационарные решения уравнений несжимаемой вязкоупругой полимерной жидкости // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 5. С. 55–69.

  5. Блохин А.М., Голдин А.Ю. О линейной неустойчивости течений несжимаемой полимерной жидкости с сильным разрывом // Ж. техн. физ. 2018. Т. 88. № 10. С. 1506–1514.

  6. Блохин А.М., Семенко Р.Е. Стационарные электрогидродинамические течения несжимаемых полимерных сред с сильным разрывом // Сиб. журнал чист. и прикл. матем. 2017. Т. 17. № 2. С. 3–12.

  7. Седов Л.И. Механика сплошной среды. М.: Наука, 1970. Т. 1. 492 с.

  8. Овсянников Л.В. Лекции по основам газовой динамики. М.: Наука, 1981. 358 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал